Формула нахождения площади прямоугольного треугольника через синус. Игры с линейкой и карандашом
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета.
Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
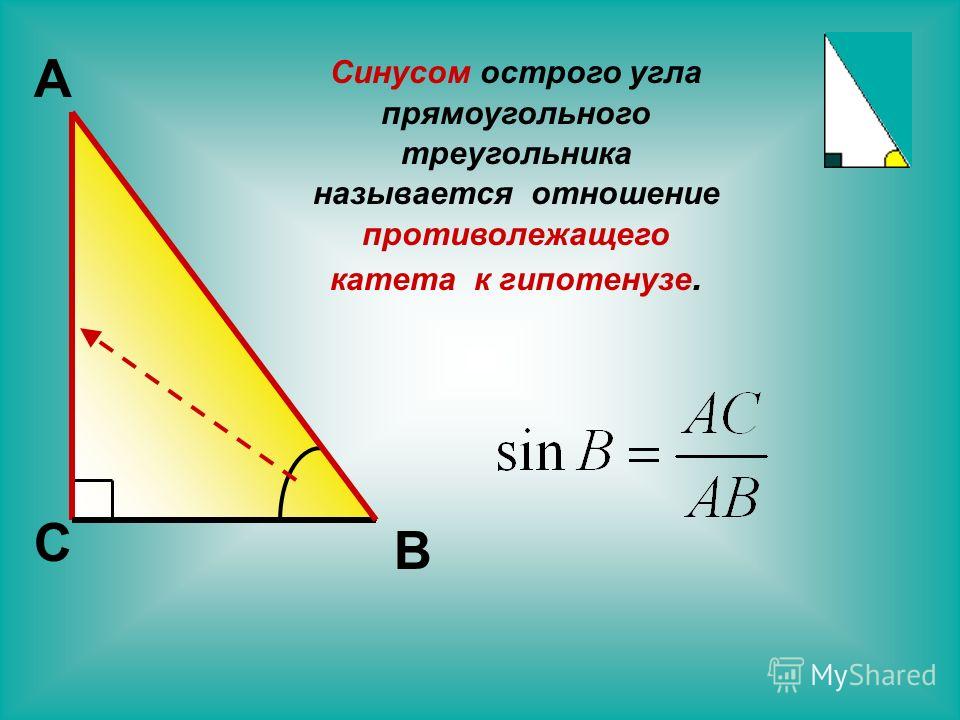
Синус угла (sin) – это отношение противолежащего катета к гипотенузе.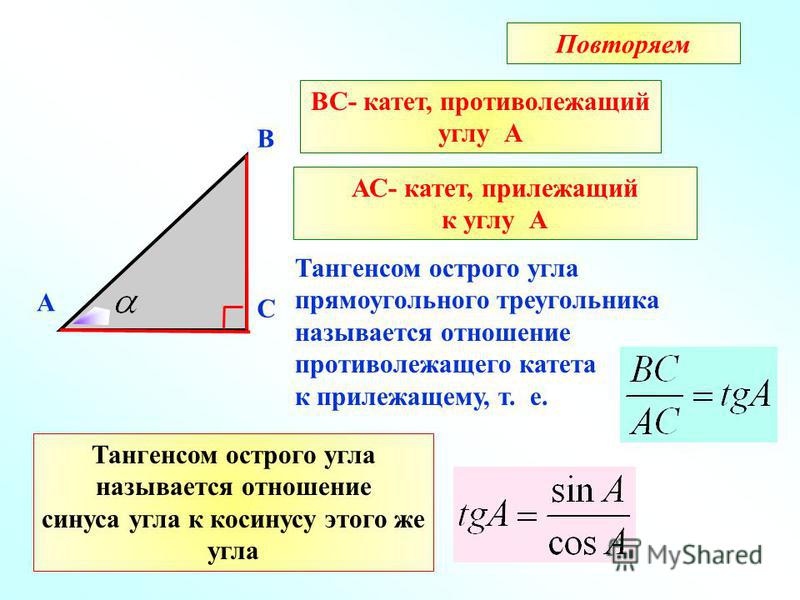
Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач.
Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.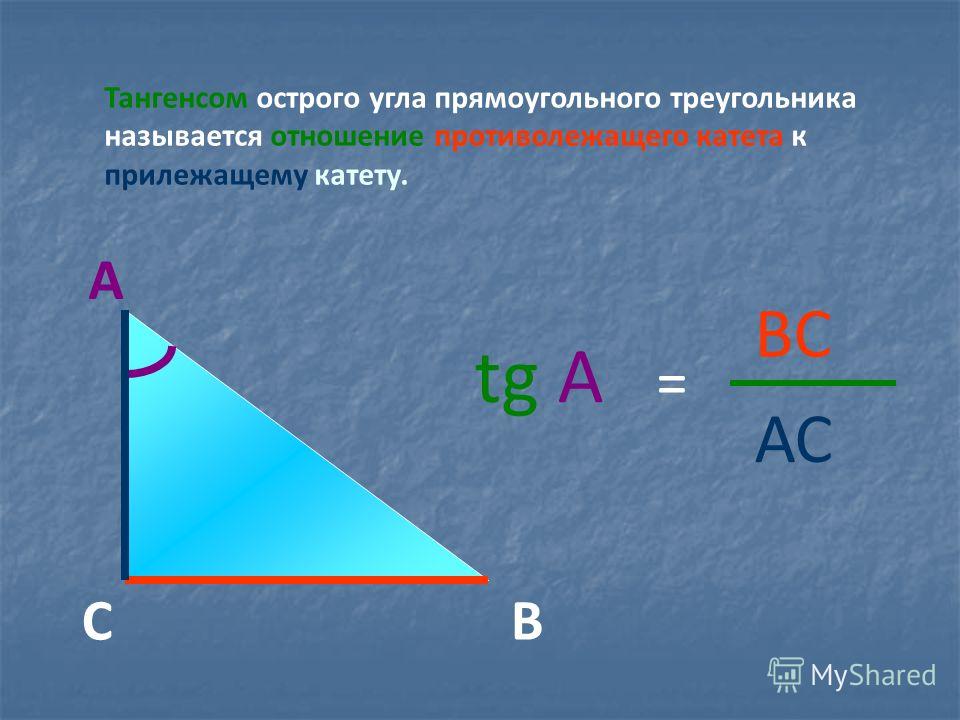
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.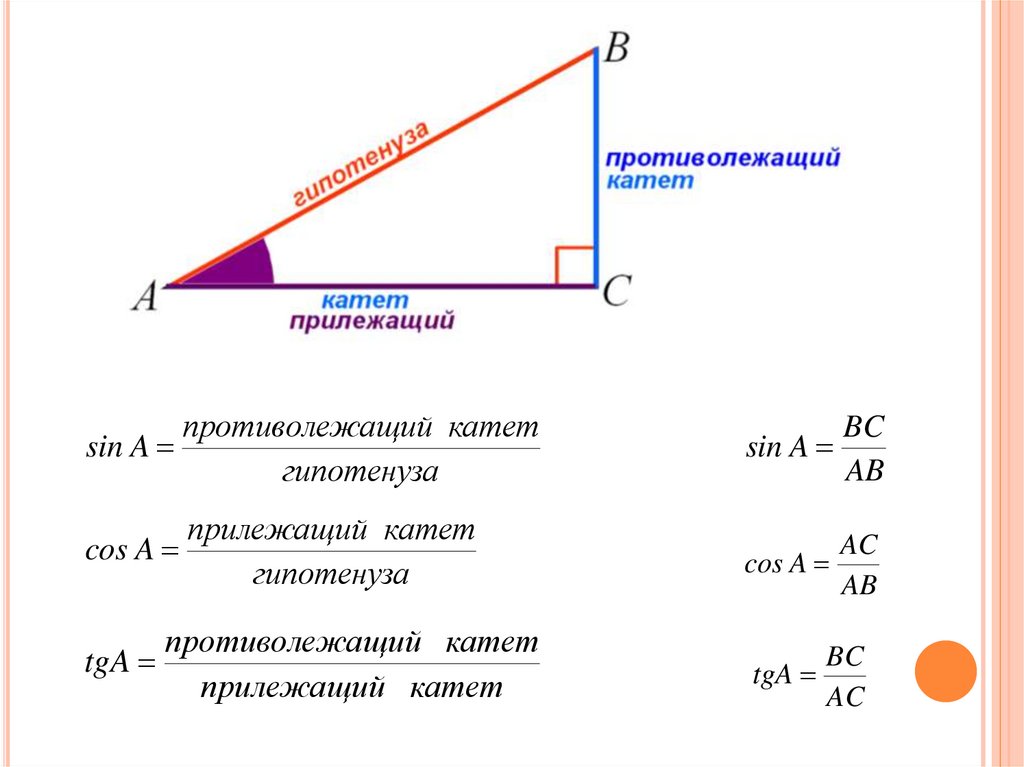
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.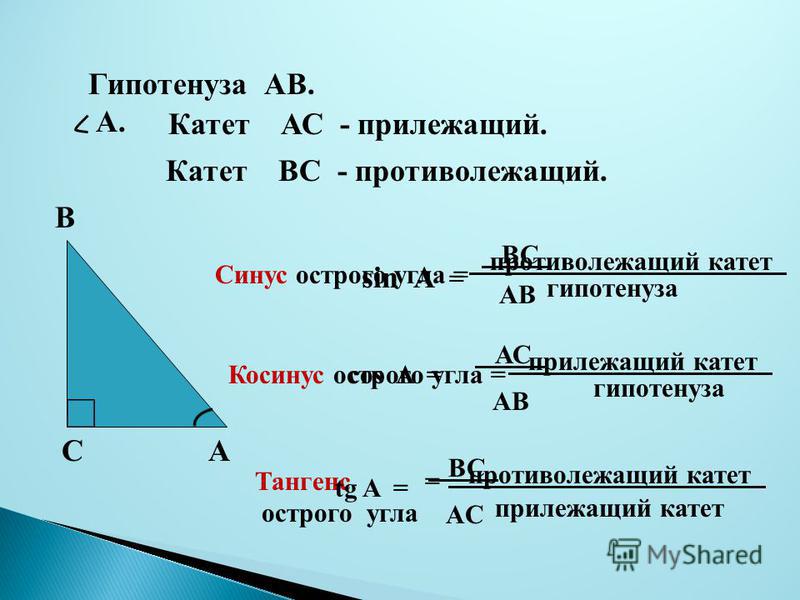
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
Доказательство:
Рассмотрим произвольный треугольник ABC. Пусть в нем сторона BC = a, сторона CA = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .
Для начала введем прямоугольную систему координат и поместим начало координат в точку С. Расположим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Сх, а точка А имела бы положительную ординату.
Если все выполнить правильно, то должен получится следующий рисунок.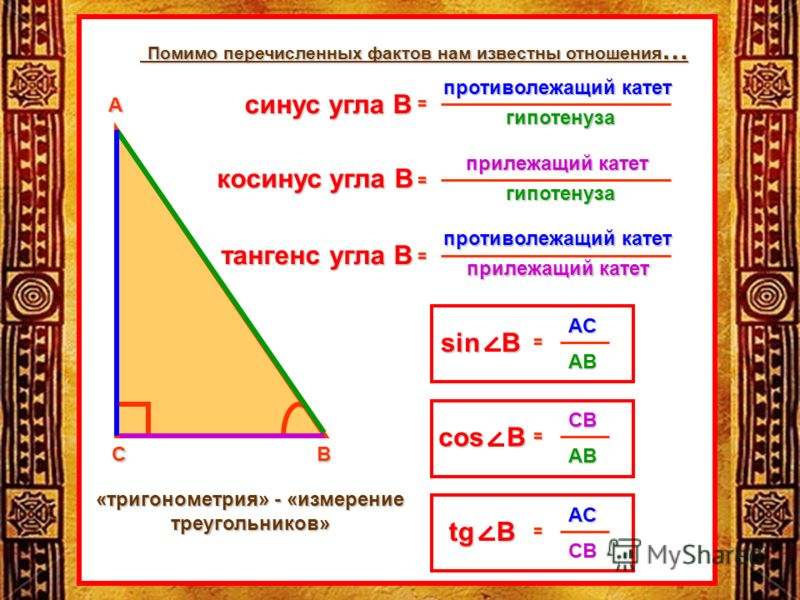
2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.
Положим S — площадь треугольника ABC. По теореме о площади треугольника имеем:
S = (1/2)*AB*AC*sin(A).
Подставим в неё имеющиеся у нас значения:
60 = (1/2)*AB*15*sin30˚ = (1/2)*15*(1/2)*AB=(15/4)*AB.
Отсюда выражаем длину стороны AB: AB = (60*4)/15 = 16.
Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.
Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла.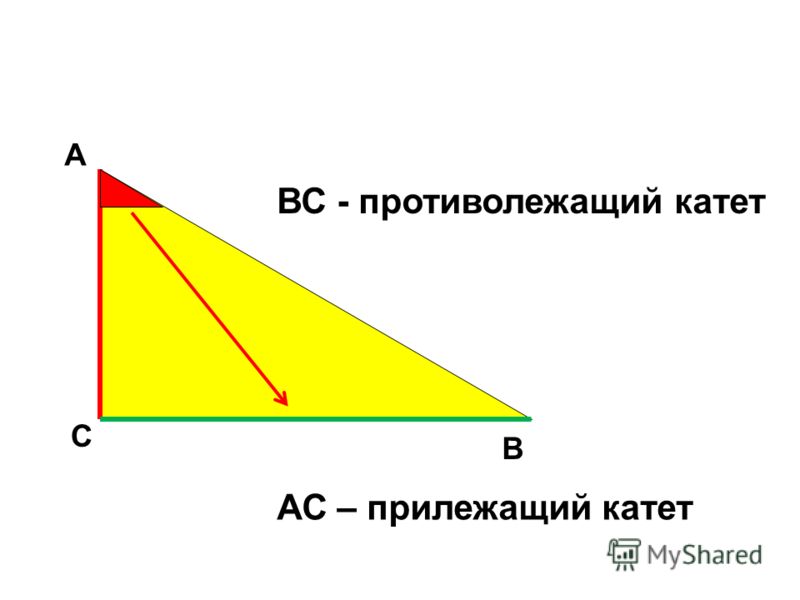
Теперь рассчитываем площадь по следующим формулам:
Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать .
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:
Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°.
Для начала найдем недостающую сторону с . По косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Теперь используя формулу, найдем
Сторону треугольника дозволено обнаружить не только по периметру и площади, но и по заданной стороне и углам. Для этого применяются тригонометрические функции – синус и косинус . Задачи с их применением встречаются в школьном курсе геометрии, а также в вузовском курсе аналитической геометрии и линейной алгебры.
Инструкция
1. Если знаменита одна из сторон треугольника и угол между ней и иной его стороной, воспользуйтесь тригонометрическими функциями – синус ом и косинус ом. Представьте себе прямоугольный треугольник НBC , у которого угол? равен 60 градусам. Треугольник НBC показан на рисунке. От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?
2.
Если в условии задачи, напротив, дан катет треугольника, обнаружьте его гипотенузу, руководствуясь дальнейшим соотношением между заданными величинами:BC=НB/sin ?По аналогии обнаружьте стороны треугольника и с применением косинус а, изменив предыдущее выражение дальнейшим образом:cos ?=НC/BC
3. В элементарной математике существует представление теоремы синус ов. Руководствуясь фактами, которые описывает данная теорема, также дозволено обнаружить стороны треугольника. Помимо этого, она разрешает обнаружить стороны треугольника, вписанного в окружность, если знаменит вестим радиус последней. Для этого воспользуйтесь соотношением, указанным ниже:a/sin ?=b/sin b=c/sin y=2RЭта теорема применима в том случае, когда знамениты две стороны и угол треугольника, либо дан один из углов треугольника и радиус описанной вокруг него окружности.
4. Помимо теоремы синус ов, существует и аналогичная ей по сути теорема косинус ов, которая, как и предыдущая, также применима к треугольникам всех 3 разновидностей: прямоугольному, остроугольному и тупоугольному.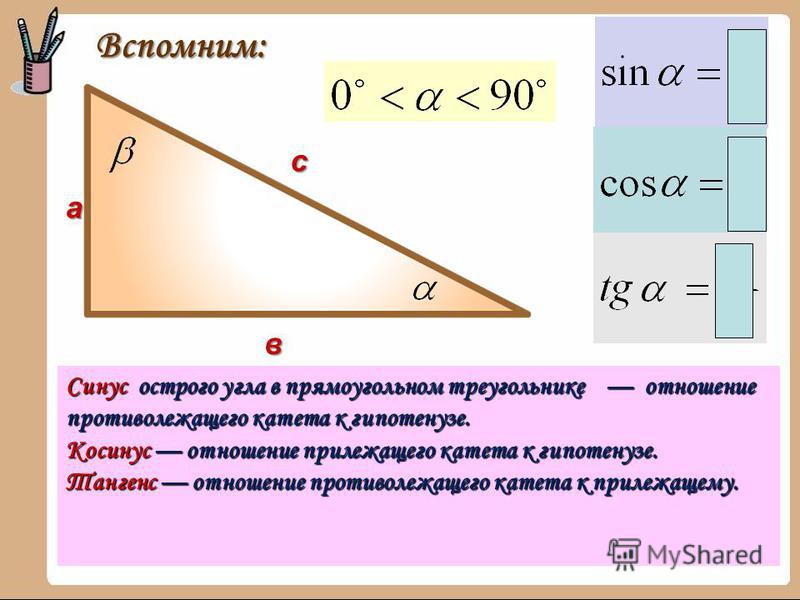
2-2ab*cos ?
Геометрическая фигура, состоящая из трёх точек, не принадлежащих одной прямой называемых вершинами, и трёх попарно соединяющих их отрезков, называемых сторонами, именуется треугольником. Существует уйма задач на нахождение сторон и углов треугольника по ограниченному числу начальных данных, одна из таких задач – нахождение стороны треугольника по одной из его сторон и двум углам .
Инструкция
1.
2. Стороны заданно треугольника дозволено обнаружить, вычислив его площадь по формулеS = 2 * R? * sin?? * sin?? * sin??,где R вычисляется по формулеR = BC/sin??, R – радиус описанной около треугольника?ABC отсюдаТогда сторону AB дозволено обнаружить, вычислив высоту, опущенную на неёh = BC * sin??,отсель по формуле S = 1/2 * h * AB имеемAB = 2 * S/hАналогичным образом дозволено вычислить сторону AC.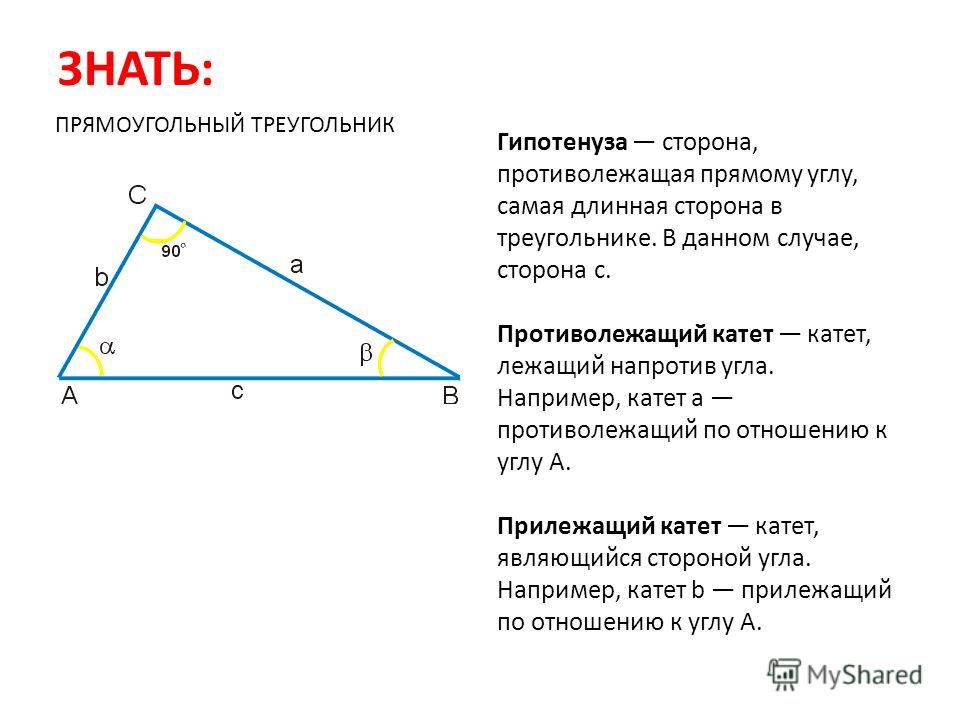
3. Если в качестве углов даны внешние углы треугольника?? и??, то обнаружить внутренние углы дозволено с поддержкой соответствующих соотношений?? = 180? – ??,?? = 180? – ??,?? = 180? – (?? + ??).Дальше действуем подобно первым двум пунктам.
Постижение треугольников ведется математиками на протяжении нескольких тысячелетий. Наука о треугольниках – тригонометрия – использует особые величины: синус и косинус.
Прямоугольный треугольник
Изначально синус и косинус появились из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было подмечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается неизменно идентичным.Именно так и были введены представления синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут использоваться не только в прямоугольных треугольниках.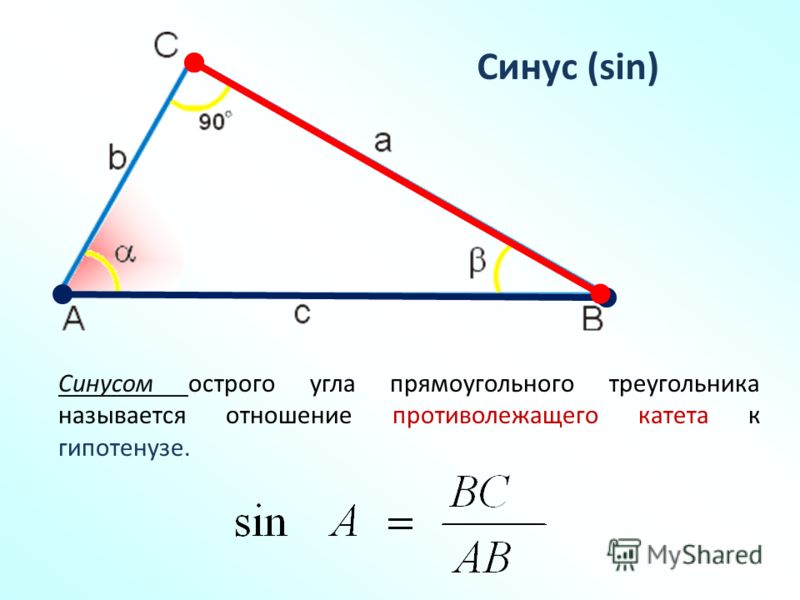
Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная – математический инструмент, показывающий, как стремительно меняется функция касательно метаморфозы ее довода. Производные применяются в алгебре, геометрии, экономике и физике, ряде технических дисциплин. При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса.
Производной синуса является косинус, а косинуса – синус, но со знаком «минус».
Применение в математике
Особенно зачастую синусы и косинусы применяются при решении прямоугольных треугольников и задач, связанных с ними. Удобство синусов и косинусов обнаружило свое отражение и в технике. Углы и стороны было примитивно оценивать по теоремам косинусов и синусов, разбивая трудные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, зачастую имеющие дело с расчетами соотношения сторон и градусных мер, тратили много времени и усилий для вычисления косинусов и синусов не табличных углов. Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов различных углов. В советское время некоторые преподаватели принуждали своих подопечных учить страницы таблиц Брадиса назубок.
Искривление носовой перегородки и/или гипертрофия носовых раковин
Носовая перегородка представляет собой фрагмент хряща и кости, разделяющий две стороны носовой полости.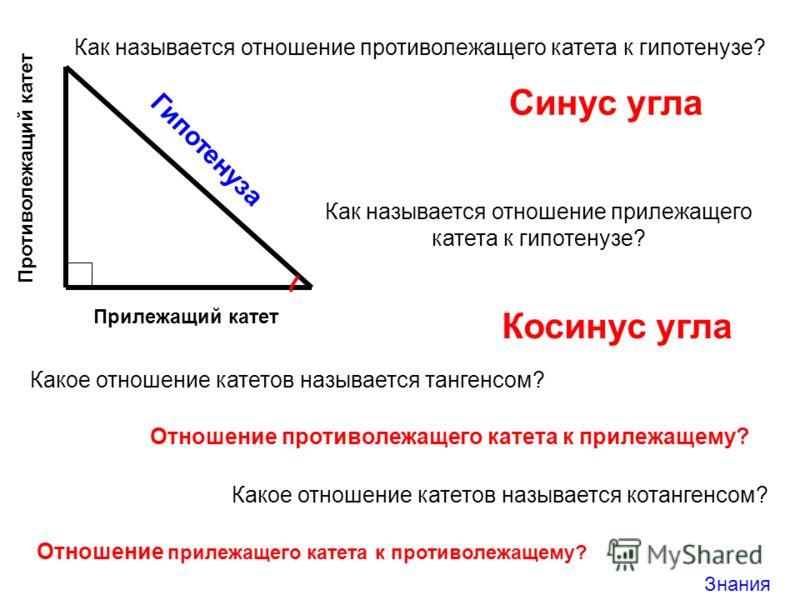
Раковины — это маленькие кости, которые выступают по бокам носовой полости и покрыты слизистой оболочкой, чтобы согревать и увлажнять поток воздуха через нос. Иногда носовая перегородка может отклоняться, вызывая заложенность носа, боль в носу, рецидивирующий синусит и/или рецидивирующие носовые кровотечения. Кроме того, носовые раковины могут быть увеличены, что еще больше способствует заложенности носа.
Как искривление перегородки, так и увеличенные носовые раковины могут вызывать уменьшение потока воздуха через нос, что приводит к хронической заложенности носа, дыханию ртом или храпу. Некоторые отклонения перегородки могут вызвать закупорку пазухи с рецидивирующим синуситом. Другие могут привести к контактным точкам, которые могут привести к боли в носу или пазухах. Тем не менее, другие могут вызывать турбулентный поток воздуха, высушивая слизистую оболочку носа и иногда приводя к носовым кровотечениям. Заложенность носа обычно усиливается ночью из-за увеличения назального кровотока под действием силы тяжести в положении лежа.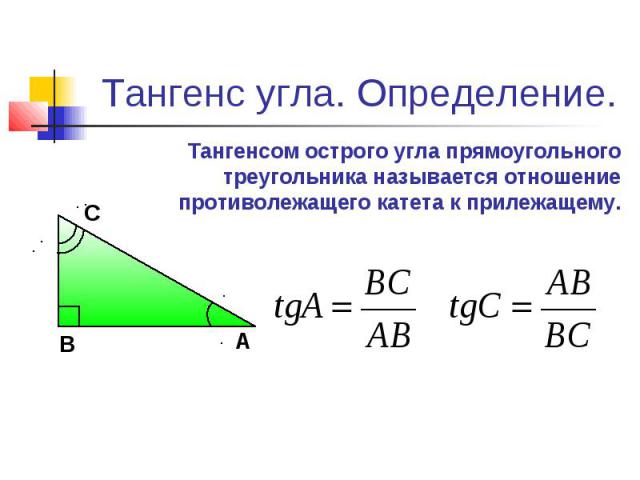
Хроническое ротовое дыхание может усилить храп или привести к сухости во рту и/или боли в горле. Обычно заложенность носа сильнее выражена на определенной стороне, но может варьироваться от стороны к стороне из-за других факторов, таких как простуда или аллергия.
Искривление носовой перегородки может быть результатом травмы носа или возникать при рождении. Нет необходимости ломать переносицу, чтобы вызвать сильное искривление перегородки. Часто незначительная травма носа может привести к перелому носовой перегородки. Перегородка может быть отклонена в одну сторону или искривлена с обструкцией с обеих сторон. Кроме того, костная шпора может выступать в полость носа или в отверстие пазухи. Увеличение носовых раковин является анатомической вариацией без особой причины. Часто носовые раковины увеличиваются на стороне, противоположной искривлению перегородки.
Во многих случаях искривление носовой перегородки или увеличение носовых раковин не вызывает проблем и не требует лечения.
Если симптомы присутствуют, обычно назначают назальные стероиды и/или противоотечные средства. Однако, если заложенность носа, боль, рецидивирующий синусит или рецидивирующие носовые кровотечения сохраняются, то перегородку можно восстановить с помощью амбулаторной процедуры, называемой септопластикой. Если носовые раковины увеличены, их можно уменьшить с помощью амбулаторной процедуры, называемой турбинопластикой. Эти две процедуры часто выполняются вместе.
Из-за высокой заболеваемости аллергическим ринитом нередко аллергия сосуществует либо с искривлением носовой перегородки, либо с увеличением носовых раковин. Аллергии вызывают отек слизистой оболочки носа, что часто делает анатомическую непроходимость более заметной. Во многих случаях лечение аллергии с помощью иммунотерапии уменьшит насморк и выделения из носа, но заложенность носа может остаться. В этой ситуации септопластика и/или турбинопластика часто используются в качестве дополнения к прививкам от аллергии, чтобы уменьшить заложенность носа.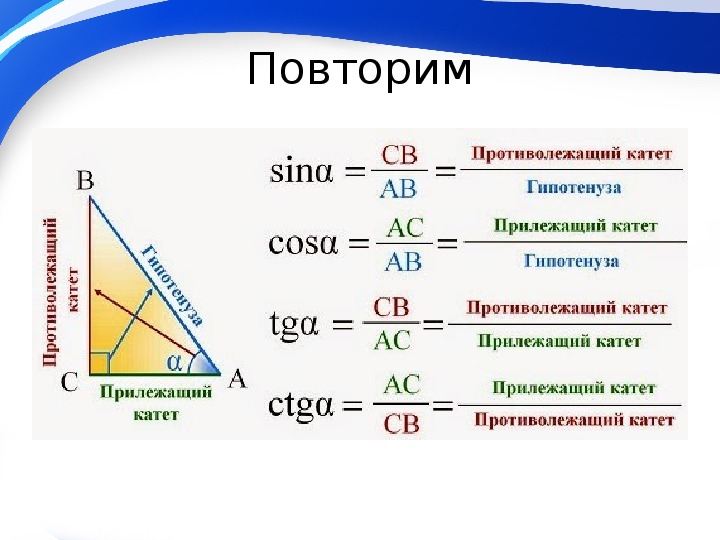
В других ситуациях, особенно после травмы носа, искривление носовой перегородки может сопровождаться деформацией спинки носа. В этих случаях может быть выполнена амбулаторная процедура, называемая септоринопластикой. С помощью этой процедуры помимо коррекции заложенности носа улучшается внешний вид носа.
Заложенность носа: виды, причины и методы лечения
Заложенность носа — распространенный симптом, часто вызываемый назальной аллергией (аллергический ринит). Со временем воспалительные состояния, такие как аллергия, вызывают отек и увеличение носовых раковин, что в конечном итоге снижает поток воздуха через нос. Заложенность носа часто чередуется несколько раз в день (это называется носовым циклом). Другие причины, такие как серьезное искривление носовой перегородки, носовые полипы или образование в носу, могут вызывать фиксированную или постоянную заложенность носа. При нарушении носового дыхания храп часто усиливается. Пациенты, которые зависят от CPAP (постоянного положительного давления в дыхательных путях) для облегчения своего обструктивного апноэ во сне, часто испытывают трудности с переносом маски ночью, когда у них заложенность носа, поскольку пассивный поток воздуха значительно снижается, когда нос закрыт.
Знание причины заложенности носа является ключом к выбору подходящего лечения.
Типы заложенности носа
1. Фиксированная заложенность носа
Фиксированная заложенность носа возникает в результате стационарных поражений в носу, которые не колеблются в зависимости от носового цикла (на них существенно не влияют изменения носового кровотока).
Причины
Искривление носовой перегородки
Наиболее частой причиной фиксированной заложенности носа является искривление носовой перегородки – состояние, при котором кость и хрящ, разделяющие две стороны носовой полости, смещены в одну сторону, что часто сопровождается шпорой, которая еще больше сужает пораженную сторону носовой полости. Приблизительно у 80 процентов людей носовая перегородка расположена не совсем по средней линии; однако легкие отклонения обычно не влияют на носовое дыхание. Умеренные и тяжелые отклонения, особенно те, которые связаны с костными шпорами, уменьшают носовой поток с одной или обеих сторон и могут даже препятствовать дренажу пазухи в тяжелых случаях.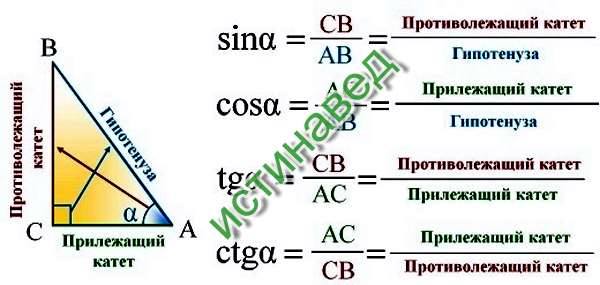
Шпоры, которые контактируют с соседними тканями в полости носа, также могут быть источником боли и повторяющихся головных болей. Многие пациенты с искривлением носовой перегородки от умеренной до тяжелой степени имеют в анамнезе переломы носа или предшествующие операции на носу.
Путь вперед
Большинство искривлений носовой перегородки могут быть визуализированы врачом, который смотрит в нос с помощью простого источника света и зеркала, чтобы увеличить отверстие ноздри. Назальная эндоскопия с гибким эндоскопом часто используется, чтобы увидеть заднюю или глубокую часть перегородки и лучше оценить анатомию до рассмотрения вопроса об операции. Лечение искривления перегородки средней и тяжелой степени с симптоматической заложенностью носа заключается в септопластике, хирургическом вмешательстве, которое включает удаление искривленных частей кости и хряща из перегородки, чтобы позволить ей занять более срединное положение.
Гипертрофированные носовые раковины
Нижние (нижние) носовые раковины согревают и увлажняют воздух, проходящий через носовые полости.
Они прикрепляются к стенкам носовых полостей и образованы костной полкой, окруженной губчатой тканью, способной быстро набухать и уменьшаться в размерах. У пациентов с длительно существующей назальной аллергией или воспалительными состояниями носовые раковины гипертрофированы или постоянно увеличены из-за хронического воспаления и связанного с этим роста тканей из-за увеличения кровотока и других факторов. В тяжелых случаях гипертрофированные носовые раковины сами по себе могут вызывать значительную заложенность носа или обструкцию. Односторонняя гипертрофия носовых раковин часто отмечается и на противоположной стороне значительного отклонения перегородки.
Путь вперед
Большинство гипертрофированных носовых раковин могут быть визуализированы врачом, который смотрит в нос с помощью простого источника света и зеркала, чтобы увеличить отверстие ноздри. Назальная эндоскопия с гибким эндоскопом часто используется, чтобы полностью увидеть носовые раковины перед рассмотрением вопроса об операции.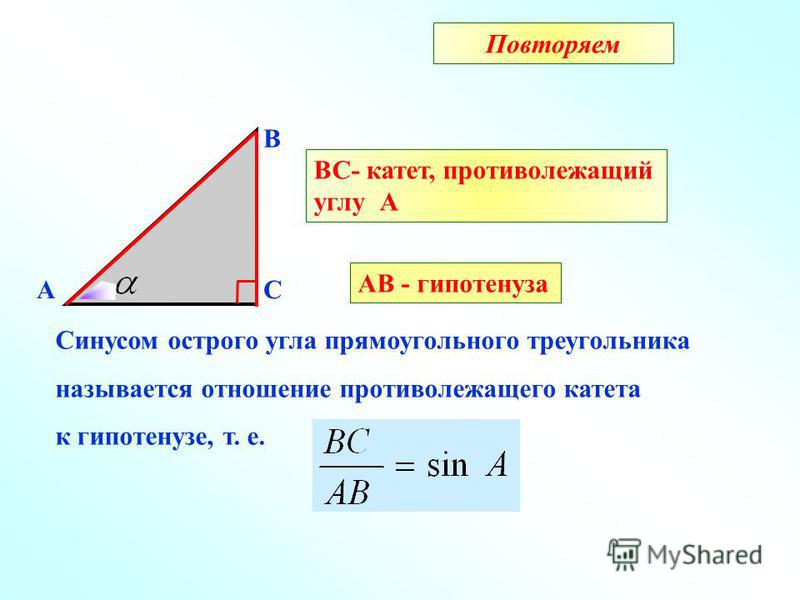
Первоначальное лечение гипертрофии носовых раковин включает назальные стероидные спреи (например, Flonase ©), используемые один или два раза в день для уменьшения воспаления и отека в течение как минимум 1 месяца. Пациентам, у которых сохраняется значительная заложенность носа, требуется хирургическое вмешательство. Радиочастотная абляция носовых раковин в офисе — это быстрая и эффективная процедура, которая уменьшает количество мягких тканей, присутствующих в носовых раковинах. В условиях операционной хирургическое уменьшение носовых раковин является обычной процедурой частичного удаления как кости, так и мягких тканей для окончательного облегчения заложенности носа.
Afrin (деконгестант для носа) Злоупотребление
Afrin© — популярный безрецептурный назальный противозастойный спрей, используемый для временного облегчения заложенности носа. При первоначальном применении обеспечивает быстрое и эффективное облегчение в большинстве случаев заложенности носа; однако использование противоотечных спреев в течение более 3 дней связано с рецидивирующей заложенностью носа, создавая цикл зависимости и, в конечном итоге, рост тканей носовых раковин, что может привести к постоянной заложенности носа.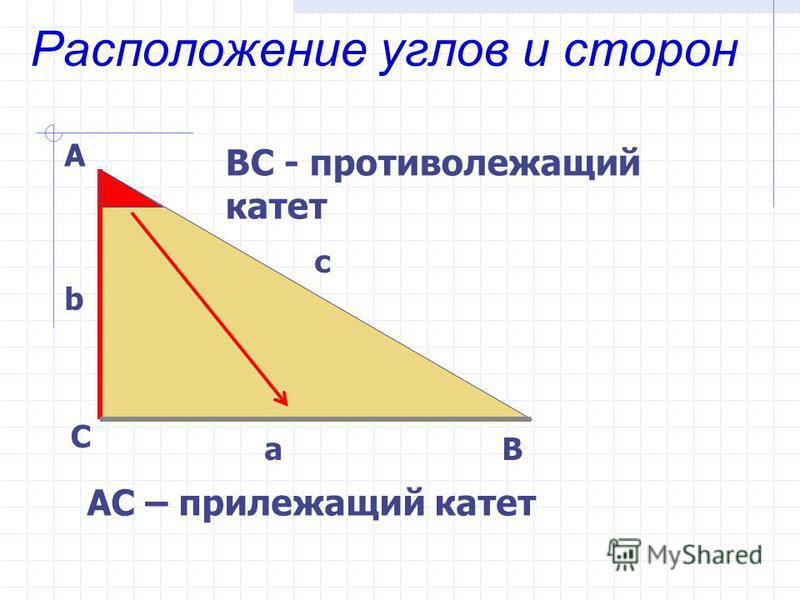
Длительное злоупотребление может привести к перфорации носовой перегородки, сильному воспалению носовых полостей и деформации носа (седловидной деформации носа).
The Way Forward
Пациенты, злоупотребляющие назальными деконгестантами, такими как Африн, должны немедленно заменить противоконгестантный спрей на назальные стероидные спреи два раза в день. В случае злоупотребления этими спреями в течение длительного периода времени пациенту, вероятно, потребуется хирургическое вмешательство, включая уменьшение носовых раковин, чтобы найти адекватное облегчение заложенности носа. Перфорированные носовые перегородки в большинстве случаев также можно исправить хирургическим путем.
2. Флуктуирующая заложенность носа
Колебания Заложенность носа носит периодический характер и часто чередуется. В большинстве случаев это вызвано легкой или умеренной гипертрофией носовых раковин, которые могут казаться бледными или иметь багровый цвет. Большинство случаев неустойчивой заложенности носа являются вторичными по отношению к хроническому риниту (хроническому воспалению полостей носа), при этом назальная аллергия является наиболее частым источником воспаления.
Причины
Аллергический ринит
Каждый пятый взрослый в США страдает аллергическим ринитом или носовой аллергией. Пациенты с аллергическим ринитом часто испытывают заложенность носа, и симптомы могут быть сезонными (если они вызваны пыльцой) или круглогодичными (если они вызваны пылью, плесенью, перхотью домашних животных и т. д.).
The Way Forward
Топические стероидные спреи для носа являются наиболее безопасным и эффективным средством для лечения заложенности носа, вторичной по отношению к аллергическому риниту. Пероральные антигистаминные препараты и местные назальные антигистаминные препараты являются другими вариантами, которые могут быть эффективными при симптомах, связанных с аллергическим ринитом. Следует избегать пероральных деконгестантов и местных деконгестантных спреев для долгосрочного облегчения симптомов. Тестирование на аллергию и иммунотерапия в виде инъекций от аллергии являются наиболее эффективными долгосрочными методами лечения аллергического ринита, который не реагирует адекватно на назальные стероидные спреи и антигистаминные препараты.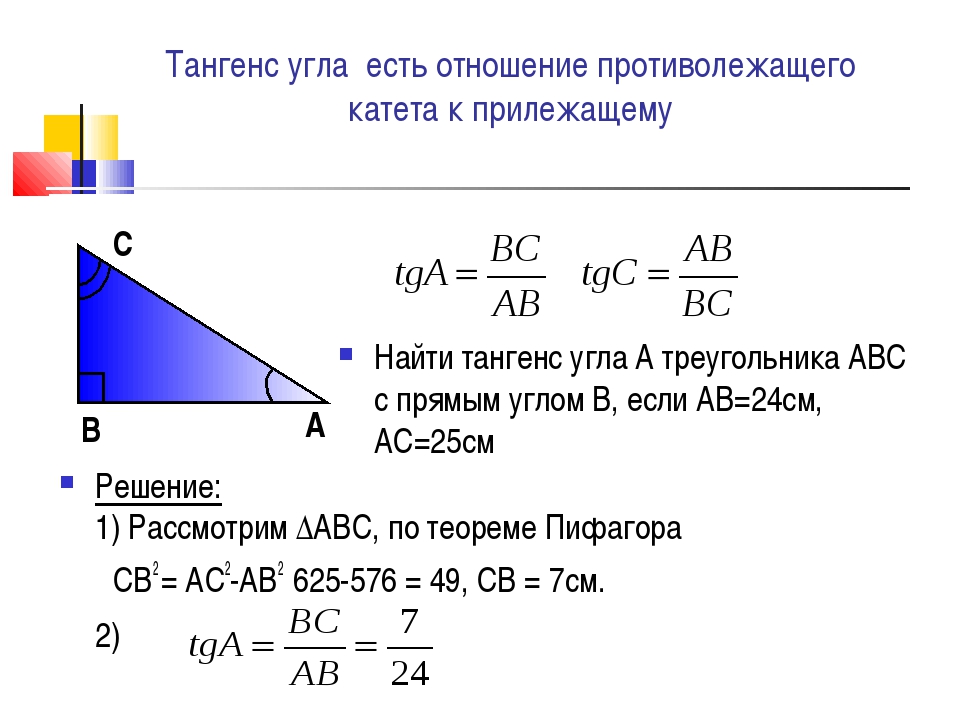
Неаллергический ринит
Неаллергические причины воспаления и отека носа встречаются реже и включают воздействие раздражителей, таких как сигаретный дым, химические пары, изменения температуры/погоды, а также прием некоторых лекарств, вызывающих отек восприимчивых тканей, таких как ротовая полость. противозачаточные и некоторые антидепрессанты.
The Way Forward
Топические назальные стероиды полезны при лечении многих случаев неаллергического ринита. Следует избегать раздражителей окружающей среды, таких как сигаретный дым. Пациентов с диагнозом вазомоторный ринит (прозрачные выделения из носа без аллергического триггера) лечат антихолинергическим назальным спреем, таким как ипратроприум (Atrovent© Nasal).
Заключение
Прерывистая или изменчивая заложенность носа вначале лечится с помощью лекарств, наиболее эффективными из которых являются назальные стероидные спреи, такие как Flonase©. Пациентам, у которых сохраняется значительная заложенность носа после 1 месяца лечения, показано хирургическое вмешательство в виде частичной резекции носовых раковин или радиочастотной абляции носовых раковин.