Синус углов: Синус, косинус угла треугольника

описание формул, примеры и решение / Справочник :: Бингоскул

Синусы углов и как их сравнивать: описание формул, примеры и решение

добавить в закладки удалить из закладок

Содержание:

Одним из видов тригонометрических функций является синус. Данная функция рассчитывается для любых углов, находящихся в окружности. Прямоугольный треугольник применяется для определения значения sin острых углов. Если угол имеет обозначение Х, алгебра предполагает использование выражения sinХ. Перед тем, как сравнивать синусы, необходимо определить тип угла, создать окружность, установить четверть этой окружности.

Как сравнивать синусы углов –

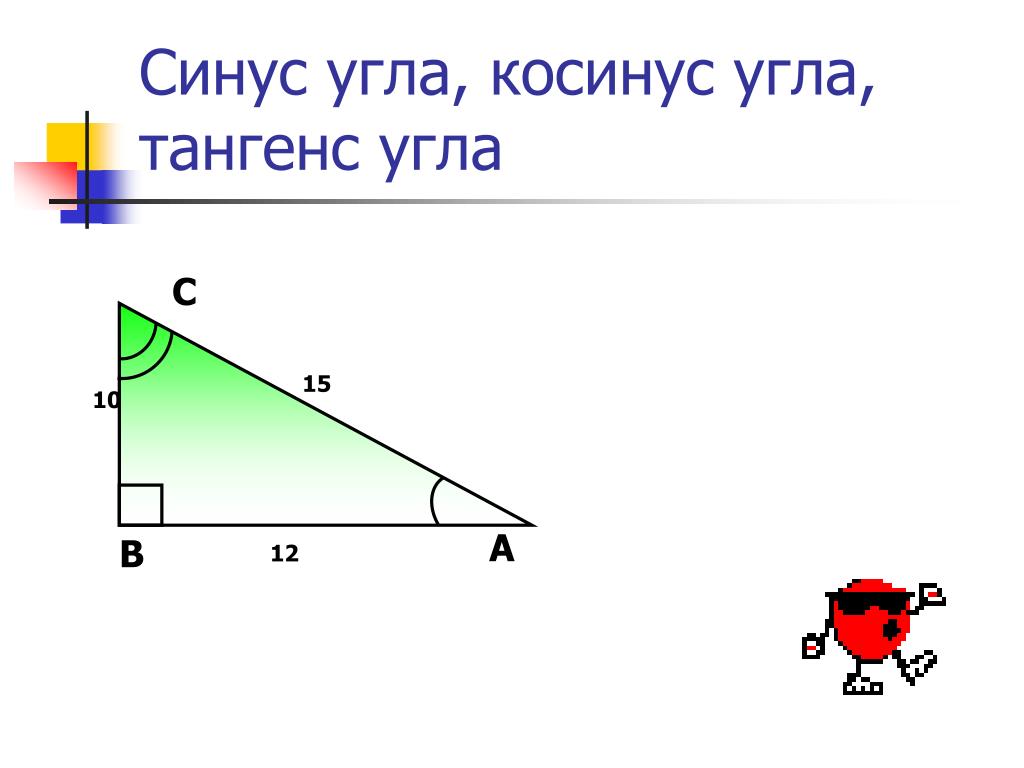
sin острого угла и пример расчета

Острый угол – угол меньше 90 градусов. Для расчета синуса необходимо рассчитать соотношение противолежащих сторон. Сравнивается катет с гипотенузой. 

Катет представляет собой одну из сторон в прямоугольном треугольнике. \propto } = 2 ( — 1 ) 2 + 22 = 25 = 255

Итог: \sin  = 25 \sqrt 5

Как сравнить синусы углов – анализ значений

Синусом называют функцию угла. Он находится в окружности, разделенной на 4 четверти. Для сравнения sin используется следующая таблица:
 

Угол	Значение
00	Всегда = 0
300	0,5
600	\sqrt {3}/2 \approx 1, 7/2 \approx 0,9
900	1

Важно запомнить: если угол находится в первой четверти, его sin будет возрастать до 90 градусов. Убывание значения отмечается во второй части окружности. Он стремится от 1 к 0. В третьей и четвертой четверти значение sin отрицательное. Для третьей части характерно стремление от нуля к -1, для 4 четверти – от -1 к 0.

Рассмотрим сравнение синусов на примерах:

1. Нужно установить соотношение между sin 195° и sin 200° . Для этого используется окружность. Местоположение 195, 200 находится на этой окружности. Это свидетельствует о том, что sin 195° > sin 200° , так как расположен ниже.
2. Определить отношение между sin 734° и sin -1066° .

Диаметр цельного круга составляет 360 градусов, двух окружностей – 720 градусов. Отсюда следует, что 734° включает два круга и 14 градусов. Если обойти три раза по кругу в обратную сторону, получится -360 х 3 = -1080 градусов. Получается, что точка -1066 – это три окружности и еще 14 градусов. Синусы точек с одинаковой градусной мерой равные. sin 734°= sin -1066°  

Поделитесь в социальных сетях:

29 июня 2021, 16:29

Математика

Could not load xLike class!

Ряд для синуса через кратные углы : Анализ-I

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

gris	Ряд для синуса через кратные углы 07.01.2016, 23:08
Заслуженный участник 13/08/08 14020	Навеяно задачей о пределе. Есть точная формула и аналогичные формулы для углов нечётной кратности, а также первый замечательный предел и следствие из него для предела косинуса. Нельзя ли как-нибудь получить из этого асимптотику для синуса около нуля до более высоких степеней? Первая степень получается точно, а потом уже не то

provincialka	Re: Ряд для синуса через кратные углы 07.01.2016, 23:26
Заслуженный участник 18/01/13 12027 Казань	Если предположить, что такая формула существует, то найти коэффициенты можно. Например, пусть . Кроме того, . Подставим эти соотношения в равенство , получим . Раскрывая скобки и сравнивая коэффициенты получаем уравнение , откуда . Но для этого нужно сначала доказать существование такого .

gris	Re: Ряд для синуса через кратные углы 08.01.2016, 00:39
Заслуженный участник 13/08/08 14020	Вот у меня то самое же получилось, правда из формулы синуса тройного угла. Там . То есть хотя бы в духе Пойа’s Правдоподобных рассуждений можно для синуса получить ряд ещё до изучения производных. А подойдя комплексно, получить кубический член для экспоненты, что позволяет найти злополучный предел. Хотя бы найти, если не доказать. Аккордеон А я, понимая, что изобретаю велосипед, подумал, что в той теме можно выйти в комплексную плоскость и попробовать подобраться к нулю не сбоку, а сверху. На Рождество так хочется чуда

ewert	Re: Ряд для синуса через кратные углы 08.01.2016, 00:45
Заслуженный участник 11/05/08 32106	provincialka в сообщении #1088832 писал(а): Если предположить, что такая формула существует, то найти коэффициенты можно. Именно что если. Скажем, общеизвестно, что и т.д. А вот доказать — естественно, отнюдь. (Оффтоп) Я в этом (в смысле ушедшем) семестре подкинул своим скубентам эту задачку в качестве развлечения. Естественно, подсказав, что там надо поиграться с кратными углами — тройными или хоть двойными (но не объясняя, как именно играться). И что вы думаете: в одной из групп сразу два человека угадали! (ну или нагуглили) В другой, правда — ни одного.

Brukvalub	Re: Ряд для синуса через кратные углы 08. 01.2016, 00:49
Заслуженный участник 01/03/06 13626 Москва	gris в сообщении #1088850 писал(а): То есть хотя бы в духе Пойа’s Правдоподобных рассуждений можно для синуса получить ряд ещё до изучения производных. Более того, можно определить синус как сумму известного степенного ряда, тогда никакие Пойи совсем не понадобятся.

deep blue	Re: Ряд для синуса через кратные углы 08. 01.2016, 11:33
23/11/09 173	В книге Маркушевича «Ряды» дается элементарное доказательство равенства синуса и его степенного ряда. Используется только замечательный предел, формулы кратных углов и признак сходимости Даламбера. Вкратце, схема доказательства такая: 1. Записываются формулы кратных углов верные для любого m: 2. Элементарно доказывается (используя признак Даламбера), что степенные ряды синуса и косинуса сходятся при всех x 3. На основе первого замечательного предела доказывается, что каждый член частичной суммы степенного ряда сколь угодно мало отличается от соответствующего члена в формуле кратных углов при достаточно большом m. 4. Рассматривается разность частичной суммы (длины n) степенного ряда и выражения косинуса через кратные углы (длины m>n формулы 1). это обрубок суммы в выражении косинуса через сумму кратных углов от n до m. Несложно показать, что при любых m>n он меньше чем обрубок степенного ряда косинуса. 5. Для заданного выбирается и фиксируется n так, чтобы частичная сумма степенного ряда отличалась от своего предела не более чем на . Поскольку n теперь зафиксировано, можно выбрать m>n так, чтобы каждый член разности (4) сколь угодно мало отличался от нуля и вся сумма этих членов (их n плюс еще один — ) сколь угодно мало отличалась от нуля, например не более чем на . Остается оценить . Мы уже знаем что при любых m, меньше чем обрубок степенного ряда косинуса, который меньше (по условленному в самом начале при выборе n). Итак, разность частичной суммы степенного ряда и косинуса стремится к нулю с ростом n при любых x. Следовательно сам косинус сколь угодно мало отличается от значения степенного ряда в бесконечности.

provincialka	Re: Ряд для синуса через кратные углы 08.01.2016, 13:09
Заслуженный участник 18/01/13 12027 Казань	Ну. .. решение с рядами — хорошее, только «из пушки по воробьям». Имеет скорее «эстетическую» ценность. А вообще-то рассуждения с кратными углами я использую, но не для доказательства формулы, а как «наведение» на неё. Показываю, что подобные формулы существуют и надо бы найти общий способ, как их легко выводить. После этого можно переходить к производной. Хотя… изложенная «программа» — это скорее утопия. Времени-то на досужие рассуждения не хватает!

Евгений Машеров	Re: Ряд для синуса через кратные углы 08.01.2016, 20:09
Заслуженный участник 11/03/08 8411 Москва	gris в сообщении #1088827 писал(а): Пользуясь этим выражением, получаем синус для для произвольно большого k. Затем заменяем синус малого x на x и видим искомый ряд. Вот с оценкой погрешности грустно, и непонятно, какие члены ряда правильные, а какие шум. Но первые выпишутся правильно.

Brukvalub	Re: Ряд для синуса через кратные углы 08.01.2016, 20:30
Заслуженный участник 01/03/06 13626 Москва	Евгений Машеров , ваши телодвижения даже на «пляски с бубном» не тянут! Чему вы учите нашу молодежь?

Евгений Машеров	Re: Ряд для синуса через кратные углы 08. 01.2016, 21:58
Заслуженный участник 11/03/08 8411 Москва	Зато можно догадаться, как получали ряды для синуса древние индусы, скажем.

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 10 ]

Модераторы: Модераторы Математики, Супермодераторы

функций — Проблемы с пониманием синуса, косинуса углов больше $90$ градусов

спросил 3 года 9 месяцев назад

Изменено 3 года, 9 месяцев назад

Просмотрено 2к раз

$\begingroup$

Недавно я узнал о тригонометрических функциях углов больше 9 долларов. 0$ градусов, и мне трудно понять концепцию.

Мы работали с такой диаграммой:

Мой учитель рассказал классу, что синус угла $\theta$ равен отношению между противолежащим катетом ($y$) и гипотенузой ($r $).

Я не совсем понимаю эту логику. Я знаком с тригонометрическими функциями, но насколько я их помню, они применялись к углам внутри прямоугольного треугольника, а не к углу вне его. Это кажется мне контринтуитивным.

Не должен ли коэффициент синуса (или косинуса, если на то пошло) представлять угол $180 — \theta$, расположенный внутри прямоугольного треугольника, а не вне его? Объяснение было бы очень признательно, так как это ключевая часть нашего текущего подразделения.

• функции
• тригонометрия

$\endgroup$

6

$\begingroup$

Когда тригонометрические функции, такие как синус и косинус, применяются к ситуациям, когда мы имеем дело с углами, которые больше или равны 9\circ$), как на вашей картинке. По сути, вы все еще как бы используете идею прямоугольного треугольника, но теперь вы должны принять во внимание тот факт, что стороны треугольника могут иметь отрицательные значения, потому что вся идея о том, что угол может быть больше или равен 90 градусам, возникает от единичного круга, с которым мы работаем в декартовой системе координат. Следовательно, когда $x$ отрицательно, длина соответствующей ветви имеет отрицательное значение. Когда $y$ отрицательно, длина соответствующей ветви также будет отрицательной. Имеет ли это смысл для вас?

Если мое объяснение покажется вам запутанным, вот более конкретная версия: забудьте об определении прямоугольного треугольника для углов, больших или равных 90 градусам. Это действительно не работает. Теперь вы работаете в декартовой системе координат, где гипотенуза равна $1$, $\cos\theta$ — координата x, а $\sin\theta$ — координата y.

$\endgroup$

7

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Функция синуса

Синус

• Сводка
• Синтаксис
• Аргументы
• Возвращаемое значение
• Использование
• Примеры
• Интерактивный
• Пояснение
• Определение
• Ссылки

Резюме

Функция синуса возвращает синус угла в радианах. В геометрических терминах функция возвращает вертикальную составляющую точки, образованной углом на единичной окружности.

Синтаксис

 грех(θ) 

Аргументы

Имя	Описание
θ (тета)	Угол в радианах

Возвращаемое значение

Возвращает синус угла в радианах.

Применение

Функция синуса возвращает синус числа, указанного в радианах. В геометрических терминах функция возвращает вертикальную составляющую точки, образованной соответствующим углом (тета) на единичной окружности. Например, при заданном угле в радианах (треть оборота) функция возвращает значение .

Визуально возвращаемое значение равно Y-компоненте точки на единичной окружности, соответствующей углу в радианах. Это показано на рисунке ниже, на котором показана единичная окружность в координатной плоскости XY , а угол выделен красным цветом, а вертикальная составляющая точки — синим.

Примеры

В этих примерах показано возвращаемое значение синуса для некоторых распространенных углов, образованных делением единичного круга на равные части. Обратите внимание, что постоянная окружности (тау) представляет собой полный оборот в радианах.

В этих примерах показано возвращаемое значение синуса для некоторых распространенных углов, образованных делением единичного круга на равные части.

 грех(0*ТАУ/8) = 0
 

 sin(1*TAU/8) = 0,7071... // sqrt(2)/2
 

 грех(2*ТАУ/8) = 1
 

 sin(3*TAU/8) = 0,7071... // sqrt(2)/2
 

Интерактивный

Интерактивное изображение выше визуализирует геометрическое отношение синуса к единичной окружности. Нажмите и перетащите любую из двух контрольных точек, чтобы посмотреть изменение ввода и вывода. Ввод выделен красным цветом и представляет входной угол в радианах. Выход выделен синим цветом.

Пояснение

Функция синуса является частью группы тригонометрических функций, которые возвращают отношения, связанные с геометрией окружности. Функция синуса является одной из трех основных функций: синуса, косинуса и тангенса, которые принимают угол в качестве входных данных и возвращают отношение в качестве выходных данных. График функции синуса показан ниже, который демонстрирует возможный выход функции синуса для области до , где .