Разложение в ряд Тейлора
Введите функцию, которую будете раскладывать в ряд Тейлора
Выполним разложение функции f(x) в ряд Тейлора в точки x0 до n-го члена
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.
Ряд Фурье периодических функций с периодом 2π.
Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.
Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):
Стандартная (=обычная) запись через сумму sinx и cosx
f(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2sin2x+b3sin3x+…,
где ao, a1
,a2,…,b1,b2,.. — действительные константы, т.е.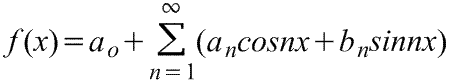 (1)
(1)
Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:
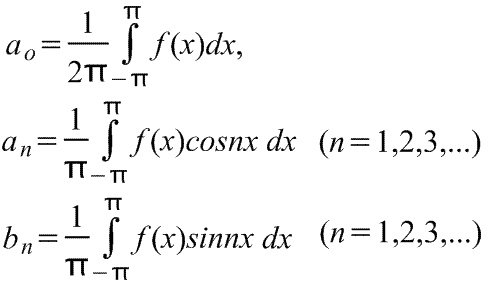
Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,
Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)
f(x)=ao+c1sin(x+α1)+c2sin(2x+α
Где ao — константа, с 1=(a12+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен an=arctg an/bn.
Для ряда (1) член (a1cosx+b1sinx) или c1sin(x+α1) называется первой или основной гармоникой, (a2cos2x+b2sin2x) или c2sin(2x+α2) называется второй гармоникой и так далее.
Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.
Ряд Фурье непериодических функций с периодом 2π.
Разложение непериодических функций.
Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.
Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .
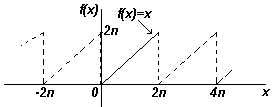
Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.
Четные и нечетные функции.
Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х2 и у=cosx.
Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.
Многие функции не являются ни четными, ни нечетными.
Разложение в ряд Фурье по косинусам.
Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,
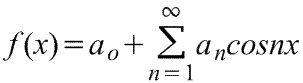
где коэффициенты ряда Фурье,
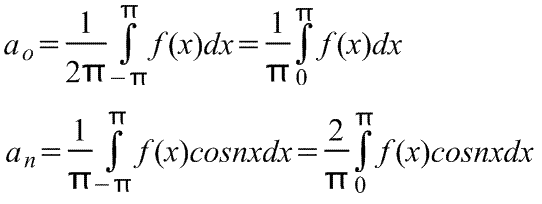
Разложение в ряд Фурье по синусам.
Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).
Следовательно,
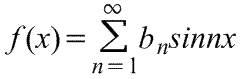
где коэффициенты ряда Фурье,
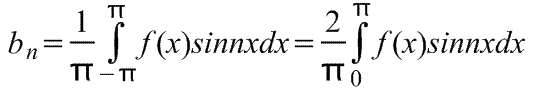
Ряд Фурье на полупериоде.
Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.
Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье ao и an

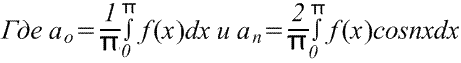
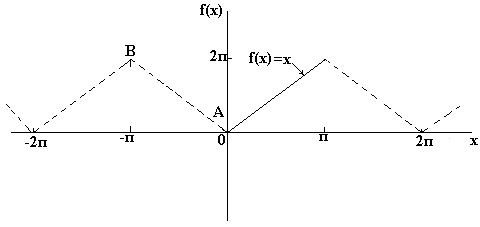
Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b
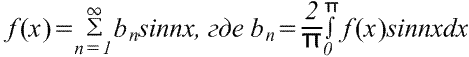
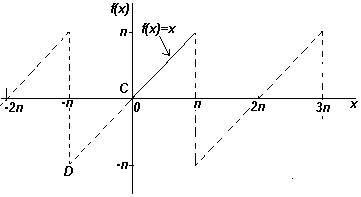
Ряд Фурье для произвольного интервала.
Разложение периодической функции с периодом L.
Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.
Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид
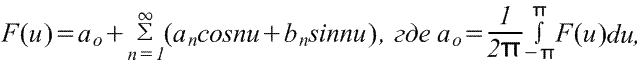
Где коэффициенты ряда Фурье,
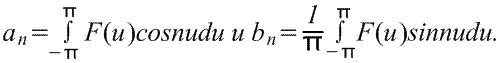
Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид
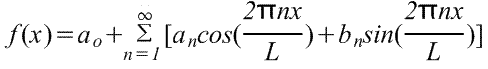
где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,
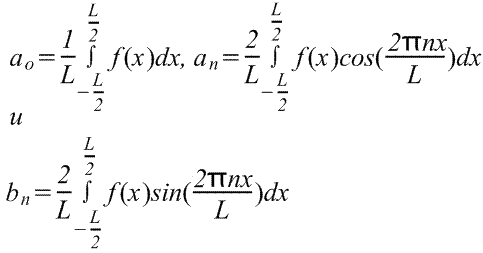
(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)
Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.
Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.
Разложение по косинусам в диапазоне от 0 до L имеет вид
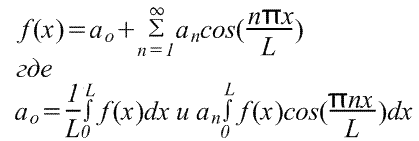
Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.
Ряд Фурье периодических функций с периодом 2π.
Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.
Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):
Стандартная (=обычная) запись через сумму sinx и cosx
f(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2sin2x+b3sin3x+…,
где ao, a1,a2,…,b1,b2,.. — действительные константы, т.е.
(1)
Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:
Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,
Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)
f(x)=ao+c1sin(x+α1)+c2sin(2x+α2)+…+cnsin(nx+αn)
Где ao — константа, с 1=(a12+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен an=arctg an/bn.
Для ряда (1) член (a1cosx+b1sinx) или c1sin(x+α1) называется первой или основной гармоникой, (a2cos2x+b2sin2x) или c2sin(2x+α2) называется второй гармоникой и так далее.
Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.
Ряд Фурье непериодических функций с периодом 2π.
Разложение непериодических функций в ряд Фурье.
Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.
Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .
Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.
Четные и нечетные функции.
Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х2 и у=cosx.
Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.
Многие функции не являются ни четными, ни нечетными.
Разложение в ряд Фурье по косинусам.
Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,
где коэффициенты ряда Фурье,
Разложение в ряд Фурье по синусам.
Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).
Следовательно,
где коэффициенты ряда Фурье,
Ряд Фурье на полупериоде.
Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам ил
Перед тем прочтением данной статьи следует просмотреть следующий материал определение многочлена Тейлора, Остатки формулы Тейлора, Коэффициенты Тейлора, ряд Тейлора.
Запишем разложения основных элементарных функций в ряд Тейлора в окрестности точки $x_{0}=0$, т.е. в ряд вида $f(x)=$$\sum\limits _{ n=0 }^{ \infty }{ \frac { { f }^{ (n) }(0) }{ n! } } { x }^{ n }$ (1), который называется рядом Маклорена.
Показательная и гиперболические функции
Пусть $f(x)=e^{x}$. Найдем производные функции: ${f}'(x)= e^{x}$, $f^{\prime\prime}( x )=e^{x}$,$\ldots$,$f^{(n)}(x)=e^{x}$. Тогда $0 < f(x) < e^{\rho }$, $0 < f^{(n)}(x) < e^{\rho }$ для любого $x\in(-\rho ,\rho )$, где $\rho > 0$ и для любого $n\in \mathbb{N}$.
Из теоремы о представлении функции в виде ее ряда Тейлора (Курс математического анализа, ст.437) следует, что ряд (1) для $f(x)=e^{x}$ сходится к этой функции на интервале $(-\rho ,\rho )$ при любом $\rho > 0$. Так как для функции $f(x)=e^{x}$ выполняются $f(0)=1$, $f^{(n)}(0)=1$ для всех $n\in \mathbb{N}$, то, по формуле (1), получаем разложение в ряд Маклорена показательной функции:
$$e^{x}=1+x+\frac{x^{2}}{2!}+ \ldots +\frac{x^{n}}{n!}+ \ldots = \sum_{n=0}^{\infty }\frac{x^{n}}{n!}, x\in \mathbb{R} (2)$$
Используя разложение (2), синус и косинус $\text{sh} \, x=\frac{e ^{x}-e ^{-x}}{2}$, $\text{ch} \, x=\frac{e ^{x}+e ^{-x}}{2}$, находим:
$$\text{sh} \, x=x+\frac{x^{3}}{3!}+ \ldots +\frac{x^{2n+1}}{(2n+1)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }\frac{x^{2n+1}}{(2n+1)!}, x\in \mathbb{R} (3)$$
$$\text{ch} \, x=1+\frac{x^{2}}{2!}+ \ldots +\frac{x^{2n}}{(2n)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }\frac{x^{2n}}{(2n)!}, x\in \mathbb{R} (4)$$
Радиус сходимости $R=+\infty $.
Тригонометрические функции
Пусть $f(x)=\sin x$. Найдем производные функции: ${f}'(x)= \cos x$, $f^{\prime\prime}(x)= -\sin x$,$\ldots$,$f^{(n)}(x)=\sin x$ при $n$ — четное. Тогда $\left | f^{(n)}(x) \right | \leq 1$, для любого $n\in \mathbb{N}$ и для любого $x\in \mathbb{R}$.
Из теоремы о представлении функции в виде ее ряда Тейлора (Курс математического анализа, ст.437) ряд (1) для $f(x)=\sin x$ сходится для любого $x\in (-\infty , \infty )$. Радиус сходимости $R=+\infty$.
Если $f(x)=\sin x$, то $f(0)=0$, $f^{(2n)}(0)=0$, ${f}'(0)=1$, $f^{(2n+1)}(0)=(-1)^{n}$ для любого $n\in \mathbb{N}$, и, по формуле (1), получаем разложение в ряд Маклорена:
$$\sin x =x-\frac{x^{3}}{3!}+ \ldots +(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}, x\in \mathbb{R} (5)$$
Пусть $f(x)=\cos x$. Найдем производные функции: ${f}'(x)= -\sin x$, $f^{\prime\prime}(x)= -\cos x$,$\ldots$,$f^{(n)}(x)=\cos x$ при $n$ — четное. Тогда $\left | f^{(n)}(x) \right | \leq 1$, для всех $x\in \mathbb{R}$, $n\in \mathbb{N}$, $f(0)=1$, ${f}'(0)=0$, $f^{(2n)}(0)=(-1)$, $f^{(2n+1)}(0)=0$ для всех $n\in \mathbb{N}$. По формуле (1):
$$\cos x =1-\frac{x^{2}}{2!}+ \ldots +(-1)^{n}\frac{x^{2n}}{(2n)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }(-1)^{n}\frac{x^{2n}}{(2n)!}, x\in \mathbb{R} (6)$$
Радиус сходимости $R=+\infty$.
Логарифмическая функция
Пусть $f(x)=\ln(1+x)$. Тогда $$f^{(n)}(x)=\frac{(-1)^{(n-1)}(n-1)!}{(1+x)^{n}} (7),$$ откуда находим $$\frac{f^{(n)}(0)}{n!}=\frac{(-1)^{(n-1)}}{n}.$$
Оценим остаток по формуле остаточного члена в интегральной форме: $$r_{n}=\frac{1}{n!}\int\limits_{0}^{x}(x-t)^{n}f^{(n+1)}(t)dt=\frac{x^{(n+1)}}{n!}\int\limits_{0}^{1}(1-\tau )^{n}f^{(n+1)}(\tau x)d\tau.$$ Используя равенство (7), получаем $$r_{n}=(-1)^{n}x^{n+1}\int\limits_{0}^{1}\frac{(1-\tau )^{n}}{(1+\tau x)^{n+1}}d\tau.$$ Пусть $\left | x \right |
Пусть $x=1$. Тогда $\left | r_{n}(1) \right |=$$\int\limits_{0}^{1}\frac{(1-\tau )^{n}}{(1+\tau )^{n+1}}d\tau$$ \leq \int\limits_{0}^{1}(1-\tau )^{n}d\tau$$ =\frac{1}{n+1}$ $\rightarrow 0.$
Если $x\in (-1,1]$, то остаточный член $r_{n}(x)$ для функции $f(x)=\ln(1+x)$ стремится к нулю при $n\rightarrow \infty.$
В итоге получаем разложение в ряд Маклорена
$$\ln(1+x)=x-\frac{x^{2}}{2}+ \ldots +(-1)^{n+1}\frac{x^{n}}{n}+ \ldots =$$ $$=\sum_{n=1}^{\infty }(-1)^{n+1}\frac{x^{n}}{n}, x\in \mathbb{R} (8)$$
Радиус сходимости $R=1.$
Степенная функция
Пусть $f(x)=(1+x)^{\alpha }$. Если $\alpha =0$, то $f(x)=1$, а если $\alpha =n$, где $n\in \mathbb{N}$, то $f(x)$-многочлен степени $n$, который можно представить в форме бинома Ньютона в форме конечной суммы:
$$f(x)=\sum\limits_{k=0}^{n}C_{n}^{k}x^{k}.$$ Покажем, что если $\alpha \neq 0$ и $\alpha \notin \mathbb{N}$, то функция $f(x)=(1+x)^{\alpha }$ представляется при каждом $x\in (-1,1)$ сходящимся к ней рядом Маклорена $$(1+x)^{\alpha }=\sum\limits_{n=0}^{\infty }C_{\alpha }^{n}x^{n} (9),$$ где $C_{\alpha }^{0}=1$, $C_{\alpha }^{n}=\frac{\alpha (\alpha -1) \ldots (\alpha -n+1))}{n!}$.
Так как $f^{(n+1)}(x)=\alpha (\alpha -1) \ldots (\alpha -n)(1+x)^{\alpha -n-1}$, то по формуле $r_{n}(x)=\frac{x^{(n+1)}}{n!}\int\limits_{0}^{1}(1-\tau )f^{(n+1)}(\tau x)d\tau$ получаем $$r_{n}(x)=A_{n}x^{n+1}\int\limits_{0}^{1}\left ( \frac{1-\tau}{1+\tau x} \right )^{n}(1+\tau x)^{\alpha -1}d\tau,$$ где $C_{n }=\frac{\alpha (\alpha -1) \ldots (\alpha -n)}{n!}.$
Выберем $m\in \mathbb{N}$ такое, чтобы выполнялось условие $\left | \alpha \right |\leq m$. Тогда для всех $n\geq m$ справедливо $\left | A_{n} \right |$$\leq \frac{m(m+1) \ldots (m+n)}{n!}$$\leq \frac{(m+n)!}{n!}=(n+1) \ldots (n+m)\leq (2n)^{m}$. Используя неравенства $\left | 1+\tau x \right |\geq 1-\tau \left | x \right |\geq 1-\tau$, $\left | 1+\tau x \right |\geq 1-\left | x \right |$, а также неравенство $\left | 1+\tau x \right |\leq 1+\left | x \right |$, получаем $0\leq \frac{1-\tau }{1+\tau x}\leq 1$.
Так как $\lim\limits_{t\rightarrow \infty }\frac{t^{m}}{a^{t}}=0$ при $\alpha > 1$, то $\lim\limits_{n\rightarrow \infty }\frac{n^{m}}{\left ( \frac{1}{\left | x \right |} \right )^{n+1}}=0$. Поэтому справедливо равенство $(1+x)^{\alpha }=\sum\limits_{n=0}^{\infty }C_{\alpha }^{n}x^{n}$. Радиус сходимости этого ряда $R=1$ при $\alpha \neq 0$ и $\alpha \notin \mathbb{N}.$
$$(1+x)^{\alpha }=$$ $$1+\alpha x+\frac{\alpha (\alpha -1)}{2!}x^{2}+ \ldots +\frac{\alpha (\alpha -1) \ldots (\alpha -n+1)}{n!}x^{n}+\ldots=$$$$1+\sum_{n=1}^{\infty }\frac{\alpha (\alpha -1) \ldots (\alpha -n+1)}{n!}x^{n}+\ldots, x\in \mathbb{R} (10)$$
- Частные случаи формулы (9):
- $\frac{1}{1+x}=1-x+x^{2}-\ldots=\sum\limits_{n=0}^{\infty }(-1)^{n}x^{n}, x\in \mathbb{R}$
- $\frac{1}{1-x}=\sum\limits_{n=0}^{\infty }x^{n}, x\in \mathbb{R}$
Спойлер
Разложить функцию в ряд Маклорена.
$$f(x)=x\cos 3x$$
$\cos 3x=1-\frac{(3x)^2}{2!}+\frac{(3x)^4}{4!}-\ldots+(-1)^{n}\frac{(3x)^{2n}}{(2n)!}+\ldots$
Раскрывая скобки, получим
$\cos 3x=1-\frac{3^{2}x^{2}}{2!}+\frac{3^{4}x^{4}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n)}}{(2n)!}+ \ldots $
Умножая левую и правую часть на $x$, получим
$x\cos 3x=x(1-\frac{3^{2}x^{2}}{2!}+\frac{3^{4}x^{4}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n)}}{(2n)!}+\ldots)$
Таким образом:
$f(x)=x\cos x=x-\frac{3^{2}x^{3}}{2!}+\frac{3^{4}x^{5}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n+1)}}{(2n)!}$
[свернуть]
Литература
Разложение в ряд Тейлора основных элементарных функций
Лимит времени: 0
Информация
Для закрепления материала рекомендуется пройти этот тест
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 4
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Математический анализ 0%
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
Похожее
Решение пределов, используя ряд Тейлора
Метод решения
Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов является разложение функций в степенной ряд Тейлора. Применение этого метода состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 при переменной x, стремящейся к нулю. Для этого, если требуется, выполняем преобразования и делаем замену переменной.
2) Раскладываем числитель и знаменатель в ряд Тейлора в окрестности точки x = 0. При этом выполняем разложение до такой степени xn, которая необходима для устранения неопределенности. Остальные члены включаем в o(xn).
Этот метод применим, если после выполнения пункта 1), функции в числителе и знаменателе можно разложить в степенной ряд.
Выполнять разложение сложных функций и произведения функций удобно по следующей схеме. А) Задаемся показателем степени n, до которого мы будем проводить разложение.
Б) Применяем приведенные ниже формулы разложения функций в ряд Тейлора, сохраняя в них члены до включительно, и отбрасывая члены с при , или заменяя их на .
В) В сложных функциях делаем замены переменных так, чтобы аргумент каждой ее части стремился к нулю при . Например,
.
Здесь при . Тогда можно использовать разложение функции в окрестности точки .
Разложение функции в ряд Тейлора, в окрестности точки , называется рядом Маклорена. Поэтому для применяемых в наших целях рядов уместны оба названия.
Применяемые свойства о малого
Определение и доказательство свойств о малого приводится на странице: «О большое и о малое. Сравнение функций». Здесь мы приводим свойства, используемые при решении пределов разложением в ряд Маклорена (то есть при ).
Далее m и n – натуральные числа, .
;
;
, если ;
;
;
;
, где ;
, где c ≠ 0 – постоянная;
.
Для доказательства этих свойств нужно выразить о малое через бесконечно малую функцию:
, где .
Разложение элементарных функций в ряд Тейлора (Маклорена)
Далее приводятся разложения элементарных функций в степенной ряд при . Как мы упоминали ранее, ряд Тейлора в окрестности точки называется рядом Маклорена.
;
;
,
где ;
;
;
,
где – числа Бернулли: , ;
;
;
;
;
;
;
;
,
;
;
.
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов с помощью ряда Тейлора.
⇓, ⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Вычислить предел последовательности, используя разложение в ряд Тейлора.
.
Решение
Это неопределенность вида бесконечность минус бесконечность. Приводим ее к неопределенности вида 0/0. Для этого выполняем преобразования.
.
Здесь мы учли, что номер элемента последовательности n может принимать только положительные значения. Поэтому . Делаем замену переменной . При . Будем искать предел считая, что x – действительное число. Если предел существует, то он существует и для любой последовательности , сходящейся к нулю. В том числе и для последовательности .
.
Раскладываем функцию в числителе в ряд Тейлора. Применяем формулу:
.
Оставляем только линейный член.
.
.
Здесь мы учли, что поскольку существует двусторонний предел , то существуют равные ему односторонние пределы. Поэтому .
Ответ
Пример 2
Все примеры ⇑ Показать, что значение второго замечательного предела можно получить, используя разложение в ряд Тейлора.
Решение
Делаем замену переменной . Тогда . При . Подставляем.
.
Для вычисления предела можно считать, что значения переменной t принадлежат любой, наперед выбранной, проколотой окрестности точки . Мы полагаем, что . Используем то, что экспонента и натуральный логарифм являются обратными функциями по отношению друг к другу. Тогда
.
Вычисляем предел в показателе, используя следующее разложение в ряд Тейлора:
.
.
Поскольку экспонента является непрерывной функцией для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.
Ответ
Пример 3
Все примеры ⇑ Вычислить предел, используя разложение в ряд Тейлора.
.
Решение
Это неопределенность вида 0/0. Используем следующие разложения функций в окрестности точки :
;
;
.
Раскладываем с точностью до квадратичных членов:
;
.
Делим числитель и знаменатель на и находим предел:
.
Ответ
Пример 4
Все примеры ⇑ Решить предел с помощью ряда Тейлора.
.
Решение
Легко видеть, что это неопределенность вида 0/0. Раскрываем ее, применяя разложения функций в ряд Тейлора. Используем приведенное выше разложение для гиперболического синуса ⇑:
(П4.1) .
В разложении экспоненты, заменим x на –x:
(П4.2) .
Далее, – сложная функция. Сделаем замену переменной . При . Поэтому мы можем используем разложение натурального логарифма в окрестности точки . Используем приведенное выше разложение, в котором переименуем переменную x в t:
(П4.3) .
Заметим, что если бы у нас была функция , то при . Поэтому подставить в предыдущее разложение нельзя, поскольку оно применимо в окрестности точки . В этом случае нам потребовалось бы выполнить следующее преобразование:
.
Тогда при и мы могли бы применить разложение (П4.3).
Попробуем решить предел, выполняя разложение до первой степени переменной x: . То есть оставляем только постоянные члены, не зависящие от x: , и линейные . Остальные будем отбрасывать. Точнее переносить в .
;
;
.
Поскольку , то в разложении логарифма мы отбрасываем члены, начиная со степени 2. Применяя, приведенные выше свойства о малого имеем:
.
Подставляем в предел:
.
Мы снова получили неопределенность вида 0/0. Значит разложения до степени не достаточно.
Если мы выполним разложение до степени , то опять получим неопределенность:
.
Выполним разложение до степени . То есть будем оставлять только постоянные члены и члены с множителями . Остальные включаем в .
;
;
;
.
Далее замечаем, что . Поэтому в разложении логарифма нужно отбросить члены, начиная со степени , включив их в . Используем разложение (П4.3), заменив t на :
.
Подставляем в исходную функцию.
.
Находим предел.
.
Ответ
.
Пример 5
Все примеры ⇑ Найти предел с помощью ряда Тейлора.
.
Решение
Будем проводить разложение числителя и знаменателя в ряд Маклорена до четвертой степени включительно.
Начнем со знаменателя. Используем свойства о малого ⇑ и разложения синуса и тангенса ⇑.
;
;
.
Теперь переходим к числителю. При . Поэтому сделать подстановку и применить разложение для нельзя, поскольку это разложение применимо при , а у нас . Заметим, что . Поэтому выполним преобразование.
.
Теперь можно сделать подстановку , поскольку при .
Разложим функцию и ее степени в ряд Тейлора в окрестности точки . Применяем приведенное выше разложение ⇑.
;
;
;
;
;
;
Далее заметим, что . Поэтому, чтобы получить разложение сложной функции с точностью до , нам нужно разложить с точностью до .
Раскладываем первый логарифм.
; ;
;
.
Разложим второй логарифм. Приводим его к виду , где при .
,
где .
Разложим z в ряд Тейлора в окрестности точки с точностью до .
Применим разложение синуса ⇑:
.
Заменим x на :
. Тогда
;
;
Заметим, что . Поэтому, чтобы получить разложение сложной функции с точностью до , нам нужно разложить с точностью до .
Раскладываем с точностью до и учитываем, что .
;
.
Находим разложение числителя.
;
;
.
Подставляем разложение числителя и знаменателя и находим предел.
;
.
Ответ
Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Автор: Олег Одинцов. Опубликовано:
Ряд Тейлора. Разложение функции в ряд Тейлора.
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
.gif)
.gif)
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1).gif) , где f(x) — функция, имеющая при х=а производные всех порядков. Rn — остаточный член в ряде Тейлора определяется выражением
, где f(x) — функция, имеющая при х=а производные всех порядков. Rn — остаточный член в ряде Тейлора определяется выражением .gif)
2)
k-тый коэффициент (при хk) ряда определяется формулой
.gif)
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при a=0 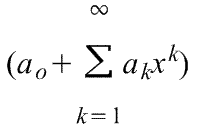
члены ряда определяются по формуле
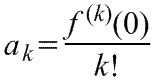
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
- Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
- Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
.gif)
Ряды Тейлора применяются при аппроксимации ( приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.Разложение в ряд Фурье — Калькулятор Онлайн
Введите функцию, которую будете разложить в ряд Фурье
Выполним разложение функции f(x)
в ряд Фурье на отрезке [a, b]
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
