Нужна помощь в аппроксимации синусоидальной функции в python с помощью ряда Тейлора
Я очень новичок в Python и пытаюсь аппроксимировать синусоидальную функцию с помощью этой серии.
Мой код выглядит так:
import math
def sin(x,n):
sine = 0
for i in range(n):
sign = (-1)**i
sine = sine + ((x**(2.0*i-1))/factorial(2**i-1))*sign
return sine
Это не дает ответа, на который я надеялся, но я очень смущен и не могу найти свою ошибку… или, может быть, я просто иду по этому совершенно неправильному пути (как я уже сказал, Я очень новичок в python и в программировании вообще).
Это похоже на программу, которую я должен был написать некоторое время назад, чтобы приблизить pi с учетом этой серии:
def piApprox(n):
pi = 0
for i in range(n):
sign = (-1)**i
pi = pi + 1.0/(2*i+1)*sign
return 4*pi
Я не знаю, полезно ли это в любом случае, но это то, что я пытался использовать, чтобы выяснить мой метод синуса.
Поделиться Источник user2141367 06 марта 2013 в 19:24
2 ответа
- Разложение в ряд Тейлора произвольной функции
Я пытаюсь получить коэффициенты разложения ряда Тейлора произвольных функций. Входная функция должна быть в виде переменных, а выходная должна содержать только коэффициенты. Я пробовал некоторые функции MATLAB, такие как ‘taylor’, но они дают все расширение в виде выражения, написанного в…
- Вычисление ряда Тейлора многомерной функции с помощью sympy
Я пытаюсь вычислить с помощью SymPy ряд Тейлора функции, которая зависит от тригонометрической функции sinc ( здесь ), чтобы упростить мою задачу, мы можем предположить, что функция, которая мне нужна, является рядом Тейлора : f(x1, x2) = sinc(x1) * sinc(x2) Моя проблема в том, что при импорте.
..
4
Ряд Тейлора для sin (x ) равен:
Сравнивая ваш код с этим определением, эти две части имеют некоторые ошибки:
x**(2.0*i-1)
factorial(2**i-1)
Минусы должны быть плюсами, а показатель в факториале должен быть умножением.
x**(2.0*i+1)
factorial(2*i+1)
Поделиться John Kugelman 06 марта 2013 в 19:27
1
Вы можете использовать символическую библиотеку SymPy для построения аппроксимированной функции с использованием рядов Тейлора:
from sympy import sin
from sympy.abc import x
# creates a generator
taylor_series = sin(x).series(n=None)
# takes the number of terms desired for your generator
taylor_series = sum([next(taylor_series) for i in range(num_of_terms)])
# creates a function that calculates the approximated sine function
mysin = sympy. lambdify((x,), taylor_series)
lambdify((x,), taylor_series)
Поделиться Saullo G. P. Castro 25 сентября 2013 в 11:58
Похожие вопросы:
Погрешность аппроксимации синуса в Java
Меня немного раздражает метод, который я написал для аппроксимации синусоидальной функции в Java. Вот она, она основана на серии Тейлора. static double PI = 3.14159265358979323846; static double eps…
Verilog код для вычисления cosx с использованием аппроксимации рядов Тейлора Я пытаюсь реализовать функцию COS X в Verilog, используя ряд Тейлора. Постановка задачи, представленная мне, выглядит следующим образом Напишите код Verilog для вычисления cosX с использованием…
«декодирование» аппроксимации ряда sin Тейлора
Я использую ряд Тейлора для вычисления sin() . Ряд Тейлора для греха: Реализация, которую я использую, выглядит следующим образом: float sine(float x, int j) { float val = 1; for (int k = j — 1; k. ..
..
Разложение в ряд Тейлора произвольной функции
Я пытаюсь получить коэффициенты разложения ряда Тейлора произвольных функций. Входная функция должна быть в виде переменных, а выходная должна содержать только коэффициенты. Я пробовал некоторые…
Вычисление ряда Тейлора многомерной функции с помощью sympy
Я пытаюсь вычислить с помощью SymPy ряд Тейлора функции, которая зависит от тригонометрической функции sinc ( здесь ), чтобы упростить мою задачу, мы можем предположить, что функция, которая мне…
Вычисление Pi с использованием ряда Тейлора C++
Я пытаюсь реализовать функцию для вычисления pi с помощью ряда Тейлора, вот мой код для этого #include <iostream> #include <math.h> using namespace std; double pi(int n) { double sum =…
какова может быть временная сложность синусоидальной функции по ряду Тейлора?
Я искал везде, даже на SO. а научные статьи в Гугле-это далеко за пределами моих умственных возможностей. x , и мне интересно, как реализовать это в python. Для простоты я думаю, что могу использовать серию…
x , и мне интересно, как реализовать это в python. Для простоты я думаю, что могу использовать серию…
Синус функция, разложение в ряд
Синус функция, разложение в ряд 137 Система единиц 24, естественная 26, когерентная 23, международная 27 [c.299]Так, если в выражениях (4.37), (4.38) ограничиться п членами разложения, то и функцию ф также представим в виде разложения в ряд по синусам с п членами. Тогда [c.86]
Уравнения п. 18 не содержат в себе никаких иных функций времени, кроме частных дифференциалов функции П поэтому, когда определяют ту часть А функции Q, которая не зависит от времени t и содержит только произвольные постоянные а,Ь,с,. . путем разложения в ряды или каким-либо иным способом, то достаточно в этих уравнениях поставить А вместо Д, и тогда мы прямо получим уравнения между величинами а,Ь,с,…, которые стали переменными, и временем t эти уравнения послужат для определения их вековых изменений, так как они совершенно свободны от всяких синусов и косинусов. [c.432]
[c.432]
В этой формуле а , а п, Ьп, Ь п являются коэфициентами разложения в ряд синусов функций .
Функция / (х) = аР четная, поэтому разложение в ряд Фурье не будет содержать синусов. Подставив в подынтегральное выражение значения для До и а также приведя функцию f (х) к 2и функции, т. е. /(х) = т [c.306]
Таким образом, рещение, соответствующее одному члену разложения функции ф в ряд по синусам, имеет вид [c.369]
Пользуясь разложением в ряд известной функции гиперболического синуса, формулу (46,2) можно записать в виде [c.178]
Предварительно рассмотрим разложение в ряд Фурье по синусам функции / (х), заданной в интервале О / — Ли равна единице при /г [c.521]
В частном случае, при большом п, коэфициенты после разложения функции a в ряд Фурье по синусам кратных дуг получаются равными
[c. 696]
696]
Выражение (3.64) представляет собой разложение функции F x) в ряд Фурье по синусам (предполагается, что такое разложение возможно). Коэффициенты этого разложения определяются известной ( рмулой [c.289]
Здесь р — целое положительное число. Для получения формулы обращения воспользуемся теорией рядов Фурье. Будем считать, что функция (х) разложима в ряд Фурье по синусам. Тогда коэффициенты разложения определяются формулами [c.81]
Это равенство есть разложение функции F(x) в ряд Фурье по синусам. Коэффициенты ряда Фурье определяются следующим выражением . [c.61]
Для определения вековых возмущений необходимо лишь вместо Q подставить непериодическую часть этой функции, т. е. первый член разложения О в ряды синусов и косинусов углов, зависящих от средних движений возмущаемой и возмущающих планет. Действительно, так как 9 является только функцией эллиптических координат этих планет, которые всегда —по крайней мере в том случае, когда эксцентриситеты и наклонения незначительны — могут быть разложены в ряды синусов и косинусов углов, пропорциональных аномалиям и средним долготам, то функцию 9 можно разложить в ряд подобного же вида, и тогда первый член, не содержащий синуса и косинуса, будет единственным, который может дать вековые уравнения.
Легко убедиться, что это уравнение однозначно определяет значение Действительно, припоминая определение гиперболического синуса и подставляя вместо показательных функций, входящих в его выражение, их разложения в степенные ряды по степеням , найдем [c.214]
Формула обращения обычно находится при помощи разложения функции в ряды по ортогональным функциям соответствующей задачи Штурма — Лиувилля. Поэтому рещения, получаемые этими методами, имеют те же принципиальные недостатки, как и решения, получаемые классическими методами. Так, формулы обращения имеют вид для синус-преобразования [c.83]
Разложение функции 8(2) в ряд по косинусам означает ее четность, т. е. мы считаем, что на поверхности МИС расположен слой вещества половинной толщины (как это и показано на рис. 3.4). При более общем разложении 8 (г) в ряд по синусам и косинусам появляется только дополнительный фазовый сдвиг у отраженной и прошедшей волн.
 Энергетические же коэффициенты отражения и прохождения при этом не изменятся.
[c.86]
Энергетические же коэффициенты отражения и прохождения при этом не изменятся.
[c.86]Здесь i z и si z — интегральные косинус и синус. Используя известные [12] разложения этих функций в ряды нри малых з, убедимся, что для Hiz) прн всех 0[c.376]
Последние формулы представляют собой разложение функций ф(а ) Ифг(а ) в ряд Фурье по синусам в интервале (О, Z).
Постоянство передаточной функции имеет место при ф [c.137]
Силовые функции Н х), Н х), Нз х), направление осей координат, коэффициенты а, рассматривают согласно изложенному в п. 12.4. При этом нужно учесть, что 033 = 0,6022 при грузовом воздействии все элементы настила основной системы (если они одинаковы) имеют один и тот же прогиб, вследствие чего а1р = а2р — 0. В третьем уравнении грузовой член представляет прогиб элемента под нагрузкой как балки, опертой на две опоры по коротким сторонам. Поэтому при удержании только первого члена из разложения нагрузки в ряд по синусам имеем
[c. 227]
227]
III. Разложение по синусам. Разложим теперь только что проанализированную функцию в ряд синусов. Допустим снова, что [c.138]
Введем следующее важное соотнощение, связывающее показательную функцию, косинус и синус и доказываемое разложением этих трех функций в степенные ряды [c.139]
Поскольку получить точное аналитическое решение дифференциального уравнения (20.12) в общем случае невозможно, будем искать его в виде бесконечного ряда. Для пластины с шарнирно опертыми по всем четырем сторонам краями удобно использовать разложение искомой функции прогиба w(x,y) в двойной тригонометрический ряд по синусам [c.436]
Обыкновенно не имеется аналитического выражения f(t), а на основании снятых индикаторных диаграмм возможно только графически представить изменение этой функции тогда разложение в ряд (4) можно выполнить графическим приемом Фишер-Хиннена i) или известным прибором гармонический анализатор , который за один обвод дает пять коэффициентов ряда синусов и пять коэффициентов ряда косинусов, что вполне достаточно для практических целей. Когда разложение тем или другим способом выполнено, мы можем уравнение (3) переписать так
[c.16]
Когда разложение тем или другим способом выполнено, мы можем уравнение (3) переписать так
[c.16]
Здесь величины, обозначенные индексом я, зависят лишь от угла а. Каждому целому значению п соответствует три таких уравнения. Если бы ) разложении функций X, Y ч Z ъ ряд Фурье входили как синусы, так и косинусы, то для каждого целого п кроме трех уравнений (16) получились бы еще три уравнения для определения коэфициентов более общего разложения в ряд Фурье эти нозые уравнения отличались бы от уравнений (16) лишь знаками перед п в двух последних уравнениях (16). Но мы для упрощения вычислений предположим, что разложение в ряд Фурье внешних сил, а следовательно, и напряжений, можно представить в следующем простом виде [c.26]
Приближенные значения сосредоточенных постоянных для всех описанных выше эквивалентных схем могут быть получены тем же способом, т. е. путем разложения в ряд параметров эквивалентной схемы вблизи частоты резонанса и приравнивания членов первого порядка в этих рядах и в аналогичных рядах, полученных для простейшей электрической цепи с сосредоточенными постоянными. Функции, выраженные через синусы, косинусы, тангенсы и котангенсы, вблизи их нулей могут быть анироксимированы последовательной цепью ЬС, а вблизи их полюсов — параллельной цепью ЬС. Область применимости каждой схемы с сосредоточенными постоянными может быть определена путем сравнения членов второго порядка в разложениях, которые рассмотрены выше.
[c.293]
Функции, выраженные через синусы, косинусы, тангенсы и котангенсы, вблизи их нулей могут быть анироксимированы последовательной цепью ЬС, а вблизи их полюсов — параллельной цепью ЬС. Область применимости каждой схемы с сосредоточенными постоянными может быть определена путем сравнения членов второго порядка в разложениях, которые рассмотрены выше.
[c.293]
Усилия, моменты, компоненты деформации и углы поворота с помощью соотношений 23.1 можно также без труда выразить через ряды вида (23.4.3). Формулы для коэффициентов этих рядов громоздки, и их приводить не будем. Заметим только, что величины Ut, S21, 5i2, H i, Нц и Ni будут при этом разложены в ряды по косинусам, а величины и , w, ТТ , Gi, G , — в ряды по синусам. Отсюда, между прочим, вытекает, что ряды для первой группы величин оказываются неполными — в них отсутствуют слагаемые, отвечающие m = 0. Это связано с тем, что для потенциальной функции Ф использовано разложение (23.4.1), в котором соответствующий член отсутствует. В дальнейшем считается, что пропорционально т, поэтому было бы бессмысленно начинать ряд для Ф с нулевого члена, но к разыскиваемому решению надо присоединить еще одно, в котором и , S i, S , Н , Я12, Ni являются функциями одного 9, а остальные перемещения, усилия и мом ты равны нулю. При помощи уравнений (23.1.7), положив в них X = Y = Z = = О, мы без труда найдем такое напряженное состояние. О)ответствующие перемещения будут
[c.343]
В дальнейшем считается, что пропорционально т, поэтому было бы бессмысленно начинать ряд для Ф с нулевого члена, но к разыскиваемому решению надо присоединить еще одно, в котором и , S i, S , Н , Я12, Ni являются функциями одного 9, а остальные перемещения, усилия и мом ты равны нулю. При помощи уравнений (23.1.7), положив в них X = Y = Z = = О, мы без труда найдем такое напряженное состояние. О)ответствующие перемещения будут
[c.343]
Однако с другой точки зрении особое значение имеет именно разложение функций в ряд по синусам или косинусам это относится к вопросу о разложении функций от времени. В 19 мы уже останавливались на причине этого с точки зрения диналгнки. [c.136]
Для определения нормальных колебаний примем, что и и V пропорциональны os( + e). Далее, поскольку кольцо образует полный круг, м и у являются периодическими функциями 0 с периодом 2я и, согласно теореме О урье, могут быть разложены в ряд по синусам и косинусам углов, кратных 9. Более того, легко показать, что каждый член любого порядка в разложении должен в отдельности удовлетворять каждому уравнению. Действительно, оказывается, что решение можно выбрать в виде
[c.177]
Более того, легко показать, что каждый член любого порядка в разложении должен в отдельности удовлетворять каждому уравнению. Действительно, оказывается, что решение можно выбрать в виде
[c.177]
В работе Морлэнда [76] в рамках плоского напряженного состояния рассмотрена задача о качении жесткого цилиндра с постоянной скоростью по однородному изотропному вязкоупругому полупространству. Скорость качения полагалась достаточно малой, так что инерционные эффекты не учитывались кроме того, касательные силы на поверхности контакта считались отсутствующими и, таким образом, контактная деформация была обусловлена лишь распределением нормального давления. Длина линии контакта полагалась малой по сравнению с диаметром движущегося цилиндра. Выведены интегральные выражения для перемещений и напряжений в вязкоупругом полупространстве. Математически задача свелась к совместному решению двух пар двойных интегральных уравнений относительно некоторых вспомогательных функций с ядрами, содержащими косинус и синус. Решение этих уравнений осуществлялось путем разложения искомых вспомогательных функций в бесконечные ряды по функциям Бесселя, в то время как для определения коэффициентов ряда требовалось решить бесконечную систему алгебраических уравнений. Если использована связь искомой функции контактного давления с найденными вспомогательными функциями и учтено, что распределение давления не имеет особенностей на краях контактной зоны, то окончательный вид распределения контактного давления представим тригонометрическими рядами. Полученные теоретические результаты проиллюстрированы числовым примером, когда реологические свойства полупространства характеризуются одним временем ретордации. Расчеты дают картину несимметричного распределения нормального давления, являющегося следствием влияния фактора времени.
[c.402]
Решение этих уравнений осуществлялось путем разложения искомых вспомогательных функций в бесконечные ряды по функциям Бесселя, в то время как для определения коэффициентов ряда требовалось решить бесконечную систему алгебраических уравнений. Если использована связь искомой функции контактного давления с найденными вспомогательными функциями и учтено, что распределение давления не имеет особенностей на краях контактной зоны, то окончательный вид распределения контактного давления представим тригонометрическими рядами. Полученные теоретические результаты проиллюстрированы числовым примером, когда реологические свойства полупространства характеризуются одним временем ретордации. Расчеты дают картину несимметричного распределения нормального давления, являющегося следствием влияния фактора времени.
[c.402]
Будем рассматривать, как основные переменные, элементы Пуанкаре (13.60) и предположим для простоты, что возмущающая функция / не зависит от времени. Тогда, если движение рассматриваемой точки принадлежит к эллиптическому типу, то Я, как это уже неоднократно отмечалось, будет периодической функцией от средней аномалии I, или от средней долготы X, 1 может быть разложена в ряд Фурье, расположенный по синусам и косинусам целых кратностей средней аномалии. Коэффициенты этого разложения будут некоторыми функциями от остальных элементов Пуанкаре, т. е. от Л, эксцентрических элементов т] и облических элементов р, д. Мы покажем те перь, что эти коэффициенты разложимы по целым, положительным степеням величин
[c.697]
Коэффициенты этого разложения будут некоторыми функциями от остальных элементов Пуанкаре, т. е. от Л, эксцентрических элементов т] и облических элементов р, д. Мы покажем те перь, что эти коэффициенты разложимы по целым, положительным степеням величин
[c.697]
Введение. Методы, изложенные в гл. I, достаточны для вычисления координат планеты в эллиптической орбите для любого момента времени по элементам этой орбиты. Для различных приложений в небесной механике необходимо иметь в распоряжении методы, которые позволят разложить координаты и функции от координат в эллиптической орбите в периодические ряды. При движении по эллипсу все конечные и непрерывные функции от координат после полного обращения тела возвращаются к исходным значениям. Поэтому такие функции разложимы в периодические ряды по любой непрерыно возрастающей угловой переменной, которая за время полного обращения тела увеличивается на 2л. Угловыми переменными, представляющими в этой связи особый интерес, являются средняя аномалия I, эксцентрическая аномалия и и истинная аномалия /. Они не являются единственными аргументами, которые могут быть рассмотрены в некоторых приложениях используются другие аргументы. Функциями, которые представляются наиболее естественными для этой цели, являются пли четные, или нечетные периодическпе функции от этпх переменных, порождающие либо ряды косинусов, либо ряды синусов. Поскольку обычно удобнее оперировать степенными рядами, чем тригонометрическими разложениями, то полезно познакомиться с разложениями в экспоненциальной форме.
[c.58]
Они не являются единственными аргументами, которые могут быть рассмотрены в некоторых приложениях используются другие аргументы. Функциями, которые представляются наиболее естественными для этой цели, являются пли четные, или нечетные периодическпе функции от этпх переменных, порождающие либо ряды косинусов, либо ряды синусов. Поскольку обычно удобнее оперировать степенными рядами, чем тригонометрическими разложениями, то полезно познакомиться с разложениями в экспоненциальной форме.
[c.58]
Важное свойство четырех функций, которые были разложены в ряды Фурье с кратными I в качестве аргументов и степенными рядами по е в качестве коэффициентов, заключается н том, что самая низкая степень е, входяп ая в коэффициент при синусе или косинусе, равна кратности I в аргументе этого члена. Степенные ряды идут далее по степеням е , так что в коэффициент при косинусе или синусе нечетного аргумента входят только нечетные степени е, а в коэффициенте члена с четным аргументом встречаются только четные степени е.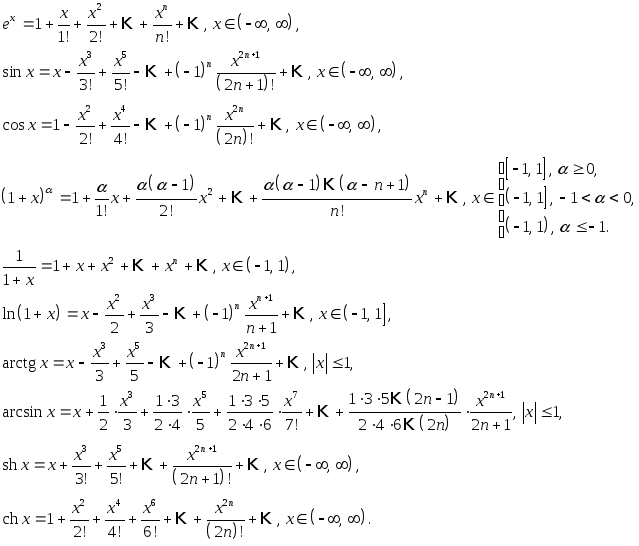 Это свойство тесно связано со свойствами разложений бесселевых функций. Оно впервые было особо отмечено Даламбером. По этой причине Браун назвал его даламберовой характеристикой.
[c.74]
Это свойство тесно связано со свойствами разложений бесселевых функций. Оно впервые было особо отмечено Даламбером. По этой причине Браун назвал его даламберовой характеристикой.
[c.74]
Можно видеть, что форма осцилляций величины (как функции 1/Я) будет, вообще говоря, совершенно отличной от формы осцилляций Л/, поскольку коэффициенты / (гХ) могут существенно отличаться друг от друга и поскольку при нечетных значениях к синус в формуле (3.30) превращается в косинус того же аргумента в формуле (3.31). В общем случае для восстановления первоначальной формы осцилляций (3.30) выходной сигнал как функцию 1/Я нужно разложить в ряд Фурье, разделить каждый коэффициент на J r ) и вновь синтезировать, взяв все компоненты с соответствующими фазами 0 , определенными при разложении. Однако в частном случае достаточно слабой модуляции коэффициенты JЛr ) пропорциональны и вид осцилляций величин Vf и d M/dH в точности совпадает на самом деле нетрудно проверить, что в этом пределе выражение (3. 31) сводится как раз к /г-му слагаемому формулы (3.20). Практически в условиях слабой модуляции амплитуды высших гармоник слишком малы, чтобы их можно было использовать. Таким образом, непосредственно записать без искажений можно только осцилляции величины dM/dH (и, возможно, d M/dH ) при детектировании на частоте со (или 2оо) и при малой амплитуде модуляции. Легко показать, что, для того чтобы коэффициент У,(гХ) отличался от (УгУХ менее чем на 1%, величина гХ должна быть меньше 0,28 это и есть критерий достаточно слабой модуляции, при которой зависимость величины 1> верно воспроизводит зависимость dM/dH.
[c.143]
31) сводится как раз к /г-му слагаемому формулы (3.20). Практически в условиях слабой модуляции амплитуды высших гармоник слишком малы, чтобы их можно было использовать. Таким образом, непосредственно записать без искажений можно только осцилляции величины dM/dH (и, возможно, d M/dH ) при детектировании на частоте со (или 2оо) и при малой амплитуде модуляции. Легко показать, что, для того чтобы коэффициент У,(гХ) отличался от (УгУХ менее чем на 1%, величина гХ должна быть меньше 0,28 это и есть критерий достаточно слабой модуляции, при которой зависимость величины 1> верно воспроизводит зависимость dM/dH.
[c.143]
Рассмотрение общей задачи о распространении импульса произвольного вида очень упрощается тем, что любую функцию можно представить в виде суммы (вообще говоря, с бесконечным числом членов) некоторых определенных функций. Физически это означает, что произвольный импульс может быть представлен как сумма (бесконечно большого числа) импульсов определенного вида.
 Подавляющее большинство приемных устройств подчиняется принципу суперпозиции, который означает, что результат нескольких одновременных воздействий представляет собой просто сумму результатов, вызванных каждым воздействием в отдельности. Принцип суперпозиции применим в том случае, когда свойства принимающей системы не зависят от того, находится ли она уже под действием принимаемого возбуждения или нет, а эта независимость всегда имеет место, если воздействие не становится слишком сильным ). Поскольку принцип суперпозиции применим, мы можем заменить произвольный импульс суммой его слагающих и рассматривать действие каждой слагаюпгей отдельно. Рациональный выбор этих слагающих, т. е. рациональный выбор метода разложения сложного импульса, позволяет чрезвычайно упростить рассмотрение задачи. Таким рациональным разложением является разложение на монохроматические волны, т. е. представление произвольной функции в виде совокупностей косинусов и синусов, введенное Фурье. Согласно теореме Фурье любая функция ) может быть представлена с какой угодно точностью в виде суммы синусоидальных и косинусоидальных функций с соответственно подобранными амплитудами, периодами и начальными фазами.
Подавляющее большинство приемных устройств подчиняется принципу суперпозиции, который означает, что результат нескольких одновременных воздействий представляет собой просто сумму результатов, вызванных каждым воздействием в отдельности. Принцип суперпозиции применим в том случае, когда свойства принимающей системы не зависят от того, находится ли она уже под действием принимаемого возбуждения или нет, а эта независимость всегда имеет место, если воздействие не становится слишком сильным ). Поскольку принцип суперпозиции применим, мы можем заменить произвольный импульс суммой его слагающих и рассматривать действие каждой слагаюпгей отдельно. Рациональный выбор этих слагающих, т. е. рациональный выбор метода разложения сложного импульса, позволяет чрезвычайно упростить рассмотрение задачи. Таким рациональным разложением является разложение на монохроматические волны, т. е. представление произвольной функции в виде совокупностей косинусов и синусов, введенное Фурье. Согласно теореме Фурье любая функция ) может быть представлена с какой угодно точностью в виде суммы синусоидальных и косинусоидальных функций с соответственно подобранными амплитудами, периодами и начальными фазами. При этом, если исходная функция периодична (с периодом Т), то периоды слагающих синусов и косинусов находятся в простом кратном отношении Т, 1 ,Т, /.1Т,. .. (представление в виде ряда Фурье). Если же функция не периодична, то в разложении содержатся не только кратные, но и все возможные периоды (представление в виде интгг-
[c.32]
При этом, если исходная функция периодична (с периодом Т), то периоды слагающих синусов и косинусов находятся в простом кратном отношении Т, 1 ,Т, /.1Т,. .. (представление в виде ряда Фурье). Если же функция не периодична, то в разложении содержатся не только кратные, но и все возможные периоды (представление в виде интгг-
[c.32]Разложения (111) проще, чем (108), так как функции Xi Q) м t/i(0) представляются тригонометрическими рядами только по косинусам, а J 2(0) и i/2(0) —только по синусам. Кроме того, для определения функций j (0) и у(0) в интервал О 02л достаточно знать разложения Х](0), X2IQ), yi(Q), г/г(0) в интервале О[c.240]
Так как все функции X, У, Хв в уравнениях (3.17) не содержат в своих разло.женпях членов ниже второго порядка относительно X, у, х, то правые части уравнений (3.19 ) будут голоморфными функциями величин г, г , Хд,. . ., г , уничтожающимися при одновременном равенстве все этих величин нулю и коэффициенты разложений которых суть периодические функции величины О, которые всегда можно представить в виде конечных рядов косинусов и синусов целых кратностей О. [c.137]
[c.137]
См. разложения степеней синуса и косинуса ио таким же функциям кратных дуг, например, в справочнике И М. Р ы ж и к и И. С. Г р а flui т е й н, Таблицы интегралов, сумм, рядов и произведений , Физматгиз, 1963. [c.156]
| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды. / / Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1.
| |||||
| Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||
| TehTab.ru Реклама, сотрудничество: info@tehtab. | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||
Приближенные вычисления — ряды Тейлора и Маклорена
Задачи на вычисление значения функций в окрестности нуля, или иной точки очень важны в математике и без специальных калькуляторов или программ найти их значение трудно. В помощь студентам, инженерам и другим специалистам приходят ряды Тейлора. Функцию раскладывают в ряд, отбирают несколько первых членов, которые вносят наибольший вклад и обеспечивают достаточную точность вычислений. После этого находят значение в заданной точке.
Рассмотрим примеры применений рядов Тейлора к приближенным вычислениям.
———————————————
Пример 1. Вычислить с точностью до 0,0001
1)
2) (9.331)
3) (9.333)
4) (9.333)
Решение. 1) Запишем заданную функцию в удобном виде
Воспользуемся формулой разложения в ряд Тейлора
и выпишем несколько членов ряда при степенях аргумента
В результате получим значение
Согласно записанной выше формуле, умножаем полученное число на 2
2)
Воспользуемся разложением синус функции в окрестности нуля
Заданное выражение перепишем в следующей форме
и подставим в формулу
Взяв только два члена ряда получаем достаточно хорошую сходимость. И такая сходимость бывает не всегда. Чем дальше отдаляемся от точки в которой развит ряд, тем больше членов разложения нужно брать для точности результата.
3)
Выпишем разложение логарифма около единицы
В данном случае подставим и просуммируем несколько членов ряда
Точный результат равный
Для обеспечения сходимости с точностью 0,0001 нужно брать больше членов ряда
Получили хорошую сходимость, но пришлось брать пять членов разложения в ряд. Это связано с тем что точка в которой искали приближенное значение находится далеко от точки разложения ряда.
Это связано с тем что точка в которой искали приближенное значение находится далеко от точки разложения ряда.
4)
Пусть имеем разложение арксинуса возле нуля
Точное значение будет следующим
Взяв два члена ряда
получим хорошую сходимость.
По аналогии с прведенными примерами поступаем и для ряда других функций.
Ряды косинусов — Справочник химика 21
При решении многих задач пределы интегрирования являются конечными, тогда как во всех приведенных выше формулах преобразований пределы интегрирования бесконечные. Преобразования с конечными пределами интегрирования реализуются на практике через ряды преобразования Фурье двумерного случая — через ряды косинусов или синусов, преобразования Ханкеля — через ряды бесселевых функций. [c.20]В зависимости от числа цилиндра сумма ряда косинусов, число которых . [c.46]
При решении различных задач применяются еще так называемые преобразования Фурье и преобразования Ханкеля с конечными пределами. Эти преобразования в основном сводятся к рядам Фурье (разложение функции на некотором ограниченном интервале в ряды косинусов и синусов), рассмотренным выше, и к рядам бесселевых функций. [c.20]
Эти преобразования в основном сводятся к рядам Фурье (разложение функции на некотором ограниченном интервале в ряды косинусов и синусов), рассмотренным выше, и к рядам бесселевых функций. [c.20]
Выражения же (2.12), (2.13) — не что иное, как некоторые усеченные ряды косинусов и ряды бесселевых функций, совпадающих с точной частотной характеристикой трансформации до некоторой граничной частоты со, или р, (рис. 4). [c.59]
При 2С = С и произвольном значении границы интервала выполнения условия (2.46) (в выражении (2.43) сОг = = 7г/Дх) получение вычислительных схем из этого условия сводится к разложению частотной характеристики трансформации в ряды косинусов, т.е. к способу, описанному в начале этого раздела для случая двухмерной задачи. [c.67]
Для реализации фильтра с такой частотной характеристикой разложим функции (4.17) в ряд косинусов на интервале со от -л до л. Для облегчения процесса разложения представим формулу (4. 17) в виде отрезков двух прямых [c.133]
17) в виде отрезков двух прямых [c.133]
Разлагая эту функцию в ряд косинусов для определения коэффициентов С/е, из формулы (2.18) в общем виде (при I = л) получим [c.133]
Фильтр с прямоугольной частотной характеристикой можно реализовать, пользуясь разложением его частотной характеристики в ряд косинусов или в ряд бесселевых функций. Например, в двухмерном случае, если обозначить через Юг = л/Ах граничную частоту спектра аномалии, то при со, определения коэффициентов вычислительной схемы, соответствующей фильтру с прямоугольной формой частотной характеристики (4.29), при а = 1 получим следующие выражения [c.143]
Для реализации оптимального или комбинированного фильтра сглаживания аномалий с частотной характеристикой (4.43) разложим последнюю в ряды косинусов на интервале -л основании формулы (2.18) получим [для упрощения процесса вычисления интегралов при расчетах значение ш, принято равным п/2 = 1,57 — вместо 1,5, соответствующего формуле (4.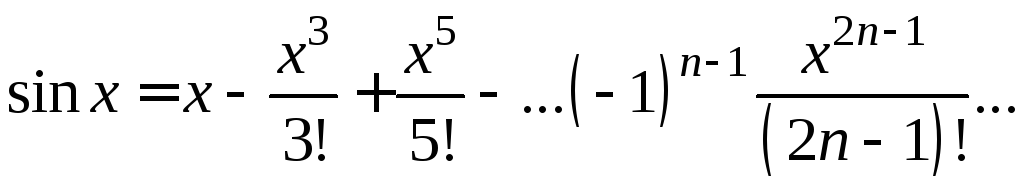 43)1, [c.147]
43)1, [c.147]
Для сравнения остановимся вначале на вычислении вторых вертикальных производных на исходном уровне задания аномалий Я = 0. Частотную характеристику вычислительной схемы этого преобразования в случае двухмерных аномалий получим, разлагая функцию со на интервале (О, Шг) в ряды косинусов вида (2.18) [c.155]
Выражения для 5 и Ф значительно упрощаются, если в (111.52) экспоненциальную зависимость и косинус разложить в ряд и получающиеся при этом мнимые члены отбросить. [c.59]
Определим функцию рассеяния f следующим образом f (т)) йц — доля всех рассеивающих соударений, которые приводят к рассеянию на такие углы в системе С), косинусы которых попадают в интервал между значениями т] и T]-f Т1 , и представим ее в впде ряда [c.53]
Решение в виде ряда получается разложением О в ряд Фурье по косинусам [c.515]
Находят приближенное значение корня этого уравнения, предполагая, что хЯо[c. 165]
165]
Известно, что любую периодическую функцию можно представить в виде ряда Фурье, т. е. бесконечного ряда синусов и (или) косинусов [c.55]
С точки зрения подобной возможности следует оценить и остальные формы точного решения основного интегрального уравнения. Нетрудно видеть, что в этом случае наиболее неудобным является решение [53], а также некоторое видоизменение этого решения, приводимое Темкиным и Левичем (см. формулу [22] их стать ), поскольку интегралы Фурье содержат расходящуюся амплитуду — гиперболический синус или косинус. Благодаря последнему обстоятельству очевидно, что утверждение Темкина и Левича (конец 2 их работы) о практической возможности приближенной замены этого интеграла Фурье соответствующими рядами Фурье не выдерживает критики. [c.293]
Предварительные замечания. Для полного описания более или менее произвольной функции нункоэффициенты разложения в ряд Тейлора, коэффициенты разложения функции в ряд Фурье по синусам и косинусам, значения непрерывной функции во всех рациональных точках и т. п.). Однако при решении задач с помощью ЭВМ имеют дело только с конечными совокупностями чисел, поэтому возникает необходимость приближенно охарактеризовать функцию конечным набором чисел. [c.16]
п.). Однако при решении задач с помощью ЭВМ имеют дело только с конечными совокупностями чисел, поэтому возникает необходимость приближенно охарактеризовать функцию конечным набором чисел. [c.16]
Если /(л) — четная функция, т. е. если/(д ) = /(—(рис. Х-1), то она разлагается в ряд по одним только косинусам [c.273]
Тригонометрический ряд может состоять только нэ косинусов или же только из синусов угла х, выраженного в радианах. Для доказательства справедливости этого положения напишем [c.573]
Если f х) — четная функция, т. е. если f (х) = f —х) (рис. Х1П-2), то она может быть разложена в ряд по одним только косинусам [c.398]
Если функция задана лишь на промежутке О х л, то приведенные выше соображения позволяют по нашему выбору разлагать данную функцию в ряд, содержащий только одни синусы или одни косинусы. Если желателен ряд с косинусами, то функция определяется в интервале от —я до О так, чтобы было f (—х) = f (х) тогда коэффициенты определяются из формул (28). Если желателен ряд с синусами, то функция определяется так, чтобы было [c.399]
Если желателен ряд с синусами, то функция определяется так, чтобы было [c.399]
Нетрудно показать, что выражение, стоящее а скобках правой части уравнения (4.13), есть разложения в ряд Фурье по косинуса.м функции [c.181]
В опытах по рассеянию молекулярных пучков на чистых поверхностях в ряде случаев наблюдалась повышенная доля зеркально отраженных молекул [6, 7]. Мы рас- сматриваем системы, в которых время контакта с поверхностью достаточно, чтобы выполнялся закон косинуса. [c.438]
Равенство (3.40) формально является разложением единицы (равномерное начальное распределение температуры) в ряд Фурье по косинусам. [c.225]
Разложим косинус в ряд Тэйлора с остаточным членом [c.123]
В ОДНИХ местах и меньшей в других. Как и любую периодическую функцию, это распределение можно представить в виде суммы синусов и косинусов (ряд Фурье), и коэффициенты при членах этого ряда оказываются равными отдельным структурным факторам, поделенным на объем элементарной ячейки. Используя предварительный набор структурных факторов, можно вычислить, таким образом, электронную плотность р(х, у, г) в зависимости от положения в кристалле. Эти вычисления довольно трудоемки, и часто предпочитают, особенно на первых стадиях структурного исследования, рассчитывать двумерные синтезы Фурье, дающие р(х, у) и т. д. Величины р(х, у) представляются в виде контурных карт, изображающих проекции электронной плотности на выбранную плоскость кристалла. Если какие-либо молекулы расположены более или менее параллельно рассматриваемой плоскости, то из проекции довольно точно можно определить положение атомов таких молекул. Положения атомов, выведенные таким путем из нескольких проекций электронной плотности, могут использоваться теперь для получения лучшего соответствия с наблюдаемыми интенсивностями, и затем строятся новые синтезы Фурье. Несколько повторений такой операции приводят, наконец, к наилучшему возможному набору параметров для исследуемой структуры. Карта электронной плотности приведена в приложении на рис.
Используя предварительный набор структурных факторов, можно вычислить, таким образом, электронную плотность р(х, у, г) в зависимости от положения в кристалле. Эти вычисления довольно трудоемки, и часто предпочитают, особенно на первых стадиях структурного исследования, рассчитывать двумерные синтезы Фурье, дающие р(х, у) и т. д. Величины р(х, у) представляются в виде контурных карт, изображающих проекции электронной плотности на выбранную плоскость кристалла. Если какие-либо молекулы расположены более или менее параллельно рассматриваемой плоскости, то из проекции довольно точно можно определить положение атомов таких молекул. Положения атомов, выведенные таким путем из нескольких проекций электронной плотности, могут использоваться теперь для получения лучшего соответствия с наблюдаемыми интенсивностями, и затем строятся новые синтезы Фурье. Несколько повторений такой операции приводят, наконец, к наилучшему возможному набору параметров для исследуемой структуры. Карта электронной плотности приведена в приложении на рис. 17. [c.315]
17. [c.315]
Однако расчет связан с принятием ряда допущений поток газа свободномолекулярный и равномерно распределен по всей входной поверхности экрана, вероятность попадания молекул в единицу телесного угла пропорциональна косинусу угла падения молекул. Молекулы, сталкивающиеся с поверхностью, отражаются диффузно. При вычислении коэффициента пропускания теплового излучения используются полученные при каждом соударении с поверхностями экранов доли молекулярных потоков. Это возможно потому, что законы отражения тепловых и [c.140]
Таким образом, если функция четная, то ее ряд Фурье (9) содержит только косинусы, а если нечетная — только синусы. Говорят, что функция разлагается в неполный ряд по косинусам или соответственно по синусам. [c.192]
Выражение для Ах» с достаточным приближением можно разложить в ряд Фурье по косинусам. [c.121]
Таким образом, с увеличением времени несимметричные компоненты первоначального распределения фо (ж) (выраженные через синусы) уменьшаются более быстро, чем симметричные компоненты (содержащие косинусы). Из этого можно сделать следующий вывод неза1шспмо от начальной формы распределения потока в последующие моменты времени распределение становится все более симметричным, если, конечно, отсутствуют дальнейшие изменения в ядерных характеристиках системы. Этот результат является следствием предположения, что делящееся вещество равномерно распределено по всему объему размножающей сферы, т. е. 2, не зависит от X. Существует еще одно важное следствие, которое может быть выведено из выражения (5.119), а именно всегда существует один член ряда (5.119), который преобладает над другими, и с увеличением времени I этот член один дает все более точную аппроксимацию всего ряда. Докажем это путем следующих рассуждений рассмотрим величину которую запишем в форме [c.143]
Из этого можно сделать следующий вывод неза1шспмо от начальной формы распределения потока в последующие моменты времени распределение становится все более симметричным, если, конечно, отсутствуют дальнейшие изменения в ядерных характеристиках системы. Этот результат является следствием предположения, что делящееся вещество равномерно распределено по всему объему размножающей сферы, т. е. 2, не зависит от X. Существует еще одно важное следствие, которое может быть выведено из выражения (5.119), а именно всегда существует один член ряда (5.119), который преобладает над другими, и с увеличением времени I этот член один дает все более точную аппроксимацию всего ряда. Докажем это путем следующих рассуждений рассмотрим величину которую запишем в форме [c.143]
Выражению (IX—28) для электростатической составляющей расклинивающего давления. можно придать следующий наглядный физический смысл. В соответств.ии с (IX—27), первое слагаемое в нем представляет собой осмотическое давление ионов в центре зазора, а второе — осмотическое давление в объеме диспероионной среды. Можно поэтому сказать, что расклинивающее давление равно разности осмотических давлений, под действием которой среда стремятся затечь в прослойку, раоклипивая ее. При малых зргачеииях ф(/г/2) разложение гиперболического косинуса в ряд сЬ [c.258]
Можно поэтому сказать, что расклинивающее давление равно разности осмотических давлений, под действием которой среда стремятся затечь в прослойку, раоклипивая ее. При малых зргачеииях ф(/г/2) разложение гиперболического косинуса в ряд сЬ [c.258]
Цисман [20] предложил в качестве характеристики поверхностной энергии полимеров использовать значения так называемого критического поверхностного натяжения. Эта величина определяется путем экстраполяции зависимости косинуса краевого угла смачивания поверхности os 6 жидкостями с различным поверхностным натяжением (а) от а к значению os 0 = 1. Ряд авторов отождествляет эту величину с собственно поверхностным натяжением твердого тела [23, 24]. Эти представления исходят из уравнений Юнга [c.312]
При п > п.1 спектральная функция Рг п) практически равна нулю, и, следовательно, если ограничиться малыми временами, например /[c.128]
ЧТО при 2а Ф d уравнение (132) значительно усложняется можно, однако, получить приближенные выражения, полагая 2ald) = 1 б, причем в области интегрирования б 1 и 2/г 1. Синусы и косинусы при этом представляются в виде степенных рядов. Выкладки мы предлагаем читателям в качестве упражнения. [c.165]
Синусы и косинусы при этом представляются в виде степенных рядов. Выкладки мы предлагаем читателям в качестве упражнения. [c.165]
Калейдоскоп формул для пи
Калейдоскоп формул для пи«…я считал, что есть две математики — алгебраическая и геометрическая, и что геометрическая математика принципиально “трансцендентна” для алгебраической. Возьмите, например, формулу длины окружности — там есть “геометрическое” число $\pi$. Или, скажем, синус — он определяется чисто геометрически.
Когда я обнаружил, что синус можно записать алгебраически в виде ряда, барьер обрушился, математика стала единой.»
— из интервью И. М. Гельфанда
«Калейдоскоп» ниже состоит из нескольких «алгебраических» формул для $\pi$ с краткими комментариями. Он также опубликован (с сокращениями) в журнале «Квант» (№5 за 2020 год).
1. Формула Виета
Одна из первых алгебраических формул для $\pi$ — это открытое в XVI веке Виетом бесконечное произведение
$$
\frac\pi2=\frac2{\sqrt2}\cdot\frac2{\sqrt{2+\sqrt2}}\cdot\frac2{\sqrt{2+\sqrt{2+\sqrt2}}}\cdot\ldots
$$
Это равенство не очень сложно доказать. 2$ (последнее равенство — это, по сути, основная теорема арифметики).
Более серьезное обсуждение вопроса можно найти, например, в книге «Введение в теорию чисел» Харди и Райта.
2$ (последнее равенство — это, по сути, основная теорема арифметики).
Более серьезное обсуждение вопроса можно найти, например, в книге «Введение в теорию чисел» Харди и Райта.
4. Формула Валлиса
Если подставить $x=\pi/2$ в разложение Эйлера синуса в бесконечное произведение, то получается равенство $$ \frac\pi2= \frac{2\cdot2\cdot4\cdot4\cdot6\cdot6\cdot\ldots}{1\cdot3\cdot3\cdot5\cdot5\cdot7\cdot\ldots} $$ Впрочем, Джон Валлис нашел эту формулу уже в середине XVII века, почти за 100 лет до формулы Эйлера, вычисляя некоторые интегралы.
В упоминавшейся выше статье Ягломов при помощи элементарной тригонометрии доказывается и формула Валлиса. А J. Wästlund нашел и доказательство (в духе «геометрического суммирования»), непосредственно связывающее произведение Валлиса с площадью круга — см. его статью (AMM, 2007) или лекцию Д. Кнута.
При помощи формулы Валлиса можно доказать, что если подкинуть монету $2n$ раз, то вероятность того, что орлов и решек выпадет в точности поровну, приблизительно равна $1/\sqrt{\pi n}$. наверх
наверх
Как разложить функцию в ряд Фурье
Разложение функций в ряды Фурье используется достаточно часто, поскольку в таком виде их удобно дифференцировать, интегрировать, использовать сдвиг функции по аргументу, а также свёртку функций. Несмотря на то, что процедура разложения функции в ряд Фурье даже в самом простом случае может быть достаточно трудоёмкой, система Вольфрам Альфа, как правило, легко справляется с этой задачей.Ряды Фурье представляются в тригонометрической и экспоненциальной (комплексной) форме:
В первом варианте в качестве базиса разложения используется система синусов и косинусов. Но при работе с рядами Фурье вместо них бывает удобнее использовать экспоненты мнимого аргумента. Видимо поэтому, Вольфрам Альфа отдает предпочтение второму варианту.
Самый простой способ разложить функцию в ряд Фурье — отправить в Вольфрам Альфа запрос вида Fourier series [функция, аргумент, количество членов ряда]. Например,
В полученном результате, как и требуется, представлены члены разложения до 5-го номера включительно; коэффициенты при сопряженных степенях экспоненты являются комплексно-сопряженными числами.
 2+t]; зависит от того, поставите ли вы между словом «Fourier» и скобкой пробел или нет.
2+t]; зависит от того, поставите ли вы между словом «Fourier» и скобкой пробел или нет.Если в запросе Fourier series не указывать явно количество членов разложения n, то система Вольфрам Альфа по умолчанию выводит четыре варианта для значений n от 0 до 3, и только для комплексной формы ряда Фурье:
Дополнительные варианты разложения для n больше 3 можно получить тут же с помощью кнопки «More». Но это относится только к графическому представлению результатов:
Таким образом, чтобы получить разложение функции в тригонометрический ряд Фурье, нужно в запросе Fourier series явно указывать количество членов разложения.
Что делать, если стоит задача найти не разложение в ряд Фурье, а коэффициенты ряда Фурье?
Прежде всего, можно использовать запрос FourierCoefficient[выражение, аргумент, n], по которому система Вольфрам Альфа выводит n-й коэффициент разложения выражения в комплексный ряд Фурье.
Например, 5-й коэффициент разложения выражения (t^2+t) в ряд Фурье можно получить так:
FourierCoefficient[t^2+t, t, 5]
Если же при не указывать явно n, то данный запрос выведет общее выражение для n-го коэффициента ряда Фурье данного выражения:
FourierCoefficient[t^2+t, t, n]
Кроме этого, Вольфрам Альфа тут же выводит также таблицу коэффициентов комплексного ряда Фурье (до 15-го члена включительно, если нажать «More»):
В этом кратком обзоре я не упомянул, как разложить функцию в ряд Фурье по синусам и косинусам или как использовать калькулятор рядов Фурье системы Вольфрам Альфа, а также ничего не сказал о двумерных рядах Фурье. Все это — темы моих будущих постов. Следите за блогом.
Все это — темы моих будущих постов. Следите за блогом.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
4.4: Ряды синусов и косинусов
4.4.1: Нечетные и четные периодические функции
Вы, наверное, заметили, что нечетная функция не имеет членов косинуса в ряду Фурье, а четная функция не имеет членов синуса в ряду Фурье. . Это наблюдение не случайно. Рассмотрим подробнее четную и нечетную периодическую функцию.
Напомним, что функция \ (f (t) \) нечетная, если \ (f (-t) = -f (t) \). Функция \ (f (t) \) даже если \ (f (-t) = f (t) \). Например, \ (\ cos {(nt)} \) четное, а \ (\ sin {(nt)} \) нечетное.k \) четно, если \ (k \) четно, и нечетно, если \ (k \) нечетно.
Упражнение \ (\ PageIndex {1} \):
Возьмите две функции \ (f (t) \) и \ (g (t) \) и определите их произведение \ (h (t) = f (t) \ , g (t) \). а) Предположим, что оба нечетные, нечетно или четно \ (h (t) \)? б) Предположим, что один четный, а другой нечетный, является ли \ (h (t) \) нечетным или четным? в) Предположим, что оба четны, является ли \ (h (t) \) нечетным или четным?
Если \ (f (t) \) и \ (g (t) \) оба нечетны, то \ (f (t) + g (t) \) нечетно. Аналогично для четных функций. С другой стороны, если \ (f (t) \) нечетно, а \ (g (t) \) четно, то мы ничего не можем сказать о сумме \ (f (t) + g (t) \).Фактически, ряд Фурье любой функции представляет собой сумму нечетной (синусоидальные) и четной (косинусные) функций.
Аналогично для четных функций. С другой стороны, если \ (f (t) \) нечетно, а \ (g (t) \) четно, то мы ничего не можем сказать о сумме \ (f (t) + g (t) \).Фактически, ряд Фурье любой функции представляет собой сумму нечетной (синусоидальные) и четной (косинусные) функций.
В этом разделе мы рассматриваем нечетные и четные периодические функции. Ранее мы определили \ (2L \) — периодическое расширение функции, определенной на интервале \ ([- L, L] \). Иногда нас интересует только функция в диапазоне \ ([0, L] \), и было бы удобно иметь нечетную (соответственно четную) функцию. Если функция нечетная (соответственно четная), все члены косинуса (соответственно синуса) исчезнут.Что мы сделаем, так это возьмем нечетное (соответственно четное) расширение функции на \ ([- L, L] \), а затем продолжим периодически до \ (2L \) — периодической функции.
Возьмем функцию \ (f (t) \), определенную на \ ([0, L] \). На \ ((- L, L] \) определите функции
\ [F _ {\ rm {odd}} (t) \ overset {\ rm {def}} {=} \ left \ {\ begin {array} {ccc} f (t) & \ rm {if} & 0 \ leq t \ leq L, \\ -f (-t) & \ rm {if} & -L Расширить \ (F_ {odd} (t) \) и \ (F_ {even} (t) \) до \ (2L \) — периодичности. Тогда \ (F_ {odd} (t) \) называется нечетным периодическим расширением \ (f (t) \), а \ (F_ {even} (t) \) называется четным периодическим расширением \ (f (t) \). Упражнение \ (\ PageIndex {2} \): Убедитесь, что \ (F_ {odd} (t) \) нечетное, а \ (F_ {even} (t) \) четное. Пример \ (\ PageIndex {1} \): Возьмем функцию \ (f (t) = t (1-t) \), определенную на \ ([0,1] \). На рис. 4.11 показаны графики нечетного и четного расширений \ (f (t) \).L f (t) \ text {cos} \ left (\ frac {n \ pi} {L} t \ right) dt = 0. \] То есть нет косинусных членов в ряду Фурье нечетного функция. Интеграл равен нулю, потому что \ (f (t) \ cos {(\ frac {n \ pi} {L} t)} \) является нечетной функцией (произведение нечетной и четной функций является нечетным), а интеграл от нечетная функция на симметричном интервале всегда равна нулю. Интересным следствием является то, что коэффициенты ряда Фурье нечетной (или четной) функции можно вычислить простым интегрированием по полуинтервалу \ ([0, L] \). Следовательно, мы можем вычислить ряд Фурье нечетного (или четного) расширения функции, вычислив определенные интегралы по интервалу, в котором определена исходная функция. Теорема 4.4.1. Пусть \ (f (t) \) — кусочно-гладкая функция, определенная на \ ([0, L] \).L f (t) g (t) \, dt, \] и следуя процедуре п. 4.2. Эта точка зрения полезна, поскольку мы обычно используем конкретный ряд, возникший из-за того, что наш основной вопрос привел к определенной проблеме собственных значений. Упражнение \ (\ PageIndex {3} \): a) Вычислите производную четного расширения \ (f (t) \), указанного выше, и убедитесь, что у нее есть скачкообразные разрывы. Используйте фактическое определение \ (f (t) \), а не его косинусный ряд! б) Почему производная четного расширения \ (f (t) \) является нечетным расширением \ (f ‘(t) \)? Ряды Фурье связаны с краевыми задачами, которые мы изучали ранее.Рассмотрим эту связь подробнее. Предположим, у нас есть краевая задача для \ (0 \ [x » (t) + \ lambda x (t) = f (t), \] для граничных условий Дирихле \ (x (0) = 0, x (L) = 0 \ ). Используя альтернативу Фредгольма (теорема 4.1.2), мы отмечаем, что до тех пор, пока \ (\ lambda \) является , а не собственным значением основной однородной задачи, существует единственное решение. Давайте посмотрим, как работает этот метод на примерах. Пример \ (\ PageIndex {3} \): Возьмем краевую задачу для \ (0 \ [x » (t) + 2x (t) = f (t) , \] , где \ (f (t) = t \) на \ (0 Обратите внимание, что b n только зависит от значений f (x)
на полуинтервале $ [0, a] $, а не на $ [- a, a] $. Александр из Гдыни, двуязычная школа
Школа № 3, Польша использовала свойства синусоидальной функции для
найти полиномиальное приближение. Как известно, полиномы — одна из самых гибких функций.
и, следовательно, могут иметь самые разные формы.3 \ более 6} $. Чтобы получить приближение $ \ sin x $, используя многочлены высших
степеней, мы должны помнить, что коэффициенты при четных степенях
должен быть равен 0. По этой причине следующая степень
полином, который можно здесь использовать, — 5-й. Андрей из Румынии использовал Taylor
серии и нарисовали графики, чтобы показать полиномиальные приближения
. Функция sin (x) представлена белым цветом, первый порядок
многочлен красным, третий — голубым, пятый — зеленым и
седьмой желтым. Можно заметить, что точность лучше
и лучше. По мере увеличения порядка полинома точность
увеличивается. Примечательно, что, используя только до седьмого порядка
полином, я получаю очень хорошее приближение функции.6 \ over 6!} + … $$ Функция выделена синим цветом, полином второго порядка фиолетовым,
четвертый — белым и шестой — красным. Я вижу, что шестой порядок
многочлен — довольно хорошее приближение в целом
интервал. Поскольку cos периодичен, интервал $ [- \ pi, \ pi] $ достаточен, и
более того, поскольку cos (x) четно, достаточно $ [0, \ pi] $. Для, $ \ log (1 + x) $, я считаю логарифм по основанию e. Здесь я
получим следующее разложение в ряд Маклаурина: $$ \ log (1 + x) = x —
{x ^ 2 \ over 2} + {x ^ 3 \ over 3} — {x ^ 4 \ over 4} + {x ^ 5 \ over 5}. Чтобы получить разложение в ряд Фурье по синусам для $ f (x) $, коэффициенты $ a_n $ должны равняться нулю (см. Ниже). Итак, пусть $ g (x) $ будет нечетной функцией , расширяющей $ f (x) $ до интервала $ [- \ pi, 0 [$, определенного в \ begin {уравнение *}
g (x) = \ left \ {
\ begin {array} {l}
\ phantom {-} f (x) & = \ phantom {-} \ dfrac {\ pi -x} {2}, \ qquad \ phantom {-} 0 \ leq x \ leq \ pi \\
\\
-f (-x) & = \ color {blue} {- \ dfrac {\ pi + x} {2}} \ qquad — \ pi \ leq x <0
\ end {массив}
\верно.
\ end {уравнение *} , график которого в $ [\ pi, \ pi] $ показан на следующем рисунке $$ g (x) = f (x) = \ frac {\ pi -x} {2}, x \ in [0, \ pi [; \; g (x) = — f (-x) = \ color {blue} {- \ frac {\ pi + x} {2}}, x \ in [- \ pi, 0] $$ Мы знаем, что разложение в тригонометрический ряд Фурье для $ g (x) $ в
интервал $ \ left [- \ pi, \ pi \ right] $ равен \ begin {уравнение *}
\ frac {a_ {0}} {2} + \ sum_ {n = 1} ^ {\ infty} \ left (a_ {n} \ cos (nx) + b_ {n} \ sin (nx) \ right),
\ end {уравнение *}
где коэффициенты — интегралы
\ begin {eqnarray *}
a_ {n} & = & \ frac {1} {\ pi} \ int _ {- \ pi} ^ {\ pi} g (x) \ cos (nx) \, dx \ qquad
п = 0,1,2, \ ldots, \\
b_ {n} & = & \ frac {1} {\ pi} \ int _ {- \ pi} ^ {\ pi} g (x) \ sin (nx) \, dx \ qquad
п = 1,2,3, \ ldots. Замечание . Для ряда косинусов Фурье нам нужно будет расширить $ f (x) $ до функции и даже , потому что тогда $ b_n $ исчезнет. Напомним, что ряд Фурье f ( x ) определяется как У нас есть следующий результат: Теорема. Эта теорема помогает определить ряд Фурье для функций, определенных только на интервале.
Основная идея — распространить эти функции на интервал а затем воспользуйтесь определением ряда Фурье. Пусть f ( x ) — функция, определенная и интегрируемая на.
Набор Определение. Пусть f ( x ), f 1 ( x ) и f 2 ( x ), как определено выше. Пример. Найдите ряд косинусов Фурье для f ( x ) = x для . Пример. Найдите ряд синуса Фурье функции f ( x ) = 1 для . Пример. Найдите ряд Фурье-синус функции для . Частный случай 2 L -периодических функций. Аналогичным образом можно расширить определения синуса Фурье и косинуса. S.O.S MATH: Домашняя страница Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard. Автор : М.А.Хамси Ряд Тейлора используется для приближения функций. Снова ограничимся рассмотрением так называемой серии Маклорена.{(4)} \ left. \ Begin {matrix} \ end {matrix} \ right | _ {x = 0} = \ sin {0} = 0 Опять же, на 4-м шаге мы получаем начальную функцию и, следовательно, дальше мы получим производные в той же последовательности. Таким образом, мы имеем значения производных в следующей последовательности: 1,0, -1,0 и так далее. На этот раз четные степени x отсутствуют, так как нули стоят рядом с соответствующими членами. для х \ дюйм Р.n}, | x | <1 Этого достаточно для решения проблем, хотя, при необходимости, проверьте наличие дополнительных расширений общих функций. A Серия Маклорена — это способ представления определенных функций, включая синусоидальную функцию, с использованием бесконечной суммы целочисленных степеней x. В общем, серия Маклорена для функции f ( x ) выглядит так: Помните, символ Σ говорит нам, что мы складываем члены в соответствии с формулой справа от символа.Нижнее уравнение сообщает нам первое число, которое мы вводим для n , а верхнее число сообщает нам последнее число, которое мы вводим для n . Поскольку у нас вверху ∞, это бесконечный ряд или тот, в котором мы складываем бесконечное количество членов. Давайте разберем формулу справа от Σ. На этом этапе вы можете подумать, что больше нечего делать, чтобы найти серию Маклорена для греха ( x ). Однако, чтобы сделать серию более полезной, мы собираемся посмотреть, сможем ли мы найти закономерность в производных синусоидальной функции. Другими словами, чтобы помочь калькулятору использовать ряд Маклорена, мы собираемся посмотреть, сможем ли мы написать ряд Маклорена для синусоидальной функции без использования записи ƒ ( n ) (0).В следующей таблице показаны производные синуса с точностью до пятой. Посмотри, сможешь ли ты найти узор. Какой узор? Получается, что ƒ ( n ) (0) = ± 1, когда n нечетное, и 0, когда n четное. Упрощение дает следующее. Чтобы записать это с обозначением Σ, нам нужно будет найти образец для терминов, отличный от того, который использовался для его создания, поскольку все остальные степени x исчезли.Обратите внимание, что у нас есть только нечетные степени x и соответствующие нечетные числа внизу каждой дроби. Поскольку нечетные числа начинаются с 1 и увеличиваются на 2 с каждым членом, мы можем представить их в суммировании выражением 2 n + 1, где n — номер члена. Затем нам нужно представить, что термины чередуются между положительными и отрицательными. Мы можем сделать это, используя (-1) n , поскольку умножение -1 на себя поочередно дает 1 и -1. Таким образом, мы можем написать следующее. Возможно, вам интересно: «Если серия Маклорена — это бесконечная серия, как мой калькулятор ее использует? Разве не потребуется бесконечное количество времени, чтобы его использовать? » Потребовалось бы бесконечное количество времени, чтобы попытаться полностью вычислить значение ряда Маклорена в определенной точке. Чтобы избежать необходимости хранить тригонометрические таблицы, калькуляторы используют ряд Маклорена для вычисления значения sin ( x ). Ряд Маклорена для функции — это ряд, заданный следующим образом. Используя это определение ряда Маклорена, мы можем определить, что синусоидальная функция может быть представлена следующим образом. Интеграл от четной функции на симметричном интервале \ ([- L, L] \) равен удвоенному интегралу функции на интервале \ ([0, L] \). Функция \ (f (t) \ sin {(\ frac {n \ pi} {L} t)} \) является произведением двух нечетных функций и, следовательно, является четной.{\ infty} a_n \ cos {\ left (\ dfrac {n \ pi} {L} t \ right)}. \]
Интеграл от четной функции на симметричном интервале \ ([- L, L] \) равен удвоенному интегралу функции на интервале \ ([0, L] \). Функция \ (f (t) \ sin {(\ frac {n \ pi} {L} t)} \) является произведением двух нечетных функций и, следовательно, является четной.{\ infty} a_n \ cos {\ left (\ dfrac {n \ pi} {L} t \ right)}. \] 2 \) для \ (0 \ leq t \ leq \ pi \ ).2} {3} -4 \ cos {(t)} + \ cos {(2t)} — \ dfrac {4} {9} \ cos {(3t)} + \ cdots \]
2 \) для \ (0 \ leq t \ leq \ pi \ ).2} {3} -4 \ cos {(t)} + \ cos {(2t)} — \ dfrac {4} {9} \ cos {(3t)} + \ cdots \] 4.4.3 Приложение
 Обратите внимание, что собственные функции этой задачи на собственные значения — это функции \ (\ sin {\ left (\ frac {n \ pi} {L} t \ right)} \).Следовательно, чтобы найти решение, мы сначала находим ряд синусов Фурье для \ (f (t) \). Запишем \ (x \) также как ряд синусов, но с неизвестными коэффициентами. Подставляем ряд для \ (x \) в уравнение и решаем неизвестные коэффициенты. Если у нас есть граничные условия Неймана \ (x ‘(0) = 0 \) и \ (x’ (L) = 0 \), мы проделываем ту же процедуру, используя ряд косинусов.
Обратите внимание, что собственные функции этой задачи на собственные значения — это функции \ (\ sin {\ left (\ frac {n \ pi} {L} t \ right)} \).Следовательно, чтобы найти решение, мы сначала находим ряд синусов Фурье для \ (f (t) \). Запишем \ (x \) также как ряд синусов, но с неизвестными коэффициентами. Подставляем ряд для \ (x \) в уравнение и решаем неизвестные коэффициенты. Если у нас есть граничные условия Неймана \ (x ‘(0) = 0 \) и \ (x’ (L) = 0 \), мы проделываем ту же процедуру, используя ряд косинусов. \ pi \ big (\ frac {1} {2} (\ sin ((n + 1) x) + \ sin ((n-1) x) \ big) dx.2-1) \ pi} \ sin (2kx).
\] Обратите внимание, что эта серия
действительно только на $ [0, \ pi] $, где $ f (x) = \ cos (x) $ было
определенный. Пусть вас не смущает то, что косинус даже на $ [- \ pi, \ pi] $. В
sine серия происходит от нечетного расширения , $ f_ {odd} $, поскольку
определено выше.
\ pi \ big (\ frac {1} {2} (\ sin ((n + 1) x) + \ sin ((n-1) x) \ big) dx.2-1) \ pi} \ sin (2kx).
\] Обратите внимание, что эта серия
действительно только на $ [0, \ pi] $, где $ f (x) = \ cos (x) $ было
определенный. Пусть вас не смущает то, что косинус даже на $ [- \ pi, \ pi] $. В
sine серия происходит от нечетного расширения , $ f_ {odd} $, поскольку
определено выше. Приближение зданий для греха (x)
 {4k + 3} (x) & = — \ cos x}.7 \ over 7!} + … $$ Простейший метод проверки точности
расширение ряда должно представить на том же графике функцию
и его расширения разного порядка.
{4k + 3} (x) & = — \ cos x}.7 \ over 7!} + … $$ Простейший метод проверки точности
расширение ряда должно представить на том же графике функцию
и его расширения разного порядка.  5 \ over 160} 1.{k-1}} {2k-1} = \ frac {\ pi} {4} долл. США
5 \ over 160} 1.{k-1}} {2k-1} = \ frac {\ pi} {4} долл. США {\ infty} \ frac {1} {n} \ sin (nx), \ qquad 0 \ leq x \ leq
\Пи ,
\ end {уравнение *}
(синус-ряд Фурье для функции $ f (x) $ в
интервал $ \ left [0, \ pi \ right] $). Мы видим, что $ f (\ pi / 2) = \ pi / 4 $. Нам просто нужно подтвердить, что для $ x = \ pi / 2 $ эта последняя серия сводится к вашей. Действительно, поскольку
\ begin {уравнение *}
\ sin \ big (\ frac {n \ pi} {2} \ big) = \ left \ {
\ begin {array} {l}
1, \ qquad n = 1,5, \ ldots, 4k + 1, \ ldots \\
0, \ qquad n = 2,4, \ ldots, 2k + 2, \ ldots \ quad (k = 0,1,2, \ ldots) \\
-1, \ quad \; n = 3,5, \ ldots, 4k + 3, \ ldots,
\ end {массив}
\верно.{k-1}} {2k-1}.
\ end {уравнение *}
{\ infty} \ frac {1} {n} \ sin (nx), \ qquad 0 \ leq x \ leq
\Пи ,
\ end {уравнение *}
(синус-ряд Фурье для функции $ f (x) $ в
интервал $ \ left [0, \ pi \ right] $). Мы видим, что $ f (\ pi / 2) = \ pi / 4 $. Нам просто нужно подтвердить, что для $ x = \ pi / 2 $ эта последняя серия сводится к вашей. Действительно, поскольку
\ begin {уравнение *}
\ sin \ big (\ frac {n \ pi} {2} \ big) = \ left \ {
\ begin {array} {l}
1, \ qquad n = 1,5, \ ldots, 4k + 1, \ ldots \\
0, \ qquad n = 2,4, \ ldots, 2k + 2, \ ldots \ quad (k = 0,1,2, \ ldots) \\
-1, \ quad \; n = 3,5, \ ldots, 4k + 3, \ ldots,
\ end {массив}
\верно.{k-1}} {2k-1}.
\ end {уравнение *} по синусу и косинусу Фурье Серия
по синусу и косинусу Фурье
где 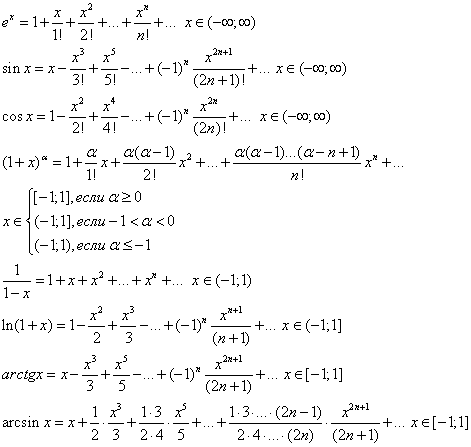 Пусть f ( x ) — функция, определенная и интегрируемая на интервале .
Пусть f ( x ) — функция, определенная и интегрируемая на интервале .
а также
а также
а также
Тогда f 1 нечетное, а f 2 четное. Легко проверить, что эти две функции определены и интегрируемы на и равны f ( x ) на.
Функция f 1 называется нечетным расширением из f ( x ),
, а f 2 называется его четным расширением .
где
где
Ответ. У нас есть
а также
Следовательно, мы имеем

Ответ. У нас есть
Следовательно
Ответ. У нас есть
что дает b 1 = 0 и для n > 1 получаем
Следовательно
Как мы делали для -периодических функций, мы можем определить ряды синуса и косинуса Фурье для функций, определенных на интервале [- L , L ].Во-первых, вспомним ряд Фурье f ( x )
где
для . 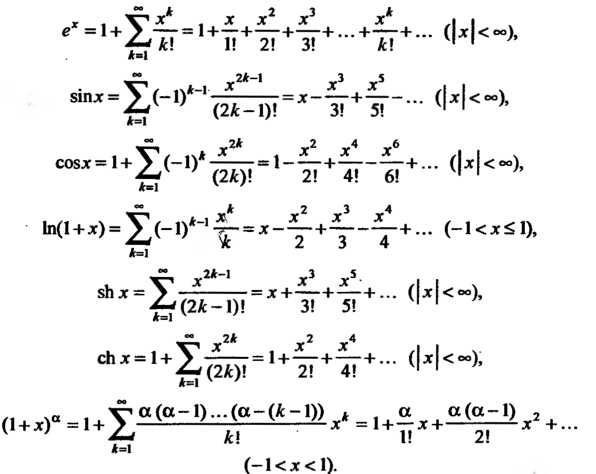 Кроме того, у нас есть
Кроме того, у нас есть
а также
Наконец, у нас есть
Наконец, у нас есть
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователя онлайн за последний час Построение ряда Тейлора для синуса и косинуса
 Прочтите нашу статью о сериале Тейлор, если вам нужно больше деталей. Как известно, для решения задач часто не хватает общей формулы. Нет необходимости изобретать велосипед каждый раз, когда вы сталкиваетесь с одной из общих функций. Более выгодный способ — запомнить несколько расширений и при необходимости использовать готовые формулы. Ранее мы рассматривали разложения Тейлора для экспоненты и логарифма (щелкните здесь, чтобы узнать подробности). Давайте продолжим и найдем формулы для синуса и косинуса.
Прочтите нашу статью о сериале Тейлор, если вам нужно больше деталей. Как известно, для решения задач часто не хватает общей формулы. Нет необходимости изобретать велосипед каждый раз, когда вы сталкиваетесь с одной из общих функций. Более выгодный способ — запомнить несколько расширений и при необходимости использовать готовые формулы. Ранее мы рассматривали разложения Тейлора для экспоненты и логарифма (щелкните здесь, чтобы узнать подробности). Давайте продолжим и найдем формулы для синуса и косинуса. Тригонометрические функции
 {2n + 1 }}
{2n + 1 }} В поисках серии Маклорена для греха (x)
Что такое серия Маклорена?
 Помните, что n ! означает, что мы умножаем все натуральные числа от 1 до на вместе. Так, например, 5! = 1 × 2 × 3 × 4 × 5. Затем ƒ ( n ) (0) представляет собой n -ю производную от ƒ, оцененную как 0.
Помните, что n ! означает, что мы умножаем все натуральные числа от 1 до на вместе. Так, например, 5! = 1 × 2 × 3 × 4 × 5. Затем ƒ ( n ) (0) представляет собой n -ю производную от ƒ, оцененную как 0. Вычисление серии Маклорена для греха (
x ) Таким образом, выписывая ряд Маклорена для sin (x), мы получаем следующее.
Таким образом, выписывая ряд Маклорена для sin (x), мы получаем следующее. Как калькулятор использует серию Маклорена?
 Вот почему ваш калькулятор не использует полную серию. Он использует только его часть. Количество используемых терминов может варьироваться от калькулятора к калькулятору, но поскольку калькуляторы могут очень быстро складывать, вычитать, умножать и делить, использование большого количества членов в ряду, даже до 100, очень выполнимо для калькулятора.Таким образом, значение, которое ваш калькулятор дает вам для синуса числа, на самом деле является приблизительным. Однако из-за природы ряда Маклорена это очень и очень точное приближение.
Вот почему ваш калькулятор не использует полную серию. Он использует только его часть. Количество используемых терминов может варьироваться от калькулятора к калькулятору, но поскольку калькуляторы могут очень быстро складывать, вычитать, умножать и делить, использование большого количества членов в ряду, даже до 100, очень выполнимо для калькулятора.Таким образом, значение, которое ваш калькулятор дает вам для синуса числа, на самом деле является приблизительным. Однако из-за природы ряда Маклорена это очень и очень точное приближение. Краткое содержание урока



 lambdify((x,), taylor_series)
lambdify((x,), taylor_series)
 ru
ru