Урок «Определение синуса, косинуса, тангенса и котангенса» | Презентация к уроку (алгебра, 9 класс) по теме:
Слайд 1
Информационно-проектный урок
Слайд 2
Тема: Определение синуса, косинуса, тангенса и котангенса.
Слайд 3
Цели урока: 1.Знать определение синуса, косинуса, тангенса и котангенса. 2.Уметь применять эти определения к решению примеров и задач. 3.Привитие творческой активности и самостоятель-ности
Слайд 4
План урока История развития тригонометрии. Повторение курса геометрии. Изучение нового материала. Закрепление
Слайд 5
Историческая справка тригонон Тригонометрия метрио (измерение треугольника)
Слайд 6
Древний Вавилон-умели предсказывать солнечные и лунные затмения. Древнегреческие учёные-составили таблицы хорд(первые тригонометрические таблицы) Учёные Индии и Ближнего Востока-положили начало радианной мере угла.
Слайд 7
Большой вклад в развитие тригонометрии внесли: Гиппарх Птолемей Франсуа Виет Эйлер Бернулли
Слайд 8
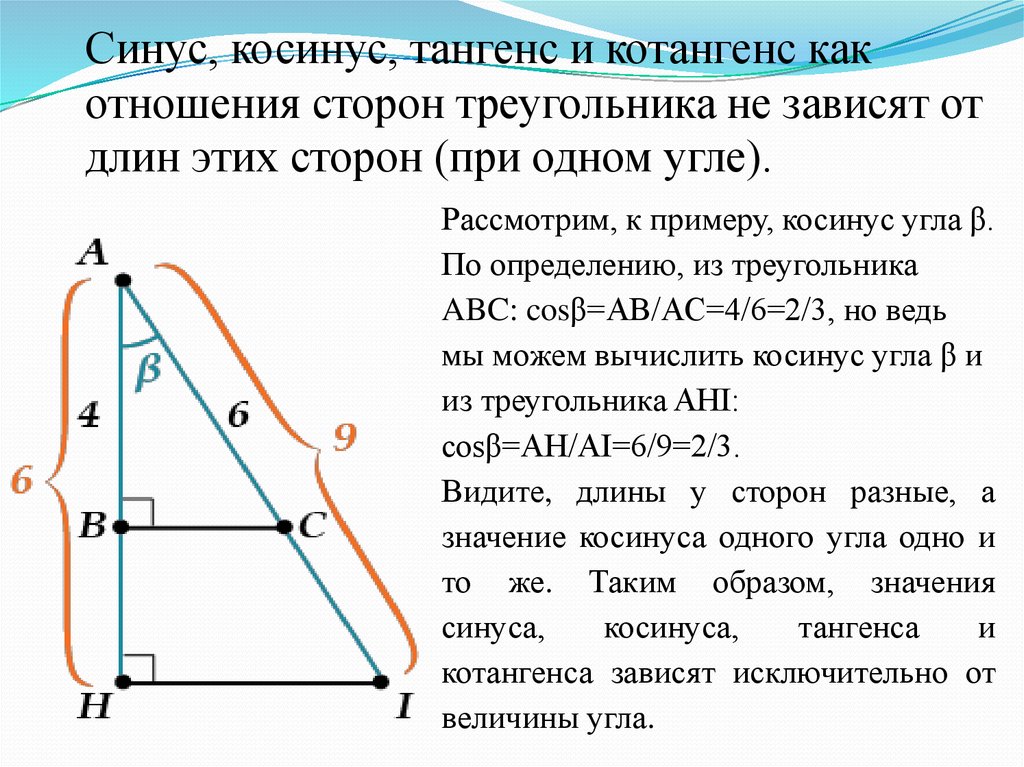
Повторение А sinC= COS C= tg C= В С ?
Слайд 9
Повторение Для единичной полуокружности y у SIN A = = Y R X COS A= = X R 0 ≤SIN A≤ 1 -1 ≤ COS A ≤1 х А В 1 -1 1
Слайд 10
Повторение Основное тригонометрическое тождество: SIN 2 X+COS 2 Х =1
Слайд 11
у х А О
Слайд 12
Угол поворота против часовой стрелки- положительный А О В У Х
Слайд 13
Угол поворота по часовой стрелке — отрицательный О х У А В
Слайд 14
Угол поворота Положительный Отрицательный В А А В 70 0 -70 0 Х У У Х o O
Слайд 15
Из курса геометрии известно: Мера угла в градусах выражается числом от 0 0 до 180 0
Слайд 16
Ответь на вопрос: Каким числом может выражаться в градусах угол поворота?
Слайд 17
В Ы В О Д: Угол поворота может выражаться в градусах каким угодно действительным числом от — ∞ до +∞
Слайд 18
Рассмотрим примеры 135 0 +360 0 n , n=0,1,-1,2,-2….
. 135 0 Х У У Х — 135 0 А В О В О А
Слайд 19
В Ы В О Д Существует бесконечно много углов поворота, при которых начальный радиус ОА переходит в радиус ОВ. В зависимости от того, в какой координатной четверти окажется радиус ОВ, угол α называют углом этой четверти.
Слайд 20
З А П О М Н И 0 0
Слайд 21
В ы в о д: Эти углы не относятся ни к какой четверти. 0 0 , ± 90 0 , ± 180 0 , ± 270 0 , ± 360 0 ….
Слайд 22
Углом какой четверти является угол β ,если: β =167 0 β =287 0 β = — 65 0
Слайд 23
Стр.153.- определение . y X Sin α = Cos= R R y X tg α = ctg α = X y
Слайд 24
Лабораторная работа
Слайд 25
В Ы В О Д: Синус, косинус, тангенс и котангенс не зависят от радиуса. Вычертите три окружности произвольного радиуса с центром в начале координат. Постройте начальный радиус ОА. Поверните начальный радиус на угол α =45 0 В каждом из случаев найдите SIN 45 0 . (смотри пример 1. стр.154.) Какой получился результат? Сделай вывод.
.
Слайд 26
Запомни Sin α , Cos α — определены при любом α . Почему?
Слайд 27
Стр.154 При каком α tg α не определён? Почему?
Слайд 28
sin α , cos α , tg α , ctg α – называют тригонометрическими функциями.
Слайд 29
Для единичной окружности: Область значения синуса и косинуса есть промежуток [ -1;1 ] Область значения тангенса и котангенса есть множество всех действительных чисел.
Слайд 30
Найти синус, косинус,тангенс и котангенс 270 0 Проверьте решение на стр.156
Слайд 31
Устно № 699 № 701
Слайд 32
Письменно № 705 Используй таблицу стр.155
Определение единичной окружности тригонометрических функций, триг. функции
Единичная окружность
Прежде чем узнать, что такое единичная окружность, полезно вспомнить, что такое числовая линия. Числовая линия — это прямая бесконечная линия с началом и единичной длиной. (OE – Единая длина, O – начало координат)
Что произойдет, если мы обернем нашу бесконечную линию вокруг окружности радиусом 1?
Каждая точка числовой прямой окажется на нашей окружности.
Каждой точке на нашей числовой прямой соответствует ровно одна точка на окружности. Этот круг называется единичным кругом. Единичная окружность — это окружность с радиусом 1. Важно, что радиус этой окружности равен 1.
Как вы знаете, на вашей числовой прямой есть положительные и отрицательные числа. Положительные числа (вверх от начала координат на картинке) воспроизводятся в положительной математической ориентации (против часовой стрелки), а отрицательные (вниз от начала координат) воспроизводятся в отрицательной математической ориентации (по часовой стрелке).
Давайте вспомним, что такое радианы. 1 радиан – это часть окружности, длина дуги которой равна радиусу. Одна целая окружность имеет $ 2 \pi$ радиан; одна половина круга имеет $\pi$ радиан и так далее.
Теперь, когда мы это вспомнили, давайте посмотрим на нашу картинку. Вы оборачиваете бесконечную линию вокруг круга. В какой-то момент вы начнете свой второй круг вокруг него, а когда вы снова завернете его, вы начнете третий и так до бесконечности.
Это означает, что бесконечно много точек с числовой прямой попадут в одни и те же места на единичной окружности.
Единица окружности радианы
Если ваша числовая линия отмечена радианами, она будет выглядеть так:
Во-первых, у вас есть обычная единичная окружность. В одной четверти круга $\frac{\pi}{2}$, в одной половине $\pi$, в трех четвертях $\frac{3 \pi}{2}$, а в одной целой $2 \пи$.
Что теперь, когда вы начнете следующий круг?
Вы снова в нуле, но теперь с 2π линии вокруг круга. Если вы добавите еще один $\frac{\pi}{2}$, это приведет вас к точке, где находится «старый» $\frac{\pi}{2}$, но теперь это значение будет $2\pi + \frac{\pi}{2} = \frac{5 \pi}{2}$. Если вы продолжите и добавите еще $\frac{\pi}{2}$, вы окажетесь в точке, где лежит «старое» π. Теперь эта точка будет равна $\frac{5 \pi}{2} + \frac{\pi}{2} = 3 \pi$. И ты продолжаешь в том же духе. 9{\circ}$ и так далее.
Разделив радианы на все меньшие и меньшие части, мы можем определить меру каждого угла.
Чаще всего используются углы 0, $\frac{\pi}{6}$, $\frac{\pi}{3}$, $\frac{\pi}{2}$ и так далее.
Вы видите здесь закономерность? Если вы наблюдаете только за первым и вторым квадрантом, вы заметите, что линии, перпендикулярные оси Y, которые проходят через $\frac{\pi}{3}$ и $\frac{2 \pi}{3}$, обрезаются. равные части оси Y. То же самое относится к $\frac{3 \pi}{4}$ и $\frac{\pi}{4}$, а также к $\frac{5 \pi}{6}$ и $\frac{\ пи{6}$.
Если вы посмотрите на первый и четвертый квадранты, вы заметите, что линии, перпендикулярные оси x $\frac{\pi}{6}$ и $\frac{11 \pi}{6}$, пересекаются от равной длины оси x, и так далее с другими углами. Это может помочь вам в их рисовании. Например, если вы получили задание нарисовать $\frac{5\pi}{6}$, вы можете просто нарисовать $\frac{\pi}{6}$ и перевести его во второй квадрант. Используя этот способ, вам нужно будет только запомнить углы в первом квадранте и перевести их.
Пример 1 : Найдите следующие углы на единичной окружности
Если у вас есть дробь, значение которой больше двух, это означает, что вы начинаете новый «круг» по кругу.
Когда вы имеете дело с такими значениями, вы должны применить процесс нахождения правильной меры угла. Это означает, что вы должны найти угол, который подходит для заданного угла, но на первом круге. Вы делаете это, вычитая с числом, кратным 2π.
Допустим, у вас есть $\frac{5 \pi}{2}$. $\frac{5\pi}{2}$ больше $2\pi$ на $\frac{\pi}{2}$. Это означает, что вы закончите первый круг и окажетесь в $\frac{\pi}{2}$.
Пример 2 : Найдите следующие углы на единичной окружности перед нашими значениями мы начинаем смотреть с нуля, но в противоположном направлении. Весь круг равен $2\pi$, а это означает, что $ -\frac{\pi}{4}$ будет иметь то же значение, что и $ 2 \pi – \frac{\pi}{4} = \frac{7 \pi}{4}$, $-\pi$ как $\pi$ и $-2 \pi$ как 0,
Базовая тригонометрия
Триггерная единичная окружность
Для каждой точки нашей единичной окружности мы хотим знать точную длину от начала координат до ее проекции на оси x и y.
Синус и косинус
Длина от начала координат до проекции точки на ось x называется косинусом , а длина от начала координат до проекции точки на ось y называется синусом .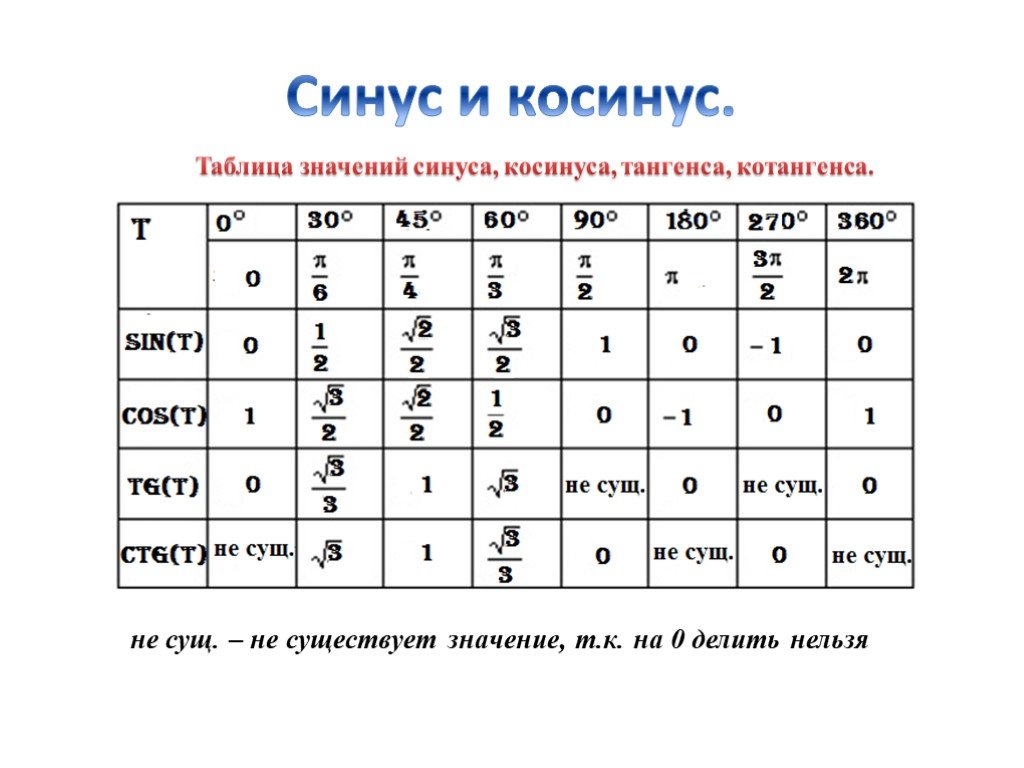
Функции синуса и косинуса — это функции, область определения которых представляет собой целое множество действительных чисел и область определения [-1, 1]. Их область значений — это множество действительных чисел между [-1, 1], потому что мы имеем дело с точками на единичной окружности, радиус которой равен 1,9.0005
Как найти угол, значения синуса и косинуса которого вам известны? Это очень просто. Если у вас есть значение синуса по умолчанию, сначала вы должны найти это значение на оси Y и провести параллельную линию от оси X через эту точку. Вы получите две точки на вашей единичной линии, которые вы соедините с началом координат. Два угла, одно плечо которых — эти линии, а второе — ось x, будут углами, которые вы ищете.
Если вам задано значение косинуса угла, вы просто найдете это значение по оси x, проведете параллельную линию от оси y через эту точку, соедините точки, которые вы получили на единичной окружности, и соедините их с началом координат. Два угла, одно плечо которых — эти линии, а второе — ось x, будут углами, которые вы ищете.
Пример 3 : Найдите углы, у которых $ sin(x) = 5$
d) $ cos(x) = 1$
Решение:
а)
б)
в) $ sin(x) = 5$. Где бы вы нарисовали свою пятёрку? Если бы вы следовали этим шагам, они вывели бы вас куда-то за пределы единичного круга. И где бы вы ни проводили параллели, ни одна из них не пересекает единичную окружность. Это из-за кодомена синуса и косинуса. Помните, что их значения могут быть только [-1,1].
г) Это просто. $ cos(x) = 1$. Это значение находится точно на числовой прямой и равно 0.
Тангенс и котангенс
Две другие очень важные тригонометрические функции называются тангенс и котангенс .
Это производные функции, но их не менее важно помнить.
Чтобы получить значение тангенса, сначала мы нарисуем линию, параллельную оси y, которая проходит через точку (1, 0).
Чтобы получить значение котангенса, сначала проведем прямую, параллельную оси x, которая проходит через точку (0, 1).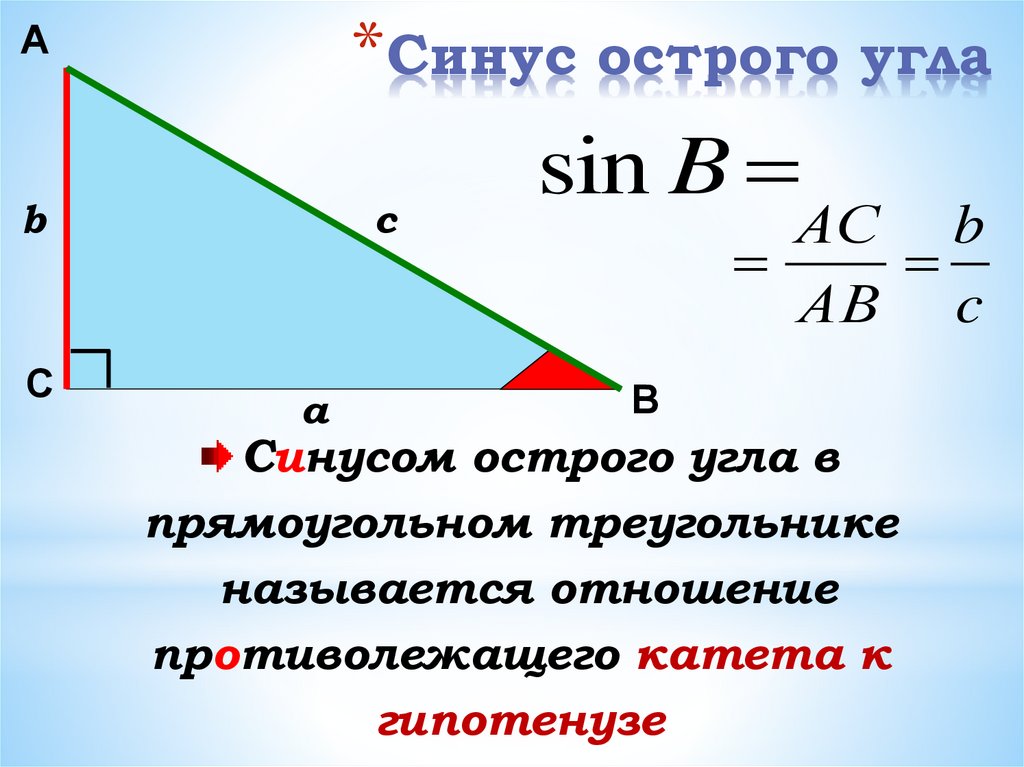
Затем мы проводим линию от начала координат до точки на единичной линии, значение которой мы ищем.
Получим два пересечения: одно с линией, перпендикулярной оси x, и второе с линией, перпендикулярной оси y.
Величина касательной в заданной нами точке равна длине от пересечения с прямой, перпендикулярной оси x и оси y. 9{-1}(a)}$ — значение функции арккотангенса, обратной функции ограниченной функции котангенса.
Теперь мы видим, что решением данного уравнения является: $x=\arccot( \frac{1}{2})$ + $k \pi , k \in \mathbf{Z}$.
Пример 5: Вычислите тангенс 60°.
Решение:
Поскольку мы знаем, что $tan(x) = \frac {sin(x)}{cos(x)}$, нам нужно знать только значения $sin(60°)$ и $ cos(60°)$.
Если мы посмотрим на единичный круг, то увидим, что $sin(60°)= \frac{\sqrt{3}}{2}$ и $cos(60°)= \frac{1}{2} $.
Теперь имеем:
$$tan(x) = \frac {sin(60°)}{cos(60°)} = \frac {\frac {\sqrt{3}}{2}}{\ frac{1}{2}}$$
$$=\frac{2 \cdot \sqrt{3}}{2}$$
$$=\sqrt{3}.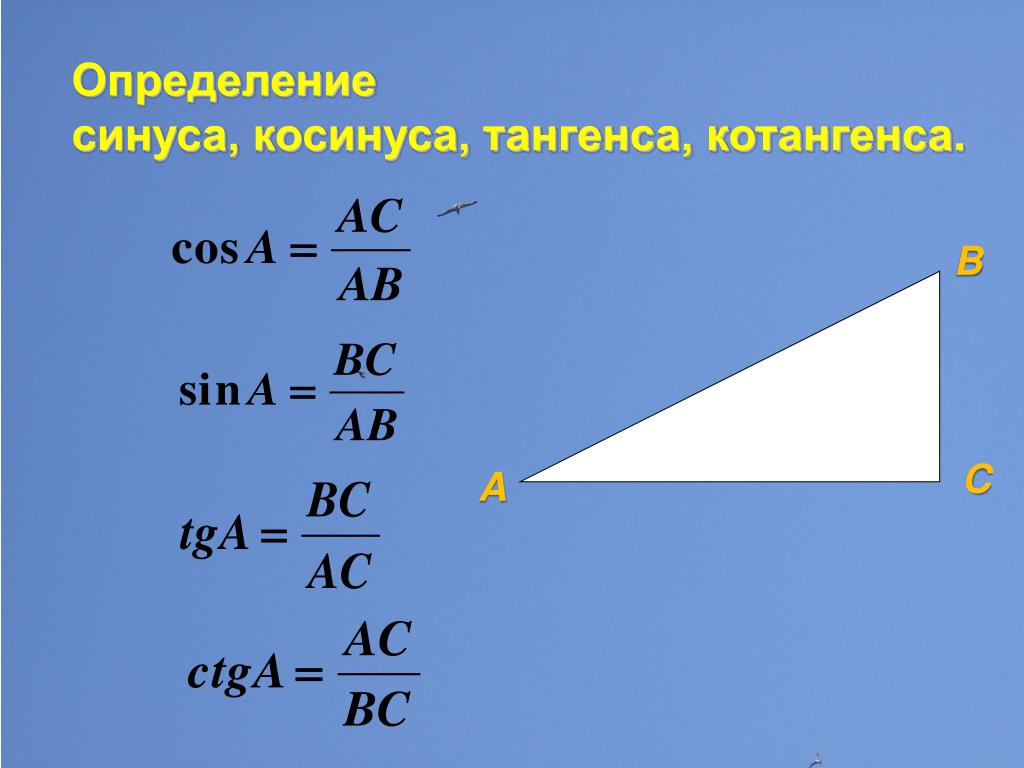
$$
Тригонометрические функции специальные углы
Специальные углы — это углы, которые имеют относительно простые значения. Следующую таблицу очень важно запомнить. Рассмотрим синус, косинус, тангенс и котангенс:
Этот урок может показаться немного сложным для запоминания, но на самом деле это не так. Вам нужно запомнить только первую строку. Cos противоположен синусу, а тангенс и котангенс являются производными от них, поэтому их всегда можно легко вычислить.
Как запомнить определения триггерных функций
Следующее руководство посвящено тому, как запомнить определения триггерных функций самым простым способом. То есть, не запоминая больше, чем необходимо. Это требует использования только трех определений, а затем некоторых общих тождеств, которые вам все равно нужно будет помнить при работе с задачами по тригонометрии. Итак, давайте посмотрим, как это работает!
реклама
Шаг 1: Запомните определения числа три.
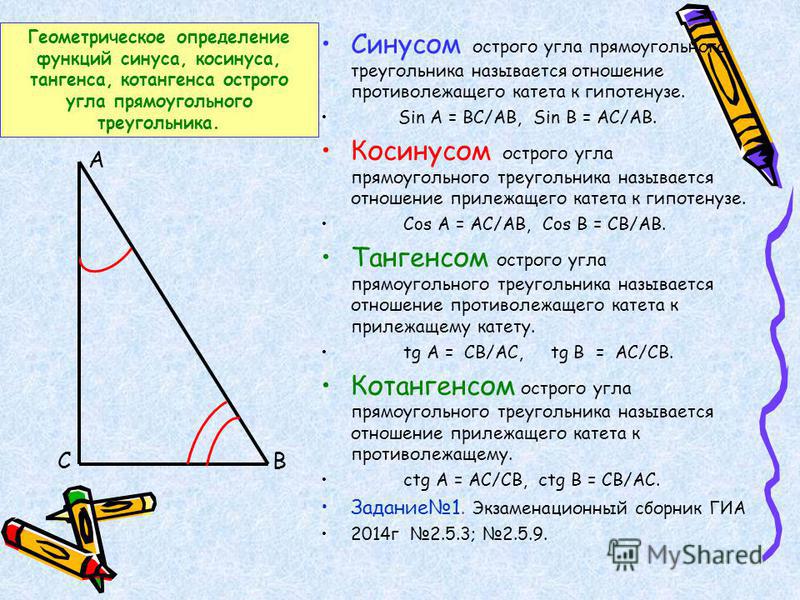Использование SohCahToaЕсли вы сможете произнести «SohCahToa» достаточное количество раз (произнесите его так, как оно пишется), то вы запомните определения синуса, косинуса и тангенса. Почему? Давайте посмотрим на этот дурацкий термин и посмотрим, что он вам говорит:
Soh
Soh — синус, противоположный гипотенузе
\(\ sin(\ theta) = \dfrac{\textrm{напротив}}{\textrm{гипотенуза}}\)
Cah
Cah – косинус, смежный по гипотенузе
\(\ cos (\ theta) = \ dfrac {\ textrm {смежный}} {\ textrm {гипотенуза}} \)
Тоа
Тоа – касательная, противоположная соседней
\(\ tan (\ theta) = \ dfrac {\ textrm {напротив}} {\ textrm {смежный}} \)
Поскольку эти три триггерные функции встречаются чаще всего, это будет очень полезно. Но как насчет других функций? Лучший способ запомнить их — работать с некоторыми общими идентичностями.
Шаг 2: Используйте взаимные тождества
Может показаться, что вы просто запоминаете больше материала здесь, но обычно вам все равно нужно знать эти тождества, так почему бы не сохранить место в мозгу и не использовать их для запоминания остальных определений ? Эти тождества:
\(\csc(\theta)=\dfrac{1}{\sin(\theta)}\)
\(\sec(\theta)=\dfrac{1}{\cos(\theta)}\)
\(\cot(\theta)=\dfrac{1}{\tan(\theta)}\)
Эти тождества говорят вам, что вы можете просто перевернуть определение синуса, косинуса и тангенса, чтобы получить определение косеканса, секанса и котангенса.
Итак:
\(\sin(\theta) = \dfrac{\textrm{напротив}}{\textrm{гипотенуза}} \rightarrow \csc(\theta) = \dfrac{\textrm{гипотенуза}}{\textrm{напротив}} \)
\(\cos(\theta) = \dfrac{\textrm{adjacent}}{\textrm{гипотенуза}} \rightarrow \sec(\theta) = \dfrac{\textrm{гипотенуза}}{\textrm{adjacent}} \)
\(\tan(\theta) = \dfrac{\textrm{напротив}}{\textrm{смежный}} \rightarrow \cot(\theta) = \dfrac{\textrm{смежный}}{\textrm{напротив}} \)
Теперь у вас есть определения всех 6 триггерных функций. Насколько это приятно?
Резюме
Если вы продолжите изучение руководств по тригонометрии Mathbootcamp, то увидите, что триггерные функции всегда записываются в этом порядке. Это связано с использованием этих тождеств для вычисления значений вместо механического запоминания каждого определения. На самом деле, возможность использовать эти тождества даже помогает позже с тем, как графически отображать функции, и иметь возможность легко идентифицировать такие вещи, как домен любой из функций.