Системы счисления формулы: Основы систем счисления / Хабр

Содержание

Система счисления. Позиционная система счисления.

Содержание:

Унарная система счисления
Непозиционная система счисления
Позиционная система счисления
Представление числа в позиционной системе счисления

Задумывались ли вы над тем, почему при сложении тех или иных чисел получается строго определённое число? А почему мы обходимся всего десятью цифрами? Странные вопросы… Дело в том, что мы привыкли проводить вычисления, используя всего одну и ту же систему счисления. Однако это было так не всегда.

Системой счисления принято называть знаковую систему, в которой были приняты определённые правила записи чисел. Знаки, с помощью которых записывают числа, мы называем цифрами, а их совокупность — алфавитом системы счисления.

Для любой системы счисления, цифры которые служат для обозначения чисел, называемые узловыми; остальные числа (алгоритмические) получаются в результате операций над узловыми числами.

В Древнем Вавилоне узловыми числами выступали 1,10,60;

Системы счисления отличаются друг от друга выбором узловых чисел и способами образования алгоритмических чисел. В информатике выделяют такие виды систем счисления, как:

унарная система;
непозиционная система;
позиционная система.

Унарная система

В самой древней и простой унарной системе счисления, для записи любых чисел использовался всего лишь один символ — в виде зарубки, выемки, узелка или камушка.

Чем больше зарубок — тем больше число. По сути, эта система является основой любого счёта. Унарная система, по-другому, ещё называется системой бирок.

Если вы думаете, что не пользуетесь этой системой счисления, тогда не считайте на пальцах!

Непозиционная система счисления

Для такой системы счисления количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.

Примерно в III тысячелетии до н.э. древние египтяне разработали десятичную непозиционную систему счисления, в которой для обозначения узловых чисел 1, 10, 100 использовались символы – иероглифы.

В большинстве непозиционных систем счисления новые числа образуются путём сложения узловых чисел.

Каноническим примером непозиционной системы счисления всегда приводится римская система счисления. В качестве узловых цифр здесь применялись заглавные буквы латинского алфавита:

I = 1,
V = 5,
X = 10,
L = 50,
C = 100,
D = 500,
M = 1000

Например, II = 1 + 1 = 2
здесь символ I обозначает единицу независимо от места в числе.

Однако римская система не может быть полностью непозиционной, так как меньшая цифра, которая стоящая слева перед большей, должна вычитаться из неё:

IV = 4, в то время как:
VI = 6

Непозиционной системой счисления являлась и кириллическая система счисления — система счисления, применяемая на территории Древней Руси до XVIII века, основанная на алфавитной записи чисел с использованием кириллицы.

Позиционная система счисления

В позиционной системе счисления, количественный эквивалент цифры как раз зависит от её положения в записи числа. Основание позиционной системы счисления соответствует количеству цифр, которые составляют её алфавит.

Основным примером позиционной системы счисления является десятичная система записи чисел, к которой мы все так уже привыкли с детства, и в которой производим все основные математические вычисления.

Алфавитом десятичной системы являются цифры от 0 до 9. Образование чисел в ней происходит следующим образом: значения цифр умножаются на их «веса» соответствующих разрядов, а затем все полученные значения складываются.

Числительными русского языка, такое значением хорошо отражается, к примеру: «пять-сот семь-десят два».

Основанием позиционной системы счисления является любое натуральное число q>1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0,1,…,q−1, каждое из которых записывается при помощи одного уникального символа; младшей цифрой всегда выступает 0.

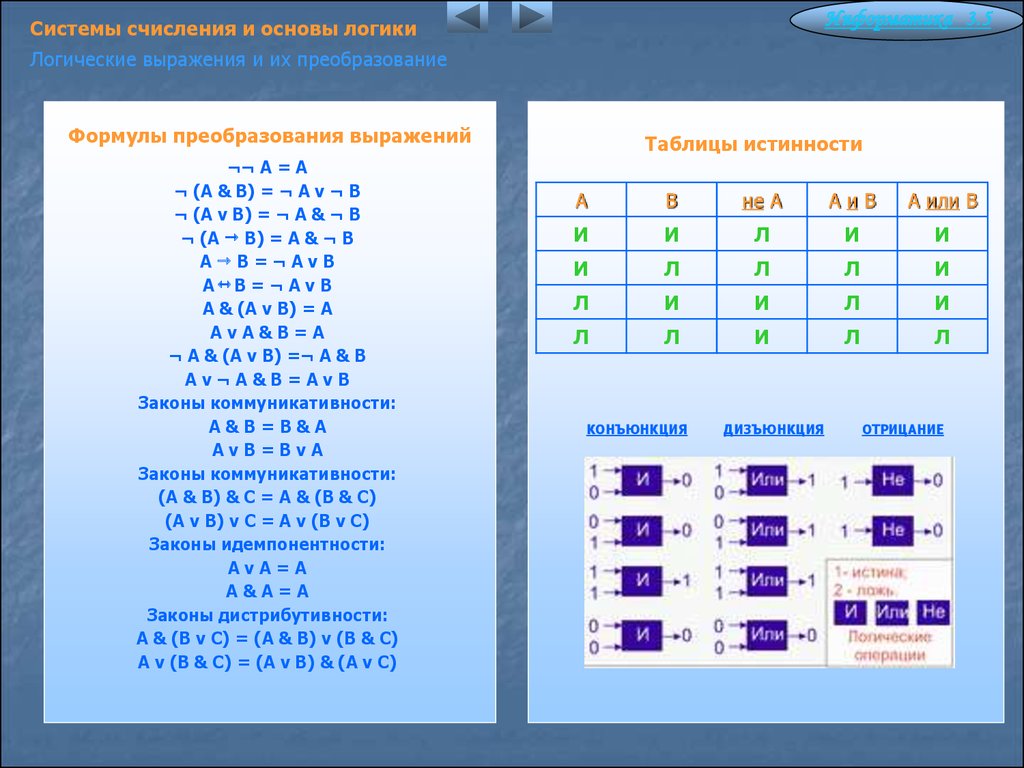
Основными преимуществами любой позиционной системы счисления являются простота выполнения арифметических операций и небольшое количество символов, используемых в записи чисел.

Представление числа в позиционной системе счисления

В позиционной системе счисления с основанием q всякое число может быть представлено по формуле (развёрнутая форма записи):

A_q=±(a_n−1⋅qⁿ⁻¹+a_n−2⋅qⁿ⁻²+…+a₀⋅q⁰+a₋₁⋅q⁻¹+…+a_−m⋅q^−m).

где:

А — число;
q — основание системы счисления;
a_i — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
q_i — «вес» i-го разряда.

Свёрнутой формой записи числа называется его представление в виде:

±a_n−1a_n−2. ..a₁a₀…a_−m

в качестве примера, возьмём десятичное число 21466,12. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме мы переходим сразу к развёрнутой записи, умножая цифры числа на «веса» разрядов и суммируя все полученные перемножения:

2⋅10⁴+1⋅10³+4⋅10²+6⋅10¹+6⋅10⁰+1⋅10⁻¹+2⋅10⁻².

Десятичная система счисления, несмотря на свою универсальность, имеет большой недостаток — она избыточна, так как имеет большой алфавит. Для компьютерной техники наиболее удобной оказалась двоичная система счисления, поэтому мы рассмотрим её в следующем уроке.

Кодирование информации Двоичная система счисления

Перевод систем счисления – таблица, правила, формулы

В решении определенного класса задач иногда удобно записывать числовые значения в разных системах счисления. Разработан ряд унифицированных правил перевода чисел между системами. О том, как выполняется перевод систем счисления, рассказано в статье.

Что такое перевод систем счисления

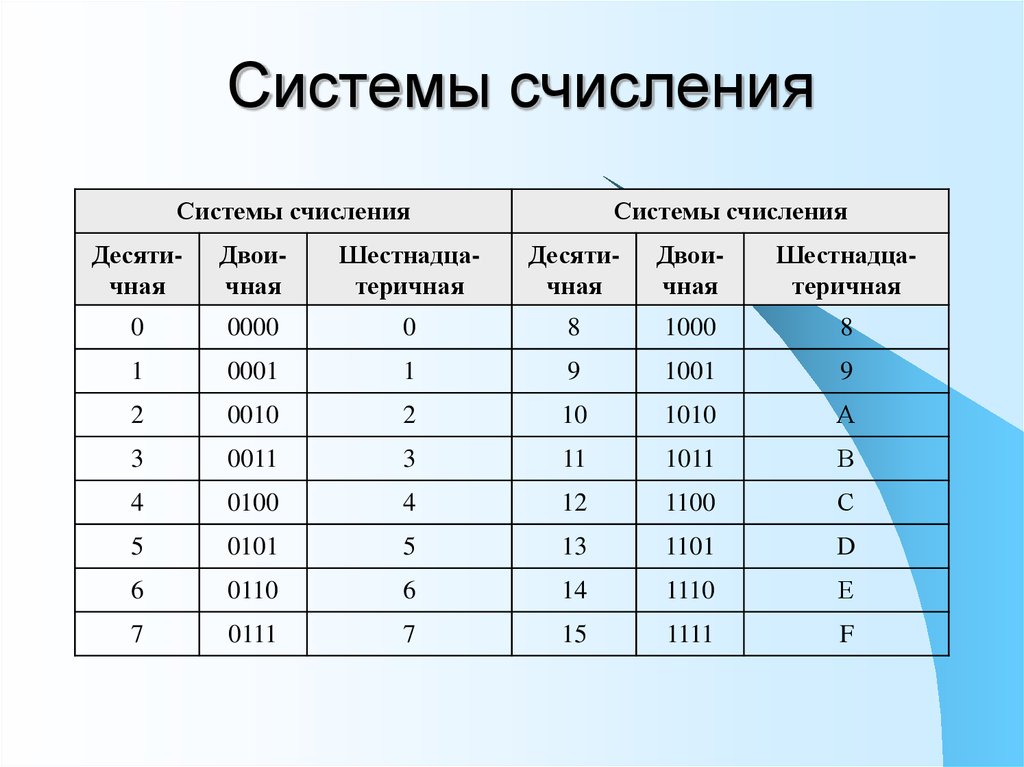
Основанием системы счисления является величина, определяющая количество символов для записи числового значения. Например, основанием двоичной системы является число 2, пятеричной, соответственно – 5.

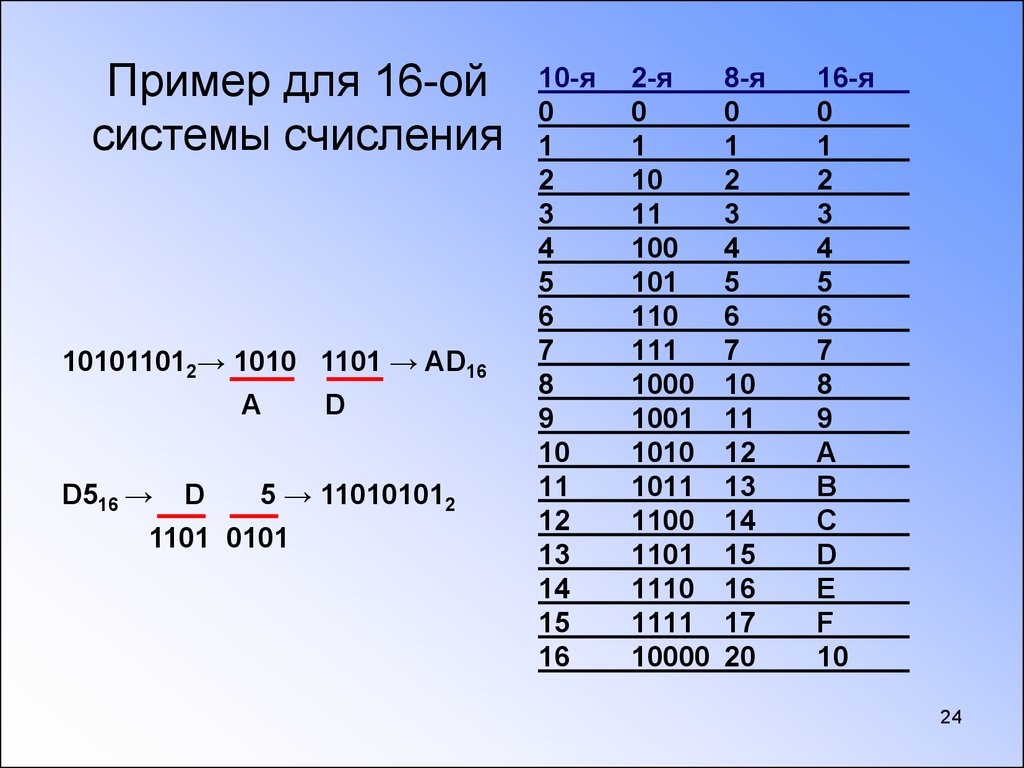
Рис. 1. Таблица: основание и алфавит различных систем счисления.

Число 15 в десятичной системе при переводе в пятеричную равно 30, а в восьмеричной будет равно 17. Шестнадцатеричный эквивалент пятнадцати представляет собой букву F. Как так получается?

Рис. 2. Таблица соответствия десятичных и шестнадцатеричных чисел.

Перевод чисел с участием десятичной системы счисления

В преобразовании чисел с участием десятичной системы приняты три строгих правила перевода.

1. Пересчет числового значения из десятичного формата в эквивалент другой системы счисления заключается в делении целой части и полученных частных, на величину основания будущей системы счисления. При этом остатки от деления записываются начиная с последнего.

Например, 15 из десятичной системы в восьмеричную переводится так: 15 / 8 = 1 (в остатке 7). Записываем итог, начиная с конечного и в данном случае единственного частного, и затем остаток. Получим 17.

Еще один пример: десятичное 125 в восьмеричной системе: 125 / 8 = 15 (5). Полученное частное больше, чем основание 8.

Продолжаем делить: 15 / 8 = 1 (7). Ответ записывается с последнего частного, а затем остатки от деления: 175.

Следует запомнить, что запись результата всегда начинает с последнего частного и остатков от деления в обратном порядке.

2. Преобразование части десятичного числа, записанной после запятой, выполняется с помощью обратной процедуры, то есть умножения, вычисляя одно за другим произведения дробных частей на основание будущей системы счисления и записывая последовательно цифры, полученные в целой части. Например, дробная часть числа 0,134 в двоичную систему переводится так (удобнее это делать столбиком):

0,134 * 2 = 0,268 (в целой части 0)

0,268 * 2 = 0,536 (0)

0,536 * 2 = 1,072 (слева от запятой 1)

0,072 * 2 = 0,144 (в целой части 0)

0,144 * 2 = 0,288 (0)

Произведения вычисляют до тех пор, пока не будет обеспечена заданная точность или в остатке не получится ноль.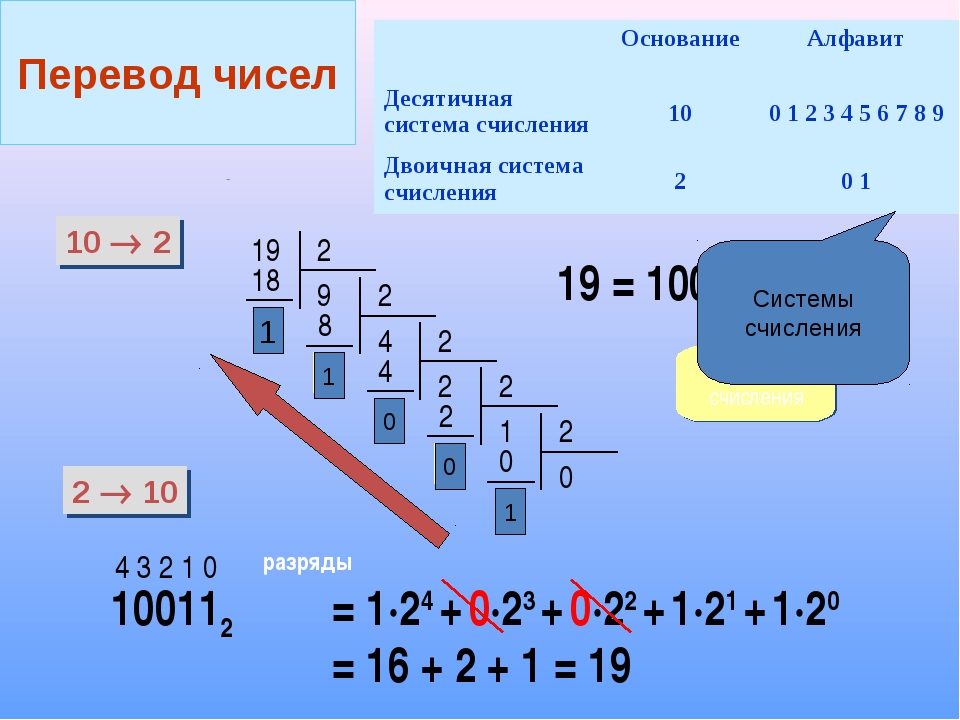 4. Перевод между этими системами и двоичной системой удобнее всего выполнять с помощью таблицы перевода систем счисления:

Рис. 3. Таблица соответствия чисел в 2-, 8- и 16-й системах счисления.

Каждое восьмеричное число представляется триадой (тремя элементами) двоичных знаков, каждое шестнадцатеричное – двоичной тетрадой (четыре элемента).

Например, 8 → 2: 134 ⇔ 001011100

16 → 2: 8F ⇔ 10001111

2 → 8: 110101 ⇔ 65

2 → 16: 11011000 ⇔ D8

Что мы узнали?

Переход между различными системами счисления выполняется по строго определенным правилам. Десятичные числа преобразуются в другие системы путем последовательного деления целой части и умножения дробной, обратный перевод выполняется с помощью полинома. Перевод между 2-, 8- и 16-ми системами выполняется по таблице.

Оценка статьи

А какая ваша оценка?

CBSE Class 9 Математические системы счисления Формулы

Вам трудно справиться с математическими формулами и уравнениями? Математические формулы кажутся сложными для запоминания? Не о чем беспокоиться. Что, если мы скажем вам, что вам больше не нужно изо всех сил ломать все математические формулы 9-го класса? Да! Вы получите формулы системы счисления в таблицах формул по математике для класса 9, разработанных экспертами в предметной области Веданту. Этот лист включает все формулы системы счисления класса 9главы мудрые.

Где найти математические формулы для 9 класса?

CBSE Class 9 Математические формулы Все главы доступны для свободного доступа и пересмотра на Vedantu.com. Вы можете просто загрузить важные математические формулы и уравнения в формате PDF для 9-го класса, чтобы легко и быстро решать задачи и получать более высокие оценки на экзаменах Совета CBSE 9-го класса в Vedantu.

Система счисления Класс 9

Натуральные числа: Имеют числовую форму -1, 2, 3, 4, 5, 6, 7, 8, 9, 10………обозначаются буквой N

Целые числа: представлены в числовой форме – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10….. …..обозначаются буквой W.

Целые числа : -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 обозначаются Z

Рациональные числа: Все числа, которые математически могут быть записаны в виде p/q, q ≠0, известны как рациональные числа, где p и q относятся к целым числам.

Иррациональные числа. Число s называется иррациональным, если его нельзя математически записать в виде p/q, где p и q — целые числа, а q ≠ 0,9.0003

Десятичное расширение: такое алгебраическое расширение в десятичной форме рационального числа является либо завершающим, либо не прекращающимся повторением. Следовательно, мы можем сказать, что число, чье десятичное представление является либо конечным, либо неконечным/повторяющимся, является тем, что мы называем рациональным числом. Имеются следующие свойства десятичного расширения:

Для иррационального числа десятичное расширение не прекращается и не повторяется.
Все рациональные и иррациональные числа можно сложить вместе.
Мы можем составить набор действительных чисел.
Вещественное число может быть как рациональным, так и иррациональным.
Если r рационально, а s иррационально, то r + s, r — s, r . s всегда будет иррациональным числом, однако r/s может быть как рациональным, так и иррациональным
Мы можем представить каждое иррациональное число на числовой прямой, используя теорему Пифагора.
Рационализация — это метод извлечения квадратных корней из знаменателя. Например, для математического выражения 2 + √6/√4, чтобы удалить, мы умножим как числитель, так и знаменатель на √4.

Система важных чисел Формула класс 9

1. Формулы полиномиальных экспрессии

Биномиальный0063 MOMOMIAL	3, 2x, 23y и т. Д.
Триномиал	x2 + 4x + 5 и т. Д.
9ply Lin Lin Lin Lin Lin Lin Lin Lin. 5 etc
Quadratic polynomial	ax2 + bx + c etc
Biquadratic polynomial	x4 + 5×3 + 2×2 + 3
Cubic polynomial	x3 + 4×2 + 5 etc

2. Coordinate Geometry Formulas

96669/

Equation of a line	ax + by + c = 0
Уравнение круга	x² +y² = R² Здесь ‘R’ относится к радиусу круга
Уравнение Allipse
Уравнение ollipse
. 0066	X²/A²+Y²/B² = 1
Уравнение Parabola	y² = 4AX
Avation a Gyerbola		Avation a Gyperbola	. = 1
Угол между двумя строками	θ = TAN² — 1 (M/1+M1M2)
Формула	√ (x2-1). −y1)²

3. Формулы для окружностей

Area of circle	πr²
Diameter of circle	2r
Circumference of circle	2πr
Угол сектора окружности	θ = (360/(πr)
Площадь сектора	(θ/9)×r²0003
Площадь кругового кольца	π × (R²−r²)
r = радиус внутренней окружности. R = радиус внешней окружности. θ = Угол между двумя радиусами.

Как выучить все формулы математических систем счисления 9 класса CBSE?

Системы счисления включают в себя различные формулы, такие как длина окружности, полиномиальные выражения, формула расстояния и т. д. Если вы не выучите все формулы должным образом, вы можете запутаться и не сможете решить вопрос. Вот несколько советов о том, как выучить все формулы CBSE Class 9.Системы счисления по математике:

Когда вы изучаете любую формулу Системы счисления по математике 9 класса CBSE, вы должны просмотреть ее определения и пояснения, данные в учебнике, чтобы понять, о чем эта формула.
После изучения формулы следует использовать решенные примеры в учебниках и справочниках, чтобы понять, как ее применять и правильно решить вопрос.
Математика CBSE класса 9 Формулы систем счисления — Система счисления, Важная формула системы счисления и часто задаваемые вопросы, доступные на Vedantu, содержат объяснения простым языком. Вы можете использовать нашу платформу, чтобы пересмотреть эти формулы и улучшить свое понимание систем счисления.
После того, как вы выучите все формулы, попробуйте решить вопросы на основе математических систем счисления 9 класса CBSE. Практикуя эти вопросы, вы научитесь использовать формулу в вопросе и улучшите свои математические навыки.
Изучая формулы математических систем счисления CBSE Class 9, вы также должны узнать, как они были получены. Изучив вывод формулы, вы сможете более четко понять ее концепцию.

Почему системы счисления важны для учащихся 9 класса CBSE, изучающих математику?

Математика является важным предметом для учащихся 9 класса CBSE. Учебная программа CBSE Class 9 по математике включает в себя множество важных понятий, которые необходимо изучить. Системы счисления являются одним из таких понятий. Изучение систем счисления действительно полезно, поскольку облегчает понимание других концепций математики для 9-го класса.

Ниже приведены некоторые другие причины, по которым вам следует изучать системы счисления:

CBSE Class 9Математические формулы систем счисления — Система счисления, Важная формула системы счисления и часто задаваемые вопросы помогут вам лучше понять действительные числа, целые числа, натуральные числа и целые числа.
Знакомство с системами счисления по математике 9 класса CBSE поможет вам с легкостью освоить другие понятия из вашей программы по математике.
Системы счисления содержат множество формул, включая полиномиальные функции, окружности и геометрию. Таким образом, изучение систем счисления по математике класса 9 CBSE также поможет вам в решении вопросов, основанных на этих темах.
Системы счисления CBSE по математике класса 9 имеют значительный вес на экзамене по математике класса 9. Если вы тщательно изучите эту концепцию, вы сможете хорошо набрать баллы на экзамене.

Преобразование чисел в различные системы счисления

Система счисления представляет собой систематический способ представления чисел с помощью символьных символов и использует базовое значение для удобной группировки чисел в компактной форме. Наиболее распространенной системой счисления является десятичная, имеющая базовое значение 10 и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Однако существуют и другие системы счисления, и они могут быть более эффективными для использования в определенных целях. Например, поскольку компьютеры используют логическую логику для выполнения вычислений и операций, они используют двоичную систему счисления, базовое значение которой равно 2.

Microsoft Office Excel имеет несколько функций, которые можно использовать для преобразования чисел в следующие системы счисления и из них:

Система счисления	Базовое значение	Набор символов
Двоичный	2	0,1
Окталь	8	0, 1, 2, 3, 4, 5, 6, 7
Десятичный	10	0, 1, 2, 3, 4, 5, 6, 7, 8 и 9
Шестнадцатеричный	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, Б, В, Г, Е, Ф

Для выполнения этой задачи используйте функцию BIN2DEC.

А	Б
Формула	Описание (Результат)
=БИН2ДЕК(1100100)	Преобразует двоичное число 1100100 в десятичное (100)
=БИН2ДЕК(1111111111)	Преобразует двоичное число 1111111111 в десятичное (-1)

Для выполнения этой задачи используйте функцию BIN2HEX.


1
2
3
4

А	Б
Формула	Описание (Результат)
= ДВИГ. 2ШЕСТ.(11111011, 4)	Преобразует двоичное число 11111011 в шестнадцатеричное с 4 символами (00FB)
= ДВИГ.2ШЕСТ.(1110)	Преобразует двоичное число 1110 в шестнадцатеричное (E)
= ДВИГ.2ШЕСТ.(1111111111)	Преобразует двоичное число 1111111111 в шестнадцатеричное (FFFFFFFFFF)

Для выполнения этой задачи используйте функцию BIN2OCT.


1
2
3
4

А	Б
Формула	Описание (Результат)
=БИН2ОКТ(1001, 3)	Преобразует двоичное число 1001 в восьмеричное с 3 символами (011)
=БИН2ОКТ(1100100)	Преобразует двоичное число 1100100 в восьмеричное (144)
=БИН2ОКТ(1111111111)	Преобразует двоичное число 1111111111 в восьмеричное (7777777777)

Для выполнения этой задачи используйте функцию DEC2BIN.

А	Б
Формула	Описание (Результат)
= ДЕК2БИН(9, 4)	Преобразует десятичное число 9 в двоичное с 4 символами (1001)
=ДЕК2БИН(-100)	Преобразует десятичное число -100 в двоичное (1110011100)

Для выполнения этой задачи используйте функцию DEC2HEX.

А	Б
Формула	Описание (Результат)
= ДЕК2ШЕСТ (100, 4)	Преобразует десятичное число 100 в шестнадцатеричное с 4 символами (0064)
= ДЕК2ШЕСТ (-54)	Преобразует десятичное число -54 в шестнадцатеричное (FFFFFFFFCA)

Для выполнения этой задачи используйте функцию DEC2OCT.

А	Б
Формула	Описание (Результат)
=DEC2OCT(58, 3)	Преобразует десятичное число 58 в восьмеричное (072)
=DEC2OCT(-100)	Преобразует десятичное число в восьмеричное (7777777634)

Для выполнения этой задачи используйте функцию HEX2BIN.


1
2
3
4

А	Б
Формула	Описание (Результат)
=HEX2BIN(«F», 8)	Преобразует шестнадцатеричное F в двоичное с 8 символами (00001111)
=HEX2BIN(«B7»)	Преобразует шестнадцатеричный B7 в двоичный (10110111)
=HEX2BIN(«FFFFFFFFFF»)	Преобразует шестнадцатеричное FFFFFFFFFF в двоичное (1111111111)

Для выполнения этой задачи используйте функцию HEX2DEC.


1
2
3
4

А	Б
Формула	Описание (Результат)
=HEX2DEC(«A5»)	Преобразует шестнадцатеричный формат A5 в десятичный (165)
=HEX2DEC(«FFFFFFFF5B»)	Преобразует шестнадцатеричный FFFFFFFF5B в десятичный (-165)
=HEX2DEC(«3DA408B9»)	Преобразует шестнадцатеричное число 3DA408B9 в десятичное (1034160313)

Для выполнения этой задачи используйте функцию HEX2OCT.


1
2
3
4

А	Б
Формула	Описание (Результат)
=HEX2OCT(«F», 3)	Преобразует шестнадцатеричное F в восьмеричное с 3 символами (017)
=HEX2OCT(«3B4E»)	Преобразует шестнадцатеричный 3B4E в восьмеричный (35516)
=HEX2OCT(«FFFFFFFF00»)	Преобразует шестнадцатеричное FFFFFFFF00 в восьмеричное (7777777400)

Для выполнения этой задачи используйте функцию OCT2BIN.

А	Б
Формула	Описание (Результат)
= ОКТ2БИН(3, 3)	Преобразует восьмеричное число 3 в двоичное с 3 символами (011)
= ОКТ2БИН(7777777000)	Преобразует восьмеричное число 7777777000 в двоичное (1000000000)

Для выполнения этой задачи используйте функцию OCT2DEC.

А	Б
Формула	Описание (Результат)
= ОКТ2ДЕКАБР (54)	Преобразует восьмеричное число 54 в десятичное (44)
= ОКТ2ДЕКАБР (7777777533)	Преобразует восьмеричное число 7777777533 в десятичное (-165)

Для выполнения этой задачи используйте функцию OCT2HEX.