Скалярные и векторные величины
Даны определения и приведены примеры скалярных и векторных величин. Описаны математические операции над векторными величинами.
Физические величины бывают скалярными и векторными
Скалярные величины
Скалярная величина (от лат. scalaris – ступенчатый) в механике – величина, каждое значение которой может быть выражено одним числом.
Примеры скалярных величин: масса тела, время, температура, длина, путь, площадь.
Более подробно функционирование опорно-двигательного аппарата человека и биомеханика мышц описаны в книге:
Биомеханика опорно-двигательного аппарата человека
Векторные величины
Если величина, кроме числового значения характеризуется еще и направлением, то она называется векторной величиной или просто вектором. То есть вектор определяется численным значением и направлением.
Примеры векторных величин: перемещение, скорость, ускорение, сила, момент силы, импульс тела.
Обозначение векторных величин
На рисунках и схемах вектор отображается отрезком прямой со стрелкой на одном конце.
Длина отрезка в выбранном масштабе выражает числовое значение векторной величины (его модуль), а стрелка указывает ее направление.
На рисунках, схемах и в тексте векторные величины обозначают несколькими способами:
1 способ. Векторная величина обозначается строчной или заглавной буквой со стрелкой или чертой над ней (рис. 1).
Рис.1. Вектор и его обозначение2 способ. Векторная величина обозначается заглавными буквами, обозначающими начало и конец вектора с чертой или стрелками над ними (рис. 1).
3 способ. Иногда векторные величины в формулах обозначаются жирным шрифтом, а скалярные — обычным. Например: F=ma
Операции над векторными величинами (векторами)
Над векторными величинами возможны следующие математические операции:
- Сложение и вычитание векторов.
- Умножение вектора на скаляр.
- Произведение векторов (скалярное и векторное).
Литература
- Петров В.А., Гагин Ю.А. Механика спортивных движений.
– М: Физкультура и спорт, 1974. – 232 с.
– М: Физкультура и спорт, 1974. – 232 с.С уважением, А.В. Самсонова
Похожие записи:
Мышечно-сухожильный комплекс
Приведена рецензия на книгу В.Т.Тураева и В.В. Тюпа «Мышечно-сухожильный комплекс: анатомия, биомеханика, спортивная практика» зав. кафедрой биомеханики НГУ…
Сила тяжести
Дано определение силы тяжести. Показано, что сила тяжести является частным случаем силы гравитации. Описаны факторы, определяющие силу тяжести:…
Сила
Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение.
Типы телосложения (конституции) по Э. Кречмеру
Описана биография Эрнста Кречмера – немецкого психиатра и психолога, разработавшего типологию тела человека. Дано описание типов телосложения…
Типы конституции женщин по И.Б. Галанту
Описана биография известного советского психиатра И.Б.Галанта, предложившего естественную систему конституциональных типов женщин.
Дана характеристика предложенных И.Б.Галантом конституциональных…
Звенья тела человека как рычаги
Дано описание опорно-двигательного аппарата (ОДА) человека как системы рычагов. Приведен пример расчета силы двуглавой мышцы плеча…
Скалярное умножение
Скалярное умножениеВ. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
Суперобложка / Обложка / Содержание
|
От автора Введение Векторы .Геометрическое определение вектора .Алгебраические операции над направленными отрезками ..Сложение направленных отрезков ..Умножение направленных отрезков на число .Проекции вектора . ..Параллельное проектирование вектора в пространстве …Проекция точки на плоскость …Проекция вектора на плоскость ..Ортогональная проекция вектора в пространстве …Ортогональная проекция вектора на плоскость …Ортогональная проекция вектора на прямую и направленную ось .Метод координат ..Коллинеарные векторы ..Компланарные векторы ..Векторы в трехмерном геометрическом пространстве ..Линейная зависимость векторов и размерность пространства .Декартова система координат ..Различные формы записи векторов ..Линейные операции над векторами в координатной форме ..Скалярное умножение векторов …Свойства скалярного умножения . ..Некоторые примеры использования скалярного умножения .Измерение площадей и объемов ..Площадь параллелограмма, построенного на векторах ..Свойства определителя второго порядка ..Задачи на применение определителей ..Объем параллелепипеда, построенного на векторах ..Определитель третьего порядка и его свойства ..Векторное произведение векторов ..Векторное умножение векторов базиса декартовой системы координат На подступах к тензорам .Преобразования координат .Скалярное умножение векторов в произвольных косоугольных координатах .Метрический тензор .Взаимный координатный базис .Ковариантные и контравариантные координаты вектора .Площадь и объем в косоугольных координатах . ..Символы Веблена ..Свойства символов Веблена ..Тензор Леви-Чивиты ..Операция векторного умножения в произвольных косоугольных координатах .Линейные преобразования или операторы .Линейный оператор и его матрица ..Примеры линейных операторов .Доказательство теоремы об определителе Тензоры .Определение тензора .Общие определения алгебраических операций с тензорами .Примеры на применение тензоров в физике ..Тензор инерции ..Тензор напряжений .Задачи ..Задачи на тождественные преобразования Методические комментарии Литература |
|
.Параллельное проектирование вектора в пространстве
.Индексная форма записи для выражений с определителями
Впервые слово «скаляр» ввел в математику Виет, но
современное значение ему придал Гамильтон (1843 г.
), назвав
скалярной величину отличную от векторной. Скалярная величина –
это величина, которая может, в отличие от векторной, быть задана
одним числовым значением. Проще говоря, скаляр – это число. По
смыслу названия, при скалярном умножении векторов должно получаться
число.
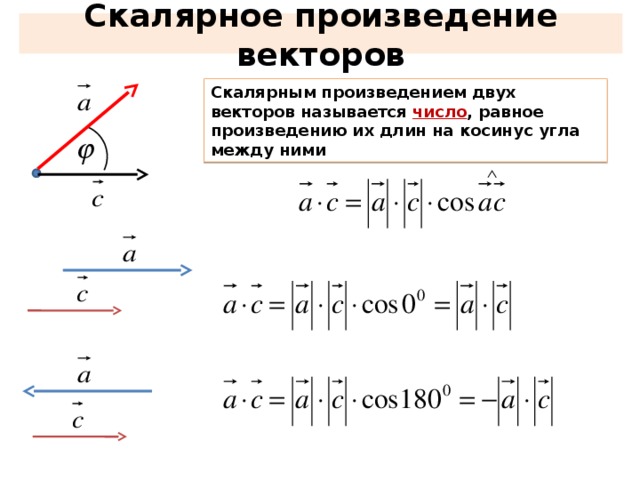
Определение скалярного произведения векторов (22)
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное умножение обычно обозначается точкой: .
Введение такой странной, на первый взгляд, операции находит как физическое, так и геометрическое оправдание.
Если
–
постоянная сила, которая действует на точку, а
– вектор перемещения этой точки, то работа A, которая
совершается силой на этом перемещении, может быть вычислена как
скалярное произведение силы на перемещение:
.
С геометрическими приложениями скалярного умножения мы познакомимся в дальнейшем.
Вспомнив, что и , мы можем записать: .
Свойства скалярного умножения
1. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда векторы взаимно ортогональны.
Пусть векторы и не равны нулю. Тогда из равенства нулю скалярного произведения следует, что , а это и означает, что .
Если же хотя бы один из векторов нулевой, то
.
С другой стороны, для нулевого вектора понятие направления не имеет
смысла. Но раз смысла нет, то любое соглашение не погрешит против
правды. Мы можем принять, что нулевой вектор параллелен любому
другому, если захотим, или, что он ортогонален к любому направлению,
что мы и сделаем. Но если нулевой вектор ортогонален к любому
другому, в том числе и нулевому же, то и этот случай не является
исключением.
2. Скалярное умножение векторов коммутативно (перестановочно).
– это сразу следует из определения.
3. Скалярное умножение ассоциативно по отношению к числовому множителю.
так же непосредственно следует из определения.
4. Скалярное умножение дистрибутивно (распределительно) относительно сложения векторов.
.
Данное свойство, несмотря на привычный вид, не является очевидным.
В самом деле (рис. 17), ,
а . Глядя на рис. 17, трудно предположить, что эти два выражения равны, однако это так.
Доказательство
Для доказательства мы используем свойства проекций.
.
Можно это свойство доказать и непосредственно вычисляя соответствующие длины и углы, но этот путь значительно дольше.
Скалярное умножение в декартовых координатах
Общее выражение для скалярного произведения в произвольных координатах значительно сложнее, и мы займемся им позже.
Для начала найдем результат скалярного умножения базисных векторов декартовой системы координат.
и аналогично .
и аналогично .
|
Полученные результаты можно свести в таблицу скалярного умножения базисных векторов. |
Теперь мы можем доказать следующее утверждение:
Скалярное произведение двух векторов равно сумме произведений их соответствующих координат: .
Доказательство
В самом деле,
. Воспользовавшись свойствами скалярного умножения и таблицей умножения для векторов базиса, мы получаем: .
..Некоторые примеры использования скалярного умножения
Длина или модуль вектора в координатной форме
Пусть произвольный вектор. Скалярное произведение этого вектора самого на себя равно:
С другой стороны, , следовательно,
и .
Расстояние между двумя точками
Пусть нам даны две точки
и
,
и требуется определить расстояние l
между ними.
Проведем из начала координат в эти точки радиусы-векторы
и
,
тогда
.
Модуль или длина вектора
как раз и будет равна этому расстоянию. Следовательно,
.
Если расстояние между двумя точками мы обозначим , полученное выражение перепишется в виде:
.
В качестве следующих примеров рассмотрим доказательство двух теорем элементарной геометрии. Этим мы убьем двух зайцев: во-первых, вспомним элементарную геометрию, во-вторых, получим удовольствие от эффективности метода.
Теорема
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Совместим векторы
и
со сторонами параллелограмма (рис. 19), тогда сумма и
разность этих векторов совпадут с его диагоналями.
и соответственно
.
Сложив эти выражения, мы получим:
.
Мы видим, что левая часть равенства – это сумма квадратов диагоналей. Правая же часть, как и следовало ожидать – сумма квадратов сторон.
Теорема
Квадрат стороны треугольника равен сумме квадратов двух других его сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.
Совместим векторы и со сторонами треугольника (рис. 20), тогда вектор совпадет с третьей его стороной.
И окончательно: .
Напомним, что a и b означают модули соответствующих векторов.
К оглавлению
Скаляр | Определение, примеры и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы. - Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю. - Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Связанный контент
Скаляр, Вектор, Матрица
(.
.. и матрицы)
Что такое скаляры и векторы?
Скаляр
имеет только величину (размер):3,044, −7 и 2½ являются скалярами
Расстояние, скорость, время, температура, масса, длина, площадь, объем, плотность, заряд, давление, энергия, работа и мощность — все это скаляры.
Вектор
имеет величину и направление :Перемещение, скорость, ускорение, сила и импульс — все это векторы.
И обратите внимание на эти специальные слова:
Расстояние против смещения
- Расстояние является скаляром («3 км»)
- Смещение — это вектор («3 км к юго-востоку»)
Вы можете пройти большое расстояние, но ваше перемещение может быть небольшим (или нулевым, если вы вернетесь в исходное положение).
Скорость против скорости
- Скорость — это то, насколько быстро что-то движется.
- Скорость — это скорость в направлении .
Сказать, что собака Ариэль бежит со скоростью 9 км/ч, (километров в час) — это скорость.
Но если сказать, что он бежит 9 км/ч на запад , то это скорость.
См. Скорость и Скорость, чтобы узнать больше.
Обозначение
Вектор часто записывается в полужирный , например a или b , поэтому мы знаем, что это не скаляр:
- , поэтому c — это вектор, он имеет величину и направление .
- , но c — это скаляр, например 3 или 12,4 .
Пример: k b на самом деле является скаляром, умноженным на k вектор b .
Вектор также можно записать в виде букв его головы и хвоста со стрелкой над ними, например:
Использование скаляров
Скаляры просты в использовании. Просто относитесь к ним как к обычным числам.
Пример: 3 кг + 4 кг = 7 кг
Использование векторов
На странице о векторах есть более подробная информация, но вот краткий обзор:
Мы можем добавить два вектора, соединив их лоб в лоб:
Мы можем вычесть один вектор из другого:
- Сначала мы меняем направление вектора, который хотим вычесть,
- , затем добавьте их как обычно:
а − б
Мы можем умножить вектор на скаляр (это называется «масштабированием» вектора):
Пример: умножить вектор
m = (7,3) на скаляр 3| а = 3 м = (3×7,3×3) = (21,9) |
Он по-прежнему указывает в том же направлении, но в 3 раза длиннее
(Теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.
)
Полярный или декартовый
Вектор может находиться в:
- Величина и направление (Полярная) форма,
- или в x и y (декартово) форма
Вот так:
| <=> | ||
| Вектор a в полярных координатах | Вектор a в декартовом Координаты |
(Прочитайте, как преобразовать их в полярные и декартовы координаты.)
Пример: вектор
13 на 22,6°В полярной форме (величина и направление):
Вектор 13 на 22,6°
Приблизительно равен 5) Декартово (x,y ) форма:
Вектор (12,5)
Попробуйте векторный калькулятор, чтобы понять, как он работает.
Умножение вектора на вектор (скалярное произведение и векторное произведение)
Как нам умножить два вектора вместе? Существует более чем один способ!
(Дополнительную информацию см. на этих страницах.) |
Больше двух измерений
Векторы также прекрасно работают в 3-х и более измерениях:
Вектор (1,4,5)
Список номеров
Таким образом, вектор можно рассматривать как список из чисел :
.- 2 числа для двумерного пространства, например (4,7)
- 3 числа для трехмерного пространства, например (1,4,5)
- и т. д.
Скаляры, векторы и матрицы
И когда мы включаем матрицы, мы получаем этот интересный шаблон:
- Скаляр — это число, например 3, -5, 0,368 и т. д. ,
- Вектор представляет собой список чисел (может быть в строке или столбце),
- Матрица — это массив чисел (одна или несколько строк, один или несколько столбцов).
