Окружность и круг 5 кл Наглядная геометрия.
Окружность
Окружностью называется фигура, состоящая из всех точек плоскости, удаленных от данной точки на данное расстояние.
Данная точка называется центром окружности, а данное расстояние – радиусом окружности. Радиусом называется также любой отрезок, соединяющий точку окружности с ее центром.
Таким образом, окружность с центром в точке О и радиусом R представляет собой фигуру, состоящую из всех точек плоскости, расстояние от которых до точки О равно R .
В режиме слайдов ответы появляются после кликанья мышкой
Отрезок, соединяющий произвольные две точки окружности, называется хордой этой окружности . Хорда, проходящая через центр окружности, называется диаметром этой окружности.
Круг
Кругом называется фигура, состоящая из всех точек плоскости, удаленных от данной точки на расстояние, не превосходящее данное.
Данная точка называется центром круга, а данное расстояние – радиусом круга.
Таким образом, круг с центром в точке О и радиусом R , представляет собой фигуру, состоящую из всех точек плоскости, удаленных от точки О на расстояние, не превосходящее R .
В режиме слайдов ответы появляются после кликанья мышкой
Круг можно представлять себе как фигуру, ограниченную окружностью.
Хордой и диаметром круга называют соответственно хорду и диаметр окружности, ограничивающей этот круг.
Упражнение 1
На сколько частей окружность делит плоскость?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ. Две.
Упражнение 2
Сколько диаметров можно провести через центр окружности?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ. Бесконечно много.
4
Упражнение 3
Найдите диаметр окружности, если известно, что он на 55 мм больше радиуса.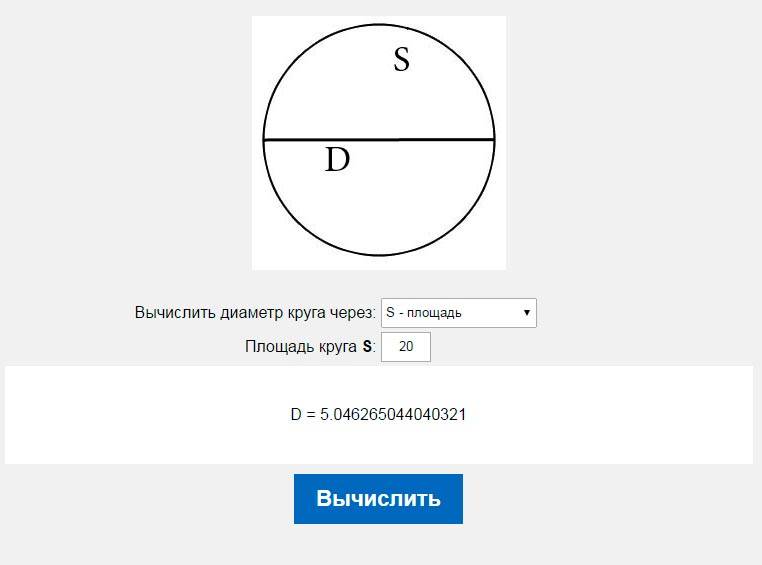
Ответ. 110 мм.
В режиме слайдов ответы появляются после кликанья мышкой
4
Упражнение 4
Найдите длину наибольшей хорды окружности, радиус которой равен 5 см.
Ответ. 10 см.
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 5
Расстояние между точками A и B равно 2 см. Найдите наименьший возможный радиус окружности, проходящей через эти точки.
Ответ. 1 см.
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 6
Изобразите центр O окружности, проходящей через данные точки A , B , C , D .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ.
8
Упражнение 7
Изобразите центр O окружности, проходящей через данные точки A , B , C , D .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ.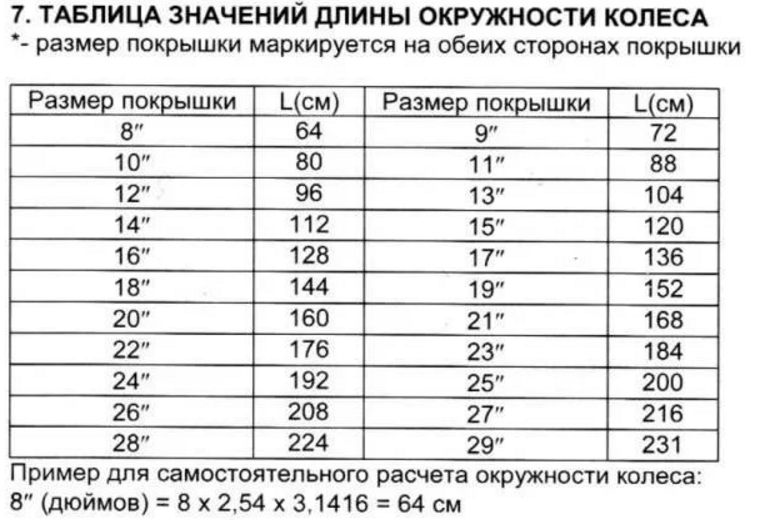
9
Упражнение 8
Сколько окружностей может проходить через две заданные точки?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ. Бесконечно много.
10
Упражнение 9
Сколько общих точек могут иметь две окружности?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: Ни одной, одну или две.
Упражнение 10
На сколько частей могут делить плоскость две окружности?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: Три или четыре.
Упражнение 11
На сколько частей делят плоскость три окружности, изображенные на рисунке?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8.
Упражнение 1 2
З акрасьте область, состоящую из всех точек A , для которых AO 1 и AP
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
14
Упражнение 1 3
З акрасьте область, состоящую из всех точек A , для которых AO 1 и AP
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
15
Упражнение 1 4
З акрасьте область, состоящую из всех точек A , для которых AO 1, AP AQ
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
16

Упражнение 1 5
На рисунке закрасьте область, состоящую из всех точек B , для которых BO 1, BP BQ 1.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
17
Упражнение 1 6
На рисунке закрасьте область, состоящую из всех точек С , для которых С O 1, С P 1 и CQ 1.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
18
Упражнение 1 7
На рисунке изображена фигура, называемая кольцом . Каким неравенствам должно удовлетворять расстояние d от точек A этого кольца до его центра O
.В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
19
Конспект по математике на тему: «Диаметр окружности»
Тема:
Диаметр окружности.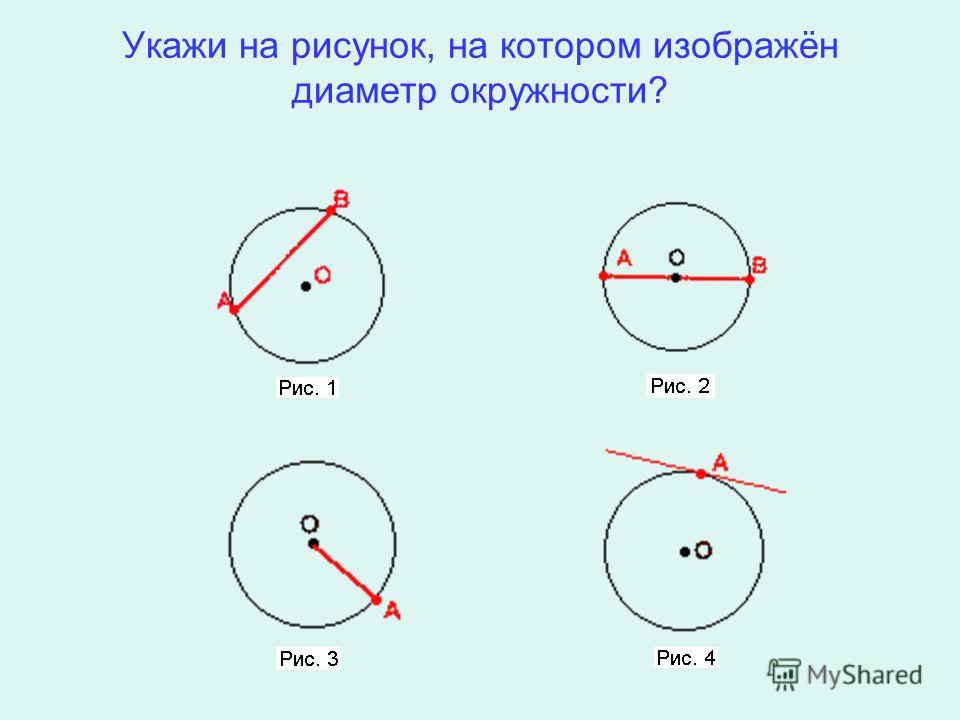
Задачи: познакомить с понятием диаметр окружности, радиус окружности, развивать пространственные представления, прививать любовь к математике.
Оборудование: дидактический материал для игры с прищепками, чертежные инструменты, индивидуальные карточки с тестовыми заданиями, дидактический материал для практической работы, дидактический материал для устного счета.
I. Организационный момент.
— Здравствуйте, ребята. Сегодня внеурочное занятие по математике и конструированию буду вести у вас я.Надеюсь сегодня вы будите внимательны и активны.
II. Вводная часть.
1. Игра с прищепками.
— Ребята у меня в руках наглядность. Она поделена на части, в каждой части картинки. В двух коробочках лежат прищепки с надписями, первая коробка это «окружность», вторая «круг».
— Вам необходимо определить какая из картинок круг, а какая окружность.
— По
очереди выходя к доске, будете цеплять прищепки.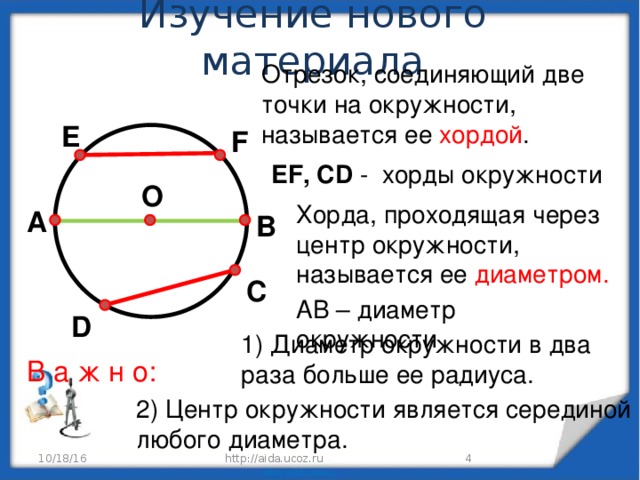
(Практическая работа детей).
III. Постановка учебной задачи.
1. Загадка.
— Вроде круг, но дело в том,
Что иначе мы зовем
Нарисованный кружок.
В чем секрет? Скажи, дружок!
Эта странная наружность
Называется…
Ответ: Окружность
— Определите тему нашего сегодняшнего занятия. (Окружность).
— Окружность – душа геометрии.
Познайте окружность, и вы не только познаете душу геометрии, но и возвысите свою душу
— Как вы понимаете это высказывание?
2. Рассказ учителя об истории.
В Древней Греции круг и окружность считались венцом совершенства.
Действительно, в каждой своей точке окружность устроена одинаковым
образом, что позволяет ей двигаться самой по себе.
Это свойство окружности сделало возможным возникновение колеса,
поскольку ось и втулка колеса должны всё время быть в соприкосновении.
В русском языке слово «круглый» тоже означает высокую степень
чего-либо: «круглый отличник», «круглый сирота», и даже «круглый
дурак».
Ещё до колеса люди использовали круглые брёвна-катки
для перевозки тяжестей.
Рисунки на стенах египетских пирамид рассказывают нам,
что именно так доставлялись огромные камни на строительство
этих пирамид.
— Найдем значение выражения.
100-99=1 80-78=2
35+5=40 44+7=51
91+8=99 72-2=70
— Расположите ответы в порядке возрастания. Прочитайте слово которое у вас получилось.(Диаметр).
— Сегодня мы с вами познакомимся с диаметром окружности.
IV. Основная часть.
1. Работа с чертежными инструментами.
-С помощью какого инструмента мы строим окружность?
-С помощью циркуля.
-Циркуль — чертежный инструмент. С ним нужно работать осторожно. Нельзя подносить к лицу или передать соседу «иглой вперед». Что это слово вам напоминает? ( Цирк и циркуль)
-Слово «циркус» в переводе с
латинского означает ни что иное, как круг.
2. Построение окружности.
—Как называется точка, которая остаётся от иголки у одной из ножек циркуля?
-Центр окружности. Поставьте карандашом эту точку.
-Слово «центр» произошло от латинского слова «центрум», которое означало палку с заостренным концом, которой погоняли быков; позднее оно означало ножку от циркуля, а потом и точку, которую оставляет циркуль на листе бумаги.
— С помощью линейки циркулем отметьте 2 сантиметра. Проведите окружность с помощью циркуля.
— Возьмите любую точку на окружности. Соедините ее с центром окружности.
-Как называется этот отрезок?
(Радиус.)
-Окружность очень похожа на колесо.
-Колесо – одно из великих изобретений, которое было сделано в 4тыс.лет до н.э. на Древнем Востоке. Так вот, «радиус» переводится не иначе, как спица колеса.
-Что такое радиус?
3. Практическая часть.
Отрезок, который соединяет какую-нибудь точку
окружности с центром – радиус.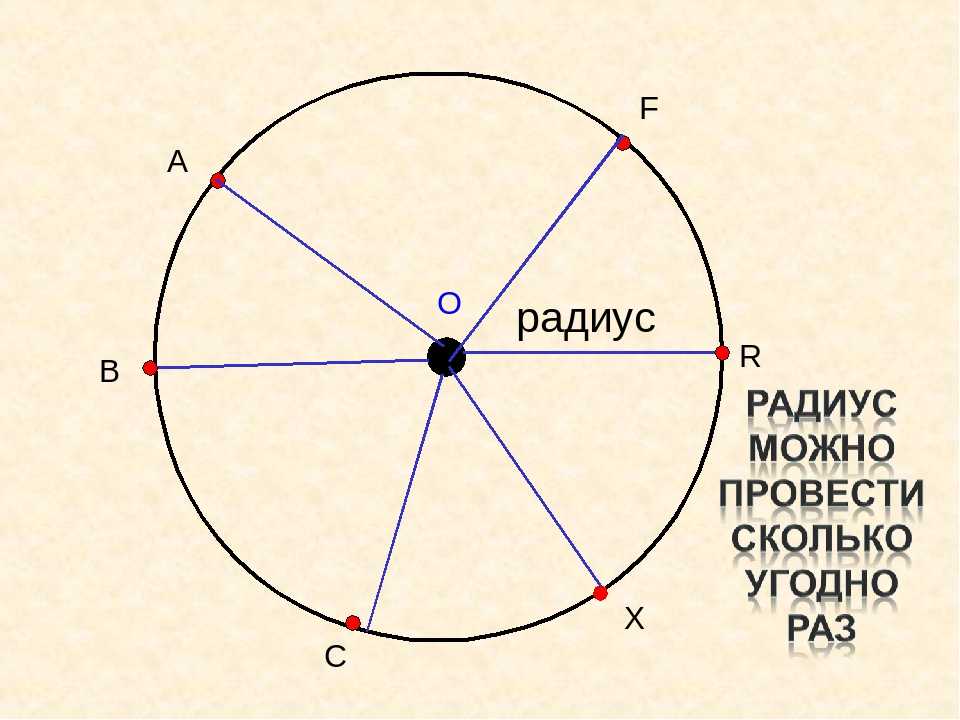
-Сколько радиусов можно провести в окружности?
(Бесконечное множество.)
— Проведите радиус вашей окружности.
-Что можно сказать о радиусах одной и той же окружности?
-Все радиусы одной окружности равны.
— Возьмите две точки на противоположенных сторонах окружности. Соедините их так чтобы они проходили через центр.
— У нас получился отрезок.
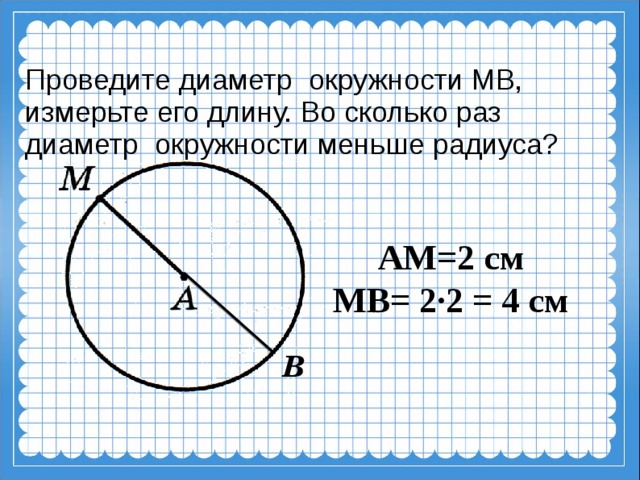
— Как он называется?(Диаметр).
Диаметр окружности- это отрезок который соединяет две противоположенные точки окружности через центр.
— Сколько диаметров можно провести в окружности? ( Бесконечно много).
— Проведите.
4. Выполнение теста.
Чтобы проверить, как вы усвоили тему, я предлагаю выполнить тест: (листочки с тестом у каждого ученика).
1. Окружность – это:
А. Замкнутая кривая линия.
Б. Ломаная линия с центром в точке О.
3. В. Замкнутая кривая линия, центр которой
одинаково удалён от всех точек окружности.
2. Диаметр — это:
А. Прямая, проходящая через центр окружности.
Б. Отрезок, соединяющий две любые точки окружности.
В. Отрезок, соединяющий две любые точки окружности и проходящий через её центр.
3. Все радиусы одной окружности:
А. Являются лучами.
Б. Равны между собой.
В. Имеют разную длину.
4. Радиус окружности – это:
А. Отрезок, соединяющий две точки окружности.
Б. Прямая, проходящая через центр.
В. Отрезок, соединяющий центр окружности и любую точку окружности.
V.Рефлексия.
Сегодня на занятии:
я узнал …
я научился…
порадовался тому, что…
— Спасибо за занятие. Мне очень понравилось, как вы работали.
4.
5. Окружность – душа геометрии.
Познайте окружность, и вы не только познаете душу геометрии, но и возвысите свою душу
Из истории.
В Древней
Греции круг и окружность считались венцом совершенства.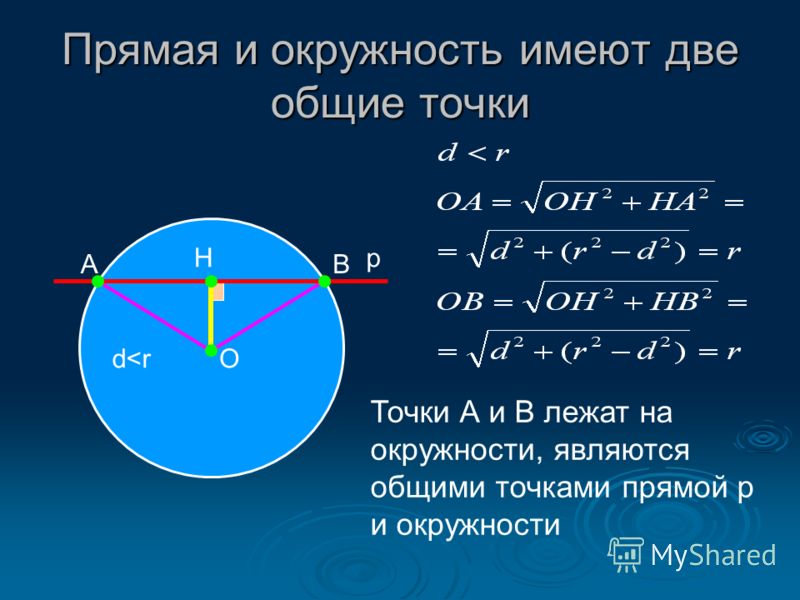
Действительно, в каждой своей точке окружность устроена одинаковым
образом, что позволяет ей двигаться самой по себе.
Это свойство окружности сделало возможным возникновение колеса,
поскольку ось и втулка колеса должны всё время быть в соприкосновении.
В русском языке слово «круглый» тоже означает высокую степень
чего-либо: «круглый отличник», «круглый сирота», и даже «круглый
дурак».
Ещё до колеса люди использовали круглые брёвна-катки
для перевозки тяжестей.
Рисунки на стенах египетских пирамид рассказывают нам,
что именно так доставлялись огромные камни на строительство
этих пирамид.
С помощью какого инструмента мы строим окружность?
С помощью циркуля.
Циркуль — чертежный инструмент. С ним нужно работать осторожно. Нельзя подносить к лицу или передать соседу «иглой вперед». Что это слово вам напоминает? ( Цирк и циркуль)
Слово
«циркус» в переводе с латинского означает ни что иное, как круг.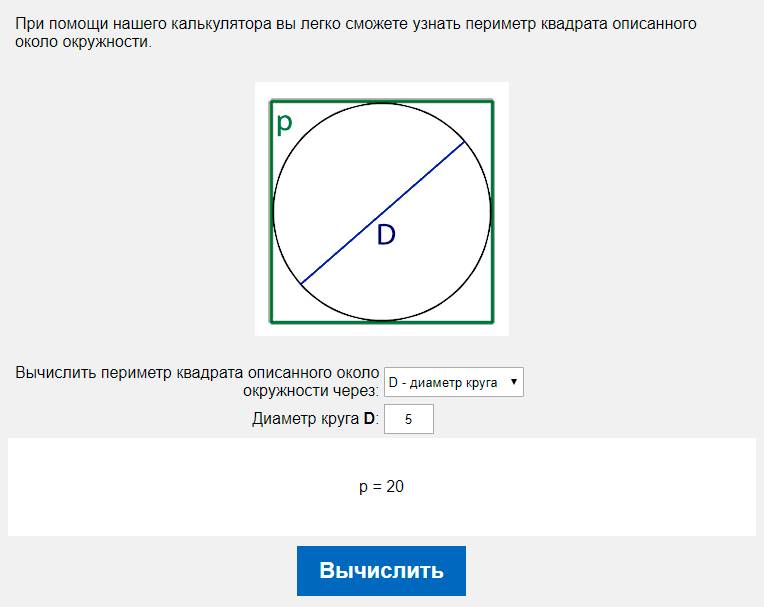
Как называется точка, которая остаётся от иголки у одной из ножек циркуля?
Центр окружности.
Слово «центр» произошло от латинского слова «центрум», которое означало палку с заостренным концом, которой погоняли быков; позднее оно означало ножку от циркуля, а потом и точку, которую оставляет циркуль на листе бумаги.
Как называется этот отрезок?
Радиус.
Окружность очень похожа на колесо.
Колесо – одно из великих изобретений, которое было сделано в 4тыс.лет до н.э. на Древнем Востоке. Так вот, «радиус» переводится не иначе, как спица колеса.
Что такое радиус?
Отрезок, который соединяет какую-нибудь точку окружности с центром – радиус.
Сколько радиусов можно провести в окружности?
Бесконечное множество.
Что можно сказать о радиусах одной и той же окружности?
Все радиусы одной окружности равны.
Такие орнаменты можно использовать для оформления различных предметов.
.
-Что можете сказать об окружностях?
Они
пересекаются.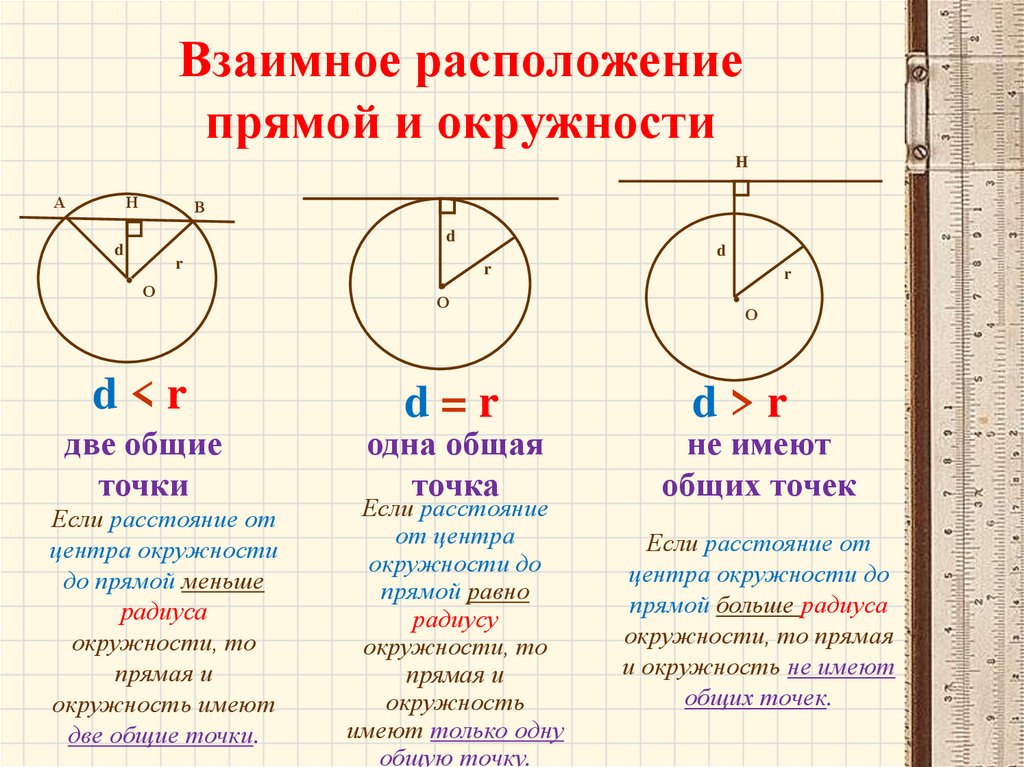
-Какой геометрической фигурой обозначим место
пересечения окружностей?
Точкой.
Соединяем эти точки.
Что получилось? (Отрезок)
Что соединяет отрезок? (2 точки на окружности)
Оказывается, в окружности, кроме радиуса, можно провести другие отрезки, которые будут соединять две любые точки окружности. Это хорды.
Итак, хорда – это отрезок, соединяющий две точки окружности.
Практическая работа.
Постройте окружность. Радиус окружности 3см. Проведите хорду. Слово «хорда» имеет несколько лексических значений. С этим словом вы встретитесь на уроках биологии.
Какие линии, кроме хорды есть в окружности?
Осевые линии.
Можно ли осевые линии назвать хордой? Почему?
Чем отличаются эти хорды от проведенных ранее хорд?
Проход через центр окружности.
Хорда, проходящая через центр окружности называется диаметром.
Диаметр обозначается буквой d .
Сколько диаметров можно провести в окружности? (Много)
Чему равен диаметр? (d=2r)
А можно ли найти радиус, если известен диаметр? Как? (r=d:2)
Итак, что мы теперь знаем об окружности?
- В окружности, кроме радиуса, можно провести хорду и диаметр
- Хорда- это отрезок, соединяющий две точки окружности;
- Диаметр – это отрезок, проходящий через центр окружности;
- «Диаметр»
в переводе с греческого поперечник.

Окружность и круг это пространственные тела или плоские фигуры?
Плоские.
А в какое геометрическое тело превратится окружность, если попадет в пространство? Шар.
Эксперимент.
Наиболее близки по форме к шару яблоки. Мы с вами сейчас проведем небольшой эксперимент. Возьмем нож и разрежем яблоко. Что у нас получилось в сечении? Круг.
Чем же круг отличается от окружности?
Круг – это площадь, ограниченная окружностью.
Окружность- это граница круга.
Закрепление.
Как называется эта фигура? Окружность.
Сколько в ней проведено радиусов, диаметров, хорд? (5,2,4)
Постройте в тетради окружность радиусом 3см.
Проведите два диаметра.
Хорд — ? 2
Диаметров — ? 2
Радиусов — ? 4
Подведение итогов.
Что нового узнали на уроке?
Чем отличается круг от окружности?
Оценивание урока.
6.
Тест
— Чтобы проверить, как вы усвоили тему, я предлагаю выполнить тест: (листочки с тестом у каждого ученика).
1. Окружность – это:
А. Замкнутая кривая линия.
Б. Ломаная линия с центром в точке О.
В. Замкнутая кривая линия, центр которой одинаково удалён от всех точек окружности.
2. Диаметр — это:
А. Прямая, проходящая через центр окружности.
Б. Отрезок, соединяющий две любые точки окружности.
В. Отрезок, соединяющий две любые точки окружности и проходящий через её центр.
3. Все радиусы одной окружности:
А. Являются лучами.
Б. Равны между собой.
В. Имеют разную длину.
4. Радиус окружности – это:
А. Отрезок, соединяющий две точки окружности.
Б. Прямая, проходящая через центр.
В. Отрезок, соединяющий центр окружности и любую точку окружности.
Взаимопроверка
—
Поменяйтесь, тетрадями, проверьте правильность выполнения работы.
2. Страница 61
— Все ли диаметры одной окружности равны между собой?
— Длина диаметра равна двум радиусам?
— Что такое радиус?
— Что такое диаметр?
-У вас на столе есть цветная бумага.
— А теперь я предлагаю вам вырезать круг радиусом 3 сантиметра.
● красный круг — если вам на уроке всё удалось
● зеленый круг – если у вас остались неразрешённые проблемы
● синий круг – если вам ещё понадобится помощь
— Давайте вспомним технику безопасности работы с циркулем, ножницами.
4. Практическая работа
5. Продолжите предложения.
Сегодня на уроке:
я узнал …
я научился…
порадовался тому, что…
— Спасибо за урок. Мне очень понравилось, как вы работали.
Q4 Верно или неверно a Два диаметра окружности обязательно пересекутся b Центр окружности.
 ..
..Перейти к
- Упражнение 4.1
- Упражнение 4.2
- Упражнение 4.3
- Упражнение 4.4
- Упражнение 4.5
- Упражнение 4.6
- Зная наши цифры
- Целые числа
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 4. Основные геометрические идеи
>
Упражнение 4.6
>
Вопрос 7
Основные геометрические идеи
>
Упражнение 4.6
>
Вопрос 7
Вопрос 7 Упражнение 4.6
В4) Скажите верно или неверно:
(а) Два диаметра окружности обязательно пересекутся.
(б) Центр круга всегда находится внутри его.
Ответ:
Решение 4:
(a) Верно.
(б) Верно.
Стенограмма видео
«Привет, ребята, добро пожаловать в Лидо домашнее задание сегодня мы делаем вопрос номер четыре что является истинным или ложным, так что это очень простое упражнение, поэтому первое это два диаметра окружности с необходимые обязательно пересекутся так это точно правильно потому что, например, если у вас есть круг вот так здесь хорошо, так что позвольте мне просто увеличить его размер хорошо, теперь предположим, что это был ваш круг прямо сейчас, например, есть диаметр, который проходит через вот так нормально и есть еще диаметр такой поэтому диаметры всегда должны быть пересекаются в одной точке который является центром круга хорошо Итак, первый пункт первый ответ абсолютно верный хорошо, что первое верно давайте перейдем ко второму центр круга всегда находится в его интерьер как вы можете видеть, это центр справа вот и центр всегда собирается быть внутри, потому что когда вы рисуете с помощью компаса, вы держите компас посередине справа от вас держите стрелку компаса, это будет всегда оставайся в центре, этого не будет снаружи здесь поэтому второй тоже правда ладно, вот и все, ребята, если у вас есть сомнения, пожалуйста, напишите это в комментарии раздел, пожалуйста, лайкните видео и подпишитесь на наш канал большое спасибо»
Связанные вопросы
По рисунку определите: (а) центр окружности (б) три радиуса (в) диаметр (г) хорду (д) две точки. ..
..
Q1) По рисунку определите: (a) центр окружности (b) три радиуса (c) диаметр (d) хорду (e)…
Q2) (a) Является ли каждый диаметр окружности также хордой? (b) Является ли каждая хорда окружности также диаметром?
а) Является ли каждый диаметр окружности также хордой? (б) Является ли каждая хорда окружности также диаметром?
Начертите любой круг и отметьте (а) его центр (б) радиус (в) диаметр (г) сектор (д) сегмент (е) точку…
Q3) Нарисуйте любой круг и отметьте (а) его центр (б) радиус (в) диаметр (г) сектор (д) сегмент (е) …
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Задание
Задание 4. 1
1
Задание 4.2
Задание 4.3
Задание 4.4
Задание 4.5
Задание 4.6
Главы
Знание наших чисел
Целые числа
играют с номерами
Основные геометрические идеи
Понимание элементарных форм
Интеллект
Фракции
DECIMAL
Симметрия
Практическая геометрия
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Круги и использование компаса
Части круга
Дуга является частью окружности.
Сектор является частью окружности между двумя радиусами.
Сегмент — это часть окружности, находящаяся между хордой и окружностью.
A полукруг является половиной круга.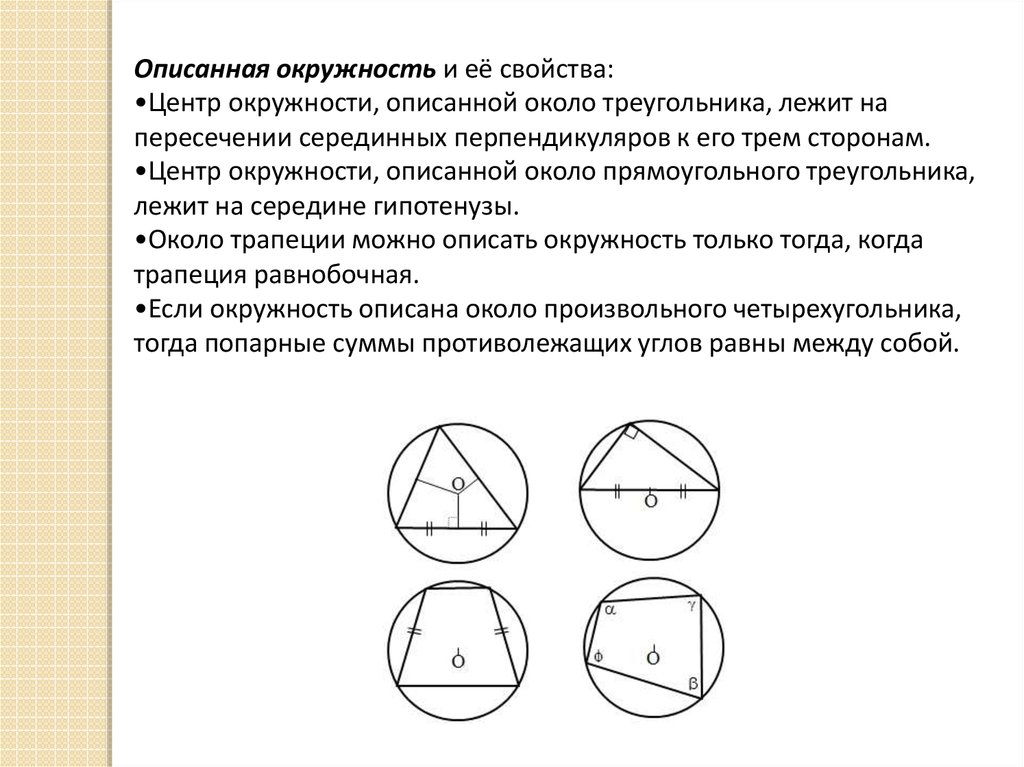
Компас
Компас — это инструмент, используемый для рисования кругов или частей окружности, называемые дугами. Он состоит из двух подвижных рычагов, шарнирно соединенных между собой. где одна рука имеет заостренный конец, а другая рука держит карандаш.
Обратите внимание, что компас также называют компасом.
Чтобы нарисовать окружность (или дугу) с помощью компаса:
- убедитесь, что шарнир в верхней части компаса затянут, чтобы не скользил
- затяните крепление для карандаша, чтобы он тоже не выскальзывал
- совместите грифель карандаша со стрелкой компаса
- нажмите на иглу и поверните ручку в верхней части циркуль для рисования окружности (или дуги)
Пример 2
С помощью циркуля начертите круг радиусом 4 см.
Решение:
Шаг 1: С помощью линейки установите расстояние от точки компаса до
грифель карандаша на 4 см.
Шаг 2: Поместите острие компаса в центр круга.
Шаг 3: Нарисуйте круг, повернув циркуль на 360°.
Деятельность 10.1
1. С помощью циркуля начертите окружность радиусом 5 см.
2. С помощью циркуля начертите круг диаметром 12 см.
3а. С помощью циркуля начертите окружность радиусом 4,5 см.
3б. Нарисуйте диаметр круга; и с помощью линейки измерьте
длина диаметра.
3с. Напишите уравнение, представляющее отношение между радиусом r ,
и диаметр д .
4а. С помощью циркуля начертите окружность радиусом 5,5 см.
4б. Начертите диаметр и обозначьте его PQ .
4с. Нарисуйте треугольник PQR , где R находится на полуокружности.

