Сколько комбинаций из 3 цифр от 1 до 3: Сколько трех значных чисел можно составить из цифр 4, 6,8, если в записи цифры не…

Сколько может быть вариантов ПИН-кода?

Статьи › Карта › Что делать если забыл пин код от карты?

Четырехзначный PIN-код можно использовать для создания 10 тыс. различных комбинаций, а шестизначный — для создания 1 млн. Однако пользователи предпочитают определенные наборы чисел и используют их намного чаще, например, 123456 и 654321, — пояснили эксперты.

1. Сколько вариантов пароля из 4 цифр?
2. Как узнать количество комбинаций кода?
3. Сколько вариантов подбора пароля из 6 цифр?
4. Какой шанс угадать 6 значный код?
5. Какие 4 значные пароли?
6. Сколько вариантов 3 цифр?
7. Сколько комбинаций из 999 цифр?
8. Сколько вариантов комбинаций из 24 цифр?
9. Сколько комбинаций 10 цифр?
10. Какие могут быть пин коды?
11. Как рассчитать все возможные варианты?
12. Сколько вариантов пароля из 6 букв?
13. Какие пароли обычно выбирают люди?
14. Сколько вариантов 6 значного кода можно составить из цифр 4 5 6 7 8 9?
15. Сколько комбинаций из 4 проводов?
16. Сколько комбинаций из цифр 1 2 3 4?
17. Как посчитать количество комбинаций кодового замка?
18. Сколько нужно цифр для пароля?

Сколько вариантов пароля из 4 цифр?

Можно сказать что это числа от 0 до 9999. 3=1000. Ваш кодовый замок имеет 1000 комбинаций паролей.

Сколько комбинаций из 999 цифр?

999). Всего комбинаций из цифр и букв может быть: 676 × 9 999 999 = 6 759 999 324 (6 млрд.

Сколько вариантов комбинаций из 24 цифр?

Вы немного ошиблись, комбинаций не 12, а из 24 чисел по 12 есть почти 3 млн. комбинаций, точнее 2 704 156 комбинаций.

Сколько комбинаций 10 цифр?

Номер автомобиля состоит из трех букв и трех цифр. Сколько различных номеров можно составить, используя 10 цифр и алфавит в 30 букв. Очевидно, что количество всех возможных комбинаций из 10 цифр по 4 равно 10.000.

Какие могут быть пин коды?

Наиболее распространенными четырехзначными PIN-кодами оказались 1234, 0000, 2580, 1111, 5555, 5683, 0852, 2222, 1212 и 1998, а шестизначными — 123456, 654321, 111111, 000000, 123123, 666666, 121212, 112233, 789456 и 159753.

Как рассчитать все возможные варианты?

Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n!(n−k)!⋅k!.

Сколько вариантов пароля из 6 букв?

N = 6*5*4*3*2*1 = 720 Ответ: 720. Как добавить хороший ответ?

Какие пароли обычно выбирают люди?

Топ-10 самых используемых паролей в России выглядит так:

• 123456;
• qwerty;
• 123456789;
• 12345;
• password;
• qwerty123;
• 1q2w3e;
• 12345678;

Сколько вариантов 6 значного кода можно составить из цифр 4 5 6 7 8 9?

= 1 * 2 * 3 = 6 комбинаций, следовательно, существует тоже 6 шестизначных чисел, удовлетворяющих условию задачи: 567489; 567498; 567849; 567894; 567948; 567984.

Сколько комбинаций из 4 проводов?

И подсчитать все возможные комбинации, то это будет 4 в 4й степени. Это 256 комбинаций.

Сколько комбинаций из цифр 1 2 3 4?

Следовательно комбинаций будет: 4 * 3 * 2 * 1 = 4! = 24.

Как посчитать количество комбинаций кодового замка?

Есть два варианта расчета количества комбинаций кодового замка по количеству его цифр. Если имеется линейная зависимость — например, замок чемодана или пин-код карточки — то число сочетаний равно N=K*K*K, то есть 1000 комбинаций, все число в промежутке 1-999 и тысячное число 000.

Сколько нужно цифр для пароля?

Что такое безопасный пароль

Хороший пароль — всегда комбинированный. В нем используются символы, буквы и цифры разного регистра. Длина пароля — желательно не менее 8 символов, а лучше не менее 12. Избегайте смысловых паролей: не используйте распространенные фразы или слова.

Сколько комбинаций можно составить из 4 цифр?

Магазины › Фикс Прайс › Замок из Фикс Прайса кодовый как открыть

Можно сказать что это числа от 0 до 9999. Значит всего возможных комбинаций 10 000. Ответ: 10 000 комбинаций.

1. Сколько комбинаций можно составить из цифр 1 2 3 4?
2. Какой шанс угадать пароль из 4 цифр?
3. Какой может быть пароль из 4 цифр?
4. Сколько комбинаций из 3 цифр 1 2 3 4 без повторений?
5. Какое количество комбинаций из 3 цифр?
6. Сколько комбинаций из 6 цифр с повторений?
7. Сколько возможных комбинаций пароля?
8. Как посчитать количество комбинаций цифр?
9. Как угадать пароль от карточки?
10. Как поставить пароль на 4 цифры?
11. Какой самый сложный пароль из цифр?
12. Какие люди ставят пароли?
13. Сколько комбинаций из 999 цифр?
14. Сколько комбинаций из 10 цифр без повторений?
15. Сколько четных трехзначных чисел можно составить из цифр 3 4 5 6 цифры не могут повторяться?
16. Сколько комбинаций из 5 цифр 12345?
17. Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5 6 без повторений?
18. Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5?
19. Какой самый лучший пин код?
20. Какой шанс угадать 6 цифр?
21. Как должен выглядеть пароль?
22. Что люди чаще всего ставят на пароль?
23. Что не должен содержать пароль?
24. Сколько четырехзначных чисел можно составить из цифр 1 2 3 4 если цифры в числе не повторяются?
25. Как посчитать количество комбинаций без повторений?
26. Сколько четырехзначных чисел можно составить из цифр 1 3 5 7 9?
27. Сколько комбинаций из 4 цифр от 1 до 2?
28. Как рассчитать количество возможных комбинаций?
29. Сколько комбинаций можно составить из 8 цифр?

Сколько комбинаций можно составить из цифр 1 2 3 4?

Следовательно комбинаций будет: 4 * 3 * 2 * 1 = 4! = 24.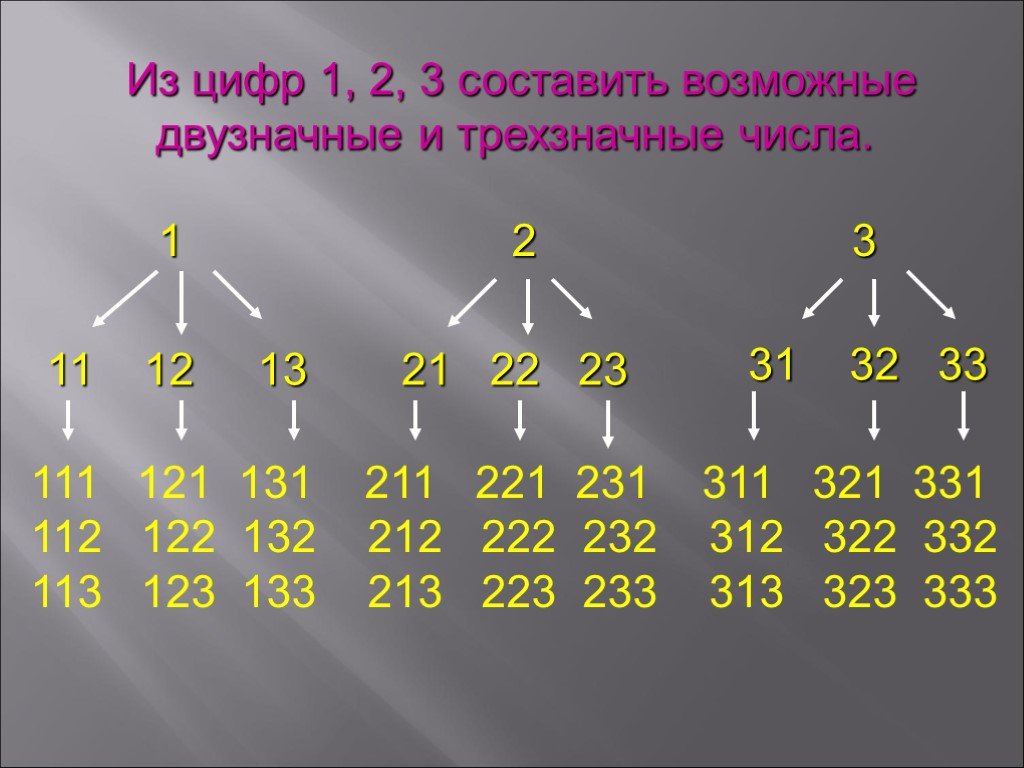

Какой шанс угадать пароль из 4 цифр?

0000, 1111, 2222, 3333, 4444, 5555, 6666, 7777, 8888, 9999. Если считать, что pin-код выбирается случайным образом, то вероятность что он состоит из четырех одинаковых цифр: 10 / 10000 = 0,001. Ответ: 0,001.

Какой может быть пароль из 4 цифр?

Наиболее распространенными четырехзначными PIN-кодами оказались 1234, 0000, 2580, 1111, 5555, 5683, 0852, 2222, 1212 и 1998, а шестизначными — 123456, 654321, 111111, 000000, 123123, 666666, 121212, 112233, 789456 и 159753.

Сколько комбинаций из 3 цифр 1 2 3 4 без повторений?

Рассмотрим комбинации из трёх цифр 1,2,3 без повторений. Таких комбинаций 6.

Какое количество комбинаций из 3 цифр?

3 = 60 способов расстановки цифр, т. е. искомое количество трехзначных чисел есть 60. (Вот некоторые из этих чисел: 243, 541, 514, 132, )

Сколько комбинаций из 6 цифр с повторений?

Допустим, есть шесть цифр. То есть N=6, и число возможных комбинации N!, 6!= 720 вариантов. k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, k — длина пароля.

Как посчитать количество комбинаций цифр?

Формула для определения количества возможных комбинаций выглядит следующим образом: nCr = n! / р!

Как угадать пароль от карточки?

PIN-код (персональный идентификационный номер) — набор цифр платежной карты, известен только держателю карты для его идентификации при осуществлении операций. Он генерируется таким образом, что его не знает ни один сотрудник (даже тот, кто выдавал вам конверт с кодом), его нельзя посмотреть ни в одной системе банка.

Как поставить пароль на 4 цифры?

Шаг 1: Откройте приложение «Настройки» и перейдите к «Touch ID и пароль». Вам нужно будет ввести шестизначный пароль для доступа к этому меню. Шаг 2: Прокрутите вниз и коснитесь параметра «сменить код-пароль. Шаг 3: Введите существующий шестизначный пароль для продолжения.

Какой самый сложный пароль из цифр?

Очень сложным и самым лучшим считается пароль от 10-12 символов длиной, с использованием заглавных, прописных букв, цифр и спецсимволов: L2jh4d61e%Fh — пример сложного и стойкого пароля.

Какие люди ставят пароли?

В частности, в десятку самых популярных паролей вошли: 123456, 123456789, qwerty, password, 12345, qwerty123, 1q2w3e, 12345678, 111111, 1234567890.

Сколько комбинаций из 999 цифр?

999). Всего комбинаций из цифр и букв может быть: 676 × 9 999 999 = 6 759 999 324 (6 млрд. 759 млн.

Сколько комбинаций из 10 цифр без повторений?

Можно сказать, что это 10-тизначное число в 36-ричной системе счисления. Количество комбинаций будет равно 3610 или 3,6561584×1015. Если символы не могут повторяться, то мы имеем дело с размещениями.

Сколько четных трехзначных чисел можно составить из цифр 3 4 5 6 цифры не могут повторяться?

Ответ: Можно составить 32 трехзначных четных числа.

Сколько комбинаций из 5 цифр 12345?

Комбинаторика. Сколько всего возможных комбинаций из пяти чисел 12345, да 120, надо лишь эти числа между собой перемножить 12345=120, но есть одно «но» нужно подсчитать еще и такие варианты как например 11234, 11123, 11112, 12234, 12333, 12222, 12344 и т.

Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5 6 без повторений?

Ответ: Можно составить 120 чисел.

Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5?

ПРИМЕР 3. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? И сколько из них с неповторяющимися цифрами? = 5× 4×3 = 60.

Какой самый лучший пин код?

Анализ позволил выявить несколько интересных фактов. Самым популярным PIN-кодом является 1234, его устанавливают почти 11% пользователей. На втором месте идёт 1111 (6%). Двадцатка самых популярных комбинаций покрывает 26,83% всех паролей, хотя при нормальном статистическом распределении она составляла бы всего 0,2%.

Какой шанс угадать 6 цифр?

Совпадение 6 чисел — шанс 0,00000012 (в процентном выражении — 0,000012%). Совпадение 5 чисел — шанс 0,000029 (0,0029%).

Как должен выглядеть пароль?

Что такое надежный пароль?:

• Не менее 12 символов. Чем длиннее ваш пароль — тем лучше.
• Содержит прописные и строчные буквы, цифры и специальные символы.
• Не содержит буквы или цифры, которые идут подряд в раскладке.
• Не основан на вашей личной информации.
• Пароль уникален для каждой вашей учетной записи.

Что люди чаще всего ставят на пароль?

Топ-10 самых используемых паролей в России выглядит так:

• 123456789;
• 12345;
• password;
• qwerty123;
• 1q2w3e;
• 12345678;
• 1234567890;
• 1q2w3e4r5t.

Что не должен содержать пароль?

Пароли НЕ ДОЛЖНЫ состоять из: Вашего имени, отчества или фамилии ни в каком виде (т. е. написаны в строчном, в прописном, в смешанном виде, задом наперед, два раза и т.

Сколько четырехзначных чисел можно составить из цифр 1 2 3 4 если цифры в числе не повторяются?

Ответ. Всего из этих цифр можно составить 120 чисел, без повтора цифр внутри них.

Как посчитать количество комбинаций без повторений?

Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n! (n−k)! ⋅k!. 15.

Сколько трехзначных чисел можно составить из цифр 1, 2 и 3?

Система счисления — это математическое значение, используемое для счета и измерения объектов, а также для выполнения арифметических вычислений. Это система письма для выражения чисел. Он дает особое представление каждому числу и представляет арифметическую и алгебраическую форму числа. Это позволяет нам выполнять арифметические операции, такие как сложение, вычитание, умножение и деление.

Уравнение — это оператор, который соединяет два алгебраических выражения с одинаковыми значениями с помощью знака «=». Например: В уравнении 9x + 4 = 7, 9x + 4 — выражение в левой части, а 7 — выражение в правой части, связанное знаком «=».

Что такое число?

Слово или символ, обозначающий количество, называется числом. Числа 2, 4, 6 и т. д. — четные числа, а 1, 3, 5 и т. д. — нечетные числа. Число — это значение, созданное слиянием целых чисел. Эти числа используются для представления алгебраических величин. Целое число — это знак из набора из 10 символов в диапазоне от 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Любая комбинация целых чисел представляет число. Размер числа зависит от количества цифр, которые используются для его формирования. Например: 126, 128, 0,356, -12, 78, 94 и т. д.

Типы чисел

Числа бывают разных типов в зависимости от шаблонов цифр, которые используются для их создания. Различные символы и правила также применяются к числам, которые классифицируют их по различным типам:

• Целые числа : Целые числа представляют собой набор целых чисел плюс отрицательные значения натуральных чисел. Целые числа не включают дробные числа, т. е. их нельзя записать в форме a/b. Диапазон целых чисел — от бесконечности на отрицательном конце до бесконечности на положительном конце, включая ноль. Целые числа представлены символом З . Целые числа — это числа, дробная часть которых равна 0, например -3, -2, 1, 0, 10, 100.
• Натуральные числа: Натуральные числа — это числа в диапазоне от 1 до бесконечности. Эти числа также известны как положительные числа или счетные числа. Мы также можем представить Натуральные числа символом N . Все целые числа, которые больше 0, являются натуральными числами. Счетные числа, такие как 1, 2, 3, 4, 5, 6.
• Целые числа: Целые числа такие же, как натуральные числа, но они также включают «ноль». . Целые числа также могут быть представлены символом Вт . Целые числа — это все натуральные числа и 0 (ноль).
• Простые числа и составные числа: Все те числа, которые имеют только два различных делителя, само число и 1, называются простыми числами. Все числа, которые не являются простыми числами, называются составными числами, кроме 0. Ноль не является ни простым, ни составным числом. Некоторые простые числа: 2, 3, 5, 53, 59, 97 и 191. Все числа больше 1 являются составными числами. Некоторые составные числа 4, 6, 9, 15, 16 и 100.
• Дроби: Дроби — это числа, записанные в виде a/b , где a принадлежит целым числам, а b принадлежит натуральным числам, т. е. b никогда не может быть 0. Верхняя часть дроби, т. е. a, называется числителем, тогда как нижняя часть, т. е. b, называется знаменателем. Пример: -1/5, 0,25, 2/5, 18/4,…
• Рациональные числа: Рациональные числа — это числа, которые могут быть представлены в форме дроби, т. е. a/b. Здесь a и b оба являются целыми числами и b ≠ 0. Все дроби — рациональные числа, но не все рациональные числа — дроби. Пример: -2/5, 0,54, 1/5, 13/4,…
• Иррациональные числа: Иррациональные числа — это числа, которые нельзя представить в виде дробей, т. е. их нельзя записать в виде a/b. Пример: √2, √3, √.434343, π,…
• Действительные и мнимые числа: Действительные числа — это числа, которые могут быть представлены в десятичной форме. Эти числа включают целые числа, целые числа, дроби и т. д. Все целые числа принадлежат к действительным числам, но не все действительные числа принадлежат к целым числам. Воображаемые числа — это все те числа, которые не являются реальными числами. Эти числа при возведении в квадрат дадут отрицательное число. √-1 представлен как i. Эти числа также называются комплексными числами. Пример: √-2, √-5,…

Перестановки и комбинации  

Перестановка – это различное расположение определенного количества компонентов, взятых по одному, по частям или по всем одновременно. Например, если у нас есть два компонента X и Y, то есть два возможных расположения: XY и YX.

Количество перестановок, когда элементы «r» расположены из общего числа «n» элементов, составляет 

ⁿ P _r = n!/(n – r)!  

Например, пусть n = 4 (A, B, C и D) и r = 2 (все перестановки размера 2). Ответ 4!/(4-2)! = 12. Итак, двенадцать перестановок — это AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB и DC.

Комбинация – это различные наборы определенного количества компонентов, взятые по одному, по частям или все вместе. Например, если у нас есть два компонента A и B, то есть только один способ выбрать два элемента, мы выбираем их оба.

Количество комбинаций при выборе ‘r’ элементов из ‘n’ элементов равно 

ⁿ C _r = n!/[(r!) × (n – r)!]

Например, пусть n = 4 (A, B, C и D) и r = 2 (все комбинации размера 2). Ответ: 4!/((4-2)! × 2!) = 6. Итак, шесть комбинаций: AB, AC, AD, BC, BD, CD.

ⁿ C _r = ⁿ C _{(n –r)}

Примечание: В том же примере у нас есть разные случаи перестановки и комбинации. Если говорить о перестановке, то АВ и ВА — разные вещи, но для отбора АВ и ВА — одно и то же.

Сколько трехзначных чисел можно составить из цифр 1, 2 и 3?

(i) разрешено ли повторение цифр?

Решение:

Ответ: 27

Метод:

Здесь общее количество цифр = 3

Предположим, что трехзначное число равно ABC.

Теперь количество цифр, доступных для A=3

Поскольку повторение разрешено,

Таким образом, количество цифр, доступных для B и C, также будет 3 (каждая).

Таким образом, общее количество трехзначных чисел, которые можно составить = 3 × 3 × 3 = 27

(ii) повторение цифр не допускается?

Решение:

Ответ: 6

Метод:

Здесь общее количество цифр = 3

число ABC.

Теперь количество цифр, доступных для A = 3,

Поскольку повторение не разрешено,

Таким образом, количество цифр, доступных для B = 2 (поскольку одна цифра уже была выбрана в A),

Аналогично, количество цифр, доступных для C = 1,

Таким образом, общее количество трехзначных чисел, которые можно составить = 3 × 2 × 1 = 6,

Похожие вопросы

Вопрос 1: Сколько трехзначных чисел можно составить из четырех цифр 1, 2, 3, 4?

(i) разрешено ли повторение цифр?

Решение:

Ответ: 64

Метод:

Здесь общее количество цифр = 4 цифра.

Теперь количество цифр, доступных для A=4

Поскольку повторение разрешено,

Таким образом, количество цифр, доступных для B и C, также будет 4 (каждая).

Таким образом, общее количество трехзначных чисел, которые можно составить = 4 × 4 × 4 = 64

(ii) повторение цифр не допускается?

Решение:

Ответ: 24

Метод:

Здесь общее количество цифр = 4

Предположим, что трехзначное число равно ABC.

Теперь количество цифр, доступных для A = 4,

Поскольку повторение запрещено,

Таким образом, количество цифр, доступных для B = 3 (поскольку одна цифра уже была выбрана в A),

Аналогично, количество цифр, доступных для C = 2.

Таким образом, Общее количество трехзначных чисел, которые можно составить = 4 × 3 × 2 = 24

Вопрос 2: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, , и 5 при условии, что –  

(i) повторение цифр разрешено?

Решение:

Ответ: 125

Метод:

Здесь общее количество цифр = 5

Пусть трехзначное число будет ABC.

Теперь количество цифр, доступных для A = 5,

Поскольку повторение разрешено,

Таким образом, количество цифр, доступных для B и C, также будет 5 (каждая).

Таким образом, общее количество трехзначных чисел, которые можно составить = 5 × 5 × 5 = 125.

(ii) повторение цифр не допускается?

Решение:

Ответ: 60

Метод:

Здесь общее количество цифр = 5

Пусть трехзначное число будет ABC.

Теперь количество цифр, доступных для A = 5,

Поскольку повторение не разрешено,

Таким образом, количество цифр, доступных для B = 4 (поскольку одна цифра уже была выбрана в A),

Аналогично, количество цифр, доступных для C = 3,

Таким образом, общее количество трехзначных чисел, которые можно составить = 5 × 4 × 3 = 60,

Вопрос 3: Сколько трехзначных четных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, если цифры могут повторяться?

Решение:

Ответ: 108

Метод:

Здесь общее количество цифр = 6

3 900.

Теперь, поскольку число должно быть четным, цифры в разряде единиц должны быть четными, поэтому число

цифр, доступных для C = 3 (поскольку 2, 4, 6 здесь четные цифры),

Поскольку повторение разрешено,

Таким образом, количество цифр, доступных для A = 6,

Аналогично, количество доступных цифр для B = 6.

Таким образом, общее количество трехзначных четных чисел, которые могут быть сформированным = 6 × 6 × 3 = 108

Вопрос 4: Сколько четырехбуквенных кодов можно составить из первых 10 букв английского алфавита, если ни одна буква не повторяется?

Решение:

Ответ: 5040

Метод:

Здесь общее количество букв = 10

Пусть 4-буквенный код будет 1234.

Теперь количество букв, доступных для 1-го места = 10,

Поскольку повторение запрещено ,

Таким образом, возможное количество букв на 2-м месте = 9 (Поскольку одна буква уже была выбрана на 1-м месте

),

Аналогично, количество букв, доступных для 3-го места = 8,

и количество буквы доступны для 4-го места = 7.

Таким образом, общее количество 4-буквенных кодов, которые можно составить = 10 × 9 × 8 × 7 = 5040

Как найти наибольшее или наименьшее количество комбинаций

Все математические ресурсы PSAT

10 Диагностика Тесты 421 практический тест Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

PSAT Math Help » Арифметика » Целые числа » Перестановка / Комбинация » Как найти наибольшее или наименьшее количество комбинаций

У Марка в шкафу 5 брюк и 7 рубашек. Он хочет носить новую комбинацию брюк и рубашки каждый день, не покупая новую одежду, как можно дольше. Сколько недель он может это делать?

Возможные ответы:

Правильный ответ:

5

Объяснение:

Фундаментальный принцип подсчета гласит, что если вы хотите определить количество способов, которыми могут произойти два независимых события, умножьте количество способов, которыми каждое событие может произойти вместе. В этом случае есть 5 * 7 или 35 уникальных комбинаций брюк и рубашек, которые может носить Марк. Если он носит одну комбинацию каждый день, он может продержаться 35 дней или 5 недель, не покупая новую одежду.

Сообщить об ошибке

Двадцать учеников участвуют в школьном конкурсе. Конкурс предлагает первый, второй и третий приз. Сколько различных комбинаций 1-го, 2-х ^-х, -х и 3-х мест может быть?

Возможные ответы:

400

8000

6840

20

4620

Правильный ответ:

6840

Объяснение:

Это задача на перестановку, потому что мы ищем количество групп победителей. Рассмотрите три позиции и количество вариантов для каждой позиции: есть 20 вариантов для 1-го места, 19за 2 место и 18 за 3 место.

20, 19, 18     

Умножьте, чтобы получить 6840.

Сообщить об ошибке

У пекаря есть четыре разных вида глазури, три разных вида посыпки и 8 разных формочек для печенья. Сколько различных комбинаций печенья может создать пекарь, если каждое печенье имеет один тип глазури и один тип посыпки?

 

Возможные ответы:

96

24

15

48

Правильный ответ:

96

Объяснение:

Так как это проблема комбинирования, и мы хотим знать, сколько различных способов могут быть созданы файлы cookie, мы можем решить ее, используя фундаментальный принцип подсчета. 4 x 3 x 8 = 96

Перемножение всех возможных вариантов.

 

 

 

Сообщить об ошибке

Если необходимо изготовить серию номерных знаков, каждая из которых имеет один и тот же образец из трех букв, за которыми следуют три цифры, сколько примерно буквенно-цифровых комбинаций возможно?

Возможные ответы:

1 тысяча

11 миллионов

180 млн.

18 тысяча

18 млн.

Правильный ответ:

18 млн.

Объяснение:

Общее количество возможных комбинаций ряда элементов равно произведению общей возможности для каждого из элементов. Таким образом, для букв есть 26 возможностей для каждого из 3-х слотов, а для чисел есть 10 возможностей для каждого из 3-х слотов. Тогда общее количество комбинаций равно: 26 х 26 х 26 х 10 х 10 х 10 = 17 576 000 ≈ 18 миллионов.

Сообщить об ошибке

Если на плоскости 8 точек, и никакие 3 из них не лежат на одной прямой, сколько уникальных прямых можно провести между парами этих 8 точек?

Возможные ответы:

30

27

28

29

Правильный ответ:

28

Объяснение:

Формула для количества прямых, определяемых n точками, никакие три из которых не лежат на одной прямой (коллинеарными), равна n(n-1)/2.

Чтобы найти количество линий, определяемое 8 точками, мы используем 8 в формуле, чтобы найти 8(8-1)/2=8(7)/2=56/2=28. (Формула получена из двух фактов: того факта, что каждая точка образует прямую с каждой другой точкой, следовательно, n(n-1), и того факта, что это отношение симметрично (т. е. если a образует прямую с b, то b образует линию с a), следовательно, деление на 2.)

 

 

Сообщить об ошибке

8 человек, запертых в комнате, по очереди берутся за руки с каждым человеком только один раз. Сколько захватов рук происходит?

Возможные ответы:

28

15

21

24

Правильный ответ: 930 30

280002

Пояснение:

Первый человек держит 7 рук. Второй держит шестерых в силу уже имеющейся помощи руки первого человека. Так продолжается до тех пор, пока не пройдут все 8 человек. 7+6+5+4+3+2+1=28.

Сообщить об ошибке

В магазине мороженого есть 5 вкусов мороженого: клубничное, ванильное, шоколадное, мятное и банановое. Сколько разных рожков для мороженого с тремя вкусами можно сделать?

Возможные ответы:

5

30

10

20

60

Правильный ответ:

10

Объяснение:

Есть 5x4x3 способов расположить 5 вкусов 3 способами. Однако в этом случае порядок вкусов не имеет значения (например, рожок с клубникой, мятой и бананом такой же, как рожок с мятой, бананом и клубникой). Итак, мы должны разделить 5x4x3 на количество способов, которыми мы можем расположить 3 разных вещи, то есть 3x2x1. Итак, (5x4x3)/(3x2x1) равно 10,  

Можно также использовать формулу комбинации для этой задачи:  _n C _r = n! / (н-р)! р!

Следовательно: ₅ C ₃ = 5! / 3! 2!

= 10

 

(Примечание. Примером задачи подсчета, в которой порядок имеет значение, является ситуация с замком или кодом доступа. Перестановка 3-5-7 для трехзначного замка или кода доступа отличается от 5- 7-3, поэтому оба должны учитываться.)

Сообщить об ошибке

В гастрономе вы можете выбрать итальянский хлеб, цельнозерновой хлеб или хлеб на закваске. Вы можете выбрать индейку или ростбиф в качестве мяса и проволоне или моцареллу в качестве сыра. Если вам нужно выбрать хлеб, мясо и сыр, сколько возможных комбинаций бутербродов у вас может быть?

Возможные ответы:

12

10

14

7

8

Правильный ответ:

12

Пояснение:

У вас есть 3 возможных вида хлеба, 2 возможных вида мяса и 2 возможных вида сыра. Умножая их, вы получаете 3*2*2, что дает вам 12 возможных комбинаций.

Сообщить об ошибке

Шеннон решила пойти пообедать в соседнее кафе. Она может приготовить бутерброд на пшеничном или белом хлебе. Кафе предлагает выбор сыра чеддер, швейцарский и американский. Из мяса Шеннон может выбрать ветчину, индейку, колбасу, ростбиф или салями. Сколько вариантов сэндвичей с сыром и мясом есть на выбор у Шеннон?

Возможные ответы:

35

20

10

30

25

Правильный ответ:

30

Объяснение:

2 варианта хлеба * 3 варианта сыра * 5 вариантов мяса = 30 вариантов сэндвичей

Сообщить об ошибке

Кафе-мороженое предлагает 36 вкусов мороженого. Вы можете заказать любой вкус в маленьком, среднем или большом размере и выбрать между вафельным рожком и чашкой. Сколько возможных комбинаций вы могли бы заказать?

Возможные ответы:

108

172

144

216

72

Правильный ответ:

216

Пояснение:

36 возможных вкусов * 3 возможных размера * 2 возможных конуса = 216 возможных комбинаций.

No related posts.