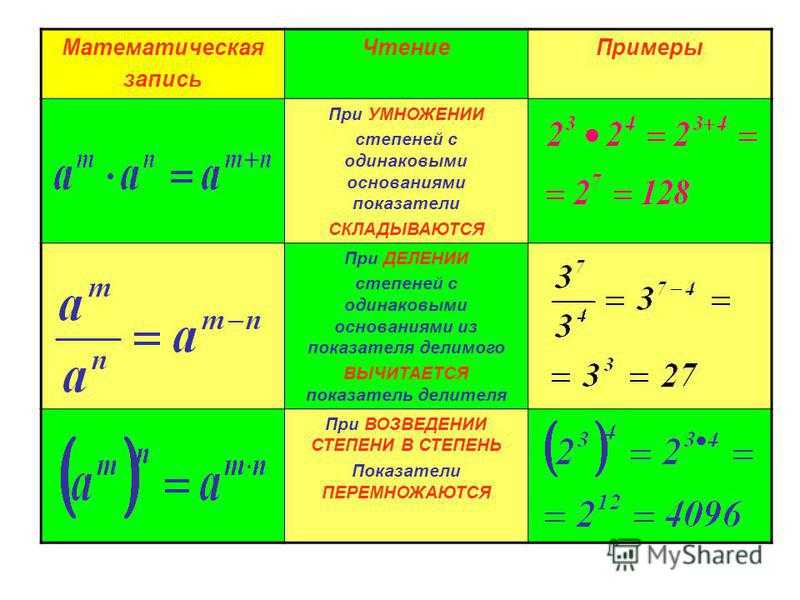
Введение в экспоненты и многочлены — Руководства по математике и статистике от Центра математики и статистики UB
Дженна Леманн
Вычисление показательных выраженийПри работе с показателями степени может быть полезнее думать о них как о множественных примерах умножения. Некоторые показатели будут более прямолинейными, но будьте осторожны при написании некоторых показателей.
Давайте рассмотрим несколько примеров вычисления экспоненциальных выражений:
В приведенном ниже выражении это иллюстрация того, что мы имеем в виду, когда говорим, что показатель степени подобен многократному умножению. Показатель степени означает, сколько раз число 2 должно быть умножено само на себя.
В следующем выражении -3 заключено в круглые скобки. Это означает, что показатель степени вне круглых скобок должен применяться ко всему числу в целом, включая его отрицательное значение.
В этом последнем выражении показатель степени стоит рядом с цифрой 3 без каких-либо круглых скобок, соединяющих отрицательное значение и цифру 3.
Использование правила продукта
При умножении двух или более одной и той же переменной с показателями степени (что означает, что они имеют одно и то же основание или букву), это как если бы вы складывали степени вместе. Ниже визуализация того, почему это так. Если мы растянем выражение так, чтобы каждый x умножался сам на себя нужное количество раз, это как если бы мы складывали степени 2 и 3 друг к другу.
Однако важно помнить, что вы можете упростить выражения таким образом только в том случае, если основное число или переменная совпадают. В приведенном ниже примере, хотя он и выглядит очень сложным, если мы разделим все числа без показателей степени и все различные переменные по типам, мы можем легко получить упрощенную версию выражения.
Итак, ответ
Степень частного правила
Сила частного правила заключается в том, что когда дробь существует в круглых скобках и встречается с показателем степени, все, что находится в круглых скобках, зависит от показателя степени. Сюда входят также любые числа, которые присоединены к переменным.
Правило частных для показателей степени
Если умножение чисел с показателями степени похоже на сложение показателей степени, то деление похоже на вычитание показателей степени.
Нулевой показатель
Для любого числа с показателем степени, равным 0, это число всегда преобразуется в 1. Постарайтесь помнить об этом, когда начнете иметь дело с более сложными уравнениями, включающими показатели степени, поскольку уравнение может быть лучше очищено путем немедленного преобразования числа или переменная с показателем степени 0 просто должна быть числом 1.
Отрицательные степени
Отрицательные показатели степени требуют, чтобы переменная преобразовывалась в дробь (а иногда и из нее) при преобразовании. В первом примере ниже x нужно перевернуть в знаменатель, чтобы избавиться от отрицательного знака в его показателе. В другом случае x нужно перевернуть в числитель, чтобы избавиться от отрицательного числа. Однако в этом случае единицу в знаменателе можно удалить, и x больше не должен быть частью дроби.
Научное обозначение
Научная нотация — это процесс, используемый для облегчения чтения очень больших или малых чисел. Чтобы перевести число в экспоненциальную запись, подсчитайте количество пробелов, которое потребуется, чтобы первая ненулевая цифра стала цифрой единицы, а затем умножьте это число на 10 на количество перемещенных цифр. Здесь мы можем увидеть пример. У нас есть число 0.000003.
Что такое многочлен?
Многочлен — это уравнение, составленное из двух или более алгебраических членов. В приведенном ниже примере каждый цвет представляет отдельный термин.
Полиномы могут состоять из некоторых или всех следующих элементов:
- Переменные:
- Константы: В приведенном выше примере константой будет число 11. Это число, которое не содержит изменяемых переменных.
- Экспоненты: Это числа, которые обычно прикрепляются к переменным
- Сложение, вычитание, умножение и деление
Что не считается многочленом?
Хотя многочлен может выглядеть по-разному, существуют некоторые правила относительно того, что не считается многочленом.
Полином НЕ:
Уравнение, содержащее деление на переменную.
Уравнение, содержащее отрицательные показатели.
Уравнение, содержащее дробные показатели.
Уравнение, содержащее радикалы.
Оценка многочленов
Вычисление многочленов ничем не отличается от решения любой другой математической задачи. обязательно используйте порядок операций. Порядок операций сокращен до PEMDAS, что означает круглые скобки, экспоненты, умножение и деление, сложение и вычитание. Для начала просто подставьте значение x или любую другую букву, с которой вы работаете, а затем используйте порядок операций, пока не получите наиболее упрощенный ответ. Посмотрите на пример ниже:
- Оценить, когда
- Шаг 1: Замена
- Шаг 2: PEMDAS
- Шаг 3: PEMDAS
- Шаг 4: PEMDAS
Добавление многочленов
При сложении многочленов помните, что складывать можно только одинаковые члены.
В приведенном ниже примере похожие термины выделены разными цветами. Не пугайтесь скобок при добавлении — просто добавляйте, как обычно.
Вычитание многочленов
Так же, как и при сложении многочленов, только одинаковые члены могут быть вычтены друг из друга. Однако в этом случае вам нужно помнить о скобках из-за минусовой стороны слева от второго многочлена. Обращайтесь со знаком минус как с -1, как если бы вы собирались умножить все в скобках на -1. Это означает, что все, что когда-то было положительным, станет отрицательным, и наоборот.
Многочлены с двумя переменными
Не отвлекайтесь на новую переменную! Правила до сих пор применяются. Просто обязательно разделите каждый тип числа по основанию, а затем упростите.
Умножение одночленов
При работе с уравнениями, включающими переменные, умножение двух одинаковых переменных приводит к «сложению» показателей степени.
Для уравнений, в которых просто есть «x» или «y», представьте, что над ними стоит 1 показатель степени.
Умножение одночленов на многочлены
При умножении одночленов на многочлены важно умножать член монома на каждый член полинома.
Использование ФОЛЬГИ
При умножении двух разных полиномов не забывайте мешать. Во-первых, умножьте две F первых переменных в каждом многочлене. Затем умножьте O внешние переменные вместе. Затем умножьте на внешних переменных. Наконец, умножьте L переменную ast каждого полинома.
Умножение биномов
При умножении двучленов важно помнить, что каждый член первого двучлена следует умножать на каждый член второго.
Умножение больших многочленов
Не пугайтесь добавленных номеров.
Просто имейте в виду, что в какой-то момент каждая переменная должна быть умножена на другие переменные. С большими полиномами, такими как этот, я обычно просто иду слева направо:
Посмотрите пример ниже.
Деление многочленов на одночлены
Деление многочлена на моном часто проще, если разбить его на более мелкие части.
Деление многочлена на другой многочлен
Решить
Шаг 1: Перепишите в порядке убывания и включите недостающие переменные ()
Шаг 2: Длинное деление, спрашивая себя: «Какое число, умноженное на 2, будет равно числу, на котором я сосредоточился?»
Шаг 3: Запишите остаток от деления на исходный многочлен
Таким образом,
Первоначально эта глава была опубликована в блоге Центра поддержки математики Балтиморского университета 13 сентября 2019 г.
степеней целых чисел | Superprof
Целые числа ведут себя по-разному в степенях.
Иногда ответ будет положительным, а в других случаях — отрицательным. Это немного сложно, но как только вы поймете, как целые числа работают с разными степенями, и именно поэтому в этом уроке вы узнаете, как найти результат целого числа, имеющего мощность. Другое слово для обозначения мощности — экспонента, так что если вы где-то читали экспоненту, не беспокойтесь, это означает то же самое. Итак, что представляет показатель степени? Показатель степени означает, сколько раз число умножается само на себя. Например, если вы видите , это значит, что вам нужно умножить само на себя и будет 3 члена. Это будет так. Если бы не было понятия показателей степени, наше вычисление могло бы идти очень долго и была бы большая вероятность того, что кто-то допустил в нем ошибку.
Степень натурального показателя целого числа равна другому целому числу. Абсолютное значение результата — это абсолютное значение основания, умноженное само на себя, как указано в показателе степени. Проще говоря, абсолютное значение умножается в соответствии со степенью, но как насчет знака? Тоже изменится? Ответ положительный, и здесь есть сложность.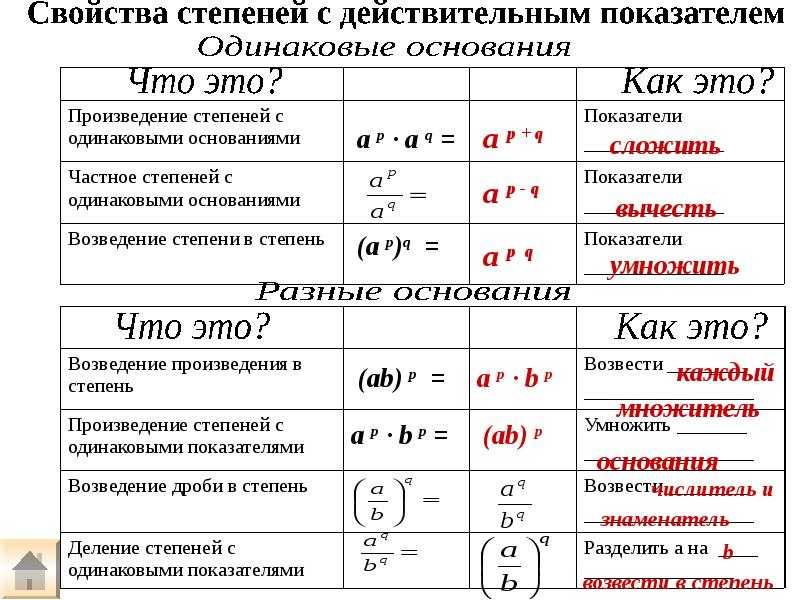
Знак тоже меняется в зависимости от мощности, но как это узнать? Не волнуйтесь, это можно определить по следующему правилу:
Правило №1
Степени четного показателя всегда положительны. Это означает, что даже если целое число имеет отрицательный знак, оно всегда будет положительным числом.
Например:
Правило № 2 имеет нечетную степень степени. Простыми словами, все, что вам нужно сделать, это умножить число в соответствии с его степенью и добавить тот же знак, который был упомянут в вопросе.
Например:
Подобно любым другим математическим операциям, они также имеют целые числа.
Свойство №1: Нулевая степень
Если возвести любое число в степень до нуля, оно всегда даст 1. Неважно, целое это число или любое другое, оно всегда будет равно 1
Свойство № 2: Стандартная степень любого числа
Сила каждого числа.
Если вы видите число, в котором не указана мощность, это означает, что оно имеет мощность . Следовательно, каждое число имеет степень .
Свойство №3: Умножение степеней с одинаковым основанием
Если есть знак умножения и одинаковые числа с разными степенями, то можно сложить обе степени. Другими словами, это другая степень с тем же основанием , а показатель степени равен сумме показателей .
Свойство №4: Разделение Полномочий с одинаковым основанием
Если есть знак деления и одинаковые числа имеют разные степени, то можно вычесть обе степени. Другими словами, это другая степень с тем же основанием, а показатель степени равен разности показателей степени.
Свойство № 5: Степень степени
Это другая степень с тем же основанием, а показатель степени равен произведению показателей степени.
Свойство № 6: Умножение степеней с одинаковым показателем
Если основания разные, но степени обоих оснований одинаковы со знаком умножения, то вы можете записать их в группу, а затем применить операция умножения.