Сложение смешанных чисел: Сложение смешанных чисел. Онлайн калькулятор

Бесплатные видеоуроки от проекта «Инфоурок»

Большая коллекция из 3243 видеоурока по 20 предметам и различным темам

УченикВероника

УчительЕвгения Вадимовна

Отличный учитель, который всегда вовлекает ученика в процесс, и сам проявляет заинтересованность в успехах ученика. Интересно слушать и работать!

УченикВероника

УчительДарья Максимовна

Дарья Максимовна замечательный, отзывчивый педагог!Обьясняет простым и доступным язык любую сложную тему- это большой плюс!! Спасибо большое моему репетитору, так как я уверена, что ОГЭ сдам на отлично !!

УченикДарья

УчительЕлизавета Владимировна

Очень качественные и продуктивные занятия. Занимаюсь не долго, но уже чувствуется прогресс. Очень милый и добрый преподаватель. Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.

УченикКарина

УчительАндрей Юрьевич

Мне понравилось заниматься с Андреем Юрьевичем. Впервые встречаю репетитора, который прежде учить языку, рассказывает про его истоки – географию, культуру, историю. Мне очень откликается такой подход. Видно, что преподаватель с большим опытом. Я очень довольна первым занятием! Буду продолжать заниматься с данным преподавателем.

УченикМия

УчительТатьяна Александровна

Ответственная, настойчивая, харизматичная, пунктуальная, высокий уровень проф подготовки, терпеливая. Наша девочка довольна, проявляет явный интерес к урокам и продвинулась в изучаемой теме. Большое спасибо вам и преподавателю Татьяне Александровне.

УченикАлёна

УчительЕлена Петровна

Прекрасный преподаватель. После восьми занятий английский стал намного лучше, многое узнала. Все понятно в объяснении, уроки на позитиве. Благодарна за работу. Искренне рекомендую.

УченикКатя

УчительЕлена Александровна

Все понравилось приятно работать с учителем. Как по мне лучше чем Елена Александровна я еще не видела учителя по русскому языку.

УченикДиана

УчительДиана Михайловна

У Дианы Михайловны занимаются английским языком две дочери: Есения и Ксения. Девочкам очень нравится преподаватель и наполнение уроков, материал преподносится в очень интересной форме, а все объяснения понятны и доступны. Девочки уже показали успехи в изучении английского языка в школе.

УченикДмитрий

УчительСветлана Анатольевна

Дмитрий прошел со Светланой Анатольевной 4 занятия и уже виден прогресс! Мальчик по натуре немного застенчивый, поначалу был немногословен, но уже хорошо разговаривает на уроках, что говорит о профессионализме педагога.

УченикАрина

УчительИрина Сергеевна

Спасибо огромное. Очень рады, что нашли этот ресурс для занятий. Ирина Сергеевна объясняет все быстро, понятно и динамично. Всего за несколько занятий наверстали упущенное по химии и прошли дальше. Обязательно будем обращаться в дальнейшем.

УченикЕлизавета

УчительРимма Николаевна

У Елизаветы есть успехи, занимается с удовольствием и заинтересованностью. Римма Николаевна очень интересно преподносит материал. Очень нравится учитель, занимаемся с удовольствием.

УченикАртём

УчительНина Ивановна

Нам понравилась Нина Ивановна, хороший человек и прекрасный педагог. Очень ответственная, трудолюбивая и толковая. Сразу нашла подход к ученику. Доходчиво объяснит любую тему. Преподаватель, в отличии от многих репетиторов не просто отбывает время, а действительно помогает.

УченикЭдуард

УчительЖанна Сергеевна

Замечательный педагог, нашла подход с первых занятий. Все очень доходчиво и понятно объясняет. Ребенку очень нравится, просит дополнительные часы для занятий.

УченикЛюдмила

УчительРита Ивановна

Добрый день! Рита Ивановна очень профессионально оценила все пробелы моего сына и нам бы хотелось продолжить с ней обучение! Занятия очень хорошие, учитель понятно все объясняет, всем рекомендую.

УченикСветлана

УчительОльга Олеговна

Спасибо Ольге Олеговне за проведённый урок в праздничный день. Здоровья, процветания, побольше радостных событий в жизни, благополучия, успехов и удачи в таком не лёгком и таком нужном труде!!! Спасибо за урок, всё понравилось!

УченикИрина

УчительТатьяна Николаевна

Очень грамотный педагог, хорошо подходит к вопросам с которыми обращаемся, подход к ребенку очень понравился, буквально на 5-8 урок у ребенка был уже прогресс и теперь любит математику. На урок математики приходим с удовольствием, подтянули свои недочеты, решаем быстро примеры, а главное сами. Спасибо за знания!

УченикПолина

УчительСветлана Михайловна

Светлана Михайловна очень хороший учитель, за урок мы разбираем много вопросов и обсуждаем правила русского языка в каждом конкретном примере. Занимаюсь с удовольствием!

УченикМария

УчительДарья Александровна

Замечательный, приятный и внимательный преподаватель. Ребенок сначала засмущался от непривычного формата урока, но Дарья Александровна, в итоге, смогла завоевать внимание и доверие дочери. Обязательно будем продолжать обучение! Спасибо!

УченикАнтон

УчительСветлана Васильевна

Репетитор быстро оценила проблемы, порекомендовала способы восполнения пробелов. Продолжим заниматься дальше, так как Светлана Васильевна доступно объясняет материал, и все сразу становится понятным. Классный репетитор, советую!

УченикСофия

УчительГалина Михайловна

Добрый день! Галина Михайловна — замечательный педагог! Мне все было очень понятно и вообще было приятно общаться! Была непонятна тема : ,, Не /ни с глаголами ,,. После того, как Галина Михайловна объяснила, все трудности были сняты. Огромное спасибо !!! 🙏

УченикЛеонид

УчительЕлена Александровна

На уроке педагог работала по индивидуальной программе, выявила пробелы в знаниях и все доходчиво разъяснила. Сложные темы, объяснили легко и понятно, сыну все очень понравилось!

УченикГалина

УчительТамара Иосифовна

Замечательный педагог и очень доброжелательный человек!!! Тамара Иосифовна очень доходчиво объяснила непонятные для меня моменты, причем из разных тем, за один урок!!! Урок проходил в спокойной и дружественной обстановке. Спасибо большое!!! Очень понравилось!!!

УченикМария

УчительВладимир Григорьевич

Спасибо большое, Вы лучший преподаватель по информатике. Как хорошо, что есть такая замечательная платформа. Спасибо всем, кто ее организовал и Вам лично. Всем друзьям и знакомым буду рекомендавать! онлайн-уроки.

УченикОльга

УчительИрина Ивановна

Очень понравился урок! Ирина Ивановна с первых минут расположил к себе ребёнка так, что даже мой непоседливый и не очень настроенный на учебу пятиклассник увлекся так, что не заметил, как пролетели 45мин. Спасибо! С удовольствием продолжим занятия!

УченикФёдор

УчительНаталия Анатольевна

Как родитель могу сказать, что самое важное — это расположить к себе ребенка. Уже после первого занятия с Наталией Анатольевной я увидела желание заниматься в глазах своей дочери. Занятие проходило очень комфортно. Понравилось, как построена программа проверочного урока.

УченикПолина

УчительМарина Михайловна

Мне очень понравилось вводное занятие, спасибо большое. За пол часа Марина Михайловна с помощью разговора поняла все мои слабые места и помогла многие из них подправить и понять. Я хочу заниматься с ней и далее.

УченикАйсултан

УчительГалина Дмитриевна

Здравствуйте! У нас был пробный урок с Галиной Дмитриевной по математике. Занимались именно логическими задачами. Учитель имеет очень хороший подход к детям и у нее есть своя отработанная хорошая методика. Хорошо объясняет, приятная. Спасибо!

УченикВиктор

УчительЮлия Анатольевна

Спасибо большое учитель объясняет очень хорошо там где ты что либо не поймёшь педагог тебе всё объяснит как раз педагог сказала повторить всё то что мне говорил предыдущий репетитор СПАСИБО БОЛЬШОЕ !!!

УченикМаксим

УчительАлёна Юрьевна

Благодарим за интересное и познавательное занятие! Преподаватель четко и внимательно ведет занятие, обращает внимание на моменты, которые необходимо доработать. Профессионально! Приятно общаться.

УченикАлександр

УчительАнастасия Сергеевна

Добрый день! Мы безумно рады, что нам посчастливилось найти такого замечательного и удивительного педагога, как Анастасия Сергеевна! Она очень интересно проводит урок, ребёнок безумно рад. Сразу чувствуется, что человек талантливый. С нетерпением ждём новый урок.

УченикЕкатерина

УчительСергей Васильевич

Спасибо за урок! Занятие очень понравилось, Сергей Васильевич все понятно и интересно обьясняет, во время урока была доброжелательная атмосфера. Также учитель посоветовал некоторые книги и способы подготовки к экзамену. Спасибо!!!

УченикКарина

УчительГулез Гаджимурадовна

Нравятся все педагоги с которыми мы занмаемся, все обладают высоким уровнем профессионализма,используют интересные и современные методы и технологии обучения. Имеет хороший уровень научно-методической подготовки. Ребенок занимается с большим интересом. Будем заниматься с Вами до окончания школы, сейчас мы в 4 классе)

УченикФеона

УчительНаталия Михайловна

За 45 минут узнала и поняла больше, чем за полгода в школе. Учитель объясняет очень понятно, доходчиво, выше школьного уровня. Однозначно этот урок не последний. С Уважением, Феона.

УченикЕкатерина

УчительНаталья Васильевна

Спасибо, Наталья Васильевна! Профессионально, четко, по делу. Педагог очень терпеливая, спокойная, уверенная. Занятие очень понравилось и ребенку и мне, маме.

УченикМаксим

УчительАлександр Александрович

Спасибо большое Александру Александровичу. Очень быстро нашел подход к ребёнку , а так же увлек математикой! Ребёнку было комфортно общаться. Надеемся встретиться на следующих занятиях.

УченикМарина

УчительНиколай Васильевич

Николай Васильевич помог за короткий срок восполнить пробелы в знаниях, за что очень благодарны! Уроки очень интересные! Будем обращаться еще к нему.

УченикМарина

УчительАлександр Сергеевич

Занятия ребенку с Александром Сергеевичем очень нравятся. Все схватывает, доволен уроками. С репетитором нашли общий язык. Мы очень благодарны Александру Сергеевичу! Хороший педагог. Спасибо.

УченикЕлизавета

УчительАлёна Игоревна

Дети понимают всё, абсолютно. В школе не понимают ничего, а с Вашими репетиторами понимают всё. Сдвиги очень большие. Алёна Игоревна хороший педагог. Все занятия результативные.

УченикДжу Уван Ми

УчительГалина Михайловна

Плохо знаю русский язык, и постоянно делаю многие ошибки в тексте и в работе. Только благодаря достуным объяснениям учителя я мог самостоятельно находить ошибки. Большое спасибо за Вашу работу и сердечные помощи в изучении русского языка!

УченикРоман

УчительИрина Алексеевна

Мой сын занимался с Ириной Алексеевной, очень понравилось, всё спокойно и понятно было показано, рассказано. Очень профессионально и качественно выстроены занятия, учитель доброжелателен, ребенку интересно заниматься.

УченикЖеня

УчительОльга Сергеевна

Ольга Сергеевна — профессинал своего дела. Высококвалифицированный педагог. По английскому нужно было именно аудирование и речь, 100% подобрали репетитора по нашему запросу. Педагог строгий — то, что нужно моему ребёнку. Мы очень довольны!

УченикНикита

УчительСарвар Шодиевич

До этого никогда не занимался у репетиторов, думал что буду сидеть ничего не понимать и всё время уйдёт зря. Однако Сарвар Шодиевич очень понятно объясняет, не подчёркивает ваши «незнания» и до упора старается всё разъяснить. Могу с уверенностью посоветовать этого репетитора каждому, кто хочет разобраться в алгебре и геометрии.

УченикВиктор

УчительЮлия Анатольевна

Спасибо большое учитель объясняет очень хорошо там где ты что либо не поймёшь педагог тебе всё объяснит как раз педагог сказала повторить всё то что мне говорил предыдущий репетитор СПАСИБО БОЛЬШОЕ !!!

УченикЭльмира

УчительЛюдмила Евгеньевна

Выражаю благодарность центру где есть такие сильные и ответственные учителя. Отдельная благодарность Людмиле Евгеньевне за опыт за знания.

УченикДарья

УчительОльга Александровна

Ольга Александровна отлично объясняет темы, с ребенком нашла общий язык моментально. Дочь занимается с удовольствием, пробелы подтянули за пару уроков. Спасибо Вам большое!

УченикОлеся

УчительГузалия Робертовна

Сыну очень понравилось заниматься с Гузалией Робертовной. Очень внимательный и доброжелательный педагог, который сразу видит слабые стороны. Всячески поощряет ребёнка и помогает поднять самооценку. Большое спасибо!

УченикДарья

УчительМария Никитична

Нравится, как преподает Мария Никитична (по программе школы + присутствует игровая минутка, ученице на занятиях не бывает скучно) Уровень знаний повысили до 5-ки, значительно расширили словарный запас. Все устраивает, рекомендует знакомым и в целом рада, что такая платформа существует.

УченикОлеся

УчительДаниил Станиславович

Спасибо. Урок понравился. Даниил Станиславович заинтересовал английским языком. Составили предположительные темы для занятий после новогодних праздников

УченикГеоргий

УчительЕкатерина Станиславовна

Грамотный, добрый, располагающий к себе педагог. С ребёнком Екатерина Станиславовна установила хороший контакт. Преподносит информацию очень доступно. Занятие проходит разнообразно, в том числе в игровой форме. Рекомендуем 5+

УченикНиколя

УчительАлла Валентиновна

Алла Валентиновна отличный преподаватель! Выявила все пробелы в знаниях Константина по русскому языку и работает над их устранением. Также помогает в работе над текущими темами урока. Уже прошли несколько занятий и продолжаем заниматься. нашла общий язык с сыном. Все нравится. Хотим заниматься дальше!

УченикПолина

УчительСветлана Григорьевна

Светлана Григорьевна просто супер учитель!!!! Все очень понятно и хорошо объясняет, прохожу с ней темы по географии 6 класса. На уроке с ней очень интересно. Уже 2 урока — одно удовольствие!!!

УченикНаталья

УчительСергей Александрович

Классный репетитор, все темы разбираются на 5+, будем обязательно продолжать обучение, также рекомендуем всем ученикам!

УченикМаксим

УчительНадежда Викторовна

Замечательный педагог, с которым нравится заниматься. Максим готовится к сдаче ОГЭ по русскому языку и занимается с репетитором с начала ноября прошлого года. За это время успели повторить пройденный материал и изучить несколько тем нового материала. Надежда Викторовна объясняет материал в доступной форме. Максим продолжит с ней занятия.

УченикАлександра

УчительИрина Борисовна

Отличный репетитор ! Ирина Борисовна обьясняет сложные темы простым и доступным языком ! Сердечно благодарю педагога за грамотность и профессионализм !!!!

УченикФеона

УчительЯнина Александровна

Преподаватель компетентный, объясняет понятно, выше школьного уровня. Быстро заполняет пробелы в знаниях. Будем сотрудничать. С Уважением, Феона.

УченикМадина

УчительМария Анатольевна

Очень чётко и понятно объяснила Мария Анатольевна. Спасибо вам. Не смотря первый раз, пробную занятия, она прям очень понравилась дочке и естественно мне💐. В дальнейшем обязательно будем заниматься с ней и подниматься.

УченикВероника

УчительЕвгения Вадимовна

Отличный учитель, который всегда вовлекает ученика в процесс, и сам проявляет заинтересованность в успехах ученика. Интересно слушать и работать!

УченикВероника

УчительДарья Максимовна

Дарья Максимовна замечательный, отзывчивый педагог!Обьясняет простым и доступным язык любую сложную тему- это большой плюс!! Спасибо большое моему репетитору, так как я уверена, что ОГЭ сдам на отлично !!

УченикДарья

УчительЕлизавета Владимировна

Очень качественные и продуктивные занятия. Занимаюсь не долго, но уже чувствуется прогресс. Очень милый и добрый преподаватель. Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.

УченикКарина

УчительАндрей Юрьевич

Мне понравилось заниматься с Андреем Юрьевичем. Впервые встречаю репетитора, который прежде учить языку, рассказывает про его истоки – географию, культуру, историю. Мне очень откликается такой подход. Видно, что преподаватель с большим опытом. Я очень довольна первым занятием! Буду продолжать заниматься с данным преподавателем.

Сложение и вычитание смешанных чисел

Урок 30.

Математика 5 класс

В этом уроке мы введем правила сложения смешанных чисел, правила вычитания смешанных чисел. И применим полученные знания на примерах

Конспект урока «Сложение и вычитание смешанных чисел»

Сегодня на уроке мы научимся складывать и вычитать смешанные числа.

На прошлом уроке мы с вами уяснили, что сумму натурального числа и правильной дроби принято записывать без знака «+». Такую сумму называют смешанным числом. Натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа. То есть

При сложении смешанных чисел пользуются переместительным и сочетательным свойствами сложения.

Пример

Найти сумму чисел  и .

В записи в тетрадях не стоит расписывать, как вы считаете достаточно написать:

Таким образом, чтобы сложить смешанные числа, нужно сложить по отдельности их целые и дробные части и записать сумму полученных чисел

.

Иногда при сложении смешанных чисел в их дробной части может получиться неправильная дробь. В этом случае из неё выделяют целую часть, и добавляют её к уже имеющейся дробной части.

Пример

Найти сумму чисел  и .

Таким образом, если при сложении дробных частей получилась неправильная дробь, то выделяют целую часть этой дроби и добавляют к уже имеющейся целой части.

Задача

На столе лежало 2  яблока. Принесли ещё 1  яблока. Сколько яблок лежит на столе?

Решение

Посмотрите, что получилось: складывали смешанные числа, а ответ выражен натуральным или можно ещё сказать целым числом.

При вычитании смешанных чисел пользуются свойством вычитания числа из суммы и свойством вычитания суммы из числа.

Пример

Найти разность дробей  и .

В тетрадях пишут короче:

Таким образом, чтобы найти разность смешанных чисел, нужно найти отдельно разность целых частей и отдельно разность дробных частей.

Есть в примерах на вычитание и «особые» случаи.

Например

Вычтем из дроби  дробь .

Запомните! Не начинайте выполнять вычитание, пока не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби.

Иногда в примерах нужно вычесть из натурального числа смешанную дробь.

Например

Найдём значение выражения .

Итоги

Чтобы сложить смешанные числа, нужно сложить по отдельности их целые и дробные части и записать сумму полученных чисел.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части.

Чтобы найти разность смешанных чисел, нужно найти отдельно разность целых частей и отдельно разность дробных частей.

Если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть.

Предыдущий урок 29 Смешанные числа

Следующий урок 31 Десятичная запись дробных чисел

Получите полный комплект видеоуроков, тестов и презентаций Математика 5 класс

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Сложение смешанных дробей — шаги, правила

Сложение смешанных дробей означает нахождение суммы смешанных дробей. Смешанная дробь – это сочетание целого числа и правильной дроби. Объединение двух или более смешанных фракций называется добавлением смешанных фракций. Давайте узнаем больше о добавлении смешанных фракций в этой статье.

1.	Сложение смешанных чисел с одинаковыми знаменателями
2.	Сложение смешанных чисел с разными знаменателями
3.	Добавление смешанных дробей и правильных дробей
4.	Часто задаваемые вопросы о добавлении смешанных фракций

Сложение смешанных чисел с одинаковыми знаменателями

Сложение смешанных чисел с одинаковыми знаменателями означает сложение тех смешанных дробей, у которых одинаковые знаменатели. Например, \(2\dfrac{2}{3}\), \(1\dfrac{1}{3}\) — смешанные дроби с одинаковыми знаменателями. Эти смешанные фракции можно сложить, используя обычные правила сложения фракций. Однако нам необходимо отметить несколько фактов о смешанных дробях, которые помогут нам легко решить эти вопросы. Вот список нескольких моментов, которые необходимо учитывать при добавлении смешанных дробей лучшим способом:

• Смешанная дробь \(a\dfrac{b}{c}\) также может быть записана как + (b/c)
• Чтобы преобразовать смешанное число в неправильную дробь, нужно умножить целое число на знаменатель правильной дроби и прибавить результат к числителю правильной дроби, сохранив знаменатель.
  Например, чтобы преобразовать \(1\dfrac{4}{7}\) в неправильную дробь, мы умножаем 1 и 7, т. е. 1 × 7 = 7, и результат прибавляем к 4, т. е. 7 + 4 = 11. Таким образом, смешанная дробь превращается в неправильную дробь и записывается как 11/7.
• Чтобы преобразовать неправильную дробь в смешанное число, нужно разделить числитель неправильной дроби на ее знаменатель. Частное становится целой частью числа, остаток становится числителем правильной дроби, а знаменатель остается прежним. Например, чтобы преобразовать 13/6 в смешанное число, мы сначала разделим 13 на 6 и получим частное как 2, а остаток как 1. Таким образом, когда 13/6 преобразуется в смешанную дробь, получается \(2\dfrac {1}{6}\)

Давайте рассмотрим пример, чтобы понять, как складывать смешанные дроби с одинаковыми знаменателями.

Пример: Добавьте смешанные дроби \(2\dfrac{2}{3}\) + \(1\dfrac{1}{3}\)

Это можно решить двумя способами.

Метод 1

• Шаг 1: Сначала складываются целые числа обеих дробей, т. е. 2 + 1 = 3
• Шаг 2: Теперь дробные части обоих чисел складываются, т. е. (2/3) + (1/3) = 3/3
• Шаг 3: Результат, полученный на шаге 2, при необходимости следует преобразовать в простейшую форму, т. е. 3/3 = 1
• Шаг 4: Теперь складываем результаты шага 1 и шага 3, т. е. 3 + 1 = 4

Следовательно, результат равен \(2\dfrac{2}{3}\) + \(1\dfrac{1}{3}\) = 4

Метод 2

Теперь давайте решить этот вопрос, используя второй метод, который является основным методом сложения дробей.

Пример: Складываем смешанные дроби \(2\dfrac{2}{3}\) + \(1\dfrac{1}{3}\)

Решение: Преобразуем смешанные дроби в неправильные дроби.

• Шаг 1: Преобразуйте обе смешанные дроби в неправильные дроби. Следовательно, \(2\dfrac{2}{3}\) станет 8/3; и \(1\dfrac{1}{3}\) станет 4/3
• Шаг 2 : Сложите дроби, добавив числители, потому что знаменатели одинаковы. Это будет 8/3 + 4/3 = 12/3.
• Шаг 3: При необходимости уменьшите дробь. Это станет 12/3 = 4. Следовательно, \(2\dfrac{2}{3}\) + \(1\dfrac{1}{3}\) = 4,

Сложение смешанных чисел с разными знаменателями

Смешанные дроби с разными знаменателями – это группа таких смешанных дробей, у которых разные знаменатели. Давайте научимся складывать смешанные дроби с разными знаменателями на примере с помощью следующих шагов.

Пример: Сложите смешанные дроби с разными знаменателями: \(3\dfrac{1}{4}\) + \(6\dfrac{1}{2}\)

Решение:

• Шаг 1: Сначала мы преобразуем данные дроби в неправильные дроби, т. е. \(3\dfrac{1}{4}\) = 13/4 и \(6\dfrac{1}{2}\) = 13/2
• Шаг 2: Теперь дроби можно записать так: (13/4) + (13/2)
• Шаг 3: Знаменатели разные, поэтому нам нужно найти наименьшее общее кратное (НОК) знаменателей, т. е. НОК 2 и 4 = 4.
• Шаг 4: С помощью НОК мы запишем их соответствующие эквивалентные дроби так, чтобы они стали похожи на дроби. Знаменатель первой дроби уже равен 4, поэтому он останется прежним, т.е. д., 13/4. Но вторая дробь изменится на 26/4
.
• Шаг 5:
  Теперь у нас есть обе дроби с одинаковыми знаменателями, то есть они были преобразованы в одинаковые дроби. Итак, мы можем их сложить, т. е. (13/4) + (26/4) = (13 + 26)/4 = 39./4
• Шаг 6: Эту неправильную дробь (39/4) можно преобразовать в смешанную дробь следующим образом: 39/4 = \(9\dfrac{3}{4}\)

Следовательно, результат \(3\dfrac{1}{4}\) + \(6\dfrac{1}{2}\) = \(9\dfrac{3}{4}\)

Другой способ сложения смешанных дробей с разными знаменателями состоит в том, чтобы сначала сложить целые части данных дробей, а затем сложить правильные дроби. Например, \(3\dfrac{1}{4}\) + \(6\dfrac{1}{2}\) = (3 + 6) + (1/4 + 1/2). Ее можно решить следующим образом.

= 9 + (1/4 + 2/4) (поскольку НОК 2 и 4 равно 4)

= 9 + 3/4

= \(9\dfrac{3}{4}\)

Таким образом, для добавления смешанных фракций можно использовать любой из двух вышеперечисленных методов.

Добавление смешанных дробей и правильных дробей

Добавление смешанных дробей и правильных дробей включает ту же процедуру, за исключением нескольких изменений. Давайте разберемся в этом на следующих примерах.

Случай 1: Смешанная дробь и правильная дробь, имеющие одинаковый знаменатель.

Пример: Добавьте смешанную дробь и правильную дробь \(3\dfrac{2}{5}\) + 1/5

Обратите внимание, что \(3\dfrac{2}{5}\) = 3 + (2/5). Следовательно,

\(3\dfrac{2}{5}\) + (1/5) = 3 + (2/5) + (1/5)

= 3 + (3/5)

= \(3\dfrac{3}{5}\)

Следовательно, \(3\dfrac{2}{5}\) + (1/5) = \(3\dfrac{3}{5}\)

Случай 2: Смешанная дробь и правильная дробь с разными знаменателями.

Пример: Добавьте смешанную дробь и правильную дробь \(5\dfrac{1}{2}\) + 2/3

\(5\dfrac{1}{2}\) + 2/3

= (11 /2) + (2/3) [Мы преобразовали \(5\dfrac{1}{2}\) в неправильную дробь, 11/2]

= [(11 × 3) / (2 × 3) ] + [(2 × 2) / (3 × 2)] [Поскольку НОК 2 и 3 равен 6]

= (33/6) + (4/6)

= 37/6

= \ (6\dfrac{1}{6}\)

Следовательно, \(5\dfrac{1}{2}\) + 2/3 = \(6\dfrac{1}{6}\).

☛ Статьи по теме

• Вычитание смешанных дробей
• Сложение дробей
• Вычитание дробей
• Сложение дробей с разными знаменателями
• Вычитание дробей с разными знаменателями
• Сложение и вычитание дробей

 

Добавление смешанных чисел Примеры

1. Пример 1: Добавьте смешанные дроби \(4\dfrac{1}{7}\) и \(5\dfrac{4}{7}\)

   Решение: Для данных смешанных дробей \(4\dfrac{1}{7}\) и \(5\dfrac{4}{7}\) мы будем использовать концепцию сложения смешанных дробей с подобными знаменатели. Так как знаменатели одинаковые, мы будем складывать целые числа отдельно и дроби отдельно и объединять их результат, чтобы получить окончательный ответ.

   \(4\dfrac{1}{7}\) + \(5\dfrac{4}{7}\)

   = (4 + 5) + (1/7 + 4/7)

   = 9 + (5/7)

   = \(9\dfrac{5}{7}\)

   Таким образом, значение \(4\dfrac{1}{7}\) + \(5\dfrac{ 4}{7}\) = \(9\dfrac{5}{7}\)

2. Пример 2: Райан хочет сшить рубашку и имеет \(20\dfrac{2}{3}\) м ткани. Он понимает, что ему нужно еще \(7\dfrac{3}{4}\) м ткани, чтобы сшить рубашку. Какова общая длина ткани, которая ему нужна?

   Решение: Общая длина ткани, необходимой для сшивания рубашки, равна сумме \(20\dfrac{2}{3}\) и \(7\dfrac{3}{4}\ ). Мы будем использовать концепцию сложения смешанных дробей с разными знаменателями, чтобы найти результат. Поскольку \(20\dfrac{2}{3}\) и \(7\dfrac{3}{4}\) имеют разные знаменатели, поэтому мы сначала преобразуем эти смешанные дроби в неправильные дроби. Итак, \(20\dfrac{2}{3}\) = 62/3 и \(7\dfrac{3}{4}\) = 31/4, и теперь нам нужно добавить 62/3 + 31/4. . Поскольку знаменатели не являются общими, найдем НОК их знаменателей и сделаем их похожими на дроби.

   НОК 3 и 4 равно 12

   62/3 = (62 × 4) / (3 × 4) = 248/12

   31/4 = (31 × 3) / (4 × 3) = 93/ 12

   После их сложения получаем,

   (248/12) + (93/12)

   = 341/12

   = \(28\dfrac{5}{12}\)

   Следовательно, общая длина ткани, необходимой для сшивания рубашки будет \(28\dfrac{5}{12}\) м.

3. Пример 3: Укажите верно или неверно в отношении добавления смешанных фракций.

   а.) \(2\dfrac{1}{2}\) + 1/2 = 3

   б.) \(2\dfrac{1}{2}\) + 1 = \(2\dfrac {1}{2}\)

   Решение:

   а.) Верно, \(2\dfrac{1}{2}\) + 1/2 = 3, поскольку знаменатели одинаковы, мы можем добавить дроби легко. 2 + 1/2 + 1/2 = 2 + 1 = 3

   b.) Неверно, \(2\dfrac{1}{2}\) + 1 = \(3\dfrac{1}{2}\), потому что, когда мы складываем целые числа, мы получаем 2 + 1 = 3 а дробь равна 1/2, поэтому сумма равна \(3\dfrac{1}{2}\), а не \(2\dfrac{1}{2}\)

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.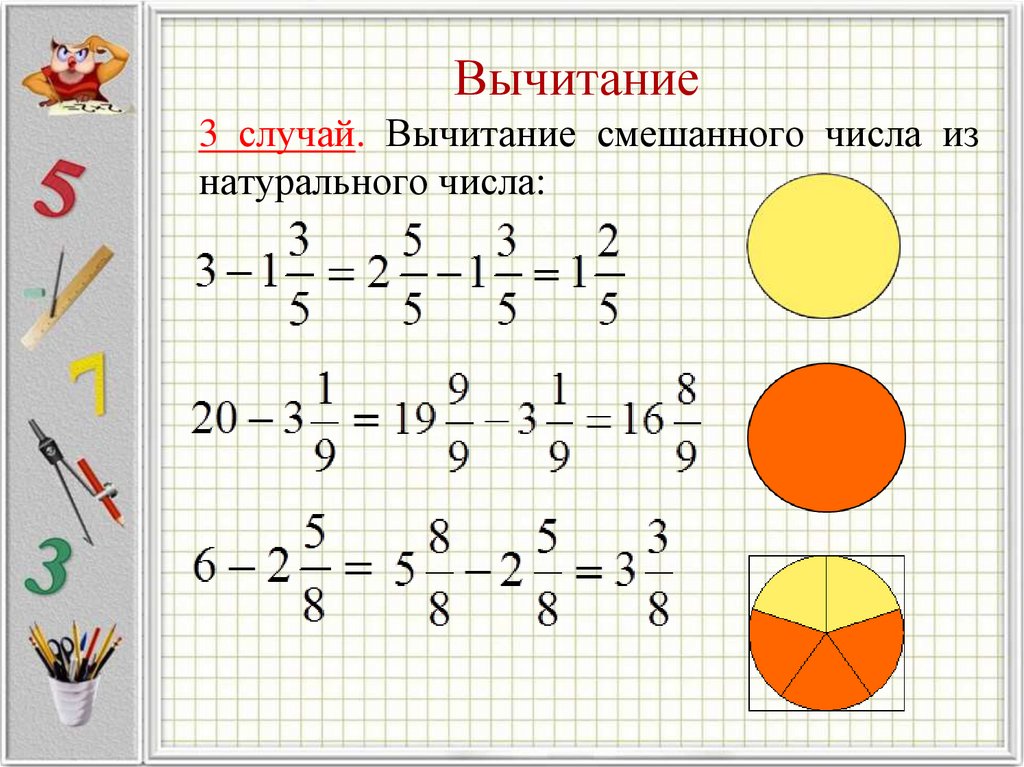

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Забронировать бесплатный пробный урок

Практические вопросы по сложению смешанных дробей

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о добавлении смешанных фракций

Как складывать смешанные номера?

Смешанные фракции можно добавлять разными способами. Если смешанные дроби имеют одинаковые знаменатели, то целая и дробная части могут быть сложены отдельно и объединены для получения результата. Для смешанных дробей с разными знаменателями их сначала преобразуют в неправильные дроби. После этого нам нужно сделать знаменатели одинаковыми, поэтому мы находим их НОК, преобразуем их в соответствующие эквивалентные дроби, а затем складываем числители.

Как складывать смешанные дроби с целыми числами?

Чтобы сложить смешанные дроби с целыми числами, мы складываем целую числовую часть смешанной дроби с заданным целым числом и, наконец, объединяем ее с дробной частью, чтобы получить результат.
Например, \(3\dfrac{3}{5}\) + 4
= 3 + (3/5) + 4
= (3 + 4) + (3/5)
= 7 + (3/5)
= \(7\dfrac{3}{5}\)

Это также можно решить, преобразовав смешанное число в неправильную дробь, а затем дроби можно сложить, используя обычный метод сложения дробей.

Каковы этапы сложения дробей и смешанных дробей?

Действия по добавлению фракций и смешанных фракций можно понять с помощью следующего примера. Например, добавим \(5\dfrac{4}{7}\) + (1/7)

• Шаг 1: Преобразуем смешанную дробь в неправильную. Здесь \(5\dfrac{4}{7}\) станет (39/7)
.
• Шаг 2: Теперь проверьте, совпадают ли знаменатели. Здесь оба знаменателя одинаковы. (39/7) + (1/7)
• Шаг 3: Если да, сложите числители обеих дробей и запишите результат над общим знаменателем. Итак, (39/7) + (1/7) = 40/7
• Шаг 4: Если знаменатели не совпадают, найдите НОК знаменателей, чтобы сделать их равными, и выполните шаг 3. Этот шаг не нужен, поскольку знаменатели одинаковы.
• Шаг 5: Предыдущий шаг дает результат в виде неправильной дроби. Превратите его в смешанную дробь. Итак, 40/7 = \(5\dfrac{5}{7}\)

Как сложить смешанные дроби с правильными дробями?

Смешанные фракции могут быть легко добавлены с правильными фракциями. Нам просто нужно преобразовать смешанные дроби в неправильные дроби, а затем сложить их по тем же правилам. Например, добавим \(2\dfrac{2}{5}\) + 3/5, выполнив следующие шаги:

• Преобразуем смешанную дробь в неправильную дробь. Таким образом, \(2\dfrac{2}{5}\) станет (12/5)
.
• Теперь проверим, совпадают ли одинаковые знаменатели. Если знаменатели совпадают, их числители можно просто сложить. Если они не совпадают, то находим их НОК, переводим в эквивалентные дроби и затем складываем. В этом случае знаменатели совпадают, поэтому их числители можно сложить. Здесь 12/5 + 3/5 = 15/5. Затем эту сумму можно упростить до наименьшей формы. Итак, 15/5 = 3,9.0042

Каковы шаги сложения смешанных дробей с одинаковыми знаменателями?

Сложение смешанных дробей с одним и тем же знаменателем можно легко выполнить, объединив целые числа отдельно и дробные части отдельно. Затем они складываются и объединяются, чтобы получить окончательный ответ.

Например, добавим \(6\dfrac{1}{6}\) + \(2\dfrac{4}{6}\)
= (6 + 2) + (1/6) + (4/6)
= 8 + (5/6)
= \(8\dfrac{5}{6}\)

Как сложить смешанные дроби с разными знаменателями?

Сложение смешанных дробей с разными знаменателями осуществляется путем преобразования смешанных дробей в неправильные дроби. Затем мы находим их НОК, преобразуем их в эквивалентные дроби и добавляем числители. Наконец, сумма преобразуется обратно в смешанную дробь.

Например, добавим \(4\dfrac{5}{8}\) + \(3\dfrac{1}{2}\)
= (37/8) + (7/2)
= (37/8) + (28/8)
= 65/8
= \(8\dfrac{1}{8}\)

Как складывать и вычитать смешанные дроби?

Сложение и вычитание смешанных дробей производится аналогичным образом. Смешанные дроби преобразуются в неправильные дроби, а затем складываются или вычитаются по обычным правилам.

Скачать БЕСПЛАТНЫЕ учебные материалы

Сложение смешанных дробей Рабочие листы

Сложение смешанных чисел с разными знаменателями

Сложение смешанных чисел

Смешанное число — это тип дроби, который состоит из двух частей: целого числа и правильной дроби. Он также известен как смешанная фракция.   

Обычно смешанное число представляет собой число между любыми двумя целыми числами. Мы часто сталкиваемся с примерами смешанных чисел в нашей повседневной жизни.

Рассмотрим дробь $3\frac{5}{8}$. Он состоит из целого числа 3 и дробной части $\frac{5}{8}$. Поскольку дробная часть $\frac{5}{8}$ имеет числитель 5, что меньше знаменателя 8, она представляет собой правильную дробь.

Итак, дробь $3\frac{5}{8}$ представляет собой смешанное число.

Как складывать смешанные числа?

Для сложения смешанных чисел (или сложения смешанных дробей) мы берем целые числа и дроби и складываем их отдельно. Затем мы соединяем их.

Давайте разберемся с этим на примере.

Пример. Найдите сумму  $2\frac{1}{8}$ и $3\frac{3}{8}$.

Здесь мы должны сложить два смешанных числа.

Первое число $2\frac{1}{8}$.

Второе число $3\frac{3}{8}$.

Визуально две дроби при сложении будут выглядеть так:

Теперь давайте посмотрим, как мы можем сложить числа $2\frac{1}{8}$ и $3\frac{3}{8}$ без помощи моделей.

Сначала складываем целые части обоих смешанных чисел.

Здесь целыми являются 2 и 3. Давайте сначала сложим их.

2 + 3 = 5

А теперь добавим дробные части.

Дробные части: $\frac{1}{8}$ и $\frac{3}{8}$. Складываем их так, как мы складывали бы две одинаковые дроби, прибавляя числитель к числителю и знаменатель к знаменателю.

$\frac{1}{8} + {3}{8}$

$= \frac{1 + 3}{8}$

$= \frac{4}{8}$

Сейчас что у нас есть отдельные суммы целых и дробей, мы сложим их вместе.

Итак, мы получаем $2\frac{1}{8} +3\frac{3}{8} =5\frac{4}{8}$    

Теперь рассмотрим пример сложения двух смешанных чисел. где наша результирующая дробь не является правильной дробью.

Например, предположим, что в одной корзине $2\frac{4}{5}$ фунтов яблок, а в другой — $3\frac{3}{5}$ фунтов. Сколько всего яблок в обеих корзинах?

Здесь, чтобы найти количество яблок в обеих корзинах, мы складываем смешанные числа $2\frac{4}{5}$ и  $3\frac{3}{5}$. Знаменатели обеих дробных частей одинаковы. Итак, чтобы сложить смешанные числа с одинаковыми знаменателями, мы складываем целые части вместе и дробные части вместе, а затем объединяем сумму двух, как показано ниже:

Складываем целую часть с целой частью и дробную часть с дробной часть.

Если сумма дробных частей является неправильным числом, преобразуйте его в другое смешанное число.

Объединить сумму целых и дробей.

Следовательно, имеется $6\frac{2}{5}$ фунтов яблок.

Математически это сложение будет выглядеть так:

$2\frac{4}{5} +3\frac{3}{5} = 2 + 3 + \frac{4}{5} + \frac{3 {5}$

$= 5 + \frac{7}{5}$

$= 5 + 1\frac{2}{5}$

$= 6\frac{2}{5}$

Сложение смешанных чисел с разными знаменателями

Теперь давайте рассмотрим пример, чтобы понять сложение смешанных чисел с разными знаменателями.

Предположим, что у Сьюзан есть $1\frac{4}{7}$ унций апельсинового сока, а у Кита  $2\frac{2}{5}$ унций апельсинового сока. Сколько апельсинового сока у них всего?

Здесь мы найдем ответ, сложив смешанные числа $1\frac{4}{7}$ и  $\frac2{2}{5}$. Здесь знаменатели обеих дробных частей разные.

Чтобы сложить смешанные числа с разными знаменателями, лучше всего преобразовать оба смешанных числа в неправильные дроби, а затем сложить их точно так же, как мы складываем две разные дроби.

Шаг 1: Преобразуйте смешанные числа в неправильные дроби.

и

Шаг 2. Сложите неправильные дроби.

Здесь нужно сложить разные дроби $\frac{11}{7}$ и $\frac{12}{5}$

Кратные 7: 14, 21, 28, 35 , 42

Кратно 5: 5, 10, 15, 20, 25, 20, 35 .

Таким образом, НОК равно 35.

Теперь преобразуем дроби в эквивалентные дроби со знаменателем в виде НОК.

$\frac{11}{7} = \frac{11}{7}  × \frac{5}{5} = \frac{55}{35}$

$\frac{12}{5} = \frac{12}{5}  × \frac{7}{7} = \frac{84}{35}$

Итак,

$\frac{11}{7} + {12}{5} = \frac{55}{35} + 8435 = 55 + 8435 = 13935

Шаг 3: Преобразуйте окончательный результат в неправильную дробь.

$\frac{139}{35}=3\frac{34}{35}$

Решенные примеры

Пример 1: Дэвид съел 3 ½ куска пиццы, а Джей съел 5 ⅔ кусочков пиццы. Сколько кусков пиццы они съели всего?

Решение : Проблема сводится к сложению смешанных чисел. Мы добавим 3 ½ + 5 ⅔.

Пример 2. Рон прошел $3\frac{2}{7}$ мили во время похода в лес, в то время как его друг прошел $2\frac{4}{7}$ мили. Какое расстояние они оба преодолели за время пути?

Решение : Мы найдем ответ, сложив смешанные числа, $3\frac{2}{7}$ и   $2\frac{4}{7}$.

Здесь целыми являются 2 и 3. Давайте сначала сложим их.

$2 + 3 = 5$

А теперь добавим дробные части.

Дробные части: $\frac{2}{7}$ и $\frac{4}{7}$.

$\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}$

Итак, мы получаем $3\frac {2}{7} +  2\frac{4}{7}=5\frac{6}{7}$

Итак, Рон и его друг преодолели $5\frac{6}{7}$ миль за поездку. .

Практические задачи

1

Найдите сумму двух смешанных дробей $4\frac{2}{6}$ и $5\frac{1}{6}$.

$6\frac{2}{6}$

$9\frac{1}{6}$

$4\frac{2}{6}$

$9\frac{3}{6}$

Правильный ответ: $9\frac{3}{6}$
$4\frac{2}{6} +5\frac{1}{6} = 4 + 5 + \frac{2}{6} + \frac {1}{6}$
$= 9 + \frac{3}{6}$
$= 9\frac{3}{6}$

2

Сэм пробежал трусцой $3\frac{1}{5} $ миль во время марафона, в то время как его друг пробежал $2\frac{1}{5}$ миль. Какое расстояние они преодолели в общей сложности?

$5\frac{2}{5}$

$5\frac{1}{5}$

$2\frac{2}{5}$

$1\frac{1}{25}$

Правильный ответ: $5\frac{2}{5}$
Мы найдем ответ, сложив смешанные числа , $3\frac{1}{5}$ и $2\frac{1}{5}$.
$3\frac{1}{5} +2\frac{1}{5} = 3 + 2 + \frac{1}{5} + \frac{1}{5}$
$= 5 + \frac {2}{5}$
$= 5\frac{2}{5}$

3

Найдите сумму $5\frac{2}{5}$ и $6\frac{4}{5}$ .