Сложение векторов.
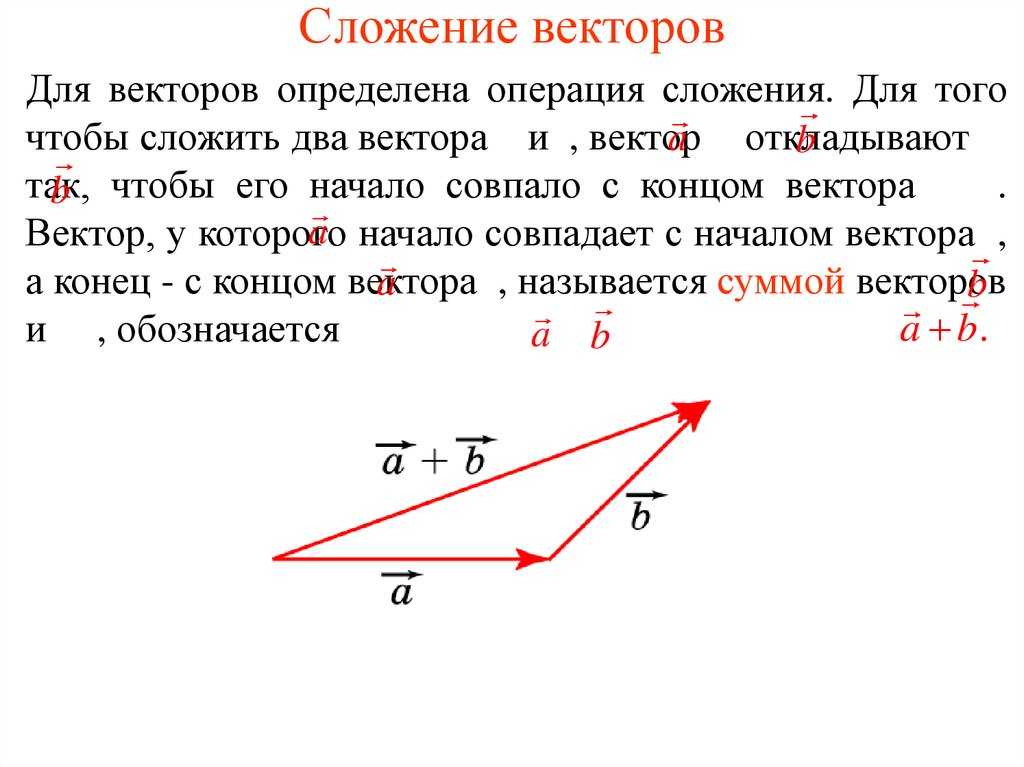
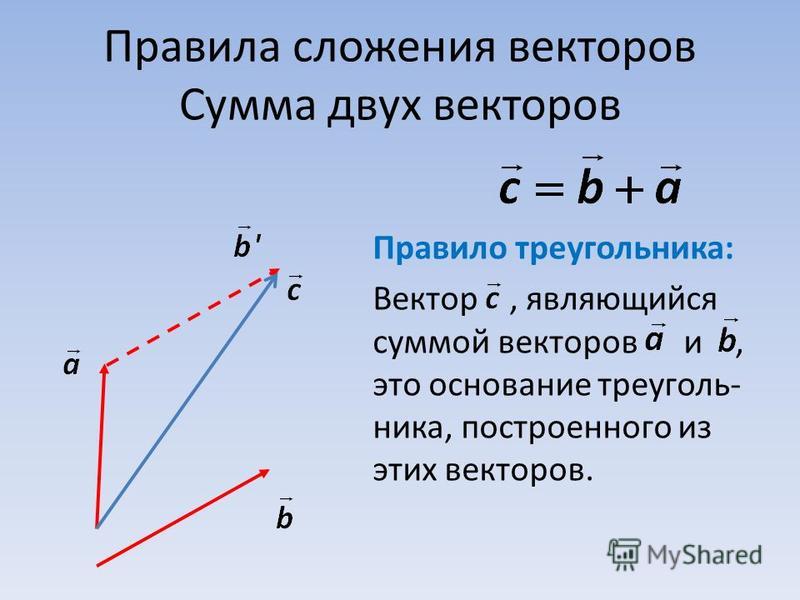
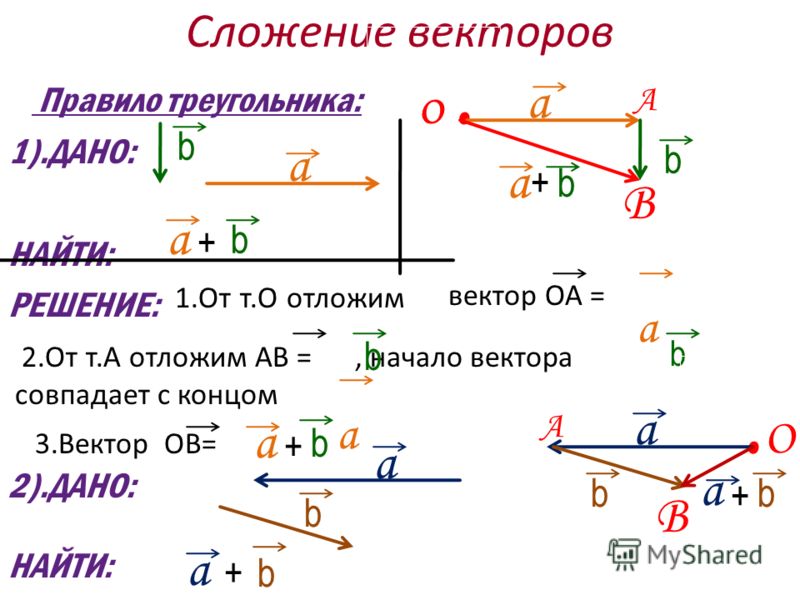
С уммой двух векторов и называется вектор , соединяющий начало вектора с концом вектора , отложенного от конца вектора .
Произведение вектора на число.
Произведение м вектора на число называется вектор, который имеет длину и который имеет направление вектора в случае и противоположное направление в случае .
Пример 3.1. Даны векторы и .
П остройте векторы: 1) ;
2) .
§ 2. Декартовы прямоугольные координаты вектора. Длина вектора.
Пусть вектор составляет угол с осью .
П роекцией вектора
на
ось
называется число, равное длине вектора (рис.3.1), взятой со знаком «плюс», если
направление вектора совпадает с направлением оси и со знаком
«минус» в противном случае.
.
Д екартовыми прямоугольными координатами вектора называются его проекции на соответствующие координатные оси .
В ектор с координатами записывают в виде или , где — единичные векторы координатных осей соответственно. Длина вектора определяется по формуле:
.
Если вектор задан точками и , то его координаты вычисляются по формулам:
.
Пример 3.2. Даны две точки и . Найдите координаты и длину вектора .
П о условию задачи , , , , , . Значит, .
.
Пример 3.3. Даны два вектора и . Найдите координаты и длину вектора .
; ;
;
.
С овместим параллельным переносом начало некоторого вектора с началом координат прямоугольной системы координат . Пусть — углы, которые образует вектор с осями координат соответственно (рис.3.2). Направление вектора определяется с помощью направляющих косинусов , , , для которых справедливы равенства:
§ 3. Скалярное произведение векторов.
С калярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними (см. рис.3.3):
.
И з рис. 3.3 видно, что .
Поэтому или . (*)
Свойства скалярного произведения.
— переместительный закон.

— распределительный закон.
Е сли то .
(или или ).
В частности, скалярное произведение единичных векторов (ортов) удовлетворяет равенствам:
Е сли векторы заданы координатами , или , , то
.
У гол между векторами и определяется по формуле:
.
В екторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.:
.
У словие перпендикулярности векторов и :
.
Пример 3.4. Векторы
и
образуют угол . Зная, что и ,
вычислите .
Зная, что и ,
вычислите .
.
П ример 3.5. Даны вершины треугольника , и . Найдите: 1) внутренний угол при вершине ;
2) .
Д ля нахождения угла найдём векторы и .
;
.
Тогда Т.е.
Согласно формуле (*)
.
ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ
1. Понятие вектора.
2. Понятие единичного и нулевого вектора.
3. Модуль вектора, формула расстояния между двумя точками.
4. Понятие коллинеарности векторов.
5. Линейные операции над векторами.
6. Понятие проекции вектора на ось.
7. Скалярное произведение векторов.
Вся элементарная математика — Средняя математическая интернет-школа
Вектор – это направленный
отрезок, соединяющий две точки в пространстве или в плоскости. Векторы
обычно
обозначаются либо маленькими буквами, либо начальной и
конечной точками. Сверху обычно ставят чёрточку.
Векторы
обычно
обозначаются либо маленькими буквами, либо начальной и
конечной точками. Сверху обычно ставят чёрточку.
Например, вектор, направленный из точки A к точке B , можно обозначить a ,
__
Нулевой вектор 0 или 0 — это вектор, у которого начальная и конечная точки совпадают, т. e . A = B . Отсюда, 0 = – 0 .
Длина (модуль) вектора a — это длина отображающего его отрезка
AB
,
обозначается | a | . В частности, | 0 | = 0.
В частности, | 0 | = 0.
Векторы называются коллинеарными ,
если их направленные отрезки лежат на параллельных прямых. Коллинеарные векторы a и b обозначаются
Три и более векторов называются компланарными , если они лежат в одной плоскости .
Сложение векторов. Так как векторы — это направленные отрезки, то их сложение может быть выполнено геометрически . (Алгебраическое сложение векторов изложено ниже, в пункте «Единичные ортогональные векторы»). Предположим , что
__ __
a = AB and b = CD ,
тогда вектор __ __
a + b = AB
+ CDесть результат выполнения двух операций:
a ) параллельного переноса одногоиз векторов таким образом, чтобы его начальная точка совпала с конечной точкой второго вектора;
б ) геометрического сложения ,
т.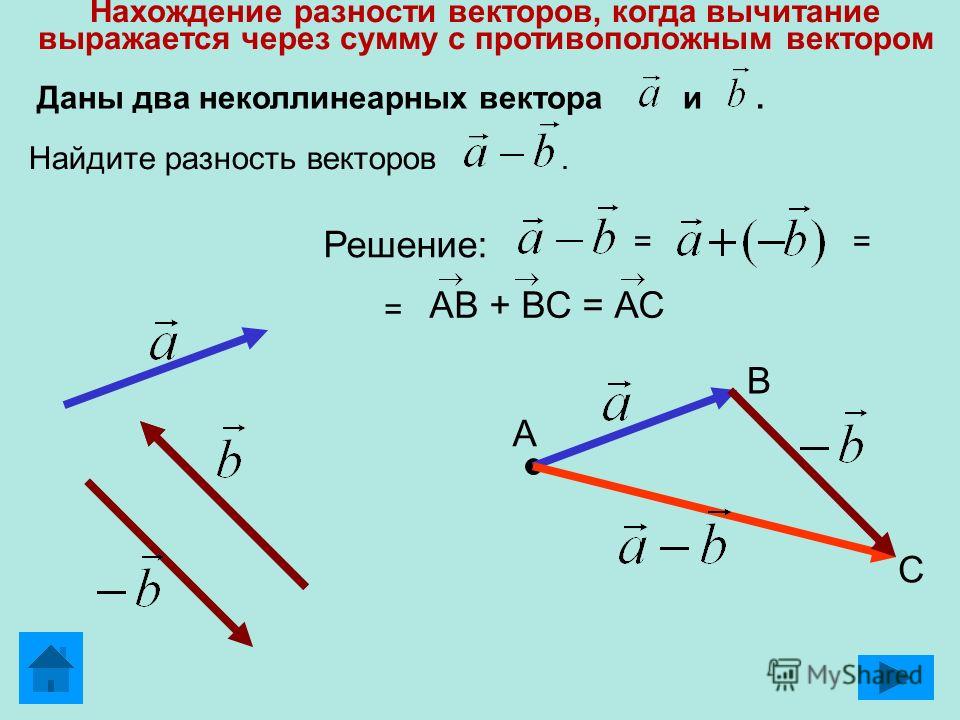 е. построения результирующего вектора, идущего от начальной точки
неподвижного вектора к конечной точке
перенесённого вектора
.
е. построения результирующего вектора, идущего от начальной точки
неподвижного вектора к конечной точке
перенесённого вектора
.
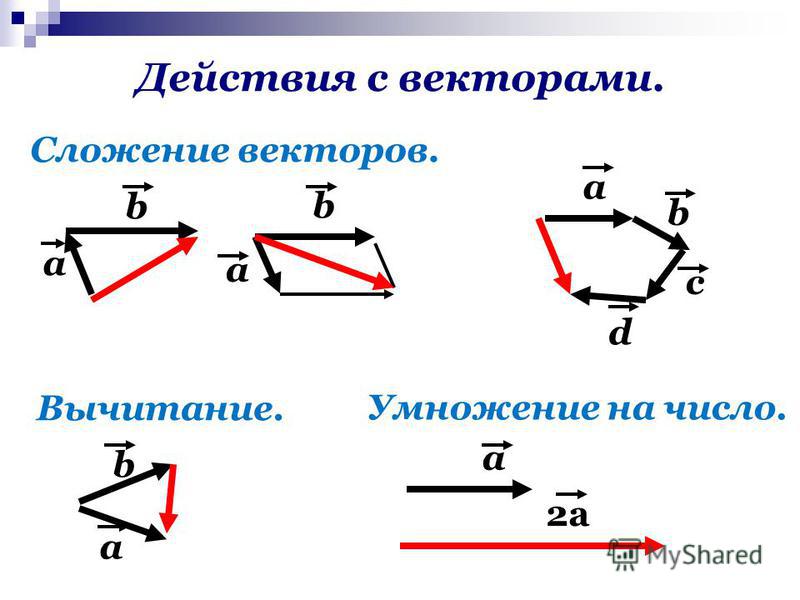
Вычитание векторов. Эта операция сводится к предыдущей путём замены вычитаемого вектора на противоположный: a – b = a + ( – b ) .
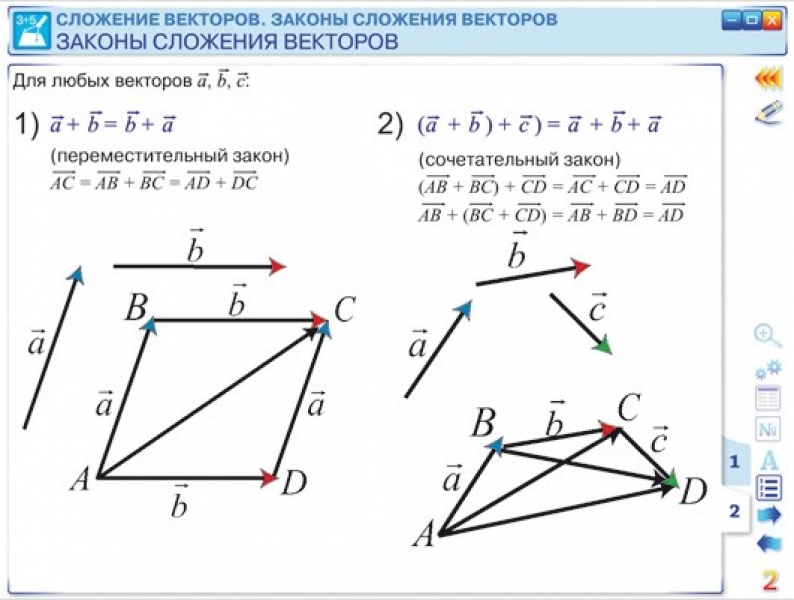
Законы сложения .
I . a + b = b + a ( П е р е м е с т и т е л ь н ы й закон ).
II
. ( a + b ) + c = a + ( b + c ) ( С о ч е т а т е л ь н ы й закон
).
( a + b ) + c = a + ( b + c ) ( С о ч е т а т е л ь н ы й закон
).
III . a + 0 = a .
IV. a + ( – a ) = 0 .
Законы умножения вектора на число.
I. 1 · a = a , 0 · a = 0 , m · 0 = 0 , ( – 1 ) · a = – a
II. m a = a m , | m a | = | m | · | a | .
III . m ( n a ) = ( m n ) a . ( С о ч е т а т е л ь н ы й
закон умножения на число ).
IV . ( m + n ) a = m a + n a , ( Р а с п р е д е л и т е л ь н ы й
m ( a + b ) = m a +
m b . закон
умножения на число ).
закон
умножения на число ).
Скалярное произведение векторов . __ __
Угол между ненулевыми векторами AB и CD – это угол, образованный векторами при их параллельном переносе до совмещения точек A и C . Скалярным произведением векторов a и b называется число, равное произведению их длин на косинус угла между ними:
Если один из векторов нулевой, то их скалярное произведение в соответствии с определением равно нулю:
( a
, 0 ) = ( 0 , b ) = 0 .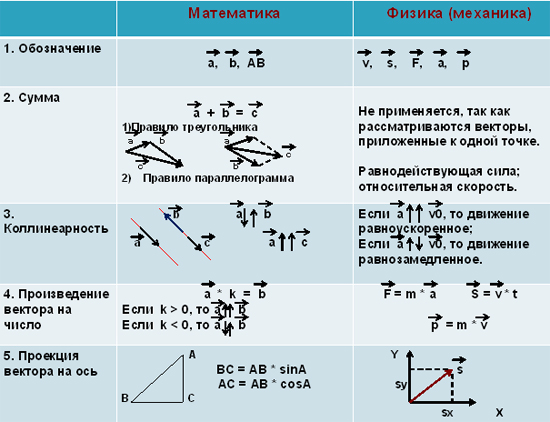
Если оба вектора ненулевые, то косинус угла между ними вычисляется по формуле :
Скалярное произведение ( a , a ), равное | a | 2 , называется скалярным квадратом. Длина вектора a и его скалярный квадрат связаны соотно шением:
Скалярное произведение двух векторов:
— положительно , если угол между векторами острый ;
— отрицательно, если угол между векторами тупой .
Скалярное произведение двух
ненулевых векторов равно нулю тогда и только тогда, когда угол между ними прямой, т.е. когда эти векторы
перпендикулярны (ортогональны):
когда эти векторы
перпендикулярны (ортогональны):
Свойства скалярного произведения. Для любых векторов a , b , c и любого числа m справедливы следующие соотношения:
I . ( a , b ) = ( b , a ) . ( П е р е м е с т и т е л ь н ы й закон )
II
. ( m a
, b ) = m ( a
, b ) .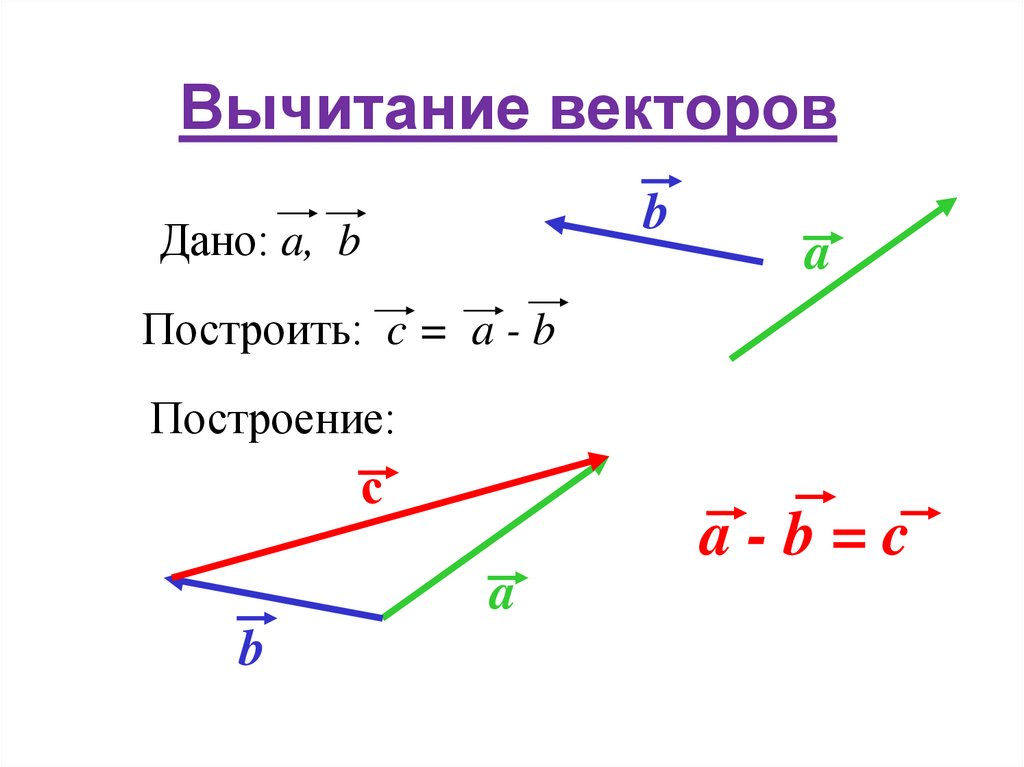
III . ( a + b , c ) = ( a , c ) + ( b , c ) . ( Р а с п р е д е л и т е л ь н ы й закон )
Единичные ортогональные векторы. В любой прямоугольной
системе координат можно ввести единичные попарно ортогональные векторы i , j и k ,
связанные с координатными осями: i – с осью Х , j – с осью
Y
и k – с осью Z .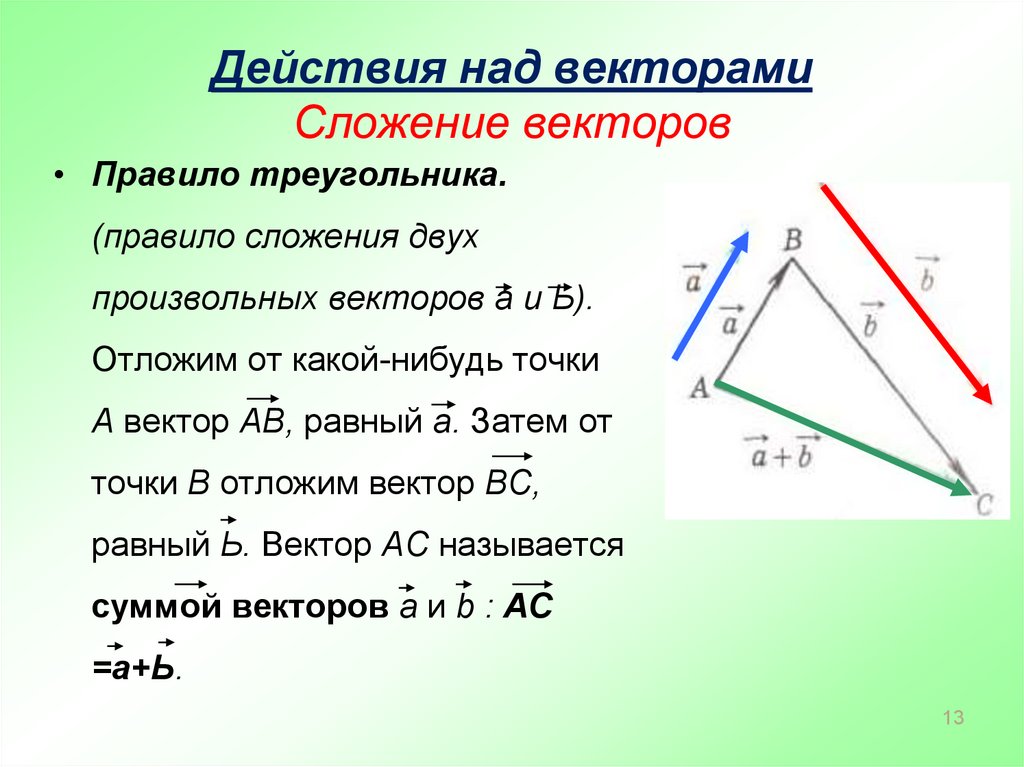 В соответствии с этим определением:
В соответствии с этим определением:
( i , j ) = ( i , k ) = ( j , k ) = 0,
| i | = | j | = | k | = 1.
Любой вектор a может быть выражен
через эти векторы единственным образом: a = x i
+ y j
+ z k .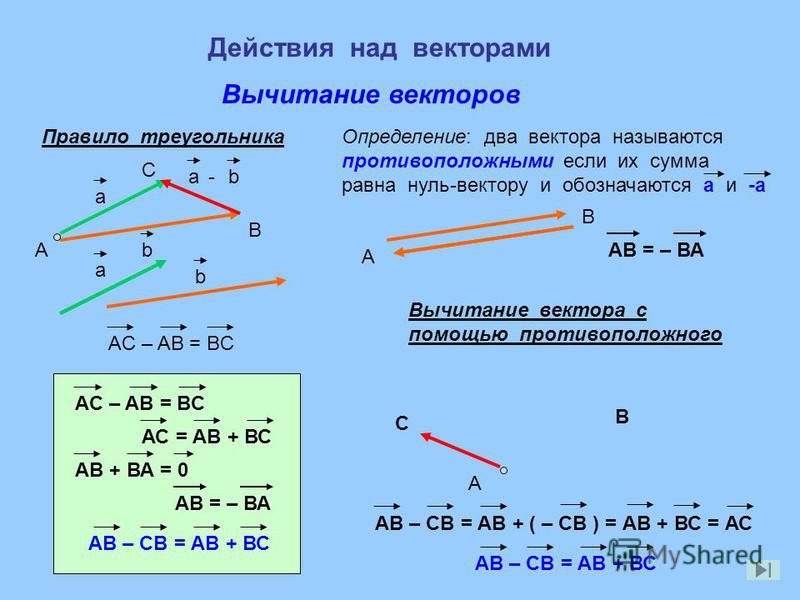 Другая форма записи
: a = ( x,
y, z ).
Здесь x , y , z
— координаты вектора a в этой системе координат. В
соответствии с последним соотношением и свойствами единичных ортогональных
векторов i
,
j
,
k скалярное произведение двух векторов
можно выразить иначе.
Другая форма записи
: a = ( x,
y, z ).
Здесь x , y , z
— координаты вектора a в этой системе координат. В
соответствии с последним соотношением и свойствами единичных ортогональных
векторов i
,
j
,
k скалярное произведение двух векторов
можно выразить иначе.
Пусть a =
( x
,
y
,
z )
; b =
( u
,
v
,
w )
. Тогда
( a , b ) = xu
+
yv
+
zw .
Тогда
( a , b ) = xu
+
yv
+
zw .
Скалярное произведение двух векторов равно сумме произведений соответствующих координат.
Длина (модуль) вектора a = ( x , y , z ) равна:
Кроме того, теперь мы получаем возможность проведения алгебраических операций над векторами, а именно, сложение и вычитание векторов может выполняться по координатам :
a + b = ( x + u , y + v , z + w ) ;
a – b = ( x – u , y – v , z – w ) .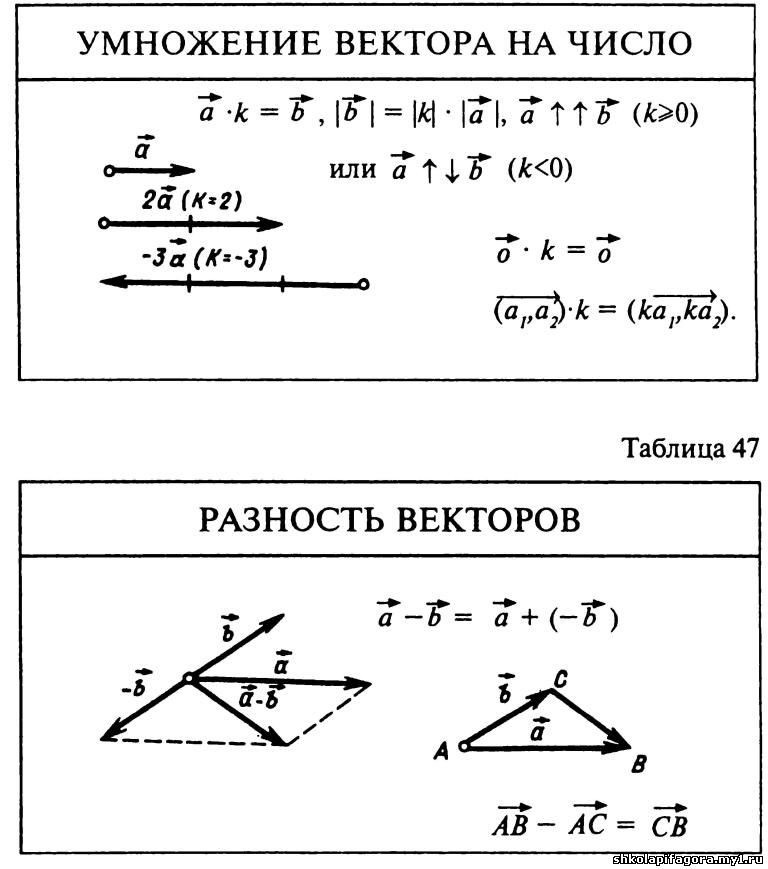
Векторное произведение векторов. Векторным произведением [ a ,
b ] векторов a и b ( в указанном порядке ) называется вектор:
Существует другая формула длины вектора
[ a, b ]
:
/\
| [ a, b ] | = | a | | b | sin ( a, b ) ,
т.
e
. длина (
модуль
) векторного произведения
векторов a и b равна
произведению длин ( модулей )
этих векторов на синус угла между ними. Иначе говоря: длина (
модуль ) вектора [ a
,
b ] численно равна площади параллелограмма, построенного на векторах a и b .
длина (
модуль
) векторного произведения
векторов a и b равна
произведению длин ( модулей )
этих векторов на синус угла между ними. Иначе говоря: длина (
модуль ) вектора [ a
,
b ] численно равна площади параллелограмма, построенного на векторах a и b .
Свойства векторного произведения
.
I . Вектор [ a , b ] перпендикулярен (ортогонален) обоим векторам a и b .
( Докажите это , пожалуйста ! ) .
II. [ a , b ] = – [ b , a ] .
III. [ m a , b ]
= m [ a , b ]
.
IV. [ a + b , c ] = [ a , c ] + [ b , c ] .
V. [ a , [ b , c ] ] = b ( a , c ) – c ( a , b ) .
VI. [ [ a , b ] , c ]
= b ( a
, c ) – a ( b
, c ) .
[ [ a , b ] , c ]
= b ( a
, c ) – a ( b
, c ) .
Необходимое и достаточное условие коллинеарности векторов
a = ( x , y , z ) и b = ( u, v, w ) :
Необходимое и достаточное условие компланарности векторов a = ( x, y, z ), b = ( u, v, w ) и c = ( p, q, r ) :
П р и м е р
. Даны векторы: a = ( 1, 2, 3 ) и b = ( – 2 , 0 ,4 ).
Даны векторы: a = ( 1, 2, 3 ) и b = ( – 2 , 0 ,4 ).
Вычислить их скалярное и векторное произведения и угол
между этими векторами.
Р е ш е н и е . Используя соответствующие формулы (см. выше), получим:
a ). скалярное произведение:
( a , b ) = 1 · ( – 2 ) + 2 · 0 + 3 · 4 = 10 ;
б). векторное произведение:
Назад
Analytical Methods – College Physics главы 1-17
3 Двумерная кинематика
Резюме
- Понимать правила сложения и вычитания векторов с использованием аналитических методов.

- Применение аналитических методов для определения векторов вертикальной и горизонтальной составляющих.
- Применение аналитических методов для определения величины и направления результирующего вектора.
Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации. Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (среди прочего) движения вдоль перпендикулярных направлений независимы. Нам очень часто нужно разделить вектор на перпендикулярные компоненты. Например, имея такой вектор, как [latex]\textbf{A}[/latex] на рисунке 1, мы можем захотеть найти, какие два перпендикулярных вектора, [latex]\boldsymbol{\textbf{A}_x}[/latex] и [латекс]\boldsymbol{\textbf{A}_y}[/латекс], добавьте, чтобы создать его.
Например, имея такой вектор, как [latex]\textbf{A}[/latex] на рисунке 1, мы можем захотеть найти, какие два перпендикулярных вектора, [latex]\boldsymbol{\textbf{A}_x}[/latex] и [латекс]\boldsymbol{\textbf{A}_y}[/латекс], добавьте, чтобы создать его.
[латекс]\boldsymbol{\textbf{A}_x}[/latex] и [латекс]\boldsymbol{\textbf{A}_y}[/latex] определены как компоненты [латекс]\textbf{A }[/latex]оси x и y. Три вектора[latex]\textbf{A},\:\boldsymbol{\textbf{A}_x},[/latex]и[latex]\boldsymbol{\textbf{A}_y}[/latex] образуют правый треугольник:
[латекс]\boldsymbol{\textbf{A}_x +\textbf{A}_y =\textbf{A}.}[/latex]
Обратите внимание, что эта связь между компонентами вектора и результирующим вектором сохраняется только для векторных величин (которые включают как величину, так и направление). Отношения не применимы только к величинам. Например, если [латекс]\boldsymbol{\textbf{A}_x=3\textbf{м}}[/латекс]восток,[латекс]\boldsymbol{\textbf{A}_y=4\textbf{м}} [/latex]север и [latex]\boldsymbol{\textbf{A}=5\textbf{ m}}[/latex]северо-восток, то верно, что векторы[latex]\boldsymbol{\textbf{ A}_x+\textbf{A}_y=\textbf{A}}.[/latex]Тем не менее, это не правда, что сумма модулей векторов тоже равна. То есть
Отношения не применимы только к величинам. Например, если [латекс]\boldsymbol{\textbf{A}_x=3\textbf{м}}[/латекс]восток,[латекс]\boldsymbol{\textbf{A}_y=4\textbf{м}} [/latex]север и [latex]\boldsymbol{\textbf{A}=5\textbf{ m}}[/latex]северо-восток, то верно, что векторы[latex]\boldsymbol{\textbf{ A}_x+\textbf{A}_y=\textbf{A}}.[/latex]Тем не менее, это не правда, что сумма модулей векторов тоже равна. То есть
[латекс]\boldsymbol{3\textbf{м}+4\textbf{м}\neq 5\textbf{м}}[/латекс]
Таким образом,
[латекс]\boldsymbol{\textbf{A}_x+\textbf{A}_y\neq\textbf{A}}[/latex]
Если известен вектор[latex]\textbf{A}[/latex], то его величина[latex]\textbf{A}[/latex]и угол[latex]\boldsymbol{\theta}[/latex] (его направление) известны. Чтобы найти[latex]\boldsymbol{\textbf{A}_x}[/latex]и[latex]\boldsymbol{A_y},[/latex] его x- и y-компоненты, мы используем следующие соотношения для прямоугольного треугольника .
[латекс]\boldsymbol{\textbf{A}_x=\textbf{A cos}\:\theta}[/latex]
и
[латекс]\boldsymbol{\textbf{A}_y=\textbf{A sin}\:\theta}. [/latex]
[/latex]
Предположим, например, что [latex]\textbf{A}[/latex] является вектором, представляющим полное перемещение человека, идущего по городу, рассмотренному в главе 3.1 «Кинематика в двух измерениях: введение» и главе 3.2 «Сложение векторов» и Вычитание: графические методы.
Рисунок 3. Мы можем использовать соотношения A x =A cos θ и A y =A sinθ 9о)=5.0\textbf{ блоков}.}[/latex] Если перпендикулярные компоненты [латекс]\boldsymbol{\textbf{A}_x}[/latex]и[латекс]\boldsymbol{\textbf{A}_y}[/latex]вектора[латекс]\textbf{A }[/latex] известны, то[latex]\textbf{A}[/latex]можно найти и аналитически. {-1}(\textbf{A}_y\:/\:\textbf{A}_x)}[/latex] используются для нахождения вектора по его перпендикулярным компонентам — то есть перейти от [латекс]\boldsymbol{\textbf{A}_x}[/latex]и[латекс]\boldsymbol{\textbf{A}_y}[/latex]к[латекс]\textbf{A }[/latex] и [latex]\boldsymbol{\theta}.[/latex] Оба процесса имеют решающее значение для аналитических методов сложения и вычитания векторов.
{-1}(\textbf{A}_y\:/\:\textbf{A}_x)}[/latex] используются для нахождения вектора по его перпендикулярным компонентам — то есть перейти от [латекс]\boldsymbol{\textbf{A}_x}[/latex]и[латекс]\boldsymbol{\textbf{A}_y}[/latex]к[латекс]\textbf{A }[/latex] и [latex]\boldsymbol{\theta}.[/latex] Оба процесса имеют решающее значение для аналитических методов сложения и вычитания векторов.
Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рисунок 5, на котором векторы[latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]добавляются для получения результирующего [латекс]\textbf{R}.[/латекс]
Рис. 5. Векторы A и B — два участка пути, а R — равнодействующее или полное перемещение. Вы можете использовать аналитические методы для определения величины и направления R . Если[latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]представляют два этапа ходьбы (два смещения), то[latex]\textbf{R}[/latex ] — полное водоизмещение.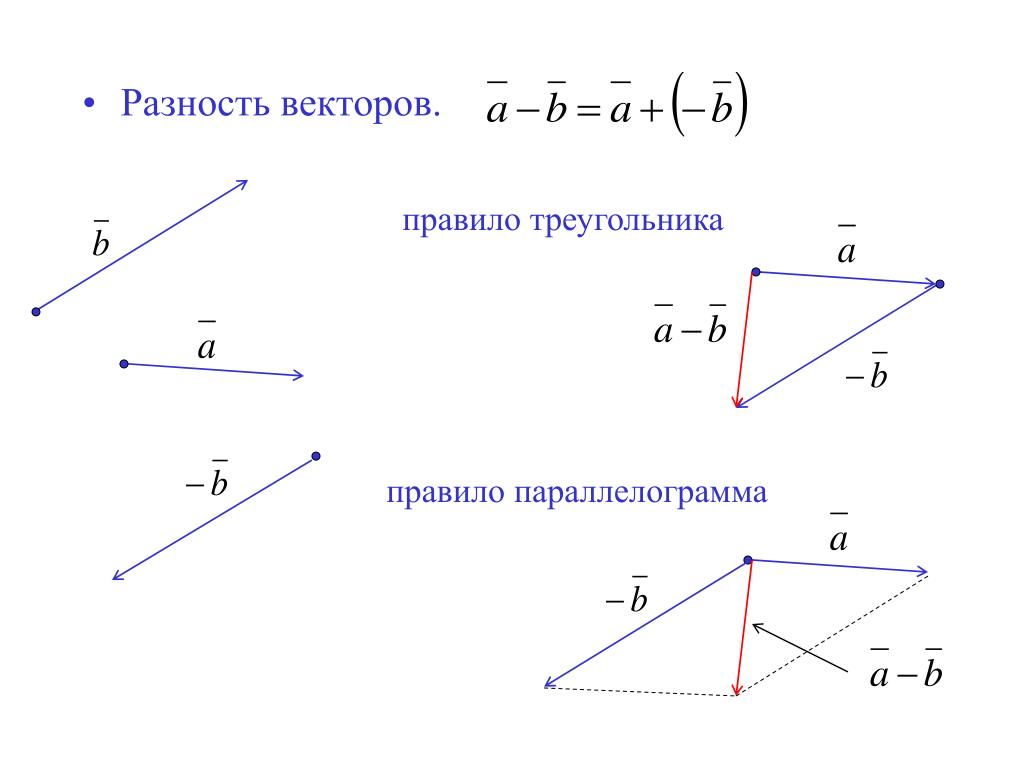 Человек, совершающий прогулку, оказывается на кончике[latex]\textbf{R}.[/latex]Есть много способов попасть в одну и ту же точку. В частности, человек мог ходить первым в 9{-1}(\textbf{A}_y\:/\:\textbf{A}_x)}.[/latex]При использовании аналитического метода сложения векторов можно определить компоненты или величину и направление вектор.
Человек, совершающий прогулку, оказывается на кончике[latex]\textbf{R}.[/latex]Есть много способов попасть в одну и ту же точку. В частности, человек мог ходить первым в 9{-1}(\textbf{A}_y\:/\:\textbf{A}_x)}.[/latex]При использовании аналитического метода сложения векторов можно определить компоненты или величину и направление вектор.
Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого вектора, которые должны быть добавлены вдоль выбранных перпендикулярных осей . Используйте уравнения [латекс]\boldsymbol{\textbf{A}_x=\textbf{A cos}\:\theta}[/latex]и[латекс]\boldsymbol{\textbf{A}_y=\textbf{A sin}\:\theta}[/latex], чтобы найти компоненты. На рисунке 6 этими компонентами являются [латекс]\boldsymbol{\textbf{A}_x},\boldsymbol{\textbf{A}_x},\boldsymbol{\textbf{B}_x},[/latex]и[латекс ]\boldsymbol{\textbf{B}_y}.[/latex]Углы, которые векторы[latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]составляют с x -ось [латекс]\жирныйсимвол{\тета_{А}}[/латекс] и [латекс]\жирныйсимвол{\тета_{В}},[/латекс] соответственно.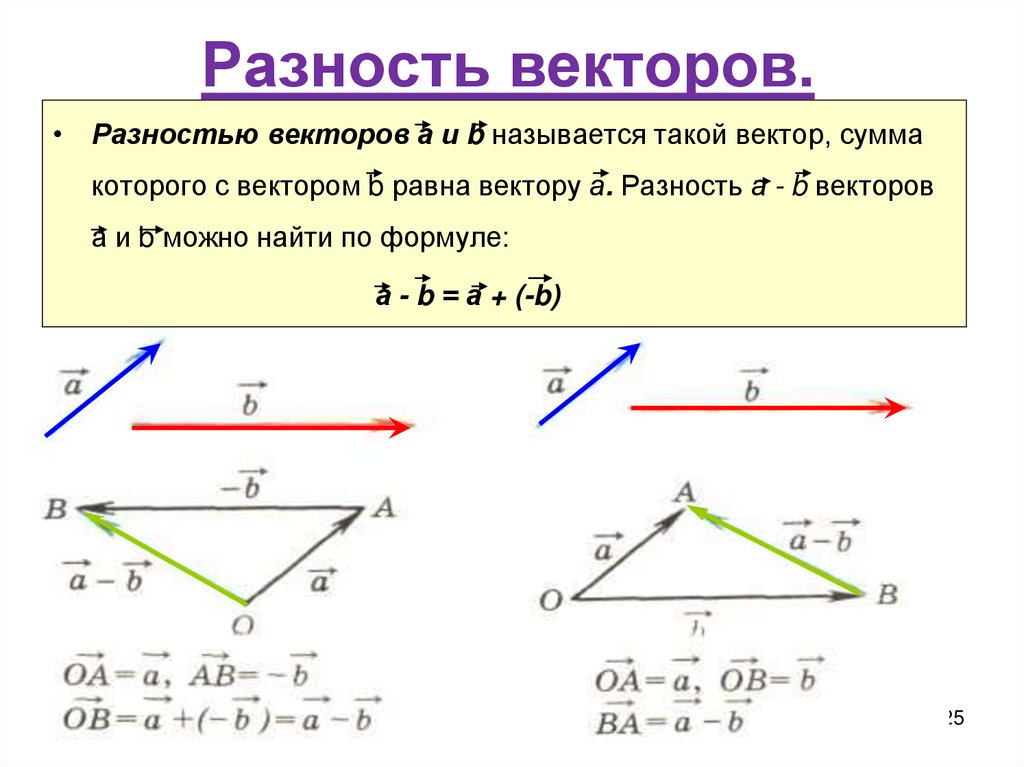
Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси . То есть, как показано на рисунке 7,
[латекс]\boldsymbol{\textbf{R}_x=\textbf{A}_x+\textbf{B}_x}[/latex]
и
[латекс]\boldsymbol{\textbf{R}_y=\textbf{A}_y+\textbf{B}_y.}[/latex]
Рисунок 7. Величина векторов A x и B x добавьте, чтобы получить величину R x результирующего вектора в горизонтальном направлении. Точно так же величины векторов A y и B y складываются, чтобы получить величину R y 29 в вертикальном направлении результирующего вектора.
Точно так же величины векторов A y и B y складываются, чтобы получить величину R y 29 в вертикальном направлении результирующего вектора.Компоненты вдоль одной и той же оси, скажем, оси x , являются векторами вдоль одной и той же прямой и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль y -ось. (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток и вторые 6 кварталов на восток, всего 9, потому что они идут в одном направлении.) Таким образом, разложение векторов на компоненты вдоль общие оси облегчают их добавление. Теперь, когда компоненты [латекса]\textbf{R}[/латекс] известны, можно найти его величину и направление.
Шаг 3. Чтобы получить величину[latex]\textbf{R}[/latex]результата, используйте теорему Пифагора: 9{-1}(\textbf{R}_y\:/\:\textbf{R}_x). o} [/latex]северо-восток.
o} [/latex]северо-восток.
Стратегия
Компоненты [latex]\textbf{A}[/latex]и [latex]\textbf{B}[/latex] вдоль x 9о)}[/латекс]
[латекс]\boldsymbol{=(34,0\textbf{м})(0,891)=30,3\текстбф{м}.}\:\:\:\:\:[/латекс]
x — и y -компоненты равнодействующей, таким образом, равны
[латекс]\boldsymbol{\textbf{R}_x=\textbf{A}_x\:+\:\textbf{B}_x =49,8\textbf{м}\:+\:15,4\textbf{м}=65,2\textbf{м}}[/латекс]
и
[латекс]\boldsymbol{\textbf{R}_y=\textbf {A}_y\:+\:\textbf{B}_y=18.1\textbf{ m}\:+\:30.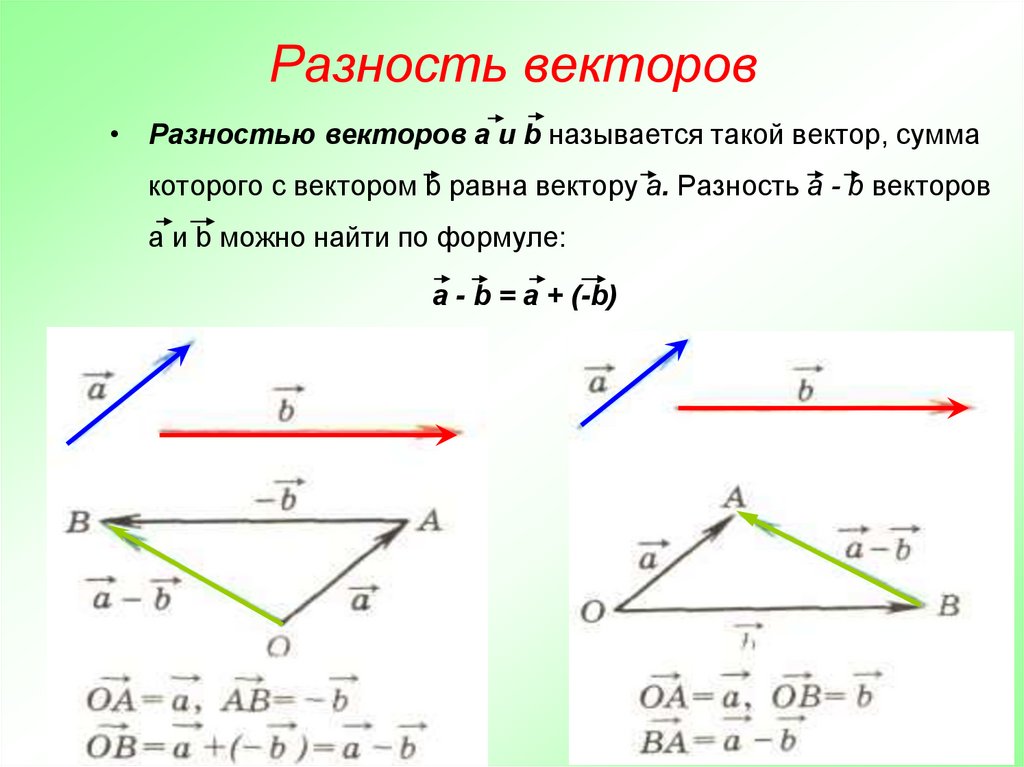 3\textbf{ m}=48.4\textbf{ m}.}[/latex]
3\textbf{ m}=48.4\textbf{ m}.}[/latex]
Теперь мы можно найти величину равнодействующей, используя теорему Пифагора: 9o.}[/latex]
Рисунок 9. Используя аналитические методы, мы видим, что звездная величина R равна 81,2 м , а ее направление 36,6 0 к северу от востока.Обсуждение
Этот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора. То есть [латекс]\boldsymbol{\textbf{A}-\textbf{B}\equiv\textbf{A}+(-\textbf{B})}.[/latex] Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты [латекс]\boldsymbol{-\textbf{B}}[/latex]являются минусами компонентов [латекс]\textbf{B}. [/latex] x – и y – Таким образом, компоненты результирующего [латекса]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{R}}[/latex] равны
[/latex] x – и y – Таким образом, компоненты результирующего [латекса]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{R}}[/latex] равны
[латекс]\boldsymbol{\textbf{R}_x=\ textbf{A}_x\:+\:(-\textbf{B}_x)}[/latex]
и
[латекс]\boldsymbol{\textbf{R}_y=\textbf{A}_y\: +\:(-\textbf{B}_y)}[/латекс]
, а в остальном метод, описанный выше, идентичен методу добавления. (См. рис. 10.)
Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующий модуль, Глава 3.4 Движение снаряда, является одним из многих, в которых использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.
Рисунок 10. Вычитание двух векторов, показанных на рисунке 5. Компоненты -B являются минусами компонентов B . Метод вычитания такой же, как и для сложения.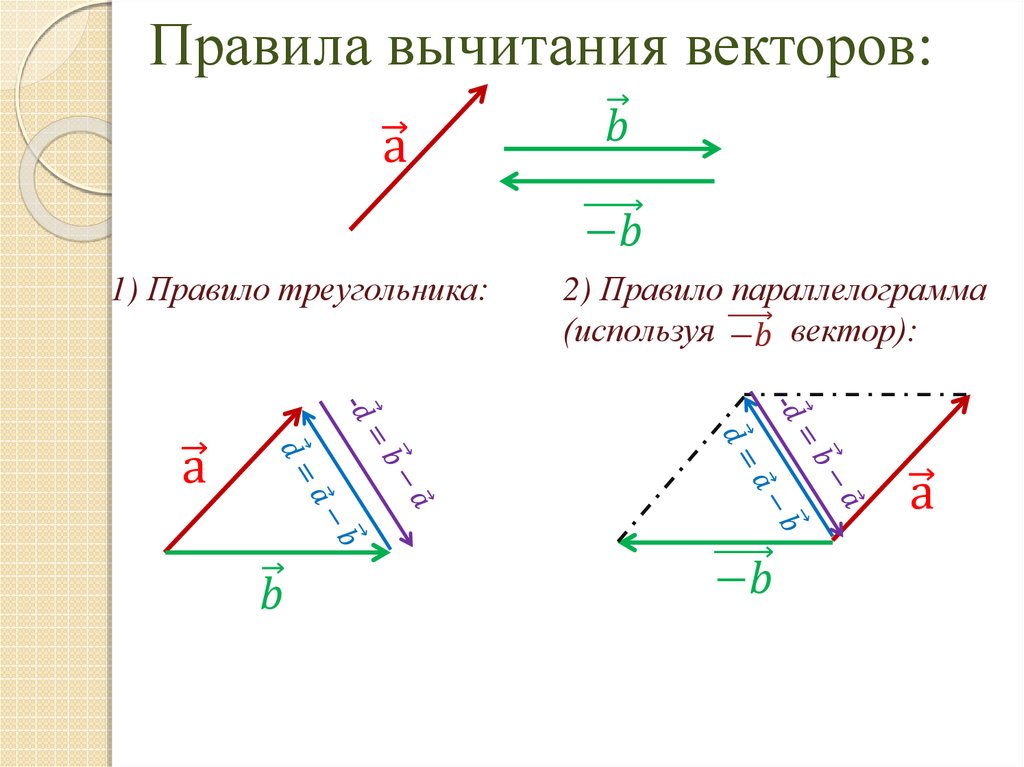
ИССЛЕДОВАНИЯ PHET: ДОБАВЛЕНИЕ ВЕКТОРОВ
Узнайте, как добавлять векторы. Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.
Рис. 11. Сложение векторов- Аналитический метод сложения и вычитания векторов включает использование теоремы Пифагора и тригонометрических тождеств для определения величины и направления результирующего вектора.
- Шаги для добавления векторов[latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]с использованием аналитического метода следующие:
Шаг 1: Определите систему координат для векторов. Затем определите горизонтальную и вертикальную составляющие каждого вектора, используя уравнения
[латекс]\boldsymbol{\textbf{A}_x=\textbf{A cos}\:\theta}[/latex]
[латекс]\boldsymbol{\textbf{B}_x=\textbf{B cos}\:\theta}[/latex]
и
[латекс]\boldsymbol{\textbf{A}_y=\textbf{A sin}\:\theta}[/latex]
[латекс]\boldsymbol{\textbf{B}_y=\textbf{B sin}\:\theta}.
 [/latex]
[/latex]Шаг 2. Сложите горизонтальные и вертикальные компоненты каждого вектора, чтобы определить компоненты [латекс]\boldsymbol{\textbf{R}_x}[/latex]и[латекс]\boldsymbol{\textbf{R}_y}[/ латекс]результирующего вектора,[латекс]\textbf{R}:[/латекс]
[латекс]\boldsymbol{\textbf{R}_x=\textbf{A}_x+\textbf{B}_x}[/latex]
и
[латекс]\boldsymbol{\textbf{R}_y=\textbf{A}_y+\textbf{B}_y}.[/latex] 9{-1}(\textbf{R}_y\:/\:\textbf{R}_x).}[/latex]
- аналитический метод
- метод определения величины и направления результирующего вектора с использованием теоремы Пифагора и тригонометрических тождеств
Учебное пособие по сложению векторов
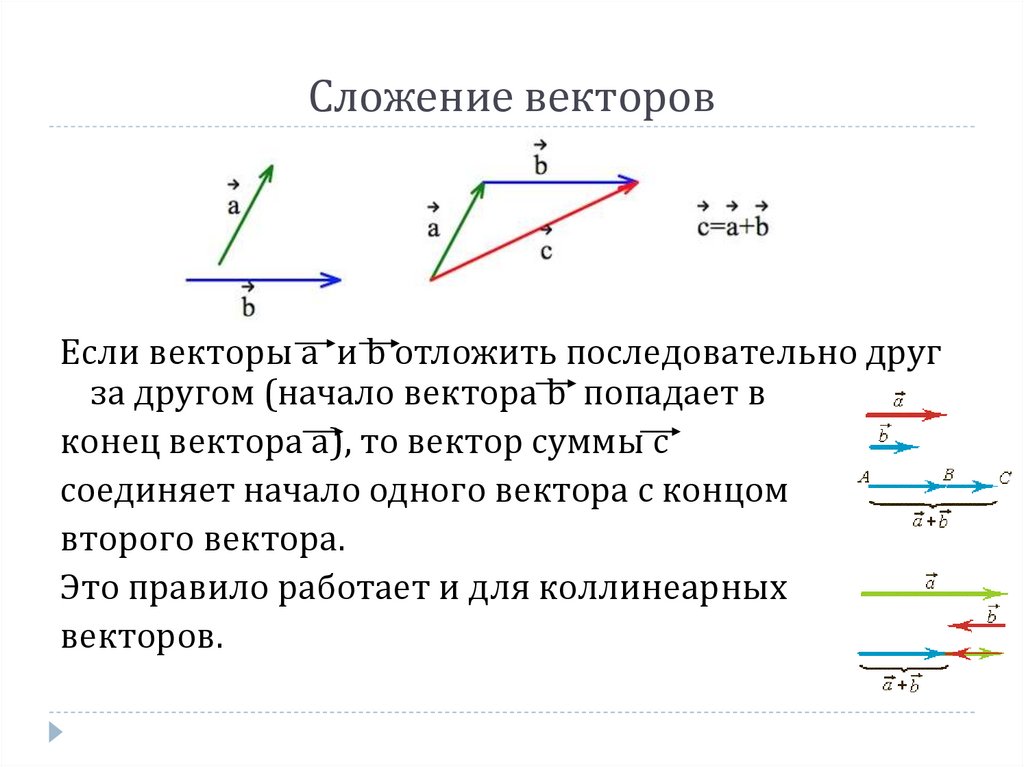
Учебное пособие по сложению векторов Скалярные количества имеют
только величина.
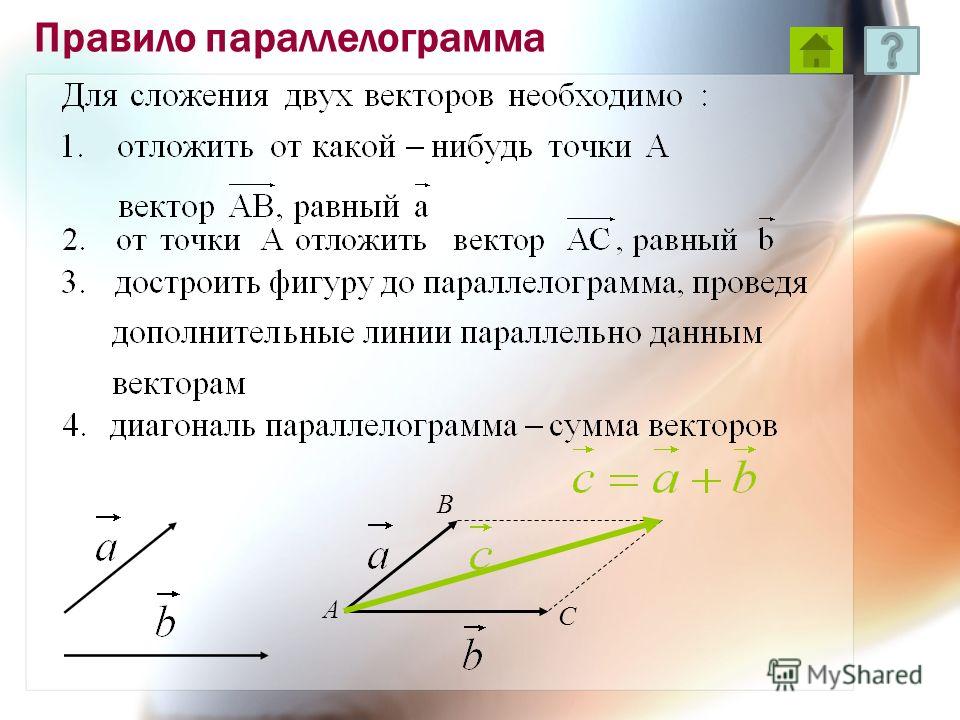 В этом разделе мы добавим те же векторы математически . Для этого мы сначала должны разложить каждый вектор на его горизонталь и вертикальные компоненты. Y = Вертикальная составляющая = Величина * Sin (θ) (Примечание: на этой диаграмме угол представлен греческим
буква θ
или «тета». В математике и естественных науках углы обычно обозначаются как таковые). Y = 3 * Sin(45°) В этом случае нет горизонтальной составляющей . X = 6 * Cos(90°) Y = 6 * Sin(90°) Y = 5 * Sin(150°) Суммируя вертикальные компоненты (значения Y): Определяем звездную величину результирующий вектор по теореме Пифагора: ArcTangent (результирующего вектора) = Арктангенс (результирующего вектора) = -4,8086237976514 На данный момент мы должны быть будьте осторожны при выборе правильного угла для результирующего вектора . 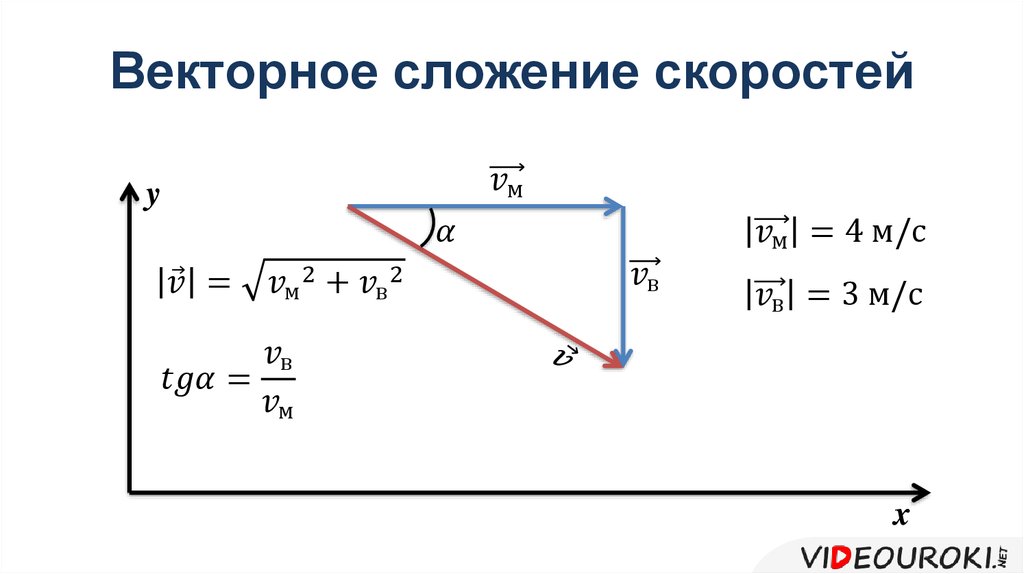 | ||


 [/latex]
[/latex] (Примерами являются температура и объем).
(Примерами являются температура и объем).  20880667536255 2 + 10.62132034355964 2
20880667536255 2 + 10.62132034355964 2