Сложение векторов по правилу треугольника определение: Какие правила сложения векторов вы знаете?

Аналитическая геометрия

Аналитическая геометрия

Привалов И.И. Аналитическая геометрия. М.: Наука, 1966. — 272 с. Учебник для студентов высших технических заведений. Содержит разделы: Аналитическая геометрия на плоскости, Аналитическая геометрия в пространстве. Много решенных примеров и задач. Оглавление ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций. § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости. 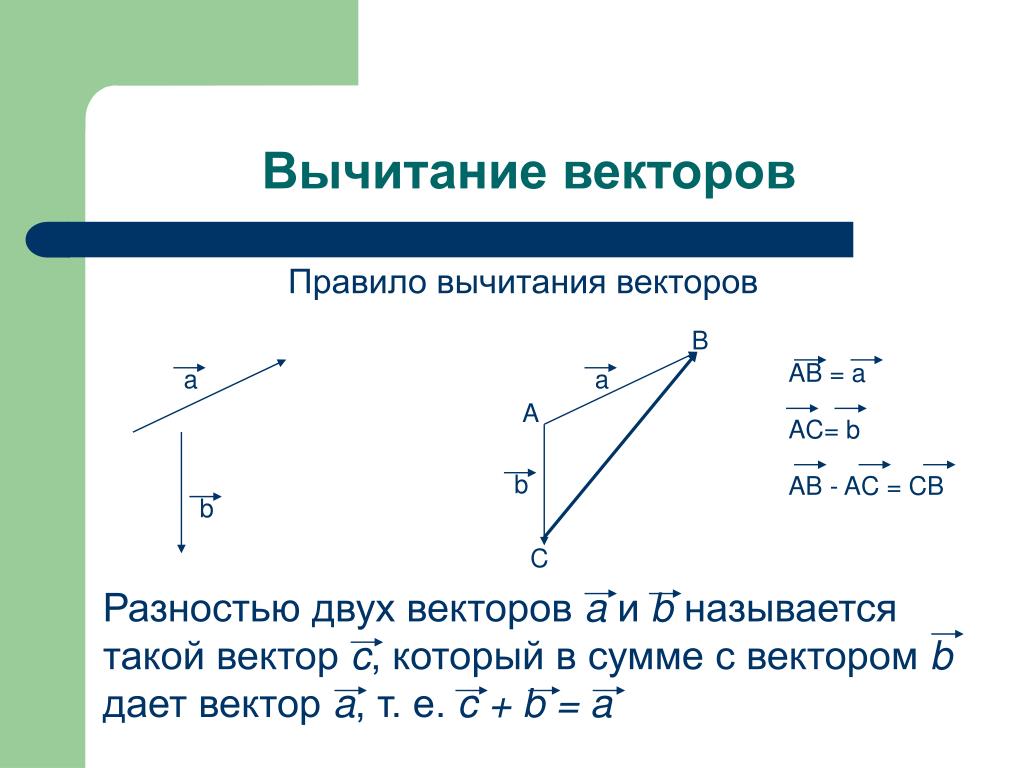§ 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры. 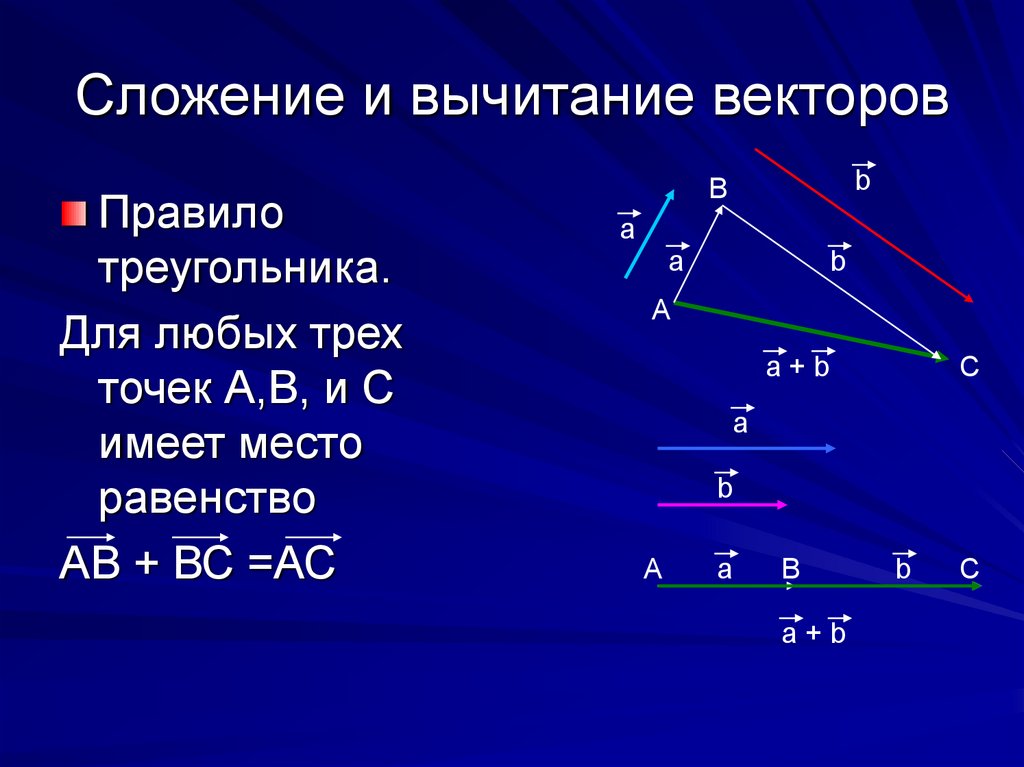§ 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии. 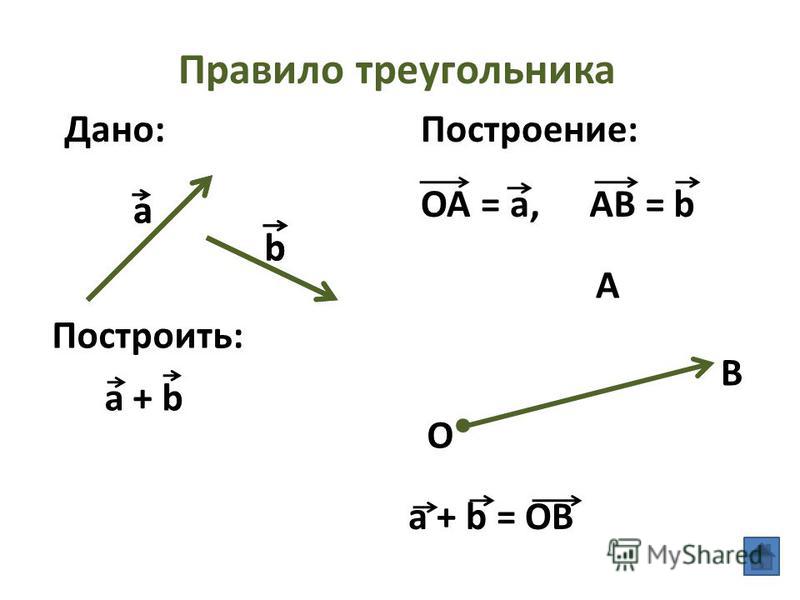Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ § 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой. § 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка. 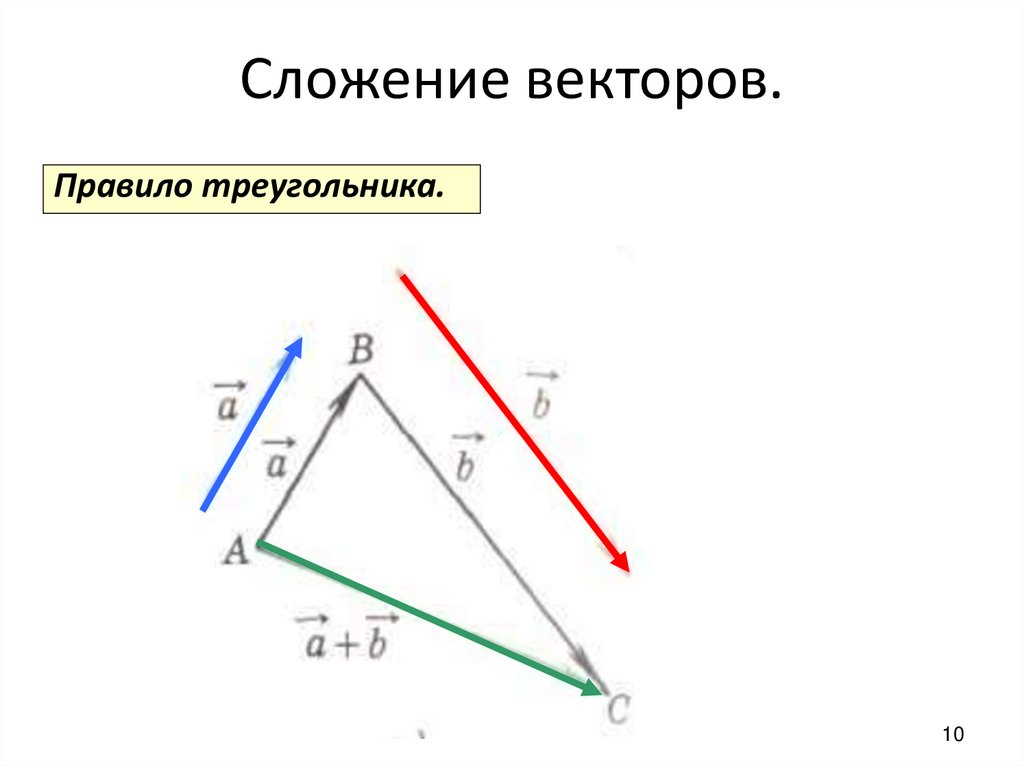Конструкции В. Г. Шухова. Упражнения Ответы

10 класс. Геометрия. Векторы в пространстве. — Сложение и вычитание векторов. Умножение вектора на число.

Комментарии преподавателя

От­ме­тим, что сло­же­ние век­то­ров про­из­во­дит­ся ана­ло­гич­но пла­ни­мет­рии, толь­ко все дей­ствия вы­пол­ня­ют­ся в про­стран­стве.

Итак, пусть за­да­ны два про­из­воль­ных век­то­ра в про­стран­стве (рис. 1):

Рис. 1. Про­из­воль­ные век­то­ры в про­стран­стве

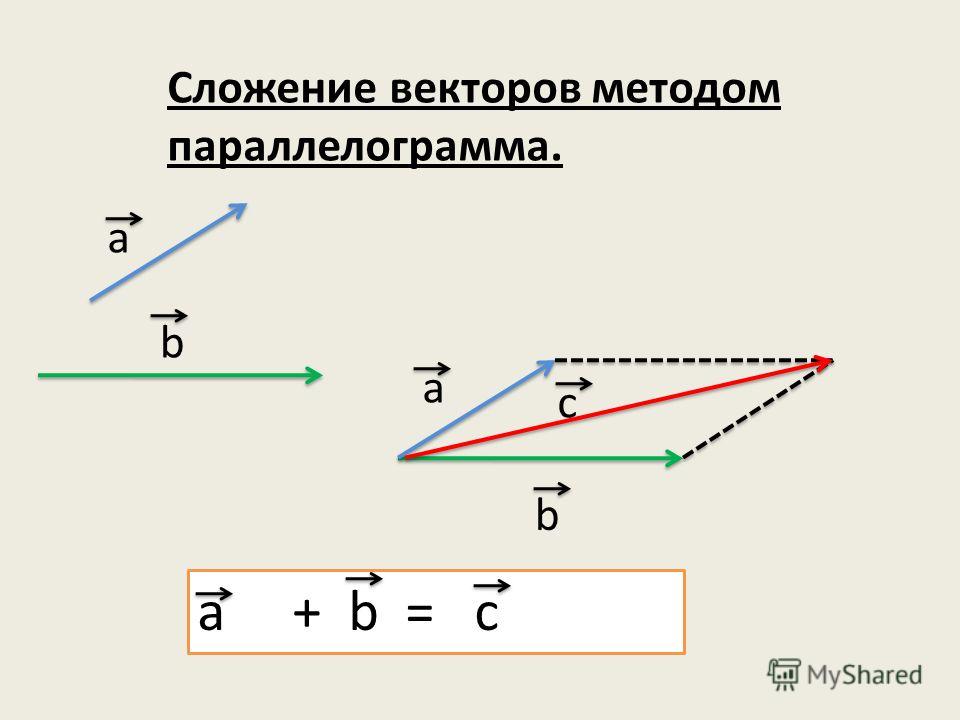
Опре­де­лим, что же на­зы­ва­ет­ся сум­мой двух этих век­то­ров.

Точно так же, как в пла­ни­мет­рии, из любой удоб­ной точки, на­зо­вем ее точ­кой А, можно един­ствен­ным об­ра­зом от­ло­жить век­тор, рав­ный век­то­ру . На­пом­ним, что за­дан­ные век­то­ры, как и любые дру­гие, сво­бод­ны, важно лишь на­прав­ле­ние и длина, сам век­тор можно па­рал­лель­но пе­ре­но­сить в любое место как на плос­ко­сти, так и в про­стран­стве. Так, мы по­лу­чи­ли век­тор  – в ре­зуль­та­те дей­ствия век­то­ра  точка А пе­ре­ме­сти­лась в точку В. Те­перь из точки В от­кла­ды­ва­ем един­ствен­но воз­мож­ным об­ра­зом век­тор , по­лу­ча­ем век­тор  – так, в ре­зуль­та­те дей­ствия век­то­ра  точка В пе­ре­ме­сти­лась в точку С. В ре­зуль­та­те точка А пе­ре­ме­сти­лась в точку С, по­лу­чен век­тор , ко­то­рый и на­зы­ва­ет­ся сум­мой век­то­ров  и  (рис. 2).

Рис. 2. Сумма двух век­то­ров в про­стран­стве

Так, по­лу­че­но пра­ви­ло тре­уголь­ни­ка для сло­же­ния век­то­ров в про­стран­стве.

Пра­ви­ло тре­уголь­ни­ка

Из любой точки про­стран­ства (точка А) от­кла­ды­ва­ем пер­вый век­тор, из конца пер­во­го век­то­ра (точка В) от­кла­ды­ва­ем вто­рой век­тор и по­лу­ча­ем точку С. Век­тор, со­еди­ня­ю­щий на­ча­ло пер­во­го век­то­ра (точка А) и конец вто­ро­го (точка С), и будет ре­зуль­ти­ру­ю­щим.

От­ме­тим, что ре­зуль­тат сло­же­ния век­то­ров не за­ви­сит от вы­бо­ра на­чаль­ной точки, су­ще­ству­ет со­от­вет­ству­ю­щая тео­ре­ма, ко­то­рая это до­ка­зы­ва­ет на ос­но­ва­нии того, что из точки можно от­ло­жить век­тор, рав­ный за­дан­но­му, един­ствен­ным об­ра­зом.

Опре­де­ле­ние

Раз­но­стью двух век­то­ров на­зы­ва­ет­ся такой тре­тий век­тор, ко­то­рый, бу­дучи сло­жен­ным со вто­рым век­то­ром, даст пер­вый век­тор.

Вве­дем раз­ность век­то­ров  и , для этого сло­жим век­тор  с про­ти­во­по­лож­ным век­то­ром :

Итак, из про­из­воль­ной точки А от­кла­ды­ва­ем век­тор , по­лу­ча­ем точку В. Чтобы по­лу­чить век­тор  мы стро­им век­тор, рав­ный век­то­ру  по длине, но про­ти­во­на­прав­лен­ный. По­лу­чен­ный век­тор от­кла­ды­ва­ем из точки В – по­лу­ча­ем точку D. Век­тор  и будет ис­ко­мым век­то­ром раз­но­сти.

Про­ил­лю­стри­ру­ем (рис. 3):

Рис. 3. Вы­чи­та­ние двух век­то­ров в про­стран­стве

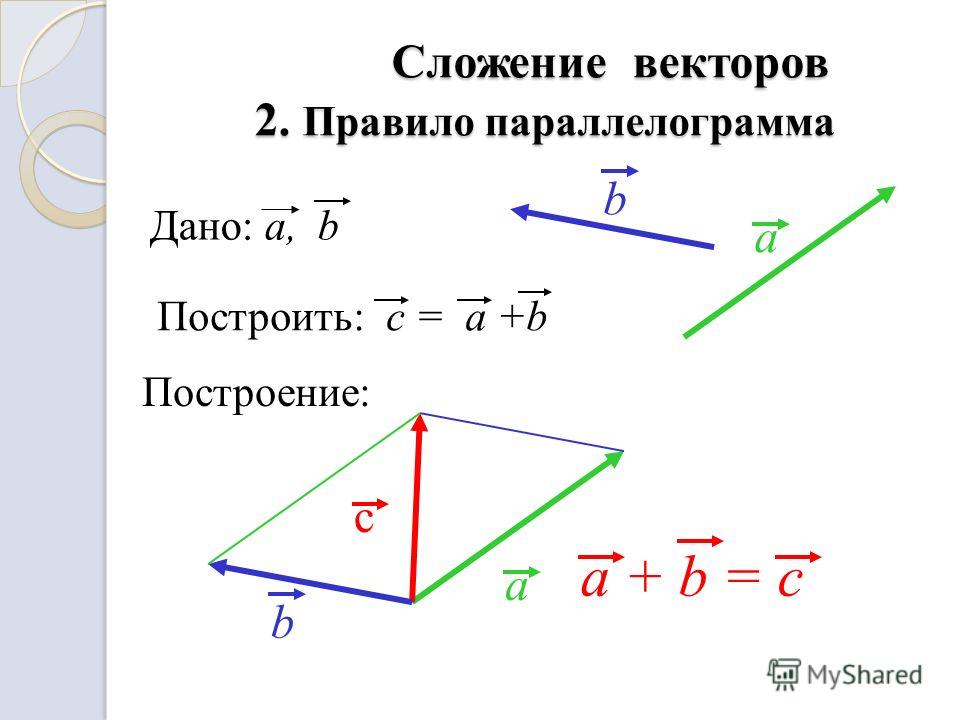
По­стро­им на за­дан­ных век­то­рах  и  па­рал­ле­ло­грамм (рис. 4):

Рис. 4. Па­рал­ле­ло­грамм на двух за­дан­ных век­то­рах

Т. к. век­тор ; ана­ло­гич­но .

По пра­ви­лу тре­уголь­ни­ка:

Так, одна из диа­го­на­лей па­рал­ле­ло­грам­ма, по­стро­ен­но­го на двух век­то­рах, со­от­вет­ству­ет сумме этих век­то­ров.

Рас­смот­рим раз­ность век­то­ров. По пра­ви­лу тре­уголь­ни­ка:

.

Так, вто­рая диа­го­наль па­рал­ле­ло­грам­ма, по­стро­ен­но­го на двух век­то­рах, со­от­вет­ству­ет раз­но­сти этих век­то­ров.

Для сло­же­ния и вы­чи­та­ния несколь­ких век­то­ров при­ме­ня­ет­ся пра­ви­ло мно­го­уголь­ни­ка. Пусть за­да­ны век­то­ры  и :

Рис. 5. Три век­то­ра в про­стран­стве

Необ­хо­ди­мо по­стро­ить век­тор .

Видим, что перед неко­то­ры­ми век­то­ра­ми стоят чис­лен­ные мно­жи­те­ли. На­пом­ним, что при умно­же­нии век­то­ра на число по­лу­ча­ем со­на­прав­лен­ный век­тор, длина ко­то­ро­го – это длина ис­ход­но­го век­то­ра, умно­жен­ная на за­дан­ное число. По­лу­чим век­то­ры  и . Век­тор  со­на­прав­лен с век­то­ром , длина его в три раза боль­ше. Век­тор  про­ти­во­на­прав­лен век­то­ру , длина его в два раза боль­ше. Про­ил­лю­стри­ру­ем (рис. 6):

Рис. 6. Умно­же­ние век­то­ра на число

При­сту­па­ем к сло­же­нию. Из про­из­воль­ной точки А от­кла­ды­ва­ем по­лу­чен­ный век­тор  – по­лу­ча­ем точку В.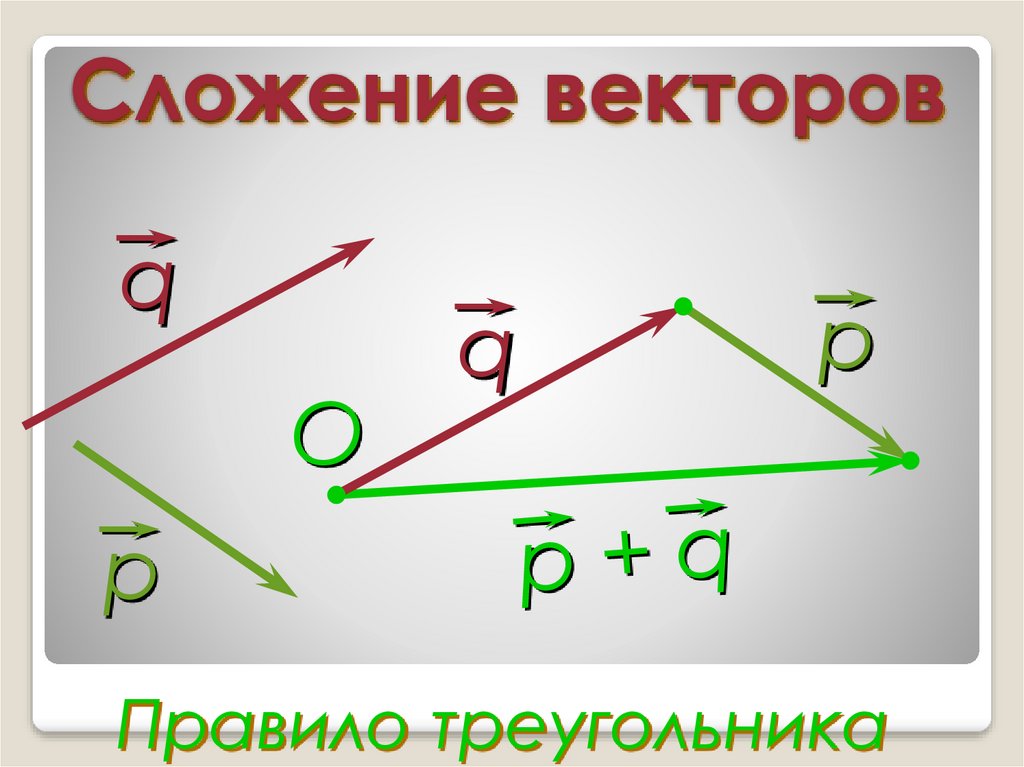 Из точки В от­кла­ды­ва­ем век­тор  – по­лу­ча­ем точку С. Из точки С от­кла­ды­ва­ем век­тор  – по­лу­ча­ем точку D. Со­глас­но пра­ви­лу мно­го­уголь­ни­ка, век­тор  со­от­вет­ству­ет ис­ко­мо­му век­то­ру :

Рис. 7. Сло­же­ние век­то­ров по пра­ви­лу мно­го­уголь­ни­ка

За­да­ча 1:

Задан тет­ра­эдр ABCD (ри­су­нок 8). До­ка­зать:

  

Рис. 8. Тет­ра­эдр, за­да­ча 1

Ре­ше­ние:

По пра­ви­лу тре­уголь­ни­ка: 

Ана­ло­гич­но: 

, ч. т. д.

По пра­ви­лу тре­уголь­ни­ка: 

Ана­ло­гич­но: , ч. т. д.

За­да­ча 2

Упро­стить вы­ра­же­ние: 

Рас­смот­рим от­дель­но сумму двух век­то­ров: , ее зна­че­ние оче­вид­но:

Про­ил­лю­стри­ру­ем (рис. 9):

Рис. 9. Сумма двух век­то­ров

Те­перь со­кра­тим про­ти­во­по­лож­ные век­то­ры:

Можно было сразу за­ме­тить:

.

В ре­зуль­та­те упро­ще­ния по­лу­че­но:

.

Итак, мы ввели опе­ра­ции сло­же­ния и вы­чи­та­ния век­то­ров, умно­же­ния век­то­ра на число в сте­рео­мет­рии, от­ме­ти­ли, что опе­ра­ции ана­ло­гич­ны таким же для пла­ни­мет­рии.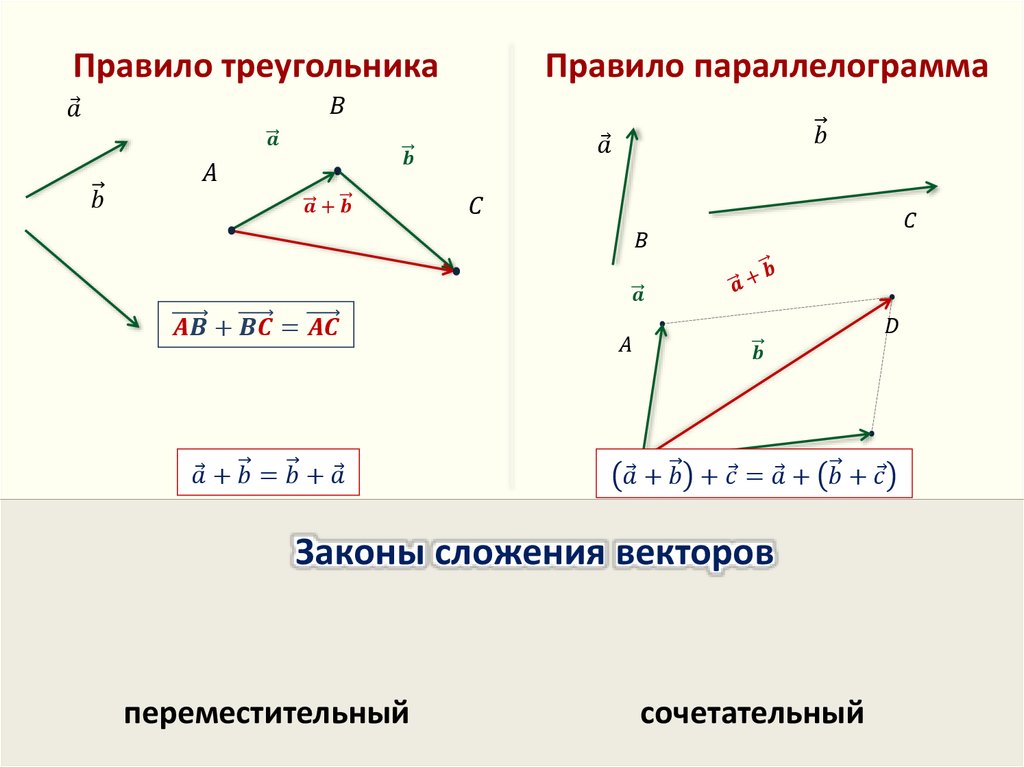 Кроме того, ре­ши­ли несколь­ко задач, ба­зи­ру­ю­щих­ся на опи­сан­ных опе­ра­ци­ях.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/vektory-v-prostranstve/slozhenie-i-vychitanie-vektorov-umnozhenie-vektora-na-chislo

http://www.youtube.com/watch?v=JQzv4c5ak-0

http://www.youtube.com/watch?v=sKCfeWlmsLk

http://azdekor.ru/Spektr/SREDN_SKOOL/MATEM/026/images/Vkt3.jpg

https://www.kursoteka.ru/teacher//index.cfm/getfile/2364/7703/4155

 http://azdekor.ru/Spektr/SREDN_SKOOL/MATEM/026/images/Vkt4.jpg

http://portfoliosmolgu.ucoz.ru/_ph/8/2/143950352.jpg?1445058118

http://www.mathprofi.ru/vektory_dlya_chainikov.html

 

Законы сложения векторов: закон треугольника, параллелограмма, многоугольника

Вектор — это физическая величина, которая имеет как величину, так и направление, такую ​​как скорость, смещение, сила и т.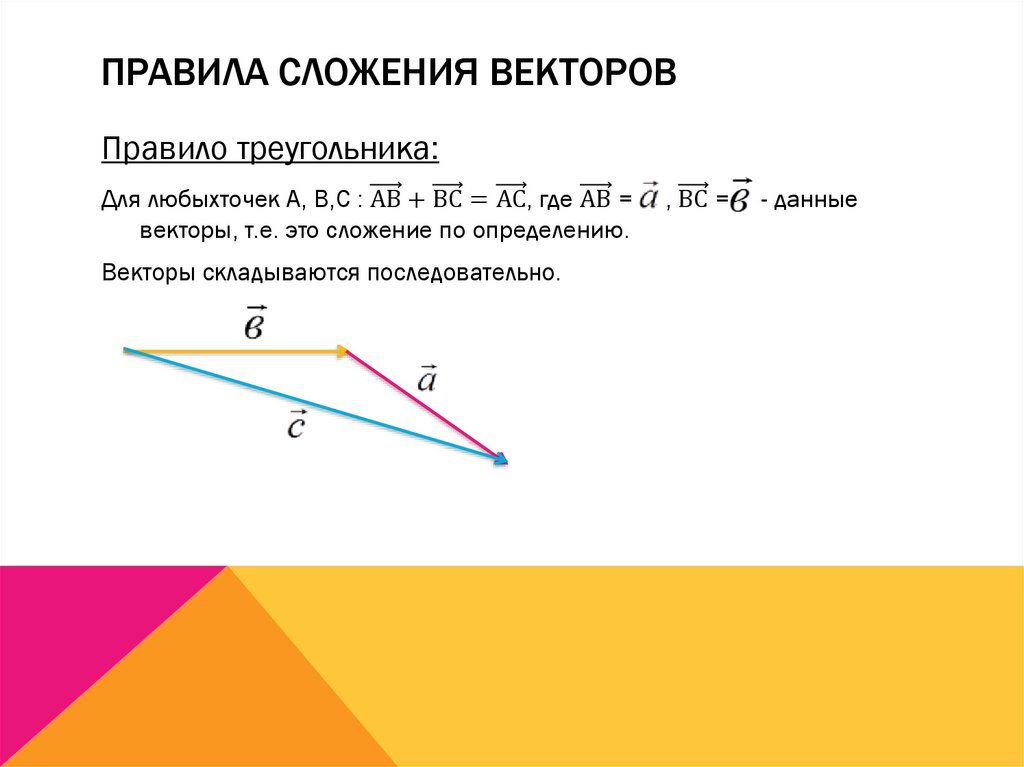 д. Мы можем сказать, что для полного описания вектору необходимы как величина, так и направление . Например, скорость 50 км/ч, север. Здесь объект движется со скоростью 50 км/ч (величина) на север (направление).

С векторами и над ними можно выполнять множество математических операций. Одной из таких векторных операций является сложение векторов. Сложение двух векторных величин невозможно с помощью обычной алгебры.

В этой статье по математике мы изучим сложение векторов и различные типы законов сложения векторов, приложения сложения векторов, свойства сложения векторов, а также решим некоторые задачи на законы сложения векторов, которые помогут вам легко понять тему .

Каковы законы сложения векторов?

Сложение векторов — это операция сложения двух или более векторов для получения векторной суммы. Векторная величина обозначается стрелкой над буквой, или жирным шрифтом, или отрезком линии со стрелкой на одном конце, где стрелка указывает направление вектора.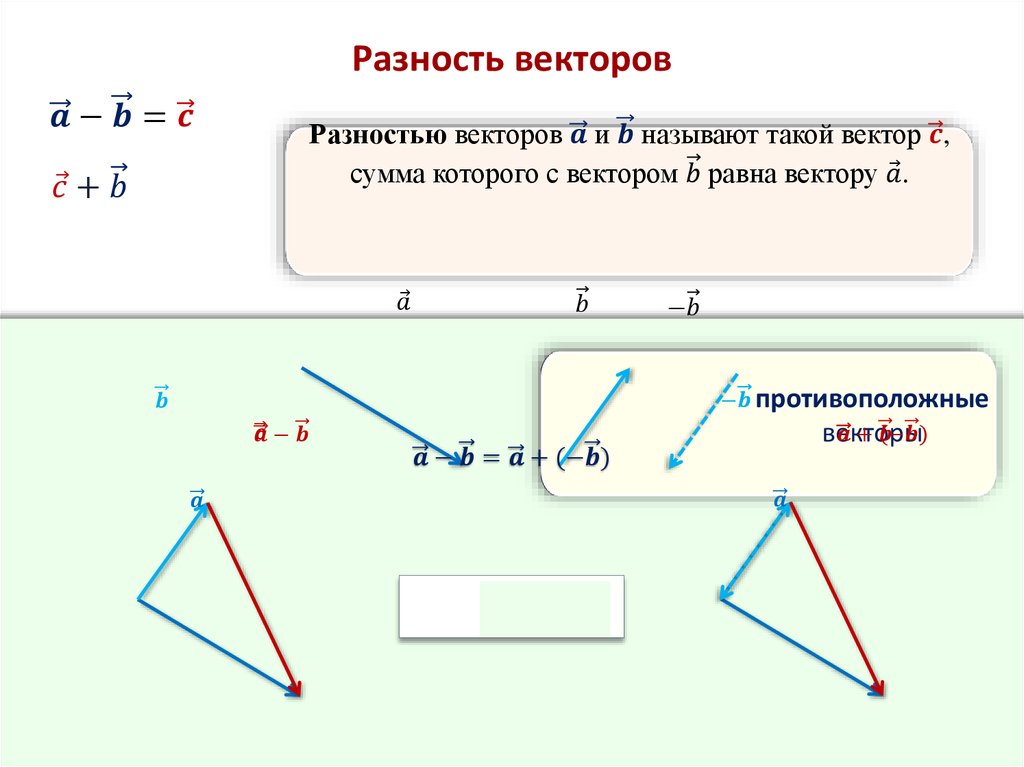

Два или более вектора могут быть равны, если они имеют одинаковую величину и направление. Когда мы умножаем векторную величину на положительное число, то изменяется ее величина, но направление остается неизменным. Однако, когда мы умножаем его на отрицательное целое число, изменяются и величина, и направление.

При добавлении векторов необходимо соблюдать некоторые условия, а именно:

• Условие 1: Два или более вектора могут быть добавлены, только если они имеют одинаковую природу.
• Условие 2: Мы не можем сложить векторную величину со скалярной величиной.

Пример сложения векторов: Предположим, что есть два вектора \(\vec{A}\) и \(\vec{B}\), где \(\vec{A}=A_{x}\hat {i}+A_{y}\шляпа{j}+A_{z}\шляпа{k}\) и \(\vec{B}=B_{x}\шляпа{i}+B_{y}\шляпа {j}+B_{z}\шляпа{k}\).

Теперь результирующий вектор или сложение векторов \(\vec{A}\) и \(\vec{B}\) определяется как

\(\vec{R}=\vec{A}+\vec {B}\) \(\vec{R}=(A_{x}\шляпа{i}+A_{y}\шляпа{j}+A_{z}\шляпа{k})+(B_{x} \шляпа{i}+B_{y}\шляпа{j}+B_{z}\шляпа{k})\)

\(\vec{R}=(A_{x}+B_{x})\шляпа{i}+(A_{y}+B_{y})\шляпа{j}+(A_{z}+ B_{z})\шляпа{k}\).

Законы сложения векторов

Существует 3 закона сложения векторов:

• 1-й закон: закон сложения векторов треугольника
• 2-й закон: закон сложения векторов параллелограмма
• 3-й закон: закон сложения векторов сложения векторов

1. Треугольный закон сложения векторов

Треугольный закон сложения векторов утверждает, что если два вектора представлены по величине и направлению двумя сторонами треугольника, взятыми в одном и том же порядке, то их равнодействующая представлена третьей стороной треугольника, взятой в обратном порядке.

Треугольный закон формулы сложения векторов

Рассмотрим два вектора \(\vec{A}\) и \(\vec{B}\) такие, что угол между ними равен \(\theta\) и их результирующий вектор суммы с использованием треугольного закона сложения векторов задается вектором R.

Формула для величины \(\left|R\right|\) и направления \(\phi\) результирующего вектора R с использованием треугольный закон векторного сложения векторов определяется выражением

\(\left|R\right| = \sqrt{(A^{2}+B^{2}+2ABcos\theta)}\) и 9{-1}\left[\frac{(Bsin\theta)}{(A+Bcos\theta)}\right]\).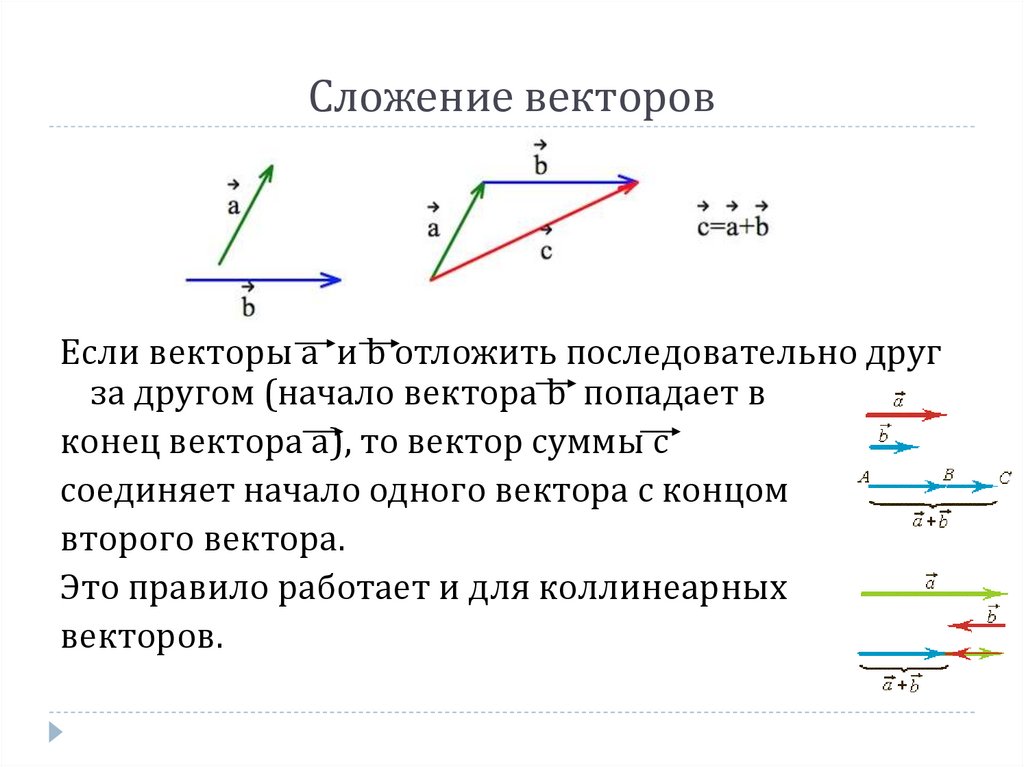

Вывод треугольного закона сложения векторов

Пусть два вектора \(\vec{A}\) и \(\vec{B}\) представлены по величине и направлению сторонами \(\vec {OP}\) и \(\vec{PQ}\) треугольника OPQ брали в том же порядке. Тогда результирующая \(\vec{R}\) будет представлена ​​замыканием стороны \(\vec{OQ}\), взятой в обратном порядке.

Чтобы найти величину равнодействующей R, проводится перпендикуляр QE из Q на стороне OP. 9{2}+2ABcos\тета)}\).

Чтобы найти направление равнодействующей, предположим, что равнодействующая R образует угол \(\phi\) с направлением вектора \(\vec{A}\). Тогда

\(\tan\phi=\frac{QE}{OE}=\frac{QE}{OP+PE}\)

Теперь OP = A и PE = B\(\cos\theta\) .

Чтобы найти QE, рассмотрим прямоугольный треугольник PEQ.

Имеем \(\sin\theta\) = \(\frac{QE}{PQ}\), или

QE = PQ \(\sin\theta\) = B \(\sin\theta\ )

\(\следовательно\) \(\tan\phi=\frac{B sin\theta}{A+B cos\theta}\).

2. Параллелограммный закон сложения векторов

Параллелограммный закон сложения векторов гласит, что если два вектора действуют вдоль двух смежных сторон параллелограмма (с величиной, равной длине сторон), оба направлены от общей вершины, равнодействующая представлена ​​диагональю параллелограмма, проходящей через ту же общую вершину.

Закон параллелограмма формулы сложения векторов

Рассмотрим два вектора \(\vec{A}\) и \(\vec{B}\) с углом \(\theta\) между ними. Сумма двух векторов \(\vec{A}\) и \(\vec{B}\) задается R, затем результирующий вектор суммы с использованием закона сложения векторов параллелограмма. Если результирующий вектор R образует угол \(\alpha\) с вектором \(\vec{A}\), формула для его величины и направления определяется формулой, 9{2}+2ABcos\тета}\).

Чтобы найти направление равнодействующей, предположим, что равнодействующая R образует угол \(\alpha\) с направлением вектора \(\vec{A}\).

В прямоугольном треугольнике OSN,

\(SN=OSsin\alpha =Rsin\alpha\),

А в прямоугольном треугольнике,

\(SN=PSsin\theta =Bsin\theta\ ).

Следовательно, \(Rsin\alpha=Bsin\theta\) ……(i)

Аналогично, \(PM=Asin\alpha=Bsin\beta\) ……..(ii)

Из уравнений (i ) и (ii), мы получаем

\(\frac{R}{sin\theta}=\frac{A}{sin\beta}=\frac{B}{sin\alpha}\)

Следовательно, \(\tan\alpha = \ frac{SN}{(OP+PN)}\)

\(tan\alpha = \frac{Bsin\theta}{(A+Bcos\theta)}\).

3. Закон сложения векторов многоугольников

Закон сложения векторов многоугольников гласит, что если стороны многоугольника взяты в одном порядке для представления множества векторов по величине и направлению, то результирующий вектор может быть представлена ​​по величине и направлению замыкающей стороной многоугольника, взятого в обратном порядке.

Полигональный закон формулы сложения векторов

Рассмотрим многоугольник с векторами \(\vec{A}\), \(\vec{B}\), \(\vec{C}\) и \ (\vec{D}\), где четыре стороны многоугольника взяты в том же порядке для представления величины и направления, затем, используя закон сложения векторов многоугольников, результирующий вектор \(\vec{R}\) определяется выражением

\(\vec{R}=\vec{A}+\vec{B}+\vec{C}+\vec{D}\).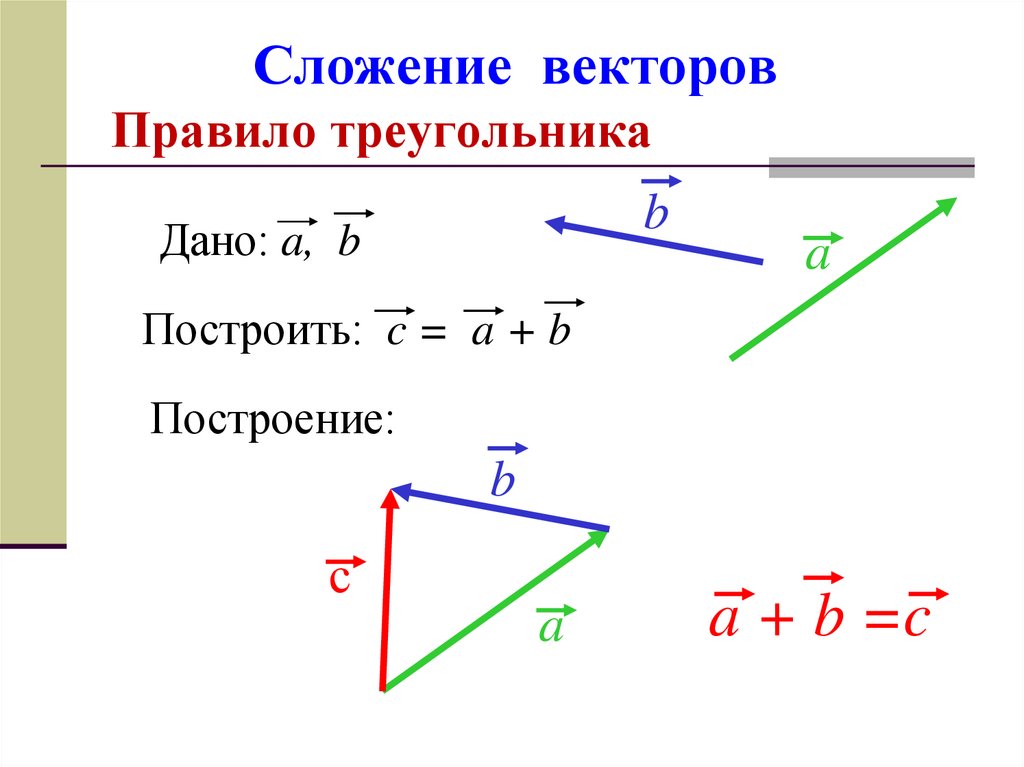

Вывод полигонального закона сложения векторов

Предположим, что существует многоугольник с 5 сторонами.

В треугольнике ABC

По треугольному закону сложения векторов имеем

AB + BC = AC ……….(i)

И, аналогично

AC + CD = AD ………..(ii )

и, AD + DE = AE ……(iii)

Аналогично проделаем это для всех сторон в многоугольнике (здесь у нас только 5-угольник).

Тогда, складывая уравнения (i), (ii) и (iii), мы получаем

AB + BC + CD + DE = AE.

Здесь AE = результирующий вектор, а остальные — нормальные стороны вектора.

Примечание. Для n-сторон это можно записать аналогично и сформулировать как приведенную выше теорему.

Добавление векторов с использованием компонентов

Наиболее распространенный способ добавления векторов — с помощью компонентов. Каждый элемент двумерной упорядоченной пары (а, b) или трехмерной тройки (а, b, с) называется компонентой вектора.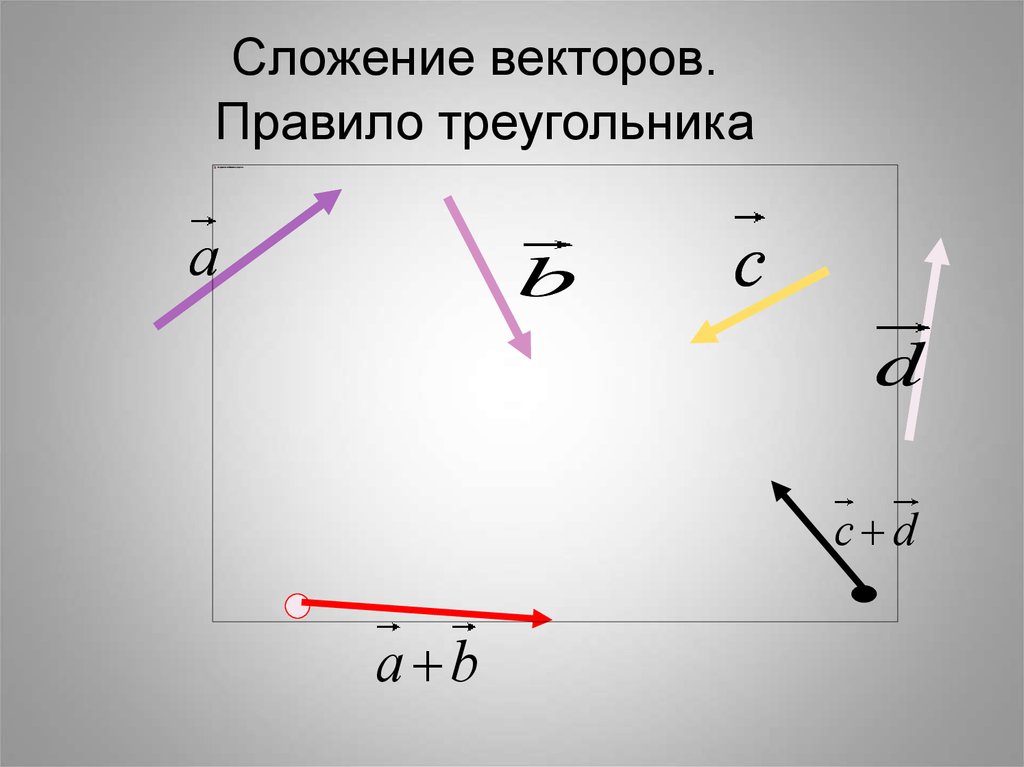 Записи соответствуют количеству единиц вектора в направлениях x, y и (для трехмерного случая) z пространства или плоскости. Другими словами, компоненты — это просто координаты точки, связанной с вектором.

• Для двумерных векторов \(a=(a_{1},a_{2})\) и \(b=(b_{1},b_{2})\) на евклидовой плоскости добавление векторов задается как \(a+b=(a_{1}+b_{1},a_{2}+b_{2})\).

• Для трехмерных векторов \(a=(a_{1}, a_{2}, a_{3})\) и \(b=(b_{1},b_{2},b_{3) })\), сложение векторов задается как \(a+b=(a_{1}+b_{1}, a_{2}+b_{2}, a_{3}+b_{3})\ ).

Важные свойства векторного сложения

Важные свойства векторного сложения приведены ниже:

Свойство 1: сложение векторов коммутативно: Если два вектора \(\vec{a}\) и \(\vec{b}\) складываются вместе, то
\(\vec{a}+\vec {b}=\vec{b}+\vec{a}\), это означает, что порядок векторов не меняет результат сложения.

Свойство 2: сложение векторов ассоциативно: Если есть три вектора \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\), то

\((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\), эта взаимная группировка векторов имеет не влияет на результат при сложении трех и более векторов вместе.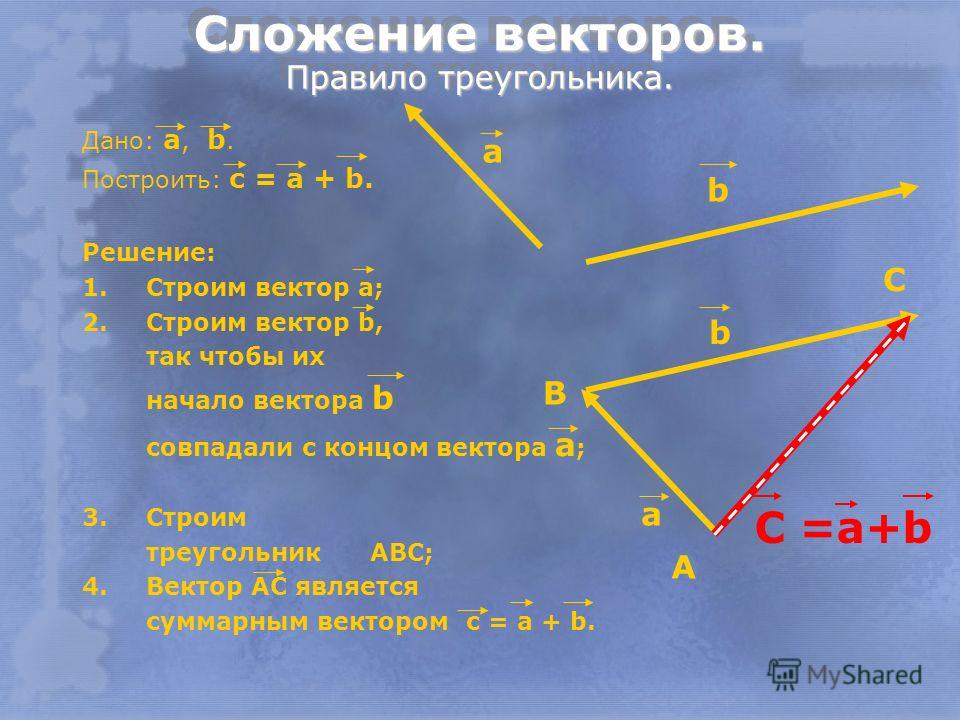

Свойство 3: сложение векторов является распределительным: Если есть два вектора \(\vec{a}\), \(\vec{b}\) и один масштабатор ‘m’, то

\(m( \vec{a}+\vec{b})=m\vec{a}+m\vec{b}\), это означает, что сумма скалярных умножений на сумму двух векторов равна сумме скалярных умноженных на двух векторов по отдельности.

Свойство 4: Существование идентичности: Для любого вектора \(\vec{a}\),

\(\vec{a}+\vec{0}=\vec{a}\). Здесь 0 — аддитивная идентичность.

Свойство 5: Существование обратного: Для любого вектора \(\vec{a}\),

\(\vec{a}+(-\vec{a})=\vec{0}\) . Здесь для каждого вектора существует аддитивный обратный.

Законы сложения векторов Примеры

Пример 1. Если векторы положения точек A(2, 5), B(3, -4) и C(7, -2) равны \(\vec{ a}\), \(\vec{b}\) и \(\vec{c}\) соответственно, затем вычислить значение \(\vec{a}+2\vec{b}-3\vec{c }\). {\circ}\) с друг с другом. Найдите величину результирующего вектора и его направление относительно \(\vec{A}\). 9{\circ}\).

Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Часто задаваемые вопросы о законах сложения векторов

В.1 Каковы 3 закона сложения векторов?

Ответ 1 Три закона сложения векторов:

1. Параллелограммный закон сложения векторов
2. Треугольный закон сложения векторов
3. Полигональный закон сложения векторов

Q.2 Что такое параллелограммный закон сложения векторов?

Ответ 2 Согласно закону сложения векторов параллелограмма, если любые два вектора a и b представляют две стороны параллелограмма по модулю и направлению, то их сумма a+b равна диагонали параллелограмма поперек их общая точка по величине и направлению.

Q.3 Что такое треугольный закон сложения векторов?

Ответ 3 Треугольный закон сложения векторов гласит, что когда два вектора представлены как две стороны треугольника с одинаковым порядком величины и направлением, величина и направление результирующего вектора представлены третья сторона треугольника.

Q.4 Что такое полигональный закон сложения векторов?

Ответ 4 Закон сложения векторов многоугольников гласит, что если количество векторов может быть представлено по величине, а также по направлению стороной многоугольника, взятого в том же порядке, то их результирующая величина представлена ​​по величине вдоль с направлением на замыкающую сторону многоугольника, взятого в обратном порядке.

Q.5 Каковы важные свойства сложения векторов?

Ответ 5 5 важных свойств сложения векторов:

1. Сложение векторов коммутативно.
2. Сложение векторов является ассоциативным.
3. Сложение векторов является дистрибутивным.
4. Наличие личности.
5. Существование инверс.

Скачать публикацию в формате PDF

Читать больше сообщений

Уравнение сферы: длина окружности, площадь поверхности и объем Формула
Алифатические углеводороды: узнайте их типы, свойства и применение
Центробежная сила: узнайте ее формулу, единицу измерения, примеры и области применения
Деструктивная дистилляция: узнайте ее процесс, продукты и области применения
Гидролиз сложных эфиров: изучение механизма и применения

Алгебра: сложение векторов

Алгебра: как сложить вектор https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 ШколаРепетиторская Академия ШколаРепетиторская Академия https://secure. gravatar.com/avatar/983a20e95a059722e4981790f518b20b?s=96&d=mm&r=g 5 октября 2012 г. 2 декабря 2014 г.

Вектор – это величина, которая имеет как величину, так и направление.

Пример: Сила, скорость, импульс и т. д.

Вектор представлен отрезком направленной линии. Если вектор имеет начальную точку P и конечную точку Q , то вектор обозначается буквой  или

PQ .

Длиной вектора называется его величина или длина или модуль . Длина вектора PQ обозначается |PQ|.

Поскольку вектор — это не просто число, его нельзя складывать так же, как числа. Есть несколько законов, которые можно использовать при сложении векторов.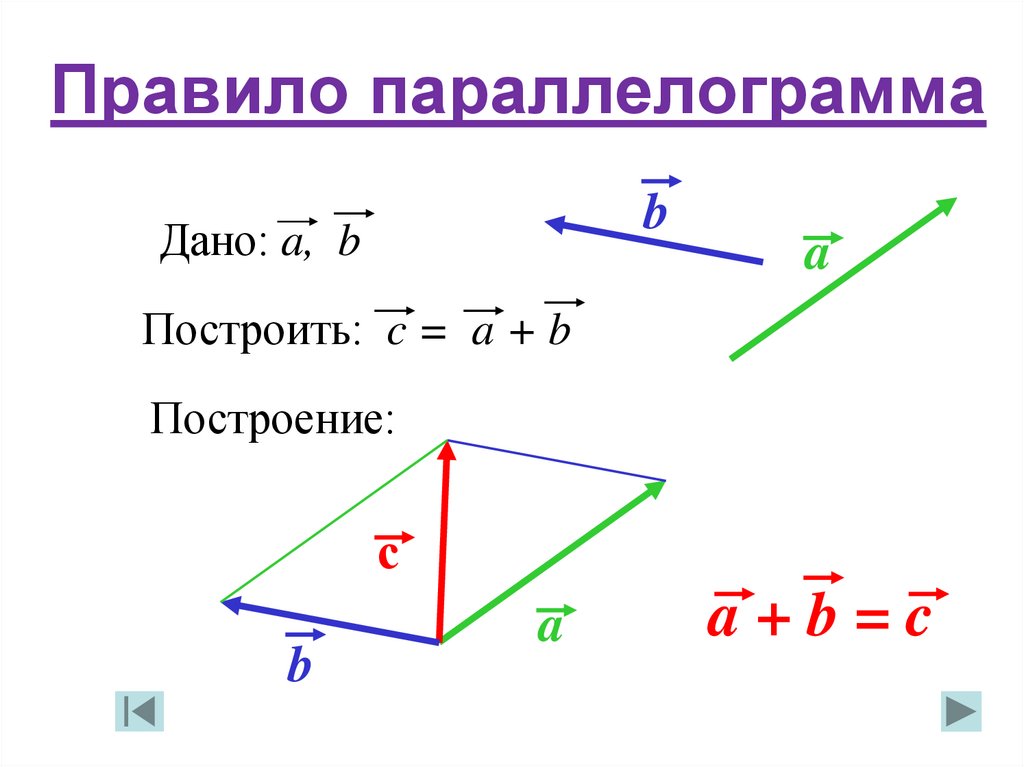

Треугольный закон сложения:

Пусть a и b — любые два вектора. Пусть O будет любой точкой. Предположим, что OA и OB — это два отрезка, такие что OA = a и AB = b. Соедините O и B . Тогда OB определяется как сумма векторов a и b .

т.е. . а+b = ОА+ОВ = ОВ.

Это известно как треугольный закон сложения .

Закон сложения параллелограммов:

Пусть OA=a и OB = b. Дополните параллелограмм OABC сторонами OA и OB . Поскольку OC параллельны AB , мы получаем OC=AB. Таким образом, мы имеем ОС=АВ=b.

Итак, OC= a+b = OA+AB = OA+OC.

i.e. The sum of two co-initial vectors OA and OC is given by OB where OB is the diagonal of the parallelogram OABC having OA и OC в качестве смежных сторон.

Это известно как закон сложения параллелограммов .

Полигональный закон векторов:

Пусть OA = a , AB = b , BC = c и CD = d .

a+b+c+d = OA+OB+OC+OD

=OB +BC + CD

= OC + CD

=OD

Таким образом, сложение векторов a , b , c и d определяется как OD .

No related posts.