Сложение вычитание и умножение векторов: Сложение и вычитание векторов. Умножение вектора на число — урок. Геометрия, 10 класс.

Операции с векторами, сложение векторов, умножение вектора на действительное число.

Рассмотрим вектор v с начальной точкой в начале координат в любой координатной системе x-y и с конечной точкой в (a,b). Мы говорим, что вектор находится в стандартном положении и ссылаемся на него как на радиус-вектор. Обратите внимание, что пара точек определяет этот вектор. Таким образом, мы можем использовать это для обозначения вектора. Чтобы подчеркнуть, что мы имеем в виду вектор, и, чтобы избежать путаницы, как правило, пишут:
v = .

Координата a есть скаляром горизонтальной компоненты вектора, и координата b есть скаляром вертикальной компоненты вектора. Под скаляром мы подразумеваем численное количество, а не векторную величину. Таким образом, это рассматривается как компонентная форма v. Обратите внимание, что a и b НЕ вектора и их не надо путать с определением компонента вектора.

Теперь рассмотрим с A = (x₁, y₁) и C = (x₂

, y₂). Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C. Таким образом, P = (x₂ — x₁, y₂ — y₁) и радиус вектор есть .

Можно показать, что и имеют одну и ту же величину и направление, и поэтому эквивалентны. Таким образом, = = 2 — x₁, y₂ — y₁ >.

Компонентная форма с A = (x₁, y₁) и C = (x₂, y₂) есть
= 2 — x₁, y₂ — y₁ >.

Пример 1 Найдите компонентную форму если C = (- 4, — 3) и F = (1, 5).

Решение Мы имеем
= = .

Обратите внимание, что вектор есть равным радиус-вектору , как показано на рисунке вверху.

Теперь, когда мы знаем, как записать вектор в компонентной форме, давайте изложим некоторые определения.

Длину вектора v легко определить, когда известны компоненты вектора. Для v = 1, v₂ >, мы имеем
|v|² = v²₁ + v²₂          Используя теорему Пифагора
|v| = √v²₁ + v²₂.

Длина, или величина ветктора v = 1, v₂ > находится как |v| = √v²₁ + v²₂.

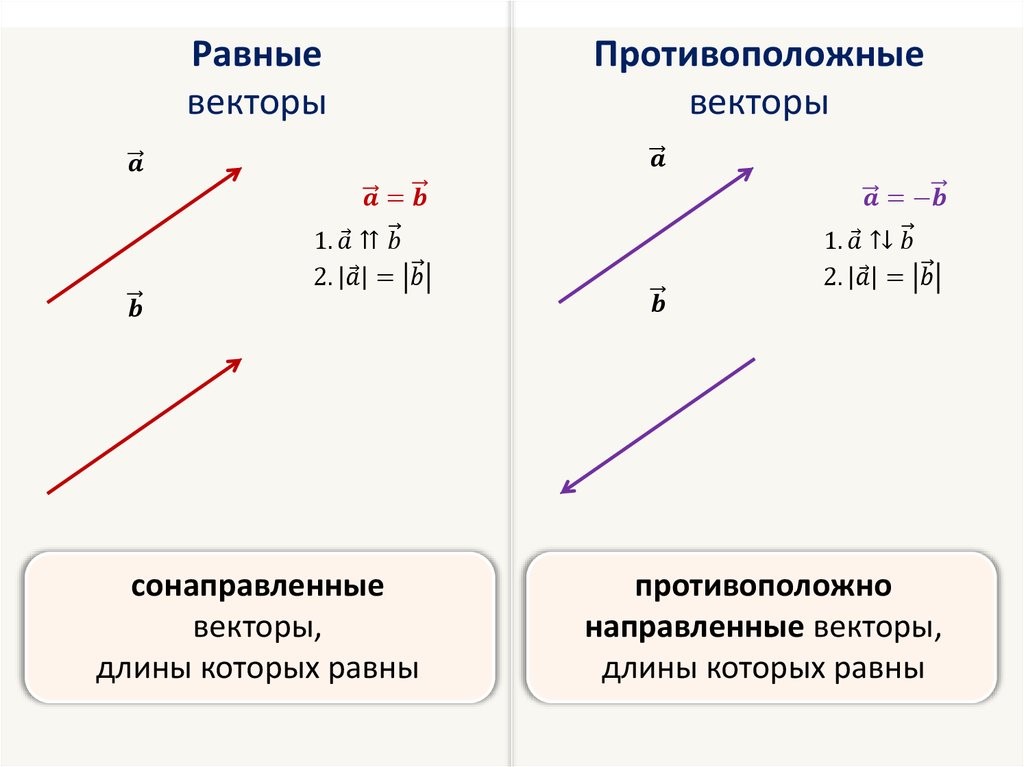
Два вектора равны или эквивалентны, если они имеют одну и ту же величину и одно и то же направление.

Пусть u = 1, u₂ > и v = 1, v₂ >. Tогда
1, u₂ > = 1, v₂ >          только если u₁ = v₁ and u₂ = v₂.

Операции с векторами

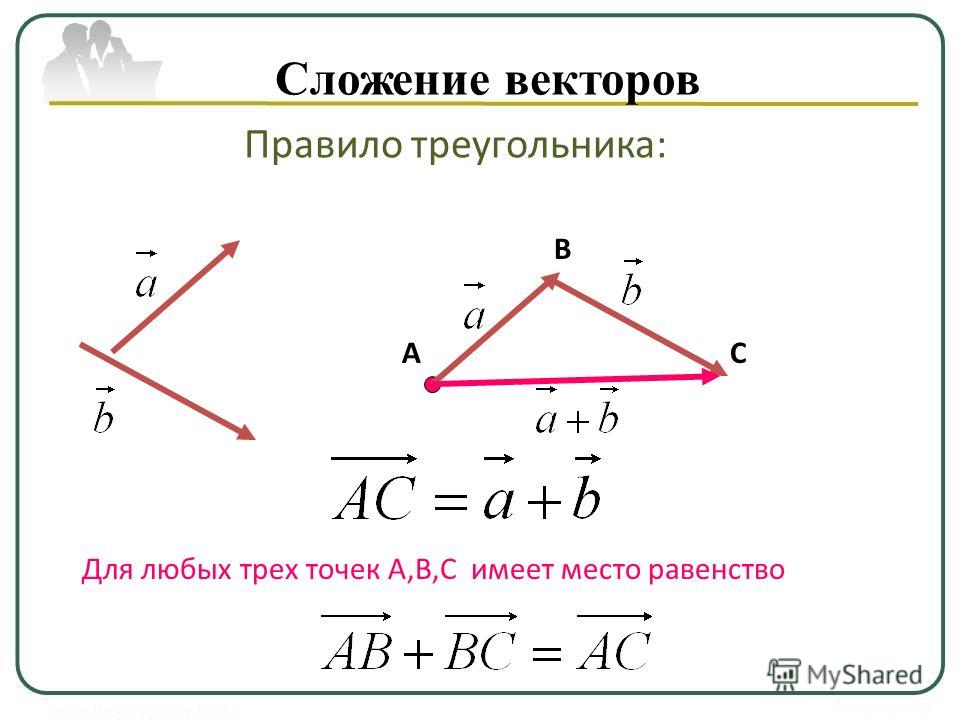Чтобы умножить вектор V на положительное число, мы умножаем его длину на это число. Его направление остается прежним. Когда вектор V умножается на 2, например, его длина увеличивается в два раза, но его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное. Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.

Для действительного числа k и вектора v = 1, v₂ >, скалярное произведение k и v есть
kv = k.1, v

2 > = 1, kv₂ >.
Вектор kv есть скалярным кратным вектора v.

Пример 2 Пусть u = и w = . Найдите — 7w, 3u и — 1w.

Решение
— 7w = — 7. = ,
3u = 3. = ,
— 1w = — 1. = .

Теперь мы можем сложить два вектора, используя компоненты. Чтобы сложить два вектора в компонентной форме, мы складываем соответствующие компоненты. Пусть u = 1, u₂ > и v = 1, v₂ >. Тогда
u + v = 1 + v₁, u₂ + v₂ >

Например, если v = и w = , тогда
v + w = =

Если u = 1, u₂ > и v = 1, v₂ >, тогда
u + v = 1 + v₁, u₂ + v₂ >.

Перед тем, как мы определим вычитание векторов нам нужно дать определение — v. Противоположный вектору v = 1, v₂ >, изображенному внизу, есть

— v = (- 1).v = (- 1)1, v₂ > = 1, — v₂ >

Вычитание векторов, такое как u — v вовлекает вычитание соответствующих компонент. Мы покажем это представлением u — v как u + (- v). Если u = 1, u₂ > и v = 1, v₂ >, тогда
u — v = u + (- v) = 1, u₂ > + 1, — v₂ > = 1 + (- v₁), u₂ + (- v₂) > = 1 — v₁, u₂ — v₂ >

Мы можем проиллюстрировать вычитание векторов с помощью параллелограмма , как мы это делали для сложения векторов.

Вычитание векторов

Если u = 1, u₂ > и v = 1, v₂ >, тогда
u — v = 1 — v₁, u₂ — v₂ >.

Интересно сравнить суммы двух векторов с разницей тех же двух векторов в одном параллелограмме. Векторы u + v и u — v есть диагоналями параллелограмма.

Пример 3 Сделайте следующие вычисления, где u = и v = .
a) u + v
b) u — 6v
c)3u + 4v
d)|5v — 2u|

Решение
a) u + v = + = = ;
b)u — 6v = — 6. = — = ;
c) 3u + 4v = 3. + 4. = + = ;
d) |5v — 2u| = |5. — 2.| = | — | = || = √(- 29)² + 21² = √1282 ≈ 35,8

Прежде чем сформулировать свойства векторного сложения и умножения, мы должны дать определение еще одному специальному вектору — нулевому вектору. Вектор, чья начальная точка совпадает с конечной точкой, называется нулевым вектором, обозначается O, или . Его величина равна 0. В сложении векторов:
v + O = v.          1, v₂ > + = 1, v₂ >
Операции над векторами обладают те же самыми свойствами, что и операции над вещественными числами.

Свойства векторного сложения и умножения

Для всех векторов u, v, и w, и для всех скаляров b и c:

1. u + v = v + u.
2. u + (v + w) = (u + v) + w.
3. v + O = v.
4 1.v = v;          0.v = O.
5. v + (- v) = O.
6. b(cv) = (bc)v.
7. (b + c)v = bv + cv.
8. b(u + v) = bu + bv.

Орты

Вектор величиной, или длиной 1 называется орт. Вектор v = есть орт, потому что
|v| = || = √(- 3/5)² + (4/5)² = √9/25 + 16/25 = √25/25 = √1 = 1.

Пример 4 Найдите орт, который имеет то же самое направление, что и вектор w = .

Решение Найдем сначала длину w:
|w| = √(- 3)² + 5² = √34. Таким образом, мы ищем вектор, с длиной 1/√34 от w и с таким же самым направлением, что и вектор w. Этот вектор есть
u = w/√34 = /√34 = .
Вектор u есть орт, потому что
|u| = |w/√34| = = √9/34 + 25/34 = √34/34 = √1 = 1.

Если v есть вектор и v ≠ O, тогда
(1/|v|)• v,          or          v/|v|,
есть орт в направлении v.

Хотя орты могут иметь любое направление, орты, параллельные осям x и y особенно полезны. Они определяются как
i =          and          j = .

Любой вектор может быть выражен как линейная комбинация орта i и j. Например, пусть v = 1, v₂ >. Tогда
v = 1, v₂ > = 1, 0 > + 2 > = v₁ + v₂ = v₁i + v₂j.

Пример 5 Выразите вектор r = как линейную комбинацию i и j.

Решение
r = = 2i + (- 6)j = 2i — 6j.

Пример 6 Запишите вектор q = — i + 7j в компонентной форме.

Решениеq = — i + 7j = -1i + 7j =

Векторные операции могут быть также выполнены, когда векторы записаны как линейные i и j.

Пример 7 Если a = 5i — 2j и b = -i + 8j, найдите 3a — b.

Решение
3a — b = 3(5i — 2j) — (- i + 8j) = 15i — 6j + i — 8j = 16i — 14j.

Углы обзора

Конечная точка P орты в стандартной позиции есть точкой на единичной окружности, определенной (cosθ, sinθ). Таким образом, орт может быть выражен в компонентной форме,
u = ,
или как линейная комбинация орт i и j,
u = (cosθ)i + (sinθ)j,
где компоненты u есть функциями угла обзора θ измеряемого против часовой стрелки от оси x к этому вектору. Так как θ изменяется от 0 до 2π, точка P отслеживает круг x² + y² = 1. Это охватывает все возможные направления ортов и тогда уравнение u = (cosθ)i + (sinθ)j описывает каждый возможный орт на плоскости.

Пример 8 Вычислите и сделайте эскиз орта u = (cosθ)i + (sinθ)j для θ = 2π/3. Изобразите единичную окружность на эскизе.

Решение
u = (cos(2π/3))i + (sin(2π/3))j = (- 1/2)i + (√3/2)j

Пусть v = 1, v₂

> с углом обзора θ. Используя определение функции тангенса, мы можем определить угол обзора их компонент v:

Пример 9 Определите угол обзора θ вектора w = — 4i — 3j.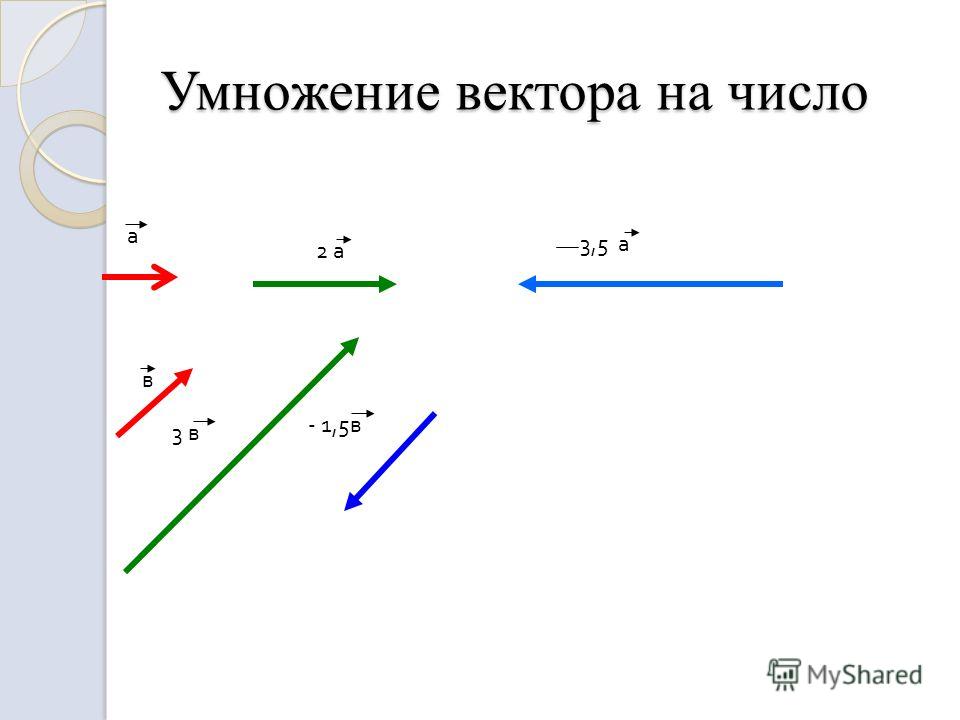

Решение Мы знаем, что
w = — 4i — 3j = .
Таким образом, имеем
tanθ = (- 3)/(- 4) = 3/4          и θ = tan^{— 1}(3/4).
Так как w находится в третьем квадранте, мы знаем, что θ есть углом третьего квадранта. Соответствующий угол есть
tan^{— 1}(3/4) ≈ 37°,          и          θ ≈ 180° + 37°, или 217°.

Это удобно для работы с прикладными задачами, а в последующих курсах, чтобы иметь способ выразить вектор так, чтобы его величина и направление могли быть легко определены или прочитаны. Пусть v это вектор. Тогда v/|v| есть орт в том же самом направлении, что и v. Таким образом, мы имеем
v/|v| = (cosθ)i + (sinθ)j
v = |v|[(cosθ)i + (sinθ)j]              Умножая на |v|

v = |v|(cosθ)i + |v|(sinθ)j.

Углы между векторами

Когда вектор умножается на скаляр, результатом есть вектор. Когда складываются два вектора, результатом также есть вектор. Таким образом, мы могли бы ожидать, что произведение двух векторов есть вектор, но это не так.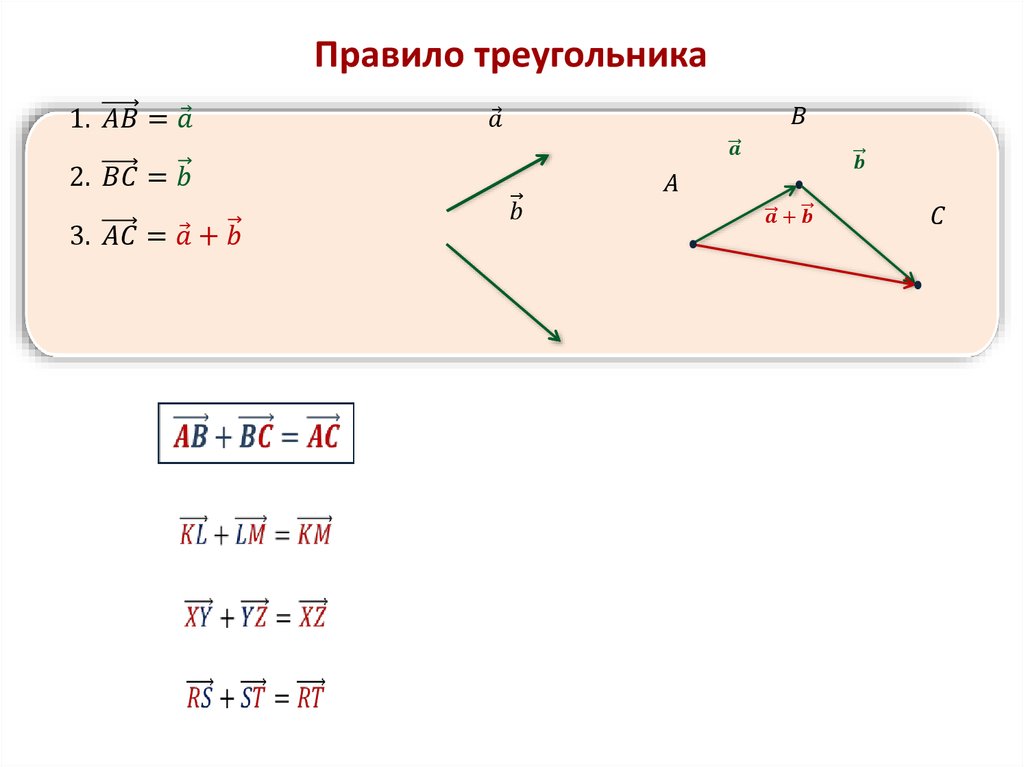 Скалярное произведение двух векторов есть действительное число или скаляр. Этот результат полезен в нахождении угла между двумя векторами и в определении, являются ли два вектора перпендикулярными.

Скалярное произведение двух векторов u = 1, u₂ > и v = 1, v₂ > is
u • v = u₁.v₁ + u₂.v₂
(Обратите внимание, что u₁v₁ + u₂v₂ есть скаляром, а не вектором.)

Пример 10Найдите скалярное произведение, когда
u = , v = и w = .
a)u • w
b)w • v

Решение
a) u • w = 2(- 3) + (- 5)1 = — 6 — 5 = — 11;
b) w • v = (- 3)0 + 1(4) = 0 + 4 = 4.

Скалярное произведение может быть использовано для нахождения угла между двумя векторами. Угол между двумя векторами это самый маленький положительный угол, образованный двумя направленными отрезками. Таким образом, θ между u и v это тот же самый угол, что и между v и u, и 0 ≤ θ ≤ π.

Если θ есть углом между двумя ненулевыми векторами u и v, тогда
cosθ = (u • v)/|u||v|.

Пример 11Найдите угол между u = и v = .

Решение Начнем с нахождения u • v, |u|, и |v|:
u • v = 3(- 4) + 7(2) = 2,
|u| = √3² + 7² = √58, and
|v| = √(- 4)² + 2² = √20.
Tогда
cosα = (u • v)/|u||v| = 2/√58.√20
α = cos^{— 1}(2/√58.√20)
α ≈ 86,6°.

Равновесие сил

Когда несколько сил действуют на одну и ту же точку на объекте, их векторная сумма должна быть равна нуля, для того, чтобы был баланс. Когда есть баланс сил, то объект является стационарным или движется по прямой линии, без ускорения. Тот факт, что векторная сумма должна быть равна нулю вывода для получения баланса, и наоборот, позволяет решать нам многие прикладные задачи с участием сил.

Пример 12 Подвесной блок 350- фунтовый блок подвешен с помощью двух кабелей. осталось. В точке А есть три силы, действующие так: W блок тянет вниз, а R и S (два кабеля) тянут вверх и наружу.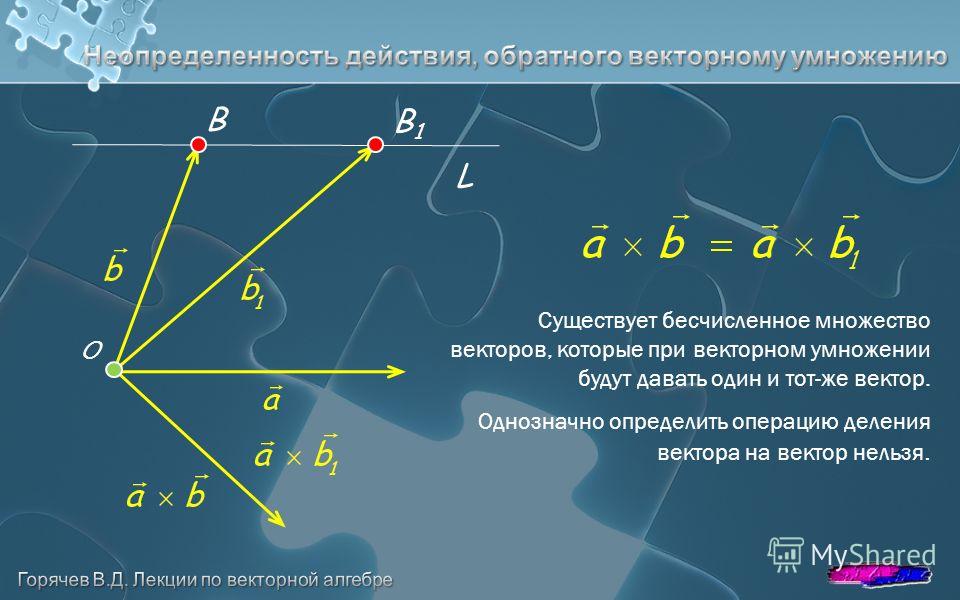 Найдите нагрузку каждого кабеля.

Решение Нарисуем диаграмму с начальными точками каждого вектора в начале кооординат. Для баланса, сумма векторов должна быть равна О:

R + S + W = О.
Мы можем выразить каждый вектор через его величину и угол обзора :
R = |R|[(cos125°)i + (sin125°)j],
S = |S|[(cos37°)i + (sin37°)j], и
W = |W|[(cos270°)i + (sin270°)j]
= 350(cos270°)i + 350(sin270°)j
= -350j          cos270° = 0; sin270° = — 1.
Заменяя R, S, и W in R + S + W + O, мы имеем
[|R|(cos125°) + |S|(cos37°)]i + [|R|(sin125°) + |S|(sin37°) — 350]j = 0i + 0j.
Это дает нам систему уравнений:
|R|(cos125°) + |S|(cos37°) = 0,
|R|(sin125°) + |S|(sin37°) — 350 = 0.
Решая эту систему, мы получаем
|R| ≈ 280 и |S| ≈ 201.
Таким образом, нагрузка на кабели 280 фунтов и 201 фунт.

Сложение и вычитание векторов

Материал урока.

Вспомним, как мы вводили понятие суммы двух векторов в планиметрии.

Сначала мы рассматривали такой пример.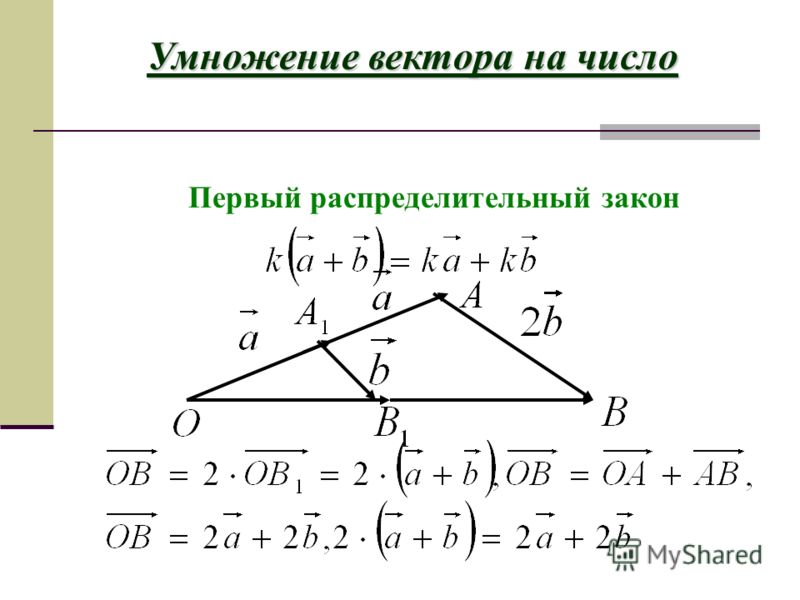

Под действием воздушных масс воздушный шар сначала двигался из точки А в точку B, а затем из точки B переместился в точку C.

Каждое из этих двух перемещений можно представить в виде вектора.  и .

Но можно ведь сказать, что в результате воздушный шар из точки А попал в точку C. И это перемещение задает вектор .

Так как перемещение из точки А в C складывается из перемещений из точки А в B и из B в C, то можно записать, что вектор .

Этот пример подводит нас к понятию суммы двух векторов.

Рассмотрим два ненулевых вектора:  и .

Отметим произвольную точку А и отложим от неё вектор , равный вектору . Далее от точки B отложим вектор , равный вектору .

Можем изобразить вектор , который называется суммой векторов  и .

Данное правило сложения векторов в пространстве, так же, как и в планиметрии, будем называть правилом треугольника.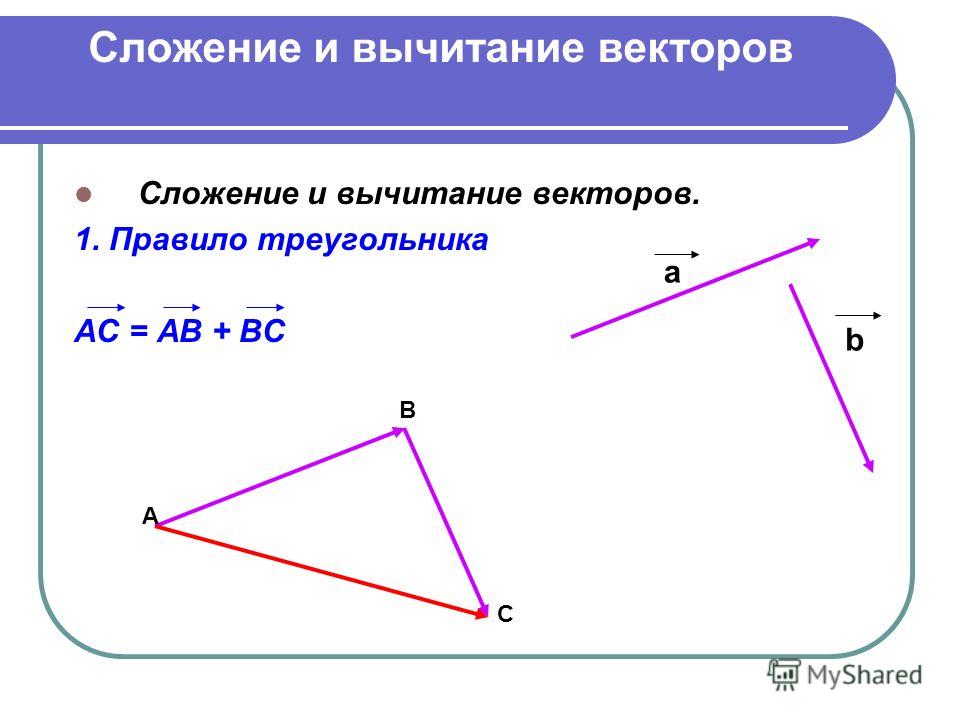

Нужно отметить, что сумма векторов  и  не зависит от выбора точки А, от которой будет отложен вектор .

Докажем это.

Найдём сумму векторов  и , но начнём откладывать их от некоторой точки А₁.

Нам необходимо доказать, что полученный вектор  равен вектору .

Из построений очевидно, что векторы  и  равны. А значит, они сонаправлены и равны по длине. То есть стороны AB и A₁B₁ четырёхугольника ABB₁A₁ параллельны и равны. И этот четырёхугольник является параллелограммом.

 

Стороны AA₁ и  BB₁ данного параллелограмма также равны и параллельны. Тогда получаем, равны векторы  и .

Аналогично, из равенства векторов  и  следует, что четырёхугольник BCC₁B₁ также является параллелограммом. А значит, равны векторы  и .

Из полученных равенств получаем, что равны векторы  и .

Поэтому четырёхугольник AA₁C₁C — параллелограмм. Его стороны AC и A₁C₁ параллельны и равны. А значит, равны векторы  и .

Что и требовалось доказать.

Итак, в точности так же, как и на плоскости, мы ввели правило треугольника сложения двух векторов в пространстве. И доказали, что сумма векторов  и  не зависит от выбора точки А, от которой будет отложен вектор .

Для любых трёх точек пространства А, B и C правило треугольника можно сформулировать так: сумма векторов  и  равна вектору .

То есть даже не строя вектор суммы можно его найти. Если конец вектора, являющегося первым слагаемым, совпадаем с началом вектора, являющегося вторым слагаемым, то началом вектора суммы является начало первого вектора, а концом — конец второго вектора.

Так же для сложения двух векторов можно применять правило параллелограмма, которое мы уже формулировали в планиметрии. Вспомним его. От произвольной точки А отложим векторы  и , равные векторам  и соответственно.

Теперь на этих векторах построим параллелограмм ABCD. Вектор  является вектором суммы векторов  и .

Для любых векторов ,  и  действуют переместительный и сочетательный законы сложения векторов.

Эти законы мы уже записывали и доказывали для векторов на плоскости.

Выполним задание.

На экране изображён параллелепипед ABCDA₁B₁C₁D₁.

Требуется назвать векторы, начало и конец которых совпадают с вершинами параллелепипеда, и которые равны соответствующей сумме векторов.

Первой рассмотрим сумму векторов  и

Чтобы сложить векторы по правилу треугольника, они должны быть отложены друг за другом, а чтобы воспользоваться правилом параллелограмма, они должны быть отложены от одной точки.

Данные векторы не подходят ни к одному правилу.

Но здесь нам поможет знание о том, что от любой точки пространства можно отложить вектор равный данному, и притом только один.

Так как перед нами параллелепипед и все его грани являются параллелограммами, то можно сказать, что есть вектор, который отложен от точки А и равен вектору  Напомним, что равными называются сонаправленные векторы, длины которых равны.

Вектор Ведь эти векторы лежат на противоположных сторонах параллелограмма, которые равны и параллельны.

От данной нам суммы перейдём к сумме векторов  и . Они отложены от одной точки, поэтому воспользуемся правилом параллелограмма. Если построить параллелограмм на этих векторах, то мы получим грань ABCD.

Диагональ AC и будет вектором суммы данных векторов.

Следующей рассмотрим сумму векторов  и .

Они уже отложены от одной точки, и на этих векторах можно построить параллелограмм ABC₁D₁. Диагональ AC₁ и будет являться вектором суммы.

Далее рассмотрим сумму векторов  и .

Вектор равен вектору . И перейдя к сумме векторов  и , не трудно заметить, что они отложены друг за другом, и именно поэтому можно применить правило треугольника. Вектор  — искомый.

Обратите внимание, пользуясь переместительным законом, можно записать, что сумма векторов  и ,  равна сумме векторов ,  и . Тогда по правилу треугольника сложения векторов для трёх произвольных точек пространства, можно сразу записать вектор суммы — . Так мы получили тот же вектор.

Теперь рассмотрим сумму векторов  и . Вектор  равен вектору . Векторы полученной суммы отложены друг за другом, поэтому вектором их суммы будет вектор .

Последней рассмотрим сумму векторов  и . Видим, что конец первого вектора в сумме совпадает с началом второго вектора.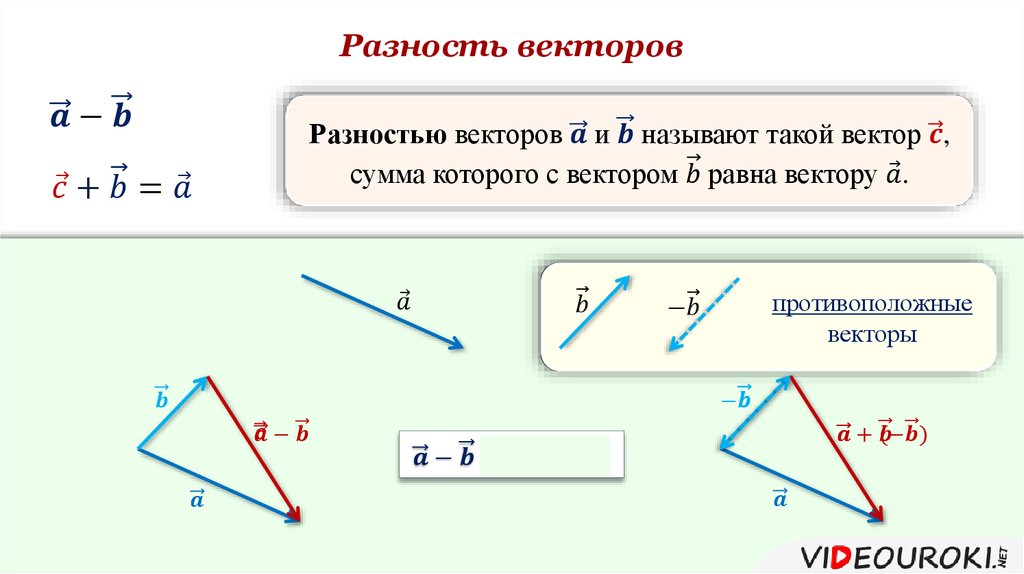 Тогда можно сразу сказать, что вектором суммы является вектор . Этот же результат мы получим, пользуясь рисунком.

Далее поговорим о разности векторов  и . Это такой вектор, сумма которого с вектором  равна вектору .

Проиллюстрируем это определение для данных векторов  и .

Итак, вектор должен являться суммой векторов  и . Тогда, отложив вектор  от начала вектора , мы без труда проведём вектор  из конца вектора  к концу вектора .

 

Действительно,  плюс  равно . А значит, вектор  равен разности векторов  и .

Таким образом, можно откладывать векторы уменьшаемое и вычитаемое от одной точки, а вектором разности будет являться вектор, направленный из конца вектора вычитаемого к концу вектора уменьшаемого.

Вы помните, что векторы называются противоположными, если их длины равны, а направления противоположны

Так вот если в данной иллюстрации у вектора  сменить направление, то есть заменить его на «», то мы получим, что вектор  равен разности векторов  и , а также, по правилу треугольника, сумме векторов  и «».

Так мы получили два способа построения вектора разности.

Рассмотрим тот же параллелепипед, что и в предыдущей задаче.

Нужно назвать векторы, начало и конец которых совпадают с вершинами параллелепипеда, и которые равны соответствующей разности векторов.

Найдём вектор разности векторов  и .

Они отложены от одной точки, поэтому вектором разности будет являться вектор, направленный из конца вектора-вычитаемого  к концу вектора-уменьшаемого . Так получаем вектор .

Применим второй способ построения вектора разности.

Нам известно, что разность векторов можно представить в виде суммы вектора уменьшаемого и вектора, противоположного вектору вычитаемому. Вектором противоположным вектору  является вектор . По правилу треугольника сложения двух векторов мы также получим вектор .

Далее рассмотрим разность векторов  и .

Они отложены от одной точки. и поэтому вектор разности будет направлен из конца вектора-вычитаемого  к концу вектора-уменьшаемого . Таким образом мы получим вектор .

Последней рассмотрим разность векторов  и . Вектор  заменим равным ему вектором . А разностью векторов  и  будет вектор . В результате и разность векторов  и  равна вектору .

Подведём итоги нашего урока.

В точности так же, как и на плоскости, на этом уроке мы с вами сформулировали правило треугольника и правило параллелограмма сложения двух векторов в пространстве, а также записали переместительный и сочетательный законы сложения векторов.

Убедившись в том, что разность векторов  и  равна сумме вектора  и вектора, противоположного вектору , мы получили два способа построения вектора разности двух векторов.

Так мы рассмотрели сложение и вычитание векторов в пространстве.

умножение, сложение векторов по правилу многоугольника

Прежде чем приступить к тематике статьи, напомним основные понятия.

Определение 1

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Определение 2

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Определение 3

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Определение 4

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Сложение двух векторов

Определение 5

Исходные данные: векторы a→ и b→ . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор AB→, равный вектору а→; из полученной точки undefined – вектор ВС→, равный вектору b→. Соединив точки undefined и C, получаем отрезок (вектор) АС→, который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

— для неколлинеарных векторов:

— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

Определение 6

Исходные данные: векторы a→ , b→, c→,d→. Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a→; затем от конца полученного вектора откладывается вектор, равный вектору b→; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B, а полученный отрезок (вектор) AB→ – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Определение 7

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a→и b→есть сумма векторов a→ и — b→.

Умножение вектора на число

Определение 8

Чтобы произвести действие умножения вектора на некое число k, необходимо учитывать следующие правила:
— еслиk>1, то это число приведет к растяжению вектора в k раз;
— если 0<k<1, то это число приведет к сжатию вектора в 1k раз;
— если k<0, то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k=1, то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

Исходные данные:
1) вектор a→и число k=2;
2) вектор b→и число k=-13.

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a→, b→, c→и произвольные действительные числа λ и μ.

1. Свойство коммутативности: a⇀+b→=b→+a→ .
   
2. Свойство ассоциативности: (a→+b→)+c→=a→+(b→+c→) .
   
3. Свойство использования нейтрального элемента по сложению (нулевой вектор 0→ ⃗). Это очевидное свойство: a→+0→=a→
4. Свойство использования нейтрального элемента по умножению (число, равное единице): 1·a→=a→. Это очевидное свойство, не предполагающее никаких геометрических преобразований.
5. Любой ненулевой вектор a→ имеет противоположный вектор -a→ и верным является равенство: a→+(-a→)=0→. Указанное свойство — очевидное.
6. Сочетательное свойство операции умножения: ( λ · µ ) · a→ = λ · ( µ·a→ ). Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
7. Первое распределительное свойство (очевидно): ( λ + µ ) · a→ = λ ·a→ + µ · a→.
8. Второе распределительное свойство: λ · (a→ +b→) = λ ·a→ + λ · b→ .
   Геометрически это свойство определяется подобием треугольников:
   

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Пример 1

Задача: упростить выражение a→-2·(b→+3·a→)
Решение
— используя второе распределительное свойство, получим: a→-2·(b→+3·a→)=a→-2·b→-2·(3·a→)
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a→-2·b→-2·(3·a→)=a→-2·b→-(2·3)·a→=a→-2·b→-6·a→
— используя свойство коммутативности, меняем местами слагаемые:a→-2·b→-6·a→=a→-6·a→-2·b→
— затем по первому распределительному свойству получаем:a→-6·a→-2·b→=(1-6)·a→-2·b→=-5·a→-2·b→Краткая запись решения будет выглядеть так:a→-2·(b→+3·a→)=a→-2·b→-2·3·a→=5·a→-2·b→
Ответ: a→-2·(b→+3·a→)=-5·a→-2·b→

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Операции над n-мерными векторами

Следующая статья

Векторное пространство

• Векторное произведение
• Векторное пространство
• Векторы на плоскости и в пространстве
• Геометрическая фигура угол
• Деление отрезка в заданном соотношении
• Все темы по математике

• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

Предмет Статистика вступит экз

Заказать такую же работу

Новая констукция валичной отжимной машины с вертикальной подачей обрабатываемого материала в зону обработки

• Вид работы:

  Курсовая работа

• Выполнена:

  13 июня 2022 г.

• Стоимость:

  4 800 руб

Заказать такую же работу

Программирование нейронных сетей

• Вид работы:

  Курсовая работа

• Выполнена:

  31 мая 2022 г.

• Стоимость:

  4 800 руб

Заказать такую же работу

Маленький сад возле жилого дома

• Вид работы:

  Курсовая работа

• Выполнена:

  23 мая 2022 г.

• Стоимость:

  4 800 руб

Заказать такую же работу

Предмет защита конфиденциальной информаци

Заказать такую же работу

Управление изменениями с помощью CICD

Заказать такую же работу

Смотреть все работы по статистике

Векторные операции: обучение сложению, вычитанию, умножению

Векторные операции включают сложение, вычитание и умножение. Векторные операции регулируются набором простых законов. В этой статье мы изучим их на примерах.

Сложение и вычитание векторов в векторных операциях

• Векторные величины не подчиняются простым арифметическим правилам сложения и вычитания. Они следуют специальному набору правил сложения и вычитания.
• Нахождение равнодействующей множества векторов, действующих на тело, называется сложением векторов. К векторным операциям относятся сложение, вычитание и умножение. Векторные операции регулируются набором простых законов. В этой статье мы изучим их на примерах.
• Два или более вектора могут быть сложены геометрически, но не алгебраически.
• Сложение векторов коммутативно по своей природе.

\(\vec{A}+\vec{B}=\vec{B} +\vec{A}\)

• Добавление отрицательного вектора к вектору называется вычитанием вектора .

\(\vec{A}+(-\vec{B})= \vec{A} – \vec{B}\)

подготовка

Законы сложения векторов в векторной операции

Существуют два закона сложения векторов или нахождения равнодействующей векторов:

1.

Закон треугольника

Согласно этому закону, если два вектора представлены двумя сторонами треугольник по величине и направлению был взят в том же порядке, то третья сторона этого треугольника представляет по величине и направлению результирующий вектор. 9{-1} {{|\vec{b}| sin\theta} \over{|\vec{a}| + |\vec{b}| cos\theta}} \end{align}\)

Чтобы получить подробную информацию о ядерной физике, кандидаты могут посетить статью по ссылке.

Q. Два вектора \(\vec{A}=2\hat{i}+6\hat{j}+9\hat{k}\) и \(\vec{B}=3\ шляпа{i}-2\шляпа{j}+2\шляпа{k}\) даны. Найдите результирующий вектор и его модуль.

Ответ. Результирующий вектор

\(\vec{C}=\vec{A}+\vec{B}=(2\hat{i}+6\hat{j}+9\hat{k})+(3 \шляпа{i}-2\шляпа{j}+2 \шляпа{k})=5\шляпа{i}+4 \шляпа{j}+11\шляпа{k}\) 92+2(6)(8)\cos60}\ \)

Вы также можете проверить подробности о законах термодинамики.

2. Закон параллелограмма

Согласно этому закону, два ненулевых вектора являются двумя смежными сторонами параллелограмма, тогда равнодействующая обоих векторов равна диагонали параллелограмма, проходящей через точку пересечения два вектора.

Здесь \(\vec{A}\) и \(\vec{B}\) — два вектора, образующие стороны параллелограмма, как показано на рисунке. Угол между двумя векторами равен θ. Результат \(\vec{R}\) из \(\vec{A}\) и \(\vec{B}\) равен углу β с вектором. 9{-1} {{|\vec{B}| sin\theta} \over{|\vec{A}| + |\vec{B}| cos\theta}} \end{align}\)

Ознакомьтесь со статьей «Применение термодинамики» здесь.

Умножение двух векторов в векторных операциях

Существуют специальные правила для произведения векторной величины.

Существует два типа произведения двух векторов:

1. Точечное или скалярное произведение

• Скалярное произведение также называется скалярным произведением или внутренним произведением.
• Скалярное произведение двух ненулевых векторов \(\vec{a}\) и \(\vec{b}\) обозначается \(\vec{a}.\vec{b}\) и дается:

, где θ — угол между двумя векторами скалярное произведение \(\vec{a}=x_1\hat{i}+y_1\hat{j}+z_1\hat{z} и \vec{b}=x_2\hat{i}+y_2\hat{j }+z_2\шляпа{z}\) определяется как:

\(a.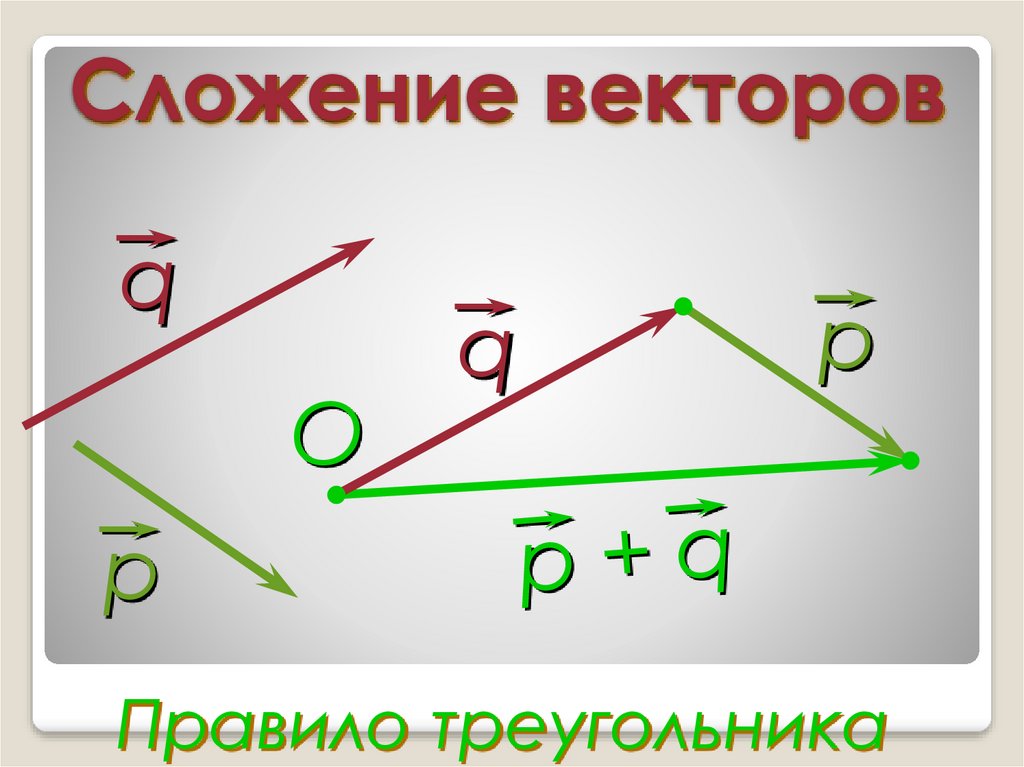 b=x{_1}x{_2}+y{_1}y{_2}+z{_1}z{_2}\)

• Угол между двумя векторами латекс]\vec{a}[/latex] и латекс]\vec{b}[/latex] определяется как:

Так как, \(\vec{a}.\vec{ b}=|\vec{a}||\vec{b}|cos\theta\) 92}=\sqrt{17}\text{ единиц.}\)

Если θ — угол между двумя векторами, то:

\(cos\theta = {{{|\vec{a}|}{|\ vec{b}|} } \over{|\vec{a}||\vec{b}|}} = {12 \over{11\sqrt 17}}\)

Подробнее об электромагнитной индукции см. здесь.

На заметку

Ортогональные векторы : Два вектора \(\vec{a}\) и \(\vec{b}\) называются ортогональными векторами, если скалярное произведение обоих векторов равно до нуля.

Два вектора, перпендикулярные друг другу, называются ортогональными векторами.

\(\vec{a}.\vec{b}=0\)

Скалярное произведение двух векторов является скалярной величиной.

Единичные векторы вдоль осей x, y и z равны i, j и k соответственно.

Затем,

\(\шляпа{i}.\шляпа{i}=\шляпа{j}. \шляпа{j}=\шляпа{k}.\шляпа{k}\)

И,

\(\шляпа{i}.\шляпа{j}=\шляпа{j}.\шляпа{k}=\шляпа{k}.\шляпа{i}=0\)

Если угол между двумя векторами \(\vec{a}\) и \(\vec{b}\) равно θ = 0°

Тогда

\(\vec{a}.\vec{b}=a\times b\)

Прочтите о звуковых волнах здесь.

2. Перекрестное или векторное произведение

Перекрестное произведение двух ненулевых векторов a и b обозначается \(\vec{a}.\vec{b}\) и задается как

\(\ vec{a}×\vec{b} = |a||b|sinθ_n\)

Направление векторного произведения двух векторов задается правилом правого винта:

Здесь мы имеем трехмерная правосторонняя прямоугольная система координат, в которой большой палец правой руки указывает в направлении положительной оси z, когда пальцы согнуты от положительной оси x к положительной оси y. Это правило правой руки.

Угол между двумя векторами \(\vec{a}\) и \(\vec{b}\) определяется выражением:

Так как, \(\vec{a}\times\vec{b}=| \vec{a}||\vec{b}|sin\theta\)

\(cos\theta = {{{\vec{a}} \times {\vec{b}} } \over{|\ vec{a}||\vec{b}|}}\)

Перекрестное произведение \(\vec{a}=x_1\hat{i}+y_1\hat{j}+z_1\hat{z} и \vec{b}=x_2\hat{i}+y_2\hat{j}+z_2\hat{z}\) определяется как:

axb =

\(\begin{bmatrix}\hat{i }&\шляпа{j}&\шляпа{k}\\
a_1&a_2&a_3\\
b_1&b_2&b_3\end{bmatrix}
\)

Чтобы получить подробную информацию о кинетической теории газов, кандидаты могут посетить статью по ссылке.

В. Найдите векторное произведение двух векторов \(\vec{a}=2\hat{i}+6\hat{j}+9\hat{z}\) и \(\vec{b} =3\шляпа{i}-2\шляпа{j}+2\шляпа{z}\) Также найдите угол между двумя векторами?

Ответ.

axb =\(\begin{bmatrix}\шляпа{i}&\шляпа{j}&\шляпа{k}\\ a_1&a_2&a_3\\ b_1&b_2&b_3\end{bmatrix}\)

=\(\begin{ bmatrix}\шляпа{i}&\шляпа{j}&\шляпа{k}\\ 2&6&9\\ 3&-2&2\end{bmatrix}\)

=\((12 +18)\шляпа{i}-(4-27)\шляпа{j}\ +(-4-18)\шляпа{k }\)

\(\vec{a}\times\vec{b}=30\hat{i}+23\hat{j}-22\hat{k}\)

Пункты, которые следует запомнить 

• Перекрестное произведение двух векторов всегда является вектором, перпендикулярным плоскости, содержащей эти два вектора.
• Перекрестное произведение двух векторов также является вектором.
• Единичные векторы вдоль осей x, y и z равны \hat{i},\hat{j}\tect{and}\hat{z} соответственно.

Тогда

\(\шляпа{i}\times\шляпа{i} = \шляпа{j}\times\шляпа{j} = \шляпа{k}\times\шляпа{k}= 0\ )

И,

\(\шляпа{i}\times\шляпа{j}=\шляпа{k}; \шляпа{j}\times\шляпа{k}=\шляпа{i}: \шляпа{ k}\times\hat{i}=\hat{j}\)

• Если угол между двумя векторами \(\vec{a}\) и \(\vec{b}\) равен θ = 0°

Затем

\(\vec{a}\times\vec{b}=|\vec{a}||\vec{b}|sin\theta = 0\)

Надеюсь, эта статья помогла вам полностью понять векторные операции. Попробуйте наше приложение Testbook, чтобы попрактиковаться и развеять все сомнения. Это абсолютно бесплатно!

Подробнее о расстоянии и перемещении см. в статье по ссылке.

Часто задаваемые вопросы о векторных операциях

В.1 Что такое треугольный закон?

Ответ 1 Согласно этому закону, если два вектора, представленные двумя сторонами треугольника по величине и направлению, взяты в одном и том же порядке, то третья сторона этого треугольника представляет по величине и направлению результирующий вектор.

Q.2 Что такое закон параллелограмма?

Ответ 2 Согласно этому закону, два ненулевых вектора являются двумя смежными сторонами параллелограмма, тогда равнодействующая обоих векторов определяется диагональю параллелограмма, проходящей через точку пересечения из двух векторов.

В.3 Что такое скалярный продукт?

Ответ 3 Скалярное произведение также называется скалярным произведением или внутренним произведением.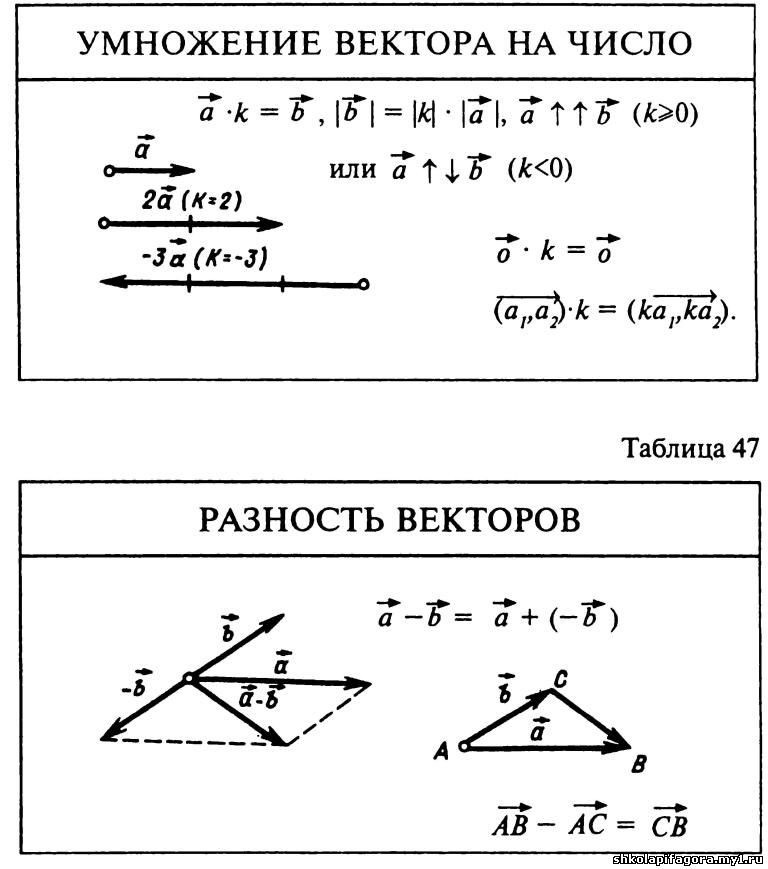

В.4 Что такое перекрестный продукт?

Ans.4 Перекрестное произведение двух ненулевых векторов a и b обозначается axb

Скачать публикацию в формате PDF

Еще на testbook.com

Уравнение движения Ньютона: вывод, определение, формула, факты и примеры решений
Векторная алгебра: изучите определения, свойства, формулы и приложения на примерах!
Горные породы Примечания: значение, типы — магматические, осадочные и метаморфические породы
Внутренняя структура Земли: земная кора, мантия и ядро
Отношения и функции: изучите типы, свойства, операции, сопоставления на примерах!

Объяснение урока: Операции с векторами в 3D

В этом объяснении мы узнаем, как выполнять операции с векторами в 3D, такие как сложение, вычитание и скалярное умножение.

Векторные операции сложения, вычитания и скалярного умножения работают в трех и более измерениях точно так же, как и в двух измерениях. Начнем с того, что вспомним, как выглядит вектор, записанный в трех измерениях.

Вектор, нарисованный в трех измерениях, имеет хвост (начальную точку) и голову (конечную точку). Направление вектора обозначено стрелкой, а длина вектора называется его величиной. Мы можем записать вектор в терминах его единичных векторов ⃑𝑖, ⃑𝑗, и ⃑𝑘 или в виде компонентов.

Определение: единичные векторы

Единичный вектор — это вектор длины (величины), равной 1. Единичные векторы в 𝑥, 𝑦 и 𝑧 направления обозначаются ⃑𝑖, ⃑𝑗 и ⃑𝑘 соответственно.

Любой вектор можно записать в виде 𝑥⃑𝑖 + 𝑦⃑𝑗 + 𝑧⃑𝑘. Альтернативно они могут быть представлены как (𝑥,𝑦,𝑧) и 𝑥𝑦𝑧.

Теперь рассмотрим формат любого вектора в пространстве, начальная точка которого находится в начале координат.

На диаграмме ниже точка 𝐴 имеет координаты (2,5,3) и вектор ⃑𝐴 (иногда обозначается как 𝑂𝐴) — это отрезок прямой от начала координат до точки 𝐴.

Из исходной точки мы перемещаемся на 2 единицы в 𝑥-направлении, на 5 единиц в 𝑦-направлении и на 3 единицы в 𝑧-направлении такой, что вектор ⃑𝐴=(2,5,3).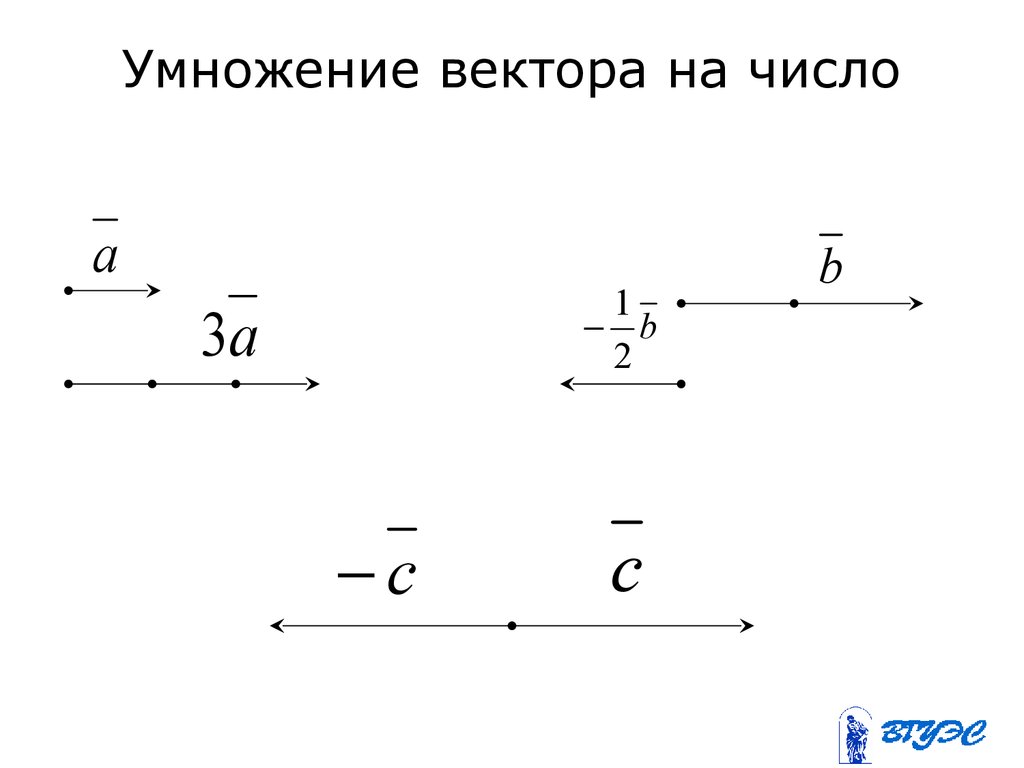

Давайте теперь вспомним некоторые ключевые определения векторов.

Определение: векторы положения

Если точка 𝐴 имеет координаты (𝑥,𝑦,𝑧), как показано на диаграмме, то вектор ⃑𝐴=(𝑥,𝑦,𝑧), где компоненты 𝑥, 𝑦 и 𝑧 — перемещения точки 𝐴 в 𝑥-, 𝑦- и 𝑧- направление от начала координат называется вектором положения.

Определение: сложение и вычитание векторов

Мы можем складывать или вычитать любые два вектора, складывая или вычитая их соответствующие компоненты.

Если ⃑𝐴=(𝑥,𝑦,𝑧) и ⃑𝐵=(𝑥,𝑦,𝑧), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦,𝑧+𝑧).

Если ⃑𝐴=(𝑥,𝑦,𝑧) и ⃑𝐵=(𝑥,𝑦,𝑧), тогда ⃑𝐴−⃑𝐵=(𝑥−𝑥,𝑦−𝑦,𝑧−𝑧).

В нашем первом примере мы покажем, как вычесть один вектор из другого, когда они оба заданы в терминах своих единичных векторов.

Пример 1. Вычитание векторов в 3D

Если ⃑𝐴=−5⃑𝑖−8⃑𝑗+6⃑𝑘 и ⃑𝐵=4⃑𝑖−3⃑𝑗+13⃑𝑘, найти ⃑𝐴−⃑𝐵.

Ответить

Мы знаем, что для того, чтобы вычесть два вектора в трех измерениях, мы вычитаем соответствующие компоненты по отдельности.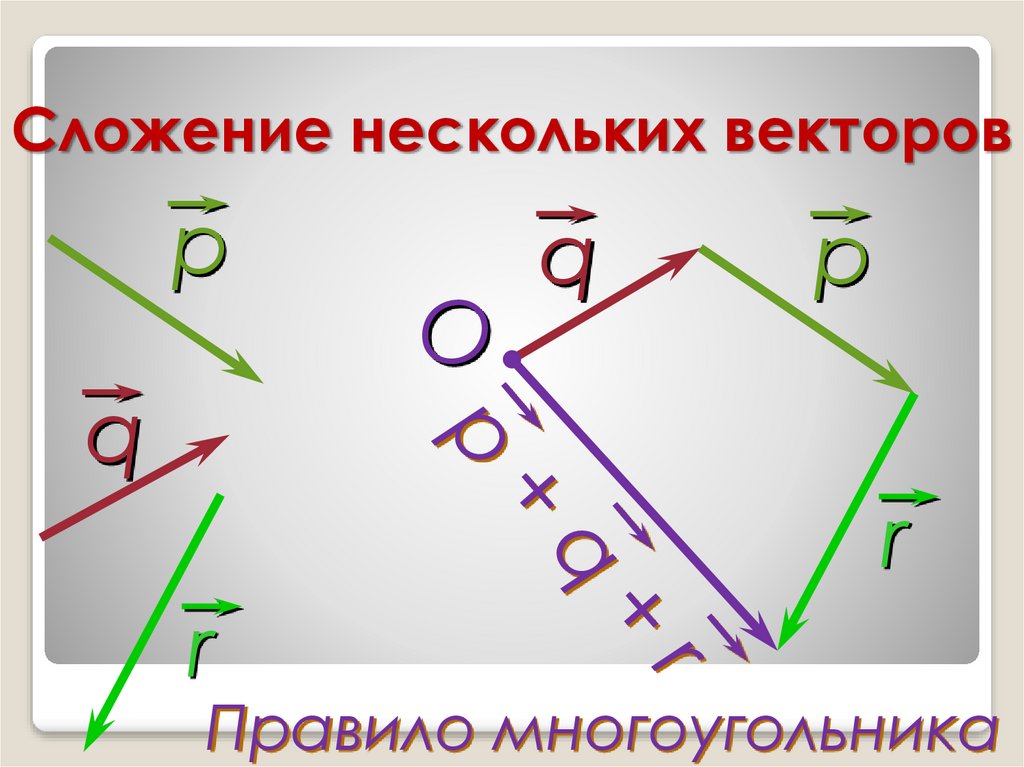 Если ⃑𝐴=(𝑥,𝑦,𝑧) и ⃑𝐵=(𝑥,𝑦,𝑧), тогда ⃑𝐴−⃑𝐵=(𝑥−𝑥,𝑦−𝑦,𝑧−𝑧).

В этом вопросе нам нужно вычесть ⃑𝑖, ⃑𝑗 и ⃑𝑘 компоненты отдельно, чтобы получить ⃑𝐴−⃑𝐵=(−5,−8,6)−(4,−3,13)=(−5−4,−8−(−3),6−13)=(−9,−5,− 7).

Следовательно, ⃑𝐴−⃑𝐵=−9⃑𝑖−5⃑𝑗−7⃑𝑘.

Давайте теперь рассмотрим, как мы можем сложить два вектора в трех измерениях.

Пример 2. Добавление векторов в 3D

Учитывая два вектора ⃑𝐴=(−2,−3,0) и ⃑𝐵=(−3,3,−2), найти ⃑𝐴+⃑𝐵.

Ответ

Мы знаем, что для сложения двух векторов в трех измерениях мы складываем соответствующие компоненты по отдельности. Если ⃑𝐴=(𝑥,𝑦,𝑧) и ⃑𝐵=(𝑥,𝑦,𝑧), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦,𝑧+𝑧).

Это означает, что ⃑𝐴+⃑𝐵=(−2+(−3),−3+3,0+(−2)).

Следовательно, ⃑𝐴+⃑𝐵=(−5,0,−2).

Мы можем распространить правило сложения и вычитания векторов в трех измерениях на вектора в 𝑛-измерениях.

Если ⃑𝐴=(𝑎,𝑎,𝑎,…,𝑎,𝑎) и ⃑𝐵=(𝑏,𝑏,𝑏,…,𝑏,𝑏), тогда ⃑𝐴+⃑𝐵=(𝑎+𝑏,𝑎+𝑏,𝑎+𝑏,…,𝑎+𝑏,𝑎+𝑏), и ⃑𝐴−⃑𝐵=(𝑎−𝑏,𝑎−𝑏,𝑎−𝑏,…,𝑎−𝑏,𝑎−𝑏).

Определение: умножение вектора на скаляр

Чтобы умножить любой вектор на скаляр, мы умножаем каждый из отдельных компонентов на этот скаляр.

Если ⃑𝐴=(𝑥,𝑦,𝑧), то 𝑘⃑𝐴=(𝑘𝑥,𝑘𝑦,𝑘𝑧), для всех вещественных констант 𝑘.

Это также можно распространить на 𝑛-мерный случай. Если ⃑𝐴=(𝑎,𝑎,𝑎,…,𝑎,𝑎), тогда 𝑘⃑𝐴=(𝑘𝑎,𝑘𝑎,𝑘𝑎,…,𝑘𝑎,𝑘𝑎).

В следующем примере мы покажем, как можно умножить вектор на скалярную величину.

Пример 3. Масштабирование трехмерного вектора

Какой вектор получится в результате масштабирования вектора ⃑𝐴=(−6,−3,−1) с коэффициентом −6?

Ответ

Чтобы умножить любой вектор на скаляр, мы умножаем каждый из отдельных компонентов на этот скаляр. Если ⃑𝐴=(𝑥,𝑦,𝑧), тогда 𝑘⃑𝐴=(𝑘𝑥,𝑘𝑦,𝑘𝑧).

В этом вопросе нам нужно умножить -6, -3 и -1 на -6. Напомним, что умножение два отрицательных числа дают положительный ответ: −6×−6=36,−3×−6=18,−1×−6=6.

Итак, умножение (−6,−3,−1) на коэффициент −6 дает нам вектор (36,18,6).

В четвертом примере мы объединим умножение вектора на скаляр с вычитанием векторов.

Пример 4. Вычитание скалярных кратных векторов

Если ⃑𝐴=(−8,9,9) и ⃑𝐵=(−6,4,9), найти 25⃑𝐴−45⃑𝐵.

Ответ

Чтобы умножить любой вектор на скаляр, мы умножаем каждый из отдельных компонентов на этот скаляр.

Поскольку ⃑𝐴=(−8,9,9), то 25⃑𝐴=25(−8,9,9)=−165 185 185.

Поскольку ⃑𝐵=(−6,4,9), тогда 45⃑𝐵=45(−6,4,9)=−245 165 365.

Чтобы вычесть два вектора в трех измерениях, мы вычитаем соответствующие компоненты по отдельности: 25⃑𝐴−45⃑𝐵=−165 185 185−−245 165 365=−165−−245,185−165,185−365=85,25,−185.

Следовательно, 25⃑𝐴−45⃑𝐵=85,25,−185.

В следующем примере мы найдем недостающий вектор в векторном выражении.

Пример 5. Поиск неизвестного вектора по векторному выражению

Если ⃑𝐴=(−1,1,1) и ⃑𝐵=(1,1,−2), определить вектор ⃑𝐶 для которого 2⃑𝐶+5⃑𝐴=5⃑𝐵.

Ответ

В вопросе сказано, что 2⃑𝐶+5⃑𝐴=5⃑𝐵, поэтому мы можем начать с переставляя и вычитая 5⃑𝐴 из обеих частей уравнения. Это дает нам уравнение 2⃑𝐶=5⃑𝐵−5⃑𝐴.

Далее вычисляем 5⃑𝐴 и 5⃑𝐵. Чтобы умножить любой вектор на скаляр, мы умножаем каждый из отдельных компонентов на этот скаляр.

Если ⃑𝐴=(−1,1,1), то 5⃑𝐴=(−5,5,5).

Если ⃑𝐵=(1,1,−2), то 5⃑𝐵=(5,5,−10).

Чтобы вычесть два вектора в трех измерениях, мы вычитаем соответствующие компоненты по отдельности.

Итак, 5⃑𝐵−5⃑𝐴=(5,5,−10)−(−5,5,5)=(10,0,−15).

Поскольку 2⃑𝐶=(10,0,−15), мы можем разделить каждый компонент на 2, чтобы вычислить вектор ⃑𝐶.

Следовательно, ⃑𝐶=5,0,−152.

Имея две точки в пространстве, мы можем применить формулу расстояния, чтобы найти расстояние между ними. Это вариант теоремы Пифагора. Данный две точки (𝑥,𝑦) и (𝑥,𝑦), расстояние 𝑑 между ними определяется выражением 𝑑=(𝑥−𝑥)+(𝑦−𝑦). 

Это можно обобщить еще больше, чтобы дать нам расстояние между точкой в ​​трехмерном пространстве и началом координат. В векторном выражении это означает, что мы можем найти длину вектора, которую мы называем величиной вектора.

Определение: Величина вектора

Величина вектора говорит нам о его длине и обозначается ‖‖⃑𝐴‖‖.

Если ⃑𝐴=(𝑥,𝑦,𝑧), то ‖‖⃑𝐴‖‖=√𝑥+𝑦+𝑧.

В нашем следующем примере мы вычислим величину векторов в трех измерениях.

Пример 6. Сравнение модулей векторных выражений

⃑𝑉 и 𝑊 — два вектора, где ⃑𝑉=(−1,5,−2) и 𝑊=(3,1,1). Сравнивая ‖‖⃑𝑉−𝑊‖‖ и ‖‖⃑𝑉‖‖−‖‖𝑊‖‖, какое количество больше?

Ответ

Чтобы вычислить величину любого вектора, мы вычисляем квадратный корень из суммы квадратов отдельных компонентов. Если ⃑𝐴=(𝑥,𝑦,𝑧), то ‖‖⃑𝐴‖‖=√𝑥+𝑦+𝑧.

Нам говорят, что ⃑𝑉=(−1,5,−2).

Итак, ‖‖⃑𝑉‖‖=(−1)+(5)+(−2)=√30.

Нам также говорят, что 𝑊=(3,1,1).

Итак, ‖‖𝑊‖‖=(3)+(1)+(1)=√11.

Это означает, что ‖‖⃑𝑉‖‖−‖‖𝑊‖‖=√30−√11≈2,1606.

Чтобы вычесть два вектора, мы вычитаем соответствующие компоненты по отдельности: ⃑𝑉−𝑊=(−1,5,−2)−(3,1,1)=(−4,4,−3).

Итак, ‖‖⃑𝑉−𝑊‖‖=(−4)+(4)+(−3)=√41.

Итак, √41≈6,4031, что больше 2,1606.

Следовательно, ‖‖⃑𝑉−𝑊‖‖ больше, чем ‖‖⃑𝑉‖‖−‖‖𝑊‖‖.

В нашем последнем примере мы продемонстрировали, что величина разности двух векторов не равна разнице между их соответствующими величины. Важно понимать, что, хотя мы можем довольно легко найти сумму или разность двух или более векторов, мы не можем применить аналогичный метод. понятие к сумме или разности их величин.

В нашем последнем примере мы вычислим возможные пропущенные значения в векторной задаче.

Пример 7. Решение векторной задачи с использованием единичных векторов

Учитывая, что ⃑𝐴=3⃑𝑖+⃑𝑗+𝑚⃑𝑘 и что ⃑𝐵 — единичный вектор, равный 15⃑𝐴, определить возможные значения 𝑚.

Ответ

Чтобы умножить любой вектор на скаляр, мы умножаем каждый из отдельных компонентов на этот скаляр.

Поскольку ⃑𝐵=15⃑𝐴, тогда ⃑𝐵=153⃑𝑖+⃑𝑗+𝑚⃑𝑘=35⃑𝑖+15⃑𝑗+𝑚5⃑𝑘.

Нам сказали, что ⃑𝐵 — единичный вектор, и мы знаем, что любой единичный вектор имеет модуль, равный 1, где ‖‖⃑𝐵‖‖=√𝑥+𝑦+𝑧, если ⃑𝐵=(𝑥,𝑦,𝑧): 35+15+𝑚5=1.

Возведение в квадрат обеих частей уравнения, 35+15+𝑚5=1,925+125+𝑚25=1.

Умножая на 25 и собирая подобные члены, 10+𝑚=25,𝑚=25−10,𝑚=15.

Если найти квадратный корень из обеих сторон, 𝑚 может быть равно √15 или −√15.

Мы закончим это объяснение повторением некоторых ключевых моментов.

Ключевые точки

• Единичный вектор имеет величину 1, а орты параллельны осям 𝑥-, 𝑦- и 𝑧 обозначаются ⃑𝑖, ⃑𝑗 и ⃑𝑘 соответственно.
• Вектор в трехмерном пространстве может быть записан в компонентной форме: (𝑥,𝑦,𝑧) или в терминах его основной единицы векторы: 𝑥⃑𝑖+𝑦⃑𝑗+𝑧⃑𝑘.
• Чтобы сложить или вычесть два вектора, мы складываем или вычитаем их соответствующие компоненты.
  Если ⃑𝐴=(𝑥,𝑦,𝑧) и ⃑𝐵=(𝑥,𝑦,𝑧), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦,𝑧+𝑧).
  Если ⃑𝐴=(𝑥,𝑦,𝑧) и ⃑𝐵=(𝑥,𝑦,𝑧), тогда ⃑𝐴−⃑𝐵=(𝑥−𝑥,𝑦−𝑦,𝑧−𝑧).
• Чтобы умножить любой вектор на скаляр, мы умножаем каждый из отдельных компонентов на этот скаляр. Если ⃑𝐴=(𝑥,𝑦,𝑧), то 𝑘⃑𝐴=(𝑘𝑥,𝑘𝑦,𝑘𝑧).
• Величина вектора — это его длина, и ее можно вычислить, адаптировав теорему Пифагора к трем измерениям. Если ⃑𝐴=(𝑥,𝑦,𝑧), то ‖‖⃑𝐴‖‖=√𝑥+𝑦+𝑧.

Графические методы – физика Колледжа Дугласа 1107

Глава 3 Двумерная кинематика

Резюме

• Понимание правил сложения, вычитания и умножения векторов.
• Применение графических методов сложения и вычитания векторов для определения перемещения движущихся объектов.

Рисунок 1. Смещение можно определить графически с помощью масштабной карты, такой как карта Гавайских островов. Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США).

Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.

На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3. 1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что символ со стрелкой над ним, такой как [latex]\vec{\text{D}}[/latex], обозначает вектор. Его величина представлена ​​курсивным символом , D, , а его направление — θ .

ВЕКТОРА В ЭТОМ ТЕКСТЕ

В этом тексте мы будем представлять вектор со стрелкой над символом. Например, мы представим количественную силу вектором [latex]\vec{\text{F}}[/latex], который имеет как величину, так и направление. Величина вектора будет представлена ​​переменной, выделенной курсивом, например, F , а направление переменной будет задано углом θ .

Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29.1 ^o к северу от востока. Рис. 3. Чтобы графически описать результирующий вектор для пешехода, идущего по городу, изображенному на рис. западная ось. Длина D стрелки пропорциональна модулю вектора и измеряется вдоль линии с помощью линейки. В этом примере величина D вектора составляет 10,3 единицы, а направление θ равно 29.1 ^o к северу от востока.

Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а конец (или кончик) вектора является конечным заостренным концом стрелки.

Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренному на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D .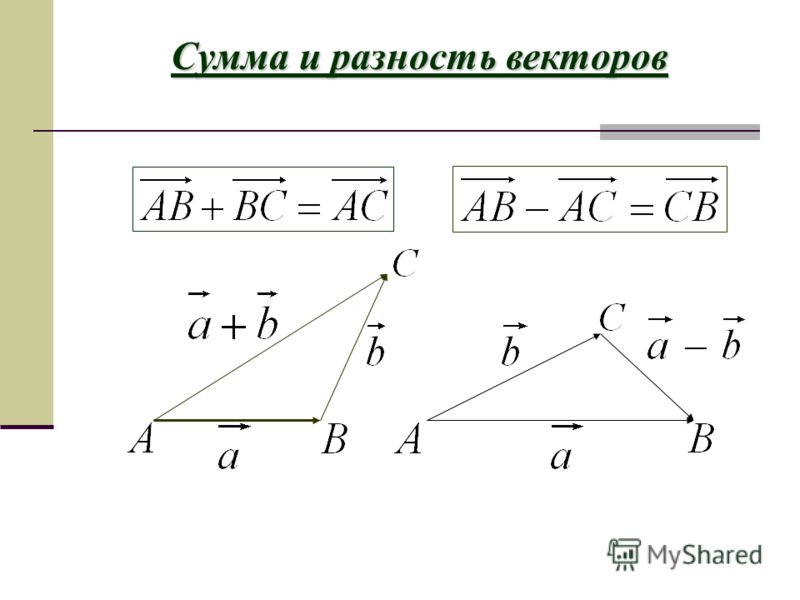 Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, составляет 29,1 ^o .

Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .

Рис. 5.

Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .

Рисунок 6.

Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .

Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.

Рисунок 7.

Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.)

Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)

Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.

Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке

Используйте графический метод сложения векторов, чтобы найти полное перемещение человека, который проходит следующие три пути (перемещения) по ровному полю. Сначала она проходит 25,0 м в направлении 49,0° к северу от востока. Затем она проходит 23,0 м в направлении 15,0° к северо-востоку. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.

Стратегия

Представьте каждый вектор смещения графически стрелкой, пометив первый [латекс]\vec{\text{A}}[/латекс], второй [латекс]\vec{\text{B}} [/latex] и третий [latex]\vec{\text{C}}[/latex], делающий длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого [латекс]\vec{\text{R}}[/латекс].

Решение

(1) Нарисуйте три вектора смещения.

Рис. 8.

(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.

Рисунок 9.

(3) Нарисуйте результирующий вектор [латекс]\vec{\text{R}}[/латекс].

Рисунок 10.

(4) Используйте линейку для измерения величины [латекс]\vec{\text{R}}[/латекс] и транспортир для измерения направления [латекс]\vec{\text {R}}[/латекс]. Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.

Рис. 11.

В этом случае видно, что полное смещение R имеет величину 50,0 м и направлено в направлении 7,0° к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0 ° к югу от востока.

Обсуждение

Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.

Рисунок 12.

Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно . Векторы можно добавлять в любом порядке.

[латекс]\vec{\text{A}}+\vec{\text{B}}=\vec{\text{B}}+\vec{\text{A}}.[/latex]

(Это верно и для сложения обычных чисел — вы получите тот же результат, сложите ли вы, например, 2 + 3 или 3 + 2).

Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\vec{\text{B}}[/latex] из [латекс]\vec{\text{A}}[/латекс], написанного [латекс]\vec{ \text{A}}-\vec{\text{B}}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием. отрицательное вектора [латекс]\vec{\text{B}} [/latex] определяется как [latex]-\vec{\text{B}}[/latex]; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано на рисунке 13. Другими словами, [latex]\vec{\text{B}}[/latex] имеет ту же длину, что и [latex]-\vec{\text{B}}[/latex] , но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.

Рисунок 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Таким образом, B является отрицательным значением -B; он имеет ту же длину, но противоположное направление.

вычитание вектора [латекс]\vec{\text{B}}[/латекс] из вектора [латекс]\vec{\текст{А}}[/латекс] затем просто определяется как добавление [латекс]- \vec{\text{B}}[/latex] в [латекс]\vec{\text{A}}[/latex]. Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.

[латекс]\vec{\text{A}}-\vec{\text{B}}=\vec{\text{A}}+(-\vec{\text{B}})[/latex]

Это аналогично вычитанию скаляров (где, например, 5 – 2 = 5 + (-2) ). Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.

Пример 2: графическое вычитание векторов: женщина, плывущая на лодке

Женщина, плывущая на лодке ночью, следует указаниям к причалу. Инструкции гласили: сначала пройти 27,5 м в направлении 66,0° к северу от востока от ее текущего местоположения, а затем пройти 30,0 м в направлении 112° к северу от востока (или 22,0° к западу от севера). Если женщина совершит ошибку и отправится в направлении 90 560, противоположном 90 561, на второй этап пути, где она окажется? Сравните это место с расположением дока.

Рисунок 14.

Стратегия

Мы можем представить первый этап пути с помощью вектора [latex]\vec{\text{A}}[/latex], а второй этап пути с помощью вектор [латекс]\vec{\text{B}}[/латекс]. Док расположен по адресу [латекс]\vec{\text{A}}+\vec{\text{B}}[/latex]. Если женщина по ошибке едет в направлении , противоположном , для второго этапа пути, она пройдет расстояние [латекс]\vec{\text{B}}[/латекс] (30,0 м) в направлении 180° – 112° = 68° к югу от востока. Мы представляем это как [латекс]-\vec{\text{B}}[/латекс], как показано ниже. Вектор [latex]-\vec{\text{B}}[/latex] имеет ту же величину, что и [latex]\vec{\text{B}}[/latex], но имеет противоположное направление. Таким образом, она окажется в месте [латекс]\vec{\text{A}}+(-\vec{\text{B}})[/latex] или [латекс]\vec{\text{A }}-\vec{\text{B}}[/латекс].

Рисунок 15.

Выполним сложение векторов, чтобы сравнить положение дока, [latex]\vec{\text{A}}+\vec{\text{B}}[/latex], с положением на который по ошибке приходит женщина, [латекс]\vec{\text{A}}+(-\vec{\text{B}})[/latex].

Решение

(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы [латекс]\vec{\text{A}}~\text{and}~-\vec{\text{ B}}[/латекс].

(2) Разместите векторы лицом к хвосту. \prime[/latex]:

Рис. 17.

В данном случае R =52,9 м и θ=90,1° к северо-востоку.

Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.

Обсуждение

Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.

Если бы мы решили пройти в три раза большее расстояние на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м, или 82,5 м, в направлении 66,0° к северу от востока. Это пример умножения вектора на положительное число 9.0020 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.

Если скаляр отрицательный, то умножение на него вектора изменяет величину вектора и дает новому вектору направление , противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор [латекс]\vec{\text{А}}[/латекс] умножается на скаляр c ,

• величина вектора становится абсолютной величиной c [латекс]\vec{\text{A}}[/латекс],
• , если c положительно, направление вектора не меняется,
• , если c отрицательно, направление меняется на противоположное.

В нашем случае c = 3 и A = 27,5 м. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.

В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например, x – и y -компоненты, или компоненты север-юг и восток-запад.

Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0° к северу от востока, и мы хотим узнать, сколько кварталов ему пришлось пройти на восток и север. Этот метод называется определением компонентов (или частей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0020 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.

PHET EXPLORATIONS: MAZE GAME

Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.

Рисунок 18. Игра «Лабиринт»

• Графический метод сложения векторов [latex]\vec{\text{A}}[/latex] и [latex]\vec{\text{B}}[/latex] включает рисование векторов на графике и добавление их методом «голова к хвосту». Результирующий вектор [latex]\vec{\text{R}}[/latex] определяется таким образом, что [latex]\vec{\text{A}}+\vec{\text{B}}=\vec{\ текст{R}}[/латекс]. Величина и направление [латекс]\vec{\text{R}}[/латекс] затем определяются с помощью линейки и транспортира соответственно.
• Графический метод вычитания вектора [латекс]\vec{\text{B}}[/латекс] из [латекс]\vec{\текст{А}}[/латекс] включает добавление противоположного вектора [латекс ]\vec{\text{B}}[/latex], который определяется как [латекс]-\vec{\text{B}}[/латекс]. В этом случае [латекс]\vec{\text{A}}-\vec{\text{B}}=\vec{\text{A}}+(-\vec{\text{B}})= \vec{\text{R}}[/латекс]. Затем обычным образом применяется метод сложения головы к хвосту, чтобы получить результирующий вектор [латекс]\vec{\text{R}}[/латекс].
• Сложение векторов равно , коммутативное , такое, что [латекс]\vec{\text{A}}+\vec{\text{B}}=\vec{\text{B}}+\vec{\text{A }}[/латекс].
• Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике и последующее размещение хвоста каждого последующего вектора в начале предыдущего вектора. Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
• Если вектор [латекс]\vec{\text{A}}[/латекс] умножить на скалярную величину c , величина произведения определяется как c [латекс]\vec{\text{A}}[/латекс]. Если c положительно, направление произведения указывает на то же направление, что и [латекс]\vec{\text{A}}[/латекс]; если c отрицательно, направление произведения указывает на направление, противоположное [латекс]\vec{\text{A}}[/латекс].

компонент (двумерного вектора)

часть вектора, указывающая либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов

коммутативный

относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму

направление (вектора)

ориентация вектора в пространстве

голова (вектора)

конечная точка вектора; расположение кончика стрелки вектора; также упоминается как «наконечник»

метод «голова к хвосту»

метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора

величина (вектора)

длина или размер вектора; величина является скалярной величиной

результат

сумма двух или более векторов

результирующий вектор

векторная сумма двух или более векторов

скаляр

количество с величиной, но без направления

хвост

начальная точка вектора; напротив наконечника или наконечника стрелки

Проблемы и упражнения

1: (A) 480 м (B) 379 м, 18,4 ^O Восток от севера

3: Северный компонент 3,21 км, восточный компонент 3.