Сложение вычитание векторов: Вычитание векторов — урок. Геометрия, 9 класс.

Сложение и вычитание векторов

Сумма векторов

Пусть даны два вектора а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) (рис. 5).

От точки А отложим отрезок АС такой, что \(\overrightarrow{AC}\) = b. Тогда, вектор с = \(\overrightarrow{OC}\) называется суммой векторов а и b и
обозначается а + b.

Таким образом, \(\overrightarrow{OA}\) + \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\). Это равенство называют
правилом треугольника сложения двух векторов.

Oчевидно, что это правило справедливо и в том случае, когда точки О, А и В лежат на одной прямой (рис. 6, 7). В частности, а + 0 = а.

Сложение векторов обладает следующими свойствами:

1. Свойство коммутативности (перестановочности): для любых векторов а и b

а + b = b + а. (1)

2. Свойство ассоциативности (сочетательности): для любых векторов а, b и с

(а + b) + с = а + (b + с). (2)

1. Пусть a = \(\overrightarrow{OA}\), b = \(\overrightarrow{OB}\). Рассмотрим случай, когда точки О, А и В не лежат на одной прямой. На отрезках ОА и ОВ построим параллелограмм OACB (рис. 8).

Тогда |ОА| = |ВС|, (ОА) || (ВС) и |ОВ| = |АС|, (ОВ) || (АС), как противоположные стороны параллелограмма. Следовательно,

а = \(\overrightarrow{OA}\)= \(\overrightarrow{BC}\), b = \(\overrightarrow{OB}\) = \(\overrightarrow{AC}\),

и поэтому

а + b = \(\overrightarrow{OA}\)+ \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\),
b + а = \(\overrightarrow{OB}\) + \(\overrightarrow{BC}\) = \(\overrightarrow{OC}\),

что и доказывает равенство (1).

Для случая, когда точки О, А, В лежат на одной прямой, доказательство можно провести самостоятельно.

2. От некоторой точки О отложим вектор \(\overrightarrow{OA}\) = а, от точки А отложим вектор \(\overrightarrow{AB}\) = b и, наконец, от точки В отложим вектор \(\overrightarrow{BC}\) = с (рис. 9, 10).

Соединим точки О и С отрезком ОС. Тогда, с одной стороны (см. рис. 9),

(а + b) + с = (\(\overrightarrow{OA}\) + \(\overrightarrow{AB}\)) + \(\overrightarrow{BC}\) =
\(\overrightarrow{OB}\) + \(\overrightarrow{BC}\)= \(\overrightarrow{OC}\)

и, с другой стороны (см. рис. 10),

а + (b + с) = \(\overrightarrow{OA}\) + (\(\overrightarrow{AB}\)+ \(\overrightarrow{BC}\)) = \(\overrightarrow{OA}\) + \(\overrightarrow{AC}\) = \(\overrightarrow{OC}\),

что и доказывает равенство (2).

Из риc. 8 видно, что сумма векторов а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) равна направленной диагонали \(\overrightarrow{OC}\) параллелограмма OACB, построенного на отрезках ОА и ОВ, т.е.

\(\overrightarrow{OA}\) + \(\overrightarrow{OB}\) = \(\overrightarrow{OC}\).

Это равенство называется правилом параллелограмма сложения двух векторов.

Так как сложение векторов ассоциативно, то сумма трех и большего числа векторов записывается без скобок. Например, вместо (а + b) + с или а + ( b + с ) пишут а + b + с.

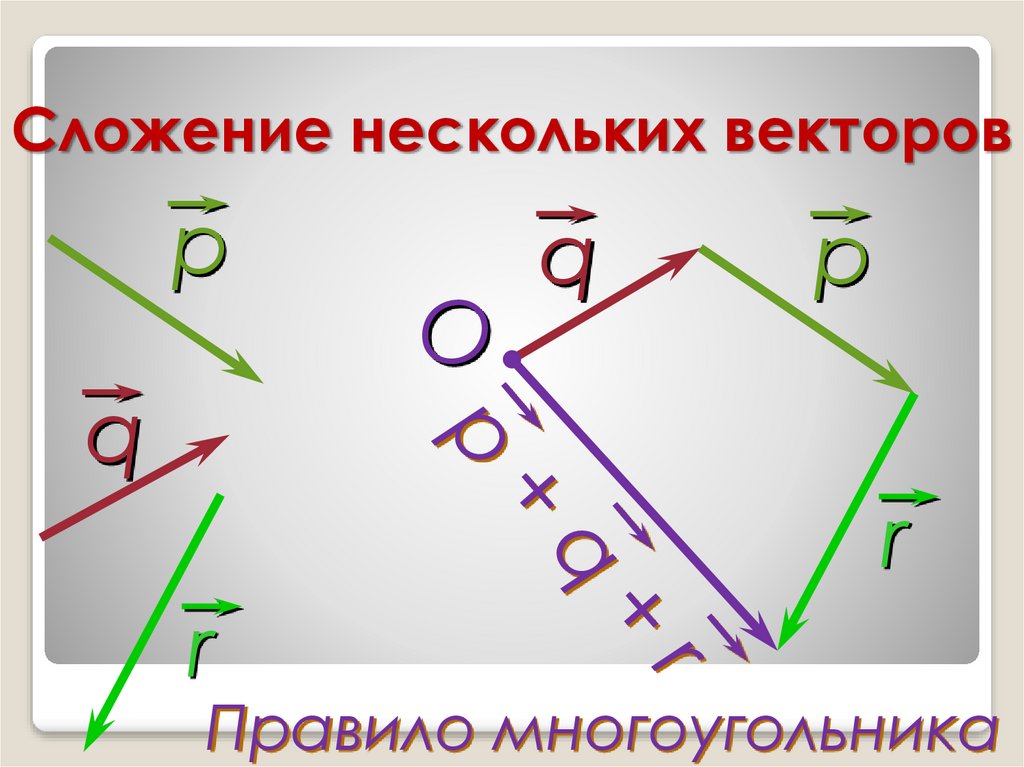
Если требуется найти сумму трех или большего числа векторов, то применяют так называемое правило многоугольника. Оно состоит в следующем.

Пусть даны векторы а, b, с, d и требуется найти их сумму.

Выберем некоторую точку О (рис. 11) и построим отрезок ОА такой, что \(\overrightarrow{OA}\) = а,
затем построим отрезок АВ такой, что \(\overrightarrow{AB}\) = b, и т. д.

Построение продолжается до тех пор, пока не будут исчерпаны все векторы-слагаемые. Направленный отрезок \(\overrightarrow{OD}\), замыкающий полученную ломаную, будет равен сумме данных векторов.

Противоположные векторы. Вычитание векторов.

Любые два вектора, сумма которых равна нулевому вектору, называются противоположными. Вектор, протипоположный вектору а, обозначается — а. Следовательно, по определению

а + (- а) = 0.

Из определения следует, что если а = \(\overrightarrow{AB}\), то — а = \(\overrightarrow{BA}\), т. е. противоположные векторы имеют одинаковую длину и противоположные направления.

Например, если ABCD — параллелограмм, то векторы \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\) противоположные (рис. 15). Векторы \(\overrightarrow{AD}\) и \(\overrightarrow{CB}\) тоже противоположные.

Для любых двух векторов а и b вектор с = а + (- b) называется разностью векторов а и b и обозначается а — b. Таким образом, по определению

а — b = а + (- b).

Если а = \(\overrightarrow{OA}\) и b = \(\overrightarrow{OB}\) (рис. 16), то

а — b = \(\overrightarrow{OA}\) — \(\overrightarrow{OB}\) = \(\overrightarrow{OA}\) + \(\overrightarrow{BO}\) = \(\overrightarrow{BO}\)+ \(\overrightarrow{OA}\) = \(\overrightarrow{BA}\).

Следовательно,

\(\overrightarrow{OA}\) — \(\overrightarrow{OB}\) = \(\overrightarrow{BA}\) (1)

Из рисунка видно, что \(\overrightarrow{BA}\) — это направленная диагональ параллелограмма ОАСВ, построенного на отрезках ОА и ОВ. Другая диагональ \(\overrightarrow{OC}\) изображает сумму векторов \(\overrightarrow{OA}\) и \(\overrightarrow{OB}\).

Нетрудно заметить, что формулу (1) можно применять, не прибегая к чертежу: для этого достаточно внимательно проследить за порядком расположения букв в записи данных и искомого векторов. Так, например,

$$ \overrightarrow{PQ} — \overrightarrow{PN} = \overrightarrow{NQ}\;\; (2)$$

Геометрия Сложение и вычитание векторов

Материалы к уроку

Конспект урока

3. Сложение и вычитание векторов

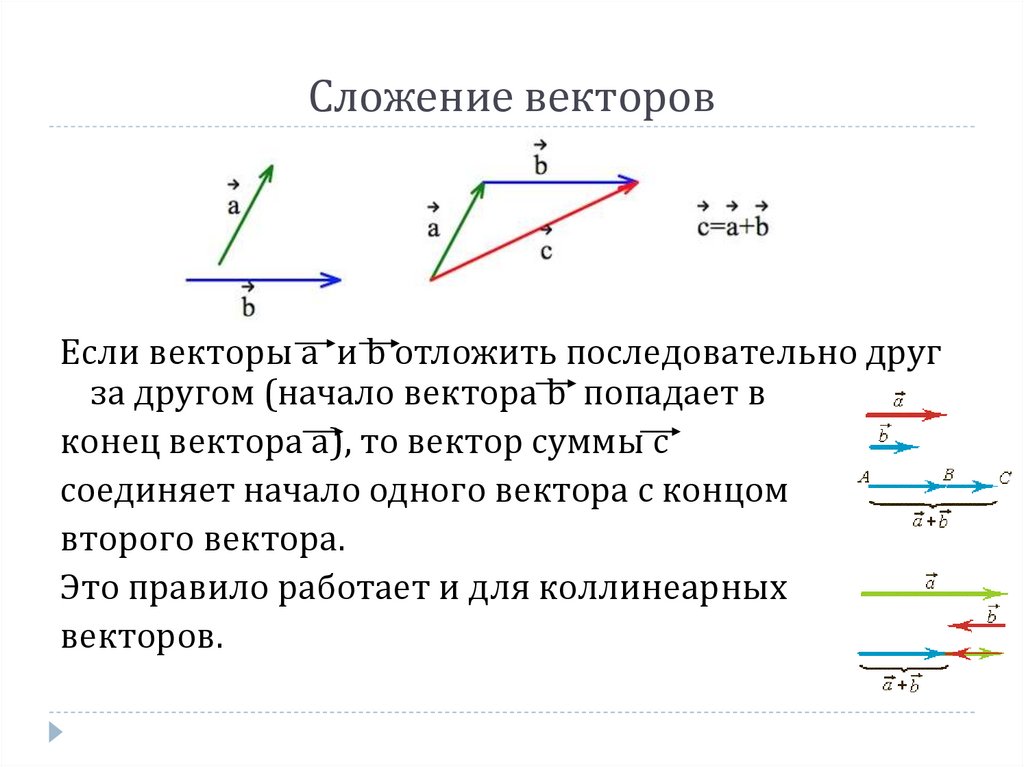
Введем правило сложения двух векторов. Пусть нам даны два неколлинеарных вектора  a и b. Отложим от произвольной точки пространства А вектор АВ, равный вектору а. Затем от точки В отложим вектор ВС, равный вектору b. Вектор АС называется суммой векторов а и b. Нужно отметить, что сумма векторов не зависит от выбора точки А. Это правило сложения векторов называется правилом треугольника.	Текст Сложение двух векторов Рисунок двух неколлинеарных векторов, треугольник, две стороны параллельны данным векторам
При сложении неколлинеарных векторов можно воспользоваться правилом параллелограмма. Пусть даны векторы а и b. От произвольной точки А отложим векторы АВ и АС, равные соответственно а и b. Достроим до параллелограмма, проведя дополнительные линии, параллельно данным векторам. Вектор AD являющийся диагональю параллелограмма, выходящий из точки А есть сумма векторов а и b.	Текст Правило треугольника Рисунок параллелепипеда
Решим задачу №327 под буквой а. На рисунке  изображен параллелепипед ABCDA1B1C1D1.Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов    AB и  A1D1 . Воспользуемся правилом параллелограмма. К вектору АВ прибавим вектор АD, равный вектору A 1D1.     Суммой этих векторов будет диагональ основания параллелепипеда, то есть вектор АС.	Текст №327(а) Рисунок параллелепипеда   По правилу параллелограмма ,
Напомним свойства сложения векторов, так как они ни чем не отличаются от свойств сложения векторов в планиметрии: Для любых трех векторов а, бэ и це, выполняются равенства 1) переместительный закон 2) сочетательный закон
Введем определение противоположных векторов. Два вектора называются противоположными, если их длины равны и они противоположно направлены Вектор минус а противоположен вектору а   Вектор DF противоположен вектору FD, и равен минус вектор FD	Противоположные векторы   Если  и – противоположные, то | |=| |,     .      и – противоположные,  = –
Определим вычитание векторов	Текст Вычитание векторов Разностью векторов    a  и   b  называется такой вектор, сумма которого с вектором  b    равна вектору a .
Разность можно найти как сумму вектора      с противоположным вектором вектору   .
Существует правило для трех точек.   Любой вектор можно представить как разность двух векторов, проведенных из одной точки. Добавляем третью точку (любую) и задаем разность из  вектора, проведенного из этой точки в конец данного вектора минус вектор, проведенный в начало.	Текст Правило трех точек       Рисунок разности векторов   (по ходу правила строить сначала вектор ВК затем вектор АК и АВ)
Решим задачу №332 На рисунке изображен параллелепипед ABCDA1B1C1D1 Представьте векторы АВ1 и DK в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.	Текст Задача №332 Рисунок параллелепипеда
Решение. Рассмотрим вектор АВ1 и воспользуемся правилом трех точек.  Третьей точкой удобно взять точку А1. Вектор, проведенный  в конец то есть в точку В1   будет А1В1 и в начало точку А – вектор А1А. Получаем АВ1 равно А1В1 минус А1А.	Текст Задача №332 Решение. Рисунок прежний
Выполним это же задание для вектора DK.  Здесь третьей точкой удобно взять точку D1. Вектор в конец ­ — D1K, в начало — D1D. Получим вектор DK равен D1K минус  D1D.	Текст Задача №332

Комментарий, было упущено свойства сложения векторов, и определение противоположного вектора.

 

Остались вопросы по теме? Наши педагоги готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать педагогаОставить заявку на подбор

Как складывать и вычитать векторы (с диаграммами)

Вектор  – это величина, с которой связаны как величина, так и направление.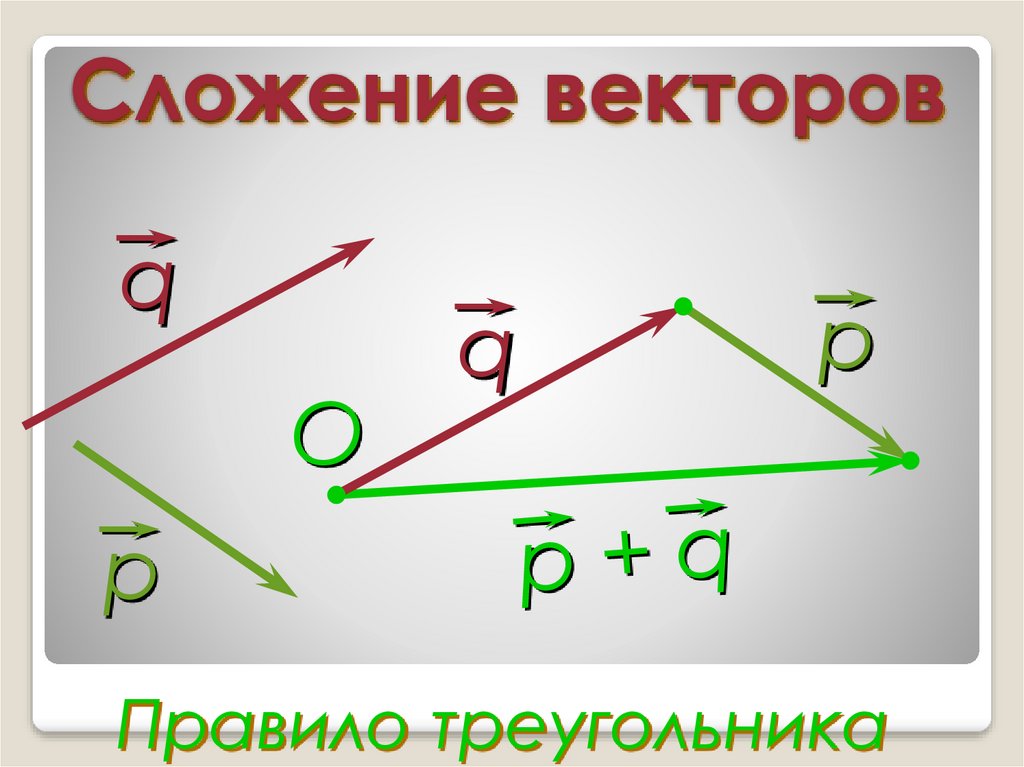 Это отличается от скалярной величины , которая соответствует только величине. Скорость является примером векторной величины. У него есть как величина (насколько быстро что-то движется), так и направление (направление, в котором оно движется).

Векторы часто рисуются в виде стрелок. Длина стрелки соответствует величине вектора, а острие стрелки указывает направление.

Существует два способа работы со сложением и вычитанием векторов. Первый — графически, манипулируя стрелочными диаграммами самих векторов. Второй — математический, дающий точные результаты.

Графическое сложение и вычитание векторов в одном измерении

При сложении двух векторов хвост второго вектора помещается на вершину первого вектора, сохраняя ориентацию вектора. Результирующий вектор  – это вектор, который начинается в конце первого вектора и направлен по прямой к вершине второго вектора.

Например, рассмотрим добавление векторов A и B , которые указывают в одном направлении вдоль линии. Мы размещаем их «кончиком к хвосту», и результирующий вектор C указывает в одном направлении и имеет длину, которая является суммой длин A и B .

Вычитание векторов в одном измерении по существу аналогично сложению, за исключением того, что вы «переворачиваете» второй вектор. Это следует непосредственно из того факта, что вычитание — это то же самое, что добавление отрицания.

Математическое сложение и вычитание векторов в одном измерении

При работе в одном измерении направление вектора может быть указано знаком. Мы выбираем одно направление как положительное (обычно «вверх» или «вправо» выбираются как положительные) и назначаем любой вектор, указывающий в этом направлении, как положительную величину. Любой вектор, указывающий в отрицательном направлении, является отрицательной величиной. При добавлении или вычитании векторов добавляйте или вычитайте их величины с соответствующими знаками.

Предположим, что в предыдущем разделе вектор A имел величину 3, а вектор B имел величину 5. Тогда результирующий вектор C = A + B = 8, вектор величина 8 указывает в положительном направлении, а результирующий вектор D = A — B = -2, вектор величины 2 указывает в отрицательном направлении. Обратите внимание, что это согласуется с графическими результатами, полученными ранее.

Совет: Будьте осторожны, добавляйте векторы только одного типа: скорость + скорость, сила + сила и так далее. Как и во всей математике в физике, единицы измерения должны совпадать!

Графическое сложение и вычитание векторов в двух измерениях

Если первый вектор и второй вектор не лежат на одной линии в декартовом пространстве, вы можете использовать один и тот же метод «кончик к хвосту», чтобы сложить или вычесть их. Чтобы добавить два вектора, просто представьте, что вы поднимаете второй и кладете его хвост на кончик первого, сохраняя при этом его ориентацию, как показано. Результирующий вектор представляет собой стрелку, начинающуюся с хвоста первого вектора и заканчивающуюся вершиной второго вектора:

Как и в одном измерении, вычитание одного вектора из другого эквивалентно переворачиванию и сложению. Графически это выглядит следующим образом:

••• Дана Чен | Science

Примечание. Иногда сложение векторов изображают графически, соединяя хвосты двух векторов слагаемых вместе и создавая параллелограмм. Результирующий вектор является диагональю этого параллелограмма.

Математическое сложение и вычитание векторов в двух измерениях

Для математического сложения и вычитания двухмерных векторов выполните следующие действия:

Разложите каждый вектор на компонент ​ x ​, иногда называемый горизонтальным компонентом, и компонент ​ y ​, иногда называемый вертикальная составляющая, используя тригонометрию. (Обратите внимание, что компоненты могут быть отрицательными или положительными в зависимости от того, в каком направлении указывает вектор)0003 y ​-компоненты обоих векторов вместе. Этот результат дает вам компоненты результирующего вектора x и y .

Величина результирующего вектора может быть найдена с помощью теоремы Пифагора.

Направление результирующего вектора можно найти с помощью тригонометрии, используя функцию арктангенса. Это направление обычно задается как угол относительно положительной оси x ​.

Тригонометрия в векторном сложении 92

Снарядное движение дает классические примеры того, как мы можем использовать эти отношения как для разложения вектора, так и для определения окончательной величины и направления вектора.

Предположим, двое играют в мяч. Предположим, вам сказали, что мяч брошен с высоты 1,3 м со скоростью 16 м/с под углом 50 градусов к горизонту. Чтобы приступить к анализу этой задачи, вам нужно будет разложить этот начальный вектор скорости на x и y компоненты, как показано:

v_{xi}=v_i\cos(\theta)=16\times\cos(50)=10,3 \text{ м/с}\\ v_{yi}=v_i\sin(\ theta)=16\times\sin(50)=12.3\text{ м/с}

Если кэтчер промахнется по мячу и он упадет на землю, с какой конечной скоростью он ударится?

Используя кинематические уравнения, мы можем определить, что конечные компоненты скорости мяча равны:

v_{xf}=10,3 \text{ м/с}\\ v_{yf}=-13,3\text{ м/ s}

Теорема Пифагора позволяет найти величину: 9{-1}\Big(\frac{-13.3}{10.3}\Big)=-52.2\степень

Пример сложения и вычитания векторов

Предположим, что автомобиль поворачивает за угол. Предположим, что v _i ​ для автомобиля находится в направлении ​ x- ​с магнитудой 10 м/с, а ​ v _f ​ находится под углом 45 градусов с положительным ​ x ​-ось со скоростью 10 м/с. Если это изменение движения происходит за 3 секунды, какова величина и направление ускорения автомобиля при повороте?

Напомним, что ускорение a  – это векторная величина, определяемая как:

a=\frac{(v_f-v_i)}{t}

_я ​ — конечная и начальная скорости соответственно (и, следовательно, тоже векторные величины).

Чтобы вычислить разность векторов ​ ​ v _f ​- ​ v _i ​, ​, мы должны сначала разложить начальный и конечный векторы скорости:

v_{xi}=10\text{ м/с}\\ v_{yi}=0\text{ м/с}\\ v_{xf}=10\cos(45)=7.07\text{ м/с s}\\ v_{yf}=10\sin(45)=7.07\text{ м/с}

Затем мы вычитаем конечные ​ x ​ и ​ y ​ компоненты из исходных ​ x ​ и ​ y ​ компоненты, чтобы получить компоненты ​ ​ v _f ​ — ​ v _i ​ ​:

Затем мы вычитаем​ x ​ и ​ y ​ компоненты:

(v_f-v_i)_x=v_{xf}-v_{xi}=7. 07-10=-2.9{-1}\Big(\frac{2.36}{-0.977}\Big)=113\степень

Объяснение урока: Сложение и вычитание векторов в 2D

В этом объяснении мы научимся складывать и вычитать векторы в 2D.

Мы знаем, что векторы могут быть представлены отрезками определенной длины (величина) и направление. Мы будем использовать их, чтобы помочь визуализировать сложение векторов и вычитание.

В рамках этого объяснения будут рассматриваться только векторы в двух измерениях; однако описанная методология может быть распространена на переносчиков в трех или более размеры.

Напомним, что единичный вектор — это вектор с величиной, равной 1, и что единичные векторы в 𝑥- и 𝑦-направлениях обозначаются ⃑𝑖 и ⃑𝑗 соответственно.

Любой двумерный вектор можно записать в виде 𝑥⃑𝑖+𝑦⃑𝑗. Они могут альтернативно быть представлено в компонентной форме как (𝑥,𝑦) или 𝑥𝑦.

Определение: Сложение векторов

Сложение векторов — это операция сложения двух или более векторов для нахождения их сумма.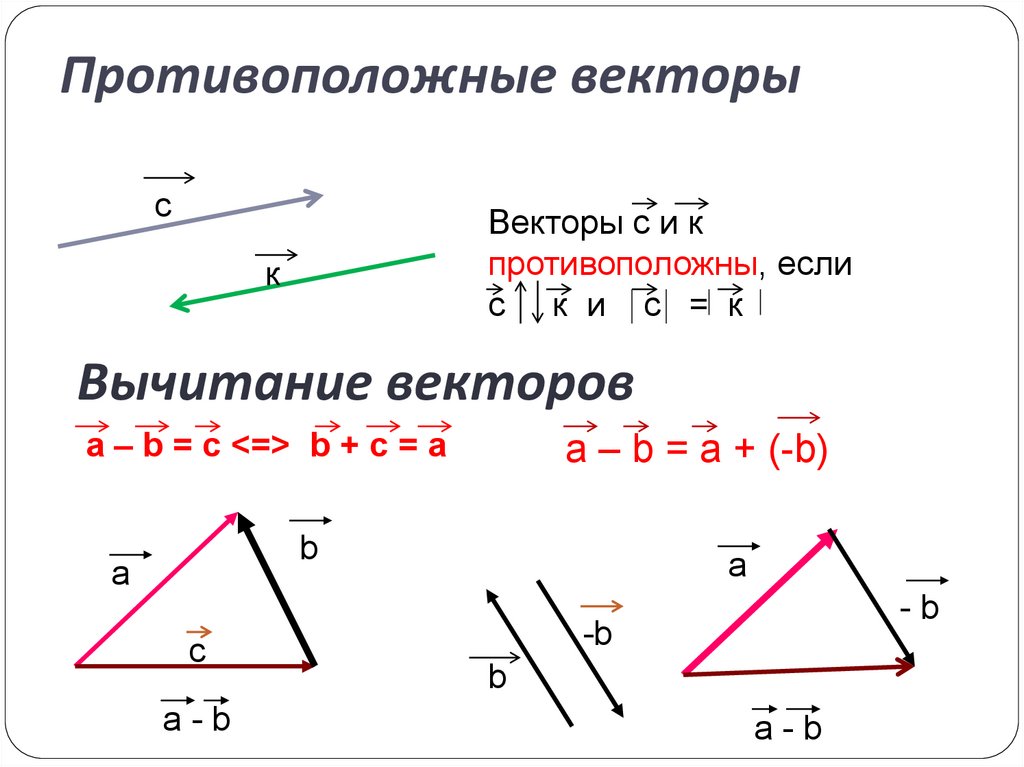

Имея два (или более) вектора в компонентной форме, мы можем найти их сумму по формуле добавление соответствующих компонентов векторов.

Например, если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).

Сложение векторов — это операция сложения двух или более векторов вместе в векторная сумма. Сумма двух и более векторов называется равнодействующей.

Сейчас мы рассмотрим пару примеров, где нам нужно сложить векторы в два размеры.

Пример 1. Нахождение суммы двух векторов

Если ⃑𝑎=(3,2) и ⃑𝑏=(4,−1), найти ⃑𝑎+⃑𝑏.

Ответ

Напомним, что в декартовых координатах сложение векторов можно выполнить с помощью добавление соответствующих компонентов векторов.

Если ⃑𝑎=(𝑥,𝑦) и ⃑𝑏=(𝑥,𝑦), тогда ⃑𝑎+⃑𝑏=(𝑥+𝑥,𝑦+𝑦).

В этом вопросе ⃑𝑎=(3,2) и ⃑𝑏=(4,−1).

Итак, ⃑𝑎+⃑𝑏=(3+4,2+(−1))=(7,1).

Таким образом, ⃑𝑎+⃑𝑏=(7,1).

Пример 2. Нахождение компонентов двух векторов и их суммы по диаграмме

На сетке единичных квадратов показаны векторы ⃑𝑢, ⃑𝑣, и ⃑𝑢+⃑𝑣.

1. Из каких компонентов состоит ⃑𝑢?
2. Из каких компонентов состоит ⃑𝑣?
3. Какие компоненты ⃑𝑢+⃑𝑣?

Ответ

Любой двумерный вектор можно записать через его 𝑥- и 𝑦-компоненты вида (𝑥,𝑦), где 𝑥 — количество единиц в положительное 𝑥-направление, а 𝑦 — количество единиц в положительном 𝑦-направление.

От начальной точки до конечной точки ⃑𝑢 идем на 2 единицы вправо и 1 единица вверх. Это соответствует 2 единицам в 𝑥-направлении и 1 единице в 𝑦-направление.

Итак, ⃑𝑢=(2,1).

От начального пункта до конечного пункта ⃑𝑣, проходим 3 единицы осталось и 4 единицы вниз. Это соответствует −3 единицам в 𝑥-направление и −4 единиц в 𝑦-направлении.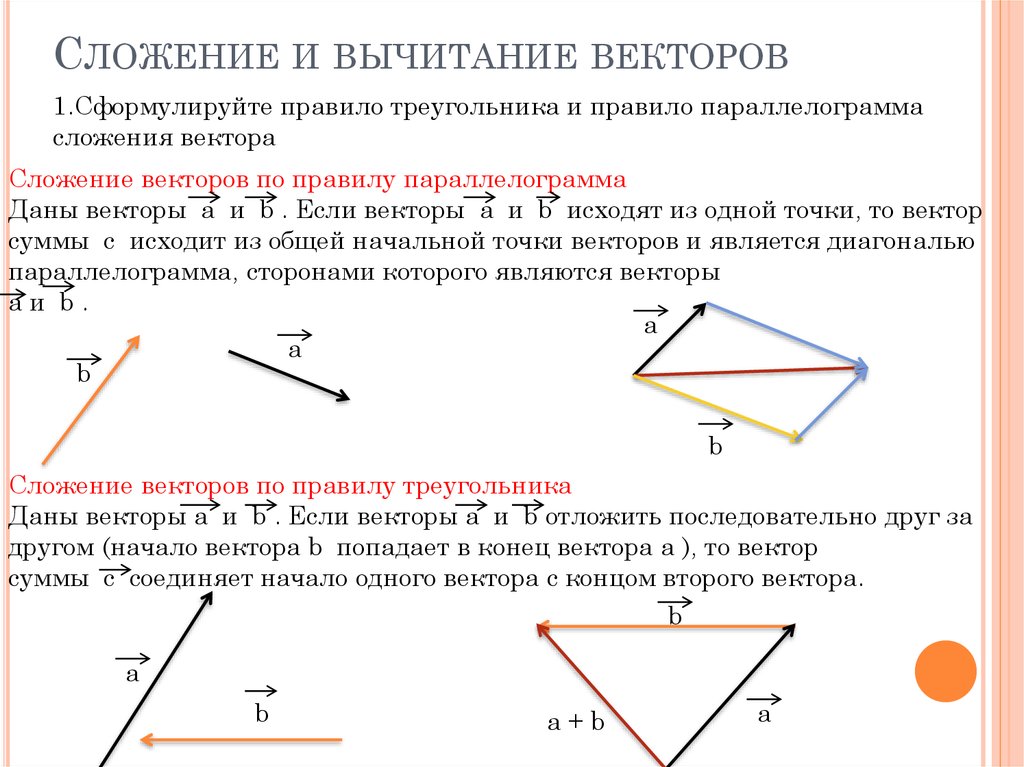

Итак, ⃑𝑣=(−3,−4).

Мы знаем, что сумма двух векторов называется равнодействующей и что в Декартовы координаты, сложение векторов можно выполнить, добавив соответствующие компоненты векторов.

Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).

С ⃑𝑢=(2,1)⃑𝑣=(−3,−4) и затем ⃑𝑢+⃑𝑣=(2+(−3),1+(−4))=(−1,−3).

Мы также могли бы прочитать эту информацию прямо из векторной диаграммы.

Из начальной точки ⃑𝑢 в конечную точку вектора ⃑𝑣, мы перемещаемся на 1 единицу влево и на 3 единицы вниз. Это соответствует -1 единице в 𝑥-направлении и −3 единицы в 𝑦-направление.

Итак, ⃑𝑢+⃑𝑣=(−1,−3).

Таким образом, ⃑𝑢=(2,1), ⃑𝑣=(−3,−4), и ⃑𝑢+⃑𝑣=(−1,−3).

Вычитание векторов — это процесс нахождения разности векторов; это операция, обратная сложению векторов.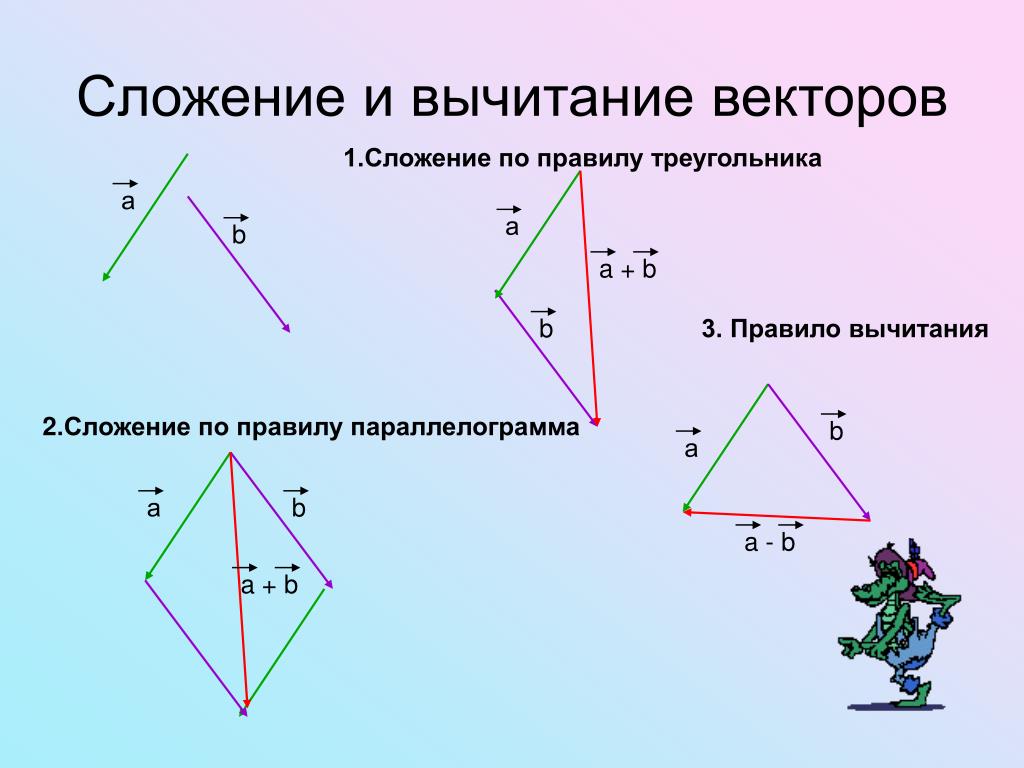

Это значит, что ⃑𝑢−⃑𝑣=⃑𝑢+−⃑𝑣. При вычитании ⃑𝑣 из ⃑𝑢, находим равнодействующую ⃑𝑢 и −⃑𝑣.

Определение: вычитание векторов

Вычитание векторов — это операция вычитания двух векторов для нахождения их разница.

Имея два вектора в компонентной форме, мы можем найти их разность по формуле вычитая соответствующие компоненты векторов.

Например, если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢−⃑𝑣=(𝑥−𝑥,𝑦−𝑦).

Стоит отметить, что эффект отрицания ⃑𝑣 является обратным в его направлении. Например, если бы у нас был вектор ⃑𝑣=(5,0), это будет вектор длины 5, параллельный оси 𝑥, указывающей слева направо. Если мы отрицаем ⃑𝑣, мы получаем −⃑𝑣=(−5,0). Величина вектора без изменений; он по-прежнему параллелен оси 𝑥, но его направление изменилось перевернутый; теперь он указывает справа налево.

Теперь мы рассмотрим еще несколько примеров, где мы будем складывать и вычитать векторы в двух измерениях.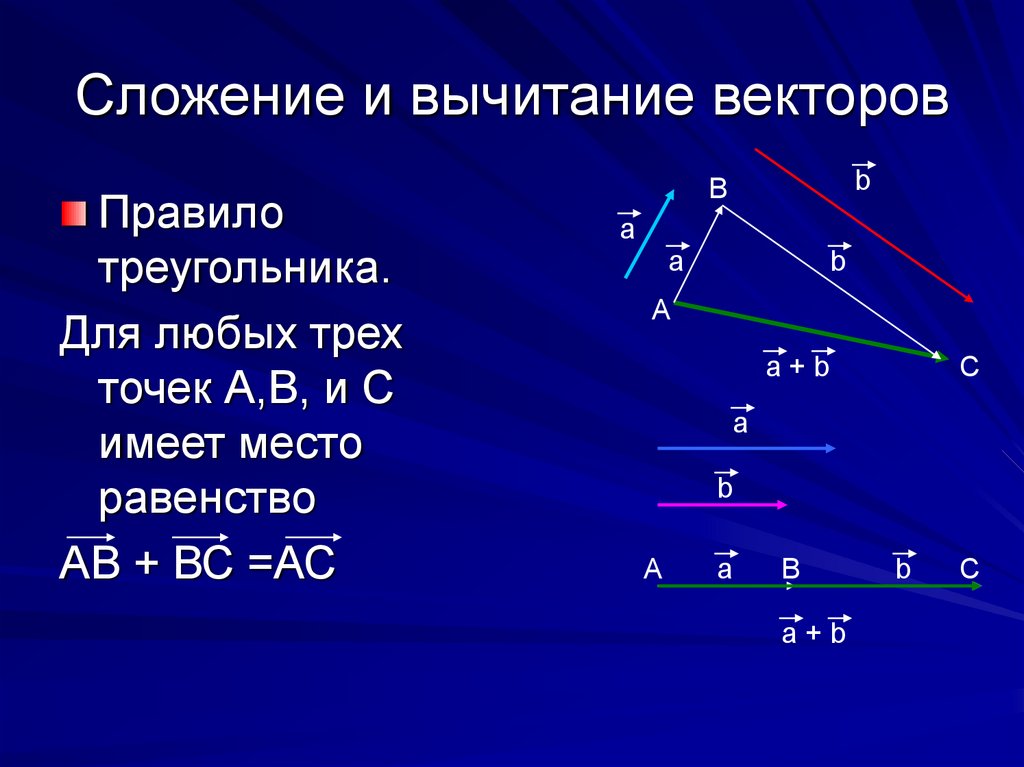

Пример 3. Вычитание векторов, выраженных в терминах единичных векторов

При заданных векторах 𝐴𝐵=3⃑𝑖−4⃑𝑗 и 𝐶𝐷=−5⃑𝑖−5⃑𝑗, рассчитать 𝐴𝐵−𝐶𝐷.

Ответ

Начнем с того, что в декартовых координатах вычитание векторов можно выполнить, вычитая соответствующие компоненты из векторы.

Если ⃑𝑢=𝑎⃑𝑖+𝑏⃑𝑗 и ⃑𝑣=𝑐⃑𝑖+𝑑⃑𝑗, тогда ⃑𝑢−⃑𝑣=(𝑎−𝑐)⃑𝑖+(𝑏−𝑑)⃑𝑗.

Итак,  𝐴𝐵 —  = 3⃑𝑖 — 4⃑𝑗 —  — 5⃑𝑖 — 5⃑𝑗 = (3 — ( — 5)) ⃑𝑖+( — 4 — ( — 5)) ⃑𝑗 = 8⃑𝑖+⃑𝑗.

Таким образом, 𝐴𝐵−𝐶𝐷=8⃑𝑖+⃑𝑗.

Пример 4. Сложение и вычитание векторов

Учитывая, что ⃑𝐴=(−2,2), ⃑𝐵=(5,2) и ⃑𝐶=(−3,−2), найти −⃑𝐴+⃑𝐵−⃑𝐶.

Ответ

Начнем с того, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.

Итак, −⃑𝐴+⃑𝐵−⃑𝐶=(−(−2)+5−(−3),−2+2−(−2))=(2+5+3,−2+2+2)=(10, 2).

Таким образом, −⃑𝐴+⃑𝐵−⃑𝐶=(10,2).

Пример 5. Поиск пропущенного вектора по заданному другому вектору и сумме двух векторов

Учитывая, что ⃑𝐴=(−4,5), и ⃑𝐴+⃑𝐵=(2,7), найти ⃑𝐵.

Ответ

Начнем с того, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.

Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦).

Поскольку ⃑𝐴=(−4,5) и ⃑𝐴+⃑𝐵=(2,7), тогда (−4,5)+⃑𝐵=(2,7)((−4,5))⃑𝐵=(2,7)−(−4,5)⃑𝐵=(2−(−4),7−5) ⃑𝐵=(6,2).вычитание из обеих сторон

Итак, ⃑𝐵=(6,2).

Пример 6. Нахождение суммы двух векторов по одному из них и разности между ними

Учитывая, что ⃑𝐴=(7,−1) и ⃑𝐴−⃑𝐵=(3,−2), найти ⃑𝐴+⃑𝐵.

Ответ

Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.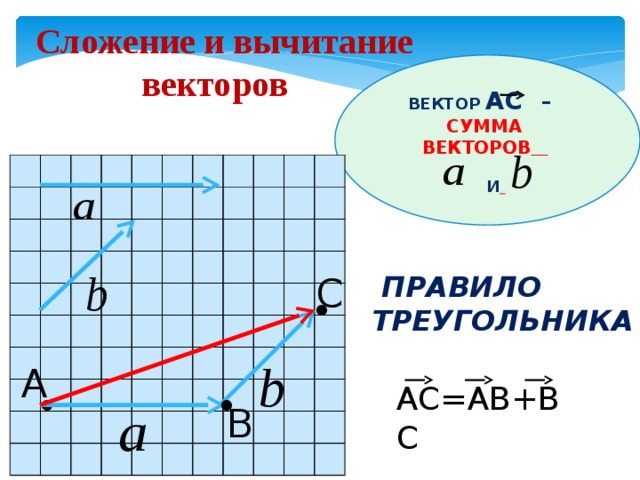

Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴−⃑𝐵=(𝑥−𝑥,𝑦−𝑦).

Так как ⃑𝐴=(7,−1) и ⃑𝐴−⃑𝐵=(3,−2), то (7,−1)−⃑𝐵=(3,−2)⃑𝐵(3,−2)⃑𝐵=(7,−1)−(3,−2)⃑𝐵=(7−3,−1−( −2))⃑𝐵=(4,1).сложение и вычитание из обеих сторон

Теперь мы вычисляем ⃑𝐴+⃑𝐵.

Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦).

Так как ⃑𝐴=(7,−1) и ⃑𝐵=(4,1), тогда ⃑𝐴+⃑𝐵=(7,−1)+(4,1)=(7+4,−1+1)=(11,0).

Итак, ⃑𝐴+⃑𝐵=(11,0).

Пример 7. Нахождение вектора по двум другим векторам и выражению между тремя векторами

Учитывая, что ⃑𝐴=(3,−2), ⃑𝐵=(−5,4), и ⃑𝐴−⃑𝐵+⃑𝐶=(6,−1), найти ⃑𝐶.

Ответ

Начнем с того, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.

Если ⃑𝐴=(𝑥,𝑦), ⃑𝐵=(𝑥,𝑦), и ⃑𝐶=(𝑥,𝑦), тогда ⃑𝐴−⃑𝐵+⃑𝐶=(𝑥−𝑥+𝑥,𝑦−𝑦+𝑦).