Сложные математические уравнения. Более сложные примеры уравнений
52. Более сложные примеры уравнений .
Пример 1
.
5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)
Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:
или, после сокращения,
5(x + 1) – 3(x – 1) = 15
5x + 5 – 3x + 3 = 15
2x = 7 и x = 3½
Рассмотрим еще уравнение:
5/(x-1) – 3/(x+1) = 4(x 2 – 1)
Решая, как выше, получим:
5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.
Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.
Для первого примера получим:
Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.
Для второго примера получим:
5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0
Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно.
Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.
Пример 2 .
Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:
(x + 3) (2x – 2) = (2x + 3) (x – 1)
2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.
Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 .
6x – 2x – 6 = 3x – 2x – 3
Перенесем неизвестные члены влево, известные вправо — получим:
3x = 3 или x = 1
Вспоминая данное уравнение
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.
Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:
2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,
что невозможно.
Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:
(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)
Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:
6x + 10 = 2x + 18
Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:
или 11 = 11
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:
(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.
Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы
4x 2 – 12x = –8
x 2 – 3x = –2
Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:
1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2
Если мы вспомним начальное уравнение
(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),
то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.
Пример 3 .
Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:
1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),
2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),
3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).
Общий знаменатель равен (x – 3)(x – 2)(x + 1).
Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:
на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:
3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.
Отсюда получим:
–x = –13 и x = 13.
Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.
Если бы мы взяли уравнение:
то, поступая совершенно так же, как выше, получили бы
3(x + 1) – 2(x – 3) = x – 2
3x + 3 – 2x + 6 = x – 2
3x – 2x – x = –3 – 6 – 2,
откуда получили бы
что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.
Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.
Математик Ян Стюарт (Ian Stewart) в своей новой книге «В поисках неизвестного: 17 уравнений, которые изменили мир» рассматривает несколько наиболее важных уравнений всех времен и приводит примеры их практического применения.
Согласно Теореме Пифагора в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Важность : Теорема Пифагора — важнейшее уравнение в геометрии, которое связывает ее с алгеброй и является основой тригонометрии. Без него было бы невозможно создать точную картографию и навигацию.
Современное использование : Триангуляция используется и по сей день, чтобы точно определить относительное расположение для GPS навигации.
Логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент.
Важность : Логарифмы стали настоящей революцией, позволив астрономам и инженерам делать расчеты более быстро и точно. С появлением компьютеров они не потеряли своего значения, поскольку все еще существенны для ученых.
С появлением компьютеров они не потеряли своего значения, поскольку все еще существенны для ученых.
Современное использование : Логарифмы важная составляющая для понимания радиоактивного распада.
Основная теорема анализа или формула Ньютона — Лейбница дает соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Важность : Теорема анализа фактически создала современный мир. Исчисление имеет важное значение в нашем понимание того, как измерять тела, кривые и площади. Она является основой многих природных законов и источником дифференциальных уравнений.
Современное использование : Любая математическая проблема, где требуется оптимальное решение. Существенное значение для медицины, экономики и информатики.
Классическая теория тяготения Ньютона описывает гравитационное взаимодействие.
Важность : Теория позволяет рассчитать силу гравитации между двумя объектами. Хотя позднее она была вытеснена теорией относительности Эйнштейна, теория все равно необходима для практического описания того, как объекты взаимодействуют друг с другом.
Современное использование : Позволяет найти наиболее энергоэффективные пути для вывода спутников и космических зондов. Также делает возможным спутниковое телевидение.
Комплексные числа
Комплексные числа — расширение поля вещественных чисел.
Важность : Многие современные технологии, в том числе цифровые фотокамеры, не могли быть изобретены без комплексных чисел. Кроме того, они позволяют проводить анализ, который нужен инженерам для решения практических задач в авиации.
Современное использование : Широко используется в электротехнике и сложных математических теориях.
Современное использование : Топология используется, чтобы понять поведение и функции ДНК.
Важность : Уравнение является основой современной статистики. Естественные и социальные науки не могли бы существовать в своей нынешней форме без него.
Современное использование : Используется в клинических испытаниях для определения эффективности лекарств по сравнению с отрицательными побочными эффектами.
Дифференциальное уравнение, описывающее поведение волн.
Важность : Волны исследуются с целью определения времени и места землетрясений, а также для прогнозирования поведения океана.
Современное использование : Нефтяные компании используют взрывчатку, а затем считывают данные от последующих звуковых волн для определения геологических формаций.
Важность : Уравнение позволяет разбивать, очищать и анализировать сложные шаблоны.
Современное использование : Используется при сжатии информации изображений в формате JPEG, а так же для обнаружения структуры молекул.
Уравнения Навье-Стокса
Уравнения Навье-Стокса
В левой части уравнения — ускорение небольшого количества жидкости, в правой — силы, которые воздействуют на него.
Важность : Как только компьютеры стали достаточно мощными, чтобы решить это уравнение, они открыли сложную и очень полезную области физики. Она особенно полезна для создания более качественной аэродинамики у транспортных средств.
Современное использование : Среди прочего, уравнение помогло в усовершенствовании современных пассажирских самолетов.
Важность : Помогли в понимании электромагнитных волн, что способствовало созданию многих технологий, которые мы используем сегодня.
Современное использование : Радар, телевидение и современные средства связи.
Вся энергия и тепло со временем исчезнет.
Важность : Имеет существенное значение для нашего понимания энергии и Вселенной через понятие энтропии. Открытие закона помогло улучшить паровой двигатель.
Современное использование : Помог доказать, что материя состоит из атомов, физики до сих пор пользуются этим знанием.
Энергия равна массе, умноженной на квадрат скорости света.
Важность : Наверное, самое известное уравнение в истории. Оно полностью изменило нашу точку зрения на материю и реальность.
Современное использование : Помогло создать ядерное оружие. Используется в GPS навигации.
Уравнение Шрёдингера
Описывает материю как волну, а не как частицу.
Важность : Перевернула представления физиков — частицы могут существовать в диапазоне возможных состояний.
Современное использование : Существенный вклад в использование полупроводников и транзисторов, и, таким образом, в большинство современных компьютерных технологий.
Оценивает количество данных в куске кода путем расчета вероятности его символов.
Важность : Это уравнение, которое открыло дверь в Информационную Эпоху.
Современное использование : В значительной степени все, что связано с обнаружением ошибок в кодировании (программировании).
Оценка изменений в популяции живых существ из поколения в поколение с ограниченными ресурсами.
Важность : Помогла в развитии , которая полностью изменила наше понимание того, как работают природные системы.
Современное использование : Используется для моделирования землетрясений и прогноза погоды.
Модель Блэка-Скоулза
Одна из моделей ценообразования опционов.
Важность : Помогла создать несколько триллионов долларов. Согласно некоторым экспертам, неправильное использование формулы (и ее производных) способствовало финансовому кризису. В частности, уравнение имеет несколько предположений, которые не справедливы на реальных финансовых рынках.
Современное использование : Даже после кризиса используются для определения цен.
Вместо заключения
В мире существует множество других важных уравнений и формул, которые изменили судьбу человечества в целом и нашу личную жизнь в частности. Среди них, модель Ходжкина-Хаксли, Фильтр Калмана и, конечно, уравнение поисковой системы Google. 2. Другие не столь широко распространены, но красота уравнения не зависит от его популярности.
2. Другие не столь широко распространены, но красота уравнения не зависит от его популярности.
Общая теория относительности
Уравнение, описанное выше, было сформулировано Альбертом Эйнштейном в 1915 году как часть инновационной общей теории относительности. Теория на самом деле произвела революцию в мире науки. Это удивительно, как одним уравнением можно описать абсолютно все, что есть вокруг, в том числе пространство и время. Весь истинный гений Эйнштейна воплощен в нем. Это очень элегантное уравнение, которое кратко описывает, как все вокруг вас связано — например, как присутствие Солнца в галактике искривляет пространство и время так, чтобы Земля вращалась вокруг него.
Стандартная модель
Стандартная модель — это еще одна из важнейших теорий физики, в ней описываются все элементарные частицы, из которых состоит вселенная. Существуют различные уравнения, способные описать эту теорию, однако чаще всего пользуются уравнением Лагранжа, французского математика и астронома 18 века. Он успешно описал абсолютно все частицы и силы, которые на них воздействуют, за исключением гравитации. Это также включает недавно открытый бозон Хиггса. Оно в полной мере сочетается с квантовой механикой и общей теорией относительности.
Он успешно описал абсолютно все частицы и силы, которые на них воздействуют, за исключением гравитации. Это также включает недавно открытый бозон Хиггса. Оно в полной мере сочетается с квантовой механикой и общей теорией относительности.
Математический анализ
В то время как первые два уравнения описывают конкретные аспекты вселенной, данное уравнение может быть использовано во всех возможных ситуациях. Фундаментальная теорема математического анализа формирует основу математического метода, известного как исчисление, и связывает две свои основные идеи — концепцию интеграла и понятие производной. Зародился математический анализ еще в древности, однако все теории были собраны воедино Исааком Ньютоном в 17 веке — он использовал их для вычисления и описания движения планет вокруг Солнца.
Теорема Пифагора
Старым добрым известным всем уравнением выражается знаменитая теорема Пифагора, которую учат все школьники на уроках геометрии. Это формула описывает, что в любом прямоугольном треугольнике квадрат длины гипотенузы, самой длинной из всех сторон (c), равен сумме квадратов двух других сторон, катетов (a и b). 2. Эта теорема удивляет многих начинающих математиков и физиков, когда они только учатся в школе и еще не знают, что им готовит новый мир.
2. Эта теорема удивляет многих начинающих математиков и физиков, когда они только учатся в школе и еще не знают, что им готовит новый мир.
1 = 0.999999999….
Это простое уравнение указывает на то, что число 0.999 с бесконечным количеством девяток после запятой, на самом деле, равно единице. Это уравнение замечательно тем, что оно крайне простое, невероятно наглядное, но все же умудряется удивить и поразить многих. Некоторые люди не могут поверить в то, что это на самом деле так. Более того, красиво и само по себе уравнение — левая его часть представляет собой простейшую основу математики, а правая скрывает в себе тайны и загадки бесконечности.
Специальная теория относительности
Альберт Эйнштейн снова попадает в список, на этот раз со своей специальной теорией относительности, которая описывает, как время и пространство являются не абсолютными понятиями, а относительными — к скорости смотрящего. Это уравнение показывает, как время «расширяется», тем сильнее замедляясь, чем быстрее человек движется. На самом деле, уравнение не является таким уж сложным, простые производные, линейная алгебра. Однако то, что оно собой воплощает, представляет абсолютно новый способ смотреть на мир.
На самом деле, уравнение не является таким уж сложным, простые производные, линейная алгебра. Однако то, что оно собой воплощает, представляет абсолютно новый способ смотреть на мир.
Уравнение Эйлера
Эта простая формула включает в себя основные знания о природе сфер. Она говорит о том, что если вы разрезаете сферу и получаете грани, ребра и вершины, то если F принять за число граней, E — за число ребер, а V — за число вершин, то вы всегда получите одно и то же: V — E + F = 2. Именно так и выглядит данное уравнение. Поражает то, что какую бы сферическую форму вы ни взяли — будь-то тетраэдр, пирамида или любая другая комбинация граней, ребер и вершин, у вас всегда получится одинаковый результат. Эта комбинаторика рассказывает людям нечто фундаментальное о сферических формах.
Уравнение Эйлера-Лагранжа и теорема Нетер
Эти понятия являются довольно абстрактными, но очень сильными. Самое интересное заключается в том, что данный новый способ мышления о физике смог пережить несколько революций в данной науке, таких как открытие квантовой механики, теории относительности и так далее. Здесь L означает уравнение Лагранжа, которое является мерой энергии в физической системе. А решение этого уравнения расскажет вам о том, как конкретная система будет развиваться с течением времени. Вариантом уравнения Лагранжа является теорема Нетер, которая является фундаментальной для физики и роли симметрии. Суть теоремы заключается в том, что если ваша система симметрична, то в ней действует соответствующий закон сохранения. Собственно говоря, главная идея этой теоремы заключается в том, что законы физики действуют повсеместно.
Здесь L означает уравнение Лагранжа, которое является мерой энергии в физической системе. А решение этого уравнения расскажет вам о том, как конкретная система будет развиваться с течением времени. Вариантом уравнения Лагранжа является теорема Нетер, которая является фундаментальной для физики и роли симметрии. Суть теоремы заключается в том, что если ваша система симметрична, то в ней действует соответствующий закон сохранения. Собственно говоря, главная идея этой теоремы заключается в том, что законы физики действуют повсеместно.
Уравнение ренормгруппы
Это уравнение также называется по имени его создателей, уравнением Каллана-Симанчика. Оно является жизненно важным базовым уравнением, написанным в 1970 году. Оно служит для того, чтобы продемонстрировать, как наивные ожидания рушатся в квантовом мире. Уравнение также имеет множество приложений, позволяющих оценить массу и размер протона и нейтрона, которые составляют ядро атома.
Уравнение минимальной поверхности
Данное уравнение невероятным образом вычисляет и кодирует те самые красивые мыльные пленки, которые образуются на проволоке, когда ее окунают в мыльную воду. Данное уравнение, однако, сильно отличается от привычных линейных уравнений из той же области, например, уравнения тепла, образования волн и так далее. Это уравнение — нелинейно, оно включает в себя воздействие сторонних сил и производных продуктов.
Данное уравнение, однако, сильно отличается от привычных линейных уравнений из той же области, например, уравнения тепла, образования волн и так далее. Это уравнение — нелинейно, оно включает в себя воздействие сторонних сил и производных продуктов.
Прямая Эйлера
Возьмите любой треугольник, нарисуйте наименьший круг, который может включить в себя треугольник, и отыщите его центр. Найдите центр массы треугольника — ту точку, которая позволила бы треугольнику балансировать, например, на острие карандаша, если бы его можно было вырезать из бумаги. Нарисуйте три высоты этого треугольника (линии, которые были бы перпендикулярны тем сторонам треугольника, от которых они рисуются) и найдите точку их пересечения. Суть теоремы заключается в том, что все три точки будут находиться на одной прямой, именно это и есть прямая Эйлера. Теорема заключает в себе всю красоту и мощь математики, открывая удивительные закономерности в самых простых вещах.
Часто, беседуя со старшеклассниками об исследовательских работах по математике, слышу следующее: «Что можно нового открыть в математике?» А действительно: может быть все великие открытия сделаны, а теоремы доказаны?
8 августа 1900 года на международном математическом конгрессе в Париже математик Дэвид Гилберт (David Hilbert) изложил список проблем, которые, как он полагал, предстояло решить в ХХ веке.В списке было 23 пункта. Двадцать один из них на данный момент решены. Последней решенной проблемой из списка Гилберта была знаменитая теорема Ферма, с которой ученые не могли справиться в течение 358 лет. В 1994 году свое решение предложил британец Эндрю Уайлз. Оно и оказалось верным.
По примеру Гилберта в конце прошлого века многие математики пытались сформулировать подобные стратегические задачи на ХХI век. Один из таких списков приобрел широкую известность благодаря бостонскому миллиардеру Лэндону Клэю (Landon T. Clay). В 1998 году на его средства в Кембридже (Массачусетс, США) был основан Математический институт Клэя (Clay Mathematics Institute) и установлены премии за решение ряда важнейших проблем современной математики. 24 мая 2000 года эксперты института выбрали семь проблем — по числу миллионов долларов, выделенных на премии. Список получил название Millennium Prize Problems:
1. Проблема Кука (сформулирована в 1971 году)
Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый.
Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей. Это говорит о том, что решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения.
Стивен Кук сформулировал проблему: может ли проверка правильности решения задачи быть более длительной, чем само получение решения, независимо от алгоритма проверки. Эта проблема также является одной из нерешенных задач из области логики и информатики. Ее решение могло бы революционным образом изменить основы криптографии, используемой при передаче и хранении данных.
2. Гипотеза Римана (сформулирована в 1859 году)
Некоторые целые числа не могут быть выражены как произведение двух меньших целых чисел, например 2, 3, 5, 7 и так далее. Такие числа называются простыми и играют важную роль в чистой математике и ее приложениях. Распределение простых чисел среди ряда всех натуральных чисел не подчиняется никакой закономерности.
Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.
3. Гипотеза Берча и Свиннертон-Дайера (сформулирована в 1960 году)
Связана с описанием множества решений некоторых алгебраических уравнений от нескольких переменных с целыми коэффициентами. Примером подобного уравнения является выражение x2 + y2 = z2. Эвклид дал полное описание решений этого уравнения, но для более сложных уравнений поиск решений становится чрезвычайно трудным.
4. Гипотеза Ходжа (сформулирована в 1941 году)
В ХХ веке математики открыли мощный метод исследования формы сложных объектов. Основная идея заключается в том, чтобы использовать вместо самого объекта простые «кирпичики», которые склеиваются между собой и образуют его подобие. Гипотеза Ходжа связана с некоторыми предположениями относительно свойств таких «кирпичиков» и объектов.
5. Уравнения Навье — Стокса (сформулированы в 1822 году)
Если плыть в лодке по озеру, то возникнут волны, а если лететь в самолете, в воздухе возникнут турбулентные потоки. Предполагается, что эти и другие явления описываются уравнениями, известными как уравнения Навье — Стокса. Решения этих уравнений неизвестны, и при этом даже неизвестно, как их решать. Необходимо показать, что решение существует и является достаточно гладкой функцией. Решение этой проблемы позволит существенно изменить способы проведения гидро- и аэродинамических расчетов.
6. Проблема Пуанкаре (сформулирована в 1904 году)
Если натянуть резиновую ленту на яблоко, то можно, медленно перемещая ленту без отрыва от поверхности, сжать ее до точки. С другой стороны, если ту же самую резиновую ленту соответствующим образом натянуть вокруг бублика, то никаким способом невозможно сжать ленту в точку, не разрывая ленту или не ломая бублик. Говорят, что поверхность яблока односвязна, а поверхность бублика — нет.
Доказать, что односвязна только сфера, оказалось настолько трудно, что математики ищут правильный ответ до сих пор.
7. Уравнения Янга — Миллса (сформулированы в 1954 году)
Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения. Тем самым они нашли путь к объединению теорий электромагнитного, слабого и сильного взаимодействий. Из уравнений Янга — Миллса следовало существование частиц, которые действительно наблюдались в лабораториях во всем мире, поэтому теория Янга — Миллса принята большинством физиков несмотря на то, что в рамках этой теории до сих пор не удается предсказывать массы элементарных частиц.
Думаю, что этот материал, опубликованный в блоге
Вставка и расчет простых математических уравнений в OneNote
OneNote для Microsoft 365 OneNote 2021 OneNote 2016 OneNote 2013 OneNote 2010 OneNote 2007 Еще. ..Меньше
..Меньше
Для простых математических подсчетов вам не потребуется калькулятор. Во время собрания, конференции или занятия можно напишите математические уравнения, а OneNote вы сможете мгновенно вычислить результаты.
-
Введите уравнение, которое вы хотите вычислить. Например, введите 95+83+416 , чтобы вычислить сумму чисел 95, 83 и 416, или корень (15), чтобы вычислить квадратный корень из 15.
-
После формулы без пробела введите знак равенства (=), а затем нажмите клавишу пробела. Ответ появится после знака равенства.
Советы:
-
Формула не должна содержать пробелов.
 Вводите числа, операторы и функции единой непрерывной строкой.
Вводите числа, операторы и функции единой непрерывной строкой. -
В кодах функций регистр символов не учитывается. Например, КОРЕНЬ(3)=, корень(3)= и Корень(3)= дают одинаковый ответ.
-
Чтобы создать новую строку после результата, нажмите клавишу ВВОД (вместо клавиши ПРОБЕЛ) после знака равенства.
-
Если вы хотите, чтобы в заметках был только ответ, вычислите его, вы можете удалить формулу, которая предшествует ему. Ответ останется в заметках.
Примеры простых вычислений
Ниже приведено несколько примеров математических выражений, которые вычисляет OneNote.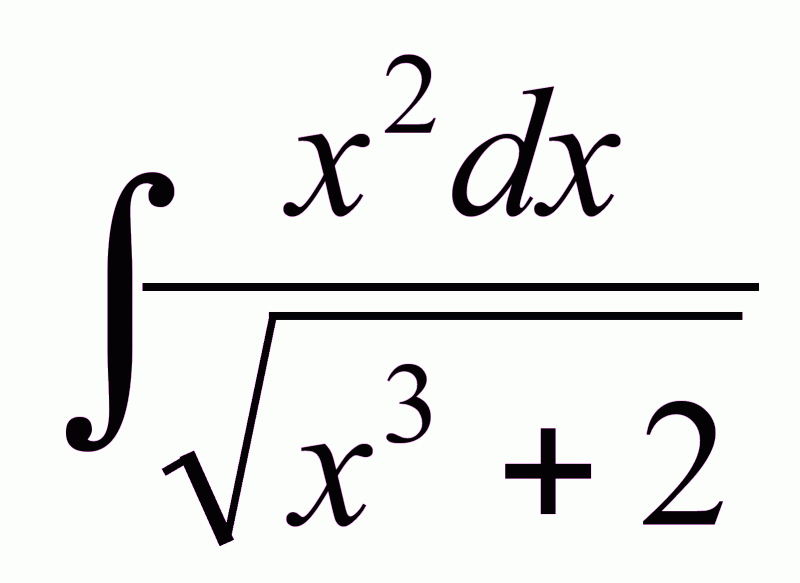
-
Среднее количество продаж продукта. Например, если общий годовой доход составляет 215 000 долларов, введите $215,000/12= и нажмите клавишу ПРОБЕЛ.
-
Общая сумма ежемесячных платежей. Например, введите 48*$129.99= и нажмите клавишу ПРОБЕЛ, чтобы посчитать стоимость 48 ежемесячных платежей, каждый из которых составляет 129,99 долларов.
-
Синус угла 30 градусов. Например, введите sin(30)= и нажмите клавишу ПРОБЕЛ.
org/ListItem»>
Более сложные математические формулы. Например, введите (6+7) / (4*sqrt(3))= и нажмите клавишу ПРОБЕЛ, чтобы получить значение вычисления (6+7), разделенное на (4, умноженное на квадратный корень из 3).
Арифметические операторы
В формулах вы можете использовать следующие операторы.
|
Оператор |
Значение |
Пример |
|
+ (знак плюса) |
Сложение |
3+3 |
|
— (знак «минус») |
Вычитание |
3-1 |
|
* (звездочка) |
Умножение |
3*3 |
|
Х (верхнего или нижнего регистра) |
Умножение |
3х3 |
|
/ (косая черта) |
Деление |
3/3 |
|
% (знак процента) |
Процент |
20 % |
|
^ (крышка) |
Возведение в степень |
3^2 |
|
! (восклицательный индекс) |
Вычисление факториала |
5! |
Математические и тригонометрические функции
Вы можете использовать в формулах математические и тригонометрические функции, приведенные в таблице.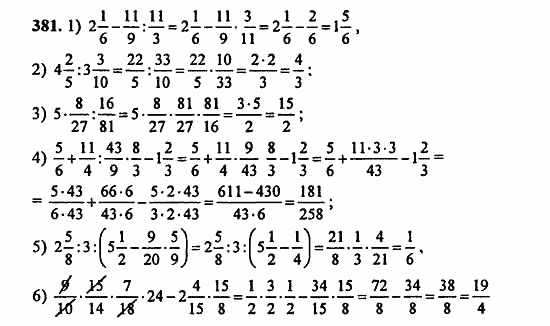
Примечание: Чтобы вычислить функцию, введите ее код (например, SQRT для квадратного корня), затем число, угол или переменные в круглых скобках, как показано в столбце «Синтаксис».
|
Функция |
Описание |
Синтаксис |
|
ABS |
Возвращает абсолютную величину числа |
ABS(число) |
|
ACOS |
Возвращает арккосинус числа |
ACOS(число) |
|
ASIN |
Возвращает арксинус числа |
ASIN(число) |
|
ATAN |
Возвращает арктангенс числа |
ATAN(число) |
|
COS |
Возвращает косинус числа |
COS(число) |
|
ГРАД |
Преобразовывает угол (в радианах) в градусы |
ГРАД(угол) |
|
LN |
Возвращает натуральный логарифм числа |
LN(число) |
|
LOG |
Возвращает натуральный логарифм числа |
LOG(число) |
|
LOG2 |
Возвращает логарифм с основанием 2 |
LOG2(число) |
|
LOG10 |
Возвращает десятичный логарифм числа |
LOG10(число) |
|
ОСТАТ |
Возвращает остаток от деления |
(число)ОСТАТ(число) |
|
ПИ |
Возвращает значение π как константу |
ПИ |
|
ФИ |
Возвращает значение Φ (золотое отношение) |
Фи |
|
ПЛТ |
Вычисляет выплаты по ссуде на основе постоянной процентной ставки, постоянного количества платежей и текущего значения общей суммы |
ПЛТ(ставка,кпер,пс) |
|
РАД |
Преобразовывает угол (в градусах) в радианы |
РАД(угол) |
|
SIN |
Возвращает синус заданного угла |
SIN(угол) |
|
КОРЕНЬ |
Возвращает положительное значение квадратного корня |
SQRT(число) |
|
TAN |
Возвращает тангенс числа |
TAN(число) |
10 увлекательных задач от советского математика
12 сентября 2021Отдых
Попробуйте решить головоломки от популяризатора математики Бориса Кордемского, не пользуясь подсказками.
Поделиться
01. Переправа через реку
Небольшой воинский отряд подошёл к реке, через которую необходимо было переправиться. Мост сломан, а река глубока. Как быть? Вдруг офицер замечает у берега двух мальчиков в лодке. Но лодка так мала, что на ней может переправиться только один солдат или только двое мальчиков — не больше! Однако все солдаты переправились через реку именно на этой лодке. Каким образом?
Показать ответ
Скрыть ответ
2. Сколько деталей?
В токарном цехе завода вытачиваются детали из свинцовых заготовок. Из одной заготовки — деталь. Стружки, получившиеся при выделке шести деталей, можно переплавить и приготовить ещё одну заготовку. Сколько деталей можно сделать таким образом из тридцати шести свинцовых заготовок?
Показать ответ
Скрыть ответ
3. Во время прилива
Недалеко от берега стоит корабль со спущенной на воду верёвочной лестницей вдоль борта. У лестницы десять ступенек; расстояние между ступеньками 30 см. Самая нижняя ступенька касается поверхности воды.
Самая нижняя ступенька касается поверхности воды.
Океан сегодня очень спокоен, но начинается прилив, который поднимает воду за каждый час на 15 см. Через какое время покроется водой третья ступенька верёвочной лесенки?
Показать ответ
Скрыть ответ
4. Девяносто девять
Сколько нужно поставить знаков «плюс» (+) между цифрами числа 987 654 321, чтобы в сумме получилось 99?
Показать ответ
Скрыть ответ
5. Для Цимлянского гидроузла
В выполнении срочного заказа по изготовлению измерительных приборов для Цимлянского гидроузла приняла участие бригада в составе опытного бригадира и девяти молодых рабочих.
В течение дня каждый из юных рабочих смонтировал по 15 приборов, а бригадир — на 9 приборов больше, чем в среднем каждый из десяти членов бригады. Сколько всего измерительных приборов было смонтировано бригадой за один рабочий день?
Показать ответ
Скрыть ответ
6. Попробуйте отвесить
В пакете находится 9 кг крупы. Попробуйте при помощи чашечных весов с гирями 50 и 200 г распределить всю крупу по двум пакетам: в один — 2 кг, в другой — 7 кг. При этом разрешается произвести только 3 взвешивания.
Попробуйте при помощи чашечных весов с гирями 50 и 200 г распределить всю крупу по двум пакетам: в один — 2 кг, в другой — 7 кг. При этом разрешается произвести только 3 взвешивания.
Показать ответ
Скрыть ответ
7. Смышлёный малыш
Три брата получили 24 яблока, причём каждому досталось столько яблок, сколько ему было лет три года назад. Самый младший, мальчик очень смышлёный, предложил братьям такой обмен яблоками:
— Я, — сказал он, — оставлю себе только половину имеющихся у меня яблок, а остальные разделю между вами поровну. После этого пусть средний брат тоже оставит себе половину, а остальные яблоки даст мне и старшему брату поровну, а затем и старший брат пусть оставит себе половину всех имеющихся у него яблок, а остальные разделит между мной и средним братом поровну.
Братья, не подозревая коварства в таком предложении, согласились удовлетворить желание младшего. В результате… у всех оказалось яблок поровну. Сколько же лет было малышу и каждому из остальных братьев?
Показать ответ
Скрыть ответ
8.
 Раздробить на части
Раздробить на частиРаздробите 45 на четыре части так, что если к первой части прибавить 2, от второй отнять 2, третью умножить на 2, а четвёртую разделить на 2, то все результаты будут равными. Сумеете сделать?
Показать ответ
Скрыть ответ
9. Посадка деревьев
Пятиклассникам и шестиклассникам было поручено посадить деревья по обе стороны улицы по равному количеству на каждой стороне.
Чтобы не ударить лицом в грязь перед шестиклассниками, пятиклассники вышли на работу пораньше и успели посадить 5 деревьев, пока пришли старшие ребята, но оказалось, что они сажали деревья не на своей стороне.
Пришлось пятиклассникам идти на свою сторону и вновь начинать работу. Шестиклассники, конечно, справились с задачей раньше. Тогда учитель предложил:
— Пойдём, ребята, поможем пятиклассникам!
Все согласились. Перешли на другую сторону улицы, посадили 5 деревьев, отдали, значит, долг, да ещё успели посадить 5 деревьев, и вся работа была закончена.
— Хоть вы пришли раньше нас, а всё-таки мы вас обогнали, — посмеялся один шестиклассник, обращаясь к младшим ребятам.
— Подумаешь, обогнали! На 5 деревьев только, — возразил кто-то.
— Нет, не на 5, а на 10, — зашумели шестиклассники.
Спор разгорался. Одни настаивают на том, что на 5, другие пытаются как-то доказать, что на 10. Кто же прав?
Показать ответ
Скрыть ответ
10. Четыре теплохода
В порту пришвартовались 4 теплохода. В полдень 2 января они одновременно покинули порт. Известно, что первый теплоход возвращается в этот порт через каждые 4 недели, второй — через каждые 8 недель, третий — через 12 недель, а четвёртый — через 16 недель.
Когда в первый раз теплоходы снова сойдутся все вместе в этом порту?
Показать ответ
Скрыть ответ
Задачи для этой подборки взяты из сборника «Математическая смекалка» Бориса Кордемского, который выходил в издательстве «Альпина Паблишер».
Читайте также 🔥
- 15 занимательных задач для тренировки ума и сообразительности
- 11 хитрых советских головоломок для проверки логики и сообразительности
- 5 задач, которые предлагают решить на собеседованиях в Google и других компаниях
5 проблем с изучением математики из-за слабо развитых исполнительных функций
Исполнительные функции играют большую роль в успешном решении математических задач. Они помогают детям применять на практике известную им информацию и развивать новые навыки. Поэтому, когда у ребенка проблемы с исполнительными функциями, им тяжело дается математика, даже если они ее понимают.
Они помогают детям применять на практике известную им информацию и развивать новые навыки. Поэтому, когда у ребенка проблемы с исполнительными функциями, им тяжело дается математика, даже если они ее понимают.
Ниже перечислены проблемы, с которыми они обычно сталкиваются.
1. Делают домашнюю работу быстро и неправильно
Некоторые дети с проблемами с исполнительными функциями могут быть импульсивными или нетерпеливыми. Они делают домашнее задание быстро и кое-как. Когда дело касается математики, детям нужно хорошо понимать задание, но дети с проблемами с исполнительными функциями, скорее всего, не будут вчитываться в задачу и думать о том, что им нужно делать, они сразу приступают к решению.
Например, ребенок может предположить, что задача решается сложением, потому что так было вчера. Спеша начать, он не замечает, что в сегодняшней задаче во всех примерах стоит знак минус, а не плюс. Таким образом, он все решает неправильно.
2. Испытывают трудности с применением новых правил на практике
Для того, чтобы научиться новому, необходимо находить новые решения новых задач. Для этого необходимо обладать гибким умом, а также останавливаться и думать, прежде чем действовать. Но дети с проблемами с исполнительными функциями часто застревают на том, что уже знают. В результате, им трудно отступить назад, чтобы придумать другое решение проблемы.
Для этого необходимо обладать гибким умом, а также останавливаться и думать, прежде чем действовать. Но дети с проблемами с исполнительными функциями часто застревают на том, что уже знают. В результате, им трудно отступить назад, чтобы придумать другое решение проблемы.
Например, когда ребенок изучает дроби, он будет настаивать, что ¼ больше, чем ½, потому что он знает, что 4 больше, чем 2. Однако в этом случае, чем знаменатель больше, тем дробь меньше. Чтобы узнать, какая дробь больше, ему нужно понять эту систему, выучить новое правило.
3. Отвечают, не задумываясь
Некоторые дети с проблемами с исполнительными функциями решают задачи, основываясь на опыте. Вместо того, чтобы оценивать каждую ситуацию осознанно, они дают ответ автоматически. Когда дело доходит до математики, они могут игнорировать ключевую информацию в задаче и из-за этого испытывают трудности с составлением уравнений.
Предположим, ребенок решает задачи на сложение. 3 + 3 будет 6, так он и отвечает. Потом он видит 3 – 3 и тоже пишет 6 в ответе. Дело не в том, что он не знает, как вычитать, но он видит 3 и 3 и отвечает первое, что приходит ему в голову.
Потом он видит 3 – 3 и тоже пишет 6 в ответе. Дело не в том, что он не знает, как вычитать, но он видит 3 и 3 и отвечает первое, что приходит ему в голову.
4. Теряются посередине комплексных математических задач
При решении сложных математических задач важную роль играет рабочая память. Известная информация, освоенная раньше (например — формула, ответ из прошлой задачи, пример упражнения из учебника) может помочь в решении новой проблемы, но дети с плохой рабочей памятью легко теряются в выстраивании нужных действий.
Вот пример. Деля в столбик, ребенок забывает, что должен спустить остаток после вычитания. Он не может вспомнить, что ему делать дальше и сдается или приходит к неверному ответу.
Также, ученики часто должны показывать процесс своего решения задач. Для этого они используют черновик, на котором показывают пошагово, как они пришли к такому решению. Но дети с проблемами с исполнительными функциями неорганизованны. Они расписывают информацию по листку вразброс, что путает не только учителя, но и их самих.
5. Не осознают свои ошибки
Детям необходимо осознавать свое развитие и свои достижения. Дети с проблемами с исполнительными функциями не могут проанализировать свою работу. Им просто не может прийти в голову, что ответ не имеет смысла и им нужно найти свою ошибку или обратиться за помощью.
Допустим, такой ребенок заканчивает свой тест по математике раньше времени. Несмотря на то, что у него есть дополнительное время, он не проверяет работу на наличие ошибок – он не видит в этом смысла, так как уверен в том, что сделал все правильно.
Как Вы можете помочь?
Если проблемы с исполнительными функциями стоят на пути изучения математики у Вашего ребенка, ему можно помочь преодолеть их с помощью различных методов.
Начните с того, что приучите его вчитываться в задачу, прежде чем приступать к ее решению. Пусть он подчеркивает вопросы и выделяет маркером важные пункты (включая знаки «плюс» и «минус»). Он должен оценить, знает ли он, как решить проблему и нужна ли ему помощь. Пусть задаст себе вопросы, вроде «чем похожа и чем отличается эта задача он предыдущей?».
Пусть задаст себе вопросы, вроде «чем похожа и чем отличается эта задача он предыдущей?».
Помогите ребенку создать свой собственный список того, на что ему нужно обратить внимание прежде, чем сдать работу на проверку. Научите его самостоятельно проверять свою работу и выявлять ошибки.
Одним из наиболее эффективных инструментов для развития исполнительных функций является онлайн методика Fast ForWord. Эта методика воздействует на самый корень проблем, связанных с нарушением развития исполнительных и когнитивных функций и благодаря этому быстро и навсегда устраняет их.
Помогите Вашему ребенку со сложной домашней работой по математике:
Вот то, что нужно помнить, помогая ребёнку с трудной домашней работой по математике:
Для начала, непонимание чего-либо сильно действует на нервы. Поддержите ребёнка и пресекайте весь негатив, который возникает в процессе работы.
Попросите ребёнка показать примеры задачи.
 Например, похожую задачу, которую они решали в классе или пример из учебника, к которому прилагается правильный ответ.
Например, похожую задачу, которую они решали в классе или пример из учебника, к которому прилагается правильный ответ.Если Ваш ребёнок не нашёл примера задачи, попытайтесь найти помощь в интернете. В учебнике Вашего ребёнка есть заголовки или какие-то ключевые слова, по которым можно найти статьи или примеры задач в интернете. Попробуйте несколько сайтов, в них наверняка подробно написано, как решать подобные задачи.
После того, как Вы найдёте пример задачи, спросите у ребенка, как ее решал учитель. Имея перед глазами решённый пример, ребёнок может вспомнить, как учитель решал задачу.
Используйте пример задачи, чтобы понять, как пошагово решить ее. Запишите каждый шаг, который помнит Ваш ребёнок, решая вместе первую задачу. Это напомнит Вашему ребёнку, что математика — это процесс. Записывая рассуждения за Вашим ребёнком, Вы создадите список, который ребёнок может отдать учителю, чтобы показать, что он старался, даже если у него ничего не вышло.
 Используя этот список, учитель может объяснить, где именно ребёнок ошибся, чтобы в будущем он смог решить эту задачу.
Используя этот список, учитель может объяснить, где именно ребёнок ошибся, чтобы в будущем он смог решить эту задачу.
Чего стоит избегать, помогая ребёнку с домашней работой по математике?
Вот что нельзя делать в случае, если ребёнок обратился к Вам за помощью с домашней работой по математике:
Не начинайте с вопросов вроде «а что тебе учитель сказал делать?» Если бы Ваш ребёнок помнил, что ему сказал учитель, он бы, наверное, не просил у Вас помощи.
Не надо сразу связываться с учителем. Дети, которые испытывают трудности с обучением или концентрацией внимания, легко сдаются и злятся, если у них что-то не получается, но важно показать им, что надо пытаться найти выход из ситуации, прежде чем просить помощи у учителя.
Не ограничивайтесь запиской, вроде «мой ребёнок не выполнил домашнее задание, так как не понял его». Предоставьте учителю информацию о том, что именно не понял ребёнок.
 Так будет легче найти пробел и заполнить его.
Так будет легче найти пробел и заполнить его.
Выводы
Математика — это процесс. Изучите этот процесс вместе с вашим ребёнком.
Предлагая ребёнку примеры похожих задач, вы поможете ему решить трудную домашнюю работу.
Помогая ребёнку решить задачу, ведите заметки, это поможет разобрать задачу и найти то, с чем ребёнок испытывает трудности.
Если записанный процесс помог ребёнку решить задачу — отлично! Если нет, эти заметки можно показать учителю, который поможет найти ошибку.
Источник
по математике для 5 класса — Герасимов
по матем по математике
Не даются умножение и деление, а формулы и дроби вызывают апатию? Не спешите к репетитору! Есть более действенный и менее дорогостоящий способ постичь азы науки о числах — решебник. С ним все по плечу!
Издание подготовлено группой педагогов, которые постарались облегчить участь учащихся 5 класса, часами бьющихся над «домашкой» по математике. Пособие включает:
Пособие включает:
- понятные и лаконичные комментарии к параграфам базового учебника; пошаговые пути решений и разъяснения к ним; задачи для шлифовки пройденного материала;
Решебник по математике для 5-го класса – друг и наставник школьника. Пригодится подспорье и родителям. С ним припомнится школьная программа, а значит последует помощь ребенку. Алгоритм ежедневных тренировок прост и незамысловат:
Прочесть условие Найти правильное решение Свериться с эталоном
Задачки и уравнения перестанут пугать, увлекая юного исследователя более сложными аспектами предмета, а также стимулируя взлет показателей успеваемости. — твой верный помощник в изучении такой непростой, но крайне важной дисциплины!
по математике для 5 класса Герасимов.
Resheba. top
13.01.2017 10:12:32
2017-01-13 10:12:32
Источники:
Https://resheba. top/matematika-5-klass-gerasimov
(решебник) по математике 6 класс Герасимов » /> » /> .keyword { color: red; }
по матем по математике
В данном -сборнике собраны все ответы на задания по математике 6 класса. С их помощью родители смогут проверить правильность выполнения домашних уроков и проверочных работ ребенком. Кроме того, готовые задания по курсу математики для 6 класса помогут школьнику выполнить домашние и факультативные задания самостоятельно и без ошибок.
С их помощью родители смогут проверить правильность выполнения домашних уроков и проверочных работ ребенком. Кроме того, готовые задания по курсу математики для 6 класса помогут школьнику выполнить домашние и факультативные задания самостоятельно и без ошибок.
В каких ситуациях рекомендуется использовать решебник по математике Герасимова?
Зачастую на уроке школьник не усваивает всю информацию, поэтому возникает необходимость дополнительного повторения пройденного материала, подобных задач и математических примеров. Благодаря нашим ответам к учебнику 6 класса по математике, родители и ученики смогут разобрать сложные моменты, которые были не до конца понятны на уроке.
Данный учебно-методический комплекс поможет не только ученикам, но и родителям. Ведь зачастую у взрослых на проверку домашней работы остается совсем мало времени. Теперь нет необходимости погружаться в материал, вдумчиво и долго вникать в математические примеры из школьной программы, ведь помочь проверить успеваемость ребенка можно с помощью .
Шестиклассники смогут после самостоятельного выполнения заданий осуществить самоконтроль и разобрать непонятные моменты решения задач, не дожидаясь помощи родителей. Это существенно сэкономит время детей и приучит к самостоятельности, которая должна развиваться в шестом классе.
В случае непосещения занятий в школе, подросток не всегда в силе освоить изучение новой программы. помогут разобрать новый материал и закрепить уже пройденный. Самые сложные математические примеры и темы станут простыми и понятными, что в свою очередь повысит уровень успеваемости.
Незаменимую помощь готовые ответы окажут и для учителей. Молодым педагогам помогут быстро проверить тетради школьников, значительно сэкономив время работы. Опытным педагогам всегда будет полезно и интересно разобрать новые способы решения, казалось бы, знакомых задач. Также с помощью готовых подсказок можно значительно разнообразить школьную методику изучения нового материала и повторение пройденного: составить дополнительные карточки, индивидуальные задания. Используя решебник по математике можно быстро составить план работы.
Используя решебник по математике можно быстро составить план работы.
Готовые домашние решения к данному курсу по математике содержат упражнения на счет десятичных дробей. Также вы узнаете, что такое проценты и пропорции. С данной книгой вы без труда сможете научиться строить самые сложные графики, узнаете, что такое рациональные и множественные числа. Подробно познакомитесь с основными геометрическими фигурами, такими как: круг, треугольник и окружность.
Теперь нет необходимости погружаться в материал, вдумчиво и долго вникать в математические примеры из школьной программы, ведь помочь проверить успеваемость ребенка можно с помощью .
Resheba. top
30.07.2018 8:06:58
2018-07-30 08:06:58
Источники:
Https://resheba. top/matematika-6-klass-gerasimov
по Математике 5 класс Герасимов часть 1 » /> » /> .keyword { color: red; }
по матем по математике
Пятиклассники начинают изучать основы алгебры. Очень важно, чтобы в этот момент ребенок не отстал в изучении, так как если он не поймет основ, то и дальнейший материал он не сможет усвоить. Когда он понимает вычисления, ему становится интересна математическая наука.
Очень важно, чтобы в этот момент ребенок не отстал в изучении, так как если он не поймет основ, то и дальнейший материал он не сможет усвоить. Когда он понимает вычисления, ему становится интересна математическая наука.
Очень большое место в изучении предмета занимает практика. Чем больше задач решит школьник, тем проще он будет решать следующие задания. Переходя от параграфа к последующему подразделу ученик будет набираться опыта и знаний. В конце книги есть Ответы к номеру (на вопрос), так что малец всегда может проверить правильно ли он решил упражнение.
Математика – это прикладная наука, то есть математика является инструментом для решения примеров в других разделах, поэтому нельзя допускать, чтобы дети отставали по этой дисциплине. Практика развивает логику, смекалку, повышает творческую деятельность и развивает личность в целом.
Решебник Герасимова по математике для 5 класса содержит задания по темам:
Практика развивает логику, смекалку, повышает творческую деятельность и развивает личность в целом.
Megaresheba. ru
06.10.2020 4:35:38
2020-10-06 04:35:38
Источники:
Https://megaresheba. ru/gdz/matematika/5-klass/gerasimov
Задачи по математике для 2 класса, 3500 занимательных заданий с ответами и решением — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Математические диктанты 2 класс, часть 2
Сложение и вычитание с переходом через разряд
Выполни вычисления столбиком.
Вариант 1
а) 30 – 18; г) 94 – 49; ж) 39 + 39;
б) 61 – 38; д) 38 + 18; з) 96 – 7;
в) 17 + 17; е) 91 – 24; и) 54 + 46.
Какую закономерность в ответах ты видишь?
Вариант 2
а) 46 + 45; г) 18 + 46; ж) 29 + 8;
б) 91 – 9; д) 93 – 38; з) 63 – 35;
в) 36 + 37; е) 18 + 28; и) 52 – 33.
Какую закономерность в ответах ты видишь?
Запиши решение столбиком и вычисли.

45 увеличь на 38.
Найди разность чисел 74 и 36.
На сколько 47 меньше 55?
Найди сумму чисел 46 и 18.
Уменьши 61 на 46.
Уменьшаемое 54, вычитаемое 28. Найди разность.
Из 83 вычти 48.
К 36 прибавь 37.
Первое слагаемое 38, второе – 49. Чему равна сумма?
Сколько получится, если из 60 вычесть 16?
Проверь решение примеров, записывая их в столбик. Найди ошибки.
а) 26 + 35 = 61; е) 35 + 49 = 84;
б) 43 – 15 = 28; ж) 6 + 29 = 89;
в) 18 = 42 = 50; з) 51 – 29 = 22;
г) 38 + 13 = 51; и) 54 + 18 = 72;
д) 74 – 48 = 26; к) 37 + 39 = 76.
Найди ошибки в решении примеров. Реши примеры верно.
1 10
а) _36 б) _92 в) _37 г) _71 д) _35
18 7 5 15 19 54 95 87 64 16
Выполни вычисления, записывая решения столбиком.
_54 _60 _48 _37 _76 _73 _70 _18
37 15 24 4 24 19 26 54
_97 _92 _42 _33 _40 _84 _54 _35
18 29 18 48 29 57 28 48
_14 _60 _37 _52 _44 _62 _17 _34
27 29 44 38 49
Вычисли, записывая решение каждого действия столбиком.
 Стрелка покажет, какое действие нужно выполнить с полученным результатом.
Стрелка покажет, какое действие нужно выполнить с полученным результатом.
а) 15 + 37 + 18 – 36 – 17 + 28 – 19 + 74 …
б) 49 + 25 – 18 + 24 – 63 +36 – 28 – 9 …
в) 54 – 18 – 29 + 56 – 48 +37 + 18 – 61 …
г) 95 – 37 – 29 + 57 – 48 +54 – 14 – 58 …
д) 14 + 39 + 38 – 74 + 48 – 26 + 51 – 62 …
е) 90 – 37 – 26 + 45 – 54 +28 + 46 – 78 …
ж) 34 + 16 – 27 + 69 – 73 + 15 + 37 – 35 …
з) 23 + 8 + 29 – 33 + 56 – 45 + 27 – 46 …
и) 96 – 27 – 58 + 39 + 27 – 56 + 75 – 57 …
к) 15 + 37 – 38 + 67 – 33 – 19 + 57 – 38 …
7. Реши круговые примеры. Ответ каждого предыдущего является началом следующего. Начни с примера, обозначенного *.
Вариант 1
_94 _91
* _ 35 67 24 _ 13
59 48
94
_53 _32
38 19
_27
26 _74
_61 39
24
_67 _37
35 37
Вариант 2
* _97
28 _ 42
69 13
_ 69 _27
27 63
_29 _ 85
56 36
_73
_74
47 _49
24
_ 90 _ 18
7 56
Уравнение.

2-й класс
Тип урока: урок введения новых знаний.
Цель: дать учащимся новое математическое понятие «уравнение».
Задачи:
- Образовательная: сформировать представление об уравнении, решение уравнений;
- Развивающая: развивать умение сравнивать, анализировать; совершенствовать вычислительные навыки;
- Воспитательная: формировать культуру общения в классом коллективе.
Оборудование урока:
- Учебник Математика 2 класс 1 часть М.И. Моро и др.
- Мультимедийный проектор, компьютер, презентация.
Ход урока
I.
Самоопределение к деятельности.
Психологический настрой: Покажите вашу прямую спинку, покажите правую руку, умные глазки. Подарите мне и друг другу добрые улыбки.
Подарите мне и друг другу добрые улыбки.
С новой темой познакомится класс.
Сегодня узнаем мы без сомнения
«Имя» этого выражения: х+4=12.
II.
Актуализация знаний и фиксация затруднений в деятельности.
– А сейчас нас ждет интересная работа – устный счет.
Назовите действия и компоненты. (Слайд 2)
- 30 + 7 = 37
- 47 – 5 = 42
Найдите значения выражений. (Слайд 3)
- 32 + 2 =
- 13 + 20 =
- 40 – 7 =
- 53 – 20 =
- х + 3 = 33
– Со всеми выражениями справились? (Нет)
– Чем отличается последнее выражение?
III.
Постановка учебной задачи.
– Такое выражение называется – уравнением. Умеем ли мы решать уравнение? (Нет) (Слайд 4)
– Чему будем учиться на уроке? (Решать уравнения, составить алгоритм решения уравнений)
IV.

Построение проекта выхода из проблемной ситуации, затруднения.
– Давайте разберемся, что же такое уравнение. Прочтите выражения. (Слайд 5)
- … — 4 = 6
- 2 + … = 8
- … + 3 = 7
- 9 — … = 5
– Что объединяет эти выражения? (Это примеры с неизвестным)
– Что нужно знать, чтобы решить их? (Необходимо знать состав чисел, название действий, название компонентов, нахождение неизвестных компонентов)
– Чтобы открыть новое, нам необходимо хорошо повторить то, что мы уже знаем.
| 1С + 2С = СУММА | У – В = Р | |
| 1С = СУММА – 2С | У = Р + В | |
| 2С = СУММА – 1С | В = У — Р |
Вывод: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. (Слайд 6)
(Слайд 6)
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое. (Слайд 7)
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
– В математике принято вместо отсутствующего компонента писать буквы латинского алфавита:
х (икс), а (а), b (бе) c (це) и другие. (Слайд 8)
– Попробуем сделать вывод из всего сказанного.
Вывод: уравнение – это … (х + 3 = 33) равенство, содержащее … (х + 3 = 33) неизвестное число, которое надо найти. (Слайд 9)
– Что надо сделать с неизвестным числом? ( Его надо найти)
– Как обозначается неизвестное число? (Латинскими буквами)
– Молодцы, ваша работа достойна похвалы. А сейчас проверьте себя, прочтите в учебнике на странице 68.
– Давайте составим алгоритм решения уравнения. (Слайд 10)
Алгоритм решения уравнений:
- Прочитай уравнение.

- Назови действие, компоненты.
- Вспомни, как найти неизвестный компонент.
- Запиши и вычисли.
- Проверь.
V.
Первичное закрепление учебного материала.
– А теперь давайте решать уравнения. Что нам поможет сделать это? (Алгоритм) (Слайд 11)
VI. Самостоятельная работа.
– Пользуясь алгоритмом, решите самостоятельно уравнения на стр. 68 №1.
Вариант 1. Верхнюю строку.
Вариант 2. Нижнюю строку.
– Взаимопроверка работы. (Слайды 12, 13)
VII.
Включение новых знаний в систему и повторение.
– Из данных выражений найдите уравнения и запишите их номера: (Слайды 14, 15)
- 8 – 4 = 4
- 6 – х = 4
- 12 + х = 20
- а – 6
- а – 6 = 18
- 13 – 1 = 12
- 10 + у
- 10 + у = 23
VIII.

Рефлексия деятельности.
– Назовите тему урока, над которой работали сегодня.
– Какую цель ставили перед собой?
– Выполнили?
– Так что такое уравнение?
7 способов помочь младшему школьнику с математикой
Предположим, что математика уже в начальной школе ребёнка идёт туго, со скрипом. Трудно и скучно складывать и вычитать, не говоря уже о чём-то более сложном. Новые темы никак не хотят укладываться в голове. Писательница и мама троих детей Ксения Букша рассказывает, основываясь на собственном опыте, как помочь ребёнку освоить математику.
Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу
Раскладываем трудности по полочкам
На уровне 1–5-го классов неспособных к математике детей не бывает. Но бывают дети с конкретными трудностями, которые можно и нужно преодолеть. Подумаем, почему ребёнку трудно с математикой.
Вот возможные варианты или их комбинации.
- Плохо считает, нет навыка счёта.
 Не очень хорошо знаком с числами.
Не очень хорошо знаком с числами. - Не может вникнуть в суть поставленной задачи, с трудом понимает, что надо делать. Пробует все варианты («Так неправильно? Тогда попробую разделить», «В три раза больше — здесь нужен плюс или минус?»).
- Усваивает шаблонное решение, но не может его доработать. Столкнувшись с малейшим изменением условий, впадает в ступор.
- Не умеет читать сложные тексты. В результате не понимает ни описания правил, ни текста задачи. Если на пальцах объяснить, что надо делать, сразу решает нормально.
- В голове не укладываются концепции. С трудом их понимает и быстро забывает. Такой ребёнок может сто раз услышать объяснение, что такое икс (неизвестное), но так и не понять.
- Не развит навык наглядного представления. Не может представить себе, нарисовать схематичную картинку, «увидеть в уме».
- Короткое внимание: всё понимает, но делает кучу ошибок, особенно в длинных сложных примерах.
Как видим, математика раскладывается на множество разных навыков. Когда мы выяснили, в чём проблема, мы можем её решать. Заранее прошу прощения у учителей и методистов: я всего лишь родитель, а мои мысли по этому поводу — всего лишь частное мнение, хотя я стараюсь его обосновывать.
Когда мы выяснили, в чём проблема, мы можем её решать. Заранее прошу прощения у учителей и методистов: я всего лишь родитель, а мои мысли по этому поводу — всего лишь частное мнение, хотя я стараюсь его обосновывать.
Ждём, пока созреет способность абстрактно мыслить
Мозг нейротипичного ребёнка дозревает до абстрагирования и обобщения далеко не сразу. У некоторых это происходит раньше, у других позже. Например, не все дети могут соотнести число и количество. Для очень многих и во 2–3-м классе есть только «15 яблок», а просто «15» нет.
При этом они как-то привыкают оперировать числами, и пробел в базовом понимании не очень заметен, пока речь не заходит о чуть более сложных вещах. Например, именно им трудновато понять, почему не может быть «полтора» в ответе на вопрос «сколько землекопов?». А уж когда начинаются проценты или задачи на скорость и расстояние, становится совсем сложно.
Стоит вернуться назад к конкретике. Возможно, для понимания дробей пока нужно проговаривать «в числителе арбузы, в знаменателе мальчики; 21 арбуз достался 42 мальчикам — каждому по половинке арбуза». Даже в пятом классе почти все концепции ещё можно заземлить до конкретики.
Даже в пятом классе почти все концепции ещё можно заземлить до конкретики.
Развиваем навыки счёта
Просто учиться считать — это скучно. Нам помогут всевозможные игры с числами. Для начала — усложнённые ходилки с 2–3 кубиками (когда за один ход максимум — 18 очков, а не 6), потом — разнообразные игры в кости, где нужно считать очки.
Самая простая игра известна мне под названием «единичка»: игроки по очереди бросают один кубик (или два, или три), пытаясь добраться до сотни очков. Серия прерывается, когда у игрока выпадает хотя бы одна единичка: в этом случае очки за эту серию сгорают, и нужно уметь остановиться вовремя.
Очень рекомендую покер на костях. В этой игре есть ряд комбинаций, каждую из которых надо выбросить за три попытки. Эти попытки можно копить. Игроки делают ходы по очереди, выигрывает тот, кто первым выполнит все комбинации. Помимо простого навыка складывания очков, покер постепенно развивает тонкое понимание случайности и вероятности, просчитываемого риска и шансов. В такой покер может научиться играть даже шести- или семилетка.
В такой покер может научиться играть даже шести- или семилетка.
Для отработки деления и умножения мы с дочкой говорили о числах как о «родственниках». Например, у числа 72 очень большая «семья»: у него есть «детки» 24 и 36, есть «внуки» — 2, 3, 4, 6, 12, 18. А вот число 37 не завело себе никакой «семьи», оно простое. Зато если «поженить» его с другим «одиночкой» — 41, у них получится вместе 78, теперь можно «заводить детей и внуков». Это хорошо помогает ориентироваться в таблице умножения.
Учим видеть и наглядно обобщать задачу
Чтобы хорошо схематизировать, надо уметь выделять именно то, что важно для условия задачи, и схематично изображать это на картинке. Сначала мы учимся выделению главного. Это знаменитые игры «что лишнее?», в которых может быть и несколько ответов. Арбуз, аист, абрикос, виноград — что лишнее? Смотря по какому признаку.
В учебнике Петерсон есть чудесные задачи, загромождённые кучей ненужных данных или лишённые необходимых условий. В задании автор просит найти и выделить только те условия, которые нужны для решения, а если их нет — указать, чего не хватает. Научившись видеть задачу, можно перейти к схематизации.
Научившись видеть задачу, можно перейти к схематизации.
Многие дети вообще не понимают, зачем рисовать схемы к задачам и почему это проще. Всё потому, что схемы эти даны готовыми. Но по какому принципу они строятся? Почему, например, неважно, какой длины сам поезд, если он едет из А в Б? Как нарисовать «3 часа»? А «все груши, посаженные мальчиками»?
Можно вместе рисовать схемы разных задач, а потом предлагать ребёнку придумывать похожие. Такие задания есть и в учебниках, но там их мало. Для некоторых эта трудность вообще определяет все отношения с математикой, да и вообще с упорядочиванием данных, абстрагированием, обобщением, поиском решения.
Оттачиваем логику
Логика — один из инструментов, которые нужны всем. Нет людей, которые были бы не склонны к логике, есть те, у кого она «не поставлена». Это как умение орудовать шуруповёртом: научиться может каждый, у кого есть руки. Вы можете сами оценить, насколько железная у вас логика. Я очень люблю вот этот чудесный тест.
Человека с логикой не способна заморочить никакая пропаганда или реклама, его не запутает недобросовестный банк, он гораздо лучше ориентируется в окружающем мире.
С детьми можно начать с простых силлогизмов, которые иногда звучат смешно, но приводят к пониманию очень важных штук. Например, услышав от кого-нибудь сентенцию «мальчики не плачут», ребёнок может уточнить: «некоторые или все?»
Если дети не проходят понятие множества, стоит хоть немножко вместе с ним порисовать «кружочки» (не обязательно сразу вводить все понятия) и порешать соответствующие задачи: вот мальчики, вот коты, а вот те, кого зовут Вася. Где мальчики, которых зовут не Вася? А где тут девочки? А где кот Барсик?
Развиваем воображение
Воображение необходимо для всего, что связано с математикой и логикой. (Я даже не пишу «как ни странно», потому что это совершенно не странно.) Особенно умение мыслить образами.
Я очень люблю игру, в которой родитель и ребёнок по очереди задают друг другу «графические загадки», не имеющие точного ответа. Каждый рисует серию непонятных геометрических фигур или их комбинаций (точка в треугольнике, молния и круг, несколько кругов, касательные…), а другой дорисовывает их так, чтобы получилась картинка. Чем остроумнее решение, тем больше удовольствия получают оба игрока.
Каждый рисует серию непонятных геометрических фигур или их комбинаций (точка в треугольнике, молния и круг, несколько кругов, касательные…), а другой дорисовывает их так, чтобы получилась картинка. Чем остроумнее решение, тем больше удовольствия получают оба игрока.
Существует много древних и новых игр, в которых нужно складывать узоры из деталей и фрагментов яйца (колумбово яйцо), квадрата, по-разному раскрашенных граней кубика («Сложи узор»). Есть и трёхмерные наборы, например «Пентамино». Речь не о том, чтобы выполнять задания, хотя все эти наборы можно использовать и так, но именно о творчестве из имеющихся деталей и об умении увидеть образ.
А можно ещё вырезать снежинки, дорисовывать симметричных бабочек и человечков, придумывать шифры, рисовать лабиринты и карты. Всё это и есть развитие математического воображения.
Учим ребёнка вычленять, чего конкретно он не понимает (метакогниция)
Я уже не раз писала про неё — и в связи с математикой, и в связи с сочинениями. Вкратце метакогниция — это умение «понимать, как я думаю», «знать, чего именно я не знаю», осознание своего мыслительного процесса. Именно этому почти никогда не учат в школе, а иногда даже портят уже развитую способность. Предполагается ведь, что есть простые и сложные способы решения той или иной задачи. Часто это так и есть, но порой гораздо ценнее умение идти самому и по шагам проверять себя: «Так нужно делать? Я прав?»
Вкратце метакогниция — это умение «понимать, как я думаю», «знать, чего именно я не знаю», осознание своего мыслительного процесса. Именно этому почти никогда не учат в школе, а иногда даже портят уже развитую способность. Предполагается ведь, что есть простые и сложные способы решения той или иной задачи. Часто это так и есть, но порой гораздо ценнее умение идти самому и по шагам проверять себя: «Так нужно делать? Я прав?»
Совместные рассуждения (и я не про математику) ценны и тем, что сближают ребёнка и родителя, и тем, что мы показываем, как проходит процесс думания. Он не должен быть гладким и автоматическим. В нём есть тупики, неожиданные повороты. «Наше первоначальное предположение неверно, а это значит, что нужно идти не по дороге 1, а по дороге 2». Кстати, это пригодится и в школьной математике, когда нужно будет понимать доказательства теорем. Ведь хорошо запоминается только то, что прошёл сам своим умом, когда смог повторить чужие рассуждения и знаешь в них каждый поворот.
Распечатанные рабочие листы для задач по математике для второго класса
Проблемы со словами могут быть сложной задачей для учащихся, особенно для второклассников, которые, возможно, еще учатся читать. Но вы можете использовать базовые стратегии, которые будут работать практически с любым учеником, даже с теми, кто только начинает изучать письменные навыки.
Инструкции и стратегии
Чтобы помочь второклассникам научиться решать задачи со словами, научите их выполнять следующие действия:
- Изучите математическую задачу: Прочтите слово «задача», чтобы понять ее общий характер.Поговорите со своими учениками о проблеме и обсудите, какие части являются наиболее важными.
- Прочтите математическую задачу: Прочтите вопрос еще раз. На этот раз сосредоточьтесь на конкретных деталях проблемы. Какие части проблемы связаны друг с другом?
- Задайте вопросы о задействованных операциях: Поразмышляйте еще раз.
 Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения. - Спросите себя о предпринятых шагах: Просмотрите каждый сделанный шаг.Определите, кажется ли ваш ответ разумным. Если возможно, сверьте свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.
- Завершите: Просмотрите текст словесных задач, которые вы будете решать, чтобы определить любые слова, которые вы не узнаете. Перечислите их и определите их значение, прежде чем решать проблемы. Напишите краткие определения терминов для справки при решении проблемы.
Решение проблем
Изучив эти стратегии, используйте следующие бесплатные распечатки задач со словами, чтобы студенты могли практиковать то, что они узнали.Есть только три рабочих листа, потому что вы не хотите перегружать своих второклассников, когда они только учатся решать задачи со словами.
Начните медленно, при необходимости повторите шаги и дайте своим ученикам возможность усвоить информацию и освоить словесные методы решения проблем в расслабленном темпе. В печатных материалах содержатся термины, которые будут знакомы молодым студентам, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
В печатных материалах содержатся термины, которые будут знакомы молодым студентам, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
Д. Рассел
В эту распечатку включены восемь математических задач, которые покажутся второклассникам многословными, но на самом деле они довольно просты.Задачи на этом листе включают задачи со словами, сформулированные в виде вопросов, например: «В среду вы видели 12 малиновок на одном дереве и 7 на другом дереве. Сколько всего малиновок вы видели?» и «У всех ваших 8 друзей есть двухколесные велосипеды, сколько всего это колес?»
Если студенты озадачены, прочитайте задачи вслух вместе с ними. Объясните: как только вы вычеркнете слова, это будут простые задачи сложения и умножения, где ответ на первый будет следующим: 12 робинов + 7 робинов = 19 малиновок; а ответ на второй будет: 8 друзей x 2 колеса (для каждого велосипеда) = 16 колес.
Д. Рассел
Рассел
Эта последняя печатная форма в наборе содержит немного более сложные задачи, такие как эта, связанная с деньгами: «У вас есть 3 квартала, и ваша выписка обошлась вам в 54 цента. Сколько денег у вас осталось?»
Чтобы ответить на этот вопрос, предложите учащимся изучить проблему, а затем прочитать ее всем классом. Задайте такие вопросы, как: «Что может помочь нам решить эту проблему?» Если учащиеся не уверены, возьмите три четверти и объясните, что они равны 75 центам. Тогда задача превращается в простую задачу вычитания, поэтому завершите ее, указав числовую операцию на доске следующим образом: 75 центов — 54 цента = 21 цент.
Задачи по обучению словарю во 2-м классе
Если вы ищете лучший способ научить словесным задачам и, что более важно, хотите, чтобы ваши ученики были более успешными в решении словесных задач, я здесь, чтобы помочь. Учить словесные задачи во 2-м классе не должно быть проблемой.
Почему во 2-м классе так сложно учить словесные задачи?
Когда я только начал преподавать, я учил своих учеников использовать ключевые слова, подчеркивать и обводить, выделять и вставлять рамку… и все же это не помогло. Они все еще не знали, когда складывать, а когда убирать.
Они все еще не знали, когда складывать, а когда убирать.
И мои ученики не понимали и не успевали лучше.
Не помогало то, что я постоянно не учил и не позволял своим ученикам практиковаться в решении словесных задач.
Задачи со словом всегда были источником разногласий для моих учеников, независимо от того, в каком классе я преподавал (1-й, 2-й и 4-й), и всегда были тем, что я преподавал наугад в рамках принятой математической программы.
Большинство учебных программ по математике предлагают следующее:
- Задачи на 1 или 2 слова в конце каждого урока, но на самом деле не предлагают способ научить учеников решать задачи со словами
- 1 глава о «решении задач»
И серьезно, ни то, ни другое полезно.
Я хотел, чтобы мои ученики ежедневно практиковались в стратегических задачах.
И знаете что? Когда я начал последовательно и стратегически преподавать задачи со словами во 2-м классе, мои ученики были менее разочарованы и гораздо более искусно решали задачи со словами.
Итак, какое решение?
Сейчас я следую 4-дневному плану обучения и оцениваю его на 5-й день.
Я больше не учу ключевые слова или подчеркивание, обводку, выделение и / или бокс… вместо этого я учу своих учеников искать закономерности в том, как структурированы проблемы со словами… ситуации со словами.
Кроме того, я посвящаю 5-10 минут каждый день обучению и практике словесных задач.
Как я узнаю, чему учить?
Начну со стандарта.
Честно говоря, что бы я ни преподаю, именно здесь я начинаю. Мне нужно точно знать, чего я ожидаю, чтобы потом я мог помочь своим ученикам справиться с этим.
Стандарт Common Core для 2-го класса гласит:
CCSS.MATH.CONTENT.2.OA.A.1
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e. g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.

Хотя многие штаты больше не используют термин «Common Core», многие принятые ими стандарты совпадают или, по крайней мере, схожи.
MAFS.2.OA.1.1 (стандарты Флориды)
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e.g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Итак, второклассники должны уметь решать:
- Сложение / вычитание в пределах 100
- Одно- и двухступенчатое
- Добавить к
- Взять из
- Соединить
- Разобрать
- Сравнить
Когда вы посмотрите на то, что должны делать второклассники, неудивительно, что учить словесные задачи так сложно, не говоря уже о том, что студенты действительно их осваивают.
Как я учу задачи по словам во 2-м классе:
В начале года ученики знакомятся с нашей рутинной задачей со словом после первых двух недель в школе.
Я объясняю, что задачи со словами похожи на истории, которые мы должны читать и понимать, что происходит в рассказе. Мы называем эти слова «проблемными ситуациями».
Затем я учу студентов, что есть 4 вещи, которые они всегда должны делать, решая задачу со словами:
- Напишите числовое предложение
- Используйте стратегию для решения
- Я объясняю студентам, что я не могу залезть в их мозг, чтобы увидеть, что они думают, и если я не знаю, о чем они думают, я не может помочь им лучше решать проблемы со словами.
- Учащиеся могут рисовать картинки, использовать семейство фактов, базовые 10 блоков и / или стандартный алгоритм.
- Вычисление
- Я смотрю, чтобы убедиться, что ученик дал правильный ответ.
- Ответ в предложении
- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки». Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.

- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки». Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.
Запуск рутинной задачи со словом — это все о моделировании и рутине. Студентам не нужно много времени, чтобы научиться этому.
Я проделал за вас тяжелую работу — у меня на весь год есть задачи по словам во 2-м классе, готовые для вас!
Что такое рутинная задача для 2-х классов?
По понедельникам я использую слово «проблемная ситуация». Я считаю полезным, чтобы студенты «разыгрывали» ситуацию. Используйте пример на ситуационном плакате / диаграмме привязки, чтобы показать учащимся образец.(Я учу студентов, что подчеркнутые части числового предложения — это известные нам части, а квадрат представляет неизвестное.)
Смоделируйте и решите практическую задачу со словами и поделитесь своими отзывами со студентами.
В течение следующих 3 дней мы моделируем и решаем задачу со словом, которая имеет ту же ситуацию, что и понедельник. Так что мы не скучаем. Это очень систематично.
Наконец, по пятницам ученики самостоятельно решают 2 задачи со словами, следуя той же ситуации, которую мы использовали всю неделю.
Для дифференциации или расширения учащиеся могут написать задачу на обратной стороне своего экзамена, которая соответствует той же ситуации, которую они изучали на этой неделе. Это отличный способ узнать, действительно ли студенты понимают ситуацию, которую мы узнали на той неделе.
Возможно вам понравится:
Давайте подключимся!
Instagram // Pinterest // Facebook // Учителя платят учителям
многоступенчатых уравнений | 2-й класс по математике
Научитесь решать многоступенчатые уравнения
😎 Итак, вы научились складывать и вычитать числа.
Что произойдет, если вам нужно будет сложить и вычесть в одном уравнении? 🤔
👉 Давайте посмотрим на пример:
У вас в ланч-боксе 5 печений . Ваш друг дает вам еще 3 файлов cookie.Вы съели 2 печенья. Сколько файлов cookie у вас осталось?
Мы начинаем с , записывая уравнение для задачи.
5 + 3 — 2 =?
Как вы решите это многошаговое уравнение ? 🤔
Решите многоэтапных уравнений с помощью , упрощая одну операцию за раз.
😃 Операция — это слово для сложения или вычитания.
👉 Идем с слева направо . Итак, сначала мы начнем с сложения.
5 + 3 = 8
Теперь мы можем переписать наше исходное уравнение и поместить 8 вместо 5 + 3 .
А теперь вычитаем!
8 — 2 = 6
Отличная работа! 👏 Наш ответ: 6.
Другой пример
👉 Давайте попробуем это уравнение.
20-11 + 5 =?
✅ На этот раз вычитание — первая операция, которую мы упростили, .
20-11 = 9
Теперь мы можем поставить 9 вместо первого уравнения.
Все, что нам осталось сделать, это добавить!
9 + 5 = 14
Отличная работа! 👍
Теперь вы можете переходить к практике.
примеров общих основных математических задач для 2-го класса — математический класс [2021]
Примеры операций и алгебраического мышления
Эти стандарты просят студентов работать со сложением и вычитанием различными способами, включая простые вычисления и более сложные решения проблем.
- В классе мисс Винки 24 ученика. Однажды к ним пришли еще трое детей, но четверо из обычных учениц мисс Винки отсутствуют. Сколько детей в классе в этот день? Покажите свое решение как минимум двумя способами.
- Автобус номер три обычно занимает 14 минут, чтобы добраться от автобусной остановки Сьюзи до ее школы. Сегодня автобус застревает в пробке еще на 5 минут. Сколько времени нужно, чтобы добраться от автобусной остановки Сьюзи до школы?
- Карлос и его семья любят гулять.В минувшие выходные собрали 28 желудей! Карлос уронил 6 из них по дороге домой и отдал 2 своему младшему брату. Сколько желудей у него осталось?
- Что на семь больше четырех? Что на четыре меньше семи?
- Джозеф покупает пачки жевательной резинки для своих друзей и семьи. Если в каждой пачке есть пять палочек жевательной резинки, а Джозеф покупает три пачки, сколько палочек жевательной резинки покупает Джозеф?
Числа и операции в десятичных примерах
Эти стандарты основываются на чувстве числа учащихся, предлагая им понять, что представляет каждая цифра в трехзначном числе и как разные числа соотносятся друг с другом.
- Что означает цифра «7» в числе 374? Как можно представить эту «7» цифрами? Используете блоки по основанию десять?
- Если вы пропускаете счет от 10 до 200, сколько раз вам придется считать?
- Что на десять больше, чем 67? Как вы можете ответить на этот вопрос, не производя вычислений?
- Как решить задачу 34 — 17? Покажите свою работу, используя как минимум две разные стратегии.
Примеры измерений и данных
Стандарты в этой области просят ваших учеников измерять длину предметов и работать с длиной в контексте решения проблем.Они также просят ваших второклассников поработать над задачами, требующими времени, денег и базового представления данных.
- Измерьте длину трех разных предметов в классе. Объясните, как вы решили, какой измерительный инструмент использовать для каждого объекта, и запишите их измерения, используя наиболее подходящую единицу измерения.
- Если в прошлом году рост Сисси составлял 48 дюймов, а в этом году она выросла на три дюйма, то какого она роста сейчас?
- Школа начинается в 8:50 каждое утро.
 Обед — через три часа десять минут после начала учебного дня. Когда будет ланч?
Обед — через три часа десять минут после начала учебного дня. Когда будет ланч? - Если у Лоуренса две четверти и пятак, сколько у него денег?
- Джоди хочет, чтобы ее мама купила ей куклу и кукольное платье. Кукла стоит 36 долларов, а платье — 11 долларов. Сколько денег Джоди просит маму вообще потратить?
- Вместе со своим классом создайте гистограмму, показывающую, сколько букв содержится в именах учащихся в вашем классе. Вместе обсудите график и объясните, что он показывает и что заставляет вас думать.
Примеры геометрии
Эти стандарты требуют, чтобы учащиеся могли рисовать и распознавать формы и разбивать их в соответствии с контрольными дробями.
- Как вы называете двухмерную форму с пятью сторонами?
- Нарисуйте прямоугольник. Разделите прямоугольник на три ряда и три столбца квадратов одинакового размера. Сколько всего квадратов в прямоугольнике?
- Нарисуйте круг. Разделите круг на три равные части. Как вы называете эти акции?
Контрольный список навыков для 2-го класса: математика
Контрольные листы подготовки ко второму классу
Математика
Номера, операции и решение проблем
- Считает по 1, 2, 5 и 10 с
- Определяет, упорядочивает и записывает цифры от 0 до 100
- Знает факты сложения и вычитания до 50
- Складывает и вычитает двузначные числа до 99 без перегруппировки
- Показывает начальное понимание разряда
- Делает разумные оценки количеств
- Обозначает целые, половину, трети и четверти
- Называет и использует порядковые номера, такие как первый, второй, третий и т.
 Д.
Д. - Отображает и определяет положительные целые числа в числовой строке
Геометрия и измерения
- Обозначает и рисует основные формы
- Исследует и решает простые пространственные и измерительные задачи, используя манипуляторы (практические объекты, которые можно подсчитать или сортировать) и чертежи.
- Признает и использует стандартные измерительные инструменты, такие как линейки, весы и термометры.
- Понимает основные концепции пространственных отношений, симметрии и отражений.
Математика в действии: определение времени, счет денег, реальная математика
- Распознает и добавляет деньги к 1 доллару.00
- Показывает время с точностью до часа
- Использует рисунки и слова для описания математического мышления
- Собирает и записывает данные с помощью таблиц, списков, диаграмм и графиков
- Считывает график или диаграмму и делает выводы
- Классифицирует, сортирует и сравнивает физические объекты по множеству схем классификации и шаблонов (сходство, различие, звук, цвет, текстура, размер, вес, температура, продолжительность и т.
 Д.).
Д.). - Создает, копирует и расширяет шаблоны с действиями, объектами и словами
Советы для родителей, которые помогут детям чувствовать себя уверенно при решении числовых и числовых задач:
- Создайте банку для монет, в которую вы бросаете мелочь и даете своему ребенку регулярную работу по сортировке и подсчету этих монет (с вашей помощью) на регулярной основе.
- Ведите общий семейный календарь и пусть ваш ребенок отмечает дни, считает дни до предстоящих событий и отслеживает дни рождения.
- Поощряйте ребенка помогать рассортировать банки и коробки в кладовой по размеру или весу.
- Включите ребенка в простые кулинарные упражнения и моделируйте его из мерных чашек или ложек; опишите, что вы делаете, когда используете эти измерительные инструменты.
- Играйте в игры на счет, когда находитесь в машине или на прогулке; выберите «магическое число» и предложите ребенку определить это количество собак, затем магическое количество больших деревьев или красных машин и т.
 д.
д.
навыков математики для 2-го класса, чему научится ваш ребенок
Во втором классе по математике дети начинают работать с большими числами и лучше понимают их значение. Студенты также изучают повседневные навыки, такие как определение времени, работа с деньгами и измерение.
Мы, родители, можем помочь нашим детям преуспеть во втором классе по математике, узнав больше о том, что они собираются изучать.В течение года ваш ребенок научится:
1. Считать в пределах 1000
Второклассники учатся читать и записывать числа до 1000. Они учатся пропускать счет на 5, 10 и 100, поскольку замечают закономерности среди чисел.
Дома: Создайте возможности для чтения и записи трехзначных чисел. Например, попросите ребенка прочитать числа на этикетках с питанием.
Вы также можете попросить ребенка устно пропустить счет на 10 или 100 секунд. Начните с 10 или 100, а затем предложите второкласснику не учитывать другие числа, например 60 или 204.
2. Понимание разряда в трехзначных числах
По мере того, как дети учатся считать с точностью до 1000, они будут более внимательно смотреть на трехзначные числа. Глядя на закономерности в числах, дети начинают понимать числовую ценность.
Дома: помогите своему ребенку, спросив, сколько единиц, десятков и сотен в трехзначных числах.
3. Сравните трехзначные числа
Узнав о разрядах и счетах в пределах 1000, второклассники смогут сравнивать трехзначные числа.Они смогут использовать свои знания о числовой стоимости, чтобы посмотреть на два числа и сказать, какое из них больше или меньше другого. Дети узнают, как использовать символы и = для сравнения трехзначных чисел.
Дома. Помогите ребенку отработать навыки сравнения, задав такие вопросы, как «Что больше: 943 или 783?» Развивайте мышление ребенка, спрашивая, почему одно число больше другого.
4. Складывать и вычитать в пределах 1 000
Во втором классе дети привыкают складывать и вычитать числа в пределах 100.Они решают одно- и двухэтапные задачи со словами, например: «У Тимми было 39 игрушечных машинок. Он получил еще 12, затем отдал 18. Сколько машин осталось у Тимми? »
После работы над сложением и вычитанием в пределах 100 дети будут использовать свои знания трехзначных чисел, чтобы практиковать сложение и вычитание в пределах 1000.
Дома: составьте несколько словесных задач, подобных приведенной выше, используя любимые игрушки или еду вашего ребенка.
5. Измерение
Второклассники развивают свое понимание измерения, оценивая длины и измеряя их с использованием различных единиц. Они сравнивают длины, аналогично тому, как они проводят сравнение с числами, и используют сложение и вычитание, чтобы узнать, насколько длиннее или короче объекты.
Дома: дайте ребенку линейку и попросите его измерить три разных предмета в доме. Затем попросите ребенка расположить предметы в порядке от самого короткого до самого длинного и объяснить, насколько каждый предмет длиннее или короче других.
Затем попросите ребенка расположить предметы в порядке от самого короткого до самого длинного и объяснить, насколько каждый предмет длиннее или короче других.
6. Определение времени с точностью до ближайших пяти минут
В первом классе учащихся познакомили с функцией определения времени.Теперь второклассники могут расширить свое понимание времени до ближайших пяти минут. Дети также смогут отличить AM от PM.
Попросите вашего ребенка научиться определять время с точностью до пяти минут — напомните ему использовать AM и PM!
7. Задачи со словами, связанные с деньгами
Второклассники решат множество задач со словами, связанных с сложением и вычитанием, в том числе с деньгами.
Дома: дайте ребенку стопку монет и задание посчитать общую сумму.Или поиграйте в «магазин» и попросите ребенка попрактиковаться в покупке предметов на разные суммы денег, а затем вычислить, сколько центов осталось.
8. Картинка и гистограммы
Картинка и гистограммы
Во втором классе ваш ребенок научится пользоваться картинками и гистограммами до четырех категорий.
Предложите ребенку пройти опросы дома и представить собранные данные в виде графика.
Приятно провести время, погрузившись в математику для второго класса!
Нашли это полезным? Ознакомьтесь с нашими руководствами по математике от детского сада до 5 класса
Написано Лили Джонс, Лили Джонс любит учиться всему.Она была воспитателем детского сада и первого класса, инструктором по обучению, разработчиком учебной программы и наставником учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
О Komodo — Komodo — это увлекательный и эффективный способ улучшить математические навыки K-5. Komodo, разработанный для детей от 5 до 11 лет для использования в домашних условиях, использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в напряженный семейный распорядок. Komodo помогает пользователям развить беглость и уверенность в математических вычислениях — , не задерживая их долгое время за экраном .
Komodo помогает пользователям развить беглость и уверенность в математических вычислениях — , не задерживая их долгое время за экраном .
Узнайте больше о Komodo и о том, как он помогает тысячам детей каждый год лучше учиться по математике — вы даже можете попробовать Komodo бесплатно.
Задачи по математике для 2-го класса — миссис Латс и мисс Уилл
2 класс
GO Math
2016-2017
Цели и учебные цели
Глава 1: Числовые концепции
числа до 20 как четные или нечетные.
· Напишите уравнения с равными слагаемыми для представления четных чисел.
· Используйте разряд для описания значений цифр в двузначных числах.
· Напишите 2-значные числа в развернутой форме.
· Записывайте двузначные числа в форме слова, развернутой и стандартной форме.
· Применяйте концепции разряда, чтобы найти эквивалентные представления чисел.
· Решайте проблемы, находя различные комбинации десятков и единиц для представления двухзначных чисел, используя стратегию «найти образец».
· Расширить последовательности подсчета в пределах 100 на 1, 5 и 10
· Расширить последовательности подсчета в пределах 1000 на 1, 5, 10 и 100 секунд.
Глава 2: Числа до 1 000
· Записывайте трехзначные числа в развернутой и стандартной форме.
· Применяйте концепции разряда, чтобы найти эквивалентные представления чисел.
· Определите на 10 больше, на 10 меньше, на 100 больше или на 100 меньше, чем любое заданное число
· Расширьте числовые шаблоны, считая на 10 или 100.
· Решайте проблемы, связанные со сравнением чисел, используя стратегию «создать модель».
· Сравните 3-значные числа, используя символы .
Глава 3: Основные факты и взаимосвязи
· Используйте двойные факты как стратегию для нахождения сумм для почти двойных фактов.
· Вспомните суммы основных фактов, используя свойства и стратегии.
· Вызов сумм для сложения фактов, используя стратегию «сделать десять».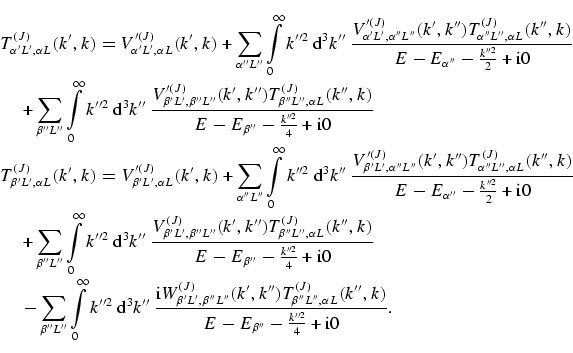
· Найдите суммы трех слагаемых, применяя коммутативные и ассоциативные свойства сложения.
· Используйте обратную зависимость сложения и вычитания, чтобы вспомнить основные факты.
· Вспомните различия основных фактов, используя умственные стратегии.
· Найдите различия на числовой прямой, чтобы разработать мысленную стратегию разложения для упрощения фактов.
· Используйте линейчатые модели для представления различных ситуаций сложения и вычитания.
· Решайте проблемы с участием равных групп, используя стратегию «разыграй все».
· Напишите уравнения, используя повторное сложение, чтобы найти общее количество объектов в массивах.
Глава 4: 2-значное дополнение
· Найдите сумму, разделив однозначное сложение, чтобы двузначное сложение стало кратным 10.
· Используйте компенсацию для развития гибкое мышление для сложения двух цифр.
· Применяйте концепцию разряда при использовании стратегии разделения для двухзначного сложения.
· Модель 2-значного сложения с перегруппировкой.
· Нарисуйте быстрые картинки и запишите сложение двух цифр, используя стандартный алгоритм.
· Запишите сложение двух цифр, используя стандартный алгоритм.
· Практикуйте сложение двух цифр с перегруппировкой и без нее.
· Перепишите задачи горизонтального сложения по вертикали в стандартном формате алгоритма.
· Решайте задачи, связанные со сложением двух цифр, используя стратегию «нарисовать диаграмму».
· Представляйте ситуации сложения числовыми предложениями, используя символ для неизвестного числа.
· Найдите суммы трех двузначных чисел.
· Найдите суммы четырех двузначных чисел.
Глава 5: Вычитание двух цифр
· Разделите однозначное вычитание на части, чтобы вычесть его из двузначного числа.
· Разделите 2-значное вычитаемое, чтобы вычесть его из 2-значного числа.
· Модель вычитания двух цифр с перегруппировкой.
· Нарисуйте быстрые картинки и запишите двузначное вычитание, используя стандартный алгоритм.
· Запишите двузначное вычитание, используя стандартный алгоритм.
· Практикуйте вычитание двух цифр с перегруппировкой и без нее.
· Перепишите задачи горизонтального вычитания по вертикали в стандартном формате алгоритма.
· Используйте сложение, чтобы найти различия.
· Решайте задачи вычитанием двух цифр, используя стратегию «нарисовать диаграмму».
· Представляйте ситуации вычитания числовыми предложениями, используя символ неизвестного числа.
· Анализируйте текстовые задачи, чтобы определить, какие операции использовать для решения многоступенчатых задач.
Глава 6: Сложение и вычитание 3-х цифр
- Нарисуйте быстрые картинки для представления 3-значного сложения.
- Примените концепцию разряда при использовании стратегии разделения для 3-значного сложения.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки единиц.

- Запишите 3-значное сложение с использованием стандартного алгоритма с возможной перегруппировкой десятков.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки единиц и десятков.
- Решайте задачи, связанные с вычитанием трех цифр, используя стратегию «создать модель».
- Запишите сложение трех цифр с использованием стандартного алгоритма с возможной перегруппировкой сотен.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки сотен и десятков.
- Запись вычитания с использованием стандартного алгоритма, когда в уменьшаемом значении есть нули.
Глава 7: Деньги и время
- Найдите общую стоимость коллекций в десять центов, пятак и центов.
- Закажите монеты в коллекции по стоимости, а затем найдите общую стоимость.
- Обозначает денежные суммы меньше доллара с использованием двух различных комбинаций монет.

- Покажите один доллар разными способами.
- Найдите и запишите общую ценность денежных сумм, превышающих доллар.
- Решайте словесные задачи, связанные с деньгами, используя стратегию «разыграй это».
- Сообщите и запишите время с точностью до часа и получаса.
- Сообщите и запишите время с точностью до 5 минут.
- Сообщите и запишите время, используя A.M. и П.
Глава 8: Длина в обычных единицах
- Используйте конкретные модели для измерения длины объектов в дюймах.
- Сделайте дюймовую линейку и используйте ее для измерения длины предметов.
- Оцените длину предметов, мысленно разделив их на дюймы.
- Измерьте длину объектов с точностью до дюйма с помощью дюймовой линейки.
- Решайте задачи сложения и вычитания, связанные с длинами объектов, используя стратегию «рисовать диаграмму».
- Измерьте длину объектов в дюймах и футах, чтобы изучить обратную зависимость между размером и количеством единиц.

- Оцените длину предметов в футах.
- Выберите подходящие инструменты для измерения различной длины.
- Измерьте длину объектов и используйте линейный график для отображения данных измерений.
Глава 9: Длина в метрических единицах
- Используйте конкретную модель для измерения длины объектов в сантиметрах.
- Оцените длину объектов в сантиметрах, сравнив их с известной длиной.
- Измерьте длину предметов с точностью до сантиметра с помощью сантиметровой линейки.
- Измерьте длину объектов в сантиметрах и метрах, чтобы изучить обратную зависимость между размером и количеством единиц.
- Оцените длину объектов в метрах.
- Измерьте, а затем найдите разницу в длине двух объектов.
Глава 10: Данные
· Соберите данные в опросе и запишите эти данные в итоговую таблицу.
· Интерпретируйте данные в графических изображениях и используйте эту информацию для решения проблем.
· Сделайте графические изображения для представления данных.
· Интерпретируйте данные в виде гистограмм и используйте эту информацию для решения проблем.
· Создавайте гистограммы для представления данных.
· Решайте проблемы, связанные с данными, используя стратегию построения графика.
Глава 11: Понятия геометрии и дроби
· Определите трехмерные формы.
· Определите трехмерные формы по количеству граней, ребер и вершин.
· Создавайте трехмерные формы, используя кубы и другие объекты.
· Назовите 3-4-5-6-сторонние формы в соответствии с количеством сторон и вершин,
· Определите углы в двухмерных формах.
· Сортировка двухмерных фигур по их атрибутам.
· Разделите прямоугольники на квадраты одинакового размера и найдите общее количество этих квадратов.
· Определите и назовите равные части кругов и прямоугольников половинками, третями или четвертями.
· Формы разделов для отображения половин, третей или четвертей.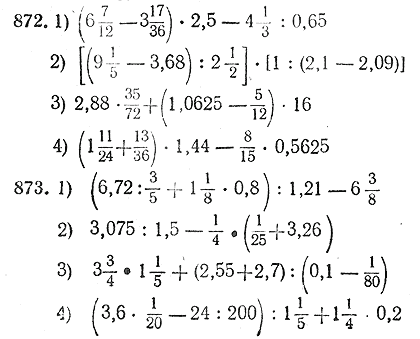
· Определите и опишите одну равную часть как половину трети или четверть целого.
10 Сногсшибательных математических уравнений – Сборник Reasoner
В большинстве случаев математическое уравнение – это просто то, что вы запоминаете для контрольной по математике. Но иногда уравнение может быть чем-то большим — оно может быть самостоятельным произведением искусства, не имеющим никакой реальной цели, кроме удовольствия. Для сегодняшнего поста я собрал десять самых поразительных, ослепительных и безумных уравнений для этой цели. Эти десять уравнений должны убедить любого, что математика — это нечто большее, чем заучивание формул.
1. Тождество Эйлера
Очень известное уравнение, тождество Эйлера связывает кажущиеся случайными значения пи, е и квадратный корень из -1. Многие считают его самым красивым уравнением в математике.
Более общая формула:
Когда значение равно -1, а равно 0, в результате тождество Эйлера равно -1 + 1 = 0.
2. Формула произведения Эйлера
Символ слева — бесконечная сумма, а справа — бесконечное произведение. Это уравнение, снова теоретизированное Леонардом Эйлером, связывает натуральные числа (n = 1, 2, 3, 4, 5 и т. д.) в левой части с простыми числами (p = 2, 3, 5, 7, 11, д.) с правой стороны. Более того, мы можем выбрать в качестве s любое число больше 1, и уравнение верно.
Левая сторона представляет собой обычное представление дзета-функции Римана.
3. Интеграл Гаусса
Функция сама по себе является очень уродливой функцией для интегрирования, но когда она выполняется по всей прямой, т. е. от минус бесконечности до бесконечности, она дает удивительно чистый ответ. На первый взгляд, конечно, не очевидно, что площадь под кривой равна квадратному корню из числа пи.
Эта формула имеет чрезвычайно важное значение в статистике, поскольку она представляет собой нормальное распределение.
4. Мощность континуума
Мощность континуума
Это утверждает, что мощность действительных чисел равна мощности всех подмножеств натуральных чисел. Это показал Георг Кантор, основатель теории множеств. Он примечателен тем, что утверждает, что континуум не является счетным, т.к.
Похожим утверждением является континуум-гипотеза, в которой утверждается, что между и нет кардинальности. Интересно, что у этого утверждения есть очень странное свойство: его нельзя ни доказать, ни опровергнуть.
5. Аналитическое продолжение факториала
Факториальная функция обычно определяется как n! = n(n-1)(n-2)…1, но это определение «работает» только для положительных целых чисел. Интегральное уравнение делает факториал также для дробей и десятичных знаков. И отрицательные числа, и комплексные числа…
Тот же интеграл для n-1 определяется как гамма-функция.
6. Теорема Пифагора
Вероятно, самое известное уравнение в этом списке.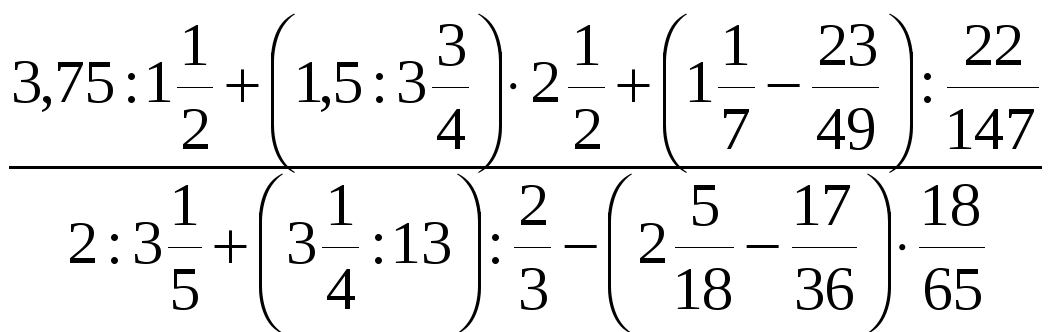 Теорема Пифагора связывает стороны прямоугольного треугольника, где a и b — длины сторон, а c — длина стороны. гипотенуза. Он также связывает треугольники с квадратами.
Теорема Пифагора связывает стороны прямоугольного треугольника, где a и b — длины сторон, а c — длина стороны. гипотенуза. Он также связывает треугольники с квадратами.
7. Явная формула для последовательности Фибоначчи
где (обратите внимание, что это число является золотым сечением). Хотя многие люди знакомы с последовательностью Фибоначчи (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д., где каждое число представляет собой сумму двух предыдущих чисел), мало кто знает, есть формула для вычисления любого заданного числа Фибоначчи: формула, которую мы привели выше, где F(n) — n-е число Фибоначчи. То есть, чтобы найти 100-е число Фибоначчи, не обязательно вычислять первые 99 номеров. Вы можете просто подбросить 100 в формулу.
Удивительно, но даже со всеми квадратными корнями и делениями ответ всегда будет точным положительным целым числом.
8. Базельская задача
Это уравнение говорит, что если вы возьмете обратное число всех квадратных чисел, а затем сложите их все вместе, вы получите пи в квадрате больше шести.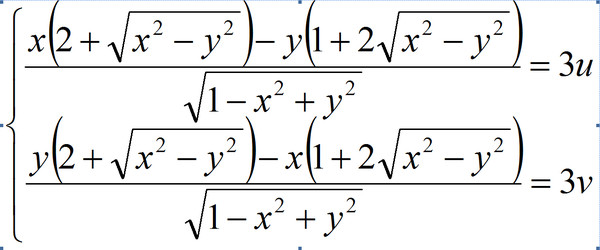 Это было доказано Эйлером. Обратите внимание, что эта сумма — просто функция в левой части уравнения 2 (формула произведения Эйлера) ранее в этом посте, где s = 2. Эта формула — дзета-функция Римана, мы можем сказать, что дзета 2 равна пи в квадрате. больше шести.
Это было доказано Эйлером. Обратите внимание, что эта сумма — просто функция в левой части уравнения 2 (формула произведения Эйлера) ранее в этом посте, где s = 2. Эта формула — дзета-функция Римана, мы можем сказать, что дзета 2 равна пи в квадрате. больше шести.
9. The Harmonic Series
Это несколько неинтуитивно, потому что здесь говорится, что если вы сложите несколько чисел, которые будут уменьшаться (и в конечном итоге станут равными нулю), они все равно достигнут бесконечности. Тем не менее, если вы возведете все числа в квадрат, в сумме это не даст бесконечности (в сумме получится пи, возведенное в квадрат на шесть). Гармонический ряд, если вы посмотрите внимательно, на самом деле представляет собой просто дзета от 1.
10. Явная формула для функции счета простых чисел
где определяется как
Вот значение этого уравнения на английском языке:
Простые числа — это числа, у которых нет других делителей, кроме 1 и самих себя. Простые числа меньше 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83. , 89, 97. Из этого уже ясно, что для простых чисел нет очевидной закономерности: в некоторых сериях чисел вы получите много простых чисел, в других сериях вы не найдете простых чисел, и имеет ли серия много простых чисел или отсутствие простых чисел кажется совершенно случайным.
Простые числа меньше 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83. , 89, 97. Из этого уже ясно, что для простых чисел нет очевидной закономерности: в некоторых сериях чисел вы получите много простых чисел, в других сериях вы не найдете простых чисел, и имеет ли серия много простых чисел или отсутствие простых чисел кажется совершенно случайным.
В течение очень долгого времени математики пытались найти закономерность в простых числах. Приведенное выше уравнение представляет собой явную функцию для количества простых чисел, меньшего или равного заданному числу.
Вот что означают все буквы:
- — функция подсчета простых чисел, которая дает количество простых чисел, меньших или равных заданному числу. Например, так как существует 3 простых числа (2, 3, 5), меньшие или равные 6.
- — функция Мёбиуса, которая дает 0, -1 или 1 в зависимости от простой факторизации n.
- — логарифмическая интегральная функция, которая определяется как интеграл от 1/(log t) до x.

- — любой из нетривиальных нулей дзета-функции Римана.
Удивительно, но эта формула всегда дает точное целое число! Это означает, что для любого числа мы можем подставить это число в это уравнение и получить количество простых чисел, меньших или равных этому числу. Тот факт, что это уравнение существует, означает, что в простых числах есть какая-то закономерность, хотя нам, возможно, еще рано его понимать.
Дополнительную информацию по математике можно найти в другом моем блоге Epic Math. Кроме того, для одного из своих занятий я написал немного более подробное объяснение (pdf) для № 10, но будьте осторожны — оно предназначено для склонных к математике.
Если вам понравился этот пост, обязательно ознакомьтесь с продолжением «10 удивительных математических фактов».
Нравится:
Нравится Загрузка…
11 самых красивых математических уравнений
(Изображение предоставлено Shutterstock/RT Wohlstadter (открывается в новой вкладке)) 92, получивший большую часть общественной славы, многие менее известные формулы имеют своих сторонников среди ученых. LiveScience попросила физиков, астрономов и математиков назвать их любимые уравнения; вот что мы нашли.
LiveScience попросила физиков, астрономов и математиков назвать их любимые уравнения; вот что мы нашли.Связанный: Из чего состоит Вселенная? Математика, говорит ученый
Общая теория относительности
(Изображение предоставлено Shutterstock/R.T. Wohlstadter )Приведенное выше уравнение было сформулировано Эйнштейном как часть его новаторской общей теории относительности в 1919 г.15. Теория произвела революцию в том, как ученые понимают гравитацию, описав силу как искривление ткани пространства и времени.
«Меня до сих пор удивляет, что одно такое математическое уравнение может описать, что такое пространство-время», — сказал астрофизик Научного института космического телескопа Марио Ливио, назвав это уравнение своим любимым. «Весь истинный гений Эйнштейна воплощен в этом уравнении». [Викторина Эйнштейна: проверьте свои знания о гении]
«Правая часть этого уравнения описывает энергетическое содержание нашей Вселенной (включая «темную энергию», которая приводит в движение текущее космическое ускорение)», — объяснил Ливио.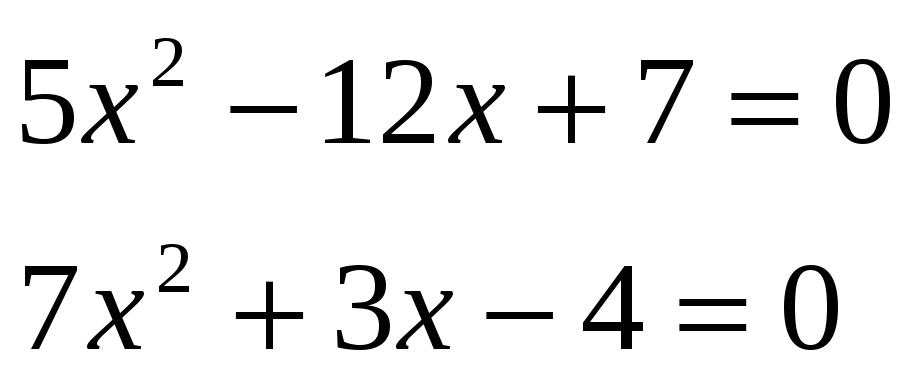 «Левая часть описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна масса и энергия определяют геометрию и, соответственно, кривизну, которая является проявлением того, что мы называем гравитацией». [6 странных фактов о гравитации]
«Левая часть описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна масса и энергия определяют геометрию и, соответственно, кривизну, которая является проявлением того, что мы называем гравитацией». [6 странных фактов о гравитации]
«Это очень элегантное уравнение», — сказал Кайл Крэнмер, физик из Нью-Йоркского университета, добавив, что уравнение раскрывает связь между пространством-временем, материей и энергией. «Это уравнение говорит вам, как они связаны — как присутствие Солнца искривляет пространство-время, так что Земля движется вокруг него по орбите и т. д. Оно также говорит вам, как развивалась Вселенная после Большого взрыва, и предсказывает, что должно черные дыры.»
Стандартная модель
(Изображение предоставлено Shutterstock/R.T. Wohlstadter (открывается в новой вкладке)) Еще одна господствующая теория физики, стандартная модель, описывает совокупность элементарных частиц, которые, как считается, в настоящее время составляют нашу Вселенную.
Теория может быть заключена в основное уравнение, называемое стандартной моделью Лагранжа (названное в честь французского математика и астронома 18-го века Жозефа Луи Лагранжа), которое было выбрано физиком-теоретиком Лэнсом Диксоном из Национальной ускорительной лаборатории SLAC в Калифорнии в качестве его любимая формула.
«Он успешно описал все элементарные частицы и силы, которые мы наблюдали в лаборатории на сегодняшний день, кроме гравитации», — сказал Диксон LiveScience. «Это включает, конечно, недавно открытый бозон Хиггса, phi в формуле. Он полностью согласуется с квантовой механикой и специальной теорией относительности».
Однако стандартная модельная теория еще не объединена с общей теорией относительности, поэтому она не может описывать гравитацию. [Инфографика: объяснение стандартной модели]
Исчисление
(Изображение предоставлено Shutterstock/agsandrew (открывается в новой вкладке)) В то время как первые два уравнения описывают отдельные аспекты нашей Вселенной, другое любимое уравнение можно применять ко всем видам ситуаций.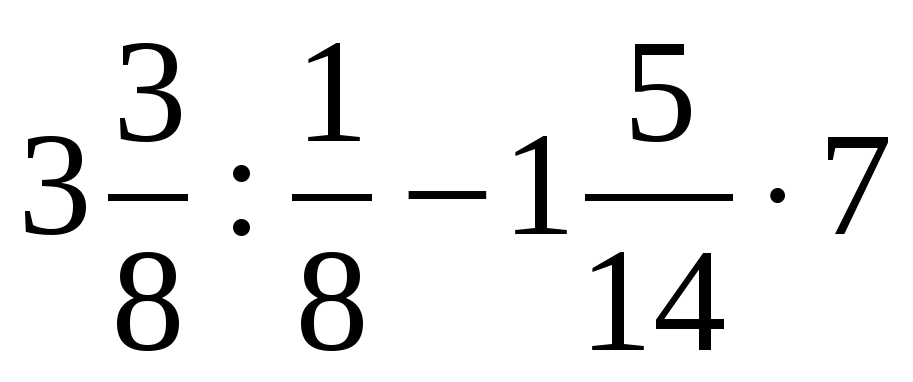 Основная теорема исчисления составляет основу математического метода, известного как исчисление, и связывает две его основные идеи, понятие интеграла и понятие производной.
Основная теорема исчисления составляет основу математического метода, известного как исчисление, и связывает две его основные идеи, понятие интеграла и понятие производной.
«Проще говоря, [это] говорит о том, что чистое изменение гладкой и непрерывной величины, такой как пройденное расстояние, за заданный интервал времени (т.е. разница значений величины в конечных точках времени интервал) равен интегралу скорости изменения этой величины, то есть интегралу скорости», — сказала Мелкана Бракалова-Тревитик, заведующая кафедрой математики Фордемского университета, выбравшая это уравнение своим любимым. «Фундаментальная теорема исчисления (FTC) позволяет нам определить чистое изменение за интервал на основе скорости изменения за весь интервал».
Семена исчисления зародились в древние времена, но большая часть их была собрана в 17 веке Исааком Ньютоном, который использовал исчисление для описания движения планет вокруг Солнца.
Теорема Пифагора.
.Эта формула описывает, как для любого прямоугольного треугольника квадрат длины гипотенузы, 92
«Самым первым математическим фактом, который меня поразил, была теорема Пифагора», — сказала математик Дайна Таймина из Корнельского университета. «Я тогда был ребенком, и мне казалось таким удивительным, что это работает в геометрии и работает с числами!» [5 ошеломляющих математических фактов]
«Я тогда был ребенком, и мне казалось таким удивительным, что это работает в геометрии и работает с числами!» [5 ошеломляющих математических фактов]
1 = 0,999999999….
(Изображение предоставлено Shutterstock/Tursunbaev Ruslan )Это простое уравнение, утверждающее, что число 0,999, за которым следует бесконечная цепочка девяток, эквивалентно единице, принадлежит математику Стивену Строгацу. Корнельского университета.
«Мне нравится, насколько это просто — все понимают, что там написано, — и в то же время провокационно», — сказал Строгац. «Многие люди не верят, что это может быть правдой. Это также прекрасно сбалансировано. Левая сторона представляет собой начало математики, правая сторона представляет тайны бесконечности».
Специальная теория относительности
(Изображение предоставлено Shutterstock/optimarc (открывается в новой вкладке)) Эйнштейн снова попал в список со своими формулами специальной теории относительности, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее относительными в зависимости от скорости наблюдателя. Приведенное выше уравнение показывает, как время растягивается или замедляется, чем быстрее человек движется в любом направлении.
Приведенное выше уравнение показывает, как время растягивается или замедляется, чем быстрее человек движется в любом направлении.
«Дело в том, что это действительно очень просто», — сказал Билл Мюррей, физик частиц из лаборатории CERN в Женеве. «Там нет ничего, что не мог бы сделать отличник, никаких сложных производных и алгебры следов. Но то, что он воплощает, — это совершенно новый взгляд на мир, целостное отношение к реальности и наше отношение к ней. неизменный космос сметается и заменяется личным миром, связанным с тем, что вы наблюдаете. Вы переходите от пребывания вне вселенной, глядя вниз, к одному из компонентов внутри нее. Но концепции и математику может понять каждый, кто хочет к.»
Мюррей сказал, что предпочитает уравнения специальной теории относительности более сложным формулам более поздней теории Эйнштейна. «Я никогда не мог следовать математике общей теории относительности», — сказал он.
Уравнение Эйлера
(Изображение предоставлено: Shutterstock/Jezper )Эта простая формула заключает в себе что-то чистое о природе сфер:
граней, ребер и вершин, и пусть F — количество граней, E — количество ребер и V — количество вершин, вы всегда получите V — E + F = 2», — сказал Колин Адамс, математик из Уильямс-колледжа в Массачусетс.
«Возьмем, к примеру, тетраэдр, состоящий из четырех треугольников, шести ребер и четырех вершин», — пояснил Адамс. «Если вы сильно подуете на тетраэдр с гибкими гранями, вы можете округлить его до сферы, так что в этом смысле сферу можно разрезать на четыре грани, шесть ребер и четыре вершины. И мы видим, что V – E + F = 2. То же верно для пирамиды с пятью гранями — четырьмя треугольными и одной квадратной — с восемью ребрами и пятью вершинами» и любой другой комбинацией граней, ребер и вершин.
«Очень крутой факт! Комбинаторика вершин, ребер и граней фиксирует что-то очень фундаментальное в форме сферы», — сказал Адамс.
Уравнения Эйлера-Лагранжа и теорема Нётер
(Изображение предоставлено Shutterstock/Marc Pinter ) «Это довольно абстрактно, но удивительно мощно», — сказал Кранмер из Нью-Йоркского университета. «Круто то, что такой взгляд на физику пережил некоторые крупные революции в физике, такие как квантовая механика, теория относительности и т. д.»
д.»
Здесь L означает лагранжиан, который является мерой энергии в физической системе, такой как пружины, рычаги или элементарные частицы. «Решение этого уравнения говорит вам, как система будет развиваться со временем», — сказал Кранмер.
Побочный продукт уравнения Лагранжа называется теоремой Нётер в честь немецкого математика 20-го века Эмми Нётер. «Эта теорема действительно фундаментальна для физики и роли симметрии», — сказал Кранмер. «Неформально теорема состоит в том, что если ваша система обладает симметрией, то существует соответствующий закон сохранения. Например, идея о том, что фундаментальные законы физики сегодня такие же, как и завтра (временная симметрия), подразумевает, что энергия сохраняется. идея о том, что законы физики здесь такие же, как и в космическом пространстве, подразумевает, что импульс сохраняется. Симметрия, возможно, является движущей концепцией в фундаментальной физике, в первую очередь благодаря вкладу [Нётер]».
Уравнение Каллана-Симанзика
(Изображение предоставлено Shutterstock/R. T. Wohlstadter )
T. Wohlstadter )«Уравнение Каллана-Симанзика — это жизненно важное уравнение из первых принципов 1970 года, необходимое для описания того, как наивные ожидания не оправдаются. в квантовом мире», — сказал физик-теоретик Мэтт Страсслер из Университета Рутгерса.
Это уравнение имеет множество применений, в том числе позволяет физикам оценивать массу и размер протона и нейтрона, составляющих ядра атомов.
Основы физики говорят нам, что сила гравитации и электрическая сила между двумя объектами обратно пропорциональны квадрату расстояния между ними. На простом уровне то же самое верно для сильного ядерного взаимодействия, которое связывает протоны и нейтроны вместе, образуя ядра атомов, и которое связывает кварки вместе, образуя протоны и нейтроны. Однако крошечные квантовые флуктуации могут немного изменить зависимость силы от расстояния, что имеет драматические последствия для сильного ядерного взаимодействия.
«Это предотвращает уменьшение этой силы на больших расстояниях и заставляет ее захватывать кварки и объединять их, чтобы сформировать протоны и нейтроны нашего мира», — сказал Штрасслер. «Уравнение Каллана-Симанзика связывает этот драматический и трудно поддающийся расчету эффект, важный, когда [расстояние] примерно равно размеру протона, с более тонкими, но более легкими для расчета эффектами, которые можно измерить, когда [ расстояние] намного меньше протона».
«Уравнение Каллана-Симанзика связывает этот драматический и трудно поддающийся расчету эффект, важный, когда [расстояние] примерно равно размеру протона, с более тонкими, но более легкими для расчета эффектами, которые можно измерить, когда [ расстояние] намного меньше протона».
Уравнение минимальной поверхности
(Изображение предоставлено Shutterstock/MarcelClemens )«Уравнение минимальной поверхности каким-то образом кодирует красивые мыльные пленки, которые образуются на границах проводов, когда вы опускаете их в мыльную воду», — сказал математик Фрэнк Морган из колледжа Уильямс. . «Тот факт, что уравнение является «нелинейным» и включает в себя степени и произведения производных, является закодированным математическим намеком на удивительное поведение мыльных пленок. Это контрастирует с более известными линейными уравнениями в частных производных, такими как уравнение теплопроводности, волновое уравнение и уравнение Шрёдингера в квантовой физике».
Прямая Эйлера
(Изображение предоставлено Патриком Ионом/Mathematical Reviews/AMS) Глен Уитни, основатель Музея математики в Нью-Йорке, выбрал другую геометрическую теорему, имеющую отношение к прямой Эйлера, названную в честь швейцарского математика и физика XVIII века Леонарда Эйлера.
«Начните с любого треугольника», — объяснила Уитни. «Нарисуйте наименьший круг, содержащий треугольник, и найдите его центр. Найдите центр масс треугольника — точку, в которой треугольник, если его вырезать из листа бумаги, балансировал бы на булавке. Нарисуйте три высоты треугольника. треугольника (линии, проведенные из каждого угла перпендикулярно противоположной стороне), и найдите точку, где они все пересекаются. Теорема состоит в том, что все три точки, которые вы только что нашли, всегда лежат на одной прямой, называемой «прямой Эйлера» треугольник».
Уитни сказала, что теорема заключает в себе красоту и силу математики, которая часто обнаруживает удивительные закономерности в простых, знакомых формах.
Подписывайтесь на Клару Московиц в Твиттере @ClaraMoskowitz или LiveScience @livescience. Мы также есть в Facebook и Google+.
Клара имеет степень бакалавра астрономии и физики Уэслианского университета, а также диплом о высшем образовании в области научного письма Калифорнийского университета в Санта-Круз. Она писала для Space.com и Live Science.
Она писала для Space.com и Live Science.
мягкий вопрос — Можете ли вы привести пример сложной математической задачи, которую легко решить?
Спросил
Изменено 1 год, 11 месяцев назад
Просмотрено 19 тысяч раз
$\begingroup$
Я работаю над презентацией проекта и хотел бы проиллюстрировать, что часто бывает трудно или невозможно оценить, сколько времени займет выполнение задачи. Я хотел бы подчеркнуть это, представив три математические задачи (вероятно, доказательства), которые на первый взгляд кажутся одинаково сложными. Но…
- Одно легко решить (или доказать)
- Сложно решить (или доказать)
- И один невозможен
Итак, если математик не может просто посмотреть на задачу и сказать: «Я могу решить ее за день, неделю или месяц, как может кто-то еще, кто действительно решает задачу? Сама природа решения проблем заключается в том, что мы не знаем, где находятся решения, и поэтому мы не знаем, сколько времени потребуется, чтобы добраться до них.
Мы будем очень признательны за любой вклад или предложения.
- мягкий вопрос
$\endgroup$
12
$\begingroup$
Это не совсем то, о чем вы просите, но оно должно очень хорошо служить той же цели.
Примерно в 1920 году Гильберт выступил с докладом, в котором обсуждал сложность различных проблем.
Он сказал, что за последние годы в аналитической теории чисел был достигнут большой прогресс, и он надеется, что доживет до доказательства гипотезы Римана. 9{\sqrt2}$ был установлен в 1929 году — Гильберт дожил до этого.
Fermat, как известно, продержался до 1990-х годов.
И Гипотеза Римана до сих пор не доказана.
Смысл рассказа не в том, чтобы высмеять Гильберта. Суть этой истории в том, что если даже Гильберт, сильнейший математик своего времени, мог так ошибаться в оценке относительной сложности различных математических задач, то это должно быть действительно трудно сделать, что, я думаю, и является точка, которую вы пытаетесь сделать.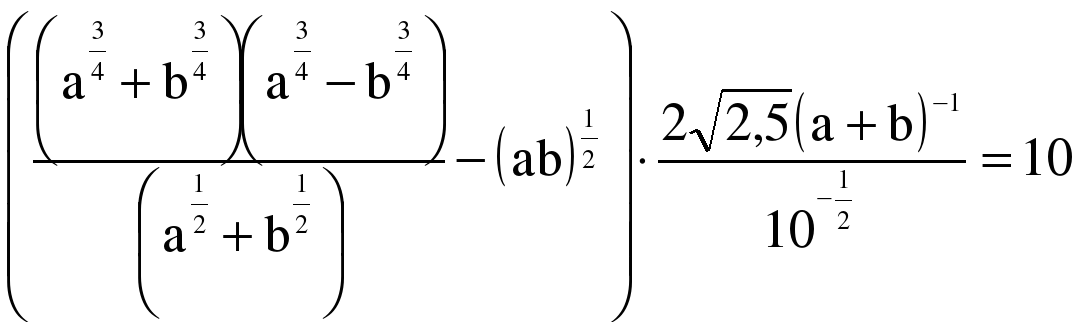 93 = п$.
93 = п$.
1) При $n = 29$ легко найти решение: $(x,y,z) = (3,1,1)$.
2) При $n = 33$ найти решение сложнее, но одно известно: $$ (х, у, г) = (8866128975287528, -8778405442862239, -2736111468807040). $$ Это было обнаружено в 2019 году Эндрю Букером. См. https://people.maths.bris.ac.uk/~maarb/papers/cubesv1.pdf и https://www.youtube.com/watch?v=ASoz_NuIvP0.
3) Здесь я ранее использовал $n = 42$, говоря, что мы ожидаем, что это сумма трех кубов в $\mathbf Z$, но что представление $42$ в такой форме в настоящее время не было известно в то время, когда я писал это . Сейчас (сентябрь 2019 г.3$. Я не хочу обновлять этот ответ снова и снова, поэтому я просто скажу, что мы ожидаем, что каждое целое число $n \not\equiv 4, 5 \bmod 9$ представляет собой сумму трех кубов в $\mathbf Z$ и для такого общего $n$ это все еще открытая проблема.
$\endgroup$
3
$\begingroup$
Один набор, который (я думаю) соответствует вашим требованиям и для которого утверждения доступны многим:
- Докажите, что $\sqrt{2}$ иррационально
- Докажите, что $e$ иррационально
- Докажите, что $e+\pi$ иррационально
$\endgroup$
6
$\begingroup$
Знаменитым примером, хотя он может потребовать больше информации, чем вам хотелось бы, является проблема Бернсайда, которая задает следующий вопрос: если группа конечно порождена и обладает тем свойством, что каждый элемент имеет порядок $n$ для некоторого фиксированного положительного целое число $n$, обязательно ли оно конечно?
- При $n = 2$ ответ положительный по прямому рассуждению.
 m $ где $m$ — количество генераторов.
m $ где $m$ — количество генераторов. - Для $n = 3, 4, 6$ ответ по-прежнему положительный, но аргумент сложнее.
- Для $n = 5$ проблема остается открытой! (Я думаю. Согласно Википедии, по крайней мере, конкретный случай двух генераторов все еще открыт.)
$\endgroup$
1
$\begingroup$
Легко умножить два 20-значных простых числа, но что, если бы вам пришлось разложить их произведение на множители? У вас есть простая проблема и сложная проблема. 9{\cdot}}}}}}=2$, Решите для $x$.
2 — Гипотеза Пуанкаре (Каждое односвязное замкнутое 3-многообразие гомеоморфно 3-сфере.).
3 — Гипотеза континуума (Первая проблема Гильберта). Этот вопрос неразрешим.
Комментарии:
1 — Эта задача выглядит очень сложной. Как найти $x$, когда мы возводили его до него бесконечное количество раз, и это должно быть равно $2$.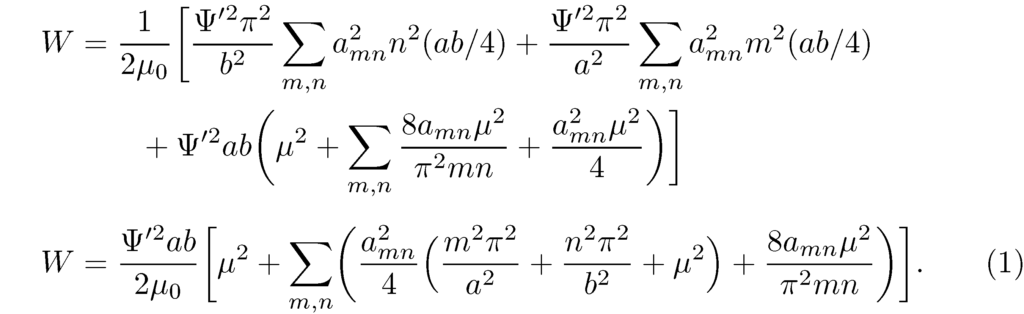 2}{6}$. (И есть аналогичные утверждения для дзета-функции четных целых чисел).
2}{6}$. (И есть аналогичные утверждения для дзета-функции четных целых чисел).
$\zeta(3)$ иррационально. Известен, но не ранее 1978 года. Здесь у нас есть иррациональность, но нет замкнутого выражения в терминах понятных констант. (Кроме того, насколько мне известно, нет никаких оснований ожидать существования такого выражения).
$\zeta(5)$ иррационально. Открытым. Мы знаем, что $\zeta(2k+1)$ бесконечно часто является иррациональным, и хотя бы одно из $\zeta(5)$, $\zeta(7)$, $\zeta(9)$ и $\zeta( 11) $ иррационально.
(Ссылки на более подробную информацию см. в этом посте. В статье Википедии о теореме Апери также перечислены некоторые результаты.) 9a (8b+7)$ и, хотя и не невозможно, доказательство значительно сложнее, чем два предыдущих.
$\endgroup$
$\begingroup$
Иногда проблема, которая кажется очень сложной, оказывается «легкой», потому что кто-то был достаточно умен, чтобы посмотреть на нее правильно. Два примера этого:
Два примера этого:
а. Построить множество негомильтоновых плоских 3-валентных 3-связных графов (такие графы могут быть реализованы выпуклыми 3-мерными многогранниками). Условие Гринберга обеспечивает отличный подход к легкому поиску таких графов: http://en.wikipedia.org/ вики/Гринберг%27s_theorem
б. Задача Клее в художественной галерее: найти количество вершинных охранников, которые иногда необходимы и всегда достаточны, чтобы «увидеть» всю внутреннюю часть плоского простого многоугольника с n вершинами. В. Чватал и Стив Фиск нашли простые способы ответить на этот вопрос: http://en.wikipedia.org/wiki/Art_gallery_theorem
$\endgroup$
$\begingroup$
Вы рассмотрели знаменитую классификацию всех конечных простых групп? См. здесь для истории этого усилия. Кроме того, тесно связанная с этим гипотеза Бернсайда (192}{6}$
$\zeta(1+it) \neq 0$
$\zeta(s)=0$ $\имплицит$ $\Re(s)= 1/2$, если $s$ лежит в правой полуплоскости.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
мягкий вопрос — Способы написать «50»
Вопрос
Изменено 7 лет, 9 месяцев назад
Просмотрено 34k раз
$\begingroup$
Закрыто . Этот вопрос должен быть более целенаправленным. В настоящее время ответы не принимаются.
Этот вопрос должен быть более целенаправленным. В настоящее время ответы не принимаются.
Хотите улучшить этот вопрос? 92}$$
Какие еще творческие способы я могу превзойти его торт?
Должен отметить, что он учитель начальных классов. Теперь он ЛЮБИТ математику, и я точно могу показать ему множество выражений. Я не хочу, чтобы они были настолько сложными, чтобы для их решения требовалась степень магистра, но они, безусловно, должны быть достаточно интересными, чтобы вызвать у него восхищение. Элементарные функции хороши, суммирование тоже хорошо, интегралы можно объяснить, так что это тип выражения, который я ищу…
РЕДАКТИРОВАТЬ:: Я хотел бы отметить, что здесь мы говорим о торте, так что с этого момента полагайтесь на свое суждение. Подумайте об обычном прямоугольном торте и о том, насколько он велик. Следовательно, длинные цепочки чисел, комплексные интегралы и длинные суммы не будут работать. Я ценю ответы, но мне нужны более компактные выражения. 2$. 9{2\operatorname{Li}_1(\frac12)}\operatorname{Li}_2\left(\frac{\Gamma'(1)}{\Psi(1)}\right)}$
2$. 9{2\operatorname{Li}_1(\frac12)}\operatorname{Li}_2\left(\frac{\Gamma'(1)}{\Psi(1)}\right)}$
$\endgroup$
7
$\begingroup$
Я пошел навестить его, когда он лежал больной в больнице. Я приехал в такси номер $50$ и заметил, что это был довольно скучный номер. «Нет, — ответил он, — это очень интересное число. Это наименьшее число, которое можно представить как произведение 25 долларов и 2 долларов двумя разными способами». https://mathoverflow.net/a/219{11}n-2n\right)-10=50$$
Используя только 5 и 0: $5,5\фракция{505}{5}-5,55=50$$ Что-то аккуратное, используя шаблон 1…7,1: $$1\cdot 2+3\cdot 4+5\cdot 6+7-1=50$$ Где $x_n$ обозначает $x$ в системе счисления $n$: $302_4=50$$ $200_5=50$$ $32_{16}=50$$ $$62_8=50$$
Если $\alpha=\#A$ утверждает, что $\alpha$ является кардиналом $A$, то:
$$\#\{x\in\mathbb{N}:5 $\endgroup$ $\begingroup$ Разложение на простые множители 9{10}(2n-1) \mod 10$$
$$50=1212_3$$
$$\left(4+\frac{4}{4}\right)\dfrac{\binom{4}{4-\frac{4}{4}}}{0,4}=50$$ $\endgroup$ $\begingroup$ Можно использовать римский вариант с $$\Huge{L}$$ Или с $$\begin{array}{c} \\ \\ \end{array}$$ $$\begin{array} {ccccccccccccc} \Huge{X}&&&&&&&&&&&&&&\Huge{X}\\ \\ \\ \\
&&&&&&\Huge{X}\\ \\ \\ \\ \Huge{X}&&&&&&&&&&&&&\Huge{X} \end{массив}\\ $$ 92}dx$$ можно усложнить, но на торте не влезет 🙂 $\endgroup$ 2 Очень активный вопрос . Люди, которые любят математику, и люди, которые ее ненавидят, сходятся в одном: вам всего 9 лет0127 действительно занимается математикой, если вы садитесь и пишете формальные уравнения. Эта идея настолько широко распространена, что предлагать обратное — значит «начинать драку», — говорит Мария Дружкова, преподаватель математики и основатель Natural Math, сайта для детей и родителей, которые хотят включить математику в свою повседневную жизнь. Математики дорожат своими формальными доказательствами, считая их лучшим выражением своей профессии, в то время как антиматематики не верят, что большая часть математики, которую они изучали в школе, применима к «реальной жизни». Но на самом деле «в нашей повседневной жизни мы делаем очень много вещей, которые глубоко математические, но на первый взгляд могут не выглядеть таковыми», — говорит Кристофер Дэниелсон, преподаватель математики из Миннесоты и автор ряда книг. Из всей математики алгебра, кажется, вызывает наибольшее раздражение, и некоторые люди даже пишут целые книги о том, почему студенты не должны терпеть ее, потому что, как они утверждают, она удерживает студентов вернулся с выпускного. Но если вы готовите, вы, скорее всего, занимаетесь алгеброй. При приготовлении еды часто приходится мыслить пропорционально, а «рассуждение с пропорциями — один из краеугольных камней алгебраического мышления», — рассказывает Дружкова Mental Floss. Вы также мыслите алгебраически всякий раз, когда корректируете рецепт, будь то для большего количества людей или потому, что вам нужно заменить или уменьшить количество ингредиентов. Люси Кинтанилья Однако, рассуждая пропорционально, вы можете просто прийти к выводу, что, поскольку у вас на одну треть меньше яиц, вы должны использовать на одну треть меньше муки. Вы также мыслите пропорционально, когда учитываете время приготовления различных блюд и соответственно планируете, чтобы все элементы вашего ужина были готовы одновременно. Например, на приготовление риса обычно уходит в три раза больше времени, чем на приготовление сплющенной куриной грудки, поэтому имеет смысл начинать сначала с риса. «Люди занимаются математикой по-своему, — говорит Дружкова, — даже если они не могут делать это очень формализованно». iStock Создание музыки включает в себя множество различных типов математики, от алгебры и геометрии до теории групп и теории паттернов и выше, а также ряд математиков (включая Пифагора и Галилей), а музыканты соединили эти две дисциплины (Стравинский утверждал, что музыка — это «нечто вроде математического мышления»). Но простое прослушивание музыки может заставить вас мыслить математически. Когда вы узнаете музыкальное произведение, вы идентифицируете звуковой паттерн. Шаблоны являются фундаментальной частью математики; ветвь, известная как теория паттернов, применяется ко всему, от статистики до машинного обучения. Дэниэлсон, который учит детей закономерностям на уроках математики, говорит, что понимание структуры закономерности жизненно важно для понимания математики на более высоких уровнях, поэтому музыка — отличный способ: «Если вы думаете о том, как две песни имеют сходство, удары, размер, или вы создаете гармонии, вы работаете над структурой паттерна и попутно делаете некоторые действительно важные математические размышления». Так что, возможно, вы не занимались математикой на бумаге, если спорили с друзьями о том, был ли прав Том Петти, подав в суд на Сэма Смита в 2015 году из-за песни «Останься со мной», звучащей очень похоже на «Я не отступлю». но вы все еще думали математически, когда сравнивали песни. И этот ушной червь, которого ты не можешь выгнать из головы? Он следует схеме: вступление, куплет, припев, проигрыш, конец. Когда вы распознаете такие паттерны, вы также распознаете симметрию (которая в поп-песне обычно включает в себя припев и хук, потому что они повторяются). Симметрия [PDF] лежит в основе теории групп, но она также является ключом к геометрии, алгебре и многим другим математическим дисциплинам. Шерил, Flickr // CC BY-SA 2.0 Дружкова, заядлая вязальщица, говорит, что ее часто интригуют очень математические дискуссии, которые коллеги-рукодельницы ведут в Интернете о лучших узорах. Дружкова не единственная любительница математики, которая установила связь между геометрией и вязанием крючком. Математик из Корнелла Дайна Таймина обнаружила, что вязание крючком — идеальный способ проиллюстрировать геометрию гиперболической плоскости или поверхности с постоянной отрицательной кривизной, такой как лист салата. Гиперболическая геометрия также используется в навигационных приложениях и объясняет, почему плоские карты искажают размеры рельефа, из-за чего Гренландия, например, на большинстве карт выглядит намного больше, чем она есть на самом деле. iStock Если вы играете в бильярд, пул или снукер, весьма вероятно, что вы используете тригонометрические рассуждения. В статье 2010 года [PDF] математик из Луизианы Рик Мабри изучил тригонометрию (и базовое исчисление) пула, сосредоточив внимание на прямом ударе. В баре в Шривпорте, штат Луизиана, он нацарапал уравнения на салфетках для каждого выстрела и вычислил самый сложный удар прямо из всех. Большинство опытных игроков в бильярд сказали бы, что это когда целевой шар находится на полпути между лузой и битком. Но это, согласно уравнениям Мабри, оказалось неверным. У самого сложного удара была удивительная особенность: расстояние от битка до лузы было ровно в 1,618 раза больше расстояния от целевого шара до лузы. Нужно ли учитывать золотое сечение при выборе места для битка? Нет, если только вы не хотите доказать свою точку зрения или настроить кого-то на проигрыш. Вы выполняете триггер автоматически. Акулы у бассейна, должно быть, знали об этом, потому что кто-то выбросил математические салфетки Мабри. iStock Многие учащиеся не изучают исчисление в средней школе или даже в колледже, но краеугольным камнем этой области математики является оптимизация — или выяснение того, как получить наиболее точное использование пространства или отрезка времени. Рассмотрим проект по благоустройству дома, в котором вы столкнулись с облицовкой плиткой чего-то, форма которого не соответствует геометрической формуле, такой как круг или прямоугольник, например, асимметричное основание унитаза или отдельно стоящая раковина. Суммы Римана (названные в честь немецкого математика 19-го века) имеют решающее значение для объяснения интегрирования в исчислении, так как являются реальным введением в более точную фундаментальную теорему. График суммы Римана показывает, как можно найти площадь кривой, строя прямоугольники вдоль оси абсцисс, или горизонтальной оси, сначала до кривой, а затем над ней, а затем усредняя расстояние между перекрытием и недокрытием до получить более точное измерение. Математика всегда вокруг нас , куда бы мы ни пошли. И это потому, что математика настолько широка, что охватывает сложение и вычитание, деление, дроби, графики, округление, решение уравнений, алгебру, неравенства, переменные, статистику, подстановку, тригонометрию, вычисления, распределительное свойство, симметрию, целые числа, простые числа, вероятность, значение, векторы, фигуры, последовательность, пропорции и многое другое! Будь то строительство вашего дома, планировка улиц в вашем районе, простое действие по запуску автомобиля или включению посудомоечной машины, когда вы делаете что-то своими руками или играете на пианино, сложная и базовая математика действительно везде. Не существует ни одного объекта, который не был бы каким-то образом результатом математики в действии , которую вы будете изучать на уроках математики в школе и далее на дополнительных уроках математики. Сложные уравнения с множеством неизвестных, радикальные математические теоремы, восходящие к древности, к открытиям конца двадцатого века, сформировали наш мир. И с каждой новой концепцией наше понимание физического мира вокруг нас растет. В 2013 г., Известный британский математик и ученый Ян Стюарт опубликовал книгу под названием «17 уравнений, которые изменили мир» (изд. Роберт Лаффонт). Поскольку математика является широким применением материи , а не открытием, мы не можем приписать одному человеку изобретение самой математики (если только вы не хотите быть очень глубоким и сказать, что создатель нашей вселенной несет ответственность за рождение математики!). Тем не менее, мы можем оглянуться на , когда математика начала играть роль в жизни людей. Неудивительно, что свидетельства показывают, что даже те, кто жил в доисторические времена, имели некоторое понимание математических понятий , записи которых были найдены на многих предметах, таких как кости и настенная резьба. Маркировка показала бы, что они использовали рациональное мышление при обучении тому, как решать простые математические задачи , такие как сложение вещей на площади поверхности. Так что же побудило их заинтересоваться математикой в первую очередь? Течение времени, например, заинтриговало бы их. Вычисляя, сколько времени им осталось охотиться за едой до захода солнца, возможно, для ответа на этот вопрос они обратились бы к астрономии. The Star Garden утверждает, что: «Кости Ишанго около 20 000 лет, и на ней есть ряд выемок, вырезанных в трех столбцах. Узоры в этих числах могут указывать на то, что они были сделаны кем-то, кто понимал сложение, вычитание , умножение, деление и простые числа». Далее они говорят, что: «Люди поняли геометрию и алгебру примерно к 2000 г. до н. длина окружности к ее диаметру. Примерно к 1500 г. до н.э. вавилоняне также знали о теореме Пифагора, которая показывает, как связаны длины сторон прямоугольных треугольников». Теорема названа в честь древнегреческого математика Пифагора (хотя некоторые говорят, что эта концепция предшествует ему), что показывает, что, хотя все математические теоремы и формулы просто существуют и ждут своего открытия, мы можем, по крайней мере, похвалить некоторых людей за их обнаружение или отрабатывая их. В своей краткой истории математики веб-сайт The Star Garden добавляет: «Кеплер также был вдохновлен Пифагором и считал, что движение планет порождает музыку. Он использовал математику, чтобы показать, что планеты вращаются вокруг Солнца по эллипсам и, к 1619 г., он смог определить время, необходимое каждой планете для обращения по орбите, и их относительное расстояние от Солнца. В 1687 году Ньютон опубликовал свой закон всемирного тяготения. Это было новаторским, потому что оно показало, что не только абстрактные математические принципы, такие как недавно изобретенное исчисление, могут быть применены к тому, что мы наблюдаем в природе, но и то, что законы, ответственные за движение планет, также ответственны за движение объектов. Современник Ньютона, Лейбниц, открыл еще одну связь между математикой и природой, когда впервые рассмотрел идею фракталов. […] Математики двадцатого века, такие как французский математик Гастон Джулия и польско-французско-американский математик Бенуа Мандельброт, были вдохновлены Лейбницем на создание собственных сложных фракталов. К этому времени квантовая механика и теории специальной и общей теории относительности немецкого швейцарско-американского физика Альберта Эйнштейна показали, что природа подчиняется законам математики, даже когда это противоречит нашему здравому смыслу понимания мира».0003 Итак, как мы видим, математика всегда присутствовала на протяжении всей истории человечества, но ряд значительных прорывов появился благодаря опытным математикам, которые пришли их найти. Ниже мы рассмотрим некоторые из самых известных математических уравнений. В завершение истории математики важно отметить, что, несмотря на то, что человечество не развивалось с использованием математических понятий, математика всегда играла свою роль на планете. Еще до появления людей математика диктовала всю природу, а также источники энергии и животных, украшавших Землю, благодаря ее необходимости в воспроизводстве и жизни в целом. Лучшие репетиторы по математике Поехали Если вам интересно, почему математика так важна и какое влияние оказывает каждое основное уравнение, читайте дальше, чтобы узнать 10 революционных формул , которые помогут вам обучение математике на другой уровень. Конечно, нет конца количеству существующих математических формул и выражений (некоторые могут сказать, что их список бесконечен!), но здесь мы сосредоточимся на некоторых наиболее известных алгебраических уравнениях и приведем некоторые полезные обозначения. Не забывайте, Superprof может помочь вам найти идеального репетитора по математике, если вы захотите получить помощь по математике с помощью онлайн-репетитора! Это, безусловно, одна из самых известных теорем. Даже спустя годы после вашего последнего урока математики его название легко приходит на ум. Возможно, вы знаете это наизусть, но давайте быстро повторим: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратных корней длин двух других сторон. Эта теорема, датируемая 530 г. до н. э., по сей день является одной из основ математики и вносит свой вклад в историю математики с момента ее открытия. Это уравнение необходимо для понимания геометрии и тригонометрии, и оно действительно сформировало наше понимание этих разделов математики. Говорят, что мы перешли от евклидовой геометрии к неевклидовой геометрии. С тех пор, благодаря Пифагору и его знаменитому уравнению, теперь легко вычислить длины, углы и доказать, что данный треугольник является прямоугольным . Эту концепцию часто можно встретить в сферах строительства и архитектуры. Логарифмы, популяризированные Джоном Нейпиром в 1610 году, сочетают в себе обратные и экспоненциальные функции, а также противоположности. Логарифмы часто используются в формулах, используемых в науке для измерения сложности алгоритмов и фракталов, а также в формулах для подсчета простых чисел. До появления современных компьютеров вычисления с использованием логарифмов были наиболее распространенным способом умножения больших чисел и позволяли выполнять более быстрые вычисления. , но, прежде всего, помог сделать рывок в областях математики, физики, техники и астрономии . Существует 3 типа логарифмов: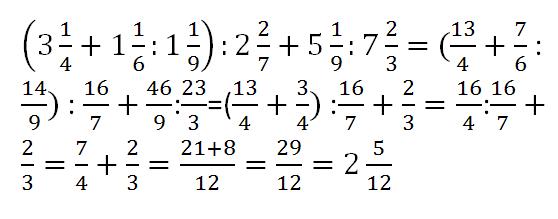 Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа.
Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа. 5 способов решать сложные математические задачи в уме, даже не осознавая этого
 книги, в том числе Common Core Math для родителей для чайников , рассказывает Mental Floss. Наше математическое мышление включает в себя не только алгебру или геометрию, но и тригонометрию, исчисление, вероятность, статистику и любой из по крайней мере 60 видов математики [PDF]. Вот пять примеров.
книги, в том числе Common Core Math для родителей для чайников , рассказывает Mental Floss. Наше математическое мышление включает в себя не только алгебру или геометрию, но и тригонометрию, исчисление, вероятность, статистику и любой из по крайней мере 60 видов математики [PDF]. Вот пять примеров. 1. КУЛИНАРИЯ // АЛГЕБРА
 Скажем, например, вы хотите испечь блины, но у вас осталось только два яйца, а по рецепту требуется три. Сколько муки следует использовать, если по оригинальному рецепту требуется одна чашка? Поскольку одна чашка равна 8 унциям, вы можете вычислить это, используя следующее алгебраическое уравнение: n/8 : 2/3.
Скажем, например, вы хотите испечь блины, но у вас осталось только два яйца, а по рецепту требуется три. Сколько муки следует использовать, если по оригинальному рецепту требуется одна чашка? Поскольку одна чашка равна 8 унциям, вы можете вычислить это, используя следующее алгебраическое уравнение: n/8 : 2/3.
2. ПРОСЛУШИВАНИЕ МУЗЫКИ // ТЕОРИЯ ОБРАЗОВ И СИММЕТРИЯ

3. ВЯЗАНИЕ С ВЯЗЬЕМ И КРЮЧКОМ // ГЕОМЕТРИЧЕСКОЕ МЫШЛЕНИЕ
 для своих проектов, даже если они часто будут настаивать на том, что плохо разбираются в математике или не интересуются ею. И все же такие поделки не могут быть сделаны без геометрического мышления: когда вы вяжете шапку спицами или крючком, вы создаете полусферу, которая подчиняется геометрической формуле.
для своих проектов, даже если они часто будут настаивать на том, что плохо разбираются в математике или не интересуются ею. И все же такие поделки не могут быть сделаны без геометрического мышления: когда вы вяжете шапку спицами или крючком, вы создаете полусферу, которая подчиняется геометрической формуле. 4. ИГРА В ПУЛ // ТРИГОНОМЕТРИЯ
 Чтобы загнать шар в лузу, используя другой шар, нужно понимать не только то, как измерять углы визуально, но и триангуляцию, которая является краеугольным камнем тригонометрии. (Триангуляция — удивительно точный способ измерения расстояния. Задолго до того, как стали возможными полеты с двигателем, геодезисты использовали триангуляцию для измерения высоты гор от их основания и отклонялись всего на несколько футов.)
Чтобы загнать шар в лузу, используя другой шар, нужно понимать не только то, как измерять углы визуально, но и триангуляцию, которая является краеугольным камнем тригонометрии. (Триангуляция — удивительно точный способ измерения расстояния. Задолго до того, как стали возможными полеты с двигателем, геодезисты использовали триангуляцию для измерения высоты гор от их основания и отклонялись всего на несколько футов.) Это число представляет собой золотое сечение, которое встречается повсюду в природе и, по-видимому, на бильярдных столах.
Это число представляет собой золотое сечение, которое встречается повсюду в природе и, по-видимому, на бильярдных столах. 5. ЗАМЕНА ПЛИТКИ В ВАННОЙ // ВЫЧИСЛЕНИЕ
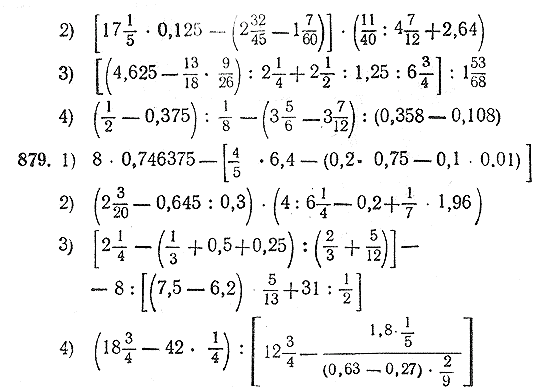 Вот здесь-то и пригодится фундаментальная теорема исчисления, которую можно использовать для точного вычисления площади объекта неправильной формы. Размышляя о том, как эти плитки лучше всего подходят к изгибу этой раковины или унитаза, и какую часть каждой плитки нужно отрезать или добавить, вы используете рассуждения, подобные тому, что делается в сумме Римана.
Вот здесь-то и пригодится фундаментальная теорема исчисления, которую можно использовать для точного вычисления площади объекта неправильной формы. Размышляя о том, как эти плитки лучше всего подходят к изгибу этой раковины или унитаза, и какую часть каждой плитки нужно отрезать или добавить, вы используете рассуждения, подобные тому, что делается в сумме Римана. 10 математических уравнений и формул, которые изменили мир

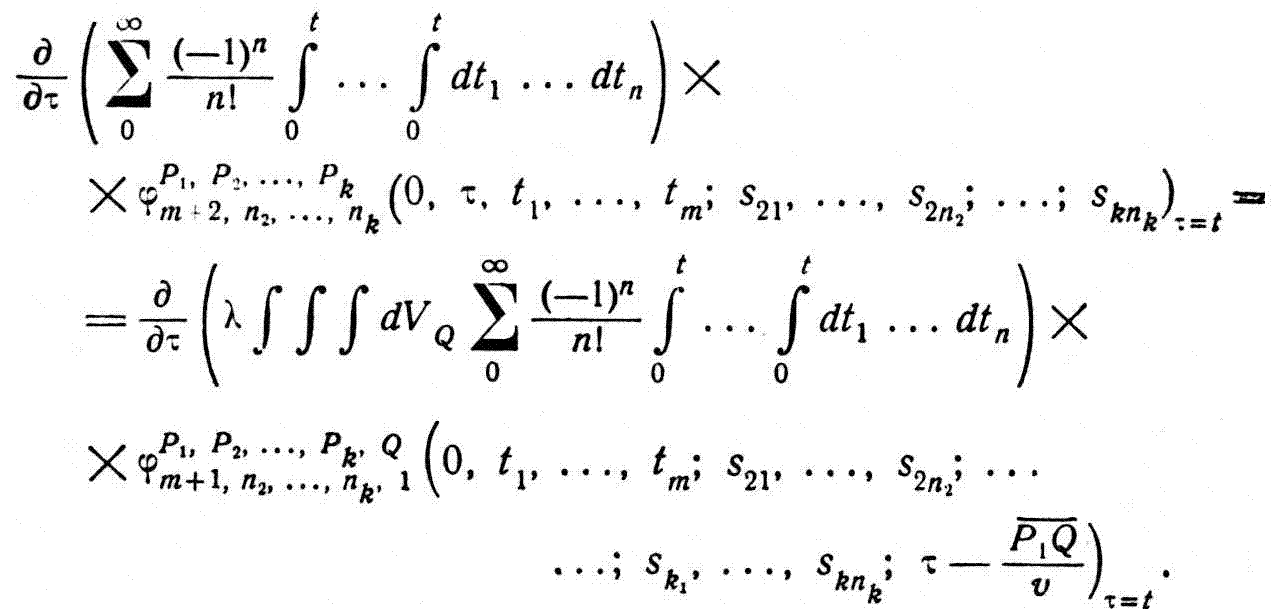
Сколько лет математическим формулам?

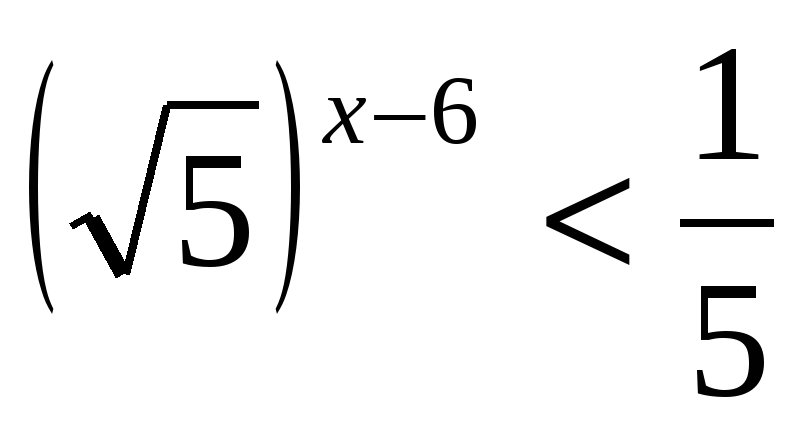
 на земле. Ньютон также считал, что вселенную можно понимать как математический объект, и описывал Бога как «сведущего в механике и геометрии».
на земле. Ньютон также считал, что вселенную можно понимать как математический объект, и описывал Бога как «сведущего в механике и геометрии».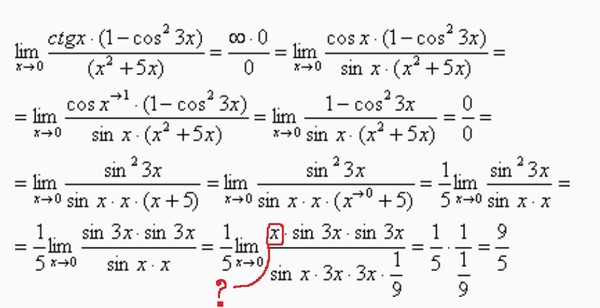
10 знаменитых математических уравнений

Теорема Пифагора
Когда теорема Пифагора встречается с искусством (Источник: commons.wikimedia.org)
Логарифмы

Например, в случае с основанием 10 логарифм (log): Log (1) = 0, log (10) = 1, log (100) = 2.
Такие вычисления полезны в, для например, покер, а в решение головоломок .
Закон всемирного тяготения
Кто никогда не слышал о знаменитом законе всемирного тяготения Исаака Ньютона ? Вы знаете историю о яблоке, которое упало на голову великого мыслителя, когда он созерцал луну в ночном небе, в 1687 году.
Закон всемирного тяготения в его современной форме (Источник: Wikipedia.org) связь между этими двумя телами (луной и яблоком), что Ньютон тогда задавался вопросом: почему луна не падает с неба? Ответ очевиден — сейчас: Он «поддерживается» гравитационной силой .
Так родился знаменитый закон всемирного тяготения Ньютона : «Астральные тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональна квадрату расстояния между их центрами».
Через 200 лет после Ньютона Эйнштейн заменил эту теорию гравитации своей теорией относительности.
Теория относительности
Независимо от того, разбирается ли человек в математике или физике или ничего не знает о математическом словаре, всем известна знаменитая формула Альберта Эйнштейна: E = mc² .
E представляет энергию, m массу тела и c скорость света (Источник: publicdomainpictures.net – Даниэле Пеллати) Эта формула, которая иллюстрирует теорию относительности (ограниченную теорию относительности и общую теорию относительности) произвела революцию в нашем понимании физика до этого момента.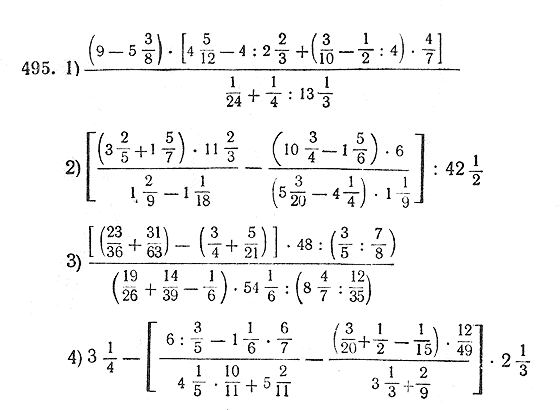
Он остается важным и по сей день, так как показывает, что материя может быть преобразована в энергию и наоборот.
Ограниченная теория относительности представила идею о том, что скорость света является универсальной константой, которая не изменяется, и что течение времени неодинаково для тел, движущихся с разными скоростями.
Общая теория относительности Эйнштейна описывает гравитацию, в которой пространство и время искривлены и свернуты: серьезное изменение в нашем понимании после закона всемирного тяготения Ньютона.
Даже сегодня Теория относительности Эйнштейна остается важной в нашем понимании происхождения, структуры и судьбы нашей Вселенной.
Математика помогает нам лучше понимать окружающий мир и является вездесущей силой в нашей повседневной жизни.
Теория хаоса
Теория хаоса показала нам, что невозможно с уверенностью предсказать, что произойдет в будущем. Это изучение поведения динамических систем .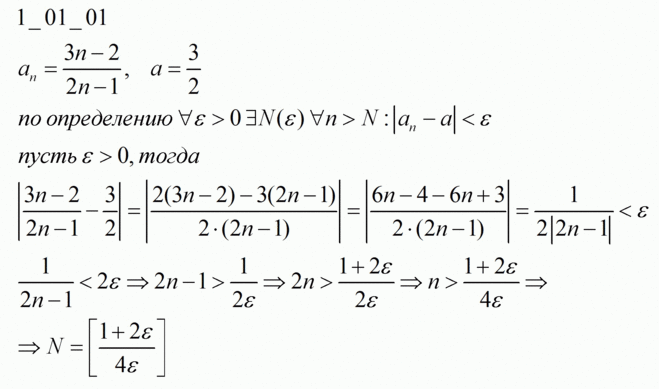 Отличная тема для изучения математики.
Отличная тема для изучения математики.
Эта теория доказывает, что никакие реально существующие процессы нельзя предсказать с уверенностью. Теория Роберта Мэя более поздняя, датируется 1975 годом. Она описывает процесс, который постоянно развивается с течением времени.
В своей формуле Мэй хотел объяснить, что хаотичное поведение (подобно климату, который испытывает многочисленные изменения погоды от момента к моменту) может через несколько дней привести к изменениям в других совершенно других системах.
Самой известной иллюстрацией является так называемый «эффект бабочки», который показывает, что взмах крыльев бабочки в Бразилии может привести к урагану или торнадо в Азии.
Турбулентность в концевом вихре крыла самолета (Источник: Национальное управление по аэронавтике и исследованию космического пространства (НАСА))Другими словами, самые незначительные вещи могут оказывать неожиданное влияние на окружающую среду, вблизи и вдали.
Множество факторов, связанных с событием, делает его непредсказуемым.
Доступны лучшие репетиторы по математике
Поехали
Тождество Эйлера
Тождество Эйлера считается » — лучшее из уравнений на уроках математики, потому что оно описывает маловероятную комбинацию пяти математических констант.
Тождество Эйлера — это равенство, где e — число Эйлера, основание натуральных логарифмов, i — мнимая единица, которая удовлетворяет условию i2 = − 1, а π равно пи, отношение длины окружности к ее диаметру (Источник: Wikipedia.org)Уравнение Эйлера (опубликованное Леонардом Эйлером в 1755 г.) применимо в случае идеальной жидкости
Почему это Уравнение имеет значение? Потому что оно использует три основных арифметических действия: сложение, умножение и возведение в степень .
Представлены пять констант: «0», аддитивная идентичность; «1» — мультипликативная идентичность; сказочный пи; «е», являющееся основанием натуральных логарифмов и числом, которое широко используется в математическом анализе; и «i», мнимая единица комплексных чисел, встречающихся в уравнениях с 3 неизвестными.
Это уравнение, украшающее Дворец Декуверт в Париже, проложило путь к развитию топологии, ветви современная математика .
Преобразование Фурье
Преобразование Фурье делит время на несколько частот и простых волн подобно тому, как призма разделяет свет на составляющие его цвета.
Преобразование Фурье (Источник: Wikipedia.org)Преобразование Фурье позволяет нам иметь дело с непериодическими функциями.
Другим примером может быть магнитное или акустическое поле , которое определяется как сигнал. Преобразование Фурье — это его спектр, поскольку оно деконструирует такое поле.
Найдите урок математики здесь, на сайте Superprof.
Обложка альбома Pink Floyd «Dark Side of the Moon» (Источник: Flickr.com — Эль Сильвер)Эта теория потрясла землю, потому что внезапно стало возможным понять структуру более сложных волн, таких как человеческая речь .
Сегодня эта теория, восходящая к 1822 году, лежит в основе современной обработки и анализа сигналов, а также обработки данных .
Уравнения Максвелла
Уравнения Максвелла описывают взаимодействие электрических зарядов, а также объясняют электрические токи и магнитные поля.
Уравнения Максвелла, также называемые уравнениями Максвелла-Лоренца, являются фундаментальными законами физики.
Они лежат в основе нашего понимания взаимосвязи между электричеством и магнетизмом и входят в число основных фундаментальных законов современной физики.
Уравнения Максвелла составляют основу классического электромагнетизма (Источник: commons.wikimedia.org)Существует 4 формы уравнений Максвелла:
- Уравнение Максвелла-Гаусса
- Уравнение Максвелла-Томсона
- Уравнение Максвелла-Фарадея
- Уравнение Максвелла-Ампера
Второй закон термодинамики Закон термодинамики (также известный как принцип Карно по имени его первооткрывателя в 1824 г.) неопровержимо доказывает, что физические явления необратимы, особенно когда происходят тепловые изменения.

Принципы термодинамики – это основные законы, управляющие термодинамикой.
Этот принцип несколько раз модифицировался и переформулировался и приобрел широкую популярность в 1873 году благодаря Людвигу Больцману и Максу Планку.
Сади Карно, первый, кто сформулировал второй закон термодинамики (Источник: архив истории математики MacTutor)В то время как первый закон термодинамики указывает, что энергия может обмениваться между физическими системами в виде тепла и работы . Второй закон вводит другую величину, известную как энтропия .
Это принцип изменения и эволюции, поскольку он определяет, в каком направлении возможны преобразования энергии потенциала.
Следовательно, некоторые химические превращения возможны, а другие никогда не будут. Можно с уверенностью сказать, например, что если положить кубик льда в чашку с горячим кофе, то кубик льда растает, а кофе никогда не замерзнет.
Уравнение Шредингера
Уравнение Шрёдингера, сформулированное австрийским физиком Эрвином Шрёдингером в 1925 году, является фундаментальным уравнением квантовой механики .
Зависимое от времени уравнение Шрёдингера (Источник: wikipedia.org)Поскольку общая теория относительности Эйнштейна помогла объяснить Вселенную в больших масштабах, это уравнение проливает свет на поведение атомов и субатомных частиц .
Уравнение Шрёдингера объясняет изменения частицы во времени. Он описывает состояния частицы, из которых можно описать любое состояние.
Это уравнение ставит настоящий философский вопрос: состоит ли материя из наличия возможных физических состояний (твердых, жидких, газообразных)?
Эрвин Шредингер, австрийский физик, лауреат Нобелевской премии (Источник: commons.wikimedia.org) Применение этого уравнения можно найти в современных технологиях, включая ядерную энергию, твердотельные компьютеры и лазеры.
Как мы видим, на протяжении всей истории человечества и особенно с 18 века математические уравнения изменили наше понимание мира, в котором мы живем, и нашу способность решать математические задачи. Они служат нам каждый день в нашей повседневной жизни, на уроках математики или более или менее прямым образом.
F формулы и уравнения, о которых вы можете узнать на уроках алгебры , это квадратные формулы, одновременные уравнения, дифференциальные уравнения, многошаговые, двухшаговые и одношаговые уравнения, полиномиальные уравнения, линейные уравнения, экспоненциальные функции, а также системы уравнения.
Призы и награды по математике
Существует ряд неотъемлемых наград, присуждаемых людям, часто называемым гениями, которые преуспевают в различных областях математики , обычно предлагая решение математической задачи. Это престижные награды с абсолютной ценностью и ценностью, некоторые из которых даже считаются эквивалентными получению Нобелевской премии.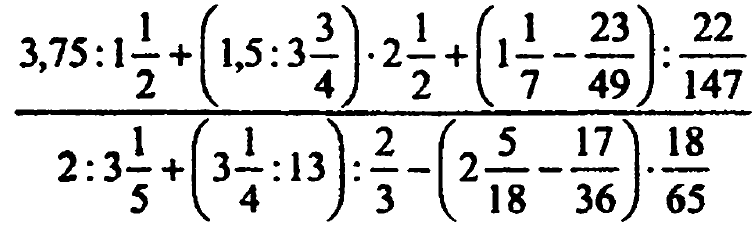 Таким образом, лишь немногие избранные получают эти награды, подчеркивающие их математические достижения.
Таким образом, лишь немногие избранные получают эти награды, подчеркивающие их математические достижения.
Ниже приведены некоторые из этих наград.
Медаль Филдса
Медаль Филдса — одна из самых известных наград, вручаемая математикам , которые достигли чего-то удивительного в своей карьере, работая с числами, уравнениями и т. д., например, открыли важную теорию или концепцию.
Официально лауреаты этой премии награждаются Международной медалью за выдающиеся открытия в области математики (можно понять, почему ее чаще называют просто Филдсовской медалью), и она вручается только раз в четыре года до четырех математиков. моложе 40 лет. Это означает, что большинство лауреатов этой престижной премии можно отнести к молодым, подающим надежды математикам с большими надеждами на будущее.
Абелевская премия
Еще одна авторитетная номинация, Абелевская премия, присуждается королем Норвегии математику, выдающемуся в своей области математических исследований .
Он назван в честь Нильса Хенрика Абеля, который в 2001 году, когда он был впервые создан, был популярным норвежским математиком.
Премия Вольфа по математике
Израильский фонд Вольфа ежегодно присуждает шесть различных премий, одна из которых – Премия Вольфа по математике.
Эта награда существует с 1978 года и считается большой честью для номинанта. Некоторые известные имена, получившие эту награду, включают Эндрю Уайлса, Джона Милнора и других.
Медаль Черна
Одна из новейших наград в области математики — Меда Черна, которая с 2010 года присуждается за достижения в области математики. свои руки на одной из этих престижных наград до сих пор. Он выдается на Международном конгрессе математиков и включает денежный приз в размере 250 000 долларов США (очевидно, чтобы помочь финансировать дальнейшие исследования или улучшить обучение в других областях математики).
Первым получателем в 2010 году стал Луис Ниренберг, а победителем в 2014 году стал Филлип Гриффитс.
Так почему же нет Нобелевской премии для математиков ?
В мире математических фактов кто-то скажет, что причина этого в том, что у жены Альфреда Нобеля был роман с известным математиком, но теперь мы знаем, что это неправда, поскольку Нобель даже не женился при жизни. Проще говоря, его работа, связанная с научными вопросами, означала, что эти предметы были ему ближе, чем математические выражения.
Проверьте онлайн-уроки математики здесь, на сайте Superprof.
Математики, изменившие мир
Если вам, как и нам, интересно, почему за всю историю математики не было ни одного упоминания о женщинах-математиках , то этот раздел для вас! Разговоры об уравнениях и неравенствах…!
Несмотря на то, что многие женщин принимали участие в математических открытиях , как и их сверстники-мужчины, об их способности решать задачи редко сообщалось. Ниже приведены лишь некоторые из женщин, у которых со временем помог сформировать математику .
Гипатия
Гипатия была дочерью греческого математика Теона и стала главой школы платоников в Александрии, Египет, где преподавала астрономию и философию.
Эта высокоинтеллектуальная женщина была убита в 415 г. н.э., заклейменна религиозными группами как сатанистка, однако считается, что она была влиятельным гением , который в свое время внес значительный вклад в опубликованные тексты своего знаменитого отца.
Софи Жермен
Говорят, что Мари-Софи Жермен была одержима теориями чисел и исчислением , вдохновленными чтением об Архимеде.
Это был 18 век, и некоторые учебные заведения не позволяли женщинам учиться под своей крышей. Поэтому Жермен приняла личность студента-мужчины, чтобы она могла учиться в математической академии только для мужчин в Париже.
К сожалению, хотя некоторые знают о ее блестящей работе над Великой теоремой Ферма, она так и не была официально признана, и она умерла, известная только как незамужняя женщина без профессии.
Узнайте больше о Софи Жермен с онлайн-репетитором по математике.
Кэролайн Гершель
Кэролайн Гершель была первой женщиной, получившей золотую медаль Королевского астрономического общества в 1828 году после того, как она открыла семь новых комет.
Гершель стала оплачиваемым помощником своего брата-астронома Уильяма, и пара открыла планету Уран в 1781 году, прежде чем сделать многочисленных значительных открытий собственных до своей смерти в возрасте 9 лет.7.
Ада Лавлейс
При известном отце, поэте лорде Байроне, не зря Лавлейс прозвали Чародейкой! Тем не менее, в отличие от своего отца, она была гораздо более талантлива, когда ее просили координировать систему счисления, а не решать какие-либо задачи со словами.
Лавлейс по профессии был пионером компьютеров викторианской эпохи, который сотрудничал с Чарльзом Бэббиджем над первыми программируемыми компьютерами в середине 19 века.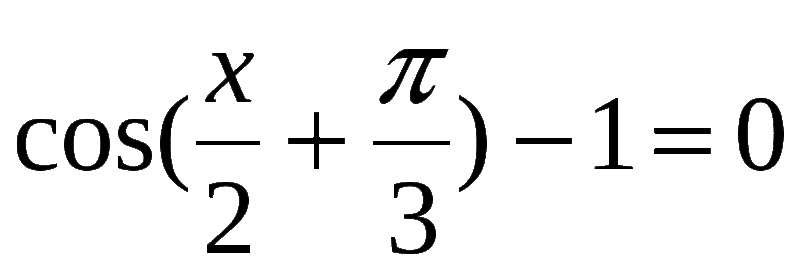 Даже сейчас можно видеть, что ее идеи настолько опередили свое время, что, возможно, поэтому она не была признана за ее вклад в область математики до 19 века.50-е годы – более 100 лет после того, как она выполняла эту работу.
Даже сейчас можно видеть, что ее идеи настолько опередили свое время, что, возможно, поэтому она не была признана за ее вклад в область математики до 19 века.50-е годы – более 100 лет после того, как она выполняла эту работу.
Софья Ковалевская
И последнее, но не менее важное: Ковалевская, родившаяся в Москве в 1850 году, внесла около очень важных вкладов в математический анализ в Германии.
Поскольку ее способности были замечены ее дядей в первую очередь, она давала частные уроки, однако позже была вынуждена выйти замуж.
Она, наконец, победила неравенство и разделение между мужчинами и женщинами и стала первой женщиной, получившей звание профессора в Северной Европе.
Другие влиятельные женщины-математики
Посмотрите ниже на еще несколько женщин, которые исторически были связаны с математикой, и почему.
| Name | Mathematical idenity |
|---|---|
| Emmy Noether | Innovator in higher algebra |
| Florence Nightingale | Inventor of pictorial ways to display statistics |
| Joan Clarke | Famous code- выключатель |
| Dame Jocelyn Bell Burnell | Astronomy pioneer |
| Radia Perlman | Leader in the field of computer science |
Taking Mathematics Into The Future
What will be the next major mathematical innovation ?
Какое новое математическое открытие перевернет наши нынешние представления о жизни? Смогли бы вы стать известным математиком благодаря квадратному уравнению, алгебраической функции, тригонометрическому прорыву или даже открытию нового понятия, такого как теорема Пифагора?
В качестве альтернативы, возможно, вы внесете что-то совершенно новое в таблицу , открыв новое целое число, о существовании которого мы никогда не знали, разработав интеллектуальный графический калькулятор или упростив математику с помощью устройства для решения уравнений или приложения для системы уравнений.

 В списке было 23 пункта. Двадцать один из них на данный момент решены. Последней решенной проблемой из списка Гилберта была знаменитая теорема Ферма, с которой ученые не могли справиться в течение 358 лет. В 1994 году свое решение предложил британец Эндрю Уайлз. Оно и оказалось верным.
В списке было 23 пункта. Двадцать один из них на данный момент решены. Последней решенной проблемой из списка Гилберта была знаменитая теорема Ферма, с которой ученые не могли справиться в течение 358 лет. В 1994 году свое решение предложил британец Эндрю Уайлз. Оно и оказалось верным. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей. Это говорит о том, что решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения.
Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей. Это говорит о том, что решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения. Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.
Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.
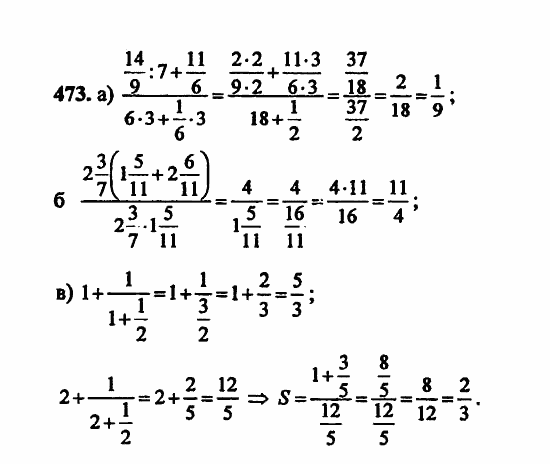 Доказать, что односвязна только сфера, оказалось настолько трудно, что математики ищут правильный ответ до сих пор.
Доказать, что односвязна только сфера, оказалось настолько трудно, что математики ищут правильный ответ до сих пор. Вводите числа, операторы и функции единой непрерывной строкой.
Вводите числа, операторы и функции единой непрерывной строкой. Например, похожую задачу, которую они решали в классе или пример из учебника, к которому прилагается правильный ответ.
Например, похожую задачу, которую они решали в классе или пример из учебника, к которому прилагается правильный ответ. Используя этот список, учитель может объяснить, где именно ребёнок ошибся, чтобы в будущем он смог решить эту задачу.
Используя этот список, учитель может объяснить, где именно ребёнок ошибся, чтобы в будущем он смог решить эту задачу. Так будет легче найти пробел и заполнить его.
Так будет легче найти пробел и заполнить его.
 Стрелка покажет, какое действие нужно выполнить с полученным результатом.
Стрелка покажет, какое действие нужно выполнить с полученным результатом.
 Не очень хорошо знаком с числами.
Не очень хорошо знаком с числами. Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.

 Вы съели 2 печенья. Сколько файлов cookie у вас осталось?
Вы съели 2 печенья. Сколько файлов cookie у вас осталось?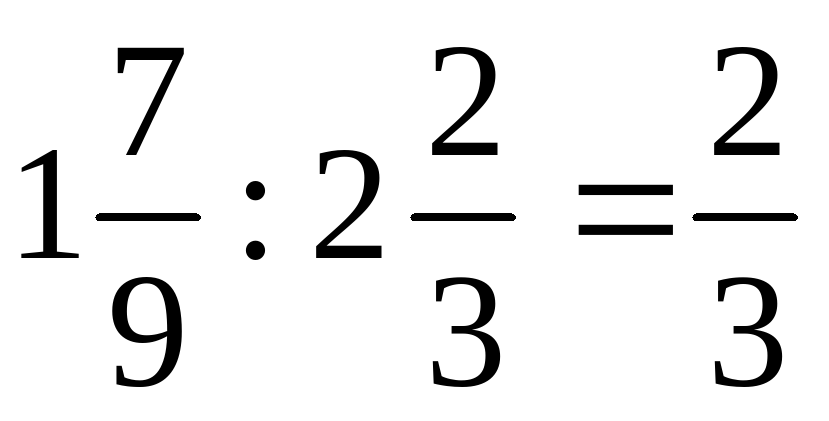 Обед — через три часа десять минут после начала учебного дня. Когда будет ланч?
Обед — через три часа десять минут после начала учебного дня. Когда будет ланч?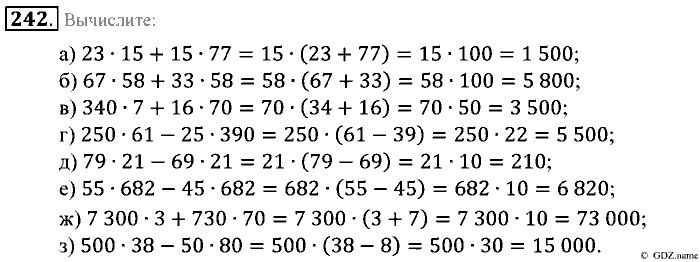 Д.
Д. Д.).
Д.).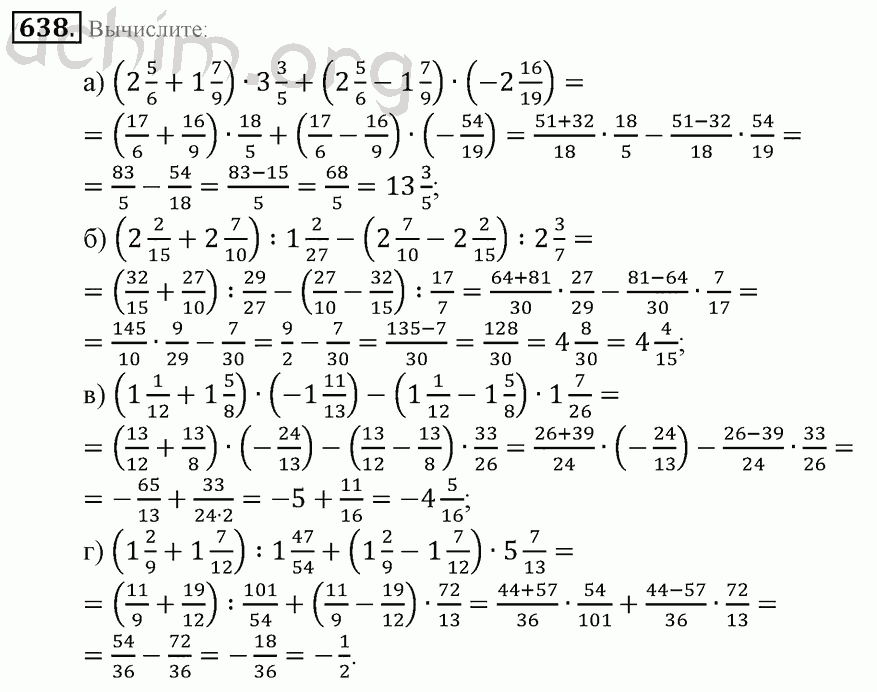 д.
д. Картинка и гистограммы
Картинка и гистограммы 


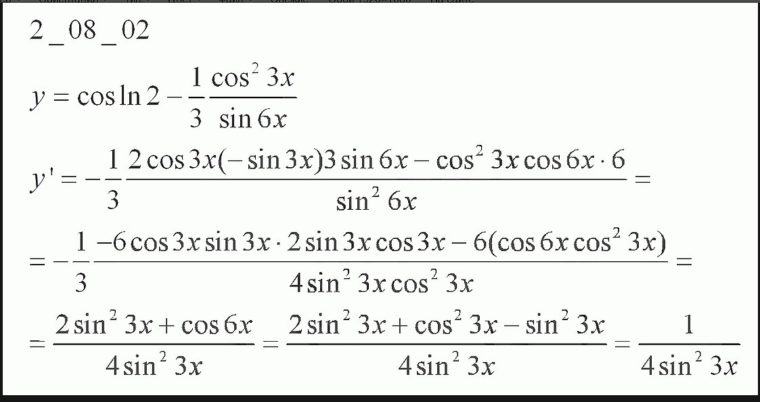
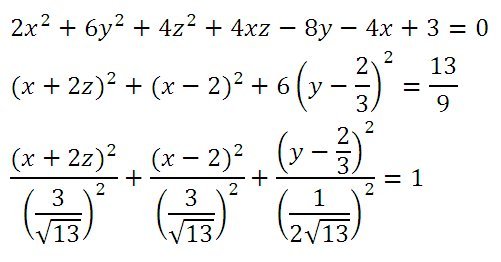 m $ где $m$ — количество генераторов.
m $ где $m$ — количество генераторов.