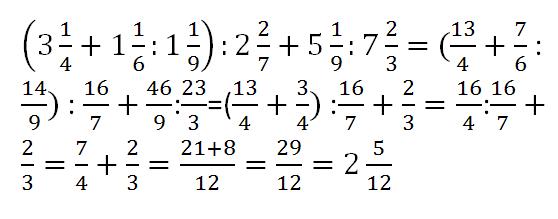Сложный математический пример: Сложные примеры по математике, которые вгоняют в краску неучей

Сложные математические примеры, которые не всем по плечу

Познавательное

23 Янв 2023

Что бы ни говорили гуманитарии, но базовые знания по математике должны быть у каждого. Они непременно пригодятся в повседневной жизни. Так что держать свой мозг в тонусе можно и нужно всегда. Для этого можно периодически решать сложные математические примеры. Несколько подобных мы сегодня предлагаем для тебя.

Сложные математические примеры

Итак, первый пример — это задачка с девятками. Казалось бы, нет ничего сложного. В общем, это действительно так. Но все-таки придется вспомнить порядок выполнения действий. А это, судя по результатам опросов в Сети, удается далеко не всем. Так какой же ответ правильный?

Второй пример затрагивает еще один популярный миф, который почему-то гуляет по Сети. Здесь нужно вспомнить, есть ли какое-то преимущество у умножения перед делением? Сколько копий было сломлено по этому поводу… Но все-таки правильный ответ может быть только один.

А в конце предлагаем немного расслабиться. Это всего лишь нечто сродни системы уравнений. Всё очень просто, ведь правильный ответ можно найти, решая каждое уравнение по отдельности. Так что главное — не спеши, и у тебя всё получится…

Переглянути цей допис в Instagram

Допис, поширений Antoha (@7second2)

Ответы

В общем, в первом примере главное — знать, что деление и умножение имеют приоритет. Так что ни в коем случае нельзя выполнять действия подряд. Другими словами, пример, который изображен на картинке, превращается в такой: 9 + 1 + 81 – 9 = 82. И только так!

© Depositphotos

Что касается этой задачки, то мне неоднократно приходилось видеть людей, которые свято верят, что у умножения есть преимущество над делением. Кто-то даже скрины предоставлял из какого-то учебника, который, правда, существует едва ли не в единственном экземпляре. Запомни раз и навсегда: умножение и деление — действия одного порядка. Так что их следует выполнять слева направо.

© Depositphotos

Вернемся к нашему примеру. Будем постепенно его упрощать, помня, что там есть еще и скобки. Итак, 3 / 3 (3 * 3) * 3 / 3 + 3 = 3 / 3 * 9 * 3 / 3 + 3 = 1 * 9 * 3 / 3 + 3 = 27 / 3 + 3 = 9 + 3 = 12.

© Depositphotos

И последняя задачка. Из первого примера легко понять, что А = 39 / 3 = 13. Переходим ко второму примеру. Зная результат первого, понимаем, что В = (25 + 13) / 2 = 19. Соответственно С = 50 – 19 – 6 = 25. Значит, под знаком вопроса у нас скрывается число 57.

Выводы

В любой ситуации всегда нужно уметь возвращаться к истокам. А наши сегодняшние примеры именно такими и являются. Нельзя переходить к чему-то большому и трудному, забывая о базовых знаниях.

© Depositphotos

Искренне надеемся, что ты справился с задачками без ошибок. Своими результатами непременно поделись в комментариях. Мы обязательно прочтем твои вердикты по поводу этого материала.

Поделиться

математика пример школа

Автор статьи

Редакция «Boom»

Редакция Boom — это неутомимые искатели крутых видео, о которых хочется рассказать всей планете. Каждый день мы знакомим любимого читателя с невероятными событиями и интригующими жизненными историями. Наша задача — делать скучный мир веселее, а лучшие видеоролики со всего мира помогают нам в этом.

Раскрытие скобок и порядок действий до 1000 (сложные примеры)

130,00 ₽

Примеры на порядок действий в пределах 1000: содержат 2 пары скобок и 5 математических действий: сложение, вычитание, умножение и деление. С ответами. Для печати А4.

Количество товара Раскрытие скобок и порядок действий до 1000 (сложные примеры)

Артикул: i-2363 Категория: Для учебы Метки: Порядок действий, 3 класс, 4 класс

• Описание
• Детали
• Отзывы (0)

Описание

Программа «Сложные примеры на порядок действий до 1000» представляет собой тренажер счета, где нужно выполнить вычисления в правильной последовательности действий.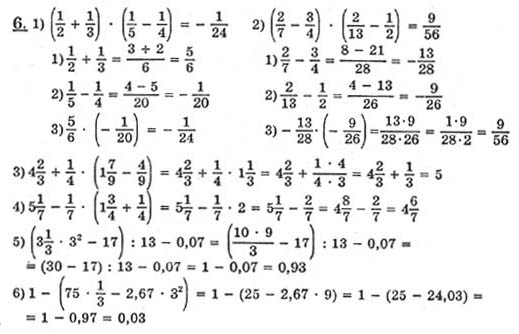 Эти задания выделятся отдельным этапом, так как они способствуют развитию логического мышления ребенка. Именно поэтому нужна практика, чтобы закрепить понимание очередности вычислений.

Формируются примеры на порядок действий в пределах 1000, которые включают скобки (2 ед.), а также

от пяти и более математических операций (сложение, вычитание, умножение, деление).

Программа написана в Excel с помощью макросов. Формируются карточки на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. В конце карточки формируются ответы на примеры, которые можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.

Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл, сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.

Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.

Другие программы, которые помогут закрепить навыки счета в пределах 1000:

• • Порядок действий в пределах 1000 (все действия)
  • Цепочки примеров в пределах 1000 (все действия)
  • Умножение и деление по типам (табличное, внетабличное, круглых чисел)
  • Сложение и вычитание в столбик
  • Умножение и деление в столбик
  • Выражения с именованными числами

На сайте представлен каталог программ, в котором все программы распределены по группам.

С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Вам также будет интересно…

• Сложение и вычитание в столбик

  Оценка 5.00 из 5

  70,00 ₽В корзину

• Умножение и деление в столбик

  Оценка 4.67 из 5

  100,00 ₽В корзину

• Деление с остатком на число (с выбором уровня сложности)

  Оценка 5.00 из 5

  80,00 ₽В корзину

• Задание на неделю 3 класс

  130,00 ₽В корзину

• Продолжить ряд чисел

  125,00 ₽В корзину

• Задачи на движение (разные виды)

  100,00 ₽В корзину

• Выражения с именованными числами (разные единицы измерения)

  90,00 ₽В корзину

• Задание на неделю 4 класс

  140,00 ₽В корзину

• Умножение и деление по типам (табличное, внетабличное, круглых чисел)

  120,00 ₽В корзину

Применение комплексных чисел в реальной жизни

Применение комплексных чисел в реальной жизни

Джозия Ву

Начнем с основ.

В раннем возрасте нас учили считать положительными числами, такими как один, два или три. Позже в начальной школе нас также познакомили с отрицательными числами: например, -19 — это отрицательное число. Я также предполагаю, что вы знакомы с квадратными корнями (если нет, вам следует пересмотреть). Студентов обычно учат, что нельзя извлекать квадратный корень из отрицательных чисел. Но что, если бы мы могли?

Вам может быть интересно: «Как можно извлечь квадратный корень из отрицательного числа?» На самом деле, математики до 16 века тоже так думали. Так было до тех пор, пока итальянский математик Джероламо Кардано не нарушил соглашение, изобретя мнимые числа в отчаянной попытке решить кубические уравнения. На протяжении всей истории математики всегда любили нарушать собственные правила: помимо извлечения квадратного корня из отрицательного числа, Рамануджан однажды доказал, что 1 + 2 + 3 + 4… вплоть до бесконечности равно -1/12. Другой математик, Георг Кантор, доказал, что четных чисел столько же, сколько целых положительных.

Поэтому то, что сделал Кардано, не было редкостью (по крайней мере, в исторических записях).

Так что же такое мнимое число? Мнимое число кратно i = √-1. Например, √-25 — мнимое число, потому что его можно переписать как √-25 = √25 × -√1 = 5i. Кроме того, можно добавить действительное число к мнимому числу, чтобы получить комплексное число. Чтобы продемонстрировать это, можно добавить 3, действительное число, к 3i, мнимому числу, чтобы получить комплексное число 3+3i.

Иллюстрация Итана Лана

Обычная визуализация комплексных чисел — это использование диаграмм Аргана. Чтобы построить это, представьте себе декартову сетку, где ось X представляет собой действительные числа, а ось Y — мнимые числа.

Важным свойством комплексных чисел является формула Эйлера: она утверждает, что каждое комплексное число можно переписать в виде re =r(cos + i sin ), где e=2,71828… — постоянная Эйлера, r — это «расстояние» комплексного числа от начала координат и угол комплексного числа от положительной действительной оси (против часовой стрелки, в радианах). Слева иллюстрация к этому.

Многие математики называют формулу Эйлера самым красивым математическим результатом в истории. Его эстетическая красота заключается в том, что он подразумевает волшебную связь между действительными числами и мнимыми числами. Хотя я хотел бы продемонстрировать элегантное доказательство этой формулы, оно, к сожалению, выходит за рамки этой статьи.

Приложения

1.

Обработка сигналов

Предположим, что пианист записывает в музыкальной студии. Он приглашает вас в игру — угадать, какие ноты он играет, не глядя на рояль. Как человек, у которого нет идеального слуха (способность определить ноту на слух), как бы вы выиграли в этой игре?

Оказывается, есть способ всегда определить, какие ноты он играет, не обманывая. Во-первых, запишите его игру в программе для редактирования аудио. Программное обеспечение сохранит запись в форме сигнала.

Затем можно применить преобразование Фурье к сигналу формы волны, чтобы выяснить, какие частоты преобладают в записи. Это можно показать, выведя «пики» в результирующем частотном распределении после применения преобразования Фурье. Поскольку имеются очевидные пики на частотах 256 Гц и 391 Гц (соответствующие C4 и G4 соответственно), мы можем сделать вывод, что пианист должен был играть на фортепиано C и G.

Знание расположения пиков невероятно важно для аудиоредакторов и музыкальных продюсеров. Они могут не только определить источник любого фонового шума, но и использовать его частоту в качестве эталона для их устранения с помощью средств эквалайзера (EQ).

Идея преобразования Фурье довольно гениальна; он предполагает, что любую сложную волну можно разложить на несколько синусоидальных волн с различными частотами. Что делает преобразование Фурье, так это то, что оно предсказывает, какая частота, вероятно, будет эквивалентна одной из таких синусоидальных волн. Он делает это, «оборачивая» волну вокруг начала координат в комплексной плоскости и вычисляя сумму комплексных координат всех возможных точек на обернутой волне.

2. Анализ цепи переменного тока

Комплексные числа также используются при расчетах тока, напряжения или сопротивления в цепях переменного тока (AC означает переменный ток, то есть ток, величина и направление которого меняются во времени). Обычно комплексные числа (точнее, формула Эйлера) применяются для вычисления разности потенциалов между двумя источниками питания переменного тока во времени. Справа пример такого расчета.

Чтобы найти суммарную разность потенциалов, просто сложить вместе VA и VB не получится. Однако мы можем выразить оба напряжения как действительную часть (координата x на диаграмме Аргана) комплексного числа.

* Общепринято использовать j вместо i для представления мнимых чисел при анализе цепей, чтобы избежать путаницы с током (символом которого является i или I).

Затем мы можем сложить комплексные числа и разложить на множители:

Кроме того, комплексные числа также используются для выражения величины и фазы импеданса в цепи переменного тока. Импеданс очень похож на сопротивление — он замедляет электроны в цепи. Отличие состоит в том, что импеданс вызывает фазовый сдвиг электрического тока, а сопротивление — нет. Импеданс имеет место в обычных электрических компонентах, таких как катушки индуктивности и конденсаторы, поэтому крайне важно иметь комплексное числовое представление. Как правило, комплексные числа служат для представления фазы, что необходимо для анализа цепей переменного тока.

3. Квантовая механика

Квантовая механика — это область физики, изучающая движения и взаимодействия между субатомными частицами, в основном бозонами (например, фотоном) и фермионами (например, нейтроном). Он обеспечивает математическое описание их поведения с точки зрения вероятностей. Фактически, комплексные числа составляют фундаментальную основу квантовой механики. Значение уравнения Шредингера для квантовой механики аналогично значению второго закона Ньютона для классической физики; они оба обеспечивают разумное математическое предсказание положения и импульса частицы. Система комплексных чисел важна для этой области, потому что это удобный язык для выражения волновых функций без нарушения правил. Кроме того, прямое применение квантовой механики заключается в том, что она ускорила распространение химии. В 1927, Вальтер Хайтлер (не Гитлер!) и Фриц Лондон сформулировали теорию валентной связи. Одной из основных задач квантовой механики является нахождение волновой функции субатомной частицы. Проще говоря, волновая функция представляет собой сложное распределение вероятностей, указывающее возможные положения частицы в определенное время. Фундаментальная формула квантовой механики, в которой роль волновой функции значительна,

— это уравнение Шредингера: с использованием упомянутого выше уравнения Шредингера. Используя формулу, они доказали, что два атома в молекуле водорода на самом деле «делят» электроны, образуя то, что мы знаем как ковалентную связь. Сразу после этого несколько других химиков продолжили развивать свою теорию связи, например, открытие Линусом Полингом резонанса и орбитальной гибридизации. Таким образом, без развития квантовой механики ученые не смогли бы ни открыть электронную структуру атомов, ни придумать концепцию связи между атомами.

Иллюстрация Итана Лана

Библиография

Обработка сигналов (преобразование Фурье)

Star, Zach. «Математика обработки сигналов | Z-преобразование, дискретные сигналы и многое другое». www.ютуб. com, 2019 г., https://www.youtube.com/watch?v=hewTwm5P0Gg&t=1350s&ab_channel=ZachStar.

«Анализ Фурье». En.Wikipedia.Org, 2020, https://en.wikipedia.org/wiki/Fourier_analysis. По состоянию на 9 ноября 2020 г.

Чан, Джастин. «Применение преобразования Фурье: обработка сигналов». www. youtube.com, 2017, https://www. youtube.com/watch?v=9uv3-m8jkVg&ab_channel=JustinChan. По состоянию на 9 ноября 2020 г.

Заключение

Хотя мы не можем физически визуализировать комплексные числа, трудно отрицать их важность для научного сообщества. Комплексные числа прекрасно демонстрируют роль математики в науке — она действует как мощный язык для описания сложных явлений и всеобъемлющий инструментарий для решения сложных задач.

Анализ цепи переменного тока

Стар, Зак. «Использование мнимых чисел в реальном мире». Www.Youtube.Com, 2018 г., https://www.youtube.com/watch?v=_ h59ilnTmW4&t=630s&ab_channel=ZachStar.

«Комплексные числа и векторы». https://Www.Electronics-Tutorials.Ws/, 2020, https://www.electronics-tutorials.ws/accircuits/complex-numbers.html.

Джонсон, Роберт. «Использование комплексных чисел в анализе цепей и обзор алгебры комплексных чисел». 2020, http://www.its.caltech.edu/~jpelab/phys1cp/AC%20Circuits%20and%20 Complex%20Impedances.pdf

Квантовая механика

ДеКросс, Мэтт и др. «Уравнение Шредингера | Блестящая вики по математике и науке». Блестящий. Org, 2020, https://brilliant.org/wiki/schrodinger-equation/, по состоянию на 9 ноября 2020 г.

Карам, Рикардо, изд. к. Зачем нужны комплексные числа в квантовой механике? Несколько ответов для вводного уровня. Университет Копенгагена, 2020 г.,

https://www.ind.ku.dk/english/research/didactics-of-physics/Karam_AJP_Complex_numbers_in_QM. pdf.

Трехо, Мигель. «Математика уравнения Шредингера: дуальность волна-частица и уравнение теплоты». Medium, 2020 г., https://towardsdatascience.com/themath-behind-schr%C3%B6dinger-equationthe-wave-particle-duality-and-the-heatequation-d5837bf4b13f.

профессий, использующих комплексные числа | Work

Автор David Weedmark Обновлено 8 марта 2021 г.

Как любой студент, изучающий алгебру, вероятно, спросит учителя: «Кто вообще когда-либо использует комплексные числа?» Очевидный ответ, конечно же, «учителя математики». Но это только начало.

Большинство ученых и инженеров, а также каждый математик должны иметь представление о комплексных числах. Физики и инженеры-электрики могут регулярно работать с комплексными числами. Возможно, вы не знаете о комплексных числах, но применение комплексных чисел в реальном мире видно любому, кто изучает или анализирует вещи, которые колеблются или напоминают волны.

Простое объяснение комплексных чисел

Комплексное число содержит два типа чисел: действительные числа и мнимые числа. Реальные числа — это почти любые числа, которые вы используете, например 1, 2, 3 и т. д., а мнимое число — это любое число, которое можно выразить как отрицательный квадратный корень. 92 — 2x + 5 = 0 ​ не имеет ни действительного решения, ни мнимого решения (отрицательный квадратный корень). Однако у него есть два комплексных числовых решения: 1 + 2i и 1 — 2i.

Комплексные числа и мнимые числа окружают нас все время и, как скажет вам любой математик, они не менее реальны (или менее важны), чем такие числа, как 1, 2 и 3. Использование комплексных чисел в нашей повседневной жизни почти всегда остаются незамеченными, но они окружают вас всякий раз, когда вы включаете свет, берете в руки гитару или даже смотрите, как дерево качается на сильном ветру.

Применение комплексных чисел в физике

Важной и увлекательной областью современной физики является квантовая механика, которая фокусируется на поведении субатомных частиц. Квантовая механика предоставляет нам математические описания и предсказания того, как ведут себя и взаимодействуют субатомные частицы, выраженные в терминах вероятностей. В основе квантовой физики лежат комплексные числа, которые используются для таких вещей, как предсказание положения или импульса частицы с помощью уравнений, наиболее известным из которых является уравнение Шредингера.

Без комплексных чисел физики и химики не смогли бы понять, как работают атомы и как они взаимодействуют. Например, комплексные числа, лежащие в основе квантовой физики, помогли ученым понять, что атомы соединяются в молекулы, обмениваясь электронами. Это было неотъемлемой частью как химии, так и физики на протяжении большей части прошлого века.

Другая область физики, в которой комплексные числа становятся очень важными, — это область оптики. Если вы когда-либо изучали интерференцию волн, вы имели дело с комплексными числами.

Применение комплексных чисел в технике

Как объясняет профессор Роберт Джонсон в статье, опубликованной Калифорнийским технологическим институтом, комплексные числа используются всякий раз, когда величина имеет как фазу, так и величину. Хотя это включает оптику и квантовую механику в физике, это также включает электронику. Инженеры-электронщики, работающие с синусоидальными колебаниями напряжения и тока, используют комплексные числа.

Комплексные числа и мнимые числа, которые они содержат, не ограничиваются только электроникой. Любой инженер, вероятно, столкнется с ними, объясняет Kaiser Science, и ему придется работать с ними, когда необходимо учитывать колебания. Это включает в себя конструкцию мостов, которые могут качаться на ветру, если они не будут тщательно спроектированы, и даже конструкцию амортизаторов в вашем автомобиле.

Применение комплексных чисел в финансах и экономике

Любой, кто занимается финансами или экономикой, также может столкнуться с ситуациями, когда им необходимо работать с комплексными числами. Комплексные числа и комплексный анализ, описанные в Issu, являются важной частью экономических моделей, в которых для анализа капитала используются разностные уравнения.