Помогите решить / разобраться (М)
| Amateur_3D |
| ||
27/03/16 |
| ||
| |||
| Lia |
| |
20/03/14 | ||
| ||
| Lia |
| ||||
20/03/14 |
| ||||
| |||||
| svv |
| |||
23/07/08 |
| |||
| ||||
| Amateur_3D |
| ||
27/03/16 |
| ||
| |||
| svv |
| |||
23/07/08 |
| |||
| ||||
| Amateur_3D |
| ||
27/03/16 |
| ||
| |||
| svv |
| |||
23/07/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
Собственные значения, собственные векторы матрицы
Вы можете ознакомиться и скачать презентацию на
тему Собственные значения, собственные векторы матрицы.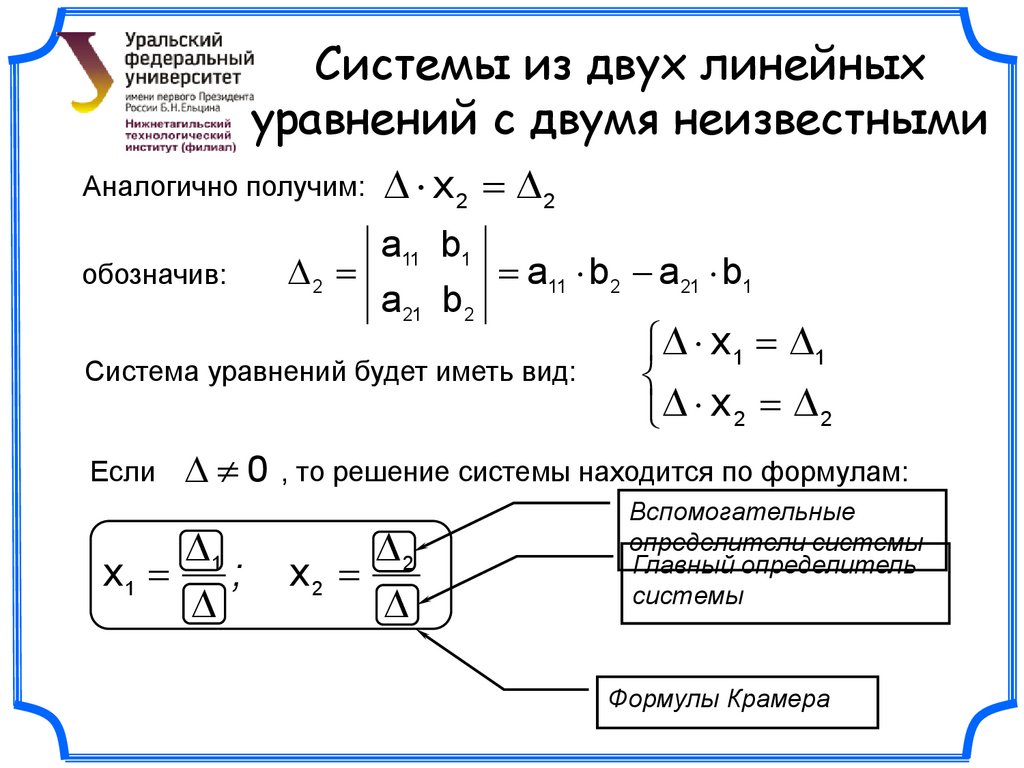 Доклад-сообщение содержит 26 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Доклад-сообщение содержит 26 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Слайд 1
Описание слайда:
СОБСТВЕННЫЕ ЗНАЧЕНИЯ СОБСТВЕННЫЕ ЗНАЧЕНИЯ, СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 2
Описание слайда:
Собственные значения матрицы
Рассмотрим квадратную матрицу порядка с постоянными действительными элементами
Определение. Число называется собственным значением, а ненулевой вектор называется соответствующим собственным вектором матрицы если выполняется равенство:
Число называется собственным значением, а ненулевой вектор называется соответствующим собственным вектором матрицы если выполняется равенство:
Слайд 3
Описание слайда:
Собственные значения матрицы Определение. Множество всех собственных значений матрицы называется спектром матрицы. Замечание. Представим равенство (1) в сл. виде: или единичная матрица порядка . Равенство (2) является системой линейных алгебраических уравнений относительно вектора .
Слайд 4
Описание слайда:
Собственные значения матрицы
Система вида (2) всегда совместна, так как всегда имеет нулевое решение. Система (2) имеет тривиальное (нулевое ) решение, если определитель матрицы
Система (2) имеет ненулевые решения , если
Система (2) имеет тривиальное (нулевое ) решение, если определитель матрицы
Система (2) имеет ненулевые решения , если
Слайд 5
Описание слайда:
Собственные значения матрицы
Слайд 6
Описание слайда:
Собственные значения матрицы Вычислив определитель, разложив его по элементам первой строки, и сгруппировав подобные члены, получим алгебраическое уравнение степени относительно , а где постоянные действительные числа Многочлен ой степени относительно называется характеристическим многочленом матрицы
Слайд 7
Описание слайда:
СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
Согласно основной теореме алгебры характеристическое уравнение всегда имеет ровно корней (с учетом их кратности), которые в общем случае являются комплексными числами. Теорема. Любая постоянная квадратная матрица
порядка имеет с учетом кратности ровно
собственных значений, совпадающих с корнями
характеристического уравнения.
Теорема. Любая постоянная квадратная матрица
порядка имеет с учетом кратности ровно
собственных значений, совпадающих с корнями
характеристического уравнения.
Слайд 8
Описание слайда:
СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
Слайд 9
Описание слайда:
СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
Слайд 10
Описание слайда:
СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
Слайд 11
Описание слайда:
СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ
Слайд 12
Описание слайда:
Свойства собственных значений матрицы
Слайд 13
Описание слайда:
Свойства собственных значений матрицы
Слайд 14
Описание слайда:
СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 15
Описание слайда:
Линейная зависимость векторов
Определение .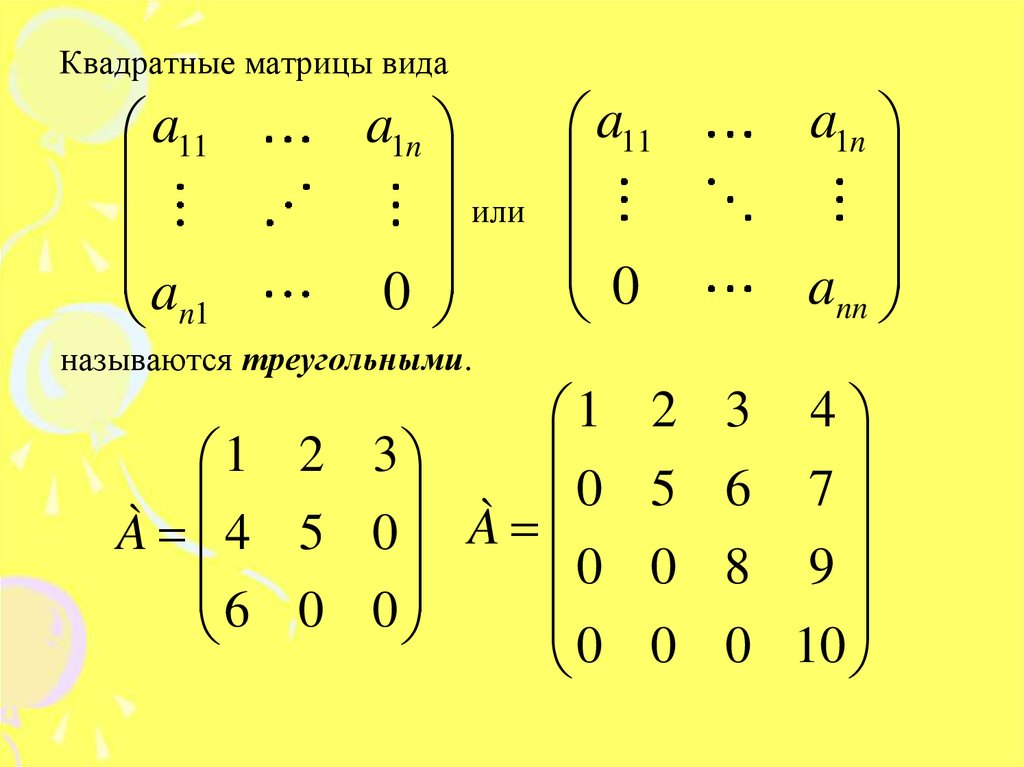 Векторы линейного векторного пространства называются линейно зависимыми, если существуют числа
, не все равные нулю, такие, что справедливо равенство:
. (1 )
Определение . Векторы линейного векторного пространства называются линейно независимыми, если выполнение равенства (1) возможно только при условии:
.
Векторы линейного векторного пространства называются линейно зависимыми, если существуют числа
, не все равные нулю, такие, что справедливо равенство:
. (1 )
Определение . Векторы линейного векторного пространства называются линейно независимыми, если выполнение равенства (1) возможно только при условии:
.
Слайд 16
Описание слайда:
СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 17
Описание слайда:
СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 18
Описание слайда:
СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 19
Описание слайда:
СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 20
Описание слайда:
СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 21
Описание слайда:
СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 22
Описание слайда:
СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ
Слайд 23
Описание слайда:
Примеры
Слайд 24
Описание слайда:
Примеры
Слайд 25
Описание слайда:
Слайд 26
Описание слайда:
Собственные значения матричного калькулятора
Поиск инструмента
Поиск инструмента в dCode по ключевым словам:Просмотр полного списка инструментов dCode
Собственные значения матрицы
Инструмент для вычисления собственных значений матрицы. Собственные значения матрицы — это значения, которые позволяют уменьшить связанные эндоморфизмы.
Собственные значения матрицы — это значения, которые позволяют уменьшить связанные эндоморфизмы.
Результаты
Собственные значения матрицы — dCode
Метки: Матрица
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике и задачах, геокэшинге решать каждый день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор собственных значений
Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
См. также: Собственные векторы матрицы — Характеристический многочлен матрицы — Диагонализация матрицы
Калькулятор собственных векторов
⮞ Перейти к: Собственные векторы матрицы
Ответы на вопросы (FAQ)
Что такое собственное значение матрицы? (Определение)
Собственные значения для любой квадратной матрицы $ M $ размера $ m \times m $ (2×2, 3×3, 4×4 и т. д.) — это скалярные значения, отмеченные символом лямбда $ \lambda $, которые связаны с собственным вектором $ \vec{v} $, такой как $$ M.\vec{v} = \lambda \vec{v} $$
д.) — это скалярные значения, отмеченные символом лямбда $ \lambda $, которые связаны с собственным вектором $ \vec{v} $, такой как $$ M.\vec{v} = \lambda \vec{v} $$
Практически собственных значения $ \lambda $ матрицы $M$ являются корнями ее характеристический многочлен $P$ as $(M-\lambda I_m).\vec{v} = 0 $$ (с $I_m$ единичной матрицей размера $m$).
92 — 4x — 5 = (x + 1) (x-5) $. Корни $P$ находятся вычислением $P(M)=0 \iff x= -1$ или $x=5$. собственных значения матрицы $M$ равны $-1$ и $5$.NB: связанные собственные векторы: $ \begin{bmatrix} 1 \\ 2 \end{bmatrix} $ для $ 5 $ и $ \begin{bmatrix} -1 \\ 1 \end{bmatrix} $ для $ -1 $
Сколько собственных значений у матрицы?
Квадратная матрица размера/размера $ n $ имеет $ n $ собственных значений . Однако будьте осторожны, некоторые собственные значения могут быть одинаковыми, чтобы узнать количество различных собственных значений (без кратности) затем вычислить различные корни характеристического многочлена матрицы.
Зачем вычислять собственные значения матрицы?
Собственные значения — это числа, характеризующие матрицу. Эти числа важны, потому что, связанные со своими собственными векторами, они позволяют определить собственные направления матрицы и выразить ее в базисе в упрощенной форме (см. Диагонализация матрицы), что облегчает вычисления.
Как доказать, что значение является собственным значением матрицы?
Чтобы определить, что значение λ является собственным значением матрицы $ M $, покажите, что существует ненулевой вектор $ \vec{x} $ такой, что $ M . \vec{x} = \лямбда . \vec{x} $. Если это уравнение имеет решение для $\vec{x}$, то $\lambda$ является собственным значением матрицы $M$.
Почему собственные значения иногда являются комплексными числами?
Если корни характеристического полинома не имеют значений на вещественном множестве $\mathbb{R}$, то они вычисляются на комплексном множестве $\mathbb{C}$, которое вводит комплекс собственные значения .
Этот случай может иметь место, даже если значения матрицы являются действительными числами.
Сложные собственные значения не имеют физического смысла и обычно исключаются из расчетов механики/физики и т.д.
Почему собственные значения?
Собственные значения называются eigen , потому что это немецкое слово, означающее собственно , характеристика .
Исходный код
dCode сохраняет право собственности на исходный код «Собственные значения матрицы». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Собственные значения матрицы», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Собственные значения Матрицы» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Собственные значения матрицы» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
д.) и все данные загрузка, сценарий или доступ к API для «Собственные значения матрицы» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Собственные значения матрицы» или любых ее результатов разрешено, если вы цитируете dCode!
Бесплатный экспорт результатов в виде файла .csv или .txt осуществляется нажатием значка export
Ссылка на источник (библиография):
Собственные значения матрицы на dCode.fr [онлайн-сайт], получено 2023-03 -25, https://www.dcode.fr/matrix-eigenvalues
Резюме
- Калькулятор собственных значений
- Калькулятор собственных векторов
- Что такое собственное значение матрицы? (Определение)
- Как вычислить собственные значения матрицы?
- Сколько собственных значений у матрицы?
- Зачем вычислять собственные значения матрицы?
- Как доказать, что значение является собственным значением матрицы?
- Почему собственные значения иногда являются комплексными числами?
- Почему собственные значения?
Похожие страницы
- Eigenvectors of a Matrix
- Matrix Diagonalization
- Characteristic Polynomial of a Matrix
- Spectral Radius of a Matrix
- Jordan Normal Form Matrix
- Rank of a Matrix
- Schur Decomposition (Matrix)
- DCODE’S TOOLS LIST
Поддержка
- Paypal
- Patreon
- Подробнее
Форум/Помощь
Ключевые слова
Eigenvalue, Eigen, Valuex, Valuex, Veriox, Velecter, Veriox, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valux, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Valuex, Matrix. 0003
0003
Ссылки
▲
Калькулятор обратной матрицы — онлайн Калькулятор обратной матрицы
Калькулятор обратной матрицы вычисляет значение обратной матрицы для заданной матрицы. Предположим, мы умножаем матрицу на заданную матрицу, и произведение является мультипликативным тождеством. Тогда такая матрица называется обратной к данной матрице.
Что такое калькулятор обратной матрицы?
Калькулятор обратной матрицы — это онлайн-инструмент, который помогает вычислить обратную матрицу для заданной матрицы 2 × 2. Если определитель матрицы равен 0, то матрица, обратная такой, не может существовать. Чтобы использовать это Калькулятор обратной матрицы , введите значения в поля ввода.
Калькулятор обратной матрицы
ПРИМЕЧАНИЕ. Введите не более 3 цифр.
Как пользоваться калькулятором обратной матрицы?
Чтобы найти обратную матрицу с помощью онлайн-калькулятора обратной матрицы, выполните следующие действия:
- Шаг 1: Перейдите к онлайн-калькулятору обратной матрицы Cuemath.

- Шаг 1: Введите значение матрицы в соответствующие поля ввода калькулятора обратной матрицы.
- Шаг 2: Нажмите кнопку «Вычислить» , чтобы найти результирующую обратную матрицу.
- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор обратной матрицы?
Предположим, у нас есть матрица, заданная A. Обратную матрицу обозначим через A -1 . Когда эти две матрицы перемножаются, мы получаем мультипликативное тождество. Таким образом, А.А. -1 = I. Чтобы существовала обратная матрица, ее определитель не должен быть равен 0. Кроме того, матрица должна быть квадратной. Шаги для вычисления обратной матрицы 2 × 2 следующие:
- Шаг 1: Найдите определитель данной матрицы.
- Шаг 2: Найдите матрицу кофакторов.
- Шаг 3: Найдите транспонированную матрицу кофакторов.
 Это также известно как сопряжение матрицы.
Это также известно как сопряжение матрицы. - Шаг 4: Разделите сопряженную матрицу, полученную на шаге 3, на определитель из шага 1. Это даст обратную матрицу.
В дополнение к шагам, упомянутым выше, для нахождения обратной матрицы 2 × 2 можно также использовать следующую формулу.
A = \(\begin{bmatrix} a & b\\ c & d \end{bmatrix}\)
A -1 = \(\frac{1}{\begin{vmatrix} A \end {vmatrix}}adjA\)
A -1 = \(\frac{1}{ad — bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix}\)
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Примеры решения на калькуляторе обратной матрицы }\) и проверить его с помощью калькулятора обратной матрицы.
Решение:
Дано: A = \(\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}\)
A -1 = \(\frac{1}{ объявление — bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix}\)
A -1 = \(\frac{1}{4 — 6}\begin{bmatrix} 4 & -2\\ -3 & 1 \end{bmatrix}\)
A -1 = \(\begin{bmatrix} -2 & 1\\ 1,5 & -0,5 \end{bmatrix}\)
Пример 2:
Найдите обратную матрицу A = \(\begin{bmatrix} -10 & 4\\ 3 & -1 \end{bmatrix}\) и проверьте это с помощью калькулятора обратной матрицы.


 03.2016, 19:13
03.2016, 19:13  Нахождение собственных векторов.
Нахождение собственных векторов. Нахождение собственных векторов.
Нахождение собственных векторов. Нахождение собственных векторов.
Нахождение собственных векторов.
 Ошибка банальная: перемножал скалярно, а надо матрица на матрицу.
Ошибка банальная: перемножал скалярно, а надо матрица на матрицу. В материальчике, которым Вы руководствовались, написано: «Пусть – произвольная вещественная матрица», а для вычисления собственных векторов без всяких оговорок предлагается вычислять произведение преобразующих матриц , как Вы и поступали. Но в общем случае это произведение не даёт собственные векторы, только в специальном. Вы с этим не согласны?
В материальчике, которым Вы руководствовались, написано: «Пусть – произвольная вещественная матрица», а для вычисления собственных векторов без всяких оговорок предлагается вычислять произведение преобразующих матриц , как Вы и поступали. Но в общем случае это произведение не даёт собственные векторы, только в специальном. Вы с этим не согласны?
 Это также известно как сопряжение матрицы.
Это также известно как сопряжение матрицы.