Сочетания и размещения формулы: Перестановки, размещения и сочетания. Формулы. – основные формулы. Перестановки, размещения, сочетания. Задачи по теории вероятностей с решением онлайн

Размещение — Википедия

В комбинаторике размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.

Пример 1: ⟨1,3,2,5⟩{\displaystyle \langle 1,3,2,5\rangle } — это 4-элементное размещение из 6-элементного множества {1,2,3,4,5,6}{\displaystyle \{1,2,3,4,5,6\}}.

Пример 2: некоторые размещения элементов множества {1,2,3,4,5,6}{\displaystyle \{1,2,3,4,5,6\}} по 2: ⟨1,2⟩{\displaystyle \langle 1,2\rangle } ⟨1,3⟩{\displaystyle \langle 1,3\rangle } ⟨1,4⟩{\displaystyle \langle 1,4\rangle } ⟨1,5⟩{\displaystyle \langle 1,5\rangle } … ⟨2,1⟩{\displaystyle \langle 2,1\rangle } ⟨2,3⟩{\displaystyle \langle 2,3\rangle } ⟨2,4⟩{\displaystyle \langle 2,4\rangle } … ⟨2,6⟩{\displaystyle \langle 2,6\rangle }…

В отличие от сочетаний, размещения учитывают порядок следования предметов. Так, например, наборы ⟨2,1,3⟩{\displaystyle \langle 2,1,3\rangle } и ⟨3,2,1⟩{\displaystyle \langle 3,2,1\rangle } являются различными, хотя состоят из одних и тех же элементов {1,2,3}{\displaystyle \{1,2,3\}} (то есть совпадают как сочетания).

Заполнить ряд — значит надо поместить на каком-нибудь месте этого ряда какой-либо объект из данного множества (причем каждый объект можно использовать всего лишь один раз). Ряд, заполненный объектами данного множества, называется размещением , т.е мы разместили объекты на данных местах. ^[1]

Количество размещений из n по k, обозначаемое Ank{\displaystyle A_{n}^{k}}, равно убывающему факториалу:

Ank=nk_=(n)k=n(n−1)⋯(n−k+1)=n!(n−k)!=(nk)k!{\displaystyle A_{n}^{k}=n^{\underline {k}}=(n)_{k}=n(n-1)\cdots (n-k+1)={\frac {n!}{(n-k)!}}={\binom {n}{k}}k!}.

Последнее выражение имеет естественную комбинаторную интерпретацию: каждое размещение из n по k однозначно соответствует некоторому сочетанию из n по k и некоторой перестановке элементов этого сочетания; число сочетаний из n по k равно биномиальному коэффициенту (nk){\displaystyle {\tbinom {n}{k}}}, в то время как перестановок на k элементах ровно k! штук.

При k = n количество размещений равно количеству перестановок порядка n:^[2][3][4]

Ann=Pn=n!{\displaystyle A_{n}^{n}=P_{n}=n!}.

Справедливо следующее утверждение:Ann−1=Ann{\displaystyle A_{n}^{n-1}=A_{n}^{n}}. Доказывается тривиально:

Ann−1=n!(n−(n−1))!=n!(n−n+1)!=n!=Ann{\displaystyle A_{n}^{n-1}={\frac {n!}{(n-(n-1))!}}={\frac {n!}{(n-n+1)!}}=n!=A_{n}^{n}}.

Все 60 вариаций без повторения трех из пяти чисел

Размещение с повторениями или выборка с возвращением^[5] — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз.

Количество размещений с повторениями[править | править код]

По правилу умножения количество размещений с повторениями из n по k, обозначаемое A¯nk{\displaystyle {\bar {A}}_{n}^{k}}, равно:^[6][2][5]

A¯nk=nk{\displaystyle {\bar {A}}_{n}^{k}=n^{k}}.

Например, количество вариантов 3-значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:

A¯103=103=1000{\displaystyle {\bar {A}}_{10}^{3}=10^{3}=1000}.

Ещё один пример: размещений с повторениями из 4 элементов a, b, c, d по 2 равно 4² = 16, эти размещения следующие:

aa, ab, ac, ad, ba, bb, bc, bd, ca, cb, cc, cd, da, db, dc, dd.

Все 125 вариантов с повторением трех из пяти чисел

Комбинаторика: основные правила и формулы.

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и  принципы  комбинаторики  используются  в  теории  вероятностей для подсчета  вероятности  случайных  событий и,  соответственно, получения законов распределения случайных величин. Это,  в  свою  очередь,  позволяет  исследовать  закономерности массовых случайных явлений, что является весьма важным для правильного понимания  статистических  закономерностей, проявляющихся в природе и технике.

 

Правила сложения и умножения в комбинаторике

Правило суммы.  Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m  способами.

 

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

 

Правило произведения.  Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n

3 способами и так до k-го действия, которое можно выполнить n_k  способами, то все k действий вместе могут быть выполнены:

способами.

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Решение

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

 Сочетания без повторений. Сочетания с повторениями

 Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно

выбрать m из n различных предметов?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Решение

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

 Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

 Размещения без повторений. Размещения с повторениями

 Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

 

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение.

В  данной  задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким  образом,  задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

 

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Решение

Можно  считать,  что  опыт  состоит  в 5-кратном выборе  с возращением одной из 3 цифр (1, 3, 7). Таким образом,  число  пятизначных  номеров  определяется  числом  размещений с повторениями из 3 элементов по 5:

.

 Перестановки без повторений. Перестановки с повторениями

 Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Решение

Генеральной  совокупностью  являются 4  буквы слова  «брак» (б, р, а, к). Число  «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинако

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

     При решении задач по комбинаторике используют следующие важные понятия

Размещения

      Рассмотрим следующую задачу.

      Задача.   9   карточек пронумерованы числами   1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .   Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

      Решение.Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.

      На первое место можно положить одну из   9   карточек. Для этого есть   9   способов. В каждом из этих   9   способов на второе место можно положить одну из оставшихся   8   карточек. Таким образом, существует

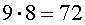
способа, чтобы положить карточки на первое и второе места. В каждом из этих   72   способов на третье место можно положить одну из оставшихся   7   карточек. Следовательно, существует

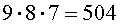
способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих   504   способов на четвертое место можно положить одну из оставшихся   6   карточек. Отсюда вытекает, что существует

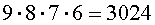
различных способа, чтобы выложить в ряд   4   карточки из набора, состоящего из   9   пронумерованных карточек. Таким образом, при выкладывании карточек можно получить   3024   различных четырехзначных числа.

      Ответ:   3024.

      При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

      Определение 1. Рассмотрим множество, содержащее   n   элементов, и все его упорядоченные подмножества, содержащие   k   элементов. Каждое из этих подмножеств называют размещением из   n   элементов по   k   элементов.

      Если обозначить символом 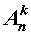 число размещений из   n   элементов по   k   элементов, то будет справедлива формула:

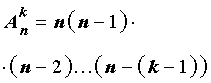(1)

      В соответствии с определением факториала, формулу (1) можно также записать в виде:

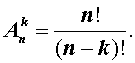
      В задаче множеством из   n   элементов является исходный набор из   9   пронумерованных карточек, а упорядоченным подмножеством из   k   элементов –   4   карточки, выложенные в ряд.

      Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из   9   элементов по   4   элемента, т.е. число

      В соответствии с формулой (1),

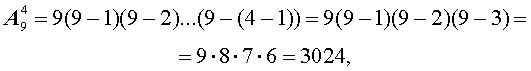
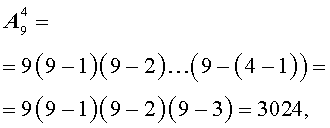
что и было получено в задаче.

      Замечание 1. Введенные в данном разделе размещения также называют размещениями без повторений.

      Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула

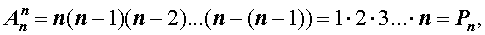
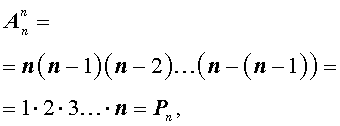
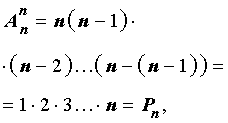
смысл которой заключается в следующем.

      Утверждение. Размещение из   n   элементов по   n   элементов является перестановкой из   n   элементов.

Сочетания

      Определение 2. Рассмотрим множество, состоящее из   n   элементов. Каждое его подмножество, содержащее   k   элементов, называют сочетанием из   n   элементов по   k   элементов.

      Число сочетаний из   n   элементов по   k   элементов обозначается символом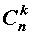

      Замечание 3. Важно отметить, что, в отличие от определения размещений, рассмотренные в определении сочетаний подмножества, содержащие   k   элементов, не являются упорядоченными. Поэтому, если в каждом подмножестве, содержащем   k   элементов (из определения 2), совершить всевозможные перестановки, количество которых равно   k ! ,   то мы получим все размещения.

      Таким образом, справедлива формула:

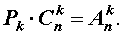
      Следовательно,

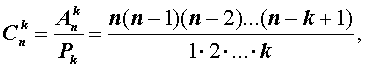
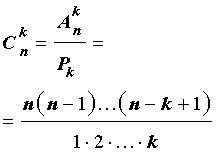
откуда вытекает формула

(2)

      Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):

      В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):

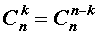
      Замечание 4. С разделом справочника «Сочетания» близко связан раздел «Бином Ньютона», где приведены и доказаны свойства чисел сочетаний.

   С понятиями факториала числа   n   и перестановок из   n   элементов можно познакомиться в разделе «Комбинаторика: факториалы и перестановки» нашего справочника.

 

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Комбинаторика. Размещения, перестановки, сочетания | Математика, которая мне нравится

В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.

Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.

Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.

Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.

В дальнейшем важную роль будет играть следующая

Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .

Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.

Размещения, перестановки, сочетания

Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .

Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .

Теорема. Число размещений множества из элементов по элементов равно

   

Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:

   

Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?

Решение. Искомое число трехполосных флагов:

   

Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.

Так, все различные перестановки множества из трех элементов — это

   

Очевидно, перестановки можно считать частным случаем размещений при >.

Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле

   

Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?

Решение. Искомое число расстановки ладей

   

по определению!

Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”).

Числа

Все сочетания из множества по два — .

.

Свойства чисел {\sf C}_n^k

1. .

Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.

2. .

Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .

Треугольник Паскаля

В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .

.

Теорема.

   

Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?

1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член

   

2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке

   

   

   

Домножим числитель и знаменатель этой дроби на :

   

   

Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?

Искомое число способов

   

Задачи.

1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :

   

Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.

Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?

Элементы комбинаторики. Перестановки, размещения, сочетания

Ниже калькулятор, подсчитывающий число перестановок, размещений и сочетаний. Под ним, как водится, ликбез, если кто подзабыл.

Элементы комбинаторики. Перестановки, размещения, сочетания

Число перестановок из n

 

Число размещений из n по m

 

Число размещений из n по m с повторениями

 

Число сочетаний из n по m

 

save Сохранить extension Виджет

Итак, есть множество из n элементов.

Вариант упорядочивания данного множества называется перестановкой (permutation).
Например, есть множество, состоящее из 3 элементов — А, В, и С. Пример перестановки — СВА. Число всех перестановок из n элементов:

Пример: Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА

Если из множества n элементов выбирают m в определенном порядке, это называется размещением (arrangement).
Пример размещения из 3 по 2: АВ или ВА — это два разных размещения. Число всех размещений из n по m

Пример: Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ

Также бывают размещения с повторениями, как ясно из названия, элементы на определенных позициях могут повторяться.
Число всех размещений из n по m с повторениями:

Пример: Для случая А, В, С число всех размещений из 3 по 2 с повторениями равно 3*3 = 9. Размещения: AA, АВ, АС, ВА, BB, ВС, СА, СВ, CC

Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием (combination).
Пример сочетания из 3 по 2: АВ. Число всех сочетаний из n по m

Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ

Приведем до кучи формулу соотношения между перестановками, размещениями и сочетаниями:

Обратите внимание, что внизу

Комбинаторика — основные понятия и формулы с примерами

Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.

Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.

Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.

Представители того научного мира пытались найти методы решения таких задач, их базовые правила и понятия, утвердить уникальные формулы и уравнения для тех, кто ещё не встречался с ними. Такая информация в наше время называется информацией «для чайников».

Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное.

Что такое комбинаторика в математике

Суть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов.

В интернете есть учебники по информатике и математике для детей, школьников, сборники материалов и задач для начинающих, где в доступном виде объяснена «занимательная» комбинаторика. Нужно твердо выяснить, как решать подобные задачи.

В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики — на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней.

Основные понятия

Их несколько:

1. Элемент – любой объект или явление, входящий в искомое множество.
2. Сочетание – подмножества, находящиеся в произвольном порядке в исходном множестве.
3. Перестановка – элементы во множестве находятся в строго определенном порядке.
4. Размещение – упорядоченные подмножества в исходном множестве.

Правило произведения

Является одним из основных правил при решении таких задач и звучит так:

При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами.

Рассмотрим на конкретных примерах.

Задача №1.

В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку?

Ответ прост: 2 * 6 = 12.

Задача №2.

Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету?

Решение аналогично: 1 * 2 * 3 * 4 = 24.

Причем левую часть можно записать гораздо проще: 4!

! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже).

Задача №3.

Сколько двузначных чисел можно составить из 2 цифр?

Ответ: 2! = 2.

Задача №4.

Сколько десятизначных чисел можно составить из 10 цифр?

10! = 3628800.

Правило суммы

Тоже является базовым правилом комбинаторики.

Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз.

Задача №5.

В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?

Ответ: 5 + 3 + 7 + 9 = 24.

Сочетания с повторениями и без повторений

Под этим термином понимают комбинации в произвольном порядке из множества n по m элементов.

Число сочетаний равно количеству таких комбинаций.

Задача №6.

В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта?

Решение простое:

Где 4! – комбинация из 4 элементов.

С повторениями чуть сложней, комбинации считаются по такой формуле:

Задача №7.

Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.

В этом случае:

Размещения с повторениями и без повторений

Под этим определением понимают набор m элементов из множества n элементов.

Задача №8.

Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов?

Ответ прост:

А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом:

Задача №9.

Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.

Решение:

Перестановки с повторениями и без повторений

Под этим термином понимают все возможные комбинации из n элементного множества.

Задача №10.

Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр?

Решения, согласно вышеприведенной формуле, следующие:

5! = 120;

6! = 720;

7! = 5040.

А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!

Задача №11.

В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?

Ответ прост: 4! / (3! * 1!) = 4.

Комбинаторные задачи с решениями

Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.

Типы задач	Что требуется найти	Методы решения
Магический квадрат	Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат).	Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам.
Задача размещения	Стандартная производственная задача (например, в лоскутной технике) — найти возможные способы разложения количества продуктов в ячейки в определенном порядке.	Включения и исключения. Как правило, применяется при доказательстве различных выражений.
Задачи про торговцев	Суть — найти все возможные пути прохождения людей из пункта А в пункт В.	Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения.

Заключение

Стоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач.

Сочетание — Википедия

Материал из Википедии — свободной энциклопедии

В комбинаторике сочетанием из n{\displaystyle n} по k{\displaystyle k} называется набор k{\displaystyle k} элементов, выбранных из данного множества, содержащего n{\displaystyle n} различных элементов.

Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-элементные сочетания, подмножества, k=3{\displaystyle k=3}) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n=6{\displaystyle n=6}) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

В общем случае число, показывающее, сколькими способами можно выбрать k{\displaystyle k} элементов из множества, содержащего n{\displaystyle n} различных элементов, стоит на пересечении k{\displaystyle k}-й диагонали и n{\displaystyle n}-й строки треугольника Паскаля.^[1]

3х элементные подмножества 5 элементного множества

Число сочетаний из n{\displaystyle n} по k{\displaystyle k} равно биномиальному коэффициенту

(nk)=Cnk=n!k!(n−k)!.{\displaystyle {n \choose k}=C_{n}^{k}={\frac {n!}{k!\left(n-k\right)!}}.}

При фиксированном n{\displaystyle n} производящей функцией последовательности чисел сочетаний (n0){\displaystyle {\tbinom {n}{0}}}, (n1){\displaystyle {\tbinom {n}{1}}}, (n2){\displaystyle {\tbinom {n}{2}}}, … является:

∑k=0n(nk)xk=(1+x)n.{\displaystyle \sum _{k=0}^{n}{\binom {n}{k}}x^{k}=(1+x)^{n}.}

Двумерной производящей функцией чисел сочетаний является

∑n=0∞∑k=0n(nk)xkyn=∑n=0∞(1+x)nyn=11−y−xy.{\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{n}{\binom {n}{k}}x^{k}y^{n}=\sum _{n=0}^{\infty }(1+x)^{n}y^{n}={\frac {1}{1-y-xy}}.}

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз. В частности, количество монотонных неубывающих функций из множества {1,2,…,k}{\displaystyle \{1,2,\dots ,k\}} в множество {1,2,…,n}{\displaystyle \{1,2,\dots ,n\}} равно числу сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k}.

Число сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k} равно биномиальному коэффициенту

C(n)k=((nk))=(n+k−1n−1)=(n+k−1k)=(−1)k(−nk)=(n+k−1)!k!⋅(n−1)!.{\displaystyle C_{(n)}^{k}=\left(\!\!{\binom {n}{k}}\!\!\right)={\binom {n+k-1}{n-1}}={\binom {n+k-1}{k}}=(-1)^{k}{\binom {-n}{k}}={\frac {(n+k-1)!}{k!\cdot (n-1)!}}.}

Доказательство

Пусть имеется n{\displaystyle n} типов объектов, причём объекты одного типа неотличимы. Пусть имеется неограниченное (или достаточно большое, во всяком случае, не меньше k{\displaystyle k}) количество объектов каждого типа. Из этого ассортимента выберем k{\displaystyle k} объектов; в выборке могут встречаться объекты одного типа, порядок выбора не имеет значения. Обозначим через xj{\displaystyle x_{j}} количество выбранных объектов j{\displaystyle j}-го типа, xj≥0{\displaystyle x_{j}\geq 0}, j=1,2,…,n{\displaystyle j=1,2,\dots ,n}. Тогда x1+x2+⋯+xn=k{\displaystyle x_{1}+x_{2}+\dots +x_{n}=k}. Но число решений этого уравнения легко подсчитывается с помощью «шаров и перегородок»: каждое решение соответствует расстановке в ряд k{\displaystyle k} шаров и n−1{\displaystyle n-1} перегородок так, чтобы между (j−1){\displaystyle (j-1)}-й и j{\displaystyle j}-й перегородками находилось ровно xj{\displaystyle x_{j}} шаров. Но таких расстановок в точности (n+k−1k){\displaystyle {\tbinom {n+k-1}{k}}}, что и требовалось доказать.■

При фиксированном n{\displaystyle n} производящей функцией чисел сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k} является:

∑k=0∞(−1)k(−nk)xk=(1−x)−n.{\displaystyle \sum _{k=0}^{\infty }(-1)^{k}{-n \choose k}x^{k}=(1-x)^{-n}.}

Двумерной производящей функцией чисел сочетаний с повторениями является:

∑n=0∞∑k=0∞(−1)k(−nk)xkyn=∑n=0∞(1−x)−nyn=1−x1−x−y.{\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{\infty }(-1)^{k}{-n \choose k}x^{k}y^{n}=\sum _{n=0}^{\infty }(1-x)^{-n}y^{n}={\frac {1-x}{1-x-y}}.}

• Р. Стенли. Перечислительная комбинаторика. — М.: Мир, 1990.