Сокращение дробей со степенями и буквами 8 класс: Сокращение алгебраических дробей — урок. Алгебра, 8 класс.

§ Алгебраические дроби. Сокращение алгебраических дробей

Алгебраические дроби. Сокращение Сложение и вычитание алгебраических дробей Умножение алгебраических дробей Деление алгебраических дробей

Прежде чем перейти к изучению алгебраических дробей рекомендуем вспомнить, как работать с обыкновенными дробями.

Запомните!

Любая дробь, в которой есть буквенный множитель, называется алгебраической дробью.

Примеры алгебраических дробей.

; 

a − b

a + b

;  ; 

m + n

n

; 

7(x + 1)

3

Как и у обыкновенной дроби, в алгебраической дроби есть числитель (наверху) и знаменатель (внизу).

Сокращение алгебраической дроби

Алгебраическую дробь можно сокращать. При сокращении пользуются правилами сокращения обыкновенных дробей.

Напоминаем, что при сокращении обыкновенной дроби мы делили и числитель, и знаменатель на одно и тоже число.

Алгебраическую дробь сокращают таким же образом, но только числитель и знаменатель делят на один и тот же многочлен.

Рассмотрим пример сокращения алгебраической дроби.

Определим наименьшую степень, в которой стоит одночлен «a» . Наименьшая степень для одночлена «a» находится в знаменателе — это вторая степень.

Разделим, и числитель, и знаменатель на «a²». При делении одночленов используем свойство степени частного.

Напоминаем, что любая буква или число в нулевой степени — это единица.

Нет необходимости каждый раз подробно записывать, на что сокращали алгебраическую дробь. Достаточно держать в уме степень, на которую сокращали, и записывать только результат.

Краткая запись сокращения алгебраической дроби выглядит следующим образом.

Важно!

Сокращать можно только одинаковые буквенные множители.

Нельзя сокращать

Можно сокращать

Другие примеры сокращения алгебраических дробей.

Как сократить дробь с многочленами

Рассмотрим другой пример алгебраической дроби. Требуется сократить алгебраическую дробь, у которой в числителе стоит многочлен.

Важно!

Сокращать многочлен в скобках можно только с точно таким же многочленом в скобках!

Ни в коем случае нельзя сокращать часть многочлена внутри скобок!

Неправильно

Правильно

Определить, где заканчивается многочлен, очень просто. Между многочленами может быть только знак умножения. Весь многочлен находится внутри скобок.

После того, как мы определили многочлены алгебраической дроби, сократим многочлен «(m − n)» в числителе с многочленом «(m − n)» в знаменателе.

Примеры сокращения алгебраических дробей с многочленами.

Вынесение общего множителя при сокращении дробей

Чтобы в алгебраических дробях появились одинаковые многочлены иногда нужно вынести общий множитель за скобки.

Рассмотрим пример.

В таком виде сократить алгебраическую дробь нельзя, так как многочлен
«(3f + k)» можно сократить только со многочленом «(3f + k)».

Поэтому, чтобы в числителе получить «(3f + k)», вынесем общий множитель «5».

Сокращение дробей с помощью формул сокращенного умножения

В других примерах для сокращения алгебраических дробей требуется
применение формул сокращенного умножения.

В первоначальном виде сократить алгебраическую дробь нельзя, так как нет одинаковых многочленов.

Но если применить формулу разности квадратов для многочлена «(a² − b²)», то одинаковые многочлены появятся.

Другие примеры сокращения алгебраических дробей с помощью формул сокращенного умножения.

Алгебраические дроби. Сокращение Сложение и вычитание алгебраических дробей Умножение алгебраических дробей Деление алгебраических дробей

---

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:

Отправить

---

Сокращение алгебраических дробей: правило, примеры.

Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.

Смысл сокращения алгебраической дроби

В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.

Сокращение алгебраической дроби представляет собой аналогичное действие.

Определение 1

Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.

К примеру, алгебраическая дробь 3·x2+6·x·y6·x3·y+12·x2·y2  может быть сокращена на число 3, в итоге получим: x2+2·x·y6·x3·y+12·x2·y2 . Эту же дробь мы можем сократить на переменную х, и это даст нам выражение 3·x+6·y6·x2·y+12·x·y2. Также заданную дробь возможно сократить на одночлен 3·xили любой из многочленов x+2·y, 3·x+6·y, x2+2·x·y или 3·x2+6·x·y.

Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.

Все ли алгебраические дроби подлежат сокращению?

Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1.

С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.

В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3·x23·y совершенно понятно, что общим множителем является число 3.

В дроби -x·y5·x·y·z3 также мы сразу понимаем, что сократить ее возможно на х, или y, или на х·y. И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.

Например, дробь x3-1×2-1  мы можем сократить на х-1, при этом указанный общий множитель в записи отсутствует. А вот дробь x3-x2+x-1×3+x2+4·x+4  подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя.

Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.

Правило сокращения алгебраических дробей

Правило сокращения алгебраических дробей состоит из двух последовательных действий:

• нахождение общих множителей числителя и знаменателя;
• в случае нахождения таковых осуществление непосредственно действия сокращения дроби.

Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.

Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a,b,c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a·cb·c , в котором мы сразу замечаем общий множитель c. Вторым шагом – выполняем сокращение, т.е. переход к дроби вида ab .

Характерные примеры

Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:

55=1;-23-23=1;xx=1;-3,2·x3-3,2·x3=1;12·x-x2·y12·x-x2·y;  

и т.п.

Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).

К примеру, 241260=2·2·2·32·2·3·3·5·7=23·5·7=2105

Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:

241260=23·322·32·5·7=23-232-1·5·7=2105  

(числитель и знаменатель разделены на общий множитель 22·3). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:

241260=23·322·32·5·7=2322·332·15·7=21·13·135=2105

По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.

Пример 1

Задана алгебраическая дробь -27·a5·b2·c·z6·a2·b2·c7·z . Необходимо произвести ее сокращение.

Решение

Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:

-27·a5·b2·c·z6·a2·b2·c7·z=-3·3·3·a·a·a·a·a·b·b·c·z2·3·a·a·b·b·c·c·c·c·c·c·c·z==-3·3·a·a·a2·c·c·c·c·c·c=-9·a32·c6

Однако, более рациональным способом будет запись решения в виде выражения со степенями:

-27·a5·b2·c·z6·a2·b2·c7·z=-33·a5·b2·c·z2·3·a2·b2·c7·z=-332·3·a5a2·b2b2·cc7·zz==-33-12·a5-21·1·1c7-1·1=·-32·a32·c6=·-9·a32·c6 .

Ответ: -27·a5·b2·c·z6·a2·b2·c7·z=-9·a32·c6

Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число.

Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).

Пример 2

Задана дробь 25·x0,3·x3. Необходимо выполнить ее сокращение.

Решение

Возможно сократить дробь таким образом:

25·x0,3·x3=25310·xx3=43·1×2=43·x2

Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т.е. на НОК (5, 10) = 10. Тогда получим:

25·x0,3·x3=10·25·x10·0,3·x3=4·x3·x3=43·x2 .

Ответ: 25·x0,3·x3=43·x2

Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.

Пример 3

Задана рациональная дробь 2·a2·b2+28·a·b2+98·b2a2·b3-49·b3 . Необходимо ее сократить.

Решение

Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:

2·a2·b2+28·a·b2+98·b2a2·b3-49·b3=2·b2·(a2+14·a+49)b3·(a2-49)

Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:

2·b2·(a2+14·a+49)b3·(a2-49)=2·b2·(a+7)2b3·(a-7)·(a+7)

Хорошо заметно, что возможно сократить дробь на общий множитель b2·(a+7). Произведем сокращение:

2·b2·(a+7)2b3·(a-7)·(a+7)=2·(a+7)b·(a-7)=2·a+14a·b-7·b

Краткое решение без пояснений запишем как цепочку равенств:

2·a2·b2+28·a·b2+98·b2a2·b3-49·b3=2·b2·(a2+14a+49)b3·(a2-49)==2·b2·(a+7)2b3·(a-7)·(a+7)=2·(a+7)b·(a-7)=2·a+14a·b-7·b

Ответ: 2·a2·b2+28·a·b2+98·b2a2·b3-49·b3=2·a+14a·b-7·b.

Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.

Пример 4

Дана алгебраическая дробь 15·x-27·x3·y5·x2·y-312 . Необходимо осуществить ее сокращение, если это возможно.

Решение

На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:

15·x-27·x3·y5·x2·y-312=x·15-27·x2·y5·x2·y-312

Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x2·y. Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:

x·15-27·x2·y5·x2·y-312=x·-27·-72·15+x2·y5·x2·y-15·312==-27·x·-710+x2·y5·x2·y-710

Теперь становится виден общий множитель, осуществляем сокращение:

-27·x·-710+x2·y5·x2·y-710=-27·x5=-235·x

Ответ: 15·x-27·x3·y5·x2·y-312=-235·x .

Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.

Как сократить дроби? Методы, примеры

Важный шаг, который мы делаем, решая дроби, — это приведение их к простейшей форме. Хоть мы и уменьшаем их для упрощения, значение дроби остается неизменным. Уменьшенная дробь эквивалентна исходной дроби. Фактически исходная дробь и уменьшенные дроби образуют пару эквивалентных дробей. В этом уроке мы научимся сокращать дроби тремя разными способами.

1.	Как сократить дроби?
3.	Методы сокращения дробей
4.	Дроби в числовой строке
5.	Как сократить дроби с переменными?
6.	Часто задаваемые вопросы о сокращении дробей

Как сократить дроби?

Сокращение дробей означает упрощение дроби, при котором мы делим числитель и знаменатель на общий делитель до тех пор, пока общий делитель не станет равным 1. Другими словами, дробь больше нельзя разделить на одно и то же целое число, отличное от 1. Например, рассмотрим дробь 8/24. Вот пошаговый процесс уменьшения дроби.

• Шаг 1: Запишите множители числителя и знаменателя. Делители 8 равны 1, 2, 4 и 8, а множители 24 равны 1, 2, 3, 4, 6, 8, 12 и 24
• Шаг 2: Определите общие делители числителя и знаменателя. Общие делители чисел 8 и 24 равны 1, 2, 4 и 8
.
• Шаг 3: Делите числитель и знаменатель на общие делители до тех пор, пока у них не будет общего делителя, кроме 1. Полученная таким образом дробь имеет сокращенную форму.

Начнем делить на 2: (8 ÷ 2) / (24 ÷ 2) = 4/12. Мы будем продолжать делить на 2, пока не сможем двигаться дальше. Итак, имеем (4 ÷ 2) / (12 ÷ 2) = 2/6 = (2 ÷ 2) / (6 ÷ 2) = 1/3. Следовательно, сокращенная форма 8/24 равна 1/3

Возьмем другой пример.

Пример: Уменьшите дробь, 10/20. Найдем общий делитель числителя и знаменателя. Повторяйте процесс до тех пор, пока не останется общих факторов. 5 является общим делителем как 10, так и 20. Разделив числитель и знаменатель на 5, мы получим 10/20 = (10 ÷ 5) / (20 ÷ 5) = 2/4. Дробь уменьшается до 2/4 на первом шаге. Теперь 2 — это общий множитель 2 и 4. Уменьшая дробь дальше, (2 ÷ 2) / (4 ÷ 2) = 1/2. Следовательно, сокращенная форма 10/20 равна 1/2.

Давайте посмотрим на рисунок, приведенный ниже. Первый круг имеет 2 заштрихованные части из 8 полных частей, тогда как второй круг имеет только одну заштрихованную часть из 4 полных частей. Следует отметить, что заштрихованная часть одинакова в обоих кругах. Таким образом, мы можем сделать вывод, что 2 равные части из 8 равных частей равны 1 равной части из 4 равных частей.

Методы сокращения дробей

Сократить дробь означает максимально упростить дробь. Чтобы найти редуцированные формы дробей, мы просто упростим дробь до ее наименьшей формы. Давайте рассмотрим три простых метода сокращения дробей.

Метод эквивалентных дробей

Эквивалентные дроби имеют одинаковое значение независимо от их числителей и знаменателей.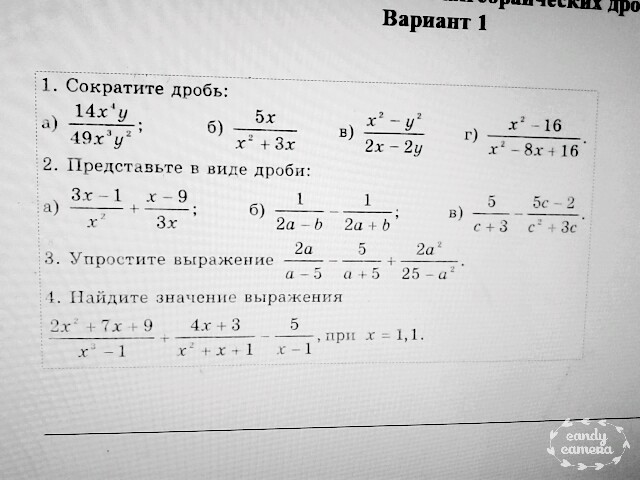 Ниже приведены шаги по уменьшению дробей методом эквивалентных дробей.

• Шаг 1: Найдите любой общий множитель числителя и знаменателя.
• Шаг 2: Разделите числитель и знаменатель на общий множитель.
• Шаг 3: Повторяйте тот же шаг в полученной дроби до тех пор, пока не останется общих делителей, отличных от 1.

Метод GCF

GCF (наибольший общий делитель) двух или более чисел — это наибольшее число среди всех общих делителей данных чисел. Ниже приведены шаги по уменьшению фракций методом GCF.

• Шаг 1: Найдите наибольший общий делитель (НОД) числителя и знаменателя.
• Шаг 2: Разделите числитель и знаменатель на GCF. Полученная таким образом фракция является восстановленной фракцией.

Метод факторизации простых чисел

Факторизация простых чисел — это способ представления числа в виде произведения его простых множителей. Ниже приведены шаги по уменьшению дробей методом простой факторизации.

• Шаг 1: Найдите разложение числителя и знаменателя на простые множители.
• Шаг 2: Сократите общие делители числителя и знаменателя.
• Шаг 3: Уберите оставшиеся числа в числителе и знаменателе, чтобы найти уменьшенную дробь.

Дроби в числовой строке

Мы уже знаем, как представлять целые числа на числовой прямой. Мы также можем показать дроби на числовой прямой и определить эквивалентные дроби на числовой прямой с помощью следующего примера и шагов.

• Шаг 1: Нарисуйте 6 линий, на концах которых отмечены два целых числа.
• Шаг 2: Разделите каждую числовую строку на равные части, как показано на рисунке. Например, начиная с первой числовой строки, мы видим, что она разделена на две равные части и деление отмечено дробью 1/2. Точно так же вторая числовая строка делится на три равные части, а деления отмечены дробями 1/3 и 2/3. Точно так же для всех числовых строк деления отмечены дробями.
• Шаг 3: После этого шага мы можем легко идентифицировать эквивалентные дроби, проверяя их длину от нуля. Например, мы можем идентифицировать дроби 1/2, 2/4, 3/6 и 4/8 как эквивалентные дроби, потому что, если мы посмотрим на их длину (расстояние) от 0, мы обнаружим, что они имеют одинаковую длину. Точно так же 1/3 и 2/6 являются эквивалентными дробями, потому что они представляют одинаковое расстояние на числовой прямой.
• Шаг 4: Таким образом, с помощью этого метода можно легко отметить и идентифицировать эквивалентные дроби на числовой прямой.

Как сократить дроби с переменными?

Переменные — это такие буквы, как a, b, c, x, y, z и т. д., которые появляются в математическом выражении и представляют неизвестные значения. Дроби могут иметь переменные вместе с числами. Чтобы сократить дробь с переменными, выполните шаги, указанные ниже:

• Шаг 1: Сгруппируйте одинаковые члены вместе. Например, в дроби (8а — а + 2а)/(12а). Сгруппируем подобные члены a. Упрощая числитель, получаем 9.а. Дробь теперь уменьшается до 9a/12a
.
• Шаг 2: Найдите общие множители и сократите их. 9а / 12а = (3 × 3 × а) / (3 × 4 × а). Отменив общие множители и упростив, получим дробь, уменьшенную до 3/4
.

Советы и рекомендации по сокращению дробей

Итак, теперь вы знаете три способа приведения дроби к ее простейшей форме. Вот несколько приемов, которые помогут вам быстро сократить дроби. Следуйте этим советам и рекомендациям, сводя дроби к их простейшей форме.

• Если числитель или знаменатель дроби является простым числом, то дальнейшее упрощение дроби невозможно.
• Дробь, в числителе которой 1, не может быть сокращена дальше.
• Чтобы уменьшить неправильную дробь, сначала запишите ее как смешанную дробь и следуйте тому же методу упрощения правильной дроби.

Темы, связанные с сокращением дробей

• Дроби
• Эквивалентные дроби
• Сложение и вычитание дробей
• Сравнение дробей
• Упрощение дробей
• Делитель
• Наибольший общий делитель
• Длинная дивизия
• Неправильные дроби

 

Примеры сокращения дробей

1. Пример 1: Сократите следующие фракции методом GCF. а) 16/64, б) 18/81

   Решение: Мы будем использовать метод GCF для сокращения дробей.

   а) Наибольший общий делитель 16 и 64 равен 16. Разделив числитель и знаменатель на 16, получим дробь, уменьшенную до 1/4. 16/64 = (16 ÷ 16) / (64 ÷ 16) = 1/4. Следовательно, сокращенная форма 16/64 равна 1/4

   б) Наибольший общий множитель 18 и 81 равен 9. Разделив числитель и знаменатель на 9, получим дробь, уменьшенную до 2/9. 18/81 = (18 ÷ 9) / (81 ÷ 9) = 2/9. Следовательно, сокращенная форма 18/81 равна 2/9.

2. Пример 2. Сократите следующие дроби методом простой факторизации. а) 3/15, б) 20/60

   Решение: Для сведения дробей методом простой факторизации находим простые множители числителя и знаменателя.

   а) Найдем разложение чисел 3 и 15 на простые множители. Разложение на простые множители 3 = 3 и разложение на простые множители 15 = 3 × 5. Сократив общие делители, мы получим 1/5. Следовательно, сокращенная форма 3/15 равна 1/5

   б) Давайте найдем разложение чисел 20 и 60 на простые множители. Разложение 20 на простые множители = 2 × 2 × 5 и разложение на простые множители 60 = 2 × 2 × 3 × 5. Сократив общие делители, мы получим 1/3. Следовательно, сокращенная форма 20/60 равна 1/3

   .

3. Пример 3: Сократите дробь (x ² + 5x + 6) / (x+3) ²

   Решение: Чтобы сократить дроби с переменными в вопросе, мы разложим выражения на множители даны в числителе и знаменателе.

   Числитель x ² + 5x + 6 можно разложить на множители как x ² + 5x + 6 = (x + 2) (x + 3). Теперь (х ² + 5х + 6) / (х+3) ² = (х + 2) (х + 3) / (х+3) ² . Сокращая общие множители, мы получаем (x + 2) / (x + 3). Следовательно, сокращенная форма дроби (x ² + 5x + 6) / (x+3) ² равна (x + 2) / (x + 3)

   .

перейти к слайдуперейти к слайдуперейти к слайду

Помогите ребенку наглядно представить, как работают числа!

Наша методология основана на визуальном обучении. Почувствуйте разницу, которую создают более 5000 визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о сокращении дробей

Как сократить большие дроби?

Для сокращения больших дробей разделим числитель и знаменатель крупной дроби на простые простые множители, чтобы привести ее к простейшему виду. Еще один простой способ сократить большие дроби — разделить числитель и знаменатель на их GCF. Это делает расчет быстрее и проще.

Как сократить смешанные дроби?

Смешанные дроби можно сократить после преобразования в неправильную дробь. Это можно сделать, используя формулу: \(\dfrac{(\text{Whole}\times\text{Знаменатель})+\text{Числитель}}{\text{Знаменатель}}\). После преобразования смешанной дроби в неправильную дробь ее можно при необходимости сократить. Например, \(5\dfrac{3}{7}=\dfrac{(5\times 7)+3}{7}=\dfrac{38}{7}\). Другой способ сокращения смешанных дробей состоит в том, чтобы разделить целое число и сократить только дробную часть смешанной дроби. Например, чтобы уменьшить \(3\dfrac{4}{8}\), мы сохраним 3 отдельно и уменьшим 4/8 до 1/2, так что окончательная уменьшенная дробь будет \(3\dfrac{1}{ 2}\)

Почему GCF используется в сокращении дробей?

При сокращении дробей мы используем НОД для деления числителя и знаменателя, потому что НОД (наибольший общий множитель) — это наибольшее число, которое делит числитель и знаменатель, поэтому дроби становится легче сокращать. Другие общие множители числителя и знаменателя меньше, и поэтому для уменьшения дроби требуется больше времени и действий. Например, сократим дробь: 12/18. GCF 12 и 18 равен 6. Таким образом, мы можем использовать 6, чтобы разделить числитель и знаменатель всего за один шаг. (12 ÷ 6)/(18 ÷ 6) = 2/3

Как дроби приводятся к наименьшему виду?

Чтобы привести дробь к простейшей форме, разделите числитель и знаменатель на наибольший общий множитель. Например, уменьшим 16/64. Наибольший общий множитель 16 и 64 равен 16. Итак, разделим числитель и знаменатель на 16. (16 ÷ 16) / (64 ÷ 16) = 1/4. Следовательно, сокращенная форма 16/64 равна 1/4.

Как уменьшить дроби?

Для приведения дроби к простейшей форме используются следующие шаги:

• Найдите наибольший общий делитель числителя и знаменателя.
• Разделите числитель и знаменатель на наибольший общий множитель. Полученная таким образом фракция имеет простейшую форму.

Как проще всего сократить дробь?

Один из самых простых способов привести дробь к простейшей форме — это разделить числитель и знаменатель дроби на их наибольший общий множитель (НОД).

Как сокращать дроби с помощью показателей?

Чтобы сократить дроби с показателями степени, примените правила возведения степени к числителю и знаменателю. Например, (a/b) ⁿ = a ⁿ /b ⁿ , где «a» и «b» — числитель и знаменатель соответственно, а «n» — показатель степени дроби. После вычисления дроби с использованием правил экспоненты приведите дробь к простейшей форме. Например, уменьшим (2/4) ³ . Это можно сократить и записать как (1/2) ³ , а затем, используя правила экспоненты, это можно записать как 1 ³ /2 ³ = 1/8.

Что такое неправильная дробь?

Дробь, у которой числитель больше знаменателя, называется неправильной дробью. Например, 7/4

Как преобразовать неправильную дробь в смешанную дробь?

Чтобы преобразовать неправильную дробь в смешанное число, нужно разделить числитель на знаменатель. Затем мы записываем частное как целое число, остаток как новый числитель, а знаменатель остается прежним. Например, чтобы преобразовать 26/7 в смешанную дробь, мы разделим 26 на 7. Это даст 3 в качестве частного и 5 в остатке. Итак, смешанная дробь будет \(3\dfrac{5}{7}\)

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист по дробям

Расширение и сокращение дробей — Уроки Wyzant

Вас могут попросить сделать две вещи: увеличить и уменьшить (или упростить) дроби. Расширить дробь
означает сделать ее «больше», а уменьшить дробь — значит сделать ее «меньше».

Расширяющиеся дроби

Расширение дробей означает их «увеличение». Например, допустим, вы съели 3/8
той пиццы, но ваш друг хотел знать, сколько шестнадцатых вы съели. Вам нужно было бы
расширить 3/8, чтобы дать ему ответ. Расширение дроби НЕ
меняет то, сколько вы съели (или съели), оно просто меняет то, как вы сообщаете человеку
, что вы съели. Вы бы расширили дробь следующим образом:

Посмотрите на знаменатели. На что нужно умножить 8, чтобы получить 16? Подумайте о своих
таблицах умножения на 8. 8 раз что дает вам 16? Ну, мы знаем, что 8 х 2 = 16. Значит,
что мы расширяем дробь на 2. Знаменатель у вас уже расширен,
значит надо еще расширить верхушку. Для этого вы берете то же число
, которое вы использовали для нижнего умножения (в данном случае 2), и умножаете это число
на верхнее число (числитель). Он сказал бы: 3 x 2 = ? Что такое 3 х 2? Мы знаем
, что ответ на этот вопрос равен 6, поэтому 6 теперь наш новый числитель. Когда мы сложим вместе
, мы получим 6/16, поэтому мы знаем, что 3/8 в расширенном виде равно 6/16. Тогда вы можете
скажи своему другу, что ты съел 6/16 пиццы. Это то же самое, что вы изначально считали
, 3/8, но это другой способ сказать ему.

Позвольте мне показать вам еще раз. На этот раз я дам вам дробь и
число, на которое мы расширяем, и вы сами получите новую дробь.

Расширить 3/4 на 5.

Подумайте: расширьте числитель (верхнее число). 3 х 5 = ? Мы знаем, что 3 х 5 = 15, поэтому
наш новый числитель равен 15. Далее расширяем знаменатель. 4 х 5 = ? Мы знаем, что 4
х 5 = 20, поэтому 20 — наш новый знаменатель. Итак, вся наша расширенная дробь равна 15/20.
15/20 по-прежнему означает то же, что и 3/4, просто это другой способ написания.

Сокращение (упрощение) дробей

Теперь поговорим о сокращении дробей. Сокращение дробей (также известное как упрощение дробей
) противоположно их расширению. Иногда мы видим действительно большие дроби
можно написать (или сказать) проще. Например, вы не стали бы говорить кому-то
, что съели 75/200 пиццы, вы бы хотели сказать это проще, чтобы он
или она могли вас понять. Для этого вам нужно будет уменьшить (упростить)
дробь. Есть два разных способа сделать это, я покажу вам оба из них.

Первый способ — попытаться вычислить наибольшее число, которое делится как на
, так и на числитель и знаменатель вашей дроби. Я собираюсь использовать 5/20 для моего примера.
Я хочу придумать число, которое можно разделить и на 5, и на 20. Я могу положить 5 в число
и на 5, и на 20. Затем я беру задуманное число (5) и делю числитель
и знаменатель на это число. В этом примере 5 ÷ 5 = 1, а 20 ÷ 5 = 4. Итак, теперь
мой новый числитель равен 1, а мой новый знаменатель равен 4, что делает дробь равной 1/4.

Это будет выглядеть так:

Сейчас я покажу вам второй способ. Для второго способа нужно перечислить простые множители
каждого номера. В этом случае простые множители числа 5 равны 1 и 5. Простые множители
числа 20 равны 2 x 2 x 5. Вы бы поместили их туда, где они принадлежат частям дроби
бар, так что 1 x 5 будет продолжаться. вверху (куда идет числитель), а 2 x 2 x 5 будет
внизу (куда идет знаменатель). Это будет выглядеть так:

Теперь вы должны искать какие-либо общие факторы между двумя числами.