Логические основы ЭВМ — презентация онлайн
Похожие презентации:
Пиксельная картинка
Информационная безопасность. Методы защиты информации
Электронная цифровая подпись (ЭЦП)
Этапы доказательной медицины в работе с Pico. Первый этап
История развития компьютерной техники
От печатной книги до интернет-книги
Краткая инструкция по CIS – 10 шагов
Информационные технологии в медицине
Информационные войны
Моя будущая профессия. Программист
1.Алгебра
высказываний
4. Логические
операции
2.Логические
переменные
5. Виды логических
операций
3.Логические
функции
6. Таблица
истинности функций
Алгебра логики – это раздел
математики, изучающий
сложные высказывания,
рассматриваемые со стороны
их логических значений
(истинности или ложности) и
логических операций над
ними.
Алгебра логики возникла в
середине 19 века в трудах
английского математика
Джорджа Буля.
представляло собой попытку
решать традиционные
логические задачи
алгебраическими методами.
Алгебра высказываний
Алгебра высказываний была
разработана для того, чтобы
определять истинность или
ложность составных
высказываний, не вникая в
их содержание
Основными элементами логики высказываний
являются логическая переменная и
логическая формула Некоторые
логические выражения необходимо
преобразовать, чтобы их было удобно читать,
упростить для дальнейшего использования
или просто подогнать для имеющихся
элементов (например, в электронике).
Для таких действий, для изменения
изначального выражения без внесения
изменений в результат, используют
тождественно истинные высказывания.
Логические
переменные
Логические переменные– простые
высказывания, содержащие только
одну мысль.
Обозначаются буквами латинского
алфавита:
A, B, C…
Логические переменные могут
принимать лишь два значения:
«ИСТИНА» (1) или «ЛОЖЬ» (0)
6.
СПОСОБЫ ЗАПИСИ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙИстинаЛожь
И
Л
True T
False F
1
0
Например, два простых
высказывания:
А=
«2 2 = 4» истина (1)
В = «2 2 = 5»
ложь (0)
являются логическими
переменными
А
и
В
В алгебре высказываний
высказывания
обозначаются именами
логических переменных,
которые могут принимать
лишь два значения:
«ИСТИНА» (1) или
«ЛОЖЬ» (0)
В алгебре высказываний
над логическими
переменными (над
высказываниями) можно
производить
определенные логические
операции, в результате
которых получаются
новые высказывания
Составные
высказывания
Высказывания, состоящие из
нескольких простых суждений и
содержащие в себе более, чем одну
простую мысль, называются
логическими функциями
Обозначаются F(A,B,C…)
Также могут принимать значения
«ИСТИНА» или «ЛОЖЬ» в
зависимости от того, какие значения
имеют входящие в их состав
логические переменные и от
действий над ними
Каждое составное высказывание можно
выразить в виде формулы (логического
выражения), в которую входят логические
переменные, обозначающие высказывания, и
знаки логических операций, обозначающие
логические функции.
Для записи составного высказывания в виде
логического выражения на формальном языке
в составном высказывании нужно выделить
простые высказывания и логические связи
между ними.
запишем в форме логического выражения
составное высказывание «(2*2=5 или 2*2=4) и
(2*2 5 или 2*2 4)».Проанализируем составное
высказывание. Оно содержит два простых
высказывания:
А= «2*2=5» — ложно (0)
В= «2*2=4» — истинно (1)
Тогда составное высказывание можно записать
в следующей форме: «(А или В) и ( А или В)».
ЛОГИЧЕСКАЯ ОПЕРАЦИЯ
способ построения сложного
высказывания из данных
высказываний, при котором значение
истинности сложного высказывания
полностью определяется значениями
истинности исходных высказываний.
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция
Объединение двух или
нескольких
высказываний в одно с
помощью союза «И»
называется операцией
логического
умножения, или
конъюнкцией
Запись конъюнкции на формальном
языке алгебры высказываний
F(A,B) = A & B
или
F(A,B) = A B
Также может встретиться запись,
типа:
F(A,B) = A * B
или
F(A,B) = A and B
F(A,B) = A B
Логическая функция,
полученная в результате
конъюнкции, истинна
тогда и только тогда,
когда истинны все
входящие в него
логические переменные
Конъюнкция.
Определитеистинность логической функции
1) «2
2) «2
3) «2
4) «2
2
2
2
2
=
=
=
=
5»
5»
4»
4»
И
И
И
И
«3
«3
«3
«3
3
3
3
3
=
=
=
=
10»
9»
10»
9»
Истинна только функция (4)
Значение логической
функции определяется
по ее таблице истинности
Таблица истинности
показывает какие
значения принимает
логическая функция
при всех возможных
значениях логических
переменных
Таблица истинности
для конъюнкции
A
B
2 2 = 5 3 3 = 10
2 2=5
3 3=9
2 2 = 4 3 3 = 10
2 2=4 3 3=9
A B
ЛОЖЬ
ЛОЖЬ
ЛОЖЬ
ИСТИНА
A
0
0
1
1
B
0
1
0
1
A B
0
0
0
1
Объединение двух или
нескольких
высказываний в одно с
помощью союза «ИЛИ»
называется операцией
логического сложения,
или дизъюнкцией
Запись дизъюнкции на
формальном языке
алгебры высказываний
F(A,B) = A B
Также может встретиться запись,
типа:
F(A,B) = A + B
или
F(A,B) = A or B
F(A,B) = A B
Логическая функция,
полученная в результате
дизъюнкции, истинна
тогда, когда истинна хотя
бы одна из входящих в
него логических
переменных
Дизъюнкция.
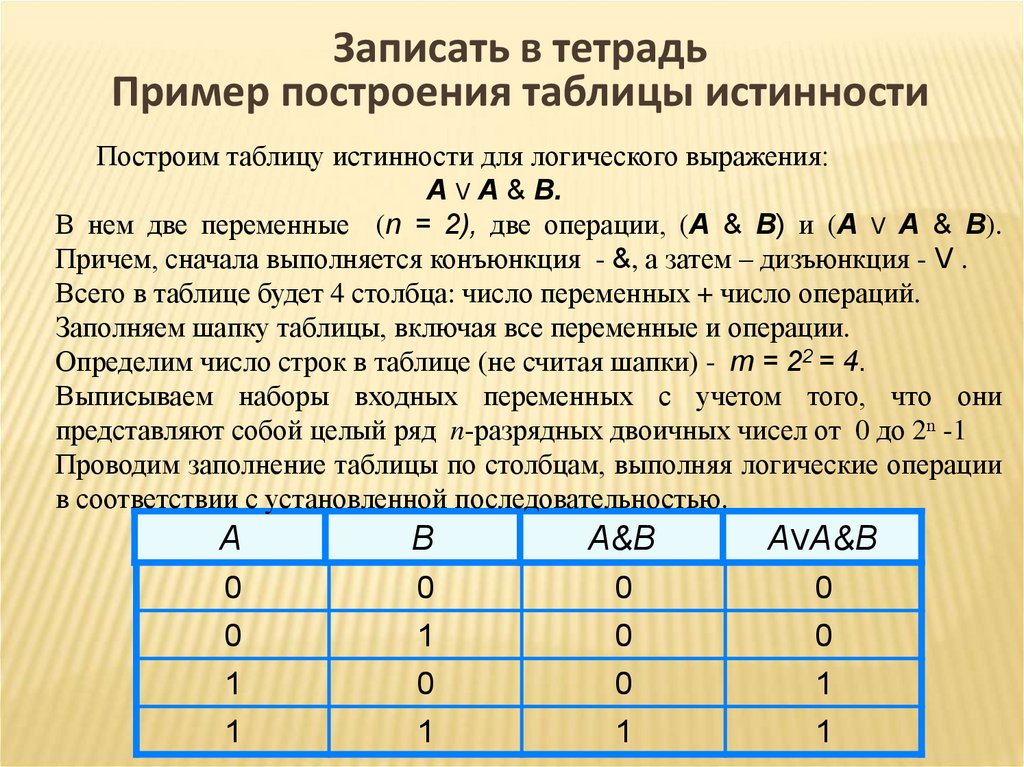Определитеистинность логической функции
1)
2)
3)
4)
«2
«2
«2
«2
2
2
2
2
=
=
=
=
5»
5»
4»
4»
ИЛИ
ИЛИ
ИЛИ
ИЛИ
«3
«3
«3
«3
Ложна только функция
(1), остальные истинны
3
3
3
3
=
=
=
=
10»
9»
10»
9»
Таблица истинности
для дизъюнкции
A
B
2 2 = 5 3 3 = 10
2 2=5
3 3=9
A B
ЛОЖЬ
ИСТИНА
2 2 = 4 3 3 = 10
ИСТИНА
2 2=4
ИСТИНА
3 3=9
Таблица истинности
для дизъюнкции
A
0
0
1
1
B
0
1
0
1
A B
0
1
1
1
Присоединение частицы
«НЕ» к высказыванию
называется операцией
логического отрицания,
или инверсией
Запись инверсии на формальном
языке алгебры высказываний
F(A) = ¬A
или
F(A) = Ā
Также может встретиться
запись, типа:
F(A) = not А
F(A) = Ā
Логическое отрицание
(инверсия) делает
истинное высказывание
ложным, а ложное –
истинным
[логическая отрицательная
единица, перевертыш]
Инверсия
Пусть
A = «2 2 = 4»
– истинное
высказывание, тогда
F(A) = «2 2 ≠ 4»
– ложное высказывание
Таблица истинности
для инверсии
А
¬А
0
1
1
0
Дополнительные
логические функции
Импликацию и эквивалентность можно
выразить через конъюнкцию, дизъюнкцию
и отрицание, поэтому их называют
дополнительными логическими функциями:
Импликация:
А → В = ¬A В или
А В = ¬A В или
А В = ¬A В
Эквивалентность:
А ↔ В = (¬A В) (¬B A) или
А В = (¬A В) (¬B A) или
А ≡ В = (¬A В) (¬B A)
Объединение двух
высказываний, из которых
первое является условием, а
второе – следствием из него,
связанных между собой
словами «если…то»,
называется импликацией
(логическим следованием)
Импликация ложна
тогда и только тогда,
когда
условие истинно,
а следствие ложно
Пример:
Если выучишь материал, то сдашь зачет
Это высказывание ложно только тогда, когда материал
выучен, а зачет не сдан, т.
к. сдать зачет можно ислучайно, например если попался единственный знакомый
вопрос или удалось воспользоваться шпаргалкой
Таблица истинности
для импликации
A
B
A→B
0
0
1
0
1
1
1
0
0
1
1
1
Эквивалентность
Эквивалентность (равнозначность)–
это логическая операция,
объединяющая два простых
высказывания в одно составное и,
которое является истинным
тогда и только тогда, когда
оба исходных высказывания
одновременно либо истинны, либо
ложны.
Таблица истинности
для эквивалентности
A
B
A B
0
0
1
0
1
0
1
0
0
1
1
1
ПРИВЕДИТЕ ПРИМЕРЫ КОНЪЮНКЦИИ
Приведите примеры истинной и
ложной конъюнкции двух или
нескольких высказываний.
Приведите примеры истинной и
ложной дизъюнкции двух или
нескольких высказываний.
Как в русском языке может
обозначаться дизъюнкция?
Найдите правильно построенное отрицание
суждения «Все воздушные шары зелёные»:
Все воздушные шары не зелёные.
Не верно, что все воздушные шары зелёные.
Докажите свою точку зрения с помощью
определения. Запишите отрицания
следующих высказываний:
Сегодня хорошая погода.
Число 3 — чётное.
Некоторые млекопитающие не живут на суше.
Во всякой школе некоторые ученики
увлекаются программированием.
39. Запишите схематически следующие высказывания
Быть иль не быть — вот в чемвопрос.» (Шекспир)
А V Ā <=> В
«Если хочешь быть красивым,
поступи в гусары.» (К. Прутков)А => В
Ядерная энергия — это не
электричество, не тяготение, просто
химия — словом, неизвестно что.
А <=> B v C < = > D v P
Если краткость — сестра таланта, то
сокращение — дитя гения. А => В
Формула Высказывание
A
В
не A
не B
AиB
A или B
Зверь полосатый
Зверь хищный
Тигр Волк Бурундук Заяц Медведь
English Русский Правила
Логические операторы
← предыдущая следующая →
В этом уроке описаны логические операторы.
JavaScript поддерживает три логических оператора: || (ИЛИ), ! (НЕ), которые очень часто используются в условных конструкциях, например if, while или for. Благодаря логическим операторам можно объединять два выражения в одно более сложное.
JavaScript: Табnица истинности
Основными логическими или булевыми операциями, названными в честь одного из математиков — Джорджа Буля (1815-1864), являются:
- ИЛИ
||– логическое сложение (дизъюнкция) – OR; - И
&&– логическое умножение (конъюнкция) – AND; - НЕ
!– логическое отрицание (инверсия) – NOT.
Логические операторы работают с операндами так же, как и с булевыми значениями, возвращая true или false, поэтому эти операции можно описать таблицей истинности, в которой полностью описано их поведение:
| X | Y | X || Y | X && Y | !X |
|---|---|---|---|---|
| false | false | false | false | true |
| true | false | true | false | false |
| false | true | true | false | true |
| true | true | true | true | false |
Из этой таблицы видно, что результатом работы оператора ИЛИ || будет false, только если оба его операнда – false; результатом оператора И && будет true, только если оба из его операндов – true.
Оператор НЕ ! прост – он получает один операнд и возвращает обратное значение.
Логические операторы не требуют, что бы их операнды были логическими значениями. Стоит отметить, что все значения в языке JavaScript являются либо истинными false.
На заметку: Ложными (false) значениями являются false, null, undefined, 0, –0, NaN и "" (пустя строка). Все другие значения, включая все объекты, являются истинными (true).
Логическое И (&&)
Логический оператор И && выполняет логическую операцию конъюнкции двух булевых значений. Конъюнкция – это сложное логическое выражение, которое считается истинным true только в том случае, когда оба его операнда (выражения) являются истинными true, во всех остальных случаях данное сложное выражение ложно false.
Примеры:
Выполнить код »
Часто оператор И && используется совместно с двумя выражениями сравнения:
Выполнить код »
Операторы сравнения, согласно таблицы приоритетов, имеют более высокий приоритет, чем логические операторы && и ||, поэтому приведенное выше выражение можно писать без скобок.
Для оператора && не обязательно, чтобы его операнды бьли булевыми значениями. Он принимает любые значения, поскольку они могут быть преобразованы в булевы.
Например, в следующем примере число 1 будет воспринято как true, а 0 – как false:
Выполнить код »
Логическое И && начинает работу с вычисления левого операнда. Если получившееся значение может быть преобразовано в false (например, null, undefined, 0
–0, NaN или ""), значит, результат выражения равен false или непреобразованному значению левого выражения.
Поэтому вычисление и преобразование второго операнда не выполняется. В противном случае, если значение слева является истинным, тогда результат всего выражения определяется значением справа. Поэтому, когда значение слева является истинным, оператор && вычисляет и возвращает значение справа:
Выполнить код »
Итак, оператор && вычисляет операнды слева направо до первого ложного false аргумента и возвращает его значение, а если все операнды истинные true – то возвращается значение последнего. Если первый операнд – false, то результат будет false, и остальные значения игнорируются.
Такое поведение оператора &&, позволяющее экономить ресурсы и не вычислять правый аргумент, иногда называют «короткой схемой вычислений».
Это особенно заметно, когда выражения, имеющие побочные эффекты (присваивания, инкременты, декременты и вызовы функций), помещаются в правую часть оператора &&:
Выполнить код »
При выполнении логического И && в этом коде возникает ошибка, потому что переменная y не объявлена.
Значение левого операнда – true, поэтому интерпретатор переходит к оценке правого операнда. Если изменить значение левого операнда на false, ошибка не возникает:
Выполнить код »
В этом примере переменная y тоже не определена, но правый операнд никогда не оценивается, потому что левый операнд равен false. Используя оператор И &&, помните о так называемой «сокращенной схеме его вычисления».
Логическое ИЛИ (||)
Оператор логическое ИЛИ || вычисляет дизъюнкцию (логическим сложением) двух операндов. Если хотя бы один или оба операнда преобразуются в true, он возвращает true или непреобразованное значение. Если же оба операнда преобразуются в false, он возвращает false или непреобразованное значение.
Логическое ИЛИ ||, как и логическое И && поддерживает сокращенные вычисления.
В этом прмере правый операнд не оценивается, потому что левый эквивалентен значению true, например:
Выполнить код »
Если же левый операнд имеет значение false или значение, которое может быть преобразовано в false, оператор || переходит к вычислению значения правого операнда, и возвращает его значение:
Выполнить код »
На заметку: Логическое ИЛИ || вычисляет операнды слева направо до первого истинного значения и возвращает его, а если все значения ложные – то возвращает последнее значение.
Логическое НЕ (!)
Оператор логического НЕ ! является унарным оператором, помещаемым перед одиночным операндом. Он преобразует значение своего операнда в булево значение, затем инвертирует это значение в противоположное и возвращает, полученное в результате инвертирования, булево значение.
Вот некоторые примеры:
Выполнить код »
Таким обазом, оператор ! всегда возвращает true или false, поэтому его можно использовать для преобразования любого значения x в его логический эквивалент, дважды применив этот оператор: !!x.
Выполнить код »
Комбинирование логических операторов
Оператор НЕ !, будучи унарным, имеет высокий приоритет (16) и тесно связан с своим аргументом. Приоритет оператора И && больше, чем приоритет оператора ИЛИ || – соответственно 6 и 5.
Учитывая приоритетность логических операторов, следующие проверки на идентичность дают истинный true результат при любых значениях выражений x и y:
Выполнить код »
В следующем коде сначала будет вычислено правое логическое И &&, а уже потом – &&:
Выполнить код »
Изменить результат сложного выражения можно применив в нужном месте кода скобки ():
Выполнить код »
Итоги
- Логическое И
&&возвращаетtrueтогда и только тогда, когда оба операнда преобразуются вtrue.
- Логическое ИЛИ
||возвращаетtrueесли хотя бы один или оба операнда преобразуются вtrue. - Операторы
&&и||поддерживают сокращенное вычисление: если первого операнда достаточно для определения результата, второй операнд не оценивается. Так, если первый операнд логического И&&эквивалентен значениюfalse, то второй операнд не оценивается. В случае с логическим ИЛИ||наоборот, правый операнд не оценивается, если левый эквивалентен значениюtrue. - Логическое отрицание НЕ
!используется для инверсии (переворачивание смысла) логического значения своего операнда и всегда возвращаетtrueилиfalse. - С помощью двух логических НЕ
!!можно преобразовать значение операнда в его логический эквивалент. - Логические операторы
!,&&и||имеют разные приоритеты – соответственно16, 6 и 5. B (циркумфлекс)Введите таблицу истинности
Введите «0», «1» или «x».
Таблица истинности (2 входа) Выход 0 0 0 1 1 0 1 1 Таблица истинности (3 входа) Выход 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Таблица истинности (4 входа) Выход 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 Таблица истинности (5 входов) Выход 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 1 0 1 1 0 0 0 1 1 0 1 0 1 1 1 0 0 1 1 1 1 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 0 0 1 1 1 0 1 0 0 1 0 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 Таблица истинности (6 входов) Выход 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 1 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 1 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 9№ Kmap -Simplifier -Google Suce
ALLBILDERVIDEOSNEWSMAPSSHOPPINGBücher
SUCOPTIONEN
MEINTEST DU: KAMP -SIMPLIFIE Решатель карты Карно, который составляет км-карту, показывает, как группировать термины, показывает упрощенное логическое уравнение и рисует схему до 6 .
..4_переменных · 3_переменных · 2_переменных · Таблица истинности
Средство расчета карт Карно — Чарли Коулман
charlie-coleman.com › Experiments › kmap
Позволяет пользователю вводить значения для карты Карно и получать логические выражения для вывода.
Решатель KMap | Решение булевой алгебры
www.boolean-алгебра.com › kmap
Упрощение и решение выражений булевой алгебры. Подробные шаги, логические схемы, KMap, таблица истинности и викторины. Все в одном калькуляторе логических выражений.
Karnaugh Map Builder and Solver
ictlab.kz › extra › Kmap
Чтобы решить выражение вручную, выберите количество переменных выше и оставьте ввод выражения пустым. … Вы можете получить более подробную информацию по …
Калькулятор карты Карно (решатель Kmap) — AtoZmath.com термины Сумма произведения, Произведение суммы показывает упрощенное логическое уравнение 2,3,4,5,6,7,8 Переменная с использованием .
..MathBunny/karnaugh-map-simplifier — GitHub
github.com › MathBunny › karnaugh-map-simplifier Карта Карно …
karnaugh-map-simplifier · Темы GitHub
github.com › темы › karnaugh-map-simplifier
kmap-solver — это инструмент командной строки для решения и визуализации карт Карно до 4 переменных . nodejs cli typescript karnaugh-map command-line-tool karnaugh-map- …
Karnaugh Map Simplifier
www.horatiulazu.ca › проекты › karnaugh › общие
Что делает эта программа? Цель этой программы — упростить выражения булевой алгебры. Программное обеспечение использует Карты Карно, которые представляют собой сетку …
Документация по упрощению карт Карно — Horatiu Lazu
www.horatiulazu.ca › проекты › сайт karnaugh ›
Добро пожаловать. Добро пожаловать на сайт документации программного обеспечения Karnaugh Map Simplifier. Цель этого веб-сайта — предоставить документацию как для разработчиков, так и .
B (циркумфлекс)
..
..