Соответственные и накрест лежащие углы: Углы при пересечении двух прямых

Содержание

Теория параллельных прямых. Теория треугольника, страница 13

Рис.3.20

Рис.3.21

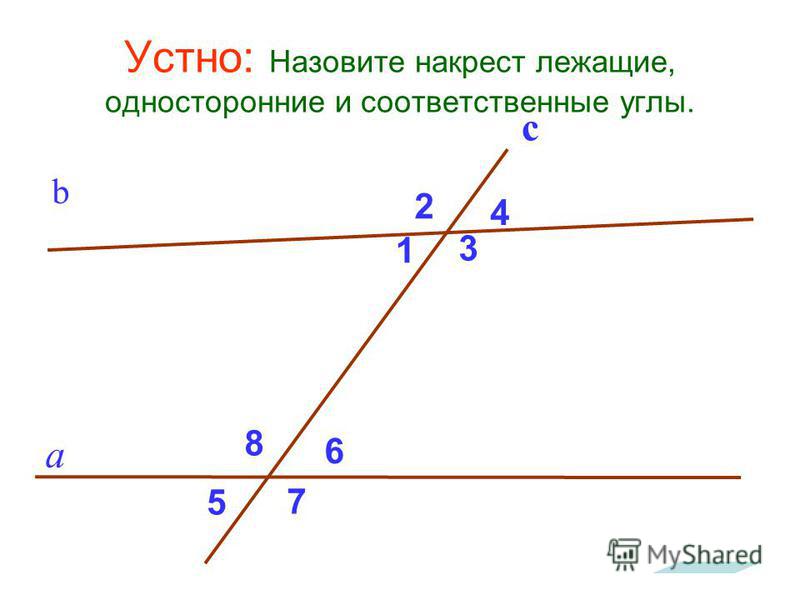
Эти углы принято называть внутренними односторонними, так как они расположены внутри параллельных прямых и в одной полуплоскости относительно секущей.

Раз одни и те же углы составляют пары и внутренних односторонних и внутренних накрест лежащих углов, то между ними должна быть связь. Посмотрите внимательнее на рисунки 3.20 и 3.21.

Пара внутренних накрест лежащих углов, например 2 и 4, и пара внутренних односторонних углов, например 1 и 2, имеют один общий угол – 2,а углы 1 и 4 – смежные, то есть Ð1+Ð4=180º. Значит, если углы 2 и 4 равны, то сумма углов 1 и 2 равна 180º, и наоборот. Поэтому верно утверждение

Если внутренние накрест лежащие углы равны, то сумма внутренних односторонних углов равна 180

°. И обратно: если сумма внутренних односторонних углов равна 180°, то внутренние накрест лежащие углы равны.

Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей. На рисунке справа углы 1 и 3– соответственные.

Из равенства внутренних накрест лежащих углов следует равенство соответственных и наоборот (Докажите это утверждение самостоятельно).

Объединим три утверждения, связывающие различные виды углов в одно.

Утверждение 3.1. Внутренние накрест лежащие углы равны, сумма внутренних односторонних углов равна 180°, соответственные углы равны — это три эквивалентных высказывания. То есть справедливость одного из них влечет справедливость остальных двух.

Раз верно утверждение 3.1, то мы можем сформулировать еще два признака параллельности прямых.

Теорема 3.3(II признак параллельности двух прямых).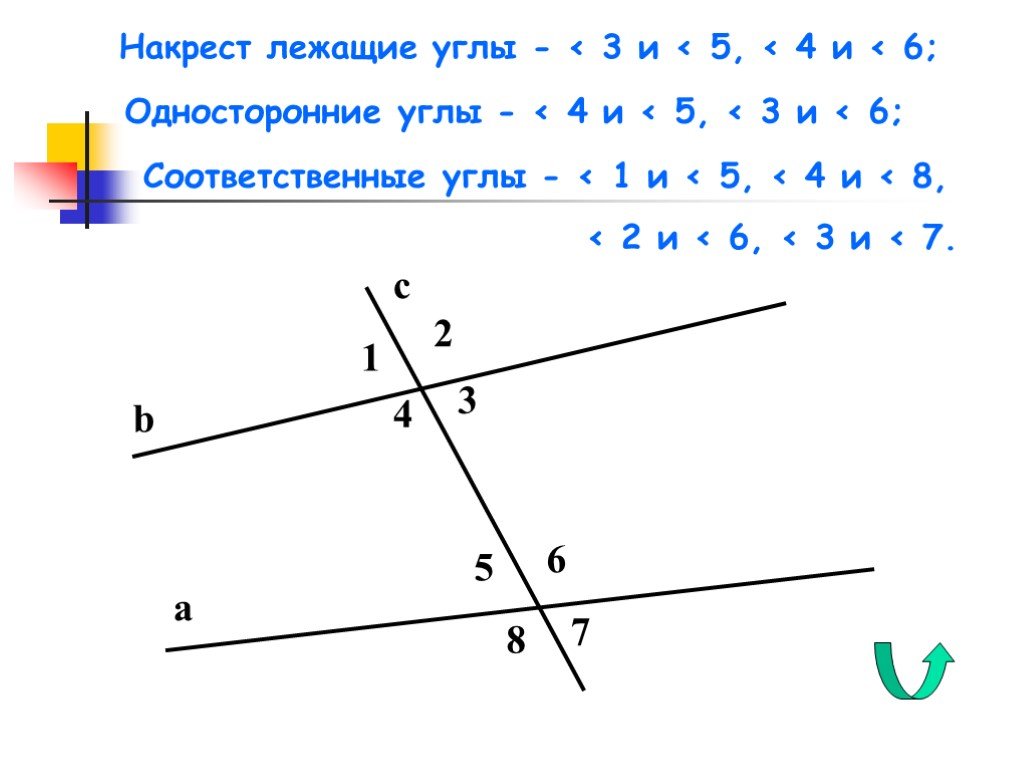 Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Задание 3. Сформулируйте и докажите обратное утверждение.

Теорема 3.4(III признак параллельности двух прямых). Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Задание 4. Как формулируется и доказывается обратное утверждение?

Обобщая вышеизложенное, можно сказать, что параллельность двух прямых можно определить по углам, которые эти прямые образуют с третьей прямой, пересекающей их (секущей).

Утверждение 3.2. Прямые параллельны, соответственные углы равны, внутренние накрест лежащие углы равны, сумма внутренних односторонних углов равна 180

° — это четыре эквивалентных высказывания. То есть справедливость одного из них влечет справедливость остальных двух.

Это утверждение следует из теорем 3.1, 3.2 и утверждения 1.

С помощью теорем, которые являются признаками параллельности двух прямых, можно доказать, что противоположные теоремы также верны.

Признаки не параллельности прямых.

I признак не параллельности прямых.

Если при пересечении двух прямых секущей внутренние накрест лежащие углы не равны, то прямые не параллельны.

Докажите это утверждение и сформулируйте обратное.

II признак не параллельности прямых.

Если при пересечении двух прямых секущей соответственные углы не равны, то прямые не параллельны.

Докажите эту теорему и сформулируйте обратную ей.

III признак не параллельности двух прямых.

Параллельные прямые. (7 класс) — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

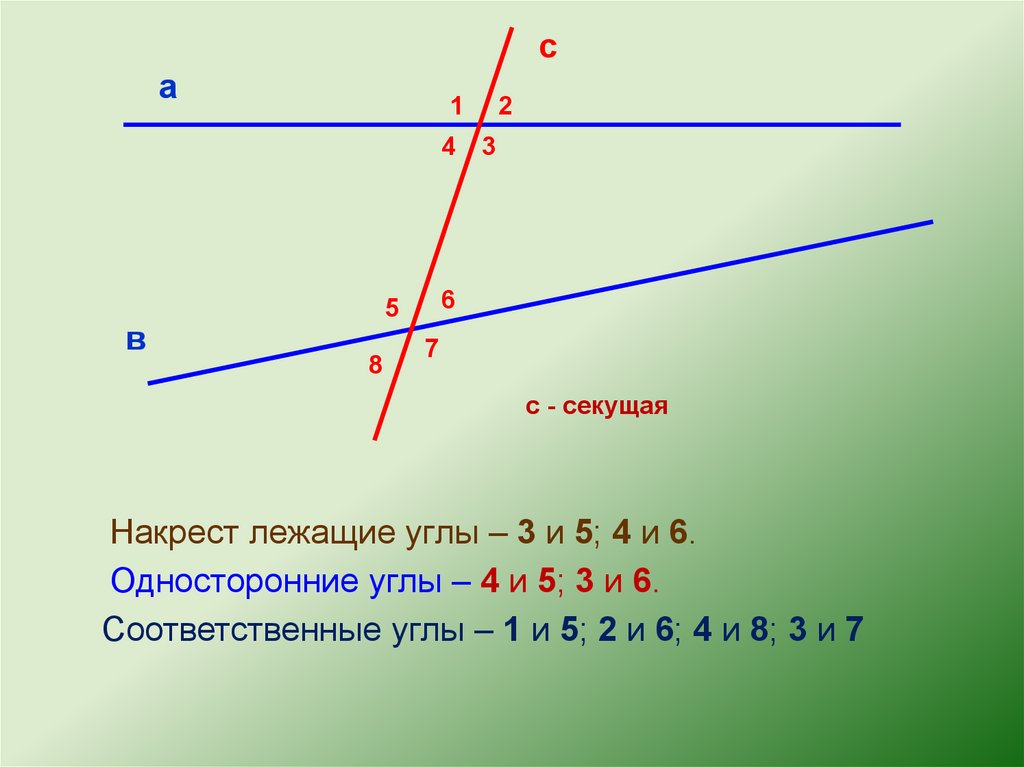
Найди пары накрест лежащих углов и щелкни по
ним мышкой.
Вертикальные углы
Односторонние углы
∠2 и ∠ 4
c
Вертикальные углы
1
4
а
2
Вертикальные углы
3
5 6
8 7
∠1 и ∠3
∠5 и ∠7
b
∠1 и ∠8
ВЕРНО!
∠3 и ∠5
Тренировочные задания.
∠4 и ∠5
ВЕРНО!

∠4 и ∠6
Односторонние углы
∠3 и ∠6
Соответственные углы
∠2 и ∠6
∠1 и ∠6
Найди пары соответственных углов и щелкни по
Вертикальные углы
ним мышкой.
Односторонние углы
∠2 и ∠4
∠4 и ∠5
c
Вертикальные углы
∠1 и ∠3
1
4
∠3 и ∠7
а
2
Вертикальные углы
3
5 6
8 7
ВЕРНО!
∠5 и ∠7
b
Односторонние углы
∠3 и ∠6
Смежные углы
∠1 и ∠8
∠7 и ∠6
ВЕРНО!
ВЕРНО!
∠2 и ∠6
∠1 и ∠5
ВЕРНО!
Тренировочные задания.

∠4 и ∠8
∠1 и ∠6
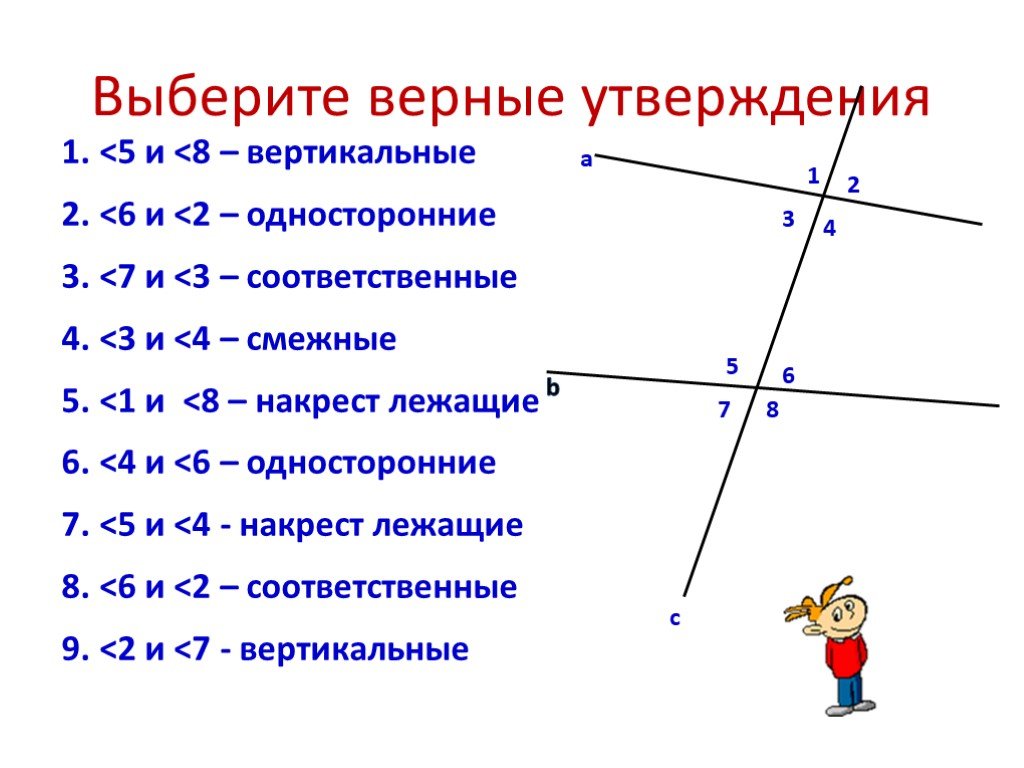
Найди пары односторонних углов и щелкни по
ним мышкой.
c
1
4
а
2
3
5 6
8
7
Тренировочные задания.
b
∠2 и ∠4
∠3 и ∠5
∠1 и ∠3
∠3 и ∠7
∠5 и ∠7
∠5 и ∠6
∠1 и ∠8
∠7 и ∠6
∠2 и ∠6
∠4 и ∠5
∠3 и ∠6
∠1 и ∠6
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.

Если при пересечении двух прямых секущей
накрест лежащие углы равны, то прямые
параллельны.
c
460
460
a
aIIb
b
Если при пересечении двух прямых секущей накрест
Условие теоремы
лежащие углы равны,
то прямые параллельны.
Заключение теоремы
Дано: НЛУ 1 = 2.
а, b, c- секущая.
c
А
а
В
b
Доказать: aIIb.
Доказательство: 1 случай
Если углы 1 и 2 прямые,
то прямые а и b
перпендикулярны
к прямой АВ, следовательно,
aIIb.
Н
c
А
а
О
В
Н1
b
2 случай
ДП
т.О – середина АВ
ОН a
Bh2=AH
АОН= ВОН1 (1 признак)
Углы 3 и 4 равны,
значит, т.

Н1 лежит на
продолжении луча ОН,
т.е. точки О, Н и Н1 лежат
на одной прямой!
Углы 5 и 6 равны,
значит, угол 6 – прямой .
Значит, прямые a и b
перпендикулярны к

прямой НН1, поэтому они
параллельны!
Если при пересечении двух прямых секущей
соответственные углы равны, Условие теоремы
то прямые параллельны.
Заключение теоремы
c
Дано: СУ 1 = 2.
а, b, c- секущая.
а
Доказать: aIIb.
Доказательство:
b
1 = 2
2 = 3, т. к. они
1 = 3
вертикальные
Углы 1 и 3 НЛУ,
следовательно, aIIb.
Если при пересечении двух прямых секущей
соответственные углы равны, то прямые
параллельны.
c
420
420
a
b
aIIb
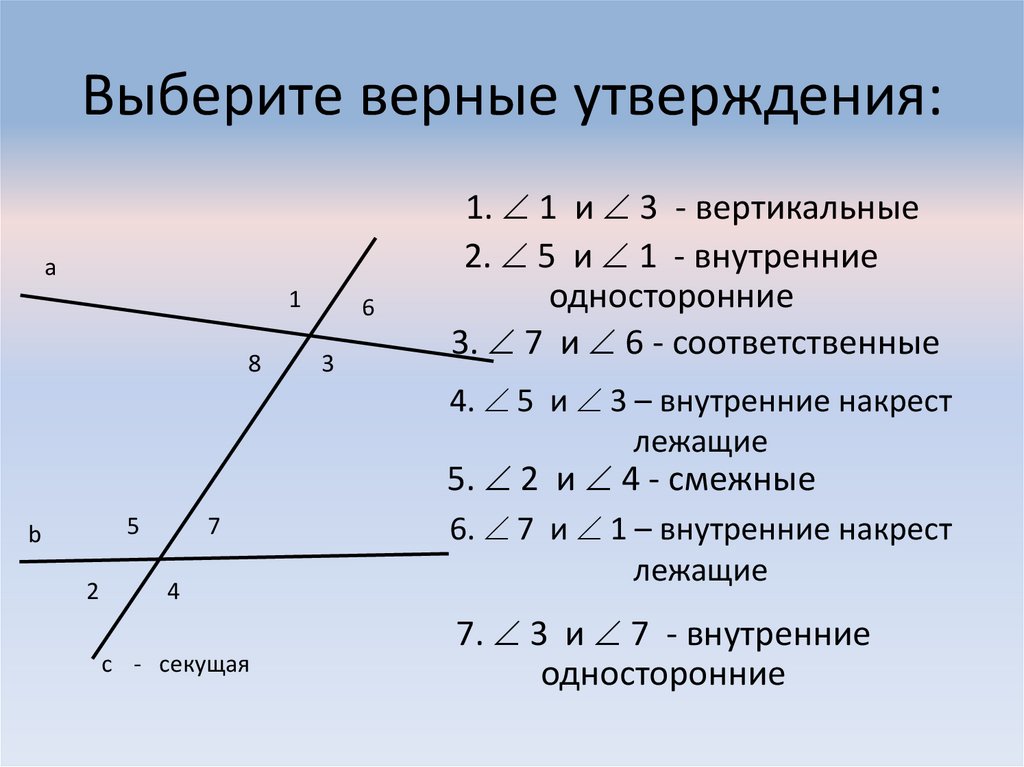
Если при пересечении двух прямых секущей сумма
односторонних углов равна 1800, Условие теоремы
Заключение теоремы
то прямые параллельны.
c
Дано: ОУ 1 + 2 = 1800.
а, b, c- секущая.
а
Доказать: aIIb.
Доказательство:
b
1 + 2=1800
3 + 2=1800, т.

к.
1 = 3
они смежные

Углы 1 и 3 НЛУ,
следовательно, aIIb.
Если при пересечении двух прямых секущей сумма
односторонних углов равна 1800, то прямые
параллельны.
c
a
1380
420
b
aIIb

English Русский Правила

секущих и их специальные пары углов — Криста Кинг Математика

Существует множество специальных пар углов, образующихся при пересечении секущей двух прямых

В этом уроке мы рассмотрим углы, образованные при пересечении пары параллельных прямых другой прямой, называемой «секущей».

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.

Трансверсали

Трансверсаль – это линия, которая пересекает как минимум две другие линии.

Особые пары углов

Когда секущие пересекают параллельные прямые, они образуют углы со специальными угловыми соотношениями.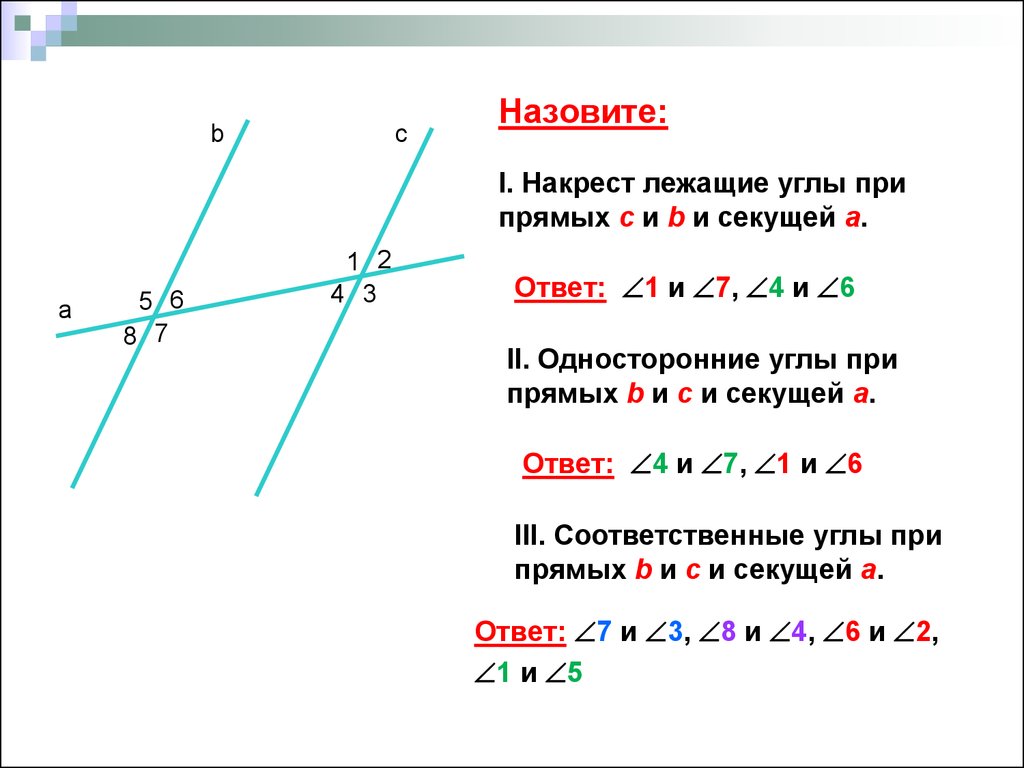 \circ???.

Типы специальных пар углов

Вертикальные углы имеют общую вершину, но лежат по разные стороны как от параллельных прямых, так и от поперечной. Пары вертикальных углов равны.

???м\угол a=m\угол b???

???м\угол с=м\угол d???

???м\угол e=m\угол f???

???м\угол g=м\угол h???

Соответствующие углы — это соответствующие углы, лежащие по одному на каждой параллельной прямой, по одну сторону от параллельных прямых и по одну сторону от поперечной. Соответствующие пары углов конгруэнтны.

???м\угол а=м\угол е???

???м\угол d=м\угол h???

???м\угол c=m\угол g???

???м\угол b=м\угол f???

Чередующиеся внутренние углы являются углами, лежащими по одному на каждой прямой на противоположных сторонах параллельных прямых и противоположных сторонах поперечной внутри параллельных прямых.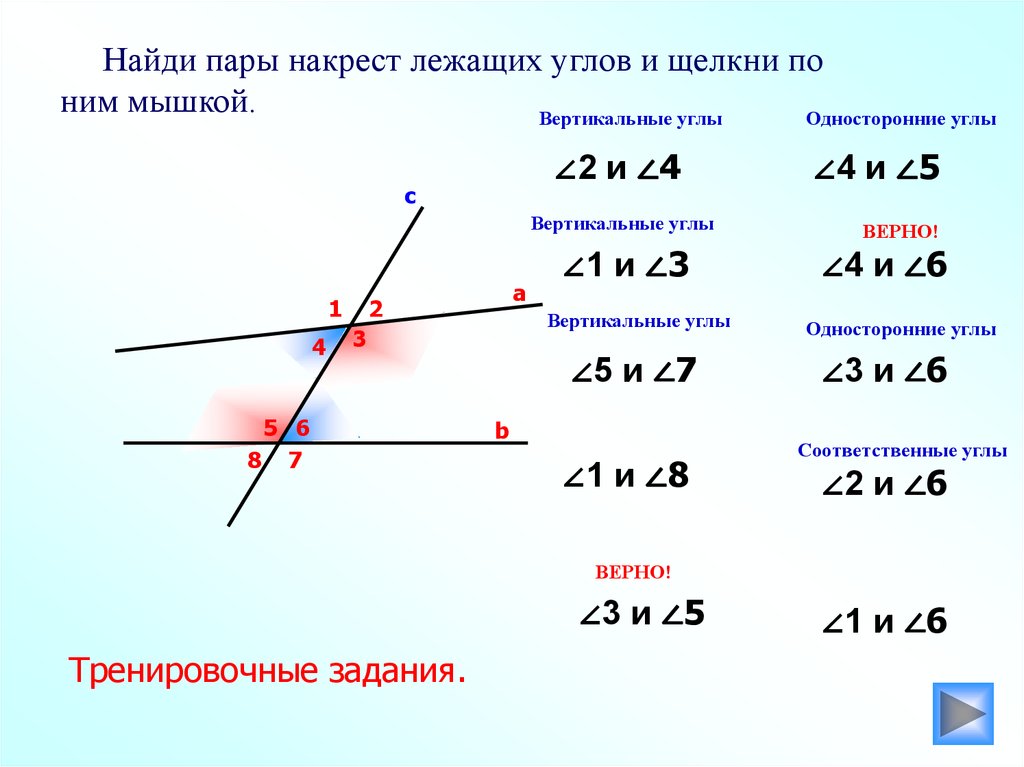 \circ???. 9\циркуляр???

Мы часто используем эти парные отношения углов для решения задач.

Работа с углами, образуемыми секущей

Пройти курс

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂

Учить больше

Пример с соответствующими и смежными парами углов

Пример

Найдите переменную. Найдите значение ???x??? до ближайшей десятой, учитывая ???m||n???.

Мы можем придумать, какие соотношения пар углов использовать.

Углы ???\угол 1??? и ???\угол 2??? конгруэнтны, потому что они являются соответствующей парой углов. Углы ???\угол 2??? и ???\угол 3??? являются дополнительными, так как являются смежными углами. Это означает, что два угла с переменными являются дополнительными, поэтому 9\ циркуляр ????

Глядя на диаграмму, мы видим, что ???\угол XYZ??? и ???\угол ЗЫР??? смежные углы, лежащие на одной параллельной прямой, значит, они дополнительные.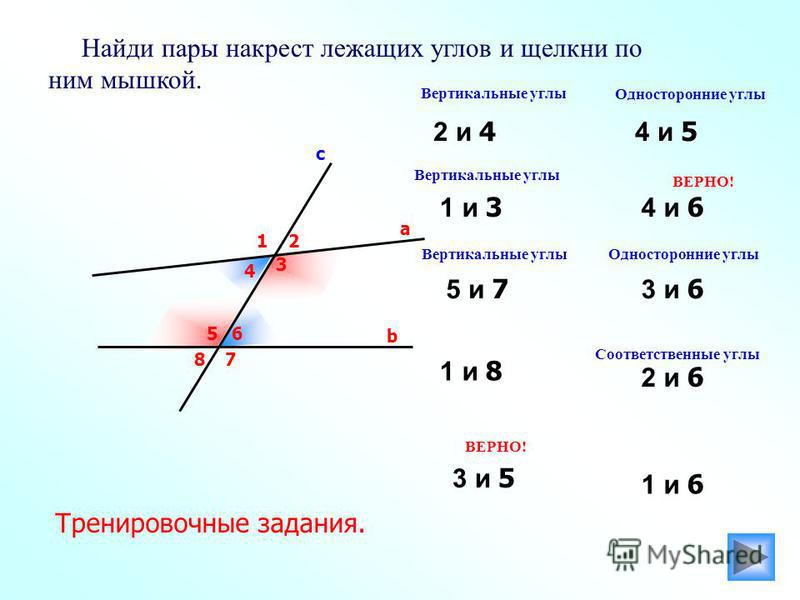

???\угол ЗЫР??? и ???\угол QYR??? являются альтернативными внутренними углами, поэтому они равны.

Теперь мы можем использовать эти факты, чтобы найти ???m\угол XYZ???. Начнем с поиска ???x???. ???м\угол ZYR=м\угол QYR??? потому что это равные углы. Итак, 9\циркуляр???

Получить доступ к полному курсу геометрии

Начать

Изучение математикиКриста Кинг 1 мая 2019 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, геометрия, секущие, углы секущих, специальные пары углов, параллельные прямые, конгруэнтные углы, дополнительные углы, вертикальные углы, соответствующие углы, чередующиеся внутренние углы, чередующиеся внешние углы, последовательные внутренние углы, смежные углы

0 лайков

Глоссарий по геометрии

остроугольный треугольник: треугольник, все углы которого меньше 90° ^o
смежная ветвь: катет прямоугольного треугольника рядом с опорным углом
высота: отрезок треугольника, соединяющий вершину с линией, содержащей противоположную сторону и перпендикулярной этой стороне
высота треугольника: отрезок, проведенный или опущенный перпендикулярно вершине треугольника к линии, содержащей противоположную сторону, высоту треугольника
Биссектриса угла: луч, делящий угол на две равные части
угол наклона: угол, измеренный ниже определенной контрольной точки (обычно линии визирования)
угол места: угол, измеренный над определенной опорной точкой (обычно линией прямой видимости)
вершина: вершина пирамиды, противоположная основанию пирамиды
апофема: длина перпендикуляра от центра правильного многоугольника до его края
дуга: изогнутая линия, являющаяся частью круга, частью окружности круга
длина дуги: мера расстояния по криволинейной линии окружности, отрезок окружности
район: количество квадратных единиц, необходимое для покрытия заданной плоской поверхности
аксиома: утверждение, которое принимается за истинное
база: конгруэнтные многоугольники, параллельные друг другу на вершине и дне призмы
биссектриса: разделить на две равные части; разделительная линия называется биссектриса
центральный уголок: угол, который пересекает окружность в двух точках и вершина которого является центром окружности
хорда: отрезок с двумя концами, лежащими на окружности
окружность: периметр круга; С = 2 π г или C = d π , где C = окружность, r = радиус и d = диаметр
составная фигура: фигура, состоящая из двух или более геометрических фигур
предположение: обоснованное предположение; предложение, которое либо истинно, либо ложно
вывод: часть «q» условного оператора, следующая за словом «then», часть, которую необходимо доказать
условное выражение: утверждение, записанное в форме если «p», то «q»
конус: трехмерная фигура, имеющая одно круглое основание и одну вершину
конгруэнтно: фигуры имеют одинаковую форму и размер, углы и стороны имеют одинаковые размеры
равные треугольники: треугольника с соответствующими сторонами одинаковой длины и соответствующими внутренними углами одинаковой меры
предположение: утверждение, которое считается верным и требует доказательства
противоречивое заявление: утверждение, заменяющее и отрицающее гипотезу и заключение исходного утверждения
обратный оператор: утверждение, заменяющее гипотезу и заключение исходного утверждения
следствие: утверждение, непосредственно вытекающее из теоремы; мини-теорема
соответствующие детали: стороны и углы, которые совпадают и имеют одинаковую форму и размер (конгруэнтны)
контрпример: пример, подтверждающий ложность гипотезы
перекрестное умножение: продукты средств и крайностей
сечение: плоская фигура, которая получается при пересечении трехмерного твердого тела плоскостью
куб: прямоугольная призма, все стороны которой равны, а все грани квадратные
цилиндр: трехмерная геометрическая фигура с двумя конгруэнтными параллельными круглыми основаниями
дедуктивное рассуждение: рассуждение, которое приводит к заключению, используя факты, определения, теоремы, постулаты или свойства
знаменатель: нижнее число в дроби
диагональ: сегмент внутри многоугольника, соединяющий несмежные вершины
диаметр: отрезок, проходящий через центр окружности, причем обе его конечные точки лежат на окружности или сфере
расширение: преобразование, которое увеличивает или уменьшает фигуру
размеры: используется для описания размера и формы объекта
край: пересечение граней в объемной фигуре
расширение: результат расширения с масштабным коэффициентом больше 1
равноугольный: все углы многоугольника равны или равны
равносторонний: все стороны многоугольника имеют одинаковую длину или равные размеры
Формула Эйлера: количество вершин плюс количество граней минус количество ребер равно 2
Теорема Эйлера: соотношение между числом граней, ребер и вершин в многограннике: V − E + F = 2
внешний уголок: удлините каждую сторону правильного многоугольника, как показано ниже, ни одна вершина не будет иметь более одного внешнего угла
лицо: плоская поверхность объемной фигуры
геометрические свойства: атрибуты или характеристики геометрической фигуры, которые поддерживаются определениями, постулатами или теоремами
большие круги: круг на поверхности сферы, центр которого совпадает с центром сферы
высота: для цилиндра: длина сегмента, перпендикулярного обоим основаниям;
для конуса: длина отрезка, перпендикулярного основанию и заканчивающегося в точке конуса
гипотенуза: сторона, противоположная прямому углу прямоугольного треугольника; это самая длинная сторона прямоугольного треугольника
гипотеза: часть «р» условного оператора, следующая за словом «если», данная информация
изображение: фигурка из трансформации
прилагаемый уголок: угол между двумя соседними сторонами многоугольника; отрезки, представляющие соседние стороны, входят в состав лучей, образующих угол
индуктивное рассуждение: рассуждение, которое приходит к выводу, обобщая утверждение на основе наблюдения закономерностей
вписанный угол: угол, который пересекает окружность в двух точках и вершина которого лежит на окружности
вписанный многоугольник: многоугольник, все вершины которого лежат на окружности
вписанный квадрат: квадрат, вершины которого лежат на окружности
перехваченная дуга: дуга окружности, лежащая внутри вписанного угла
внутренние углы: углов, расположенных внутри треугольника, по одному в каждой вершине
обратный оператор: утверждение, отрицающее как гипотезу, так и заключение исходного утверждения
неправильный многоугольник: многоугольник, стороны которого не конгруэнтны друг другу
изометрический: представление трехмерных фигур так, чтобы можно было наблюдать три стороны фигуры
равнобедренный треугольник: треугольник, в котором две стороны имеют одинаковую длину
оправдать
боковая часть: стороны:
боковая поверхность цилиндра прямоугольник
боковая поверхность конуса круглого сечения
боковой край: пересекающиеся ребра боковых граней твердого тела
ножки: стороны, прилегающие к прямому углу прямоугольного треугольника
строка: удерживает местоположение и не имеет толщины, длины или ширины; он не имеет меры ни в каком направлении
сегмент линии: часть одной линии с двумя конечными точками и всеми точками между ними
линейная пара: внутренний угол, соединенный с внешним углом, имеющим одну и ту же сторону
медиана треугольника: отрезок с концами, являющимися вершиной треугольника и серединой противоположной стороны
малая дуга: кратчайшее расстояние от одной точки окружности до другой точки окружности
несколько: произведение числа и любого целого числа
отрицание: утверждение, образованное вставкой слова «не» для изменения значения гипотезы или вывода на противоположное значение
нетто: двухмерное изображение трехмерной фигуры, которое можно сложить, чтобы сформировать фигуру
числитель: первое число в дроби
наклонный конус: конус, у которого высота не перпендикулярна основанию
наклонный цилиндр: цилиндр, в котором основания не выровнены
косая призма: призма, основания которой не выровнены должным образом
тупоугольный треугольник: треугольник с одним углом больше 90 ^o, но меньше 180 ^o (тупой угол
противоположная нога: катет прямоугольного треугольника, противоположный опорному углу
орфографический: представление трехмерных фигур с использованием двухмерных перспектив, таких как вид спереди, сбоку или сверху
идеальный квадрат: произведение квадрата целого числа или целого числа во второй степени
перпендикулярно: две линии или отрезки, пересекающиеся и образующие 90 ^o углы
самолет: имеет длину и ширину, но не толщину и высоту; плоская поверхность, простирающаяся бесконечно во всех направлениях по своей длине и ширине
точка: удерживает местоположение и не имеет толщины, длины или ширины; он не имеет меры ни в каком направлении
точка касания: точка пересечения касательной с окружностью
полигон: Замкнутая плоская фигура, образованная тремя или более отрезками, пересекающимися в своих концах
многогранник: объемная фигура, стороны которой представляют собой многоугольники
постулат: утверждение, которое принимается за истинное без доказательства
прообраз: исходное изображение до трансформации
призма: Трехмерное твердое тело с двумя параллельными и конгруэнтными основаниями, названное в честь формы основания
пропорциональный: имеющие постоянное соотношение всех соответствующих сторон между двумя фигурами
пирамида: объемная фигура с многоугольником в основании и треугольниками в качестве сторон
Теорема Пифагора: в прямоугольном треугольнике, где a и b длины катетов и c длина гипотенузы, а a ² + b
4
5 = 2
Пифагорейская тройка: набор из трех целых чисел, удовлетворяющих теореме Пифагора
радиус: расстояние от центра круга до любой точки на окружности круга или для правильного многоугольника длина от центра до вершины
соотношение: дробь
скорость изменения: отношение изменения выходного значения к изменению входного значения функции
прямоугольная призма: трехмерный объект с шестью гранями, представляющими собой прямоугольники
переходник: результат расширения с масштабным коэффициентом менее 1
опорный угол: один из двух острых углов прямоугольного треугольника, являющийся точкой отсчета
отражение: преобразование фигуры, перевернутой через линию
правильный многоугольник: замкнутая фигура, у которой все углы и все стороны равны
правильная пирамида: многогранник с многоугольным основанием и треугольниками для сторон, высота пересекает основание под прямым углом и вершину
прямой угол: угол, длина которого равна 90° ^o
правый конус: трехмерная фигура, имеющая одно круглое основание, одну вершину и высоту, пересекающую основание под прямым углом
правый цилиндр: Объемная геометрическая фигура, имеющая два конгруэнтных и параллельных основания и высоту, перпендикулярную обоим основаниям
правая призма: многогранник, состоящий из двух параллельных конгруэнтных граней, называемых основаниями
прямоугольный треугольник: треугольник, содержащий один внутренний угол с величиной 90 ^o (т.
No related posts.