Составить уравнение биссектрисы угла между прямыми в котором лежит точка: математика / Составить уравнение биссектрисы угла / Математика

тема 7

Курс “Алгебра и Геометрия”

(спец. прикладная математика, информатика, 1 курс, 1 семестр)

Тема 7. Уравнения прямой на плоскости. – 2 ч.

Содержание: общее уравнение прямой, уравнение прямой с угловым коэффициентом; угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых; уравнение прямой, проходящей через две данные точки; неполные уравнения прямой; уравнение прямой в отрезках; нормальное уравнение, расстояние от точки до прямой; полярное уравнение прямой; уравнение пучка прямых.

Цель: изучить различные способы задания прямых на плоскости их уравнениями; научиться применять уравнения прямых при решении планиметрических задач.

Форма контроля: опрос.

Задачи

Задача 1 ([8], 216). Даны уравнения двух сторон параллелограмма , и уравнение одной из его диагоналей .

Определить координаты вершин этого параллелограмма.

Задача 2 ([8], 217). Стороны треугольника лежат на прямых , , . Вычислить его площадь .

Задача 3 ([8], 218). Площадь треугольника кв. ед.; две его вершины — точки и , а третья вершина лежит на прямой . Определить координаты вершины .

Задача 4 ([8], 220). Составить уравнение прямой и построить прямую на чертеже, зная её угловой коэффициент и отрезок , отсекаемый ею на оси Oy:

1) , ; 2) , ; 3) , ; 4) , ;

5) , ; 6) , .

Задача 5 ([8], 221). Определить угловой коэффициент и отрезок , отсекаемый на оси Oy, для каждой из прямых:

1) ; 2) ; 3) ; 4) ; 5) .

Задача 6 ([8], 222). Дана прямая . Определить угловой коэффициент прямой:

1. параллельной данной прямой;

2. перпендикулярной к данной прямой.

Задача 7 ([8], 223). Дана прямая . Составить уравнение прямой, проходящей через точку :

1. параллельной данной прямой;

2. перпендикулярной к данной прямой.

Задача 8 ([8], 224). Даны уравнения двух сторон прямоугольника , и одна из его вершин . Составить уравнения двух других сторон этого прямоугольника.

Задача 9 ([8], 225). Даны уравнения двух сторон прямоугольника , и уравнение одной из его диагоналей . Найти вершины прямоугольника.

Задача 10 ([8], 226). Найти проекцию точки на прямую .

Задача 11 ([8], 227). Найти точку , симметричную точке относительно прямой .

Задача 12 ([8], 228). В каждом из следующих случаев составить уравнение прямой, параллельной двум данным прямым и проходящей посередине между ними:

1) , ;

2) , ;

3) , ;

4) , ;

5) , .

Задача 13 ([8], 253). Определить угол между двумя прямыми:

1) , ;

2) , ;

3) , ;

4) , .

Задача 14 ([8], 254). Дана прямая . Составить уравнение прямой, проходящей через точку под углом 45^o к данной прямой.

Задача 15 ([8], 272). Составить уравнения сторон треугольника, зная одну из его вершин и уравнения двух биссектрис и .

Задача 16 ([8], 273). Составить уравнения сторон треугольника, зная одну его вершину , а так же уравнения высоты и биссектрисы , проведённых из одной вершины.

Задача 17 ([8], 274). Составить уравнения сторон треугольника, зная одну его вершину , а так же уравнение высоты и биссектрисы , проведённых из различных вершин.

Задача 18 ([8], 275). Составить уравнения сторон треугольника, зная одну его вершину , а так же уравнение высоты и медианы , проведённых из одной вершины.

Задача 19 ([8], 276). Составить уравнения сторон треугольника, зная одну его вершину , а так же уравнение высоты и медианы , проведённых из различных вершин.

Задача 20 ([8], 277). Составить уравнения сторон треугольника, зная одну его вершину , а так же уравнение биссектрисы и медианы , проведённых из одной вершины.

Задача 21 ([8], 278). Составить уравнения сторон треугольника, зная одну его вершину , а так же уравнение биссектрисы и медианы , проведённых из разных вершин.

Задача 22 ([8], 286). Определить, при каких значениях и прямая параллельна оси абсцисс и отсекает на оси ординат отрезок, равный -3 (считая от начала координат). Написать уравнение этой прямой.

Задача 23 ([8], 292). Определить при каких значениях и две прямые , .

1. параллельны;

2. совпадают;

3. перпендикулярны.

Задача 24 ([8], 304). Составить уравнение прямой, которая проходит через точку и отсекает от ординарного угла треугольник с площадью, равной кв. ед.

Задача 25 ([8], 307). Через точку проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3 кв. ед. Определить точки пересечения этой прямой с осями координат.

Задача 26 ([8], 312). Вычислить величину отклонения и расстояние точки от прямой в каждом из следующих случаев:

1. , ; 2) , ;

3) , ; 4) , .

Задача 27 ([8], 324). Доказать, что прямая параллельна прямым , и делит расстояние между ними пополам.

Задача 28 ([8], 333). Точка является вершиной квадрата, одна из сторон которого лежит на прямой . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.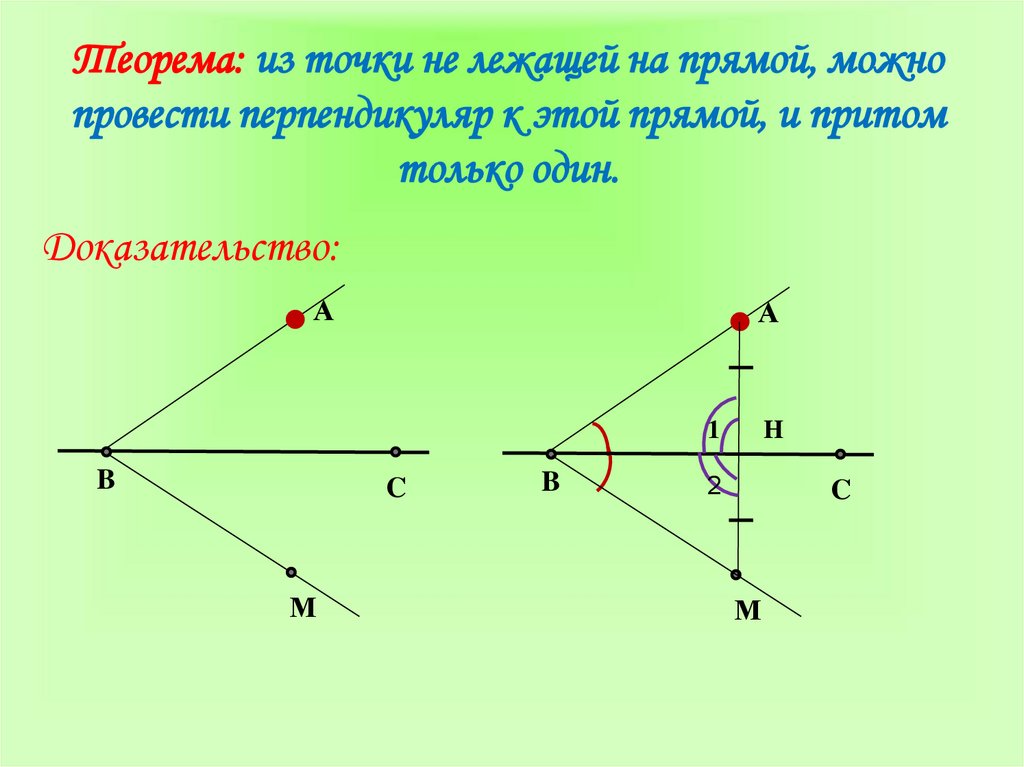

Задача 29 ([8], 336). Отклонения точки от прямых и равны соответственно -3 и -5. Определить координаты точки .

Задача 30 ([8], 339). Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми:

1) , ; 2) , ;

3) , .

Задача 31 ([8], 349). Составить уравнения биссектрисы угла между прямыми и , в котором лежит точка .

Задача 32 ([8], 353). Найти центр пучка прямых, данного уравнения .

Задача 33 ([8], 359). Даны уравнения сторон треугольника , , . Не определяя координат его вершин, составить уравнения высот этого треугольника.

Задача 34 ([8], 360). Составить уравнение прямой, проходящей через точку пересечения прямых , под углом в 45^о к прямой . Решить задачу, не вычисляя координат точки пересечения данных прямых.

Задача 35 ([8], 363). Дано уравнение пучка прямых . Найти прямые этого пучка, отрезки которых, заключённые между прямыми , , равны .

Задача 36 ([8], 364). Дано уравнение пучка прямых . Доказать, что прямая принадлежит этому пучку.

Задача 37 ([8], 381). Вывести полярное уравнение прямой, если даны:

1. угол наклона прямой к полярной оси и длина перпендикуляра , опущенного из полюса на эту прямую. Написать уравнение этой прямой в случае , ;

2. отрезок , который отсекает прямая на полярной оси, считая от полюса, и полярный угол нормали этой прямой. Написать уравнение этой прямой в случае , ;

3. угол наклона этой прямой к полярной оси и отрезок , который отсекает прямая на полярной оси, считая от полюса. Написать уравнение этой прямой в случае , .

Тема 7. Различные виды уравнения прямой на плоскости

.

Ответы

Задача 1. , , и .

Задача 2. кв. ед.

Задача 3. или .

Задача 4. 1) ; 2) ; 3) ;

4) ; 5) ; 6) .

Задача 5. 1) , ; 2) , ; 3) , ;

4) , ; 5) ; .

Задача 6. 1) ; 2) .

Задача 7. 1) ; 2) .

Задача 8. , .

Задача 9. , ; , .

Задача 10. .

Задача 11. .

Задача 12. 1) ; 2) ;

3) ; 4) ; 5) .

Задача 13. 1) ; 2) ; 3) — прямые параллельны; 4) .

Задача 14. или .

Задача 15.

, , . Указание. Если на одной стороне угла дана точка , то точка, симметричная точке относительно биссектрисы этого угла, будет лежать на другой его стороне.

Задача 16. , , .

Задача 17. , , .

Задача 18. , , .

Задача 19. , , .

Задача 21. , , .

Задача 22. , , .

Задача 22. , , .

Задача 23. 1) , или , ; 2) , или , ; 3) , – любое значение.

Задача 24. Условию задачи удовлетворяют следующие три прямые: , , .

Задача 25. Условию задачи удовлетворяют две прямые, пересекающие соответственно оси координат в точках , и , .

Задача 26. 1) , ; 2) , ; 3) , ;

4)

, — точка лежит на прямой.

Задача 28. Условию задачи удовлетворяют два квадрата; остальные стороны одного из них лежат на прямых , , ; остальные стороны другого — на прямых: , , .

Задача 29. .

Задача 30. 1) , ; 2) , ; 3) , .

Задача 31. .

Задача 32. .

Задача 33. , , .

Задача 34. , .

Задача 35. , .

Задача 36. 1)

2)

3)

Задача 38.

kletenik_14

§ 14. Нормальное уравнение прямой. Задача определения расстояния от точки до прямой

Пусть на плоскости хОу дана прямая. Проведём через начало коорди­нат перпендикуляр к данной прямой и назовём его нормалью. Обозначим

через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р.

Если а есть полярный угол нормали, p — длина отрезка(черт.10), то уравнение данной пря­ мой может быть записано в виде

х cos α + у sin α — р = 0;

уравнение этого вида называется нормальным.

Пусть дана какая—нибудь прямая и произвольная точка

Черт. 10 М*; обозначим через d расстояние точки М* от данной прямой. Отклонением точки М* от прямой называется число +d, если данная точка и начало координат лежат по разные стороны от данной прямой, и — и, если данная точка и начало координат расположены по одну сторону от данной пря­мой. (Для точек, лежащих на самой прямой, = 0.)

Если даны координаты x*, у* точки М* и нормальное уравнение прямой х cos α + у sin α -р = 0; то отклонение точки М* от этой прямой может быть вычислено по формуле = х* соs α а + у*sin α — р.

Таким образом, чтобы найти отклонение какой—нибудь точки М* от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки М*.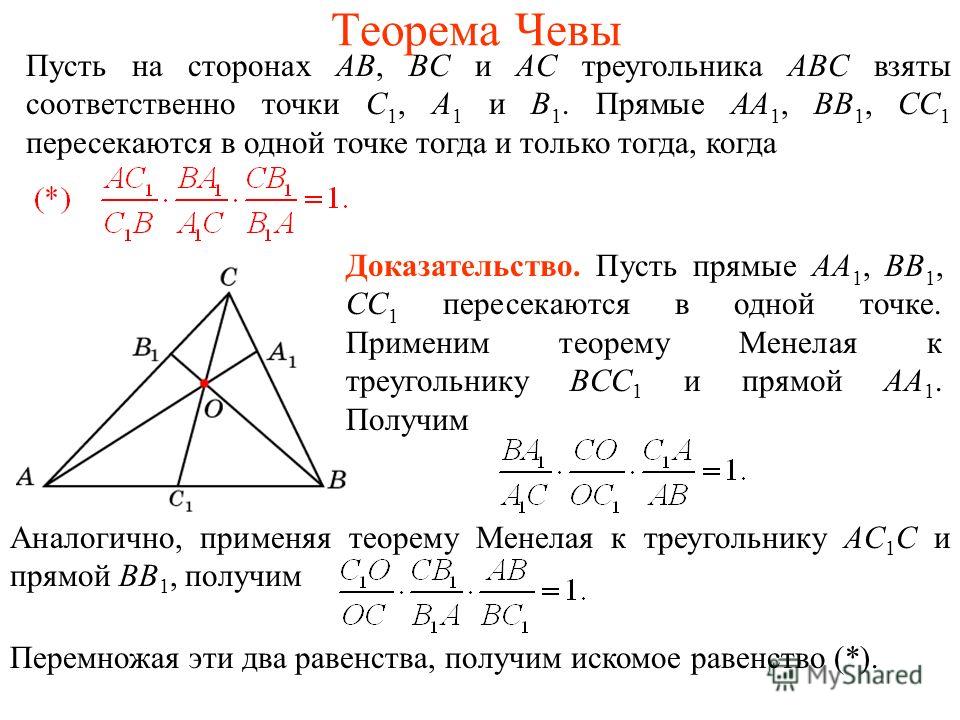 Полученное число будет равно искомому отклонению.

Чтобы найти расстояние d от точки до прямой, достаточно вычислить отклонение и взять его модуль: d =

Если дано общее уравнение прямой Аx+Bу+С=0, то, чтобы приве­сти его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель μ., определяемый формулой

Знак нормирующего множителя выбирается противоположным знаку сво­бодного члена нормируемого уравнения.

309. Определить, какие из следующих уравнений прямых являются нормальными:

1) x—y—3=0; 2) x—y—1 = 0;

3) х—у + 2 = 0; 4) —х +у — 2 = 0;

5) — х + 2 = 0; 6) х — 2 = 0; 7) у + 2 = 0; 8) — у — 2 = 0.

310. Привести общее уравнение прямой к нормальному виду в каждом из следующих случаев:

1) 4х —3у—10 = 0; 2) x —y+10 = 0;

3) 12х — 5у + 13 = 0; 4) х + 2 = 0; 5) 2х — у —= 0.

311. Даны уравнения прямых:

1) х—2 = 0; 2) х + 2 = 0; 3) у —3 = 0; 4) у + 3 = 0;

5) х+у—6 = 0; 6) х—у+2 = 0; 7) х + у+2 = 0;

8) x cos  —y sin  — q = 0, q >0;  — острый угол;

9) x cos  + y sin  + q = 0, q > 0;  — острый угол.

Определить полярный угол нормали  и отрезок р для каждой из данных прямых; по полученным значениям параметров  и р построить эти прямые на чертеже (в последних двух случаях построение прямой выполнить, считая  = 30 и q = 2).

312. Вычислить величину отклонения  и расстояние d точки от прямой в каждом из следующих случаев:

1)А(2;—1)₎ 4х + 3у+10 = 0;

2) В(0; — 3), 5х—12у—23=0;

3) Р(—2; 3), 3х —4у —2 = 0;

4) Q(l; —2), х—2у —5 = 0.

313. Уcтaнoвить_, лежит ли точка М(1; —3) и начало коорди­нат по одну или по разные стороны каждой из следующих прямых:

1) 2х—у + 5 = 0; 2) х —3у —5 = 0; 3) 3х+2у—1 = 0;

2) х—3у + 2 = 0; 5) 10х + 24у+15 = 0.

314. Точка А(2; —5) является ве2шиной квадрата, одна из сторон которого лежит на прямой

х — 2у — 7 = 0.

Вычислить площадь этого квадрата.

315. Даны уравнения двух сторон прямоугольника

3х —2у — 5 = 0, 2х + 3у + 7 = 0

и одна из его вершин А(—2; 1). Вычислить площадь этого прямо­угольника.

316. Дoкaзaть_, что прямая

2х+у+3 = 0

пересекает отрезок, ограниченный точками А(—5; 1) и В(3; 7).

317. Доказать, что прямая

2х —3у+6 = 0

не пересекает отрезка, ограниченного точками М₁(—2; —3) и М₂(1; —2).

318. Последовательные вершины четырёхугольника суть точки А(—3; 5), В(— 1; —4), С(7; — 1) и D(2; 9). Установить, является ли этот четырёхугольник выпуклым.

319. Последовательные вершины четырёхугольника суть точки А(—1; 6), B(1; —3), С(4; 10) и D(9; 0). Установить, является ли этот четырёхугольник выпуклым.

320. Даны вершины треугольника: А(—10; —13), В(—2; 3) и С(2; 1). Вычислить длину перпендикуляра, опущенного из вершины В на медиану, проведённую из вершины С.

321. Стороны АВ, ВС и СА треугольника ABC соответственно даны уравнениями

х + 21у — 22 = 0, 5х — 12у + 7 = 0, 4х — 33у + 146 = 0.

Вычислить расстояние от центра тяжести этого треугольника до стороны ВС.

322. Вычислить расстояние d между параллельными прямыми в каждом из следующих случаев:

1) 3х —4у—10 = 0, 2) 5х—12у + 26 = 0,

6х —8у + 5 = 0; 5х—12у—13 = 0;

3) 4х — 3у + 15 = 0, 4) 24х—10у + 39 = 0,

8х—6у + 25 = 0; 12х —2у —26 = 0.

323. Две стороны квадрата лежат на прямых

5х — 12у — 65 = 0, 5х — 12у + 26 = 0.

Вычислить его площадь.

324. Доказать, что прямая

5х — 2у — 1 = 0

параллельна прямым

5х —2у + 7 = 0, 5х —2у —9 = 0

и делит расстояние между ними пополам.

325. Даны три параллельные прямые

10х+15у —3 = 0, 2х+3у + 5 = 0, 2х+3у —9 = 0.

Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними.

326. Доказать, что через точку Р(2; 7) можно провести две прямые так, чтобы их расстояния от точки Q(l; 2) были равны 5. Составить уравнения этих прямых.

327. Доказать, что через точку Р(2; 5) можно провести две прямые так, чтобы их расстояния от точки Q(5; 1) были равны 3. Составить уравнения этих прямых.

328. Доказать, что через точку С(7; — 2) можно провести только одну прямую так, чтобы расстояние её от точки А(4; —6) было равно 5. Составить её уравнение.

329. Доказать, что через точку В (4; —5) невозможно провести прямую так, чтобы расстояние её от точки С(—2; 3) было равно 12.

330. Вывести уравнение геометрического места точек, отклоне­ние которых от прямой 8х—15у — 25 = 0 равно —2.

331. Составить уравнения прямых, параллельных прямой 3х—4у— 10 = 0 и отстоящих от неё на расстоянии d=3.

332. Даны две смежные вершины квадрата А(2; 0) и В(—1; 4). Составить уравнения его сторон.

333. Точка А(5; —1) является вершиной квадрата, одна из сторон которого лежит на прямой

4х — 3у — 7 = 0.

Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.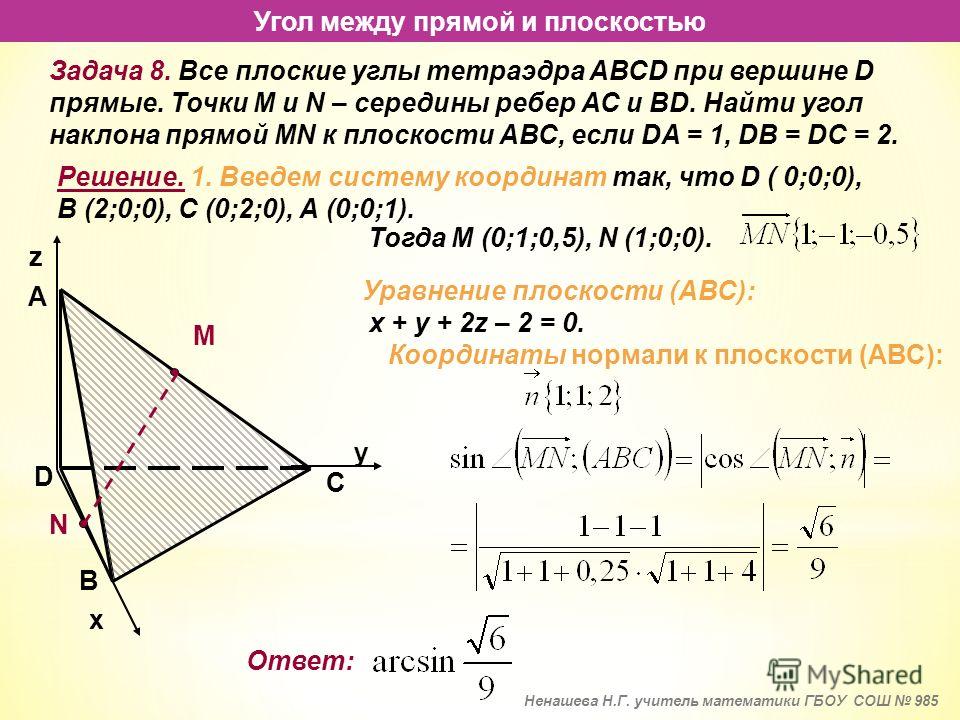

334. Даны уравнения двух сторон квадрата

4х —3у + 3 = 0, 4х—3у—17 = 0

и одна из его вершин А(2; —3). Составить уравнения двух дру­гих сторон этого квадрата.

335. Даны уравнения двух сторон квадрата

5х+12у—10 = 0, 5х+12у+29 = 0.

Составить уравнения двух других его сторон при условии, что точка M₁(—3; 5) лежит на стороне этого квадрата.

336. Отклонения точки М от прямых

5х—12у—13=0 и 3х —4у—19 = 0

равны соответственно — 3 и — 5. Определить координаты точки М.

337. Составить уравнение прямой, проходящей через точку Р(—2; 3) на одинаковых расстояниях от точек А(5; — 1) и В(3; 7).

338. Составить уравнение геометрического места точек, равно­удалённых от двух параллельных прямых:

1) 3х — у + 7 = 0, 2) х — 2у + 3 = 0, 3) 5х — 2у — 6 = 0,

3х — у — 3 = 0; х —2у + 7 = 0; х —4у + 3 = 0.

339. Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми:

1) х — 3у + 5 = 0, 2) х — 2у — 3 = 0, 3) 3х + 4у — 1 = 0,

3х—у —2 = 0; 2х + 4у + 7 = 0; 5х + 12у — 2 = 0.

340. Составить уравнения прямых, которые проходят через точку Р(2; —1) и вместе с прямыми

2х— у + 5 = 0, 3х + 6у — 1 = 0

образуют равнобедренные треугольники.

341. Определить, лежат ли точка М (1; —2) и начало коорди­нат в одном, в смежных или вертикальных углах, образованных при пересечении двух прямых:

1) 2х—у —5 = 0, 2) 4х+3у—10 = 0, 3) х — 2у— 1=0,

3х+у+10 = 0; 12х—5у —5 = 0; 3х—у —2 = 0.

342. Определить, лежат ли точки М (2; 3) и N (5; —1) в одном, в смежных или вертикальных углах, образованных при пересечении двух прямых:

1) х—3у—5 = 0, 2)2х+7у —5 = 0, 3) 12х+у— 1=0,

2х+9у —2 = 0; х + 3у + 7 = 0; 13х + 2у—5 = 0.

343. Определить, лежит ли начало координат внутри или вне треугольника, стороны которого даны уравнениями

7х —5у—11=0, 8х + 3у + 31=0, х + 8у—19 = 0.

344. Определить, лежит ли точка М (— 3; 2) внутри или вне треугольника, стороны которого даны уравнениями

х + у —4 = 0, 3х — 7у + 8 = 0, 4х — у — 31 = 0.

345. Определить, какой из углов, острый или тупой, образован­ных двумя прямыми

3х — 2у + 5 = 0 и 2х + у — 3 = 0,

содержит начало координат.

346. Определить, какой из углов, острый или тупой, образован­ных двумя прямыми

3х —5у —4 = 0 и х + 2у + 3 = 0,

содержит точку М (2; — 5).

347. Составить уравнение биссектрисы угла между прямыми 3х—у—4= 0 и 2х+6у+3 = 0, в котором лежит начало коор­динат.

348. Составить уравнение биссектрисы угла между прямыми

х—7у+5= 0, 5х+5у—3 = 0,

смежного с углом, содержащим начало координат.

349. Составить уравнение биссектрисы угла между прямыми х + 2у—11 = 0 и 3х — 6у — 5 = 0, в котором лежит точка М(1; —3).

350. Составить уравнение биссектрисы угла между прямыми

2х — 3у — 5 = 0, 6х — 4у + 7 = О,

смежного с углом, содержащим точку С (2; —1).

351. Составить уравнение биссектрисы острого угла, образован­ного двумя прямыми

3x+4y —5 = 0, 5х—12у+3 = 0.

352. Составить уравнение биссектрисы тупого угла, образован­ного двумя прямыми х—3у+ 5 = 0, 3х—у+15 = 0.

Координатная геометрия — биссектриса угла

Акшай Ядав, Бывший блестящий член, Александр Кац, а также

способствовал

Содержимое

• Уравнение биссектрисы угла
• Доказательство
• Уравнение двух биссектрис угла
• Обобщение уравнения двух биссектрис угла
• Смотрите также

Пусть линия ABABAB определяется уравнением a1x+b1y+c1=0a_1x+b_1y+c_1=0a1​x+b1​y+c1​=0, а CDCDCD определяется уравнением a2x+b2y+c2= 0a_2x+b_2y+c_2=0a2​x+b2​y+c2​=0. Пока эти прямые не параллельны (в этом случае «биссектрисы угла» не существует), эти две прямые пересекаются в некоторой точке МММ. 9{2}_2}}. a12​+b12​​a1​x+b1​y+c1​=−a22​+b22​​a2​x+b2​y+c2​​.

Обратите внимание, что эти уравнения практически идентичны; один просто «негатив» другого. Это неудивительно, так как две биссектрисы угла обязательно являются перпендикулярными прямыми.

Пусть MPMPMP — биссектриса угла ∠AMC\угла AMC∠AMC, и пусть R=(h,k)R=(h,k)R=(h,k) — точка на этой биссектрисе. Пусть L1L_1L1​ и L2L_2L2​ будут основаниями двух перпендикуляров из RRR в ABABAB и CDCDCD соответственно. Тогда треугольники MRL1MRL_1MRL1​ и MRL2MRL_2MRL2​ конгруэнтны и равны во всех отношениях. Следовательно, RL1=RL2RL_1=RL_2RL1​=RL2​. 9{2}_2}}. \end{выровнено}RL1​RL2​=a12​+b12​∣a1​h+b1​k+c1​∣​=a22​+b22​​∣a2​h+b2​k+c2​∣​ .​

WLOG, предположим, что MPMPMP находится на той же стороне AB,CDAB,CDAB,CD, что и источник (((иначе поменяйте местами PPP и Q)Q)Q). Обратите внимание, что это означает, что a1h+b1k+c1a_1h+b_1k+c_1a1h+b1k+c1 и a2h+b2k+c2ka_2h+b_2k+c_2ka2h+b2k+c2k будут иметь тот же знак, что и c1c_1c1​ и c2c_2c2 будет соответственно.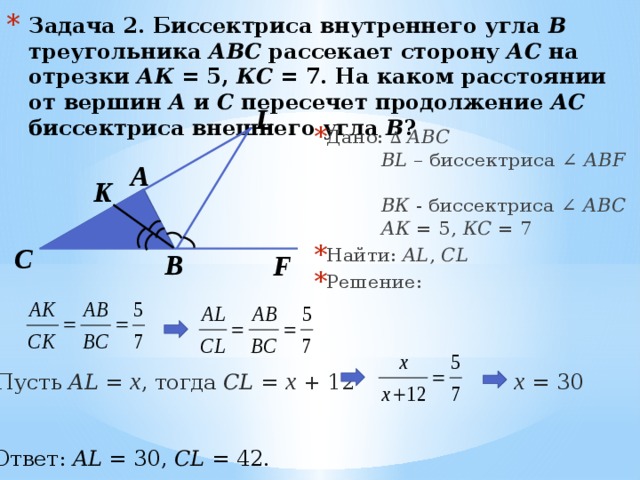 Предположим, что c1c_1c1​ и c2c_2c2​ имеют одинаковый знак (((иначе снова поменяйте местами PPP и Q)Q)Q), так что a1h+b1k+c1a_1h+b_1k+c_1a1​h+b1​k+c1​ и a2h+ b2k+c2a_2h+b_2k+c_2a2h+b2k+c2 имеют одинаковый знак. Таким образом 92 = 0 \ \ (b\ne 0), ax2+2hxy+by2=0 или ba​x2+b2h​xy+y2=0 (b​=0),

, что можно записать в виде (mx −y)(m′x−y)=0 (mx-y)(m’x-y) = 0 (mx−y)(m′x−y)=0, где mm′=ab mm’ = \ frac{a}{b} mm’=ba​ и m+m’=-2hb m+m’ = \frac{-2h}{b} m+m’=b-2h​. Обозначим углы между mx=y mx=ymx=y и m′x=ym’x=y m′x=y и осью xxx соответственно через Φ\PhiΦ и Φ′\Phi ‘Φ′. Две биссектрисы угла, внешняя и внутренняя, перпендикулярны друг другу. Таким образом, углы между биссектрисами внутреннего и внешнего угла и осью xxx могут быть выражены как Φ′+Φ2 \frac{\Phi ‘+\Phi}{2} 2Φ′+Φ​ и Φ′+Φ+π2 \frac {\Phi ‘+\Phi+\pi}{2} 2Φ′+Φ+π​ соответственно.

Теперь вспомним следующее тригонометрическое тождество:

tan⁡(α+β)=tan⁡(α)+tan⁡(β)1−tan⁡(α)tan⁡(β).\tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 — \tan(\alpha)\tan(\beta)}. tan(α+β)=1−tan(α )загар(β)загар(α)+загар(β)​.

Используя это соотношение,

tan⁡(Φ′+Φ)=tan⁡(Φ)+tan⁡(Φ′)1−tan⁡(Φ)tan⁡(Φ′)=m+m′1−mm ′=−2hb−a.(1)\begin{выровнено} \тан (\Фи ‘+\Фи) &= \frac{\tan(\Phi) + \tan(\Phi’)}{1 — \tan(\Phi)\tan(\Phi’)} \\ &= \frac {м+м’}{1-мм’} \\ &= \frac {-2h}{b-a}. \qquad (1) \end{align}tan(Φ′+Φ)​=1−tan(Φ)tan(Φ′)tan(Φ)+tan(Φ′)​=1−mm′m+m′​=b−a −2ч​.(1)​

Предположим, что есть точка (x,y) (x,y) (x,y) на одной из биссектрис угла, выделенной красным ниже, и обозначим угол биссектрисы относительно оси xxx Φbisector=Φ+ Φ′2.\Phi_\text{биссектриса} = \frac{\Phi + \Phi’}{2}.Φбиссектриса​=2Φ+Φ′​.

Снова, используя вышеприведенное тригонометрическое соотношение,

tan⁡(Φ′+Φ)=tan⁡(Φбиссектриса+Φбиссектриса)=tan⁡(Φбиссектриса)+tan⁡(Φбиссектриса)1−tan⁡(Φбиссектриса)tan⁡( Φбиссектриса)=2(yx)1−(y2x2)=2xyx2−y2.(2)\begin{выровнено} \tan (\Phi ‘+\Phi) = \tan (\Phi_\text{биссектриса}+\Phi_\text{биссектриса}) &= \frac{\tan(\Phi_\text{биссектриса}) + \tan(\Phi_\text{биссектриса})}{1 — \tan({\Phi_\text{биссектриса}})\tan(\Phi_ \text{биссектриса})} \\ &= \frac {2\left( \frac{y}{x} \right) }{1- \left( \frac{y^2}{x^2} \right) } \\ &= \frac {2xy}{x^2-y^2}.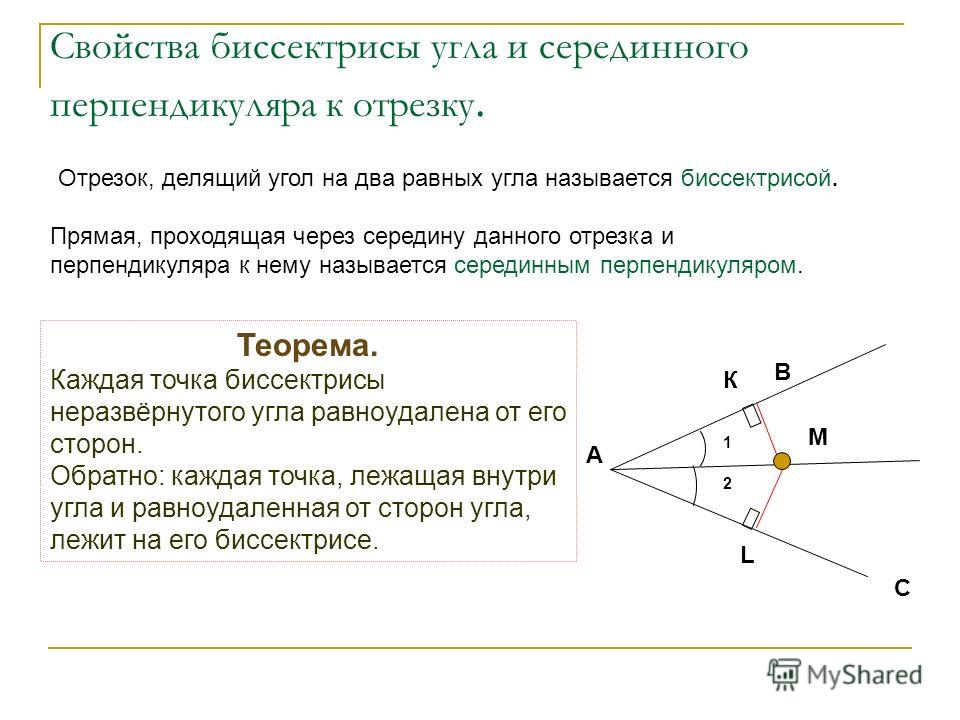 2 &= 0. \end{выровнено} hX2-(a-b)XY-hY2h(x-p)2-(a-b)(x-p)(y-q)-h(y-q)2​=0=0 .​ 92 + 2gx + 2fy + c ax2+2hxy+by2+2gx+2fy+c. Проверить, является ли

∣ahghbfgfc∣ \begin{vmatrix} a & h & g \\ h & b & f \\ g & f & c \end{vmatrix} ∣∣∣∣∣∣​ahg​hbf​gfc​∣ ∣∣∣∣∣​

равно нулю, чтобы подтвердить, что данное уравнение является парой прямых.

• Теорема о биссектрисе угла
• Расстояние между точкой и линией
• Инцентр

Цитировать как: Координатная геометрия — биссектриса угла. Brilliant.org . Извлекаются из https://brilliant.org/wiki/coordinate-geometry-angle-bisector/

Биссектрисы угла двух прямых

В этом уроке мы найдем уравнение прямых, которые делят пополам угол между двумя заданными прямыми . То есть уравнения биссектрисы угла двух прямых.

Давайте обсудим два разных метода.

Метод 1

Пусть две заданные строки будут:

L ₁ : A ₁ x + B ₁ Y + C ₁ = 0

L ₂ : A ₂ x + B ₂ : A ₂ x + B ₂ : A ₂ x + B ₂ : A ₂ x + B ₂ : A ₂

7 L ₂ : A ₂ = 0

Now, the angle bisectors of L ₁ and L ₂ are the lines that:

pass through the point of intersection L ₁ and L ₂ и

составляют равные углы л ₁ и л ₂ .

Начнем с поиска точки пересечения линий. Допустим, мы получили точку (x ₁ , y ₁ ) .

Далее нам нужно найти наклон м биссектрисы угла.

Так как они составляют один и тот же угол с L ₁ и L ₂ , используя формулу для угла между двумя линиями, мы получим:

|(м – м ₁ )/(1 + мм ₁ )| = |(м – м ₂ )/(1 + мм ₂ )|

⇒ (м – м ₁ )/(1 + мм ₁ ) = ±(м – м ₂ )/(1 + мм ₂ ) 1 9 9 м 1 0 2 0 2 0 3 9 0  и м ₂ — уклоны L ₁ и L ₂ соответственно.

Решение предыдущего уравнения даст нам два значения м , а значит получим две биссектрисы угла (по одной на каждое значение м ).

Наконец, мы можем найти их уравнения, используя форму точка-наклон.

Как вы уже поняли, этот метод достаточно сложен. Давайте перейдем к следующему, который намного элегантнее.

Способ 2

Начнем с двух предыдущих строк:

L ₂ : a ₁ x + b ₁ y + c 1₀₀₀₃

L ₂ : a ₂ x + b ₂ y + c ₂ = 0

биссектриса угла будет равноудалена от двух прямых. Взглянуть.

Если P является любой точкой на биссектрисе угла, то PA всегда будет равно PB . Почему? Потому что два треугольника POA и POB всегда будут конгруэнтны.

Мы нашли соотношение, верное для любой точки P на биссектрисе угла. Напомним, что это все, что нам нужно, чтобы найти уравнение геометрического места P (т. е. уравнение биссектрисы угла).

Теперь нам просто нужно преобразовать это в уравнение, которое включает координаты P . Предположим, что это (x, y) . Так как PA = PB , используя эту формулу, мы можем написать:

|a ₁ x + b ₁ г + к ₁ | / √(a ₁ ² + b ₁ ² ) = |a ₂ x + b ₂ y + c ₂ | / √(a ₂ ² + b ₂ ² )

А это искомое уравнение!

Удалив модуль, мы получим два уравнения (подразумевая, что у нас есть две биссектрисы угла):

(a ₁ x + b ₁ y + c ₁ ) / √(a 2 7 ₁ 7 ) 2 + б ₁ ² ) = (a ₂ x + b ₂ y + c ₂ ) / √(a ₂ ² + b ₂ ² )

( A ₁ X + B ₁ Y + C ₁ ) / √ (A ₁ ² + B ₁ ² 333333 + B ₂ ² 3333333 года) = — (A ₂ ² 3333333 года) = — (A ₂ ² 3333333 года.

No related posts.