Способ гаусса решения систем линейных уравнений: Решение систем линейных уравнений методом Гаусса

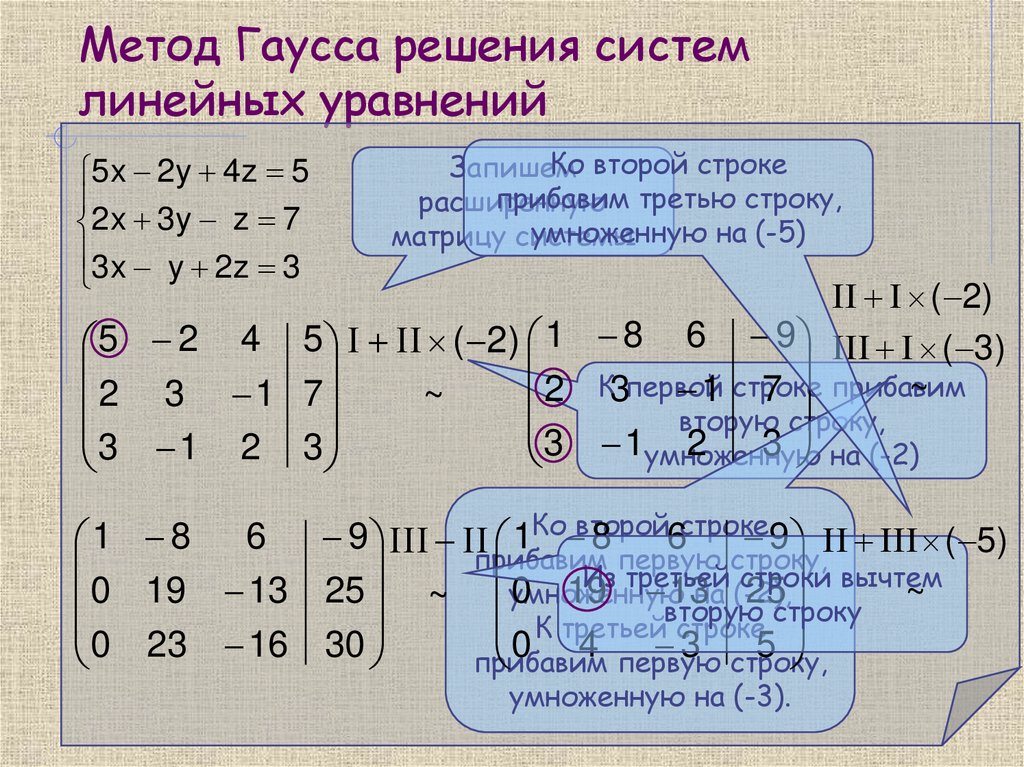
Метод Гаусса решения систем линейных уравнений

Рассмотрим квадратную систему

                                     .                                      (1)

У этой системы коэффициент a₁₁ отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x₁ не равен нулю.

Проведем следующие преобразования системы:

1) поскольку a₁₁¹0, первое уравнение оставим без изменений;

2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;

3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;

4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.

Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x₁ (это и являлось целью преобразований 1 – 4):

                                   .                                      (2)

Можно доказать, что замена любого уравнения системы новым, получающимся прибавлением к данному уравнению любого другого уравнения системы, умноженного на любое число, является эквивалентным преобразованием системы.

Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде таблицы

                                       .                                        (3)

Прямоугольную таблицу, состоящую из p строк и q столбцов, будем называть матрицей размера p´q:

                                    .

Числа a_ij называются элементами матрицы. Первый индекс фиксирует номер строки, а второй – номер столбца, в которых стоит данный элемент. Если p = q, то есть число столбцов матрицы равно числу строк, то матрица называется квадратной. Элементы a_ii образуют главную диагональ матрицы.

Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы, которую иногда называют просто матрицей системы.

Очевидно, что матрица коэффициентов квадратной системы является квадратной матрицей.

Каждую систему m линейных уравнений с n неизвестными можно представить в виде расширенной матрицы, содержащей m строк и n+1 столбцов. Каждую матрицу можно считать расширенной матрицей или матрицей коэффициентов некоторой системы линейных уравнений. Системе (2) соответствует расширенная матрица

                                     .

Преобразуем эту матрицу следующим образом:

1) первые две строки оставим без изменения, поскольку элемент a₂₂ не равен нулю;

2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;

3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.

В результате получится матрица, соответствующая системе, у которой неизвестная x₁ исключена из всех уравнений, кроме первого, а неизвестная x₂ — из всех уравнений кроме первого и второго:

                                     .

Теперь исключим  неизвестную x₃ из четвертого уравнения. Для этого последнюю матрицу преобразуем так:

1) первые три строки оставим без изменения, так как a₃₃ ¹ 0;

2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой:

                                  .

Полученная матрица соответствует системе

                                  .                                   (4)

Из последнего уравнения этой системы получаем x₄ = 2. Подставив это значение в третье уравнение, получим x₃ = 3. Теперь из второго уравнения следует, что x₂ = 1, а из первого — x₁ = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x₄, затем x₃ и т. д.).

Назовем элементарными преобразованиями матрицы следующие преобразования:

1) перемена местами двух строк;

2) умножение строки на число, отличное от нуля;

3) замена строки матрицы суммой этой строки с любой другой строкой, умноженной на некоторое число.

Если матрица A является расширенной матрицей некоторой системы, и путем ряда элементарных преобразований матрица A переводится в матрицу B, являющуюся расширенной матрицей некоторой другой системы, то эти системы эквивалентны.

Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей. Матрица коэффициентов системы (4) – треугольная матрица.

Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна.

Рассмотрим другой пример:

                              .                                (5)

Проведем следующие преобразования расширенной матрицы системы:

1) первую строку оставим без изменения;

2) вместо второй строки запишем разность между второй строкой и удвоенной первой;

3) вместо третьей строки запишем разность между третьей строкой и утроенной первой;

4) четвертую строку заменим разностью между четвертой и первой;

5) пятую строку заменим разностью пятой строки и удвоенной первой.

В результате преобразований получим матрицу

                                 .

Оставив без изменения первые две строки этой матрицы, приведем ее элементарными преобразованиями к следующему виду:

                                  .

Если теперь, следуя методу Гаусса, который также называют и методом последовательного исключения неизвестных, с помощью третьей строки привести к нулю коэффициенты при x₃ в четвертой и пятой строках, то после деления всех элементов второй строки на 5 и деления всех элементов третьей строки на 2 получим матрицу

.

Каждая из двух последних строк этой матрицы соответствует уравнению 0x₁+0x₂+0x₃+0x₄+0x₅ = 0. Это уравнение удовлетворяется любым набором чисел x₁, x₂, ¼, x₅, и его следует удалить из системы. Таким образом, система с только что полученной расширенной матрицей эквивалентна системе с расширенной матрицей вида

                                  .                                    (6)

Последняя строка этой матрицы соответствует уравнению x₃ – 2x₄ + 3x₅ = –4. Если неизвестным x₄ и x₅ придать произвольные значения: x₄ = r; x₅ = s, то из последнего уравнения системы, соответствующей матрице (6), получим x₃ = –4 + 2r – 3s. Подставив выражения x₃, x₄, и x₅ во второе уравнение той же системы, получим x₂ = –3 + 2r – 2s. Теперь из первого уравнения можно получить x₁ = 4 – r + s. Окончательно решение системы представляется в виде

                                           .

Рассмотрим прямоугольную матрицу A, у которой число столбцов m больше, чем число строк n. Если матрицу A можно разделить вертикальной чертой на две матрицы: стоящую слева треугольную матрицу размера m и стоящую справа прямоугольную матрицу, то матрицу A назовем трапециевидной или трапецеидальной. Очевидно, что матрица (6) — трапециевидная матрица.

Если при применении эквивалентных преобразований к системе уравнений хотя бы одно уравнение приводится к виду

                         0x_{1+ 0x2+ ¼0xn = bj  (bj ¹ 0),}

то система несовместна или противоречива, так как ни один набор чисел x₁, x₂, ¼, x_n не удовлетворяет этому уравнению.

Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к трапецеидальному виду и при этом система не получается противоречивой, то система совместна и является неопределенной, то есть имеет бесконечно много решений.

В последней системе можно получить все решения, придавая конкретные числовые значения параметрам r и s.

Те переменные, коэффициенты при которых стоят на главной диагонали трапецеидальной матрицы (это значит, что эти коэффициенты отличны от нуля), называются базисными. В рассмотренном выше примере это неизвестные x₁, x₂, x₃. Остальные неизвестные называются свободными. В рассмотренном выше примере это неизвестные x₄, и x₅. Свободным неизвестным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере.

Базисные неизвестные единственным образом выражаются через свободные неизвестные.

Если свободным неизвестным приданы конкретные числовые значения и через них выражены базисные неизвестные, то полученное решение называется частным решением.

Если свободные неизвестные выражены через параметры, то получается решение, которое называется общим решением.

Все бесконечное множество решений системы можно получить, придавая свободным неизвестным любые числовые значения и находя соответствующие значения базисных неизвестных.

Если всем свободным неизвестным приданы нулевые значения, то полученное решение называется базисным.

Одну и ту же систему иногда можно привести к разным наборам базисных неизвестных. Так, например, можно поменять местами 3-й и 4-й столбцы в матрице (6). Тогда базисными будут неизвестные x₁, x₂, x₄, а свободными – x₃ и x₅. Рекомендуем читателю самостоятельно привести последнюю систему к такому виду, чтобы свободными неизвестными были x₁ и x₂, а базисными – x₃, x₄, x₅.

Если получены два различных набора базисных неизвестных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число неизвестных, называемое рангом системы.

Рассмотрим еще одну систему, имеющую бесконечно много решений:

                            .

Проведем преобразование расширенной матрицы системы по методу Гаусса:

            .

Как видно, мы не получили трапецеидальной матрицы, однако последнюю матрицу можно преобразовать, поменяв местами третий и четвертый столбцы:

                                   .

Эта матрица уже является трапецеидальной. У соответствующей ей системы две свободных неизвестных – x₃, x₅ и три базисных – x₁, x₂, x₄. Решение исходной системы представляется в следующем виде:

                                          .

Приведем пример не имеющей решения системы:

                                          .

Преобразуем матрицу системы по методу Гаусса:

        .

Последняя строка последней матрицы соответствует не имеющему решения уравнению 0x₁ + 0x₂ + 0x₃ = 1. Следовательно, исходная система несовместна.

Сформулируем теперь кратко суть метода Гаусса. Полагая, что в системе  коэффициент a₁₁ отличен от нуля ( если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x₁ и переобозначить коэффициенты), преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x₁ с помощью эквивалентных преобразований описанным выше способом.

В полученной системе

                          ,

считая, что  (что всегда можно получить, переставив уравнения или слагаемые внутри уравнений и переобозначив коэффициенты системы), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x₂. Во вновь полученной системе

15. Характеристика еженедельника «Эспрессо» — лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

                             

при условии  оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x₃.

Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:

1) если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;

2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;

3) если получается система с трапецеидальной матрицей коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.

Уничтожение матриц. Устранение матриц (или система решения… | Соломон Се | Основы линейной алгебры

Устранение матриц (или решение системы линейных уравнений ) является самым первым и фундаментальным навыком в линейной алгебре. Это, наверное, первый урок из всех курсов

Прежде чем изучать решение систем линейных уравнений , вам действительно нужно ознакомиться со всеми основными терминами, иначе перейти к следующему этапу может быть очень сложно.
И в этом случае лучший способ узнать об этом — через Википедию.

JFR, основные термины: Гауссовая ликвидация , Гаусс-Джордан Эликация , Акматированная матрица , Элементарные ряды , Элементарная матрица , Row Echelon Form (ref) , Redued Row Echelon Форма (RREF) , Треугольная форма .

Это Алгоритм сокращения строк решить Систему линейных уравнений.

См. вики: исключение Гаусса
См. простую вики: исключение Гаусса
Пример: showme.com

для создания типа матрицы, называемой расширенной матрицей .
Затем элементарных операции над строками используются для упрощения матрицы.
Цель исключения Гаусса состоит в том, чтобы получить матрицу в ступенчато-строковой форме .
Если матрица имеет форму строк-ступеней , которая также называется Треугольная форма .
В некоторых определениях исключения Гаусса говорится, что результат матрицы должен быть в уменьшенной ступенчато-строковой форме .
Исключение Гаусса, которое создает уменьшенный результат матрицы строк-ступеней, иногда называют Исключение Гаусса-Жордана .

Для упрощения вот структура:

• Алгоритм: Исключение Гаусса
• Шаг 1: Перепишите систему в расширенную матрицу .
• Шаг 2: Упростите матрицу с помощью Элементарные операции со строками .
• Результат:
• Строка Эшелон Форма или
• Сокращенная Эшелон Форма

0016

• Алгоритм: Исключение Гаусса-Жордана
• Шаг 1: Перепишите систему в расширенную матрицу .
• Шаг 2: Упростите матрицу с помощью Элементарные операции со строками .
• Результат: Только в Сокращенная форма эшелона

Элементарные операции со строками используются для упрощения матрицы .

Используются три типа операций со строками:

• Тип 1: Переключение одной строки на другую ряд .
• Тип 2: Умножение строки на ненулевое число .
• Тип 3: Добавление строки из другой строки . (!Примечание: вы можете только ДОБАВИТЬ их, но не вычесть , но вы можете ДОБАВИТЬ отрицательное)

Запутанная операция: Посмотрите, где был поставлен отрицательный знак :

Предположим, цель состоит в том, чтобы найти решение для линейной системы ниже:

Сначала нам нужно превратить его в Augmented Matrix form:

Затем мы применяем Elementary Row Operations , и в результате получается Row Echelon Form :

В конце, если мы хотим, мы можем дополнительно применить некоторые операции со строками, чтобы получить матрицу in Сокращенная форма строки Echelon :

Чтение этой матрицы говорит нам о том, что решения этой системы уравнений возникают, когда x = 2, y = 3 и z = -1.

Обратитесь к этому видео-лекции: REF & RREF.

Неважно, это Квадратная матрица или нет, может быть Диагональ или Основная диагональ , или вы вообще не можете провести диагональ.
Имеет значение только ЧТО ВЫШЕ 1 И ЧТО НИЖЕ 1.

• REF: Для каждого столбца все числа ниже 1 ДОЛЖНЫ БЫТЬ 0. Не имеет значения, какие числа больше 1.
• RREF : Для каждого столбца все числа выше и ниже 1 ДОЛЖНЫ БЫТЬ 0. Нас не волнует, если в столбце нет 1.

Значит, вносим в матрицу еще один столбец, представляющий Правую часть системы уравнений, числа справа от знака =

5.

Когда мы применяем исключение к линейным уравнениям , мы работаем с обеими сторонами одновременно. Но для компьютерных программ это часто относится к Левая сторона и помните операции, например. умножьте число или сложите уравнения вместе, когда левая сторона будет закончена, примените те же операции к правой стороне.

Если для данной Матрицы было сказано, что это Расширенная Матрица , мы должны предположить, что Последний Столбец — это Столбец Решения .

• Эквивалентные системы: Линейные системы с ТАКИМ НАБОРОМ РЕШЕНИЙ.

• Эквивалентные матрицы: две матрицы, где одна матрица может быть превращена в другую матрицу с помощью элементарных операций над строками .

Или называется Курсор или Базовая или Базовая переменная .

См. это видео от mathispower4u.

Это означает значение, которое представляет неизвестную переменную в каждом столбце. В столбце нет разворота , если вы не можете получить 1 в этом столбце.

Если в столбце нет сводной точки, это означает, что эта неизвестная переменная столбца может быть любым числом , поэтому мы называем это свободной переменной .

опорные точки находятся после сокращения строк , а затем возвращаются к Исходной матрице, столбцы С опорными точками называются опорными столбцами .

Все просто: когда вы решаете одну неизвестную переменную в линейной системе, вы подставляете значение обратно в другие уравнения. Мы называем этот процесс обратной заменой .

-

SCIRP Открытый доступ

Издательство научных исследований

Журналы от A до Z

Журналы по темам

• Биомедицинские и биологические науки.
• Бизнес и экономика
• Химия и материаловедение.
• Информатика. и общ.
• Науки о Земле и окружающей среде.
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные науки. и гуманитарные науки

Журналы по тематике  

• Биомедицина и науки о жизни
• Бизнес и экономика
• Химия и материаловедение
• Информатика и связь
• Науки о Земле и окружающей среде
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные и гуманитарные науки

Публикация у нас

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Публикуйте у нас  

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Недавно опубликованные статьи

Недавно опубликованные статьи

Подпишитесь на SCIRP

Свяжитесь с нами

клиент@scirp. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт