Средние величины — задачи с решениями
Средние величины — задачи с решениямиСтатистика
Искать…
- Вы здесь:
- Главная
- Статистика
- Средние величины — задачи с решениями
Средние величины — задачи с решениями
Практическое занятие. Тема: Средние величины.
Задача по средним величинам
Имеются следующие данные:
|
Группы рабочих по количеству произведенной за смену продукции (штук) |
Число рабочих |
|
3-5 |
10 |
|
5-7 |
30 |
|
7-9 |
40 |
|
9-11 |
15 |
|
11-13 |
5 |
Исчислить среднюю выработку продукции одним рабочим за смену.
Задачи по средним величинам с решением
Имеются следующие данные о ценах и сумме продажи товара А на рынках:
|
Рынки |
Цена за единицу |
Продано на сумму, грн. |
|
1 |
2 |
500 |
|
2 |
3 |
500 |
|
3 |
2 |
500 |
Определить среднюю цену товара А.
Ход решения задачи:
Используем среднюю гармоническую простую для равных хf.
Задача по средним величинам.
Имеются данные о выполнении норм выработки рабочими:
|
Группы рабочих по выполнению норм выработки |
Число рабочих |
|
90-100 |
28 |
|
100-110 |
48 |
|
110-120 |
20 |
|
120-130 |
4 |
Определить моду и медиану.
Ход решения задачи:
Модальным является интервал 100-110, имеющий наибольшую частоту (480. Следовательно,
Для нахождения медианы достроим графу накопленных частот:
Накопленные частоты
28
76
96
100
Находим медиану:
- Назад
- Вперед
Добавить комментарий
Задачи по темам:
Примеры решения задач по теме «Средние показатели» Средняя арифметическая величина
49
Задача 2.1
Имеются данные о средней заработной плате и числе рабочих различной квалификации (табл. 2.1).
Таблица 2.1
Заработная плата и число рабочих
Квалификация рабочего | Разряд рабочего | Средняя заработная плата, ЗПi , тыс. | Число рабочих, Ni , чел. |
1. Низкая | 1; 2 | 6,0 6,5 6,8 | 1 1 1 |
2. Средняя | 3; 4 | 8,2 8,8 9,0 | 2 2 2 |
3. Высокая | 5; 6 | 10,5 12,0 12,6 | 3 5 2 |
Итого | | 19 |
Определить
среднюю заработную плату рабочих каждой
квалификации и всех рабочих.
Решение
1. Средняя заработная плата j-й квалификации рабочих (групповая средняя величина) рассчитывается следующим образом
где ФЗПj фонд заработной платы рабочих j-й квалификации; Nj число рабочих j-й квалификации.
2. Средняя заработная плата рабочих низкой (первой) квалификации может быть рассчитана по формуле простой средней, т. к. значения заработной платы этой категории рабочих не повторяются
3. Для рабочих средней квалификации средняя заработная плата рассчитывается по формуле средней взвешенной
или по формуле простой средней, т. к. статистический вес (число рабочих) одинаковый для различных значений заработной платы
4. Средняя заработная платы рабочих высокой квалификации
5.
средней арифметической взвешенной с использованием всех значений заработной платы
средней арифметической взвешенной с использованием средних значений заработной платы рабочих по каждой квалификационной группе
средней агрегатной с использованием величины фонда заработной платы и численности рабочих по каждой квалификационной группе
Задача 2.2
Имеются данные о возрасте работников предприятия в виде интервального ряда распределения работников по возрасту (графы 1, 2 или 1, 3 табл. 2.2).
Таблица 2.2
Распределение рабочих по возрасту
Номер группы работников | Возраст рабочих, лет | Число рабочих, Ni,
чел. | Удельный вес рабочих, di,, % | Средний возраст рабочих в группе, Вi, лет | ||
А | 1 | 2 | 3 | 4 | 5 | 6 |
1 | 20 25 | 200 | 10 | 22,5 | 4500 | 225,0 |
2 | 25 30 | 900 | 45 | 27,5 | 24750 | 1237,5 |
3 | 30 35 | 800 | 40 | 32,5 | 26000 | 1300,0 |
4 | 35 40 | 100 | 5 | 37,5 | 3750 | 187,5 |
Итого | 2000 | 100 | | 59000 | 2950,0 |
Определить
средний возраст работника предприятия.
Решение
Для расчета среднего возраста работника в интервальном ряду распределения необходимо определить середину интервала (графа 4 табл. 1.25). Средний возраст работника может быть рассчитан с использованием в качестве статистических весов
численности работников (графа 5 табл. 2.2)
удельного веса работников каждой группы в общей численности работников (графа 6 табл. 2.2)
Задача 2.3
Имеются данные о численности высоко- и низкоквалифицированных рабочих и средней месячной заработной плате по двум предприятиям (табл. 2.3).
Таблица 2.3
4.4.1 Расчет среднего
Содержание
Текст начинается
Навигация по теме
- 4 Исследование данных
- 4.4 Меры центральной тенденции
- 4.
 4.1 Вычисление среднего
4.1 Вычисление среднего - 4.4.2 Расчет медианы
- 4.4.3 Расчет режима
- 4.
- 4.4 Меры центральной тенденции
Среднее можно вычислить только для числовых переменных, независимо от того, являются ли они дискретными или непрерывными. Его получают, просто разделив сумму всех значений в наборе данных на количество значений. Расчет может быть выполнен из необработанных данных или для данных, агрегированных в частотной таблице. Вот несколько примеров расчета.
Пример 1. Футбольный турнир на горе Ривал
Mount Rival ежегодно принимает футбольный турнир. В этом сезоне в 10 играх лучший бомбардир хозяев поля забил 7, 5, 0, 7, 8, 5, 5, 4, 1 и 5 голов. Каков средний балл этого игрока?
Сумма всех значений равна 47 и имеется 10 значений. Следовательно, среднее значение составляет 47 ÷ 10 = 4,7 голов за игру.
Пример 2. ДТП со смертельным исходом
В следующей таблице указано количество людей, погибших в дорожно-транспортных происшествиях за 10-летний период. Каково в этот период среднее число людей, теряющих жизнь каждый год? Сколько человек ежедневно погибает в среднем в дорожно-транспортных происшествиях?
Каково в этот период среднее число людей, теряющих жизнь каждый год? Сколько человек ежедневно погибает в среднем в дорожно-транспортных происшествиях?
| Год | Смертей |
|---|---|
| 2009 | 623 |
| 2010 | 583 |
| 2011 | 959 |
| 2012 | 1 037 |
| 2013 | 960 |
| 2014 | 797 |
| 2015 | 663 |
| 2016 | 652 |
| 2017 | 560 |
| 2018 | 619 |
| Итого | 7 453 |
Общее количество умерших представлено в таблице (7453). Чтобы получить среднегодовое значение, количество смертей делится на 10, что дает 745,3 смертей в год. Чтобы получить среднесуточное значение, среднегодовое значение делится на 365, что дает примерно 2 смерти в день.
Чтобы получить среднегодовое значение, количество смертей делится на 10, что дает 745,3 смертей в год. Чтобы получить среднесуточное значение, среднегодовое значение делится на 365, что дает примерно 2 смерти в день.
Для большого набора данных может быть проще суммировать данные в таблице частот перед вычислением среднего значения. В этом случае вам необходимо взвесить каждое возможное значение по частоте значения, чтобы рассчитать итог.
Пример 3. Футбольный турнир на горе Ривал
Вернемся к футбольному турниру Mount Rival. Предположим, что соревнуются пять команд, в каждой из которых по 10 игроков, всего 50 игроков. Количество голов, забитых каждым игроком, было собрано, а результаты сведены в таблицу частоты ниже. Например, мы можем видеть, что восемь игроков забили только один гол во время турнира. Каково среднее количество голов, забитых игроками во время турнира?
| Количество забитых голов | Количество игроков |
|---|---|
| 0 | 2 |
| 1 | 8 |
| 2 | 14 |
| 3 | 12 |
| 4 | 8 |
| 5 | 4 |
| 6 | 2 |
Сначала нужно подсчитать общее количество забитых мячей. Для этого вы берете каждое наблюдаемое значение количества забитых голов, то есть значения от 0 до 6, и умножаете каждое значение на количество игроков:
Для этого вы берете каждое наблюдаемое значение количества забитых голов, то есть значения от 0 до 6, и умножаете каждое значение на количество игроков:
0 × 2 + 1 × 8 + 2 × 14 + 3 × 12 + 4 × 8 + 5 × 4 + 6 × 2 = 136
Поскольку игроков 50, среднее значение составляет 136 ÷ 50 = 2,72 гола на игрока.
- Статистика: сила данных! — Главная страница
- 1 Данные, статистическая информация и статистика
- 2 Источники данных
- 3 Сбор и обработка данных
- 4 Исследование данных
- 5 Визуализация данных
- Библиография
- Глоссарий
Что-то не работает? Есть ли устаревшая информация? Не можете найти то, что ищете?
Пожалуйста, свяжитесь с нами и дайте нам знать, как мы можем вам помочь.
Уведомление о конфиденциальности
- Дата изменения:
Статистические средние значения — среднее, мода, медиана
В статистике
среднее значение определяется как число, которое измеряет центральную тенденцию данного
набора чисел. Существует ряд различных средних значений, включая, помимо прочего,
Существует ряд различных средних значений, включая, помимо прочего,
в: среднее, медиана, мода и диапазон.
Среднее
Среднее — это то, что большинство людей обычно называют средним. Среднее значение относится к числу
, которое вы получаете, когда суммируете данный набор чисел, а затем делите эту сумму
на общее число в наборе. Среднее также правильнее называть средним арифметическим
.
Дан набор из n элементов от 1 до n
Среднее значение находится путем сложения всех и , а затем деления на общее число
, n
.
Это можно обобщить следующей формулой:
Примеры средних задач
Пример 1
Найдите среднее значение набора чисел ниже
Раствор
Первым шагом является подсчет количества чисел в наборе, который мы будем называть
n
.
Следующим шагом является сложение всех чисел в наборе
Последний шаг — найти фактическое среднее значение, разделив сумму на n
.
Среднее также можно найти для сгруппированных данных, но прежде чем мы увидим пример, давайте сначала определим частоту.
Частота в статистике означает то же, что и в повседневном использовании этого слова. Частота
элемента в наборе относится к тому, сколько таких элементов имеется в наборе. Частота
может быть от 0 до максимально возможного количества. Если вам говорят, что частота
элемента равна 3, это означает, что существует 3 с в комплекте.
Пример 2
Найдите среднее значение набора возрастов в таблице ниже
| Возраст (лет) | Частота |
|---|---|
| 10 | 0 |
| 11 | 8 |
| 12 | 3 |
| 13 | 2 |
| 14 | 7 |
Решение
Первый шаг — найти общее число эпох, которое мы обозначим как n .
Поскольку считать все возрасты будет утомительно, мы можем найти n , сложив
частоты:
Далее нам нужно найти сумму всех возрастов. Мы можем сделать это двумя способами: мы можем сложить
каждого отдельного возраста, что будет долгим и утомительным процессом; или мы можем
используйте частоту, чтобы ускорить процесс.
Поскольку мы знаем, что частота представляет собой количество представителей этого конкретного возраста, которых насчитывается
, мы можем просто умножить каждый возраст на его частоту, а затем сложить все эти произведения.
Последний шаг — найти среднее значение, разделив сумму на n
.
Среднее значение населения по сравнению со средним значением выборки
В разделе
Введение в статистику мы определили совокупность и выборку
, где выборка является частью совокупности.
В статистике есть два вида средних значений: среднее по совокупности и среднее по выборке. Среднее значение совокупности
— это истинное среднее значение всей совокупности набора данных, а выборочное среднее значение
— это среднее значение небольшой выборки совокупности. Эти различные средние значения часто встречаются как в статистике, так и в вероятности, и их не следует путать друг с другом.
Среднее значение населения представлено греческой буквой μ (произносится как мю ), в то время как среднее значение выборки
представлено x̄ (произносится как x бар ). Общее количество
элементов в популяции представлено N , а количество
элементов в выборке представлено n . Это приводит к корректировке формулы
, которую мы привели выше для расчета среднего.
Среднее значение выборки обычно используется для оценки среднего значения совокупности, когда среднее значение совокупности
неизвестно.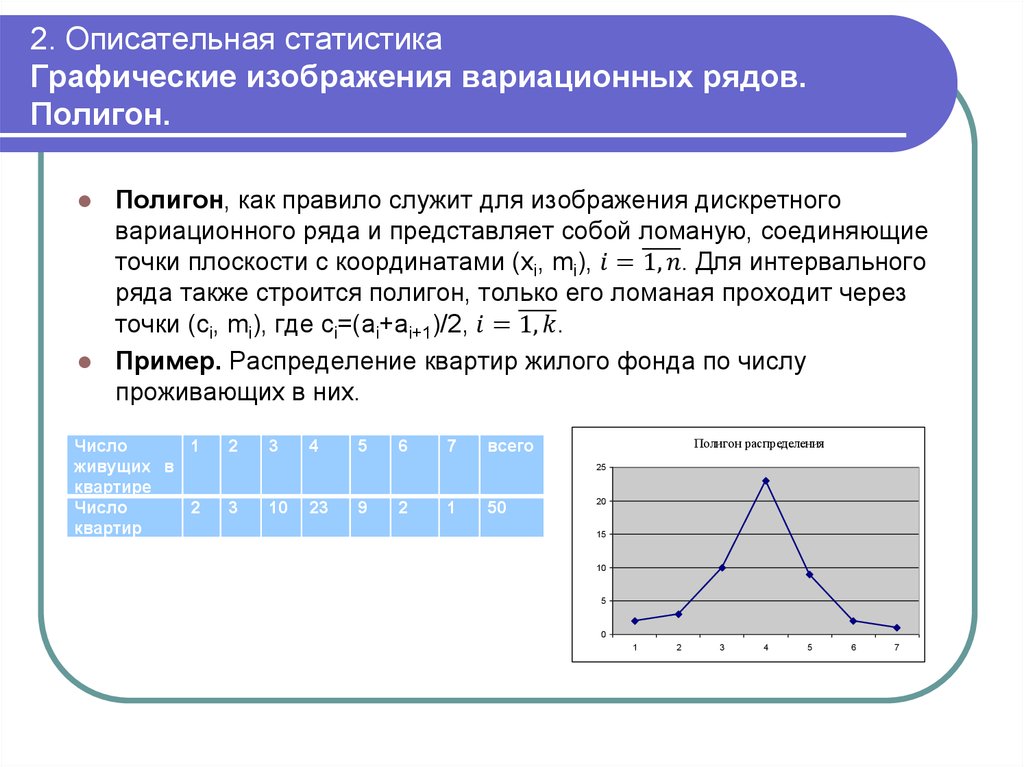 Это потому, что они имеют одинаковое ожидаемое значение.
Это потому, что они имеют одинаковое ожидаемое значение.
Медиана
Медиана определяется как число в середине данного набора чисел, расположенных
в порядке возрастания величины. Когда задан набор чисел, медианой является число
, расположенное точно в середине списка, когда вы упорядочиваете числа из
от низшего к высшему. Медиана также является мерой среднего. В статистике более высокого уровня
в качестве меры дисперсии используется медиана. Медиана важна, потому что
описывает поведение всего набора чисел.
Пример 3
Найдите медиану в наборе чисел, приведенных ниже
Решение
Из определения медианы мы должны быть в состоянии сказать, что первый шаг равен 9.0043, чтобы переставить заданный набор чисел в порядке возрастания величины, т.е. от
самого низкого до самого высокого
Затем мы проверяем набор, чтобы найти то число, которое лежит точно посередине.
Давайте попробуем другой пример, чтобы подчеркнуть кое-что интересное, что часто происходит, когда
находит медиану.
Пример 4
Найдите медиану данных
Решение
Как и в предыдущем примере, мы начинаем с перестановки данных в порядке от
наименьшего к наибольшему.
Затем мы проверяем данные, чтобы найти число, которое находится точно посередине.
Из приведенного выше видно, что в итоге мы получаем два числа ( 4 и 5 )
посередине. Мы можем найти медиану, найдя среднее значение этих двух чисел
следующим образом:
Режим
Режим определяется как элемент, который чаще всего встречается в заданном наборе из
элементов. Используя приведенное выше определение частоты, мода также может быть определена
Используя приведенное выше определение частоты, мода также может быть определена
как элемент с наибольшей частотой в заданном наборе данных.
Для данного набора данных может быть более одного режима. Пока все эти элементы
имеют одинаковую частоту и эта частота является самой высокой, все они являются
модальными элементами набора данных.
Пример 5
Найдите режим следующего набора данных.
Решение
Режим = 3 и 15
Режим для сгруппированных данных
Как мы видели в разделе о данных, сгруппированные данные делятся на классы. У нас есть определенная мода
как элемент, который имеет самую высокую частоту в данном наборе данных.
В сгруппированных данных мы можем найти два вида режима: модальный класс или класс с
самой высокой частотой и сам режим, который мы вычисляем из модального класса, используя
приведенную ниже формулу.

 р./мес.
р./мес.
 4.1 Вычисление среднего
4.1 Вычисление среднего 4.1.2
4.1.2