Применение подобия к доказательству теорем и решению задач. Средняя линия треугольника и трапеции
- Чулкова Екатерина Геннадиевна, учитель математики
Разделы: Математика
Цели урока:
- ввести определение средней линии треугольника, трапеции;
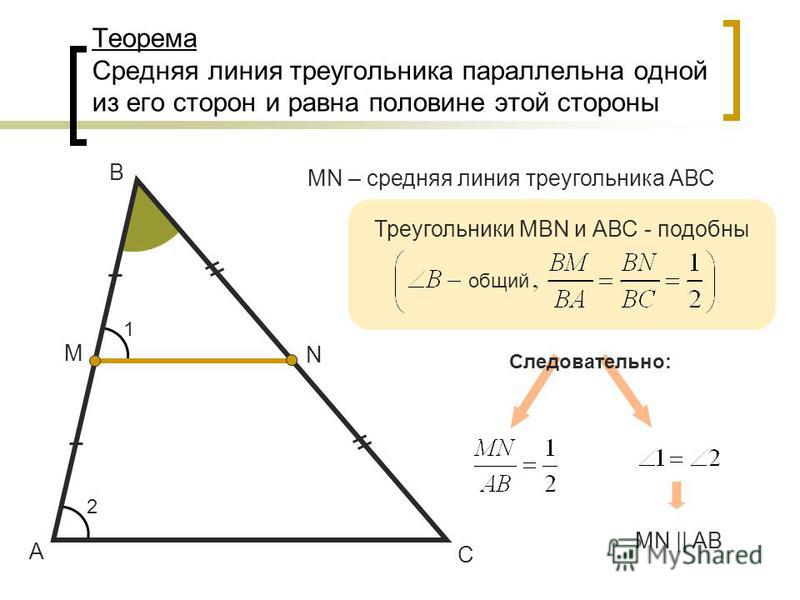
- сформулировать и доказать теорему о средней линии треугольника;
- рассмотреть решение задач на применение этой теоремы;
- пропедевтика свойства средней линии трапеции.
Ход урока
I. Организационный момент
II. Устная работа
III. Объяснение нового материала
IV. Закрепление изученного материала
V. Итоги урока
VI. Домашнее задание.
I. Оргмомент. Учитель сообщает тему урока.
Оргмомент. Учитель сообщает тему урока.
II. Устно (фронтальная работа с классом).
1. Какие треугольники называются подобными?
2. Являются ли треугольники (рис. 1) подобными? На основании какого признака подобия?
3. Что можно сказать об углах этих треугольников?
4. Какие признаки подобия треугольников вы еще знаете?
Эти факты будем использовать при решении задач.
5. Во сколько раз АВ больше МВ, а ВС больше ВN? (по рис. 2)
Что можно сказать о АВС и МВN? (рис. 2). На основании какого признака подобия?
7. Сравните площади этих треугольников?
Сделаем запись:
Имеем
Записываем в тетрадь тему урока.
III. Объяснение нового материала
- Дать определение средней линии треугольника.
- Сформулировать теорему о средней линии треугольника (предложить учащимся самостоятельно сформулировать теорему, опираясь на 9 вопрос устных упр
 Закрепление изученного материала
Закрепление изученного материала1. Чему равны средние линии треугольника со сторонами 14 см, 16 см, 20 см? Использовать модель (вырезать из цветной бумаги, заранее отметить середины сторон). Перегибая ?, обсудить с учащимися ответы.
2. №564 у.
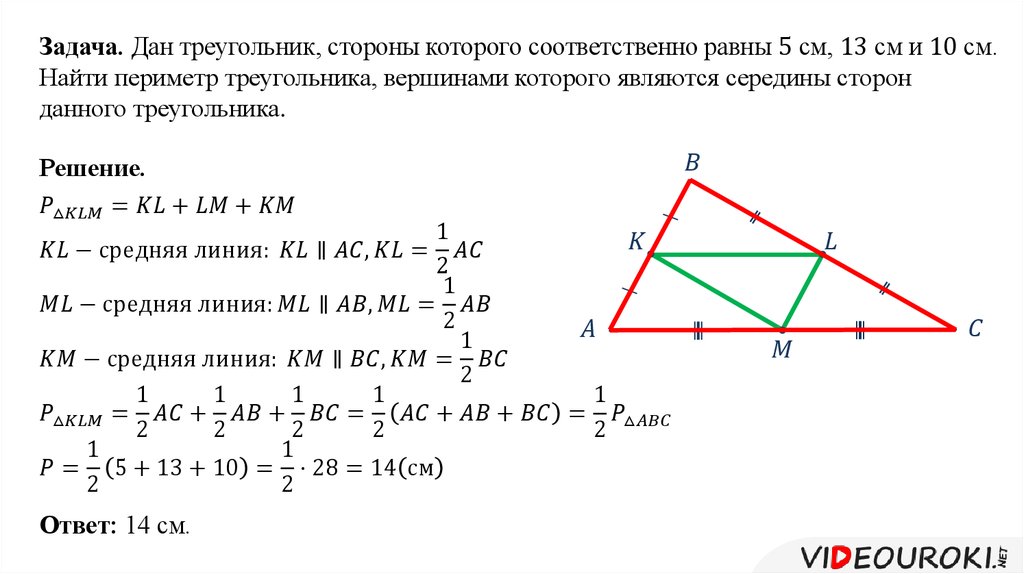
Дан треугольник, стороны которого равны 8 см, 5 см, 7 см. Найдите периметр треугольника, вершинами которого являются середины сторон данного треугольника.
Сделать вывод про периметр и площадь этого треугольника.
3. № 567 (письм)
Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Вопрос классу: Как доказать, что четырехугольник является параллелограммом?
(Надо использовать признаки параллелограмма)
Из того, что M, N – середины сторон АВ и ВС, что можно сказать об отрезке MN?
Записываем в тетрадях решение:
Из п.1 и п.2
PM = 1/2 AD; MK = 1/2 BC
PK = 1/2 (AD + BC)
Как вы думаете, как называется отрезок,
соединяющий боковые стороны трапеции? Чему он
равен? [Этот отрезок равен полусумме оснований].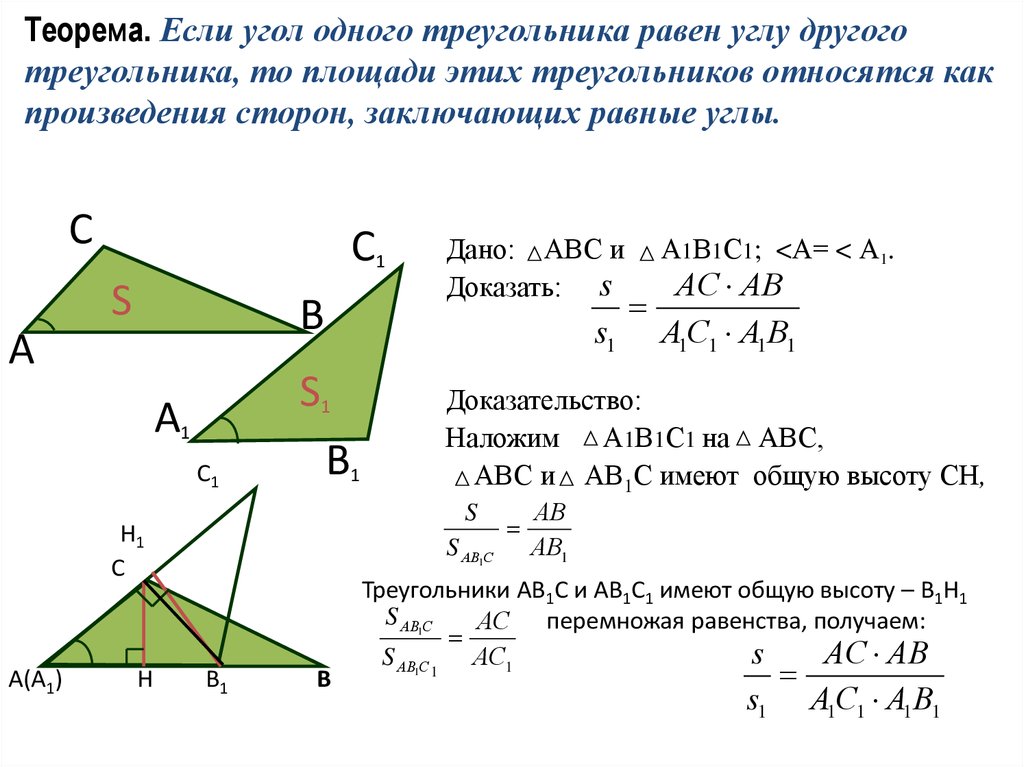
V. Подводим итоги урока
1. Возьмите белый лист (приложение 1) и выполните задание.
2. Устно (по заранее заготовленному чертежу) решение задачи
Повторить выводы, сделанные на уроке:
1) периметр треугольника, образованного средними линиями данного треугольника, вдвое меньше периметра данного треугольника;
2) площадь треугольника, образованного средними линиями данного треугольника, вчетверо меньше площади данного треугольника;
3) средние линии разбивают треугольник на четыре треугольника равной площади.
Домашнее задание.
Вопр.8 стр. 154 № 565; 566; 568(а).
Замечание:
Приложение 2 использовать как дополнение, если позволяет время.
Литература:
- Геометрия. Учебник для 7-9 кл. об/об учр. (Л.С. Атанасян и др.), М., Просвещение, 2000;
- Рабинович Е.М. Задачи и упражнения на готовых чертежах 7-9 кл., М., Илекса, 2006;
- Левитас Г.Г. Карточки для коррекции знаний по
геометрии для 8-9 кл.
 М., Илекса, 2003;
М., Илекса, 2003; - Шуба М.Ю. Занимательные задания в обучении математике, М.: Просвещение, 1994.
Средняя линия треугольника | План-конспект урока по геометрии (8 класс) по теме:
Методическая разработка урока математики в 8 классе.
Тема урока «Средняя линия треугольника».
Тип урока: урок усвоения новых знаний
Цели урока:
Образовательные:
- Ввести понятие средней линии треугольника; доказать свойство средней линии треугольника, а также теорему о пересечении медиан треугольника; рассмотреть свойства медианы и средней линии треугольника применительно к его площади; научить применять их при решении задач.
Развивающие:
- Развивать интерес с к геометрии, логическое мышление, интуицию учащихся; формировать умения чётко и ясно излагать свои мысли;
совершенствовать графическую культуру.
- Развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к исследовательской деятельности, к синтезу и анализу.
Воспитательные:
- Мотивировать детей к самообразованию.
- Воспитывать интерес к геометрии, расширять кругозор учащихся
- Прививать аккуратность в оформлении геометрических задач, культуру устной речи.
Оборудование, наглядность, электронные приложения к уроку:
Компьютер. Мультимедийный проектор. Документ камера.
Презентация Microsoft PowerPoint.
Структура урока.
Вид деятельности. | № слайдов. | мин. |
1. Постановка цели урока. Эпиграф к уроку. | 1-3 | 2 |
2. Проверка домашнего задания | 2 | |
3. Повторение изученного материала. | 4-6 | 3 |
4. Понятие средней линии треугольника и её свойство. Математический диктант | 7-9 10-14 | 12 |
5. Физкультминутка. | 1 | |
6. Свойство медиан треугольника. Следствия. | 15-17 18-21 | 15 |
7. Закрепление нового материала. Решение задач. | 22-23 | 8 |
8. Подведение итогов. | 24 | 2 |
9. Домашнее задание. | 25 | 1 |
Ход урока.
1. Вступительное слово учителя.
Эпиграфом к сегодняшнему уроку взяты слова французского писателя XIX столетия. Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом” (сайд №2).
Давайте последуем совету писателя и на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
Многие известные мыслители и писатели прошлого обращались к темам о замечательных точках и линиях треугольника. Сегодня мы тоже займемся этим интересным исследованием.
Тема нашего урока «Средняя линия треугольника». Давайте сформулируем, какие цели мы должны достичь: (учащиеся самостоятельно формулируют цели, слайд №3)
- Дать определение средней линии треугольника.
- Доказать теорему о средней линии треугольника.
- Доказать теорему о пересечении медиан треугольника.
2. Проверка домашнего задания.
С помощью документ камеры решение домашнего задания (№ 568 б) из тетради учащегося проектируется на экран. Учащийся комментирует решение.
3. Устная работа. Повторение изученного материала.
Цель: систематизировать базовые знания по теме «Подобие треугольников»; развивать логическое мышление; формировать умение четко и ясно излагать свои мысли.
Чтобы успешно выполнить цели сегодняшнего урока, нам не раз придется обращаться к признакам подобия треугольников. Какие признаки подобия треугольников вы знаете? Учащиеся формулируют признаки подобия треугольников (слайд 4-6).
4. Понятие средней линии треугольника и ее свойства.
Цели: сформулировать определение средней линии треугольника и доказать ее свойство; развивать умение сравнивать и анализировать.
— Что общего у треугольников, изображенных на рисунке? (слайд №7)
Учащиеся самостоятельно дают определение средней линии треугольника(слайд №8).
— Сколько средних линий можно построить в треугольнике?
-Средняя линия треугольника — это замечательная линия треугольника. А чем же она замечательна? Давайте сформулируем и докажем свойство средней линии треугольника (слайд №9).
Теорему учащиеся доказывают самостоятельно (задание получено сильным учащимся предварительно). С целью закрепления понятия и свойства средней линии треугольника проводится математический диктант (решение задач по готовым чертежам; слайд № 10-14). Учащиеся получают карточки, выполняют математический диктант.
Учащиеся получают карточки, выполняют математический диктант.
Математический диктант
Вариант 1 | Вариант 2 |
1)Две стороны треугольника соединили отрезком, непараллельным третьей стороне. Является ли этот отрезок средней линией данного треугольника? | 1)Точки А и В являются серединами двух сторон треугольника. Как называется отрезок АВ? |
2)В ∆АВС сторона АВ=7 см. Чему равна средняя линия треугольника, параллельная этой стороне? | 2)Средняя линия треугольника АВD, параллельная стороне ВD, равна 4 см. Чему равна сторона ВD? |
3) Дано: МК=3, KN=4, MN=5. Найти периметр треугольника АВС. | 3) Дано: АВ=3м, ВС=5м, АС=4м. Найти периметр треугольника MNK. |
4) Концы отрезка АВ лежат на сторонах треугольника, а его длина равна половине третьей стороны. Обязательно ли: АВ – средняя линия этого треугольника? | 4)Концы отрезка MN лежат на сторонах треугольника. Обязательно ли: MN – средняя линия этого треугольника? |
5) Периметр треугольника равен 5,9 см. Найти периметр треугольника, отсекаемого одной из его средних линий. | 5)Периметр треугольника равен 7,3 см. Найти периметр треугольника, отсекаемого одной из его средних линий. |
5. Физкультминутка
6. Свойство медиан треугольника
Цель: развивать логическое мышление; способность к исследовательской деятельности, к синтезу и анализу.
Вспомните, что называется медианой треугольника? (слайд №15) Укажите рисунок, на котором изображена медиана.
Свойство медиан треугольника: медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины (слайд № 16).
Теорему учащиеся доказывают самостоятельно (задание получено сильным учащимся предварительно).
-Медиану тоже считают замечательной линией треугольника. Как вы считаете, почему? Вспомните, какие треугольники называются равновеликими (слайд 17)?Давайте, исследуем следующие предположения. В треугольнике провели медиану. Как изменится площадь? (слайд № 18)
Как вы считаете, почему? Вспомните, какие треугольники называются равновеликими (слайд 17)?Давайте, исследуем следующие предположения. В треугольнике провели медиану. Как изменится площадь? (слайд № 18)
Утверждение: медиана треугольника делит его на два равновеликих треугольника. |
-В параллелограмме, площадь которого равна S, проведены диагонали. Чему равны площади образовавшихся треугольников (слайд №19)?
Следствие 1: диагонали параллелограмма делят его на четыре равновеликих треугольника.
— В треугольнике проведены три медианы. Являются ли они равновеликими (слайд № 20)?
Следствие 2: медианы треугольника делят его на шесть равновеликих треугольников.
— В треугольнике проведены средние линии. Чему равна площадь треугольника BMN (слайд № 21)?
Следствие 3: средняя линия треугольника отсекает от данного треугольник, площадь которого равна ¼ площади исходного треугольника.
7. Закрепление нового материала. Решение задач
Цель: научить учащихся применять приобретенные на уроке знания при решении задач; развивать логическое мышление; прививать аккуратность в оформлении геометрических задач; совершенствовать графическую культуру.
Задача 1. Медианы ВК и ЕМ, треугольника ВСЕ, пересекаются в точке О. Найти SMOK:SCMK (слайд №22).
Задача 2. Решите задачу устно по готовому чертежу (слайд № 23).
АА1, ВВ1, СС1 – медианы треугольника. Доказать:
|
8. Подведение итогов
Рефлексия.
- Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
- Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

- Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
- Средняя линия треугольника отсекает от данного треугольник, площадь которого равна ¼ площади исходного.
- Три средние линии треугольника разбивают его на 4 равоновеликих треугольника, площадь каждого из них равна ¼ площади исходного.
Оценки за урок.
9. Домашнее задание
П. 62, вопросы 8, 9 (стр. 160). Задачи № 616, 571.
Литература
- Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений. / Л.С. Атанасян, В.Ф Бутузов, С.Б. Кадомцев и др. – 5-е изд. – М.: Просвещение, 1995. – 335 с.: ил. – ISBN 5-09-006554-3
- Лысенко Ф. Ф. Математика. Подготовка к ЕГЭ. – Ростов – на –Дону: «Легион М», 2012.
- Алтынов П.И. Геометрия. Тесты. 7-9 кл.
- Гилярова М. Г. Поурочные разработки по геометрии: 8 класс. Волгоград: « Учитель — АСТ», 2003.
- Интернет-сайты:
Интернет-государство учителей в разделе Инфотека-Математика.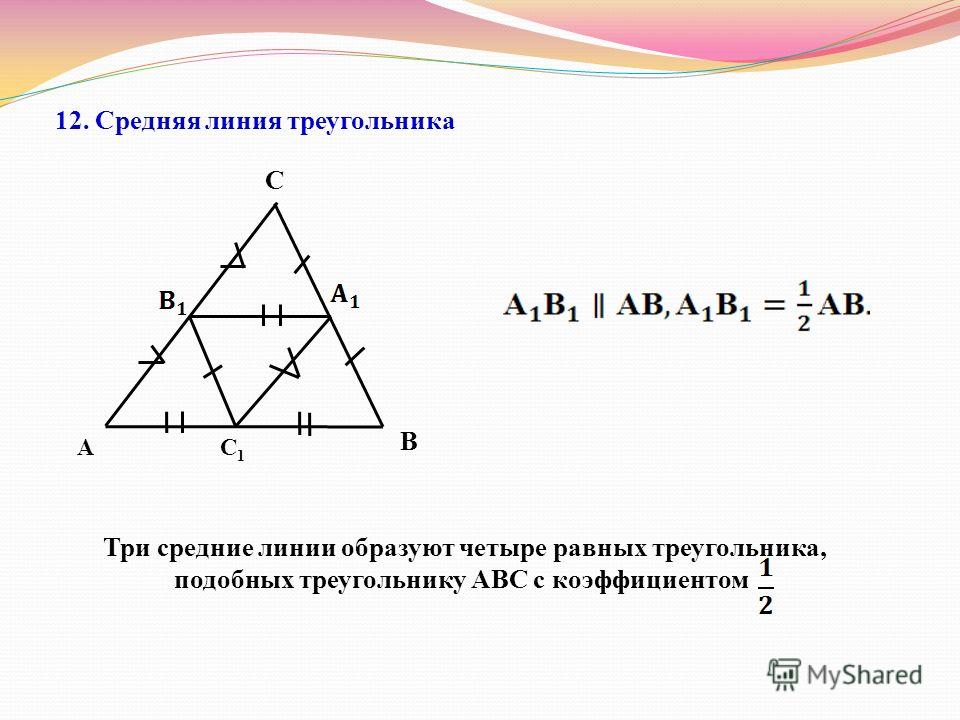 http://www.intergu.ru/infoteka/
http://www.intergu.ru/infoteka/
http://school-collection.edu.ru/
Упражнения для глаз: comp-doctor.ru/eye/eye_upr.php
подобных треугольников Теорема о средней линии треугольника
Теорема о средней линии треугольника . ТМТ. Звучит весело, да?
Хотя TMT и не так скандален, как TMZ, он делится множеством пикантных слухов о длине различных сегментов линий в мире треугольников и во всем мире. В частности, в нем говорится, что если вы соедините середины двух сторон треугольника, то вы получите срединный сегмент , волшебное существо, которое живет прямо в середине треугольника, который он называет своим домом. Средние сегменты составляют половину длины стороны, которой они идут параллельно, они делят две другие стороны пополам и пукают блестками. Нет, подождите, это единороги.
Здесь B — это середина AC , а D — это середина CE . Мы можем быть в этом уверены, потому что нам сказали, что отрезки конгруэнтны по обе стороны от обеих этих точек.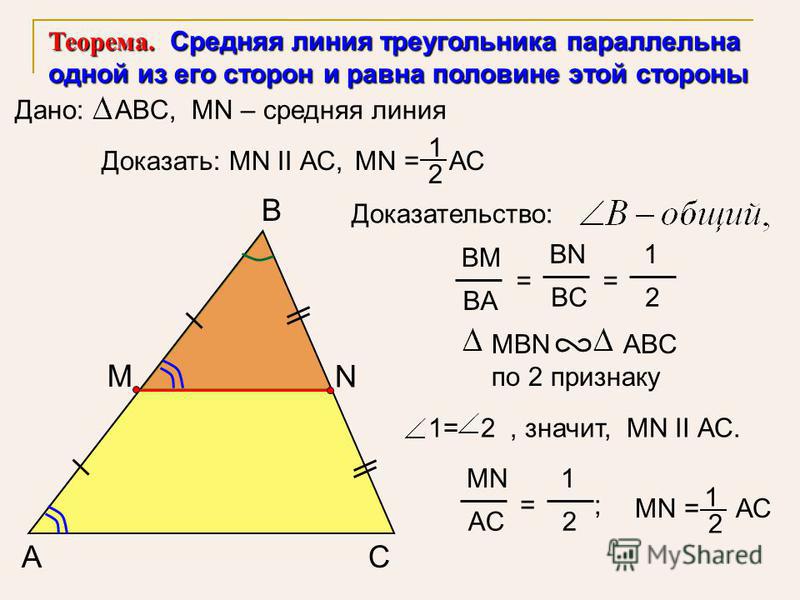 Соединив их, мы получим средний сегмент BD . TMT говорит, что BD || AE и что BD = × AE .
Соединив их, мы получим средний сегмент BD . TMT говорит, что BD || AE и что BD = × AE .
Пример задачи
Если GI = 11, какова длина FJ ?
Итак, мы видим, что GI является средним отрезком, так как FG ≅ GH , JI ≅ IH , и IH |3 | ГИ . Это означает, что FJ дважды равно GI , поэтому FJ = 2 × 11 = 22. секущей, и они образуют конгруэнтные отрезки на одной из этих секущей, то отрезки на другой секущей также конгруэнтны. В Triangle Land (разве это не забавный тематический парк?) это говорит нам о том, что если у нас есть линия, параллельная одной стороне, которая пересекает вторую сторону в ее середине, то она автоматически пересекает и третью сторону в ее середине. .
(Да, мы сказали три параллельные линии. Третья параллельная линия проходит через вершину, противоположную первой стороне. Она невидима, как воображаемый друг вашего младшего брата, Космический рейнджер Бастер.)
Она невидима, как воображаемый друг вашего младшего брата, Космический рейнджер Бастер.)
Итак, если мы посмотрим снова в ∆ FJH , где нам дано, что G является средней точкой FH и FJ || GI , тогда мы можем понять, что I является средней точкой JH . Спасибо, ТМТ.
Пример задачи
∆ VXY имеет срединный сегмент WZ , где W — середина VX . Если VX = 14 и VZ = 4, то какой длины будут VW и VY ?
Поскольку WZ является средним сегментом, мы знаем, что он делит VX и VY пополам, вот так: VW = 7. А потому что VZ = 4, VY = 8.
Но мы можем сделать еще один шаг вперед. Это следствие работает не только для конгруэнтных сегментов, но и для любых пропорциональных сегментов. Да, больше пропорций. Пожалуйста, не ненавидьте нас.
Параллельные прямые, пересекающие трансверсали, создают пропорциональные сегменты на этих трансверсалях.
В ∆ ADE мы можем установить следующие пропорции, чтобы найти недостающие длины: . Разберемся с каждым из них отдельно.
Перемножьте, чтобы получить 4 × GF = 15. Разделите обе части на 4, и мы найдем GF = 3,75.
Снова перекрестное умножение, и мы получаем 4 × AG = 40. Разделим обе части на 4 (ух ты, дежа вю) и на этот раз мы получим AG = 10.
Пример задачи
Найдите решение значения a и b .
Благодаря ТМТ и ее следствиям мы можем установить пропорции, чтобы найти недостающие длины.
7 A = 20
A = 2,857142
4 B = 42
B = 10,5
. . Этот урок даст координатное доказательство теоремы о середине треугольника. Что такое теорема о средней линии треугольника?
Если отрезок соединяет середины сторон треугольника, то этот отрезок параллелен третьей стороне и равен половине длины третьей стороны.
Вот доказательство теоремы о середине треугольника
Доказательство теоремы.
Рассмотрим следующий треугольник в системе координат.
| Дано: S — середина OQ R — середина PQ Докажите: СР || ОП СР = ОП / 2 |
| Дано: S — середина OQ R — середина PQ Докажите: СР || ОП СР = ОП / 2 |
Чтобы доказать, что SR || ОП, мы можем просто показать, что их наклоны равны.
С: ( б + 0 / 2 , | с + 0 / 2 ) | «=» б / 2 , | с / 2 ) |
| С: ( б + 0 / 2 , | с + 0 / 2 ) | «=» б / 2 , | с / 2 ) |
Р: ( а + б / 2 , | с + 0 / 2 ) | «=» а + б / 2 , | с / 2 ) |
Р: ( а + б / 2 | с + 0 / 2 ) | «=» а + б / 2 , | с / 2 ) |
Поскольку координата y одинакова для обеих точек, наклон SR равен нулю.

 М., Илекса, 2003;
М., Илекса, 2003; Признаки подобия треугольников.
Признаки подобия треугольников.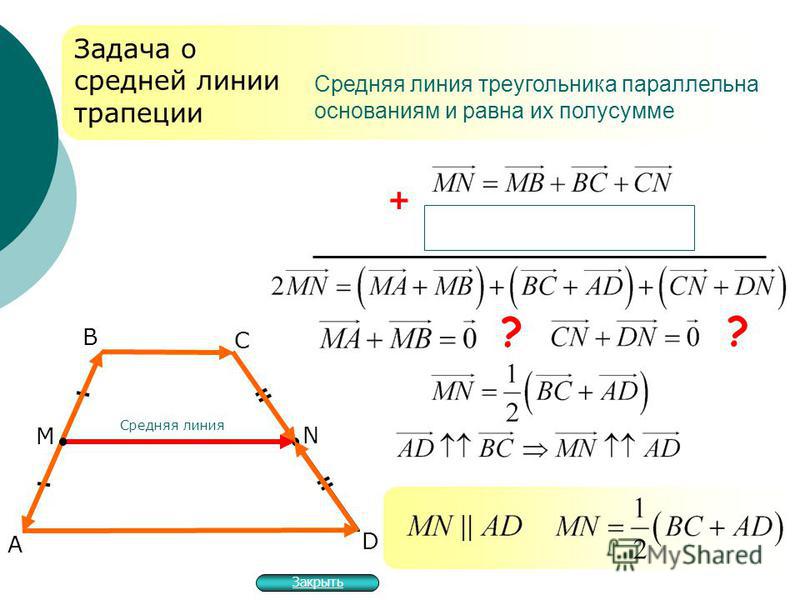 Отрезок MN параллелен третьей стороне и равен его четверти.
Отрезок MN параллелен третьей стороне и равен его четверти.