Урок по теме «Средняя линия треугольника» | Методическая разработка по геометрии (8 класс):
Конспект урока по геометрии
Тема: «Средняя линия треугольника».
Класс: 8 класс.
Урок № 37 (№1).
УМК: Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций/ Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – 2-е изд. – М.: Просвещение, 2014. – 383 с.: ил.
Цель:
образовательная: формирование понятия «средняя линия треугольника».
развивающая: развитие умения анализировать учебный материал, развитиеумения слушать и вступать в диалог.
воспитательная: воспитание самостоятельности, внимательности, целеустремленности.
Частные задачи:
- повторить определение подобных треугольников;
- повторить изученные ранее признаки подобия треугольников;
- ввести понятие «средняя линия треугольника»;
- изучить свойства средней линии треугольника;
- осуществить самоконтроль новых знаний.
Формируемые УУД:
личностные: формирование самооценки на основе успешной деятельности;
регулятивные:планировать своё действие в соответствии с поставленной задачей;умение оценивать правильность выполнения действия на уровне адекватной оценки;
коммуникативные: слушать и понимать речь других, вступать в диалог;
познавательные: ориентироваться в системе знаний; составлять ответы на вопросы.
Тип урока: комбинированный.
Оборудование: раздаточный материал (карточки с заданиями для повторения, карточка для самооценки, карточка с заданиями по новой теме).
План урока:
- Организационный этап (1 мин).
- Актуализация знаний (5 мин).
- Подготовка учащихся к работе на основном этапе урока (2 мин).
- Этап усвоения новых знаний и способов действий (8 мин).
- Этап первичной проверки понимания изученного (20 мин).
- Этап контроля и самоконтроля знаний и способов действий (1 мин).
- Подведение итогов урока (2 мин).
- Этап информации о домашнем задании (1 мин).
Ход урока:
- Организационный этап.
Цель: создать благоприятный психологический настрой на работу.
Форма работы: фронтальная.
Формируемые УУД:
личностные: планирование учебного сотрудничества с учителем и сверстниками;
регулятивные: прогнозирование своей деятельности;
коммуникативные: умение слушать и вступать в диалог;
познавательные: осознанное и произвольное построение речевого высказывания.
Деятельность учителя | Деятельность учащихся |
Приветствие учащихся. Фиксация отсутствующих на уроке. Проверка подготовленности к уроку: наличие учебника, тетради, письменных принадлежностей. | Приветствие учителя. Дежурные называют отсутствующих в классе ребят. Проверяют наличие учебных принадлежностей. |
II. Этап актуализация знаний.
Цель: актуализация опорных знаний и способов действий.
Форма работы: фронтальная.
Формируемые УУД:
личностные: смыслообразование;
регулятивные: выделение и осознание того, что уже пройдено;
коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;
познавательные: поиск и выделение необходимой информации.
Деятельность учителя | Деятельность учащихся |
Прежде чем перейти к изучению новой темы, давайте вспомним, о чем мы говорили на предыдущих уроках? Хорошо. Верно. Сколько существует признаков подобия треугольников? Давайте вспомним каждый из них. Два треугольника являются подобными, если … . по первому признаку подобия: по второму признаку подобия: по третьему признаку подобия: Правильно. Откройте тетради, запишите дату, классная работа. Задача 1: Даны точки М и N — середины сторон АВ и ВС треугольника ABC. Докажите, что MN ||AC. Назовите и запишите, что дано и что нужно найти. Сделайте чертеж к задаче. Для того, чтобы доказать, что стороны MN и AC параллельны, чем мы будем пользоваться? Мы с вами знаем, что все признаки параллельности связаны с углами. Чем мы будем пользоваться для того, чтобы доказать равенство углов? | На предыдущих уроках мы говорили о подобных треугольниках. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. Всего существует три признака подобия треугольников. два угла одного треугольника соответственно равны двух углам другого треугольника. две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны. три стороны одного треугольника пропорциональны трем сторонам другого треугольника. Открыли тетради, записывают дату, классная работа. Внимательно читают условие задачи. Пытаются решить задачу самостоятельно, один человек решает около доски. Дано: ABC – треугольник, точка М — середина стороны АВ, и N — середина стороны ВС. Доказать: MN || AC. Для доказательства параллельности сторон воспользуемся признаками параллельности прямых. Для того, чтобы доказать равенство углов воспользуемся признаками подобия треугольников. Доказательство: 1. – общий; т.к. точки М и N — середины сторон АВ и ВС. Следовательно, треугольник ABC подобен треугольнику BMN, по двум пропорциональным сторонам и углам, заключенным между этими сторонами. 2. BMN=BAC т.к. треугольник ABC подобен треугольнику BMN. 3. MN || AC т.к. BMN и BAC – соответственные при прямых МN и АС и секущей АВ. Ч.т.д. |
III. Подготовка учащихся к работе на основном этапе урока.
Цель: организовать целенаправленную работу учащихся, принятие ими цели урока.
Форма работы: фронтальная, самостоятельная.
Формируемые УУД:
личностные: формирование интереса к новому материалу;
регулятивные: целеполагание;
коммуникативные: постановка вопросов;
познавательные: самостоятельное выделение-формулирование познавательной цели.
Деятельность учителя | Деятельность учащихся |
Посмотрите на рисунок к задаче. Как бы вы назвали отрезок MN? Как вы думаете, чем мы будем заниматься сегодня на уроке? | Внимательно изучают рисунок к уже решенной задаче. Предлагают свои варианты названия отрезка MN. Сегодня на уроке мы познакомимся с «ИМЕНЕМ» отрезка MN и его свойствами. |
IV. Этап усвоения новых знаний и способов действий.
Цель: обеспечение восприятия, осмысления и первичного запоминания детьми изучаемой темы: средняя линия треугольника.
Форма работы: фронтальная, самостоятельная.
Формируемые УУД:
личностные: формирование математической компетентности;
регулятивные: планирование, прогнозирование;
коммуникативные: умение слушать и вступать в диалог;
познавательные: поиск и выделение необходимой информации.
Деятельность учителя | Деятельность учащихся |
И так, мы определили цель сегодняшнего урока. А темой сегодняшнего урока будет «Средняя линия треугольника». Запишите тему сегодняшнего урока. И так, рассматриваемый нами отрезок MN называется средней линией треугольника. Как вы думаете ребята, что же такое средняя линия треугольника? Так вот, средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Как вы думаете, а сколько средних линий можно провести в одном треугольнике? Верно, а теперь нам предстоит выяснить, какими свойствами обладает средняя линия треугольника. Для этого вернемся к рисунку и к ранее разобранной задаче. Каким свойством обладает средняя линия? Верно. Но это не единственное свойство средней линии. Как вы думаете, каким еще свойством обладает средняя линия треугольника? Еще одним свойством является то, что средняя линия равна половине основания. Давайте докажем это. (Доказательство производится с помощью учеников) Пусть дан треугольник ABC, где MN– средняя линия. Заметим, что первую часть теоремы мы с вами уже доказывали в начале урока. Теперь предлагаю доказать второе утверждение. Поиск доказательства теоремы: 1. Что нужно доказать? 2. Что для этого нужно доказать? 3. В какие треугольники входят рассматриваемые отрезки? 4.Что нужно знать, чтобы доказать подобие треугольников? 5. Какие пары равных и (или) пропорциональных элементов можно указать в данных треугольниках? 6. Какой вывод можно сделать по этим данным? 7. Какой вывод можно сделать об отрезках MN и AC? 9. Какой вывод можно сделать из доказанного? Два доказанных нами свойства можно объединить в следующую теорему, доказательство которой будет состоять из 2-х частей: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Доказанные нами свойства мы можем применять при решении различных задач. | Записывают тему урока в тетрадь. Предлагают свои варианты формулировки определения средней линии треугольника. В одном треугольнике можно провести три средние линии. Внимательно изучают уже знакомый рисунок и отвечают на вопросы учителя. Средняя линия треугольника параллельна основанию треугольника. Высказывают свои предположения относительно свойства средней линии треугольника. Записывают краткую запись вместе с рисунком в тетрадь. Дано: ABC – треугольник, MN– средняя линия. Доказать: 1. MN || AC; 2. MN = . 1. Нужно доказать, что MN = . 2. Для этого нужно доказать подобие треугольников, содержащих стороны MN и AC. 3. Рассматриваемые отрезки входят в треугольники BMN и BAC. 4. Нужно знать три пары пропорциональныхсторон, или две пары равных углов, или две пары пропорциональных сторон, и пару равных углов, заключенных между этими сторонами. 5. Для треугольников BMNи BAC: B–общий, – по условию. 6. Треугольники BMNи BAC подобны по двум пропорциональным сторонам и углу, заключенному между этими сторонами. 7. Эти отрезки относятся в отношении , т.к. треугольники BMNи BAC подобны. 9. . Доказательство: 1. B–общий, , то треугольники BMNи BAC подобны по двум пропорциональным сторонам и углам, заключенным между этими сторонами. 2. BMN=BAC, т.к. треугольники BMNи BAC подобны. 3. , т.к. треугольники BMNи BAC подобны. Следовательно, . Ч.т.д. |
V. Этап первичной проверки понимания изученного.
Цель: проверить правильность понимания и осознанности изученного материала.
Форма работы: фронтальная, самостоятельная.
Формируемые УУД:
личностные: формирование математической компетентности;
регулятивные: планирование деятельности для решения поставленной задачи, контроль полученного результата;
коммуникативные: умение слушать и вступать в диалог;
познавательные: структурирование знаний.
Деятельность учителя | Деятельность учащихся |
У каждого на столе лежит карточка с заданиями. Задача 1: Укажите номера чертежей, на которых указана средняя линия треугольника: Задача 2: Чему равна средняя линия треугольника, параллельная стороне a? 1 клетка = 1 см. Чем отличаются эти задания друг от друга? В чем сложность их выполнения? Откройте учебник на странице 152, выполним следующие упражнения письменно. № 564 Дан треугольник, стороны которого равны 8 см, 5 см и 7 см. Найдите периметр треугольника, вершинами которого являются середины сторон данного треугольника. Назовите и запишите, что дано и что нужно найти. Сделайте чертеж к задаче. Чем мы будем пользоваться для решения данной задачи? Верно. Чему у нас получится равна сторона DE? Чему равна сторона DF? Чему равна сторона EF? Как найти периметр треугольника? Чему равен периметр треугольника? Что запишем в ответ? № 567 Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма. Назовите и запишите, что дано и что нужно найти. Сделайте чертеж к задаче. Чем мы будем пользоваться для решения данной задачи? Для того, чтобы доказать, что четырехугольник является параллелограммом, чем мы будем пользоваться? Чем отличаются друг от друга и что общего у двух последних задач? В чем состоит трудность решения данных задач? | Решают задания с карточки самостоятельно в тетрадях, после проверяем устно, обсуждая способ решения. Задача 1: Средняя линия треугольника указана на чертежах 1 и 3. Задача 2: Средняя линия треугольника, параллельная стороне aравна (см) Для определения длины средней линии треугольника используется теорема (свойства средней линии). Говорят о возникших трудностях при решении задач, если они были. Открывают учебник на указанной странице и приступают к выполнению первого задания самостоятельно. Один ученик решает около доски. Дано:ABC, DEF– треугольники; AB = 5 см, BC = 8 см, AC = 7 см, AD = BD, AE = EC, BF = FC. Найти: . Для решения данной задачи воспользуемся свойствами средней линии треугольника. Решение: 1. DE – средняя линия треугольника ABC, т.к. D – середина AB, E–середина AC; Следовательно, DE = BC. DE = = 4 см. 2. DF – средняя линия треугольника ABC, т.к. D – середина AB, F–середина BC; Следовательно, DF = AC. DF = = 3,5 см. 3. EF – средняя линия треугольника ABC, т.к. E–середина AC, F–середина BC; Следовательно, EF = AB. EF = = 2,5 см. 4. = DE + DF + EF; = 4 + 3,5 + 2,5 = 10 (см). Ответ: 10 см. Дано:GHIJ–произвольный четырехугольник; MG = MJ, KG = KH, LH = LI, IN = NJ. Доказать: MKLN– параллелограмм. Для решения данной задачи воспользуемся свойствами средней линии треугольника. Для того, чтобы доказать, что четырехугольник является параллелограммом, воспользуемся признаком: Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны. Доказательство: 1. Рассмотрим треугольник JGH: MK – средняя линия, т.к. M–середина GJ, K–середина GH. Следовательно, MK || JH; и MK = JH. 2. Рассмотрим треугольник JIH: NL – средняя линия, т.к. L–середина HI, N–середина JI. Следовательно, NL || JH; и NL=JH. 3. MK || NL, т.к. MK || JH, и NL || JH. 4. MK = NL т.к. MK = JH и NL=JH. 5. MKLN– параллелограмм, т.к. MK = NL и MK || NL. (по признаку параллелограмма) Ч.т.д. Отвечают на поставленные учителем вопросы. |
VI. Этап контроля и самоконтроля знаний и способов действий.
Цель: осуществление самоконтроля и самооценки действий.
Форма работы: индивидуальная.
Формируемые УУД:
личностные: формирование правильной самооценки; умение признавать свои ошибки;
регулятивные: контроль, коррекция.
коммуникативные: поддержание здорового духа соперничества для поддержания мотивации учебной деятельности.
Деятельность учителя | Деятельность учащихся |
У каждого на столе лежит лист для самооценки, называется «Дерево успехов» Выберите изображение «яблоко» — если на уроке нам удалось выполнить все задания правильно; «цветочек» — если неплохо поработал на уроке, но что-то не совсем получилось; «листок» — если сегодня многое не получилось, но вы не отчаиваетесь. | Оценивают свою деятельность на уроке: |
VII. Подведение итогов урока.
Цель: обобщение изученного на уроке материала.
Форма работы: фронтальная.
Формируемые УУД:
личностные: саморегуляция достижений;
регулятивные: оценивание собственной деятельности;
коммуникативные: умение вести диалог;
познавательные: систематизирование и обобщение.
Деятельность учителя | Деятельность учащихся |
Чем мы занимались сегодня на уроке? Какой отрезок называют средней линией треугольника? Какими свойствами обладает средняя линия треугольника? Средняя линия треугольника встречается только в задачах, где речь идет о треугольниках? Встречались ли мы сегодня с такими задачами? Какой отсюда можно сделать вывод? Выставление оценок за урок. | Сегодня на уроке мы рассматривали понятие «средняя линия треугольника», а также познакомились с ее свойствами. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Средняя линия встречается не только в таких задачах. Да, встречались. Тогда речь в задаче шла о четырехугольниках. Применение свойств средней линии треугольника возможно для решения любых задач, где можно найти треугольники. |
VIII. Этап информации о домашнем задании.
Цель: повторение, закрепление изученного материала.
Форма работы: фронтальная.
Формируемые УУД:
личностные: воспитание волевых качеств;
регулятивные: умение учитывать ориентиры данные учителем;
коммуникативные: умение вести диалог.
Деятельность учителя | Деятельность учащихся |
А теперь откройте дневники и запишите домашнее задание: с. № 565, 566. | Открывают дневники и записывают задание на следующий урок. |
Тест Средняя линия треугольника 8 класс с ответами
Тесты по геометрии 8 класс. Тема: «Средняя линия треугольника»
Правильный вариант ответа отмечен знаком +
1. Средняя линия треугольника – это отрезок, который:
— соединяет середины трех сторон треугольника.
— соединяет две стороны треугольника.
— соединяет два треугольника.
+ соединяет середины двух сторон треугольника.
2. Выберите вариант ответа, который характеризует свойства треугольника:
— Стороны треугольника соединяются тремя точками, находящимися на одной прямой.
+ Треугольники могут быть разносторонними.
— Отрезки, соединяющиеся тремя точками, именуют вершинами.
— В равнобедренном треугольнике два основания и одна боковая сторона.
3. В каком варианте не указан вид треугольника?
В каком варианте не указан вид треугольника?
+ трехугольный
— тупоугольный
— остроугольный
— прямоугольный
4. Дан треугольник KLN, где основание NK равно 17 см. HJ – средняя линия данного треугольника. Найдите его длину:
— 34 см
— 8 см
+ 8,5 см
— 25,5 см
5. Дан треугольник MNK, вершины которого лежат на середине сторон треугольника ABC. АВ = 8 см, ВС = 7 см, СА = 5 см. Чему равен периметр треугольника MNK?
+ 10 см
— 100 см
— 30 см
— 9 см
6. Если периметр равностороннего треугольника равен 42 см, то чему равна средняя линия данного треугольника?
— 14 см
— 28 см
+ 70 мм
— 84 см
7. «Средняя линия равностороннего треугольника …». В каком варианте представлено продолжение данного суждения?
+ параллельна одной ее стороне.
— находится на одной ее стороне.
— пересекает одну ее сторону.
— перпендикулярна одной ее стороне.
8. Дан треугольник KLN, где основание NK равно 36 см. MF – средняя линия данного треугольника. Найдите его длину:
— 9 см
+ 18 см
— 8 см
— 4 см
9. Площадь треугольника RTY равна 100 см2. Чему равна площадь треугольника NMK, вершины которого лежат на середине сторон треугольника RTY?
— 50 см2
— 75 см2
+ 25 см2
— 33,3 см2
тест 10. Посмотрите на рисунок и выберите вариант ответа, в котором указано ошибочное определение:
+ AK=BM
— AK=KB
— BM=MC
— AC > BM
11. Какая фигура образуется при соединении всех трех средних линий остроугольного треугольника?
— четырехугольник
+ треугольник
— прямоугольник
— трапеция
12. Как именуются треугольники, у которых две стороны равны между собой?
+ равнобедренными
— равносторонними
— разнобедренными
— разносторонними
13. Дан треугольник ADH. GF – средняя линия данного треугольника равна 15,5 см. Чему равно основание HA треугольника ADH?
Дан треугольник ADH. GF – средняя линия данного треугольника равна 15,5 см. Чему равно основание HA треугольника ADH?
— 45,5 см
— 7,75 см
— 28 см
+ 31 см
14. Треугольники бывают:
— многоугольными
— косоугольными
+ тупоугольными
— все варианты верны
15. У равностороннего треугольника периметр равен 6240 мм. Значит, любая средняя линия данного треугольника равна:
+ 104 см
— 2080 мм
— 10,4 см
— 3120 мм
16. «… – это отрезок, благодаря чему соединяются смежные стороны». Какое слово здесь пропущено?
— Медиана
+ Средняя линия
— Перпендикуляр
— Биссектриса
17. Чему равна средняя линия треугольника?
+ половине основания треугольника
— половине суммы трех сторон треугольника
— половине суммы двух боковых сторон треугольника
— четверти гипотенузы
18. Какой вид треугольника имеет два катета и одну гипотенузу?
— равнобедренный
— правильный
+ прямоугольный
— равносторонний
19. Посмотрите на рисунок и выберите вариант ответа, в котором указано правильное определение:
Посмотрите на рисунок и выберите вариант ответа, в котором указано правильное определение:
— ΔAMK больше ΔMBH
— ΔABC = ΔAMK + ΔMBH + ΔKHC
— ΔABC = 3 ΔMKH
+ ΔAMK = ΔMKH
тест-20. Выберите вариант ответа, в котором не допущена ошибка?
+ Параллельная к гипотенузе средняя линия прямоугольного треугольника равна его медиане.
— Две средние линии прямоугольного треугольника параллельны его двум катетам.
— В прямоугольном треугольнике можно провести только одну среднюю линию.
— В прямоугольном треугольнике можно провести лишь две средних линии.
21. Дан прямоугольный треугольник NMK. GF – средняя линия, пересекающая катеты данного треугольника, равна 90 мм. Чему равна гипотенуза треугольника NMK?
— 180 см
— 45 см
— 135 мм
+ 18 см
22. Дан треугольник ABC. Сторона AB равна 7 см, сторона BC – 5 см, сторона AC – 10 см. Чему равен периметр треугольника, вершины которого лежат на сторонах треугольника ABC?
— 22 см
— 43,75 см
+ 11 см
— 350 мм
23. «В … треугольнике можно провести три средних линии». В каком варианте представлено наиболее подходящее слово вместо пропуска?
«В … треугольнике можно провести три средних линии». В каком варианте представлено наиболее подходящее слово вместо пропуска?
+ каждом
— равнобедренном
— остроугольном
— тупоугольном
24. У равностороннего треугольника периметр равен 81 мм. Значит, любая средняя линия данного треугольника равна:
— 135 мм
— 27 мм
+ 13,5 мм
— 9 см
25. Если периметр равностороннего треугольника равен 99 см, то чему равна средняя линия данного треугольника?
— 33 см
+ 16,5 см
— 66 см
— 165 см
26. Дан треугольник ABC. Сторона AB равна 46 мм, сторона BC – 89 мм, сторона AC – 97 мм. Чему равен периметр треугольника, вершины которого лежат на сторонах треугольника ABC?
— 1160 мм
— 40 см
— 232 мм
+ 11,6 см
27. «Параллельная средней линии сторона треугольника называется …». Продолжите данное предложение:
— боковой стороной
+ основанием
— катетом
— смежной стороной
28. Диагональ прямоугольника равна 18 см. Чему равна площадь четырехугольной фигуры, вершины которой находятся на середине сторон прямоугольника?
Диагональ прямоугольника равна 18 см. Чему равна площадь четырехугольной фигуры, вершины которой находятся на середине сторон прямоугольника?
— 72 см2
— 36 см2
— 324 см2
+ 81 см2
29. Дан квадрат, диагональ которого равна 36 см. Чему равны параллельные диагонали средние линии образовавших двух треугольников?
— 72 см и 36 см
+ 18 см и 18 см
— 18 см и 9 см
— 36 см и 18 см
тест_30. На сколько и на какие треугольники делят средние линии прямоугольного треугольника?
— на три прямоугольных треугольника
— на четыре равносторонних треугольника
— на три равнобедренных треугольника
+ на четыре прямоугольных треугольника
Формула средней линии равностороннего треугольника. Прямоугольный треугольник
Как найти середину треугольника: геометрическая задачка. Основные элементарные задачи евклидовой геометрии пришли к нам из древности. В них заключена сама первичная сущность и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является задача нахождения середины треугольника. Сегодня это задание рассматривается как образовательный метод развития интеллектуальных способностей школьников. В античном мире знания о том, как найти середину треугольника, применялись и на практике: в землеустройстве, при изготовлении различных механизмов и т. д. В чем суть этой геометрической головоломки?
В них заключена сама первичная сущность и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является задача нахождения середины треугольника. Сегодня это задание рассматривается как образовательный метод развития интеллектуальных способностей школьников. В античном мире знания о том, как найти середину треугольника, применялись и на практике: в землеустройстве, при изготовлении различных механизмов и т. д. В чем суть этой геометрической головоломки?
Что такое медиана? Перед решением задачи необходимо ознакомиться с простейшей геометрической терминологией, касающейся треугольников. Во-первых, каждый треугольник имеет три вершины, три стороны и три угла, от чего и произошло название этой геометрической фигуры. Важно знать, как называются линии, соединяющие вершины с противоположными сторонами: высота, биссектриса и медиана.
Высота — линия, перпендикулярная стороне, противоположной вершине, из которой она проведена; биссектриса – угол пополам; медиана делит сторону, противоположную исходящей вершине, пополам.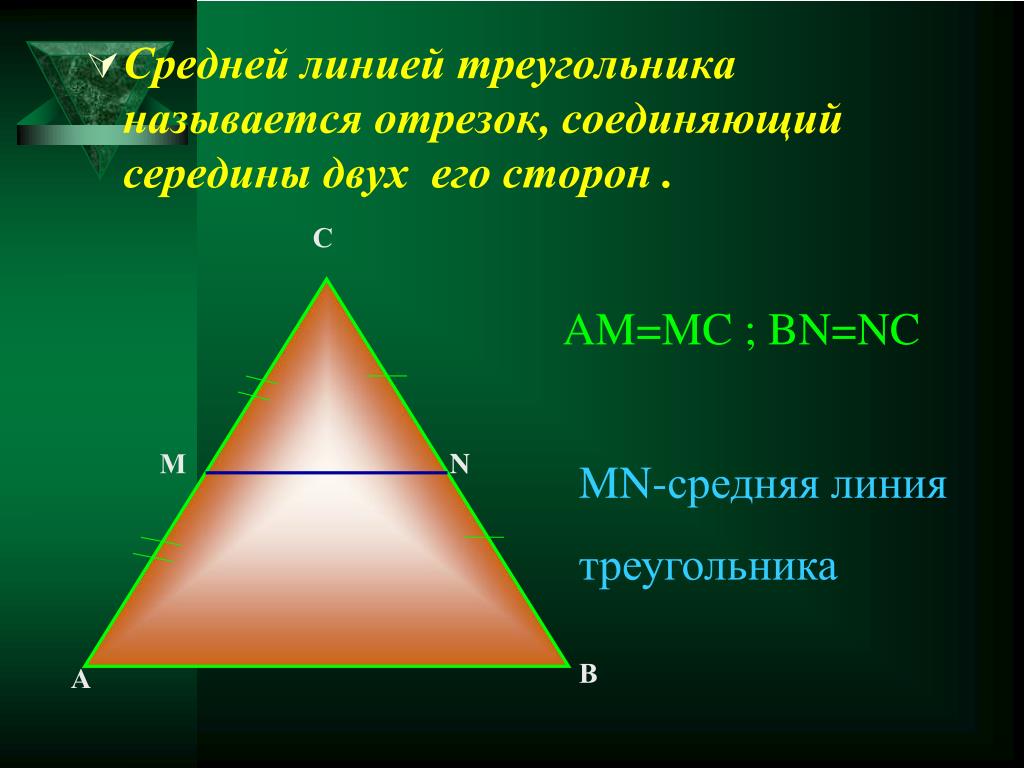 Для решения этой задачи необходимо знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника является его серединой.
Для решения этой задачи необходимо знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника является его серединой.
Найдите середины сторон треугольника. Нахождение середины отрезка также является классической геометрической задачей, для решения которой требуются циркуль и линейка без делений. Ставим стрелку циркуля в конечную точку отрезка и в середине последнего чертим полуокружность больше половины отрезка. Сделайте то же самое с другой стороны линии. Полученные полуокружности обязательно пересекутся в двух точках, потому что их радиусы больше половины исходного отрезка.
Соединяем две точки пересечения окружности прямой с помощью линейки. Эта линия пересекает исходную линию ровно посередине. Теперь, зная, как найти середину отрезка, проделываем это с каждой стороной треугольника. После нахождения всех середин сторон треугольника все готово для построения собственной середины.
Строим середину треугольника. Соединив прямыми линиями вершины треугольника с серединами противоположных сторон, мы получим три медианы.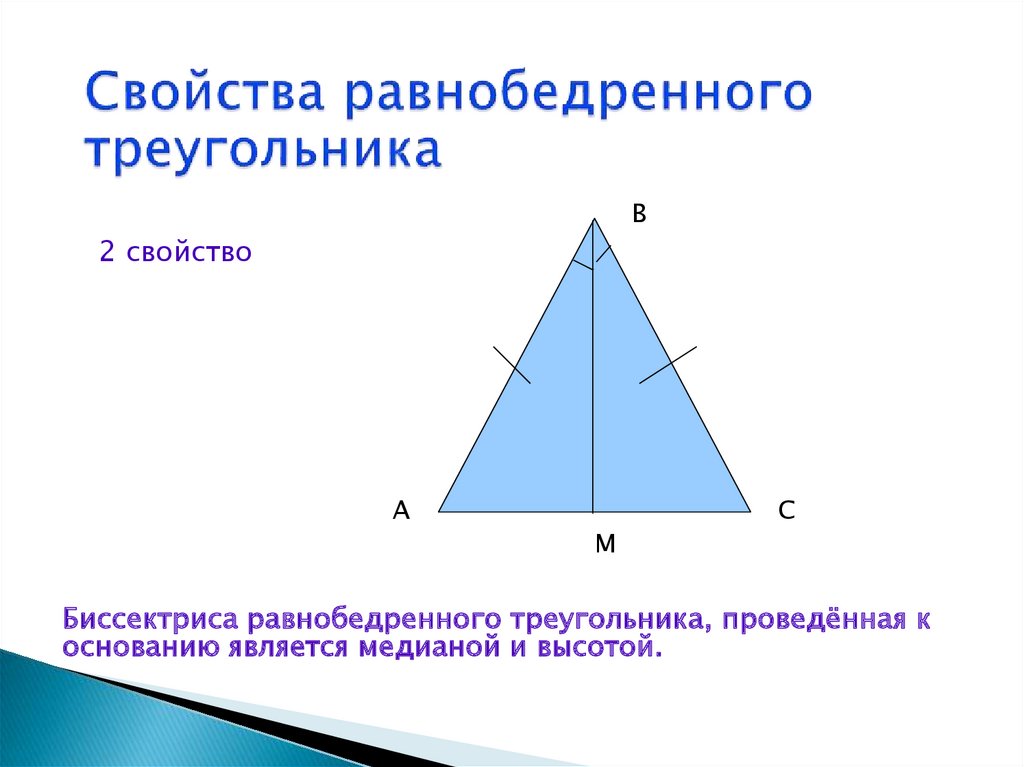 Это может кого-то удивить, но один из законов гармонии этой геометрической фигуры заключается в том, что все три медианы всегда пересекаются в одной точке. Именно эта точка и будет искомой серединой треугольника, найти которую не так уж и сложно, если знать, как построить середину отрезка.
Это может кого-то удивить, но один из законов гармонии этой геометрической фигуры заключается в том, что все три медианы всегда пересекаются в одной точке. Именно эта точка и будет искомой серединой треугольника, найти которую не так уж и сложно, если знать, как построить середину отрезка.
Интересно также, что точка пересечения медиан является не только геометрической, но и «физической» серединой треугольника. То есть, если, например, вырезать из фанеры треугольник, найти его середину и поместить эту точку на острие иглы, то в идеале такая фигура будет балансировать и не упадет. Элементарная геометрия таит в себе множество таких захватывающих «тайн», знание которых помогает постичь гармонию окружающего мира и природу более сложных вещей.
Четырехугольник, у которого параллельны только две стороны, называется трапецией .
Параллельные стороны трапеции называются ее основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если стороны равны, то такая трапеция равнобедренная. Расстояние между основаниями называется высотой трапеции.
Если стороны равны, то такая трапеция равнобедренная. Расстояние между основаниями называется высотой трапеции.
Средняя линия трапеции
Средняя линия — это отрезок, соединяющий середины сторон трапеции. Средняя линия трапеции параллельна ее основаниям.
Теорема:
Если прямая, проходящая через середину одной стороны, параллельна основаниям трапеции, то она делит вторую сторону трапеции пополам.
Теорема:
Длина средней линии равна среднему арифметическому длин ее оснований
МН || АБ || DC
AM = MD; БН = НЗ
MN средняя линия, AB и CD — основания, AD и BC — стороны
MN = (AB + DC) / 2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин ее оснований.
Основная задача : Докажите, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине основания трапеции.
Центральная линия треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и составляет половину длины третьей стороны.
Она параллельна третьей стороне и составляет половину длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне этого треугольника, то она делит третью сторону пополам.
AM = MC и BN = NC =>
Применение свойств средней линии треугольника и трапеции
Деление сегмента на определенное количество равных частей.
Задание: Разделите отрезок АВ на 5 равных частей.
Решение:
Пусть p — случайный луч с началом в точке A, не лежащий на прямой AB. Откладываем последовательно 5 равных отрезков на р АА 1 = А 1 А 2 = А 2 А 3 = А 3 А 4 = А 4 А 5
Тогда как из трапеции B 3 B 1 A 1 A 3, B 3 B 2 = B 2 B 1.
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключение получаем :
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Понятно, что для того, чтобы разделить отрезок AB на другое количество равных частей, нужно спроецировать такое же количество равных отрезков на луч р. А затем продолжить, как описано выше.
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Соответственно, каждый треугольник имеет три средние линии. Зная качество средней линии, а также длины сторон треугольника и его углов, можно определить длину средней линии.
Вам понадобится
- Стороны треугольника, углы треугольника
Инструкции
1. Пусть в треугольнике ABC MN — средняя линия, соединяющая середины сторон AB (точка M) и AC (точка N). По свойству средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине. Это означает, что средняя линия MN будет параллельна стороне ВС и равна ВС/2. Поэтому для определения длины центральной линии треугольника достаточно знать длину стороны именно этой третьей стороны . 92/4) = 0.
Поэтому для определения длины центральной линии треугольника достаточно знать длину стороны именно этой третьей стороны . 92/4) = 0.
Квадратный треугольник правильнее называть прямоугольным треугольником. Соотношение между сторонами и углами этой геометрической фигуры подробно рассматривается в математической дисциплине тригонометрии.
Вам понадобится
- — бумага;
- — ручка;
- — Столы Брадиса;
- — калькулятор.
Инструкции
1. Откройте для себя сбоку прямоугольный треугольник с опорой на теорему Пифагора. Согласно этой теореме квадрат гипотенузы равен сумме квадратов катетов: с2 = а2 + b2, где с — гипотенуза треугольника , а и b — его катеты. Чтобы применить это уравнение, вам нужно знать длину любых двух сторон прямоугольного треугольника .
2. Если размеры катетов заданы по условиям, найти длину гипотенузы. Для этого с помощью калькулятора извлеките квадратный корень из суммы катетов, каждый из которых заранее возведен в квадрат.
3. Вычислите длину одного из катетов, если известны размеры гипотенузы и другого катета. Используя калькулятор, извлеките квадратный корень из разницы между квадратом гипотенузы и известным катетом, также возведенным в квадрат.
4. Если задача содержит гипотенузу и один из соседних острых углов, используйте таблицы Брадиса. Они показывают значения тригонометрических функций для большого количества углов. Используйте калькулятор с функциями синуса и косинуса и тригонометрическими теоремами, описывающими взаимосвязь между сторонами и углами прямоугольника треугольник .
5. Найдите катеты, используя основные тригонометрические функции: a = c * sin?, B = c * cos?, где a — катет, противоположный углу ?, b — катет, примыкающий к углу ?. Таким же образом рассчитайте размеры сторон. треугольник , если даны гипотенуза и другой острый угол: b = c * sin?, a = c * cos?, где b — катет, противолежащий углу?, а катет — прилежащий к углу ?.
6. В том случае, когда мы переносим катет а и примыкающий к нему острый угол, не забываем, что в прямоугольном треугольнике сумма острых углов неизменно равна 90°: +? = 90°. Найдите величину угла, противолежащего катету а:? = 90°-?. Или воспользуйтесь формулами тригонометрического приведения: sin? = sin(90°-?) = cos?; тг? = tg(90°-?) = ctg? = 1/тг?.
7. Если имеем катет a и противолежащий ему острый угол, с помощью таблиц Брадиса, калькулятора и тригонометрических функций вычислить гипотенузу по формуле: c = a * sin?, Катет: b = a * tg?.
Видео по теме
Иногда темы, которые объясняются в школе, не всегда могут быть понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эту науку начинают делить на две части: алгебру и геометрию.
У каждого ученика могут быть способности в одном из двух направлений, но особенно в начальных классах важно понимать основы как алгебры, так и геометрии. В геометрии одной из основных тем считается раздел о треугольниках.
В геометрии одной из основных тем считается раздел о треугольниках.
Как найти среднюю линию треугольника? Давайте разберемся.
Основные понятия
Для начала, чтобы разобраться, как найти среднюю линию треугольника, важно понять, что это такое.
Для проведения средней линии ограничений нет: треугольник может быть любым (равнобедренный, равносторонний, прямоугольный). И все свойства, которые относятся к средней линии, будут работать.
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Следовательно, в любом треугольнике может быть 3 таких прямых.
Свойства
Чтобы уметь находить среднюю линию треугольника, обозначим его свойства, которые необходимо запомнить, иначе без них невозможно будет решить задачи с необходимостью обозначения длины середины линии, так как все полученные данные должны быть обоснованы и аргументированы теоремами, аксиомами или свойствами.
Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника ABC?», достаточно знать одну из сторон треугольника.

 А какие треугольники называются подобными?
А какие треугольники называются подобными?
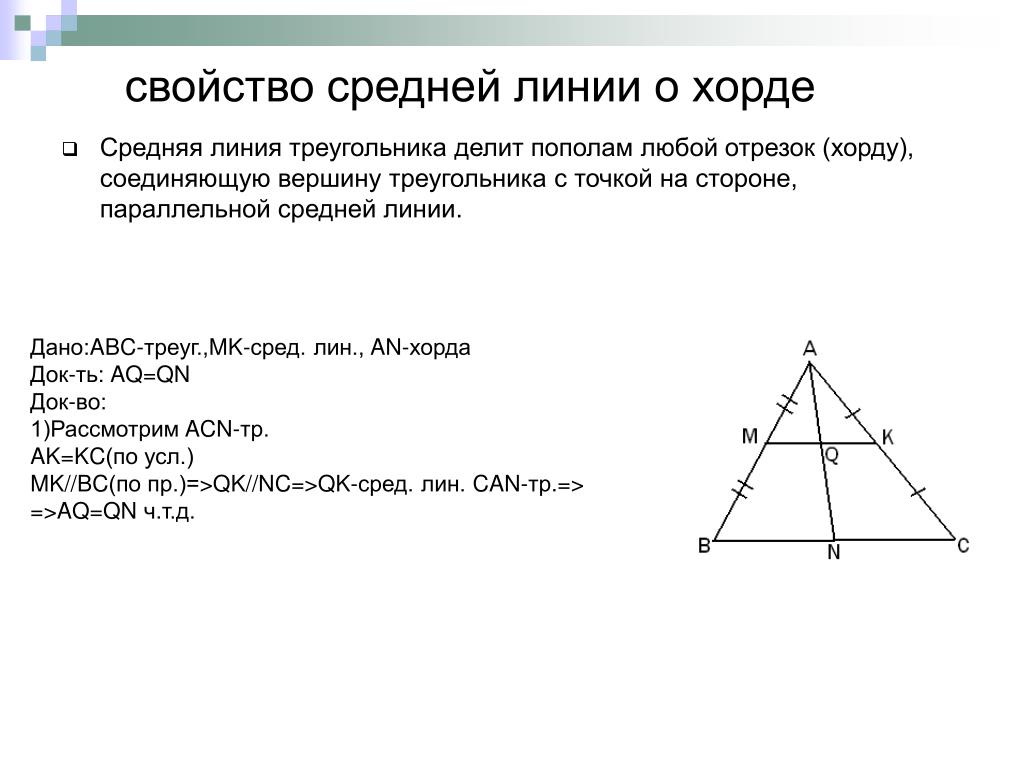
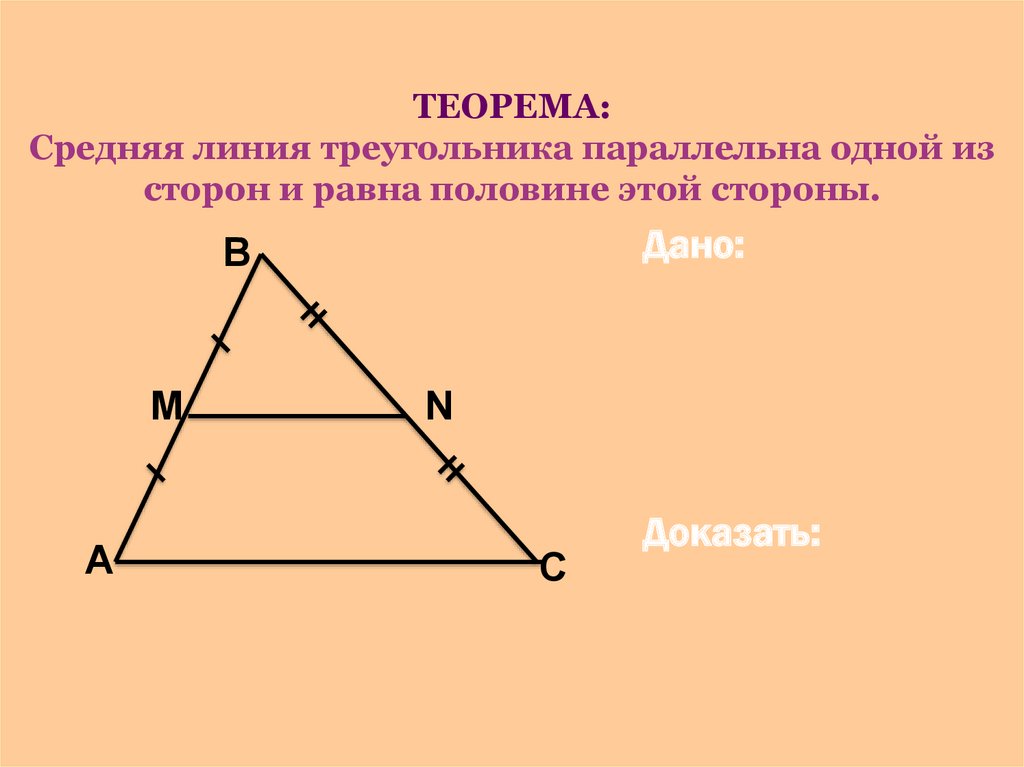 В данной задаче мы с вами рассматривали отрезок MN, который имеет свое собственное «ИМЯ» и обладает определенными свойствами.
В данной задаче мы с вами рассматривали отрезок MN, который имеет свое собственное «ИМЯ» и обладает определенными свойствами.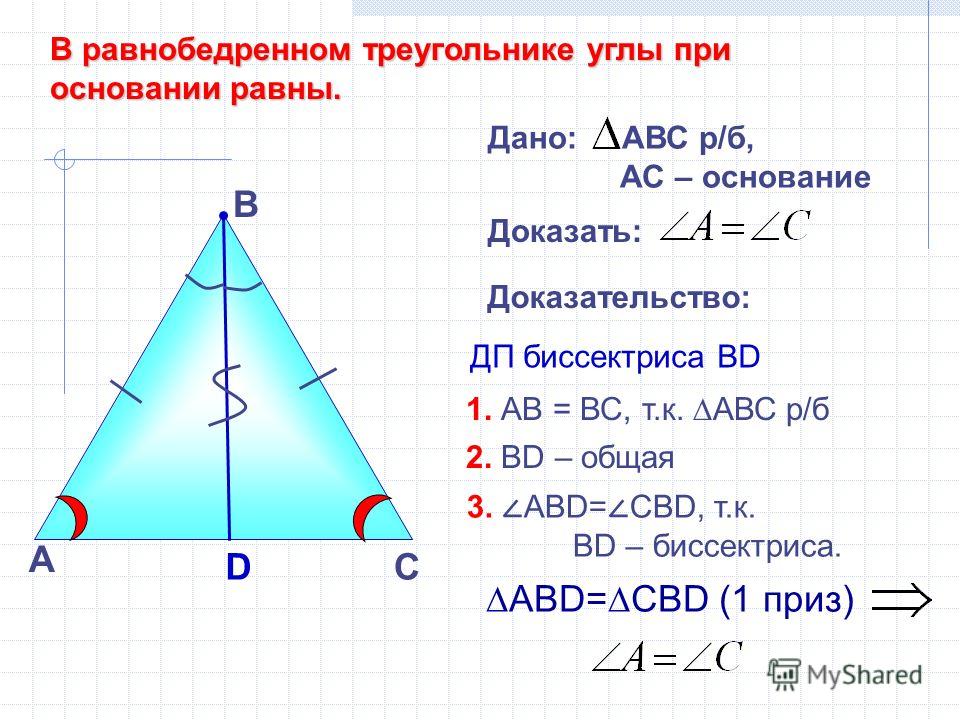
 Докажем, что MN || ACи MN = .
Докажем, что MN || ACи MN = .

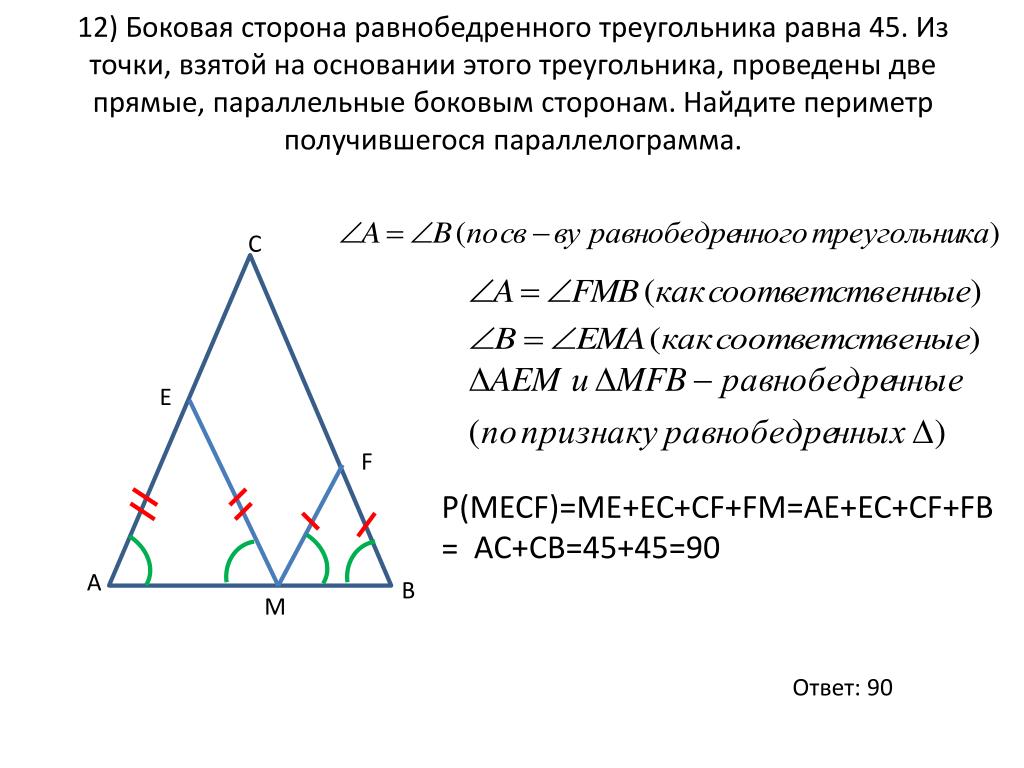

 159, вопросы 8,9.
159, вопросы 8,9.