Средняя линия треугольника
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-11-09
Средняя линия треугольника. Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была на блоге статья, в которой сии факты я предлагал просто запомнить, теперь подробнее…
Что такое средняя линия треугольника и каковы её свойства?
Определение. Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.
Понятно, что средних линий в треугольнике три. Покажем их:
Без всяких доказательств вы уже, наверное, заметили, что все четыре образованные треугольника равны. Это так, но подробнее об этом поговорим далее.
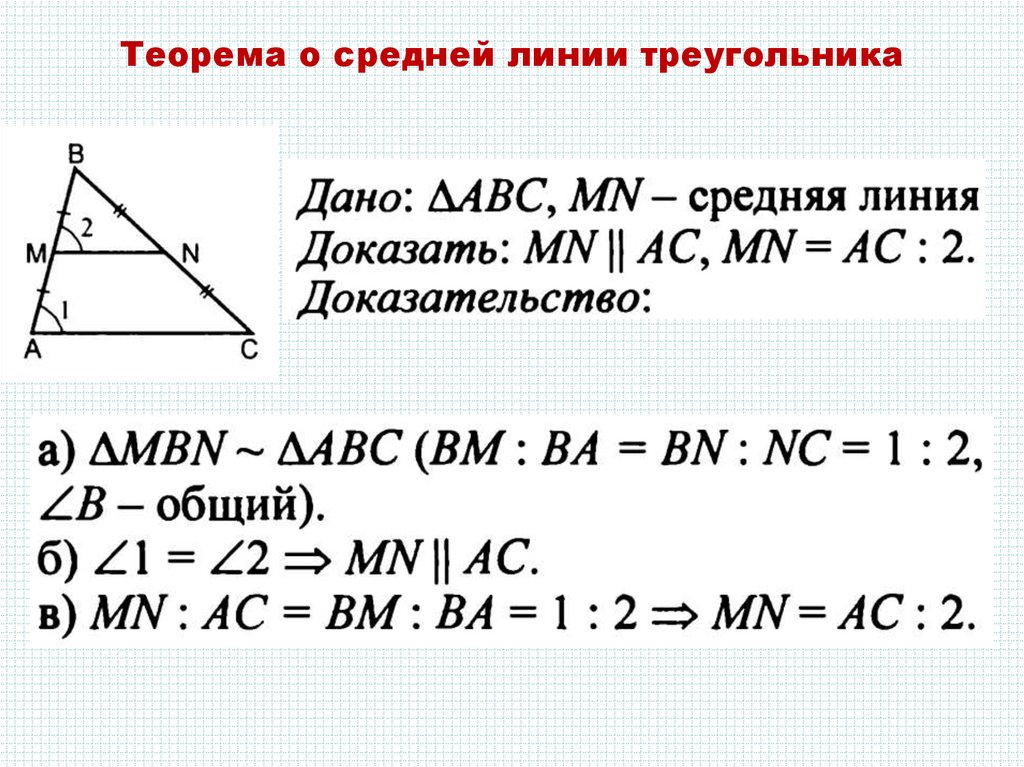
Средняя линия треугольника.
Теорема
Теорема. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Доказательство:
1. Давайте рассмотрим треугольники BMN и BAC. По условию у нас BM=MA, BN=NC. Можем записать:
Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А то что:
По признаку параллельности прямых MN||AC.
2. Также из подобия треугольников следует, что
То есть MN в два раза меньше. Доказано!
Средняя линия треугольника. Задача
Решим типичную задачу.
Задача. В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.
Решение. Конечно, прежде всего следует проверить существование треугольника MNK (а значит и существование треугольника АВС).
Сумма двух меньших сторон должна быть более третьей стороны, записываем 10+8>12. Выполнятся, следовательно треугольник существует.
Построим эскиз:
Таким образом периметр треугольника АВС равен 24+20+16=60.
Ответ: 60
*Теперь подробнее о треугольниках полученных при построении всех трёх средних линий. Их равенство легко доказывается. Посмотрите:
Равны они по трём сторонам. Конечно, и другие признаки здесь применимы. Получаем, что
Как это свойство используется в заданиях включённых в состав экзамена? Особо хочется заострить внимание на задачах по стереометрии. Есть такие типы, в которых речь идет о треугольной призме.
Например, сказано что плоскость проходит через середины сторон основания и она параллельна третьему ребру основания. Ставятся вопросы о изменении площади поверхности призмы, её объёма и другие.
Так вот. Зная и понимая информацию изложенную выше вы сразу же определите, что эта плоскость отсекает от основания указанной призмы одну четвёртую часть и задачу решите устно.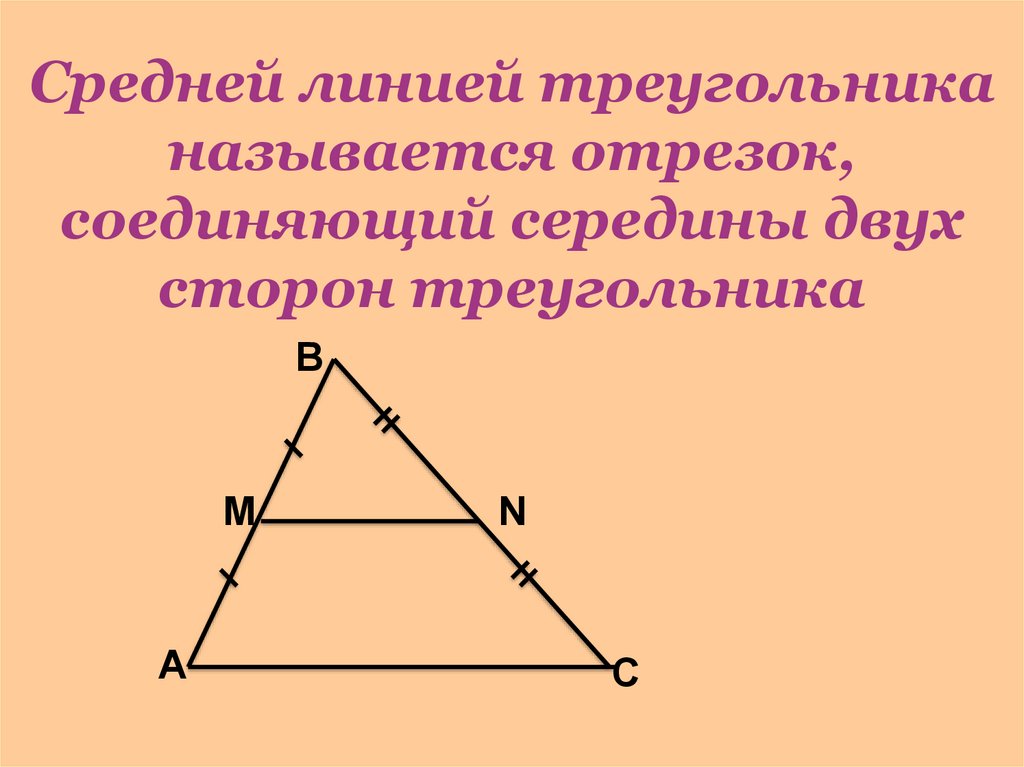
Вот статья на блоге с такими задачами.
На этом всё! Всего доброго!
Скачать материал статьи
С уважением, Александр Крутицких.
Делитесь информацией сайта в социальных сетях!
Категория: Формулы Теория | ТреугольникФормулы
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Средняя линия треугольника
Понятие средней линии треугольника
Введем понятие средней линии треугольника.
Определение 1
Средняя линия треугольника — это отрезок, соединяющий середины двух сторон треугольника (Рис. 1).
Рисунок 1. Средняя линия треугольника
Теорема о средней линии треугольника
Теорема 1
Средняя линия треугольника параллельна одной из его сторон и равна её половине.
Доказательство.
Пусть нам дан треугольник $ABC$. $MN$ — средняя линия (как на рисунке 2).
Рисунок 2. Иллюстрация теоремы 1
Так как $\frac{AM}{AB}=\frac{BN}{BC}=\frac{1}{2}$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит
Также, отсюда следует, что $\angle A=\angle BMN$, значит $MN||AC$.
Теорема доказана.
Следствия из теоремы о средней линии треугольника
Следствие 1: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.
Доказательство.
Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 3).
Рисунок 3. Иллюстрация следствия 1
По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $\angle ABB_1=\angle BB_1A_1,\ \angle BAA_1=\angle AA_1B_1$.
Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда
Аналогично доказывается, что
Теорема доказана.
Следствие 2: Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=\frac{1}{2}$.
Доказательство.
Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ (рис. 4)
Рисунок 4. Иллюстрация следствия 2
Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то
Угол $C$ — общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму признаку подобия треугольников с коэффициентом подобия $k=\frac{1}{2}$.
Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, и треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.
Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ — средние линии треугольника, то
Следовательно, по третьему признаку подобия треугольников, треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.
Теорема доказана.
Примеры задачи на понятие средней линии треугольника
Пример 1
Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найти периметр треугольника, вершины которого лежат в серединах сторон данного треугольника.
Решение.
Так как вершины искомого треугольника лежат в серединах сторон данного треугольника, то его стороны — средние линии исходного треугольника. По следствию 2, получим, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.
\[P=8см+5см+7см=20\ см\]
Ответ: $20$ см.
Пример 2
Дан треугольник $ABC$. Точки $N\ и\ M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).
Рисунок 5.
Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.
Решение.
Так как $N\ и\ M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит
\[AB=2MB,\ BC=2BN\]
По теореме 1, $AC=2MN$.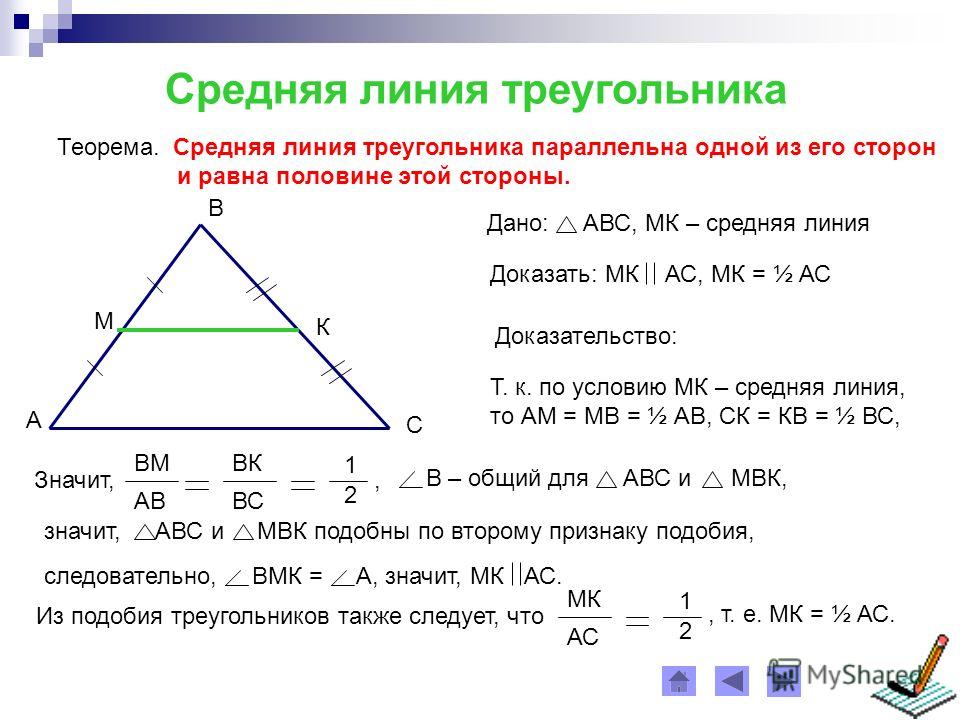
\[P_{ABC}=AB+BC+AC=2MB+2BN+2MN=2P_{BMN}=28\ см\]
Ответ: $28$ см.
Теорема средней линии треугольника| Блог Twisted One 151
Monday Math 156
28 июля 2014 г.
Для трапеции медиана (также известная как средняя линия или средний сегмент) — это отрезок, соединяющий середины сторон трапеции. В этом посте представлено доказательство того, что:
- медиана трапеции параллельна основаниям;
- длина медианы равна половине суммы длин оснований;
- середины диагоналей трапеции также лежат на ее средней линии.
(подробнее…)
Теги:Математика, Медиана, Средняя линия, Понедельник Математика, Аксиома Плейфера, Трапеция, Теорема средней линии треугольника
Опубликовано в Математика/Наука | Оставить комментарий »
Monday Math 155
21 июля 2014 г.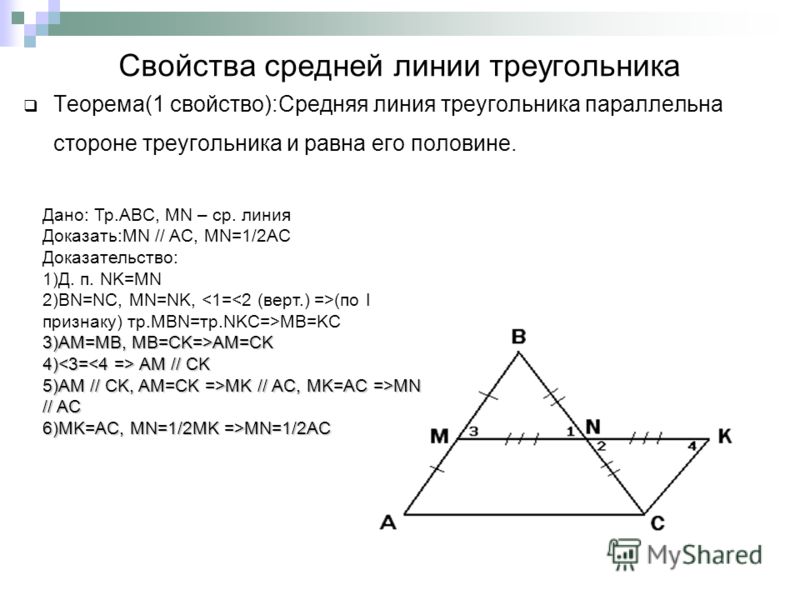
Теорема о средней линии треугольника, также называемая теоремой о средней линии, утверждает, что отрезок, соединяющий середины двух сторон треугольника, параллелен и составляет половину длина третьей стороны. Это может быть тривиально доказано с помощью подобия треугольников (условие подобия SAS) и постулата соответствующих углов. Однако более интересно доказать это, используя конгруэнтность треугольников.
Пусть D и E будут серединами сторон AB и AC соответственно ∆ ABC . Продлим отрезок DE за E до точки F так, что DE = EF , и нарисуем CF .
Так как DE = EF , AE = EC , а вертикальные углы ∠ AED и ∠ CEF 9003 равны0032 ADE ≅∆ CFE . Таким образом, CF = AD = BD . Кроме того, ∠ FCE ≅∠ DAE ; но поскольку это альтернативные внутренние углы для прямых и пересеченные секущей, мы видим, что.
Но тогда четырехугольник BCFD имеет пару противоположных сторон, BD и CF , которые имеют равную длину и параллельны, поэтому он является параллелограммом, и так. А поскольку противоположные стороны параллелограмма имеют одинаковую длину, DF = до н.э. , и поэтому DE = ½ DF = ½ до н.э. .
Мы также можем доказать аналогичную теорему: прямая, проходящая через середину одной стороны треугольника, параллельная второй стороне треугольника, делит третью сторону пополам, и что отрезок этой прямой внутри треугольника равен половине длинна параллельной стороны. Как и в случае с теоремой о средней точке, тривиально доказать с помощью подобия треугольников (на этот раз условие AA) и постулата о соответствующих углах. Итак, вместо этого мы используем аналогичную конструкцию, как указано выше.
Пусть D будет серединой стороны AB ∆ ABC , и пусть E будет точкой, где линия, проходящая через D и параллельная AC , пересекает .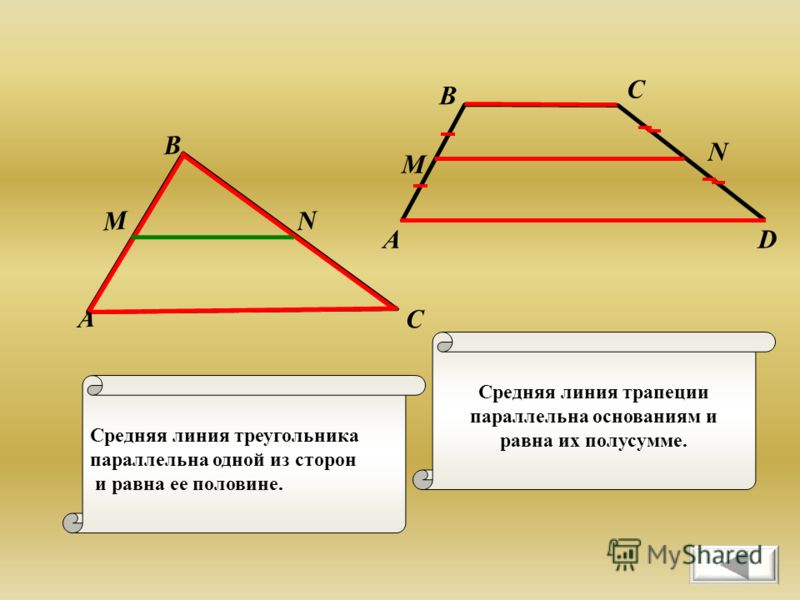
Проведите через C прямую, параллельную AB , и пусть F будет точкой пересечения
. Тогда BCFD является параллелограммом, а поскольку противоположные стороны параллелограмма имеют одинаковую длину, = CF и BC = DF . Итак, CF = BD = AD . А поскольку ∠ ADE и ∠ CFE являются альтернативными внутренними углами для прямых и разрезаны секущей , они конгруэнтны. Аналогично, ∠ DAE ≅∠ CFE , и, таким образом, по условию ASA ∆ ADE ≅∆ CFE . Таким образом, AE = EC и E , таким образом, является средней точкой AC . Мы также видим, что DE = EF , а поскольку DF = до н.э. , таким образом, DE = ½ DF = ½ BC .
Используя обе эти теоремы вместе, мы можем доказать третью: что средняя линия (средний отрезок) треугольника и медиана треугольника, пересекающая его, делят друг друга пополам.
Пусть M A , M B и M C будут серединами сторон BC , 2 AB 90 033 AB3 соответственно ∆ ABC . Таким образом, это средняя линия ∆ ABC и медиана. Пусть P будет точкой их пересечения.
По теореме о средней линии и M B M C =½ BC .
Это означает, что , и поэтому по нашей второй теореме выше относительно ∆ ABM A , мы видим, что P должно быть серединой , и M C P = ½ БМ А .
Аналогично, наша вторая теорема, примененная к треугольнику AM A C , устанавливает, что M B P = ½ CM A . Но BM A = CM A , и поэтому M B P = M C P , а также P 9 является серединой.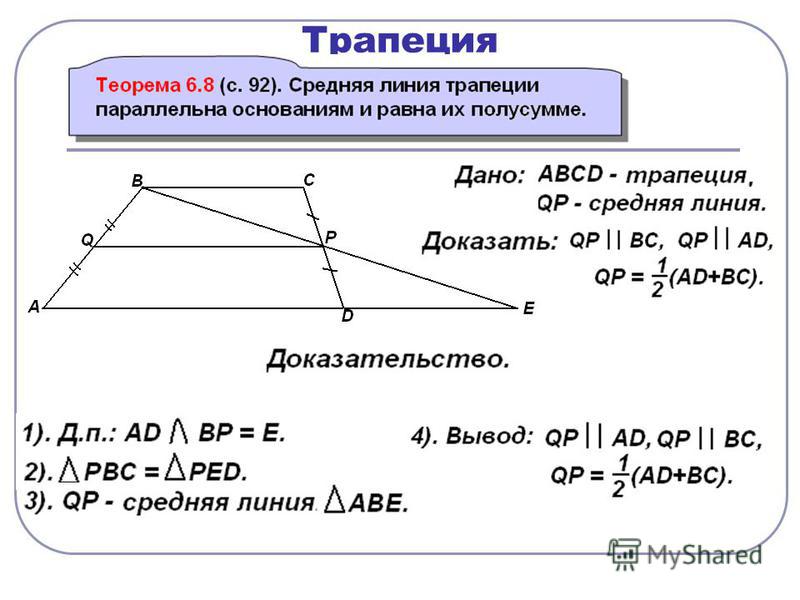
Теги:Математика, Медиана, Средняя линия, Понедельник Математика, Теорема средней линии треугольника
Опубликовано в Математика/Наука | 2 комментария »
Доказательство: Теорема о средней линии треугольника | Помощь по геометрии
Главная » Треугольники » Теорема о середине треугольника
Последнее обновление: Идо Сариг · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности
Сегодня на уроке мы докажем теорему о средней линии треугольника.
Средняя линия треугольника — это линия, соединяющая середины двух сторон:
Теорема о средней линии треугольника утверждает, что средняя линия параллельна третьей стороне, а ее длина равна половине длины третьей стороны. . Теперь мы докажем эту теорему, а также пару других родственных теорем, а также их обратные теоремы.
Задача
Показать, что в треугольнике ΔABC средний отрезок DE параллелен третьей стороне, а его длина равна половине длины третьей стороны.
Стратегия
Чтобы показать, что длины отрезков равны, мы обычно используем конгруэнтность треугольников, поэтому здесь нам нужно построить пару треугольников.
Чтобы показать конгруэнтность, нам нужно будет полагаться на то, что дано в условии задачи, и посмотреть, какие части (стороны или углы), как мы знаем, равны. В этом случае, поскольку DE является средней линией, мы знаем, что AE=EC и AD=DB, поэтому мы должны использовать одну или несколько из этих сторон в треугольниках, которые мы строим.
Нам также нужно кое-что доказать относительно DE, т. е. равной половине BC, поэтому было бы полезно, чтобы треугольник, который мы строим, имел DE в качестве стороны, с другой стороной, равной ей, которую мы могли бы построить . Имея это в виду, давайте построим новый треугольник, продолжив линию DE до точки F так, чтобы DE=EF, и соединив F с C:
Теперь легко показать, что построенный нами новый треугольник (ΔCFE) конгруэнтен ΔADE используя постулат Сторона-Угол-Сторона, и в результате этот DFCB является параллелограммом, поскольку теперь у нас есть две стороны, DB и FC, которые равны и параллельны.
А поскольку DFCB — параллелограмм, DE параллелен BC, что нам и нужно было доказать. Из конгруэнтности ΔCFE и ΔADE мы также имеем DE=EF, а поскольку DF=BC как противоположные стороны в параллелограмме, DE составляет половину BC.
Proof
(1) DE=EF //Построение
(2) AE=EC //Дано, DE – срединный отрезок
(3) ∠AED ≅ ∠CEF (DE) ΔA
// Вертикальные углы
≅ΔCFE // постулат Сторона-Угол-Сторона(5) ∠DAE ≅ ∠FCE // соответствующие углы в конгруэнтных треугольниках, (CPCTC)
(6) AB||CF // Теорема о обратных внутренних углах
(7) AD=CF // соответствующие стороны в конгруэнтных треугольниках, (CPCTC) середина
(9) CF=DB //(7), (8), транзитивность равенства
(10) DFCB — параллелограмм //две противоположные стороны параллелограмма, CF и DB, равны и параллельны
(11) DE||BC //(10), противоположные стороны параллелограмма
(12) DF=BC //(10), противоположные стороны параллелограмма
(13) DE=EF //(4) соответствующие стороны в конгруэнтных треугольниках, (CPCTC)
(14) DE= ½DF
(15) DE= ½BC //(12) , (14), замена
Об авторе
Идо Сариг — руководитель отдела высоких технологий со степенью бакалавра вычислительной техники.