Иллюстрированный самоучитель по SPSS > Непараметрические тесты > Тест Колмогорова-Смирнова (Kolmogorov-Smirnov Test) | ||||||||||||||||||
14.16. Тест Колмогорова-Смирнова для проверки формы распределения При помощи этого теста по выбору можно проверить, соответствует ли реальное распределение переменной нормальному (Гауса), равномерному, экспоненциальному распределению или распределению Пуассона. Разумеется, самым распространённым видом проверки является проверка наличия нормального распределения. Чтобы продемонстрировать работу данного теста, проверим на предмет наличия нормального распределения исходные значения холестерина, то есть переменную cho10 из файла hyper.sav.
Рис. 14.5: Диалоговое окно One Sample Kolomgorov-Smirnov Test Предварительно установленной является проверка на нормальное распределение. В окне просмотра появятся следующие результаты: One-Sample Kolmogorov-Smirnov Test (Тест Колмогорова-Смирнова для одной выборки)
a. Test distribution is Normal. (Тестируемое распределение является нормальным распределением.) Полученные результаты включают:
Отклонение от нормального распределения считается существенным при значении р < 0,05; в этом случае для соответствующих переменных следует применять непараметрические тесты. В рассматриваемом примере (значение р = 0,616), то есть вероятность ошибки не является значимой; поэтому значения переменной достаточно хорошо подчиняются нормальному распределению и можно применять параметрические тесты. | ||||||||||||||||||
Методы статистики
Колмогоров А.Н.
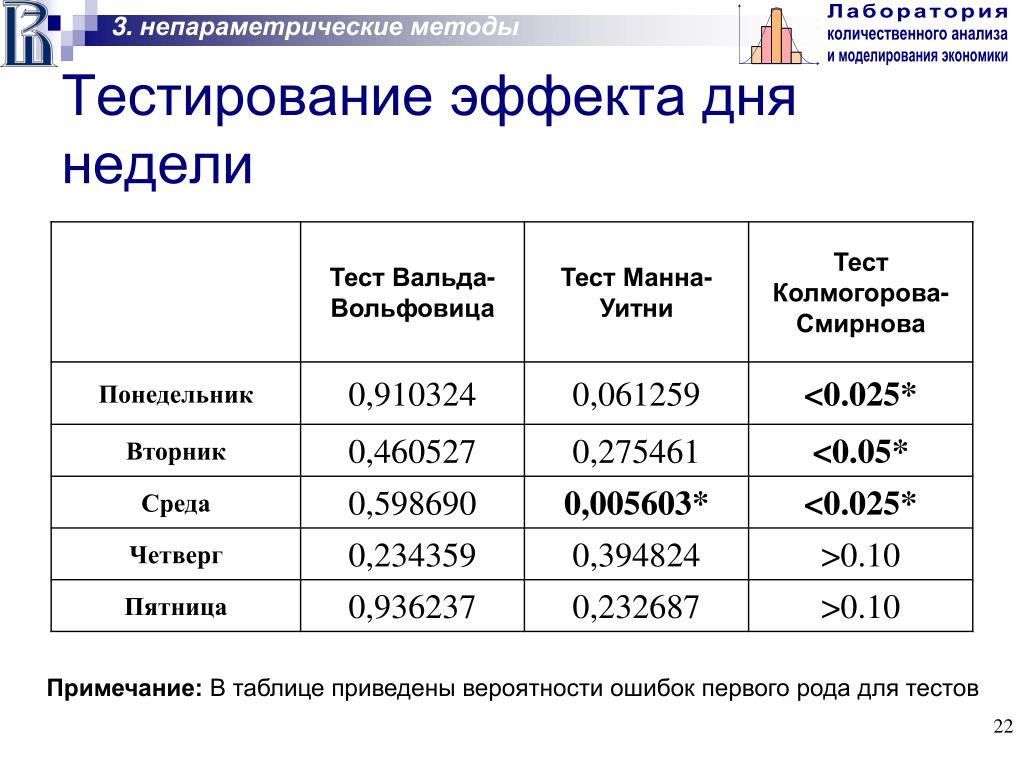
Критерий Колмогорова-Смирнова – непараметрический критерий согласия, в классическом понимании предназначен для проверки простых гипотез о принадлежности анализируемой выборки некоторому известному закону распределения. Наиболее известно применение данного критерия для проверки исследуемых совокупностей на нормальность распределения.
1. История разработки критерия Колмогорова-Смирнова
Критерий Колмогорова-Смирнова был разработан советскими математиками Андреем Николаевичем Колмогоровым и Николаем Васильевичем Смирновым.
Колмогоров А.Н. (1903-1987) — Герой Социалистического Труда, профессор Московского государственного университета, академик АН СССР — крупнейший математик XX века, является одним из основоположников современной теории вероятности.
Смирнов Н.В. (1900-1966)- член-корреспондент АН СССР, один из создателей непараметрических методов математической статистики и теории предельных распределений порядковых статистик.
Впоследствии критерий согласия Колмогорова-Смирнова был доработан с целью применения для проверки совокупностей на нормальность распределения американским статистиком, профессором Университета Джорджа Вашингтона Хьюбертом Лиллиефорсом (Hubert Whitman Lilliefors, 1928-2008). Профессор Лиллиефорс являлся одним из пионеров применения компьютерной техники в статистических расчётах.
Хьюберт Лиллиефорс2. Для чего используется критерий Колмогорова-Смирнова?
Данный критерий позволяет оценить существенность различий между распределениями двух выборок, в том числе возможно его применение для оценки соответствия распределения исследуемой выборки закону нормального распределения.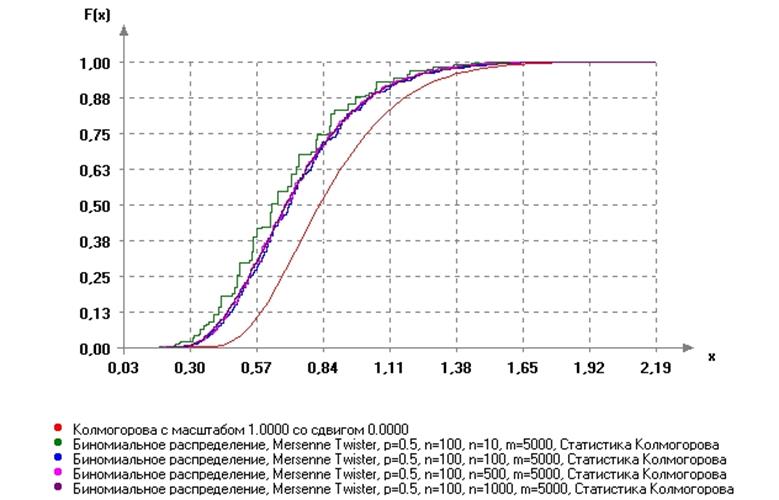
3. В каких случаях можно использовать критерий Колмогорова-Смирнова?
Критерий Колмогорова-Смирнова предназначен для проверки на нормальность распределения совокупностей количественных данных.
Для большей достоверности полученных данных объемы рассматриваемых выборок должен быть достаточно большими: n ≥ 50. При размерах оцениваемой совокупности от 25 до 50 элементов, целесообразно применение поправки Большева.
4. Как рассчитать критерий Колмогорова-Смирнова?
Критерий Колмогорова-Смирнова рассчитывается при помощи специальных статистических программ. В основе лежит статистика вида:
где sup S — точная верхняя грань множества S, Fn — функция распределения исследуемой совокупности, F(x) — функция нормального распределения
Выводимые значения вероятности основаны на предположении, что среднее и стандартное отклонение нормального распределения известны априори и не оцениваются из данных.
Однако на практике обычно параметры вычисляются непосредственно из данных. В этом случае критерий нормальности включает сложную гипотезу («насколько вероятно получить D статистику данной или большей значимости, зависящей от среднего и стандартного отклонения, вычисленных из данных»), и приводятся вероятности Лиллиефорса (Lilliefors, 1967).
В этом случае критерий нормальности включает сложную гипотезу («насколько вероятно получить D статистику данной или большей значимости, зависящей от среднего и стандартного отклонения, вычисленных из данных»), и приводятся вероятности Лиллиефорса (Lilliefors, 1967).
5. Как интерпретировать значение критерия Колмогорова-Смирнова?
Если D статистика Колмогорова-Смирнова значима (p<0,05), то гипотеза о том, что соответствующее распределение нормально, должна быть отвергнута.
Критерий согласия Колмогорова-Смирнова
Допущение нормальности > Критерий Колмогорова-Смирнова
Содержание:
- Что такое критерий Колмогорова-Смирнова?
- Как запустить тест вручную
- Тест КС в SPSS
- Использование другого программного обеспечения Таблица P-значения теста K-S
- Преимущества и недостатки
- Распределение Колмогорова-Смирнова
Что такое тест Колмогорова-Смирнова?
Тест согласия Колмогорова-Смирнова (тест K-S) сравнивает ваши данные с известным распределением и позволяет узнать, имеют ли они одинаковое распределение. Хотя тест является непараметрическим — он не предполагает какого-либо конкретного базового распределения — он обычно используется в качестве теста на нормальность, чтобы увидеть, нормально ли распределены ваши данные. Он также используется для проверки предположения о нормальности в дисперсионном анализе.
Хотя тест является непараметрическим — он не предполагает какого-либо конкретного базового распределения — он обычно используется в качестве теста на нормальность, чтобы увидеть, нормально ли распределены ваши данные. Он также используется для проверки предположения о нормальности в дисперсионном анализе.
В частности, тест сравнивает известное гипотетическое распределение вероятностей (например, нормальное распределение) с распределением, созданным вашими данными — эмпирической функцией распределения.
Тест Лиллиефорса, скорректированная версия теста K-S на нормальность , обычно дает более точную аппроксимацию распределения тестовой статистики. На самом деле, многие статистические пакеты (например, SPSS) объединяют эти два теста в качестве «скорректированного по Лиллифорсу» теста K-S.
Примечание: Если вы никогда раньше не сравнивали экспериментальный дистрибутив с гипотетическим дистрибутивом, вы можете сначала прочитать статью об эмпирическом дистрибутиве. Это короткая статья, в которой есть пример простого сравнения двух наборов данных — с использованием точечной диаграммы вместо проверки гипотезы.
Это короткая статья, в которой есть пример простого сравнения двух наборов данных — с использованием точечной диаграммы вместо проверки гипотезы.
Вернуться к началу
Как запустить тест вручную
Нужна помощь с инструкциями? Посетите нашу обучающую страницу!
гипотез для теста:
- Нулевая гипотеза
- Альтернативная гипотеза (H 1 ): по крайней мере одно значение не соответствует указанному распределению.
То есть
H 0 : P = P 0 , H 1 : P ≠ P 0 .
Где P — это распределение вашего образца (т. е. EDF), а P 0 — заданное распределение.
Общие шаги
общих шагов для запуска теста :
- Создайте EDF для ваших выборочных данных (шаги см. в Функция эмпирического распределения ),
- Укажите родительский дистрибутив (то есть тот, с которым вы хотите сравнить свой EDF),
- Постройте график двух распределений вместе.

- Измерьте наибольшее расстояние по вертикали между двумя графиками.
- Рассчитать статистику теста.
- Найдите критическое значение в таблице KS.
- Сравните с критическим значением.
Вычисление статистики теста
Статистика теста K-S измеряет наибольшее расстояние между данными EDF F (x) и теоретической функцией F 0 (x), измеренное в вертикальном направлении (Колмогоров, цит. по Stephens 1992 ). тестовая статистика определяется как:
Где (для двустороннего теста):
- F 0 (x) = cdf гипотетического распределения,
- F данные (x) = эмпирическая функция распределения ваших наблюдаемых данных.
Для одностороннего теста опустите абсолютные значения из формулы.
Если D больше критического значения, нулевая гипотеза отклоняется. Критические значения для D указаны в таблице P-значений теста KS.
В начало
Пример
Шаг 1: Найдите EDF.
Шаг 2: Укажите родительский дистрибутив. В той же статье я также рассчитал соответствующие значения для гамма-функции.
Шаг 3: Постройте график функций вместе. Снимок точечной диаграммы выглядел так:
Наибольшее вертикальное расстояние для этой диаграммы выделено желтым прямоугольником.
Шаг 4: Измерьте наибольшее расстояние по вертикали. Предположим, что я изобразил всю выборку в виде графика, и наибольшее расстояние по вертикали, разделяющее мои два графика, равно 0,04 (выделено желтым цветом).
Шаг 5: Найдите критическое значение в таблице K-S. В моей выборке 50 наблюдений. При альфа-уровне 0,05 значение таблицы K-S составляет 0,190.
Шаг 6: Сравните результаты шагов 4 и 5. Поскольку 0,04 меньше 0,190, принимается нулевая гипотеза (о том, что распределения одинаковы).
Нулевая гипотеза для теста состоит в том, что нет существенной разницы между переменной и нормальным распределением.
Подробные шаги смотрите в видео:
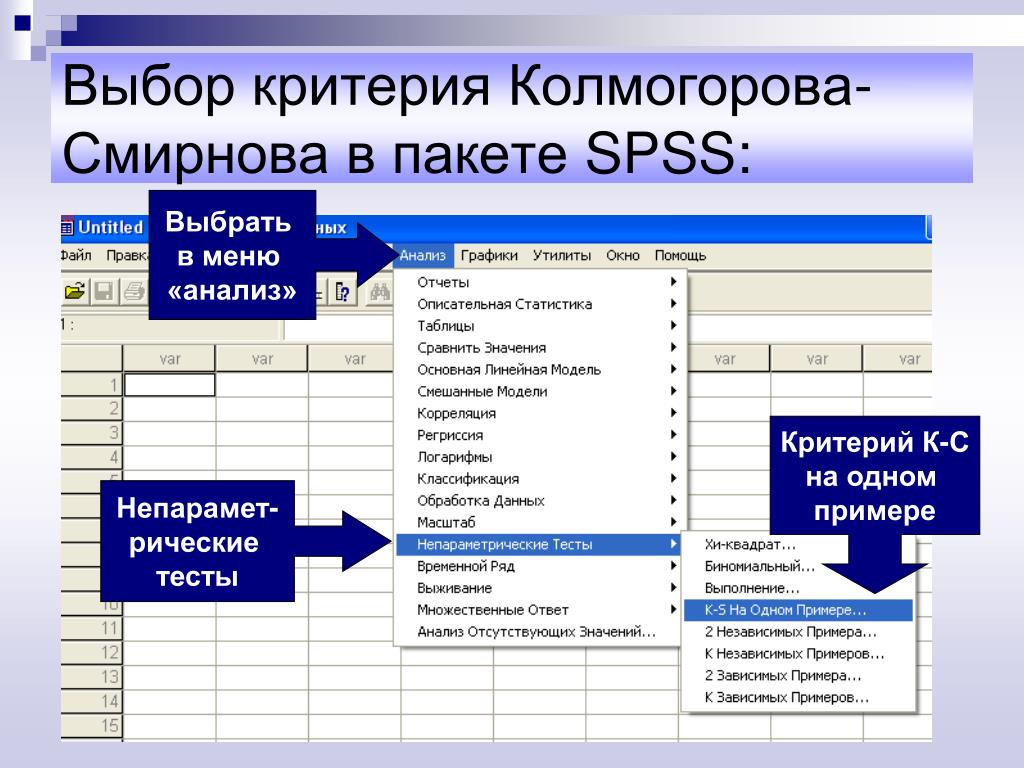
Тест Колмогорова-Смирнова (тест КС) в SPSS
Посмотрите это видео на YouTube.
Шаг 1: Анализ → описательная статистика → исследование
Шаг 2: Переместите переменные, которые вы хотите проверить на нормальность, в поле Зависимый список.
Шаг 3: (необязательно, если вы хотите проверить наличие выбросов) Нажмите «Статистика», затем установите флажок в поле «Выбросы».
Шаг 4: Нажмите Графики, затем установите флажок рядом с Гистограмма и Графики нормальности с тестами. Нажмите «Продолжить».
Шаг 5: Нажмите «Параметры», чтобы указать, как должны обрабатываться отсутствующие значения.
- Исключить наблюдения по списку: исключить все наблюдения с пропущенными значениями для выбранных переменных.
- Исключить случаи попарно: вычислить среднее значение для каждой переменной, используя все неотсутствующие ответы для этой конкретной переменной.

- Значения отчета: этот параметр влияет только на анализ факторной переменной.
Нажмите «Продолжить».
Шаг 6: Нажмите OK, чтобы запустить тест KS.
Шаг 7: Прочтите результаты в разделе «Тесты нормальности». В столбце «Sig» указано значение p. Если это значение крошечное (например, менее 0,05 для уровня альфа 5%), то вы можете отклонить нулевую гипотезу о нормальном распределении данных. Здесь большие p-значения указывают на нормально распределенные данные.
SPSS одновременно предоставляет результаты теста Шапиро-Уилка. Это может дать вам разные результаты. Вы должны читать K-S для больших размеров выборки (n ≥ 50) и Шапиро-Уилка для малых размеров выборки (< 50).
В разделе «Экстремальные значения» содержится информация о выбросах.
Использование технологии
Большинство программных пакетов могут выполнять этот тест.
R-функция ecdf создает эмпирические функции распределения. Функция R p , за которой следует имя распределения (pnorm, pbinom и т. д.), дает теоретическую функцию распределения.
д.), дает теоретическую функцию распределения.
Доступно несколько онлайн-калькуляторов, например этот и этот.
В результате использования программного обеспечения для проверки нормальности небольшие значения p в ваших выходных данных обычно указывают на то, что данные не относятся к нормальному распределению (Ruppert, 2004).
Вернуться к началу
Таблица P-значений теста K-S
Вернуться к началу
Преимущества и недостатки
Преимущества включают:
- Тест не подлежит распространению . Это означает, что вам не нужно знать базовое распределение населения для ваших данных перед запуском этого теста.
- D-статистика (не путать с D- Коэна), используемая для теста, легко вычисляется.
- Может использоваться как критерий согласия после регрессионного анализа.
- Есть нет ограничений на размер выборки ; Допустимы небольшие образцы.

- Таблицы легко доступны.
Хотя тест K-S имеет много преимуществ, он также имеет несколько ограничений
- Чтобы тест работал, необходимо указать параметры местоположения, масштаба и формы. Если эти параметры оцениваются по данным, это делает тест недействительным . Если вы не знаете эти параметры, вы можете провести менее формальный тест (например, тот, который описан в статье об эмпирической функции распределения ).
- Как правило, нельзя использовать для дискретных дистрибутивов, , особенно если вы используете программное обеспечение (большинство программных пакетов не имеют необходимых расширений для дискретного теста K-S, а ручные вычисления запутаны).
- Чувствительность выше в центре распределения и ниже на хвостах.
Вернуться к началу
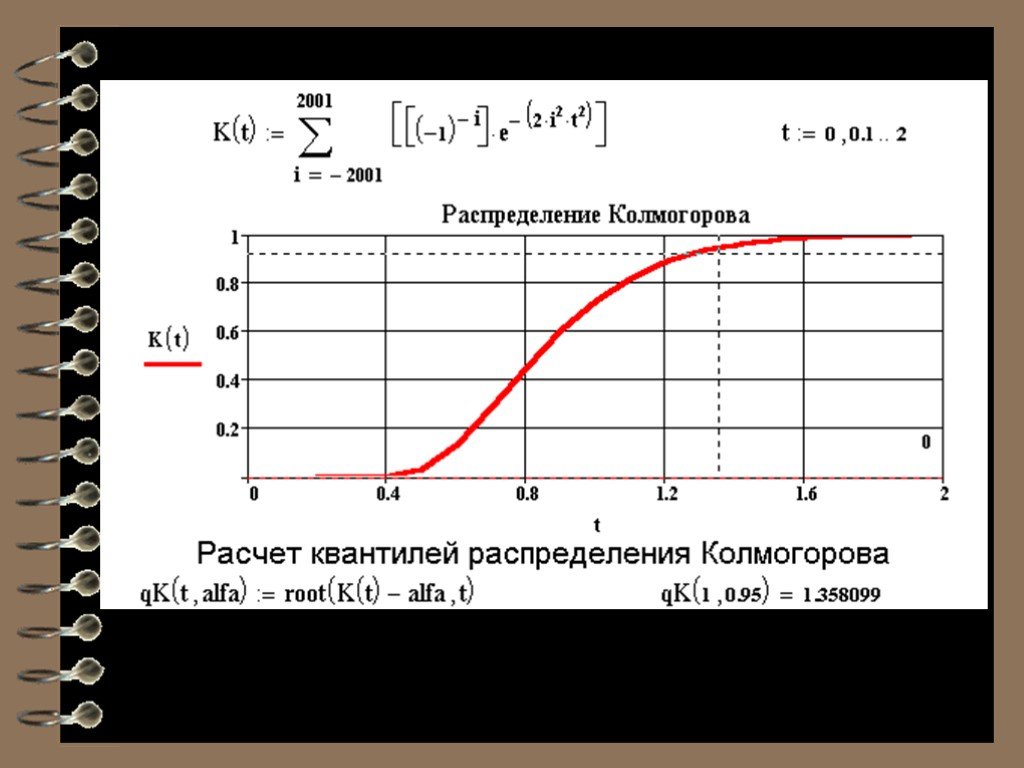
Термин «Распределение Колмогорова-Смирнова» относится к распределению статистики K-S.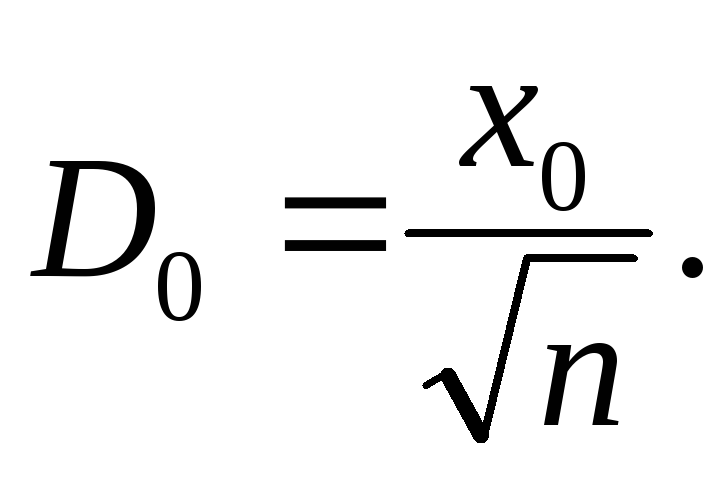 В подавляющем большинстве случаев предполагается, что основная кумулятивная функция распределения является непрерывной. В этих случаях распределение K-S может быть глобально аппроксимировано общим бета-распределением [1].
В подавляющем большинстве случаев предполагается, что основная кумулятивная функция распределения является непрерывной. В этих случаях распределение K-S может быть глобально аппроксимировано общим бета-распределением [1].
Однако для некоторых реальных приложений требуется дискретное распределение. Хотя можно подобрать дискретное распределение, работа с разрывами скачков была проблематичной. На самом деле не существует общепринятых эффективных или точных вычислительных методов, позволяющих справиться с этой ситуацией. Димитрова и др. al [2] предоставил один метод для прерывистого распределения Колмогорова-Смирнова; это приводит к точным значениям p для теста. Этот подход выходит за рамки этой статьи, но включает в себя выражение дополнительной PDF через вероятность прямоугольника для равномерной статистики порядка с помощью быстрого преобразования Фурье.
Случайная величина K-S D n с параметром n имеет кумулятивную функцию распределения D n −1/(2n) из [3]:
Распределение Колмогорова-Смирнова: Ссылки
[1] Zhang , Дж. и Ву, Ю. (2001). Бета-аппроксимация распределения статистики Колмогорова-Смирнова. Анна. Инст. Статистическая математика. Том 54. № 3, 577-584. Получено 1 ноября 2021 г. с: https://www.ism.ac.jp/editsec/aism/pdf/054_3_0577.pdf
и Ву, Ю. (2001). Бета-аппроксимация распределения статистики Колмогорова-Смирнова. Анна. Инст. Статистическая математика. Том 54. № 3, 577-584. Получено 1 ноября 2021 г. с: https://www.ism.ac.jp/editsec/aism/pdf/054_3_0577.pdf
[2] Dimitrova, D. et al. (2020). Вычисление распределения Колмогорова-Смирнова, когда лежащий в основе CDF является чисто дискретным, смешанным или непрерывным. Журнал статистического программного обеспечения. Том 95, выпуск 10 (октябрь). КС.
[3] Распределение Колмогорова–Смирнова. Получено 15 ноября 2021 г. с: http://www.math.wm.edu/~leemis/chart/UDR/PDFs/Kolmogorovsmirnov.pdf
Статьи по теме
- Тест Андерсона-Дарлинга
- Тест хи-квадрат на нормальность
- Графики нормальной вероятности
- Тест Шапиро-Уилка
Ссылки
Чакраварти, Лаха и Рой (1967). Справочник по методам прикладной статистики, том I, John Wiley and Sons, стр. 39.2-394.
Рупперт, Д. (2004). Статистика и финансы: введение. Springer Science and Business Media.
Springer Science and Business Media.
Стивенс М.А. (1992) Введение в Колмогорова (1933) Об эмпирическом определении распределения. В: Коц С., Джонсон Н.Л. (ред.) Прорывы в статистике. Серия Springer в статистике (Перспективы в статистике). Springer, New York, NY
УКАЗЫВАЙТЕ ЭТО КАК:
Stephanie Glen . «Тест Колмогорова-Смирнова на пригодность» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/kolmogorov-smirnov-test/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста Связаться с нами .
Тест Колмогорова-Смирнова (KS Test) — GeeksforGeeks
Улучшить статью
Сохранить статью
- Последнее обновление: 10 июн, 2020
Улучшить статью
Сохранить статью
Тест Колмогорова-Смирнова очень эффективный способ определить, существенно ли отличаются два образца друг от друга. Обычно используется для проверки однородности случайных чисел. Однородность является одним из наиболее важных свойств любого генератора случайных чисел, и для его проверки можно использовать критерий Колмогорова-Смирнова.
Критерий Колмогорова-Смирнова также можно использовать для проверки того, различаются ли два лежащих в основе одномерных распределения вероятностей. Это очень эффективный способ определить, существенно ли отличаются два образца друг от друга.
Статистика Колмогорова-Смирнова количественно определяет расстояние между эмпирической функцией распределения выборки и кумулятивной функцией распределения эталонного распределения или между эмпирическими функциями распределения двух выборок.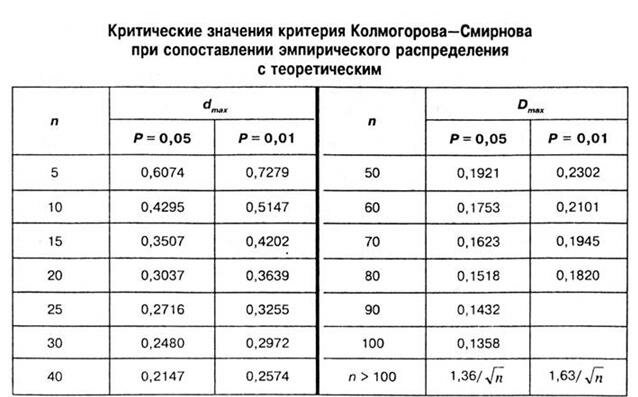
Чтобы использовать тест для проверки однородности случайных чисел, мы используем CDF (кумулятивную функцию распределения) U[0, 1].
F(x)= x for 0<=x<=1
Эмпирический CDF, Sn(x)= (количество R1, R2…Rn < x)/N массив случайных чисел , случайные числа должны находиться в диапазоне [0, 1].
Используемая гипотеза –
H0(Нулевая гипотеза): Нулевая гипотеза предполагает, что числа равномерно распределены между 0-1. Если мы можем отвергнуть нулевую гипотезу, это означает, что числа неравномерно распределены между 0-1. Неспособность отвергнуть нулевую гипотезу не обязательно означает, что числа следуют равномерному распределению.
Алгоритм:
-> Ранжировать N случайных чисел в порядке возрастания.
-> Рассчитать D+ как max(i/N-Ri) для всех i в (1, N)
-> Рассчитать D- как max(Ri-((i-1)/N)) для всех i в (1, N)
-> Рассчитать D как max(sqrt(N) * D+, sqrt(N) * D-)
-> Если D>D(альфа)
Отвергает единообразие
еще
Он не может отвергнуть нулевую гипотезу.
Ниже приведена реализация вышеуказанного алгоритма на Python:
|


 Deviation (Стандартное отклонение)
Deviation (Стандартное отклонение)


 append(random.random())
append(random.random()) 