Свойства показателей степени с примерами: умножение, деление
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Показатель степени: определение и свойства
Степень an равняется произведению числа a на само себя n-ое количество раз.
an = a * a * a… a (n раз)
В данном случае a – это основание, а n – показатель степени.
Примеры:
- 31 = 3
- 32 = 3 × 3 = 9
- 33 = 3 × 3 × 3 = 27
- 34 = 3 × 3 × 3 × 3 = 81
- 35 = 3 × 3 × 3 × 3 × 3 = 243
Произошение:
- Число a2 следует произносить как “a в квадрате”. Например, 42 – это “четыре в квадрате”.
- Число a3 произносится как “a в кубе”.
 Например, 43 – это “четыре в кубе”.
Например, 43 – это “четыре в кубе”. - Во всех остальных случаях an говорится как “a в n-ой степени”. Например, 46 – это “четыре в шестой степени”.
#1. Умножение степеней (одинаковые основания)
an ⋅ am = an+m
Пример: 22 ⋅ 23 = 22+3 = 25 = 32
#2. Степень произведения
(a ⋅ b)n = an ⋅ bn
Пример: (2 ⋅ 3)4 = 24 ⋅ 34 = 1296
#3. Деление степеней (одинаковые основания)
an / am = an-m
Пример: 25 ⋅ 23 = 25-3 = 22 = 4
#4. Степень частного
(a / b)n = an / bn
Пример: (12 / 4)3 = 123 / 43 = 27
#5. Возведение степени в степень
Возведение степени в степень
(an)m = an · m
Пример: (52)3 = 52 · 3 = 3125
#6. Степень, возведенная в степень
anm = a(nm)
Пример: 242 = 2(42) = 2(4 · 4) = 2(16) = 65536
#7. Извлечение степени из числа в степени
m√(an) = a n/m
Пример: 3√(26) = 26/3 = 22 = 2⋅2 = 4
#8. Возведение в отрицательную степень
b-n = 1 / bn
Пример: 2-4 = 1 / 24 = 1 / (2⋅2⋅2⋅2) = 1/16 = 0,0625
#9. Число в нулевой степени
a0 = 1
Пример: 100 = 1
#10. Возведение нуля в степень
0n = 0, для n>0
Пример: 07 = 0
#11. Число в первой степени
Число в первой степени
a1 = a
Пример: 151 = 15
#12. Единица в степени (любой)
1n = 1
Пример: 120 = 1
#13. Минус один в степени
(-1)n = 1, если n – четное число
(-1)n = -1, если n – нечетное число
Пример: (-1)6 = 1
#14. Возведение числа в дробную степень (в числителе – единица)
a1/n = n√a
Пример: 271/3 = 3√27 = 3
Смотрите также:
- Как возвести число в степень в Эксель
- Как извлечь корень в Эксель: квадратный, кубический, в степени
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Если числа складываются то степени.
 Правило умножение степеней с разными основаниями
Правило умножение степеней с разными основаниямиЕсли числа складываются то степени. Правило умножение степеней с разными основаниями
Если вам нужно возвести какое-то конкретное число в степень, можете воспользоваться . А сейчас мы более подробно остановимся на свойствах степеней .
Экспоненциальные числа открывают большие возможности, они позволяют нам преобразовать умножение в сложение, а складывать гораздо легче, чем умножать.
Например, нам надо умножить 16 на 64. Произведение от умножения этих двух чисел равно 1024. Но 16 – это 4×4, а 64 – это 4х4х4. То есть 16 на 64=4x4x4x4x4, что также равно 1024.
Число 16 можно представить также в виде 2х2х2х2, а 64 как 2х2х2х2х2х2, и если произвести умножение, мы опять получим 1024.
А теперь используем правило . 16=4 2 , или 2 4 , 64=4 3 , или 2 6 , в то же время 1024=6 4 =4 5 , или 2 10 .
Следовательно, нашу задачу можно записать по-другому: 4 2 х4 3 =4 5 или 2 4 х2 6 =2 10 , и каждый раз мы получаем 1024.
Мы можем решить ряд аналогичных примеров и увидим, что умножение чисел со степенями сводится к
Таким образом, мы можем, не производя умножения, сразу сказать, что 2 4 х2 2 х2 14 =2 20 .
Это правило справедливо также и при делении чисел со степенями, но в этом случае экспонента делителя вычитается из экспоненты делимого . Таким образом, 2 5:2 3 =2 2 , что в обычных числах равно 32:8=4, то есть 2 2 . Подведем итоги:
a m х a n =a m+n , a m: a n =a m-n , где m и n — целые числа.
С первого взгляда может показаться, что такое умножение и деление чисел со степенями не очень удобно, ведь сначала надо представить число в экспоненциальной форме. Нетрудно представить в такой форме числа 8 и 16, то есть 2 3 и 2 4 , но как это сделать с числами 7 и 17? Или как поступать в тех случаях, когда число можно представить в экспоненциальной форме, но основания экспоненциальных выражений чисел сильно различаются.
Тогда стоит ли вообще возиться с этим методом? Безусловно стоит. Он дает огромные преимущества, особенно при сложных и трудоемких вычислениях.
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел. 3$
3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15 - Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2 - Вычислить.
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Как умножать степени
Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?
В алгебре найти произведение степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать степени, на конкретных примерах.
Единицу в показателе степени не пишут, но при умножении степеней — учитывают:
При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:
Умножение степеней с одинаковыми основаниями
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы изучим умножение степеней с одинаковыми основаниями. Вначале вспомним определение степени и сформулируем теорему о справедливости равенства . Затем приведем примеры ее применения на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач.
Тема: Степень с натуральным показателем и ее свойства
Урок: Умножение степеней с одинаковыми основаниями (формула )
1.
 Основные определения
Основные определенияОсновные определения:
n — показатель степени,
— n -ая степень числа.
2. Формулировка теоремы 1
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
По-иному: если а – любое число; n и k натуральные числа, то:
Отсюда правило 1:
3. Разъясняющие задачи
Вывод: частные случаи подтвердили правильность теоремы №1. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
4. Доказательство теоремы 1
Дано число а – любое; числа n и k – натуральные. Доказать:
Доказательство основано на определении степени.
5. Решение примеров с помощью теоремы 1
Пример 1: Представьте в виде степени.
Для решения следующих примеров воспользуемся теоремой 1.
ж)
6. Обобщение теоремы 1
Здесь использовано обобщение:
7.
 Решение примеров с помощью обобщения теоремы 1
Решение примеров с помощью обобщения теоремы 18. Решение различных задач с помощью теоремы 1
Пример 2: Вычислите (можно использовать таблицу основных степеней).
а) (по таблице)
б)
Пример 3: Запишите в виде степени с основанием 2.
а)
Пример 4: Определите знак числа:
, а – отрицательное, так как показатель степени при -13 нечетный.
Пример 5: Замените (·) степенью числа с основанием r:
Имеем , то есть .
9. Подведение итогов
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
1. Школьный помощник (Источник).
1. Представьте в виде степени:
а) б) в) г) д)
3. Запишите в виде степени с основанием 2:
4. Определите знак числа:
а)
5. Замените (·) степенью числа с основанием r:
а) r 4 · (·) = r 15 ; б) (·) · r 5 = r 6
Умножение и деление степеней с одинаковыми показателями
На этом уроке мы изучим умножение степеней с одинаковыми показателями. Сначала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и возведении степень в степень. Затем сформулируем и докажем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью решим ряд типичных задач.
Сначала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и возведении степень в степень. Затем сформулируем и докажем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью решим ряд типичных задач.
Напоминание основных определений и теорем
Здесь a — основание степени,
— n -ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n иk справедливо равенство:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
Теорема 3. Для любого числа а и любых натуральных n иk справедливо равенство:
Все перечисленные теоремы были о степенях с одинаковыми основаниями , на этом уроке будут рассмотрены степени с одинаковыми показателями .
Примеры на умножение степеней с одинаковыми показателями
Рассмотрим следующие примеры:
Распишем выражения по определению степени.
Вывод: из примеров можно заметить, что , но это еще нужно доказать. Сформулируем теорему и докажем ее в общем случае, то есть для любых а и b и любого натурального n.
Формулировка и доказательство теоремы 4
Для любых чисел а и b и любого натурального n справедливо равенство:
Доказательство теоремы 4.
По определению степени:
Итак, мы доказали, что .
Чтобы перемножить степени с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить неизменным.
Формулировка и доказательство теоремы 5
Сформулируем теорему для деления степеней с одинаковыми показателями.
Для любого числа а и b () и любого натурального n справедливо равенство:
Доказательство теоремы 5.
Распишем и по определению степени:
Формулировка теорем словами
Итак, мы доказали, что .
Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.
Решение типичных задач с помощью теоремы 4
Пример 1: Представить в виде произведения степеней.
Для решения следующих примеров воспользуемся теоремой 4.
Для решения следующего примера вспомним формулы:
Обобщение теоремы 4
Обобщение теоремы 4:
Решение примеров с помощью обобщенной теоремы 4
Продолжение решения типичных задач
Пример 2: Запишите в виде степени произведения.
Пример 3: Запишите в виде степени с показателем 2.
Примеры на вычисление
Пример 4: Вычислить самым рациональным способом.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю. М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
2. Школьный помощник (Источник).
1. Представить в виде произведения степеней:
а) ; б) ; в) ; г) ;
2. Запишите в виде степени произведения:
3. Запишите в виде степени с показателем 2:
4. Вычислить самым рациональным способом.
Урок математики по теме «Умножение и деление степеней»
Разделы: Математика
Педагогическая цель :
Задачи :

Деятельностные единицы учения: определение степени с натуральным показателем; компоненты степени; определение частного; сочетательный закон умножения.
I. Организация демонстрации овладение учащимися имеющимися знаниями. (шаг 1)а) Актуализация знаний:
2) Сформулировать определение степени с натуральным показателем.
a n =a a a a … а (n раз)
b k =b b b b a… b (k раз) Обосновать ответ.
II. Организация самооценивания обучаемого степенью владения актуальным опытом. (шаг 2)Тест для самопроверки: (индивидуальная работа в двух вариантах.)
А1) Представьте произведение 7 7 7 7 x x x в виде степени:
А2) Представить в виде произведения степень (-3) 3 х 2
A3) Вычислите: -2 3 2 + 4 5 3
Количество заданий в тесте я подбираю в соответствии с подготовкой уровня класса.
К тесту даю ключ для самопроверки. Критерии: зачёт – не зачёт.
III. Учебно-практическая задача (шаг 3) + шаг 4. (сформулируют свойства сами ученики)
(сформулируют свойства сами ученики) В ходе решения задачи 1) и 2) учащиеся предлагают решение, а я, как учитель, организую класс на нахождение способа для упрощения степеней при умножении с одинаковыми основаниями.
Учитель: придумать способ для упрощения степеней при умножении с одинаковыми основаниями.
На кластере появляется запись:
Формулируется тема урока. Умножение степеней.
Учитель: придумайте правило деления степеней с одинаковыми основаниями.
Рассуждения: каким действием проверяется деление? а 5: а 3 = ? что а 2 а 3 = а 5
Возвращаюсь к схеме – кластер и дополняем запись – ..при делении вычитаем и дописываем тему урока. …и деление степеней.
IV. Сообщение учащимся пределов познания (как минимум и как максимум).
Учитель: задачей минимума на сегодняшний урок является научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимума: применять умножение и деление совместно.
На доске записываем: а m а n = а m+n ; а m: а n = а m-n
V. Организация изучения нового материала. (шаг 5)а) По учебнику: №403 (а, в, д) задания с разными формулировками
№404 (а, д, е) самостоятельная работа, затем организую взаимопроверку, даю ключи.
б) При каком значении m справедливо равенство? а 16 а m = а 32 ; х h х 14 = х 28 ; х 8 (*) = х 14
Задание: придумать аналогичные примеры для деления.
в) № 417(а), №418 (а) Ловушки для учеников : х 3 х n = х 3n ; 3 4 3 2 = 9 6 ; а 16: а 8 = а 2 .
VI. Обобщение изученного, проведение диагностической работы (что побуждает учеников, а не учителя изучать данную тему)(шаг 6)
Диагностическая работа.
Тест (ключи поместить на обратной стороне теста).
Варианты заданий: представьте в виде степени частное х 15: х 3 ; представьте в виде степени произведение (-4) 2 (-4) 5 (-4) 7 ; при каком m справедливо равенство а 16 а m = а 32 ; найдите значение выражения h 0: h 2 при h =0,2; вычислите значение выражения (5 2 5 0) : 5 2 .
Итог урока. Рефлексия. Делю класс на две группы.
Найдите аргументы I группа: в пользу знания свойств степени, а II группа – аргументы, которые будут говорить о том, что можно обойтись без свойств. Все ответы выслушиваем, делаем выводы. На последующих уроках можно предложить статистические данные и назвать рубрику «В голове не укладывается!»
Историческая справка. Какие числа называют числами Ферма.
П.19. №403, №408, №417
Используемая литература:
 Н. Макарычев, Н.Г. Миндюк и др.
Н. Макарычев, Н.Г. Миндюк и др.Свойства степеней, формулировки, доказательства, примеры.
После того как определена степень числа, логично поговорить про свойства степени . В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров.
Навигация по странице.
Свойства степеней с натуральными показателями
По определению степени с натуральным показателем степень a n представляет собой произведение n множителей, каждый из которых равен a . Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел , можно получить и обосновать следующие свойства степени с натуральным показателем :
- если a>0 , то a n >0 для любого натурального n ;
- если a=0 , то a n =0 ;
- если a 2·m >0 , если a 2·m−1 n ;
- если m и n такие натуральные числа, что m>n , то при 0m n , а при a>0 справедливо неравенство a m >a n .

- a m ·a n =a m+n ;
- a m:a n =a m−n ;
- (a·b) n =a n ·b n ;
- (a:b) n =a n:b n ;
- (a m) n =a m·n ;
- если n – целое положительное число, a и b – положительные числа, причем an n и a −n >b −n ;
- если m и n – целые числа, причем m>n , то при 0m n , а при a>1 выполняется неравенство a m >a n .
Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби a m ·a n =a m+n при упрощении выражений часто применяется в виде a m+n =a m ·a n .
Теперь рассмотрим каждое из них подробно.
Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называют основным свойством степени : для любого действительного числа a и любых натуральных чисел m и n справедливо равенство a m ·a n =a m+n .
Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a m ·a n можно записать как произведение . В силу свойств умножения полученное выражение можно записать как , а это произведение есть степень числа a с натуральным показателем m+n , то есть, a m+n . На этом доказательство завершено.
Приведем пример, подтверждающий основное свойство степени.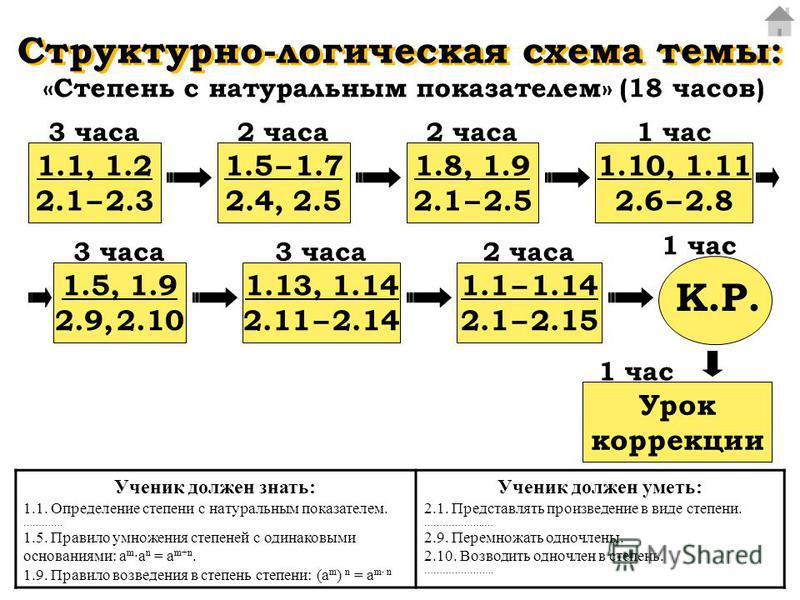 Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3 , по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 ·2 3 =(2·2)·(2·2·2)=4·8=32 и 2 5 =2·2·2·2·2=32 , так как получаются равные значения, то равенство 2 2 ·2 3 =2 5 — верное, и оно подтверждает основное свойство степени.
Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3 , по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 ·2 3 =(2·2)·(2·2·2)=4·8=32 и 2 5 =2·2·2·2·2=32 , так как получаются равные значения, то равенство 2 2 ·2 3 =2 5 — верное, и оно подтверждает основное свойство степени.
Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями. Так для любого количества k натуральных чисел n 1 , n 2 , …, n k справедливо равенство a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k .
Например, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .
Можно переходить к следующему свойству степеней с натуральным показателем – свойству частного степеней с одинаковыми основаниями : для любого отличного от нуля действительного числа a и произвольных натуральных чисел m и n , удовлетворяющих условию m>n , справедливо равенство a m:a n =a m−n .
Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0 n =0 , а при знакомстве с делением мы условились, что на нуль делить нельзя. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n), либо отрицательным числом (что происходит при m m−n ·a n =a (m−n)+n =a m . Из полученного равенства a m−n ·a n =a m и из связи умножения с делением следует, что a m−n является частным степеней a m и a n . Этим доказано свойство частного степеней с одинаковыми основаниями.
Приведем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2 , рассмотренному свойству степени отвечает равенство π 5:π 2 =π 5−3 =π 3 .
Теперь рассмотрим свойство степени произведения : натуральная степень n произведения двух любых действительных чисел a и b равна произведению степеней a n и b n , то есть, (a·b) n =a n ·b n .
Действительно, по определению степени с натуральным показателем имеем . Последнее произведение на основании свойств умножения можно переписать как , что равно a n ·b n .
Приведем пример: .
Данное свойство распространяется на степень произведения трех и большего количества множителей. То есть, свойство натуральной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .
Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .
Следующее свойство представляет собой свойство частного в натуральной степени : частное действительных чисел a и b , b≠0 в натуральной степени n равно частному степеней a n и b n , то есть, (a:b) n =a n:b n .
Доказательство можно провести, используя предыдущее свойство. Так (a:b) n ·b n =((a:b)·b) n =a n , а из равенства (a:b) n ·b n =a n следует, что (a:b) n является частным от деления a n на b n .
Запишем это свойство на примере конкретных чисел: .
Теперь озвучим свойство возведения степени в степень : для любого действительного числа a и любых натуральных чисел m и n степень a m в степени n равна степени числа a с показателем m·n , то есть, (a m) n =a m·n .
Например, (5 2) 3 =5 2·3 =5 6 .
Доказательством свойства степени в степени является следующая цепочка равенств: .
Рассмотренное свойство можно распространить на степень в степени в степени и т.д. Например, для любых натуральных чисел p , q , r и s справедливо равенство . Для большей ясности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .
Осталось остановиться на свойствах сравнения степеней с натуральным показателем.
Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.
Для начала обоснуем, что a n >0 при любом a>0 .
Произведение двух положительных чисел является положительным числом, что следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
Достаточно очевидно, что для любого натурального n при a=0 степень a n есть нуль. Действительно, 0 n =0·0·…·0=0 . К примеру, 0 3 =0 и 0 762 =0 .
Переходим к отрицательным основаниям степени.
Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m , где m — натуральное. Тогда . По правилу умножения отрицательных чисел каждое из произведений вида a·a равно произведению модулей чисел a и a , значит, является положительным числом. Следовательно, положительным будет и произведение и степень a 2·m . Приведем примеры: (−6) 4 >0 , (−2,2) 12 >0 и .
Наконец, когда основание степени a является отрицательным числом, а показатель степени есть нечетное число 2·m−1 , то . Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 17 n n представляет собой произведение левых и правых частей n верных неравенств aсвойств неравенств справедливо и доказываемое неравенство вида a n n . Например, в силу этого свойства справедливы неравенства 3 7 7 и .
Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 17 n n представляет собой произведение левых и правых частей n верных неравенств aсвойств неравенств справедливо и доказываемое неравенство вида a n n . Например, в силу этого свойства справедливы неравенства 3 7 7 и .
Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем его. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями, меньшими единицы, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше. Переходим к доказательству этого свойства.
Докажем, что при m>n и 0m n . Для этого запишем разность a m −a n и сравним ее с нулем. Записанная разность после вынесения a n за скобки примет вид a n ·(a m−n −1) . Полученное произведение отрицательно как произведение положительного числа a n и отрицательного числа a m−n −1 (a n положительна как натуральная степень положительного числа, а разность a m−n −1 отрицательна, так как m−n>0 в силу исходного условия m>n , откуда следует, что при 0m−n меньше единицы). Следовательно, a m −a n m n , что и требовалось доказать. Для примера приведем верное неравенство .
Полученное произведение отрицательно как произведение положительного числа a n и отрицательного числа a m−n −1 (a n положительна как натуральная степень положительного числа, а разность a m−n −1 отрицательна, так как m−n>0 в силу исходного условия m>n , откуда следует, что при 0m−n меньше единицы). Следовательно, a m −a n m n , что и требовалось доказать. Для примера приведем верное неравенство .
Осталось доказать вторую часть свойства. Докажем, что при m>n и a>1 справедливо a m >a n . Разность a m −a n после вынесения a n за скобки принимает вид a n ·(a m−n −1) . Это произведение положительно, так как при a>1 степень a n есть положительное число, и разность a m−n −1 есть положительное число, так как m−n>0 в силу начального условия, и при a>1 степень a m−n больше единицы. Следовательно, a m −a n >0 и a m >a n , что и требовалось доказать. Иллюстрацией этого свойства служит неравенство 3 7 >3 2 .
Свойства степеней с целыми показателями
Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.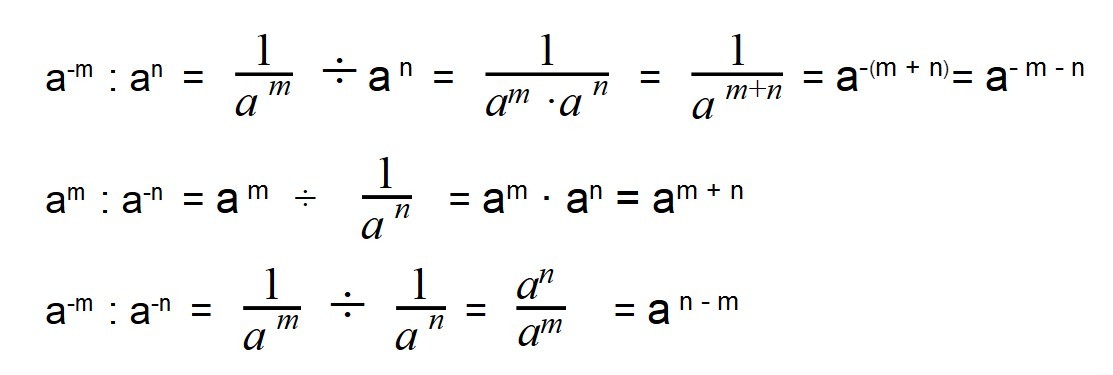
Степень с целым отрицательным показателем, а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.
Итак, для любых действительных и отличных от нуля чисел a и b , а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями :
При a=0 степени a m и a n имеют смысл лишь когда и m , и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.
Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.
Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (a p) q =a p·q , (a −p) q =a (−p)·q , (a p) −q =a p·(−q) и (a −p) −q =a (−p)·(−q) . Сделаем это.
Для положительных p и q равенство (a p) q =a p·q доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0·q =a 0 =1 , откуда (a 0) q =a 0·q . Аналогично, если q=0 , то (a p) 0 =1 и a p·0 =a 0 =1 , откуда (a p) 0 =a p·0 . Если же и p=0 и q=0 , то (a 0) 0 =1 0 =1 и a 0·0 =a 0 =1 , откуда (a 0) 0 =a 0·0 .
Теперь докажем, что (a −p) q =a (−p)·q . По определению степени с целым отрицательным показателем , тогда . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению является степенью вида a −(p·q) , которую в силу правил умножения можно записать как a (−p)·q .
Аналогично .
И .
По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.
В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a −n >b −n , которое справедливо для любого целого отрицательного −n и любых положительных a и b , для которых выполняется условие a. Запишем и преобразуем разность левой и правой частей этого неравенства: . Так как по условию an n , следовательно, b n −a n >0 . Произведение a n ·b n тоже положительно как произведение положительных чисел a n и b n . Тогда полученная дробь положительна как частное положительных чисел b n −a n и a n ·b n . Следовательно, откуда a −n >b −n , что и требовалось доказать.
Следовательно, откуда a −n >b −n , что и требовалось доказать.
Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.
Свойства степеней с рациональными показателями
Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:
- свойство произведения степеней с одинаковыми основаниями при a>0 , а если и , то при a≥0 ;
- свойство частного степеней с одинаковыми основаниями при a>0 ;
- свойство произведения в дробной степени при a>0 и b>0 , а если и , то при a≥0 и (или) b≥0 ;
- свойство частного в дробной степени при a>0 и b>0 , а если , то при a≥0 и b>0 ;
- свойство степени в степени при a>0 , а если и , то при a≥0 ;
- свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b , a0 справедливо неравенство a p p , а при p p >b p ;
- свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q .

- a p ·a q =a p+q ;
- a p:a q =a p−q ;
- (a·b) p =a p ·b p ;
- (a:b) p =a p:b p ;
- (a p) q =a p·q ;
- для любых положительных чисел a и b , a0 справедливо неравенство a p p , а при p p >b p ;
- для иррациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q .
Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем доказательства.
По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено.
Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:
По схожим принципам доказываются и остальные равенства:
Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b , a0 справедливо неравенство a p p , а при p p >b p . Запишем рациональное число p как m/n , где m – целое число, а n – натуральное. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При m>0 и am m . Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, a p p .
Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При m>0 и am m . Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, a p p .
Аналогично, при m m >b m , откуда , то есть, и a p >b p .
Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q . Мы всегда можем привести к общему знаменателю рациональные числа p и q , пусть при этом мы получим обыкновенные дроби и , где m 1 и m 2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m 1 >m 2 , что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0m 1 m 2 , а при a>1 – неравенство a m 1 >a m 2 . Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 – неравенство a p >a q .
Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 – неравенство a p >a q .
Свойства степеней с иррациональными показателями
Из того, как определяется степень с иррациональным показателем, можно заключить, что она обладает всеми свойствами степеней с рациональными показателями. Так для любых a>0 , b>0 и иррациональных чисел p и q справедливы следующие свойства степеней с иррациональными показателями :
Отсюда можно сделать вывод, что степени с любыми действительными показателями p и q при a>0 обладают этими же свойствами.
- Алгебра – 10 класс. Тригонометрические уравнения Урок и презентация на тему: «Решение простейших тригонометрических уравнений» Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы […]
- Открыт конкурс на позицию «ПРОДАВЕЦ — КОНСУЛЬТАНТ»: Обязанности: продажа мобильных телефонов и аксессуаров для мобильной связи сервисное обслуживание абонентов Билайн, Теле2, МТС подключение тарифных планов и услуг Билайн и Теле2, МТС консультирование […]
- Параллелепипед формулы Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом. Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником. Любой параллелепипед характеризуется 3 […]
- ПРАВОПИСАНИЕ Н И НН В РАЗНЫХ ЧАСТЯХ РЕЧИ С.Г.ЗЕЛИНСКАЯ ДИДАКТИЧЕСКИЙ МАТЕРИАЛ Теоретическая зарядка 1. Когда в прилагательных пишется нн? 2. Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […]
- ИНСПЕКЦИЯ ГОСТЕХНАДЗОРА БРЯНСКОЙ ОБЛАСТИ
Квитанция об оплате госпошлины(Скачать-12,2 kb)
Заявления на регистрацию для физ.
 лиц(Скачать-12 kb)
Заявления на регистрацию для юр.лиц(Скачать-11,4 kb)
1. При регистрации новой машины:
1.заявление 2.паспорт […]
лиц(Скачать-12 kb)
Заявления на регистрацию для юр.лиц(Скачать-11,4 kb)
1. При регистрации новой машины:
1.заявление 2.паспорт […] - Общество защиты прав потребителя астана Для того, что бы получить pin-код для доступа к данному документу на нашем сайте, отправьте sms-сообщение с текстом zan на номер Абоненты GSM-операторов (Activ, Kcell, Beeline, NEO, Tele2) отправив SMS на номер, […]
- Принять закон о Родовых поместьях Принять федеральный закон о безвозмездном выделении каждому желающему гражданину Российской Федерации или семье граждан участка земли для обустройства на нем Родового Поместья на следующих условиях: 1. Участок выделяется для […]
- Пивоев В.М. Философия и методология науки: учебное пособие для магистров и аспирантов Петрозаводск: Изд-во ПетрГУ, 2013. ― 320 с.ISBN 978-5-821-1647-0 PDF 3 mb Учебное пособие предназначено для студентов старших курсов, магистров и аспирантов социального и […]
Степень с отрицательным показателем. Деление степеней с одинаковым основанием. 4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю. Основание и аргумент первого логарифма — точные степени. Данное свойство распространяется на степень произведения трех и большего количества множителей. Следовательно, am−an>0 и am>an, что и требовалось доказать. Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями.
4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю. Основание и аргумент первого логарифма — точные степени. Данное свойство распространяется на степень произведения трех и большего количества множителей. Следовательно, am−an>0 и am>an, что и требовалось доказать. Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке. То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным. Вычисление значения степени называют действием возведения в степень. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).
После того как определена степень числа, логично поговорить про свойства степени. В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров. Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами.
Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров. Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами.
Приведем пример, подтверждающий основное свойство степени. Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Основное свойство дроби позволяет записать равенство am−n·an=a(m−n)+n=am.
Переход к новому основанию
То есть, свойство натуральной степени n произведения k множителей записывается как (a1·a2·…·ak)n=a1n·a2n·…·akn. Для наглядности покажем это свойство на примере. Доказательство можно провести, используя предыдущее свойство. Например, для любых натуральных чисел p, q, r и s справедливо равенство. Для большей ясности приведем пример с конкретными числами: (((5,2)3)2)5=(5,2)3+2+5=(5,2)10.
Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. Достаточно очевидно, что для любого натурального n при a=0 степень an есть нуль. Действительно, 0n=0·0·…·0=0. К примеру, 03=0 и 0762=0. Переходим к отрицательным основаниям степени. Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m, где m — натуральное.
Переходим к доказательству этого свойства. Докажем, что при m>n и 0По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями.
Операции с корнями. Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем;нодействиясостепенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения. Если мы хотим, чтобы формула a m: a n=a m — nбыла справедлива при m = n,нам необходимо определение нулевой степени. Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать.
Все эти показатели степеней требуют дополнительного определения. Если мы хотим, чтобы формула a m: a n=a m — nбыла справедлива при m = n,нам необходимо определение нулевой степени. Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать.
Вынесение показателя степени из логарифма
Если основания разные, эти правила не работают! Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств. Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами. Часто в процессе решения требуется представить число как логарифм по заданному основанию.
Свойства степеней, формулировки, доказательства, примеры.
Число n может быть абсолютно любым, ведь это просто значение логарифма. Она так и называется: основное логарифмическое тождество. Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением. В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма.
Примеры решения примеров с дробями, содержащими числа со степенями
Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице. 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения. Вот и все свойства. Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.
Логарифмическая единица и логарифмический ноль
2.a-4 есть a-2 первый числитель. В этом случае советуем поступать следующим образом. Это действие третьей ступени. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0n=0, а при знакомстве с делением мы условились, что на нуль делить нельзя. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями.
Это действие третьей ступени. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0n=0, а при знакомстве с делением мы условились, что на нуль делить нельзя. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями.
Аналогично, если q=0, то (ap)0=1 и ap·0=a0=1, откуда (ap)0=ap·0. В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. Эти неравенства по свойствам корней можно переписать соответственно как и. А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно.
Деление степеней с одинаковым основанием. Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями.
3.a-3 есть a0 = 1, второй числитель. В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. Теперь рассмотрим их на конкретных примерах и попробуем доказать.
Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать. После того как определена степень числа, логично поговорить про свойства степени.
Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an. Приведем пример, подтверждающий основное свойство степени. Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке.
Свойства степеней с натуральными показателями
Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями. Для наглядности покажем это свойство на примере. Например, для любых натуральных чисел p, q, r и s справедливо равенство. Для большей ясности приведем пример с конкретными числами: (((5,2)3)2)5=(5,2)3+2+5=(5,2)10.
Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями. Для наглядности покажем это свойство на примере. Например, для любых натуральных чисел p, q, r и s справедливо равенство. Для большей ясности приведем пример с конкретными числами: (((5,2)3)2)5=(5,2)3+2+5=(5,2)10.
Сложение и вычитание одночленов
Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. Достаточно очевидно, что для любого натурального n при a=0 степень an есть нуль. Действительно, 0n=0·0·…·0=0. К примеру, 03=0 и 0762=0. Переходим к отрицательным основаниям степени. Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m, где m — натуральное.
Переходим к доказательству этого свойства. Докажем, что при m>n и 0Осталось доказать вторую часть свойства. Следовательно, am−an>0 и am>an, что и требовалось доказать. Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами.
Следовательно, am−an>0 и am>an, что и требовалось доказать. Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами.
Если p=0, то имеем (a0)q=1q=1 и a0·q=a0=1, откуда (a0)q=a0·q. По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно.
При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Эти неравенства по свойствам корней можно переписать соответственно как и. А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно.
Основные свойства логарифмов
Вычисление значения степени называют действием возведения в степень. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание). 1. Если Вы теперь аккуратно воспользуетесь свойствами степеней (при возведении степени в степень показатели…
1. Если Вы теперь аккуратно воспользуетесь свойствами степеней (при возведении степени в степень показатели…
То есть показатели степени действительно вычитаются, но, поскольку в знаменателе у степени показатель отрицательный, при вычитании минус на минус даёт плюс, и показатели складываются. Вспомним, что называется одночленом, и какие операции можно делать с одночленами. Напомним, что для приведения одночлена к стандартному виду необходимо вначале получить численный коэффициент, перемножив все численные множители, а после этого перемножить соответствующие степени.
Переход к новому основанию
То есть, мы должны научиться различать подобные и не подобные одночлены. Сделаем вывод: подобные одночлены имеют одинаковую буквенную часть, и такие одночлены можно складывать и вычитать.
Спасибо Вам за отзыв. Если наш проект вам понравился и вы готовы помочь или принять участие в нём, перешлите информацию о проекте знакомым и коллегам. В предыдущем видео говорилось,что в примерах с одночленами может быть только умножение:»Найдем отличие этих выражений от предыдущих.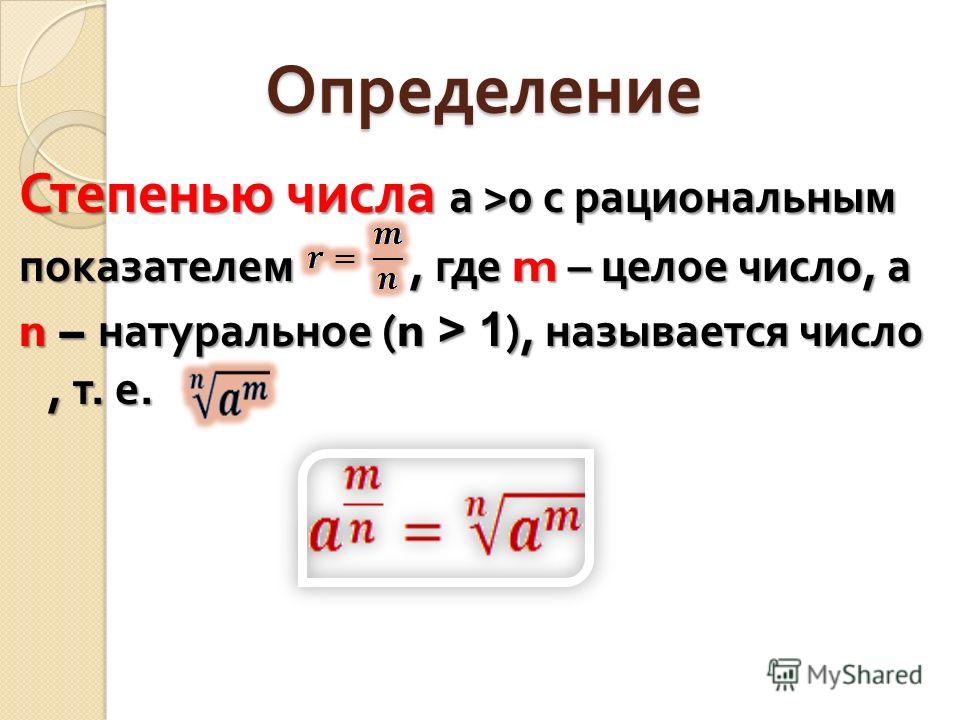
Само понятие одночлена как математической единицы подразумевает только умножение чисел и переменных, если есть другие операции, выражение уже не будет одночленом. Но вместе с тем между собой одночлены можно складывать, вычитать, делить… Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.
Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают! Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
То есть, свойство натуральной степени n произведения k множителей записывается как (a1·a2·…·ak)n=a1n·a2n·…·akn. Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует. Основание и аргумент первого логарифма — точные степени. 4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю.
Основание и аргумент первого логарифма — точные степени. 4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю.
В прошлом видеоуроке мы узнали, что степенью некоего основания называется такое выражение, которое представляет собой произведение основания на самого себя, взятого в количестве, равном показателю степени. Изучим теперь некоторые важнейшие свойства и операции степеней.
Например, умножим две разные степени с одинаковым основанием:
Представим это произведение в полном виде:
(2) 3 * (2) 2 = (2)*(2)*(2)*(2)*(2) = 32
Вычислив значение этого выражения, мы получим число 32. С другой стороны, как видно из этого же примера, 32 можно представить в виде произведения одного и того же основания (двойки), взятого в количестве 5 раз. И действительно, если пересчитать, то:
Таким образом, можно с уверенностью прийти к выводу, что:
(2) 3 * (2) 2 = (2) 5
Подобное правило успешно работает для любых показателей и любых оснований. Это свойство умножения степени вытекает из правила сохранности значения выражений при преобразованиях в произведении. При любом основании а произведение двух выражений (а)х и (а)у равно а(х + у). Иначе говоря, при произведении любых выражений с одинаковым основанием, итоговый одночлен имеет суммарную степень, образующуюся сложением степени первого и второго выражений.
Это свойство умножения степени вытекает из правила сохранности значения выражений при преобразованиях в произведении. При любом основании а произведение двух выражений (а)х и (а)у равно а(х + у). Иначе говоря, при произведении любых выражений с одинаковым основанием, итоговый одночлен имеет суммарную степень, образующуюся сложением степени первого и второго выражений.
Представляемое правило прекрасно работает и при умножении нескольких выражений. Главное условие — что бы основания у всех были одинаковыми. Например:
(2) 1 * (2) 3 * (2) 4 = (2) 8
Нельзя складывать степени, да и вообще проводить какие-либо степенные совместные действия с двумя элементами выражения, если основания у них являются разными.
Как показывает наше видео, в силу схожести процессов умножения и деления правила сложения степеней при произведении прекрасно передаются и на процедуру деления. Рассмотрим такой пример:
Произведем почленное преобразование выражения в полный вид и сократим одинаковые элементы в делимом и делителе:
(2)*(2)*(2)*(2)*(2)*(2) / (2)*(2)*(2)*(2) = (2)(2) = (2) 2 = 4
Конечный результат этого примера не так интересен, ведь уже в ходе его решения ясно, что значение выражения равно квадрату двойки. И именно двойка получается при вычитании степени второго выражения из степени первого.
И именно двойка получается при вычитании степени второго выражения из степени первого.
Чтобы определить степень частного необходимо из степени делимого вычесть степень делителя. Правило работает при одинаковом основании для всех его значений и для всех натуральных степеней. В виде абстракции имеем:
(а) х / (а) у = (а) х — у
Из правила деления одинаковых оснований со степенями вытекает определение для нулевой степени. Очевидно, что следующее выражение имеет вид:
(а) х / (а) х = (а) (х — х) = (а) 0
С другой стороны, если мы произведем деление более наглядным способом, то получим:
(а) 2 / (а) 2 = (а) (а) / (а) (а) = 1
При сокращении всех видимых элементов дроби всегда получается выражение 1/1, то есть, единица. Поэтому принято считать, что любое основание, возведенное в нулевую степень, равно единице:
Вне зависимости от значения а.
Однако будет абсурдно, если 0 (при любых перемножениях дающий все равно 0) будет каким-то образом равен единице, поэтому выражение вида (0) 0 (ноль в нулевой степени) просто не имеет смысла, а к формуле (а) 0 = 1 добавляют условие: «если а не равно 0».
Решим упражнение. Найдем значение выражения:
(34) 7 * (34) 4 / (34) 11
Так как основание везде одинаково и равно 34, то итоговое значение будет иметь такое же основание со степенью (согласно вышеуказанных правил):
Иначе говоря:
(34) 7 * (34) 4 / (34) 11 = (34) 0 = 1
Ответ: выражение равно единице.
Как умножать степень числа разным основанием. Как умножать степени, умножение степеней с разными показателями
В прошлом видеоуроке мы узнали, что степенью некоего основания называется такое выражение, которое представляет собой произведение основания на самого себя, взятого в количестве, равном показателю степени. Изучим теперь некоторые важнейшие свойства и операции степеней.
Например, умножим две разные степени с одинаковым основанием:
Представим это произведение в полном виде:
(2) 3 * (2) 2 = (2)*(2)*(2)*(2)*(2) = 32
Вычислив значение этого выражения, мы получим число 32. С другой стороны, как видно из этого же примера, 32 можно представить в виде произведения одного и того же основания (двойки), взятого в количестве 5 раз. И действительно, если пересчитать, то:
И действительно, если пересчитать, то:
Таким образом, можно с уверенностью прийти к выводу, что:
(2) 3 * (2) 2 = (2) 5
Подобное правило успешно работает для любых показателей и любых оснований. Это свойство умножения степени вытекает из правила сохранности значения выражений при преобразованиях в произведении. При любом основании а произведение двух выражений (а)х и (а)у равно а(х + у). Иначе говоря, при произведении любых выражений с одинаковым основанием, итоговый одночлен имеет суммарную степень, образующуюся сложением степени первого и второго выражений.
Представляемое правило прекрасно работает и при умножении нескольких выражений. Главное условие — что бы основания у всех были одинаковыми. Например:
(2) 1 * (2) 3 * (2) 4 = (2) 8
Нельзя складывать степени, да и вообще проводить какие-либо степенные совместные действия с двумя элементами выражения, если основания у них являются разными.
Как показывает наше видео, в силу схожести процессов умножения и деления правила сложения степеней при произведении прекрасно передаются и на процедуру деления. Рассмотрим такой пример:
Рассмотрим такой пример:
Произведем почленное преобразование выражения в полный вид и сократим одинаковые элементы в делимом и делителе:
(2)*(2)*(2)*(2)*(2)*(2) / (2)*(2)*(2)*(2) = (2)(2) = (2) 2 = 4
Конечный результат этого примера не так интересен, ведь уже в ходе его решения ясно, что значение выражения равно квадрату двойки. И именно двойка получается при вычитании степени второго выражения из степени первого.
Чтобы определить степень частного необходимо из степени делимого вычесть степень делителя. Правило работает при одинаковом основании для всех его значений и для всех натуральных степеней. В виде абстракции имеем:
(а) х / (а) у = (а) х — у
Из правила деления одинаковых оснований со степенями вытекает определение для нулевой степени. Очевидно, что следующее выражение имеет вид:
(а) х / (а) х = (а) (х — х) = (а) 0
С другой стороны, если мы произведем деление более наглядным способом, то получим:
(а) 2 / (а) 2 = (а) (а) / (а) (а) = 1
При сокращении всех видимых элементов дроби всегда получается выражение 1/1, то есть, единица. Поэтому принято считать, что любое основание, возведенное в нулевую степень, равно единице:
Поэтому принято считать, что любое основание, возведенное в нулевую степень, равно единице:
Вне зависимости от значения а.
Однако будет абсурдно, если 0 (при любых перемножениях дающий все равно 0) будет каким-то образом равен единице, поэтому выражение вида (0) 0 (ноль в нулевой степени) просто не имеет смысла, а к формуле (а) 0 = 1 добавляют условие: «если а не равно 0».
Решим упражнение. Найдем значение выражения:
(34) 7 * (34) 4 / (34) 11
Так как основание везде одинаково и равно 34, то итоговое значение будет иметь такое же основание со степенью (согласно вышеуказанных правил):
Иначе говоря:
(34) 7 * (34) 4 / (34) 11 = (34) 0 = 1
Ответ: выражение равно единице.
Если умножаются (или делятся) две степени, у которых разные основания, но одинаковые показатели, то их основания можно перемножить (или поделить), а показатель степени у результата оставить таким же как у множителей (или делимого и делителя).
В общем виде на математическом языке эти правила записываются так:
a m × b m = (ab) m
a m ÷ b m = (a/b) m
При делении b не может быть равно 0, то есть второе правило надо дополнить условием b ≠ 0.
Примеры:
2 3 × 3 3 = (2 × 3) 3 = 63 = 36 × 6 = 180 + 36 = 216
6 5 ÷ 3 5 = (6 ÷ 3) 5 = 2 5 = 32
Теперь на этих конкретных примерах докажем, что правила-свойства степеней с одинаковыми показателями верны. Решим данные примеры так, как будто мы не знаем о свойствах степеней:
2 3 × 3 3 = (2 × 2 × 2) × (3 × 3 × 3) = 2 × 2 × 2 × 3 × 3 × 3 = 8 × 27 = 160 + 56 = 216
65 ÷ 35 = (6 × 6 × 6 × 6 × 6) ÷ (3 × 3 × 3 × 3 × 3) == 2 × 2 × 2 × 2 × 2 = 32
Как мы видим, ответы совпали с теми, которые были получены, когда использовались правила. Знание этих правил позволяет упростить вычисления.
Обратите внимание, что выражение 2 × 2 × 2 × 3 × 3 × 3 можно представить в таком виде:
(2 × 3) × (2 × 3) × (2 × 3).
Это выражение в свою очередь есть нечто иное как (2 × 3) 3. то есть 6 3 .
Рассмотренные свойства степеней с одинаковыми показателями могут быть использованы в обратную сторону. Например, сколько будет 18 2 ?
18 2 = (3 × 3 × 2) 2 = 3 2 × 3 2 × 2 2 = 9 × 9 × 4 = 81 × 4 = 320 + 4 = 324
Свойства степеней также используются при решении примеров:
= 2 4 × 3 6 = 2 4 × 3 4 × 3 × 3 = 6 4 × 3 2 = 6 2 × 6 2 × 3 2 = (6 × 6 × 3) 2 = 108 2 = 108 × 108 = 108 (100 + 8) = 10800 + 864 = 11664
Правило деления степеней. При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. Примеры:
При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. Примеры:
Слайд 11 из презентации «Деление и умножение степеней» к урокам алгебры на тему «Степень»
Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке алгебры, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Деление и умножение степеней.ppt» можно в zip-архиве размером 1313 КБ.
«Деление и умножение степеней» — a2 a3 = a2+3 = a5. a3 = a · a · a. Найдем произведение a2 и a3. 100. 2+3. 5 раз. 64 = 144 = 1 0000 =. Умножение и деление степеней. 3 раза. a2 a3 =.
«Степени двойки» — 1024+. Правила перевода из одной системы счисления в другую. Гусельникова Е.В. Школа №130. Содержание. Таблица степеней двойки. Переведём число 1998 из десятичной в двоичную систему. Кислых В.Н. 11Э Зинько К.О. 11Э. Преподаватель: Выполнили: Рассмотрим схему преобразования на примере.
«Степень с отрицательным показателем» — Степень с отрицательным показателем. 5 12?3 (27?3). -2. -1. Вычислите: -3.
«Степень с рациональным показателем» — по теме: «Степень с рациональным показателем». Цели урока: I. Организационная часть. Проверка домашнего задания 1.Математический диктант 2. Взаимопроверка III.Самостоятельная работа IV. Обобщающий урок. Ход урока. Подготовка к контрольной работе V. Подведение итогов урока VI. II.
«Степень с целым показателем» — Представьте выражение в виде степени. X-12. Расположите в порядке убывания. Представьте выражение x-12 в виде произведения двух степеней с основанием x, если один множитель известен. Вычислите. Упростите.
«Свойства степени» — Обобщение знаний и умений по применению свойств степени с натуральным показателем. Вычислительная пауза. Свойства степени с натуральным показателем. Проверь себя! Применение знаний для решения различных по сложности задач. Тест. Физминутка. Развитие настойчивости, мыслительной активности и творческой деятельности.
Правило деление степеней
1. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):
(abc…) n = a n b n c n …
Пример 1. (7 2 10) 2 = 7 2 2 2 10 2 = 49 4 100 = 19600. Пример 2. (x 2 –a 2) 3 = [(x +a)(x — a)] 3 =(x +a) 3 (x — a) 3
Практически более важно обратное преобразование:
a n b n c n … = (abc…) n
т.е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.
Пример 3. Пример 4. (a +b) 2 (a 2 – ab +b 2) 2 =[(a +b)(a 2 – ab +b 2)] 2 =(a 3 +b 3) 2
2. Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:
Пример 5. Пример 6.
Обратное преобразование:. Пример 7.. Пример 8..
3. При умножении степеней с одинаковыми основаниями показатели степеней складываются:
Пример 9.2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .
4. При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого
Пример 11. 12 5:12 3 =12 5-3 =12 2 =144. Пример 12. (x-y) 3:(x-y) 2 =x-y.
5. При возведении степени в степень показатели степеней перемножаются:
Пример 13. (2 3) 2 =2 6 =64. Пример 14.
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел. 3$
3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Алгебра – 7 класс.
 n$.
n$. mathematics-tests.com
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
(2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т. e. 1 = 1, откуда следует,
e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
- Правила техники безопасности при работе утюгом Правила техники безопасности при работе утюгом. 1.Перед включением утюга в электросеть нужно проверить изоляцию шнура и положение утюга на подставке. 2.Включение и […]
- Проблемы водного налога Состояние, анализ и проблемы совершенствования водного налога При заборе воды сверх установленных квартальных (годовых) лимитов водопользования налоговые ставки в части такого превышения […]
- как составить приказ о переходе с 223фз на 44 фз Сергей Антонов 30 Ответ написан год назад Профессор 455 Ответ написан год назад Например: приказ об отмене применения положения о закупках. Оценка ответа: 0 Добавить […]
- Деление отрицательных чисел Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению. Если « a » и « b » положительные числа, то разделить число « a » на число « […]
- Разрешения D1, 960Н, 720Р, 960Р, 1080Р
Системы видеонаблюдения получают все большее распространение по всему миру.
 Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […]
Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […] - Конституционное право Российской Федерации. Баглай М.В. 6-е изд., изм. и доп. — М.: Норма, 200 7 . — 7 84 с. Настоящий учебник, представляющий собой шестое, измененное и дополненное, издание, написан известным […]
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов. 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
7 класс. Алгебра. Степень с натуральным показателем и ее свойства. — Умножение и деление степеней с одинаковыми основаниями.
Комментарии преподавателяНа этом уроке мы изучим умножение степеней с одинаковыми основаниями. Вначале вспомним определение степени и сформулируем теорему о справедливости равенства . Затем приведем примеры ее применения на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач.
Тема: Степень с натуральным показателем и ее свойства
Урок: Умножение степеней с одинаковыми основаниями (формула )
Основные определения:
Здесь a — основание степени,
n — показатель степени,
— n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
По-иному: если а – любое число; n и k натуральные числа, то:
Отсюда правило 1:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Разъясняющие примеры:
1)
2)
Вывод: частные случаи подтвердили правильность теоремы №1. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
Дано число а – любое; числа n и k – натуральные. Доказать:
Доказательство основано на определении степени.
То есть
Пример 1: Представьте в виде степени.
Для решения следующих примеров воспользуемся теоремой 1.
а)
б)
в)
г)
д)
е)
ж)
Здесь использовано обобщение:
з)
и)
к)
л)
м)
Пример 2: Вычислите (можно использовать таблицу основных степеней).
а) (по таблице)
б)
Пример 3: Запишите в виде степени с основанием 2.
а)
б)
в)
г)
Пример 4: Определите знак числа:
, а – отрицательное, так как показатель степени при -13 нечетный.
По-иному:
Пример 5: Замените (·) степенью числа с основанием r:
Имеем , то есть .
На этом уроке мы изучим деление степеней с одинаковыми основаниями. Вначале вспомним определение степени и теорему об умножении степеней с одинаковыми основаниями. Далее мы сформулируем теорему о делении степеней с одинаковыми основаниями, решим разъясняющие задачи и докажем теорему в общем случае. Затем мы применим теорему для решения различных задач, а также решим типичные задачи с использованием обеих теорем.
Тема: Степень с натуральным показателем и ее свойства
Урок: Деление степеней с одинаковыми основаниями (формула )
Основные определения:
Здесь a — основание степени,
n — показатель степени,
— n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
Разъясняющие задачи
1)
2)
Вывод: частные случаи подтвердили правильность теоремы №2. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k таких, что n > k.
Доказательство теоремы 2.
Первый способ.
Воспользуемся теоремой 1. Применим ее для степеней и .
Применим ее для степеней и .
. Разделим обе части на .
Второй способ.
Доказательство основано на определении степени
Сократим k сомножителей.
То есть для любого а и любых натуральных n и k таких, что n > k.
Пример 1: Вычислить.
Для решения следующих примеров воспользуемся теоремой 2.
а)
б)
Пример 2: Упростить.
а)
б)
в)
Пример 3: Решить уравнение.
а)
б)
Пример 4: Вычислить:
Для решения следующих примеров будем пользоваться обеими теоремами.
а) =6 или быстрее =6
б) ==81 или быстрее =81
в) == или быстрее
Пример 5: Упростить:
а) = или быстрее
б)
в) или быстрее
Источники конспекта: http://interneturok. ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/umnozhenie-stepeney-s-odinakovymi-osnovaniyami-formula-a-sup-n-sup-8727a-sup-k-sup-a-sup-n-k-sup?konspekt&chapter_id=2
ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/umnozhenie-stepeney-s-odinakovymi-osnovaniyami-formula-a-sup-n-sup-8727a-sup-k-sup-a-sup-n-k-sup?konspekt&chapter_id=2
http://interneturok.ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/delenie-stepeney-s-odinakovymi-osnovaniyami?konspekt&chapter_id=2
Источник видео: http://www.youtube.com/watch?v=IQPWIC6GXuI
Умножение и деление степеней с одинаковыми основаниями
Урок алгебры в 7 классе
Гришко Е.М., учитель математики МБОУ «СОШ №4», г.Красноперекопск, Республика Крым
Цели урока:
— вывести правила умножения и деления степеней с одинаковыми основаниями;
— дать определение нулевой степени числа, не равного нулю;
— формировать умение выполнять указанные действия со степенями.
Задачи урока:
Образовательные (формирование познавательных УУД):
— познакомить учащихся со степенью с натуральным показателем;
— тренировать способность к использованию выведенного алгоритма;
— организовать деятельность учащихся по приобретению необходимых умений и навыков;
— повторить и закрепить;
Воспитательные (формирование коммуникативных и личностных УУД):
— содействовать развитию познавательного интереса учащихся к предмету;
— прививать учащимся навыки организации самостоятельной работы;
— умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
Развивающие (формирование регулятивных УУД): развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей.
Тип урока: изучение и первичное закрепление новых знаний.
Оборудование: презентация, раздаточный материал; лист целеполагания (Приложение 1) и лист самоконтроля (Приложение 2).
Ход урока:
Презентация
I. Организационный (мотивационный) момент
Здравствуйте, ребята! Садитесь! Прежде чем начать урок, мне бы хотелось рассказать одну притчу.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому вопрос. У первого спросил: «Что ты делал целый день»? И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?». И тот ответил: «А я добросовестно выполнял свою работу». Третьему человеку задал свой вопрос мудрец и в ответ услышал: «А я принимал участие в строительстве храма!»
И тот ответил: «А я добросовестно выполнял свою работу». Третьему человеку задал свой вопрос мудрец и в ответ услышал: «А я принимал участие в строительстве храма!»
Желаю и вам, ребята, сегодня принять участие в строительстве храма ваших знаний.
II. Актуализация знаний и фиксация затруднения в деятельности (актуализировать учебный материал необходимый для изучения нового, зафиксировать затруднения в деятельности)
1. Проверка домашнего задания (Слайд 2)
Откройте тетради, запишите число и классная работа. Что было задано на дом? (№377, 386 (а,в), 388 (а-г), 400)
Проверка домашнего задания № 388.
Решение:
а) –13 + (–2)3 = –1 + (–8) = –9;
б) –62 – (–1)4 = –36 – 1 = –37;
в) –83 + (–3)3 = –512 + (–27) = –539;
г) 10 – 5 · 24 = 10 – 5 · 16 = 10 – 80 = –70;
Поменяйтесь тетрадями с партнёром по плечу, оцените работу партнёра с решением, которое представлено на доске.
2. Устная работа (Слайды 3-5)
Для дальнейшей работы по этой теме нам нужно будет вспомнить элементарные правила степеней. Ответьте на вопросы:
а) Что такое степень?
б) Чему равна степень отрицательного числа с четным показателем?
в) Чему равна степень отрицательного числа с нечетным показателем?
г) Что получится при возведении в степень с натуральным показателем числа нуль?
3. Вычислите: Слайд 6
4. Проверочная работа. Найдите значение выражения: Слайд 7
5. Работа в парах. Вычислите: Слайд 8
(Возникает затруднение при выполнении последних двух заданий)
Выход на проблему и постановка учебной задачи на урок (задачу на урок ставят сами дети)
III. Постановка цели и задач урока. Мотивация учебной деятельности
Слайд 9
Построение проекта выхода из затруднения и открытие нового знания.
Записывают тему урока и разрабатывают план действий:
— представить степени в виде произведения,
— вычислить значение степени,
— провести анализ полученного затруднения,
— записать формулу в общем виде,
— сформулировать соответствующее правило
Работа с учебником (стр.99-101)
Слайды 10-11
Вернемся к тем заданиям, где возникли затруднения в ходе устной работы
IV. Усвоение новых знаний и способов действий
Первичное закрепление (учебник «Алгебра 7 класс», автор Макарычев Ю.Н.)
№ 403 (а, е, ж,з), № 405 (а-г), № 407, 409 (а, в, д, е), 410 (а, в, д), 411 (а-г), 414 (а, в, з), 416 (а, б, в), 417 (а, б)
- № 403
Решение:
а) x5x8 = x5 + 8 = x13;
е) yy12 = y1 + 12 = y13;
ж) 2624 = 26 + 4 + 210; з) 757 = 75 + 1 = 76.
- № 405
Решение:
а) a15 = a6 + 9 = a6 ∙ a9; б) a15 = a9 + 6 = a9 ∙ a6;
в) a15 = a2 + 13 = a2 ∙ a13; г) a15 = a14 + 1 = a14 ∙ a = a ∙ a14.
- № 407
Решение:
Представим число 6 в виде суммы двух натуральных чисел всеми возможными способами:
6 = 1 + 5; 6 = 2 + 4; 6 = 3 + 3.
Значит, a6 = a ∙ a5; a6 = a2 ∙ a4; a6 = a3 ∙ a3.
- № 409
Решение:
а) m3m2m8 = m3 + 2 + 8 = m13; в) xx4x4x = x1 + 4 + 4 + 1 = x10;
д) 78 ∙ 7 ∙ 74 = 78 + 1 + 4 = 713; е) 5 ∙ 52 ∙ 53 ∙ 55 = 51 + 2 + 3 + 4 = 511.
- № 410
(При выполнении этого упражнения ученики сами определяют основание степени, которое будет являться общим для двух степеней)
Решение:
а) 58 ∙ 25 = 58 ∙ 52 = 58 + 2 = 510;
в) 615 ∙ 36 = 615 ∙ 62 = 615 + 2 = 617;
д) 0,45 ∙ 0,16 = 0,45 ∙ 0,42 = 0,45 + 2 = 0,47;
е) 0,001 ∙ 0,14 = 0,13 ∙ 0,14 = 0,13 + 4 = 0,17.
- № 411
Решение:
а) 24 ∙ 2 = 24 + 1 = 25 = 32;
б) 26 ∙ 4 = 26 ∙ 22 = 26 + 2 = 28 = 256;
в) 8 ∙ 27 = 23 ∙ 27 = 23 + 7 = 210 = 1024;
г) 16 ∙ 32 = 24 ∙ 25 = 24 + 5 = 29 = 512.
- № 414
Решение:
а) x5 : x3 = x5 – 3 = x2;
в) a21 : a = a21 – 1 = a20;
з) 0,79 : 0,74 = 0,79 – 4 = 0,75.
- № 416
Решение:
а) 56 : 54 = 56 – 4 = 52 = 25;
б) 1015 : 1012 = 1015 – 12 = 103 = 1000;
в) 0,510 : 0,57 = 0,510 – 7 = 0,53 = 0,125;
г) ;
д) 2,7313 : 2,7312 = 2,7313 – 12 = 2,73;
е) .
- Используя правила умножения и деления степеней, упростите выражение.
а) x8 ∙ x3 : x5; б) x20 : x10 ∙ x;
в) x7 : x3 : x3; г) x14 : x9 ∙ x5.
Решение:
а) x8 ∙ x3 : x5 = x8 + 3 : x5 = x11 : x5 = x11 – 5 = x6;
б) x20 : x10 ∙ x = x20 – 10 ∙ x = x10 ∙ x = x10 + 1 = x11;
в) x7 : x3 : x3 = x7 – 3 : x3 = x4 : x3 = x4 – 3 = x;
г) x14 : x9 ∙ x5 = x14 – 9 ∙ x5 = x5 ∙ x5 = x5 + 5 = x10.
- № 417
Решение:
а) = 86 : 84 = 86 – 4 = 82 = 64;
б) = 0,87 : 0,84 = 0,87 – 4 = 0,83 = 0,512;
в) = (–0,3)5 : (–0,3)3 = (–0,3)5 – 3 = (–0,3)2 = 0,09.
V. Физкультминутка
VI. Контроль и самоконтроль знаний и способов действий
Самостоятельная работа (по вариантам)
Раздается каждому учащемуся, решение можно выполнять прямо на листочках. После выполнения работы проверяются в классе, и каждый ученик оценивает себя сам.
VII. Включение в систему знаний и повторение.
Слайды 12-13
Задача «Определить во сколько раз масса земного шара больше массы всего окружающего его воздуха».
Решение. Чтобы убедиться, насколько облегчаются практические вычисления при пользовании степенным изображением больших чисел, выполним такой расчет: определим, во сколько раз масса земного шара больше массы всего окружающего его воздуха.
На каждый кв. сантиметр земной поверхности воздух давит, мы знаем, с силой около килограмма. Это означает, что вес того столба атмосферы, который опирается на 1 кв.см, равен 1 кг. Атмосферная оболочка Земли как бы составлена вся из таких воздушных столбов. Их столько, сколько кв. сантиметров содержит поверхность нашей планеты; столько же килограммов весит вся атмосфера. Заглянув в справочник, узнаем, что величина поверхности земного шара равна 510 млн. кв. км, т.е. 51 × 107 кв. км.
Рассчитаем, сколько квадратных сантиметров в квадратном километре. Линейный километр содержит 1000 м, по 100 см в каждом, т.е. равен 105 см, а кв. километр содержит (105)2 = 1010 кв. сантиметров. Во всей поверхности земного шара заключается поэтому
51 × 107× 1010 = 51 × 1017 кв. сантиметров.
Столько же килограммов весит и атмосфера Земли. Переведя в тонны, получим:
51 × 1017 : 1000 = 51 × 1017 : 103=51 × 1017-3 = 51 × 1014.
Масса же земного шара выражается числом
6 × 1021 тонн.
Чтобы определить, во сколько раз наша планета тяжелее ее воздушной оболочки, производим деление:
6 × 1021 : 51 × 1014 ≈ 106,
т. е. масса атмосферы составляет примерно миллионную долю массы земного шара
VIII. Рефлексия учебной деятельности на уроке, подведение итогов
- Дайте определение степени с натуральным показателем.
- Сформулируйте правило возведения отрицательного числа в четную степень, в нечетную степень.
- Какой знак имеет результат возведения любого числа в квадрат?
- Сформулируйте правила сложения и умножения степеней с одинаковыми основаниями.
- Чему равно значение выражения 20; (–1)1?
Заполнить пункты «знаю» и «умею» таблицы целеполагания.
Заполнение листов самоконтроля.
Пожалуйста, поделитесь своими мыслями о сегодняшнем занятии (хотите одним предложением). Вам для этого помогут слова:
Вам для этого помогут слова:
* Сегодня на уроке я закрепил…
* На что мне нужно обратить внимание…
IX. Информация о домашнем задании(Слайд 14)
П.16 выучить правила. Решить задания:
I уровень: №404, 408, 415, 418;
II уровень: №406, 412, 419 (б,г,е), 533.
Выразить массу Земли и Луны в различных единицах массы (в граммах, килограммах, в центнерах и тоннах)
Приложение 1
Лист целеполагания
Ф.И.___________________________________________
| Вопросы | Знаю | Не знаю | Хочу знать |
| Что такое степень с натуральным показателем? | |||
| Как возвести отрицательное число в степень? | |||
| Как умножать степени с одинаковыми основаниями? | |||
| Как делить степени с одинаковыми основаниями? | |||
| Как возвести число в степень с нулевым показателем? |
Приложение 2
Лист самоконтроля
Ф. И.________________________________________________
И.________________________________________________
| № | Виды работ | Оценка | |
| 1 | Проверка домашнего задания | ||
| 2 | Устная работа | ||
| 3 | Работа в парах | ||
| 4 | Самостоятельная работа по вариантам | ||
| 5 | Решение задачи | ||
| Средняя оценка: |
Используемые учебники и учебные пособия:
Учебник для общеобразовательных учреждений /Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под редакцией С.А. Теляковского
Источник: uchportal.ru
Умножение степеней примеры. Степень — свойства, правила, действия и формулы
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.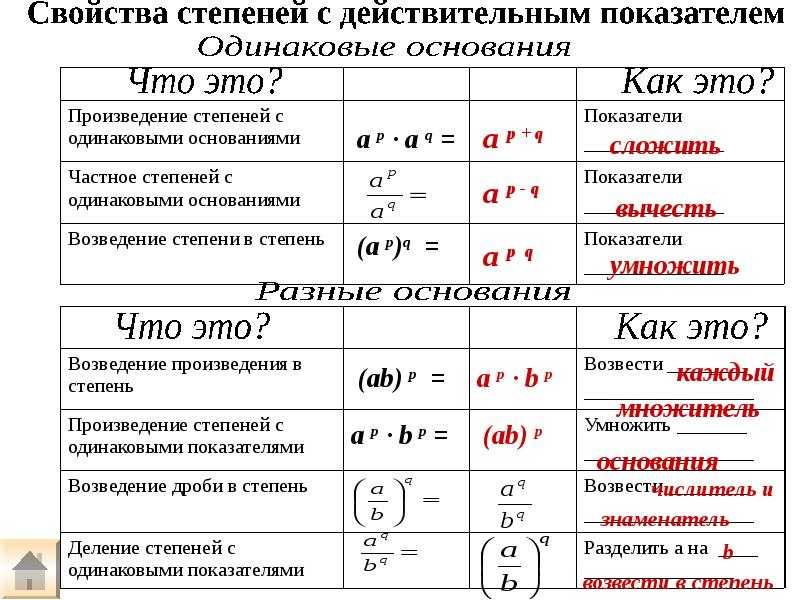
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Онлайн-калькулятор возведения в степень
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.
Математически это выглядит следующим образом:
a n = a * a * a * …a n .
Например:
- 2 3 = 2 в третьей степ. = 2 * 2 * 2 = 8;
- 4 2 = 4 в степ. два = 4 * 4 = 16;
- 5 4 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
- 10 5 = 10 в 5 степ.
 = 10 * 10 * 10 * 10 * 10 = 100000;
= 10 * 10 * 10 * 10 * 10 = 100000; - 10 4 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- a n * a m = (a) (n+m) ;
- a n: a m = (a) (n-m) ;
- (a b) m =(a) (b*m) .
Проверим на примерах:
2 3 * 2 2 = 8 * 4 = 32. С другой стороны 2 5 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично: 2 3: 2 2 = 8 / 4 =2. Иначе 2 3-2 = 2 1 =2.
(2 3) 2 = 8 2 = 64. А если по-другому? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.
А как же быть со сложением и вычитанием ? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
- 3 3 + 2 4 = 27 + 16 = 43;
- 5 2 – 3 2 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3) 2 = 2 2 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3) 3 = 8 3 = 512.
Как производить вычисления в более сложных случаях ? Порядок тот же:
- при наличии скобок – начинать нужно с них;
- затем возведение в степень;
- потом выполнять действия умножения, деления;
- после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:
- Корень n-ой степени из числа a в степени m запишется в виде: a m / n .
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b) n = a n * b n .
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?
Исходя из свойств 4 и 5 (смотри пункт выше), получается :
A (- n) = 1 / A n , 5 (-2) = 1 / 5 2 = 1 / 25.
И наоборот:
1 / A (- n) = A n , 1 / 2 (-3) = 2 3 = 8.
А если дробь?
(A / B) (- n) = (B / A) n , (3 / 5) (-2) = (5 / 3) 2 = 25 / 9.
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1…и т. д.
A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3…и т. д.
Кроме того, если (-a) 2 n +2 , n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.
Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: A m / n . Читается как: корень n-ой степени из числа A в степени m.
С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
- А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;
А r 1 ˂ А α ˂ А r 2 , r 1 ˂ r 2 – рациональные числа;
- 0˂А˂1.
В этом случае наоборот: А r 2 ˂ А α ˂ А r 1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
r 1 – в этом случае равно 3;
r 2 – будет равно 4.
Тогда, при А = 1, 1 π = 1.
А = 2, то 2 3 ˂ 2 π ˂ 2 4 , 8 ˂ 2 π ˂ 16.
А = 1/2, то (½) 4 ˂ (½) π ˂ (½) 3 , 1/16 ˂ (½) π ˂ 1/8.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
В предыдущей статье мы рассказали, что из себя представляют одночлены. В этом материале разберем, как решать примеры и задачи, в которых они применяются. Здесь будут рассмотрены такие действия, как вычитание, сложение, умножение, деление одночленов и возведение их в степень с натуральным показателем. Мы покажем, как определяются такие операции, обозначим основные правила их выполнения и то, что должно получится в результате. Все теоретические положения, как обычно, будут проиллюстрированы примерами задач с описаниями решений.
Удобнее всего работать со стандартной записью одночленов, поэтому все выражения, которые будут использованы в статье, мы приводим в стандартном виде. Если изначально они заданы иначе, рекомендуется сначала привести их к общепринятой форме.
Правила сложения и вычитания одночленов
Наиболее простые действия, которые можно проводить с одночленами – это вычитание и сложение. В общем случае результатом этих действий будет являться многочлен (одночлен возможен в некоторых частных случаях).
В общем случае результатом этих действий будет являться многочлен (одночлен возможен в некоторых частных случаях).
Когда мы складываем или вычитаем одночлены, сначала записываем в общепринятой форме соответствующую сумму и разность, после чего упрощаем получившееся выражение. Если есть подобные слагаемые, их нужно привести, скобки – раскрыть. Поясним на примере.
Пример 1
Условие: выполните сложение одночленов − 3 · x и 2 , 72 · x 3 · y 5 · z .
Решение
Запишем сумму исходных выражений. Добавим скобки и поставим между ними плюс. У нас получится следующее:
(− 3 · x) + (2 , 72 · x 3 · y 5 · z)
Когда мы выполним раскрытие скобок, получится — 3 · x + 2 , 72 · x 3 · y 5 · z . Это многочлен, записанный в стандартной форме, который и будет результатом сложения данных одночленов.
Ответ: (− 3 · x) + (2 , 72 · x 3 · y 5 · z) = − 3 · x + 2 , 72 · x 3 · y 5 · z .
Если у нас задано три, четыре и больше слагаемых, мы осуществляем это действие точно так же.
Пример 2
Условие: проведите в правильном порядке указанные действия с многочленами
3 · a 2 — (- 4 · a · c) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c
Решение
Начнем с раскрытия скобок.
3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c
Мы видим, что полученное выражение можно упростить путем приведения подобных слагаемых:
3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = = (3 · a 2 + a 2 — 7 · a 2) + 4 · a · c — 2 2 3 · a · c + 4 9 = = — 3 · a 2 + 1 1 3 · a · c + 4 9
У нас получился многочлен, который и будет результатом данного действия.
Ответ: 3 · a 2 — (- 4 · a · c) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = — 3 · a 2 + 1 1 3 · a · c + 4 9
В принципе, мы можем выполнить сложение и вычитание двух одночленов с некоторыми ограничениями так, чтобы получить в итоге одночлен. Для этого нужно соблюсти некоторые условия, касающиеся слагаемых и вычитаемых одночленов. О том, как это делается, мы расскажем в отдельной статье.
Правила умножения одночленов
Действие умножения не налагает никаких ограничений на множители. Умножаемые одночлены не должны соответствовать никаким дополнительным условиям, чтобы в результате получится одночлен.
Чтобы выполнить умножение одночленов, нужно выполнить следующие шаги:
- Правильно записать произведение.
- Раскрыть скобки в полученном выражении.
- Сгруппировать по возможности множители с одинаковыми переменными и числовые множители отдельно.
- Выполнить необходимые действия с числами и применить к оставшимся множителям свойство умножения степеней с одинаковыми основаниями.
Посмотрим, как это делается на практике.
Пример 3
Условие: выполните умножение одночленов 2 · x 4 · y · z и — 7 16 · t 2 · x 2 · z 11 .
Решение
Начнем с составления произведения.
Раскрываем в нем скобки и получаем следующее:
2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11
2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11
Все, что нам осталось сделать – это умножить числа в первых скобках и применить свойство степеней для вторых. В итоге получим следующее:
В итоге получим следующее:
2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11 = — 7 8 · t 2 · x 4 + 2 · y · z 3 + 11 = = — 7 8 · t 2 · x 6 · y · z 14
Ответ: 2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11 = — 7 8 · t 2 · x 6 · y · z 14 .
Если у нас в условии стоят три многочлена и больше, мы умножаем их по точно такому же алгоритму. Более подробно вопрос умножения одночленов мы рассмотрим в рамках отдельного материала.
Правила возведения одночлена в степень
Мы знаем, что степенью с натуральным показателем называют произведение некоторого числа одинаковых множителей. На их количество указывает число в показателе. Согласно этому определению, возведение одночлена в степень равнозначно умножению указанного числа одинаковых одночленов. Посмотрим, как это делается.
Пример 4
Условие: выполните возведение одночлена − 2 · a · b 4 в степень 3 .
Решение
Мы можем заменить возведение в степень на умножение 3 -х одночленов − 2 · a · b 4 . Запишем и получим нужный ответ:
Запишем и получим нужный ответ:
(− 2 · a · b 4) 3 = (− 2 · a · b 4) · (− 2 · a · b 4) · (− 2 · a · b 4) = = ((− 2) · (− 2) · (− 2)) · (a · a · a) · (b 4 · b 4 · b 4) = − 8 · a 3 · b 12
Ответ: (− 2 · a · b 4) 3 = − 8 · a 3 · b 12 .
А как быть в том случае, когда степень имеет большой показатель? Записывать большое количество множителей неудобно. Тогда для решения такой задачи нам надо применить свойства степени, а именно свойство степени произведения и свойство степени в степени.
Решим задачу, которую мы привели выше, указанным способом.
Пример 5
Условие: выполните возведение − 2 · a · b 4 в третью степень.
Решение
Зная свойство степени в степени, мы можем перейти к выражению следующего вида:
(− 2 · a · b 4) 3 = (− 2) 3 · a 3 · (b 4) 3 .
После этого мы возводим в степень — 2 и применяем свойство степени в степени:
(− 2) 3 · (a) 3 · (b 4) 3 = − 8 · a 3 · b 4 · 3 = − 8 · a 3 · b 12 .
Ответ: − 2 · a · b 4 = − 8 · a 3 · b 12 .
Возведению одночлена в степень мы также посвятили отдельную статью.
Правила деления одночленов
Последнее действие с одночленами, которое мы разберем в данном материале, – деление одночлена на одночлен. В результате мы должны получить рациональную (алгебраическую) дробь (в некоторых случаях возможно получение одночлена). Сразу уточним, что деление на нулевой одночлен не определяется, поскольку не определяется деление на 0.
Для выполнения деления нам нужно записать указанные одночлены в форме дроби и сократить ее, если есть такая возможность.
Пример 6
Условие: выполните деление одночлена − 9 · x 4 · y 3 · z 7 на − 6 · p 3 · t 5 · x 2 · y 2 .
Решение
Начнем с записи одночленов в форме дроби.
9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2
Эту дробь можно сократить. После выполнения этого действия получим:
3 · x 2 · y · z 7 2 · p 3 · t 5
Ответ: — 9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2 = 3 · x 2 · y · z 7 2 · p 3 · t 5 .
Условия, при которых в результате деления одночленов мы получим одночлен, приводятся в отдельной статье.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n -ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:
Определение 1
1. Главное свойство степени: a m · a n = a m + n
Можно обобщить до: a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .
2. Свойство частного для степеней, имеющих одинаковые основания: a m: a n = a m − n
3. Свойство степени произведения: (a · b) n = a n · b n
Свойство степени произведения: (a · b) n = a n · b n
Равенство можно расширить до: (a 1 · a 2 · … · a k) n = a 1 n · a 2 n · … · a k n
4. Свойство частного в натуральной степени: (a: b) n = a n: b n
5. Возводим степень в степень: (a m) n = a m · n ,
Можно обобщить до: (((a n 1) n 2) …) n k = a n 1 · n 2 · … · n k
6. Сравниваем степень с нулем:
- если a > 0 , то при любом натуральном n, a n будет больше нуля;
- при a , равном 0 , a n также будет равна нулю;
- при a
- при a
7. Равенство a n
8. Неравенство a m > a n будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.
В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными. Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: a m · a n = a m + n — то же самое, что и a m + n = a m · a n . В таком виде оно часто используется при упрощении выражений.
1. Начнем с основного свойства степени: равенство a m · a n = a m + n будет верным при любых натуральных m и n и действительном a . Как доказать это утверждение?
Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:
Это можно сократить до (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m + n . Таким образом, a m + n , значит, основное свойство степени доказано.
Разберем конкретный пример, подтверждающий это.
Пример 1
Итак, у нас есть две степени с основанием 2 . Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 2 2 · 2 3 = 2 2 + 3 = 2 5 Вычислим значения, чтобы проверить верность этого равенства.
Выполним необходимые математические действия: 2 2 · 2 3 = (2 · 2) · (2 · 2 · 2) = 4 · 8 = 32 и 2 5 = 2 · 2 · 2 · 2 · 2 = 32
В итоге у нас вышло: 2 2 · 2 3 = 2 5 . Свойство доказано.
Свойство доказано.
В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n 1 , n 2 и др. буквой k , мы получим верное равенство:
a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .
Пример 2
2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство a m: a n = a m − n , которое справедливо при любых натуральным m и n (причем m больше n)) и любом отличном от нуля действительном a .
Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0 n = 0). Условие, чтобы число m обязательно было больше n , нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m , мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.
Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:
a m − n · a n = a (m − n) + n = a m
Из него можно вывести: a m − n · a n = a m
Вспомним про связь деления и умножения. Из него следует, что a m − n – частное степеней a m и a n . Это и есть доказательство второго свойства степени.
Пример 3
Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π : π 5: π 2 = π 5 − 3 = π 3
3. Следующим мы разберем свойство степени произведения: (a · b) n = a n · b n при любых действительных a и b и натуральном n .
Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:
Вспомнив свойства умножения, запишем: . Это значит то же самое, что и a n · b n .
Пример 4
2 3 · — 4 2 5 4 = 2 3 4 · — 4 2 5 4
Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:
(a 1 · a 2 · … · a k) n = a 1 n · a 2 n · … · a k n
Пример 5
С конкретными числами получим следующее верное равенство: (2 · (- 2 , 3) · a) 7 = 2 7 · (- 2 , 3) 7 · a
4. После этого мы попробуем доказать свойство частного: (a: b) n = a n: b n при любых действительных a и b , если b не равно 0 , а n – натуральное число.
Для доказательства можно использовать предыдущее свойство степени. Если (a: b) n · b n = ((a: b) · b) n = a n , а (a: b) n · b n = a n , то из этого выходит, что (a: b) n есть частное от деления a n на b n .
Пример 6
Подсчитаем пример: 3 1 2: — 0 . 5 3 = 3 1 2 3: (- 0 , 5) 3
Пример 7
Начнем сразу с примера: (5 2) 3 = 5 2 · 3 = 5 6
А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:
Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p , q , r , s , то верно будет:
Если у нас есть любые натуральные числа p , q , r , s , то верно будет:
a p q y s = a p · q · y · s
Пример 8
Добавим конкретики: (((5 , 2) 3) 2) 5 = (5 , 2) 3 · 2 · 5 = (5 , 2) 30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Для начала сравним степень с нулем. Почему a n > 0 при условии, что а больше 0 ?
Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени a n с положительным основанием и натуральным показателем это будет верно.
Пример 9
3 5 > 0 , (0 , 00201) 2 > 0 и 34 9 13 51 > 0
Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.
Пример 10
0 3 = 0 и 0 762 = 0
Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2 · m , где m – натуральное число.
Вспомним, как правильно умножать отрицательные числа: произведение a · a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда и степень a 2 · m также положительны.
Пример 11
Например, (− 6) 4 > 0 , (− 2 , 2) 12 > 0 и — 2 9 6 > 0
А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2 · m − 1 .
Тогда
Все произведения a · a , согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a , то конечный результат будет отрицателен.
Тогда получим: (− 5) 3
Как это доказать?
a n
Пример 12
Например, верны неравенства: 3 7 (0 , 75) 124
8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Для начала нам нужно убедиться, что a m
Вынесем a n за скобки, после чего наша разность примет вид a n · (a m − n − 1) . Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m − n > 0 , тогда a m − n − 1 –отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
У нас вышло, что a m − a n
Осталось привести доказательство второй части утверждения, сформулированного выше: a m > a справедливо при m > n и a > 1 . Укажем разность и вынесем a n за скобки: (a m − n − 1) . Степень a n при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a > 1 степень a m − n больше единицы. Выходит, a m − a n > 0 и a m > a n , что нам и требовалось доказать.
Степень a n при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a > 1 степень a m − n больше единицы. Выходит, a m − a n > 0 и a m > a n , что нам и требовалось доказать.
Пример 13
Пример с конкретными числами: 3 7 > 3 2
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:
Определение 2
1. a m · a n = a m + n
2. a m: a n = a m − n
a m: a n = a m − n
3. (a · b) n = a n · b n
4. (a: b) n = a n: b n
5. (a m) n = a m · n
6. a n b − n при условии целого положительного n , положительных a и b , a
7. a m n и 0 1 a m > a n .
Если основание степени равно нулю, то записи a m и a n имеют смысл только лишь в случае натуральных и положительных m и n . В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.
Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.
Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (a p) q = a p · q , (a − p) q = a (− p) · q , (a p) − q = a p · (− q) и (a − p) − q = a (− p) · (− q)
Условия: p = 0 или натуральное число; q – аналогично.
Если значения p и q больше 0 , то у нас получится (a p) q = a p · q . Схожее равенство мы уже доказывали раньше. Если p = 0 , то:
(a 0) q = 1 q = 1 a 0 · q = a 0 = 1
Следовательно, (a 0) q = a 0 · q
Для q = 0 все точно так же:
(a p) 0 = 1 a p · 0 = a 0 = 1
Итог: (a p) 0 = a p · 0 .
Если же оба показателя нулевые, то (a 0) 0 = 1 0 = 1 и a 0 · 0 = a 0 = 1 , значит, (a 0) 0 = a 0 · 0 .
Вспомним доказанное выше свойство частного в степени и запишем:
1 a p q = 1 q a p q
Если 1 p = 1 · 1 · … · 1 = 1 и a p q = a p · q , то 1 q a p q = 1 a p · q
Эту запись мы можем преобразовать в силу основных правил умножения в a (− p) · q .
Так же: a p — q = 1 (a p) q = 1 a p · q = a — (p · q) = a p · (- q) .
И (a — p) — q = 1 a p — q = (a p) q = a p · q = a (- p) · (- q)
Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.
Доказательство предпоследнего свойства: вспомним, a − n > b − n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b .
Тогда неравенство можно преобразовать следующим образом:
1 a n > 1 b n
Запишем правую и левую части в виде разности и выполним необходимые преобразования:
1 a n — 1 b n = b n — a n a n · b n
Вспомним, что в условии a меньше b , тогда, согласно определению степени с натуральным показателем: — a n 0 .
a n · b n в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь b n — a n a n · b n , которая в итоге также дает положительный результат. Отсюда 1 a n > 1 b n откуда a − n > b − n , что нам и нужно было доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Определение 3
1. a m 1 n 1 · a m 2 n 2 = a m 1 n 1 + m 2 n 2 при a > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 (свойство произведения степеней с одинаковыми основаниями).
2. a m 1 n 1: b m 2 n 2 = a m 1 n 1 — m 2 n 2 , если a > 0 (свойство частного).
3. a · b m n = a m n · b m n при a > 0 и b > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 и (или) b ≥ 0 (свойство произведения в дробной степени).
4. a: b m n = a m n: b m n при a > 0 и b > 0 , а если m n > 0 , то при a ≥ 0 и b > 0 (свойство частного в дробной степени).
5. a m 1 n 1 m 2 n 2 = a m 1 n 1 · m 2 n 2 при a > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 (свойство степени в степени).
6. a p 0 ; если p b p (свойство сравнения степеней с равными рациональными показателями).
7. a p q при 0 0 – a p > a q
Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n -ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.
Разберем каждое свойство.
Согласно тому, что из себя представляет степень с дробным показателем, получим:
a m 1 n 1 = a m 1 n 1 и a m 2 n 2 = a m 2 n 2 , следовательно, a m 1 n 1 · a m 2 n 2 = a m 1 n 1 · a m 2 n 2
Свойства корня позволят нам вывести равенства:
a m 1 · m 2 n 1 · n 2 · a m 2 · m 1 n 2 · n 1 = a m 1 · n 2 · a m 2 · n 1 n 1 · n 2
Из этого получаем: a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2
Преобразуем:
a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2
Показатель степени можно записать в виде:
m 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 · n 2 n 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 n 1 + m 2 n 2
Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
a m 1 n 1: a m 2 n 2 = a m 1 n 1: a m 2 n 2 = a m 1 · n 2: a m 2 · n 1 n 1 · n 2 = = a m 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 · n 2 n 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 n 1 — m 2 n 2
Доказательства остальных равенств:
a · b m n = (a · b) m n = a m · b m n = a m n · b m n = a m n · b m n ; (a: b) m n = (a: b) m n = a m: b m n = = a m n: b m n = a m n: b m n ; a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = = a m 1 m 2 n 1 n 2 = a m 1 · m 2 n 1 n 2 = = a m 1 · m 2 n 2 · n 1 = a m 1 · m 2 n 2 · n 1 = a m 1 n 1 · m 2 n 2
Следующее свойство: докажем, что для любых значений a и b больше 0 , если а меньше b , будет выполняться a p b p
Представим рациональное число p как m n . При этом m –целое число, n –натуральное. Тогда условия p 0 будут распространяться на m 0 . При m > 0 и a
При этом m –целое число, n –натуральное. Тогда условия p 0 будут распространяться на m 0 . При m > 0 и a
Используем свойство корней и выведем: a m n
Учитывая положительность значений a и b , перепишем неравенство как a m n
Таким же образом при m b m , получаем a m n > b m n значит, a m n > b m n и a p > b p .
Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q , p > q при 0 0 будет верно a p > a q .
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m 1 n и m 2 n
Здесь m 1 и m 2 – целые числа, а n – натуральное. Если p > q , то m 1 > m 2 (учитывая правило сравнения дробей). Тогда при 0 1 – неравенство a 1 m > a 2 m .
Их можно переписать в следующем виде:
a m 1 n a m 2 n
Тогда можно сделать преобразования и получить в итоге:
a m 1 n a m 2 n
Подводим итог: при p > q и 0 0 – a p > a q .
Основные свойства степеней с иррациональными показателями
На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a > 0 , b > 0 , показатели p и q – иррациональные числа):
Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a > 0 , b > 0 , показатели p и q – иррациональные числа):
Определение 4
1. a p · a q = a p + q
2. a p: a q = a p − q
3. (a · b) p = a p · b p
4. (a: b) p = a p: b p
5. (a p) q = a p · q
6. a p b p
7. a p 0 , то a p > a q .
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a > 0 обладают теми же свойствами.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Понятие степени в математике вводится еще в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных своих видах. Степени — достаточно трудная тема, требующая запоминания значений и умения правильно и быстро сосчитать. Для более быстрой и качественной работы со степенями математики придумали свойства степени. Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.
Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.
Свойства степени
Мы рассмотрим 12 свойств степени, в том числе и свойства степеней с одинаковыми основаниями, и к каждому свойству приведем пример. Каждое из этих свойств поможет вам быстрее решать задания со степенями, а так же спасет вас от многочисленных вычислительных ошибок.
1-е свойство.
Про это свойство многие очень часто забывают, делают ошибки, представляя число в нулевой степени как ноль.
2-е свойство.
3-е свойство.
Нужно помнить, что это свойство можно применять только при произведении чисел, при сумме оно не работает! И нельзя забывать, что это, и следующее, свойства применяются только к степеням с одинаковыми основаниями.
4-е свойство.
Если в знаменателе число возведено в отрицательную степень, то при вычитании степень знаменателя берется в скобки для правильной замены знака при дальнейших вычислениях.
Свойство работает только при делении, при вычитании не применяется!
5-е свойство.
6-е свойство.
Это свойство можно применить и в обратную сторону. Единица деленная на число в какой-то степени есть это число в минусовой степени.
7-е свойство.
Это свойство нельзя применять к сумме и разности! При возведении в степень суммы или разности используются формулы сокращенного умножения, а не свойства степени.
8-е свойство.
9-е свойство.
Это свойство работает для любой дробной степени с числителем, равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.
Также это свойство часто используют в обратном порядке. Корень любой степени из числа можно представить, как это число в степени единица деленная на степень корня. Это свойство очень полезно в случаях, если корень из числа не извлекается.
10-е свойство.
Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.
Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.
11-е свойство.
Это свойство нужно уметь вовремя увидеть при решении, чтобы избавить себя от огромных вычислений.
12-е свойство.
Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может требовать некоторых преобразований и применения других формул. Поэтому для правильного решения мало знать только свойства, нужно практиковаться и подключать остальные математические знания.
Применение степеней и их свойств
Они активно применяются в алгебре и геометрии. Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.
Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.
Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.
Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.
Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.
Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.
Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.
С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.
Показательные уравнения и неравенства
Особое место свойства степени занимают именно в показательных уравнениях и неравенствах. Эти задания очень часто встречаются, как в школьном курсе, так и на экзаменах. Все они решаются за счет применения свойств степени. Неизвестное всегда находится в самой степени, поэтому зная все свойства, решить такое уравнение или неравенство не составит труда.
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .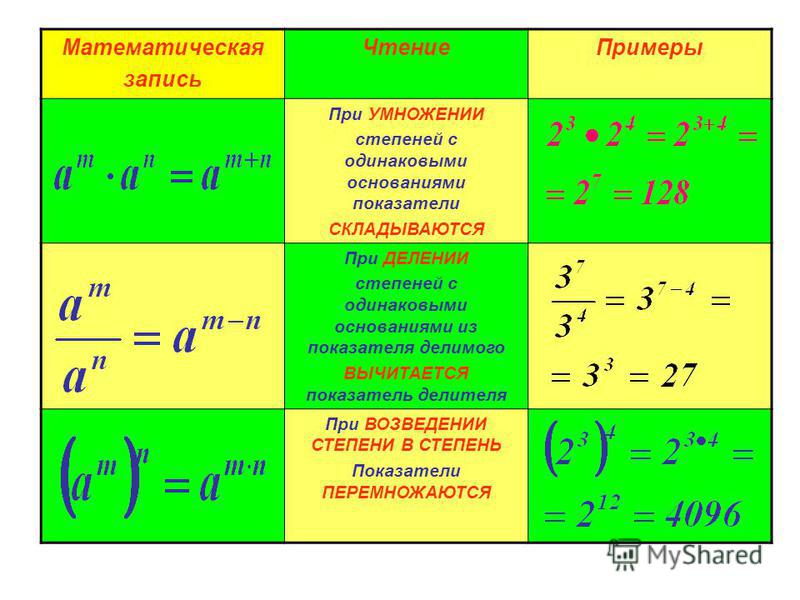 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Классы младшего дивизиона и старшего дивизиона | Лучшие колледжи
Поделиться этой статьей
- Некоторые колледжи делят свои каталоги курсов на старшие и младшие классы.

- Курсы младших классов знакомят студентов с академической дисциплиной.
- Классы старших классов обеспечивают обучение на продвинутом уровне, особенно для специальностей.
- Студенты должны проверять номера курсов при составлении расписания.
Что такое курсы старших классов? Чем они отличаются от курсов младших классов? И почему номера курсов имеют значение?
Большинство четырехгодичных колледжей делят курсы бакалавриата на младшие и старшие классы. Например, одна общепринятая система нумерации курсов классифицирует 100- и 200-уровневые классы как более низкий уровень. Во многих школах, в том числе в Университете Аризоны, эти курсы в основном предназначены для студентов первого и второго курсов.
www.bestcolleges.com — это сайт, поддерживаемый рекламой. Рекомендуемые или доверенные партнерские программы, а также все результаты поиска, поиска или подбора школ предназначены для школ, которые выплачивают нам компенсацию. Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.
Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.
Готовы отправиться в путешествие?
Напротив, классы 300-го и 400-го уровня считаются высшим дивизионом. Эти курсы предназначены в первую очередь для юниоров и пожилых людей. Курсы с номером 500 или выше обычно представляют классы для выпускников.
В других школах используются другие системы нумерации. Например, курсы нижнего уровня могут включать классы уровня 1000 и 2000, а варианты высшего уровня могут состоять из курсов уровня 3000 и 4000.
Эти различия важны для студентов. Посещение старших классов в новой области может привести к тому, что учащиеся будут изо всех сил стараться не отставать. Но недостаточное количество занятий в старших классах может сделать невозможным получение высшего образования.
Что такое курсы младших классов?
Курсы младших классов знакомят учащихся с академической дисциплиной.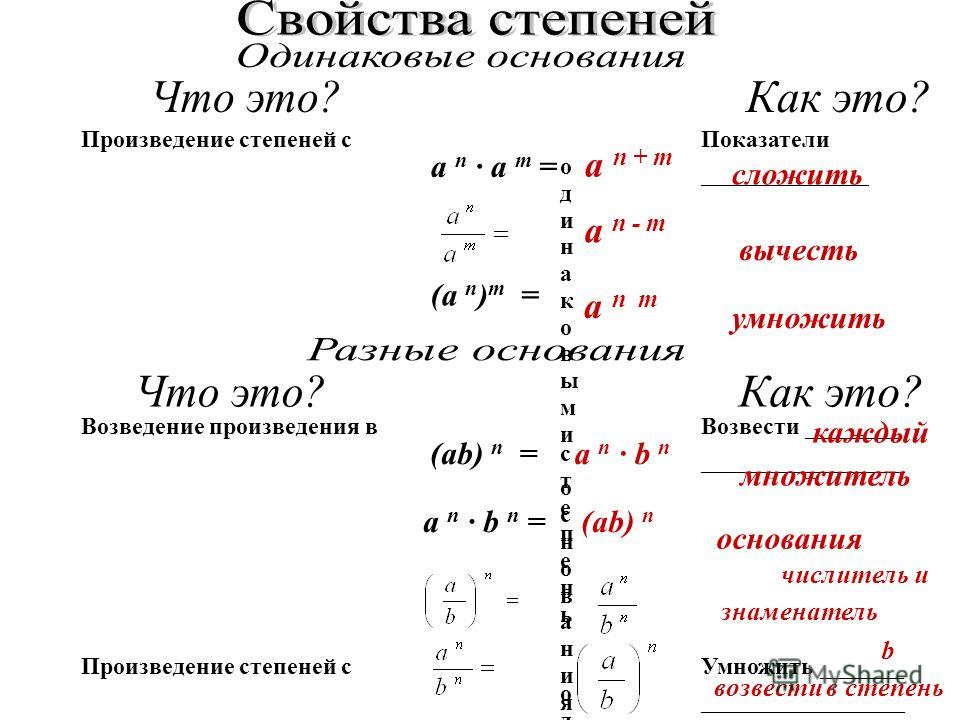 Они обеспечивают обзор основополагающих теорий, концепций и методов.
Они обеспечивают обзор основополагающих теорий, концепций и методов.
Эти вводные курсы могут охватывать большую часть информации с меньшими подробностями, чем курсы старших классов. Например, курс истории из 100 уровней может охватывать несколько столетий или даже тысячелетий. История 101 в Университете Луисвилля охватывает как минимум 1000 лет истории. Когда я вел этот курс, моя учебная программа была рассчитана на период с 3000 г. до н.э. по 1500 г. н.э.
Большинство общеобразовательных курсов относятся к низшему дивизиону. Эти курсы, такие как English 101, знакомят учащихся с обучением на уровне колледжа в различных областях, таких как гуманитарные, социальные и естественные науки. Прохождение различных курсов для младших классов может помочь первокурсникам и второкурсникам выбрать специализацию.
Студенты получают знания и академические навыки на курсах младших классов, которые готовят их к занятиям в старших классах. После приобретения основных навыков в дисциплине студенты переходят на курсы более высокого уровня.
Что такое курсы старших классов?
Курсы старших классов строятся на фундаментальных знаниях, полученных на занятиях младших классов. Эти курсы используют продвинутый подход и часто требуют, чтобы студенты обладали предварительными знаниями в этой области.
В Вашингтонском университете, например, курс «Введение в микроэкономику» состоит из 200 уровней, микроэкономика среднего уровня — из 300 уровней, а продвинутая микроэкономика — из 400 уровней. Каждый курс требует, чтобы учащиеся завершили предыдущий урок в последовательности в качестве предварительного условия.
В старших классах может быть больше чтения, более длинные проекты или исследовательские работы, а также более высокий уровень академической строгости.
Студенты обычно посещают старшие классы по своей специальности. В зависимости от дисциплины, специалистам может потребоваться пройти определенную последовательность курсов старших классов для выполнения требований отдела.
Многие колледжи устанавливают минимальное количество курсовых работ старших курсов для выпускников. Например, в Техасском университете в Остине студенты должны набрать 36 кредитов в старших классах, чтобы получить степень бакалавра. Университет Южной Флориды требует 42 кредита высшего уровня для получения степени бакалавра. Студенты, не соответствующие требованиям, не могут получить степень.
Когда следует посещать курсы старших классов?
Когда учащиеся должны посещать курсы старших классов? И когда им следует избегать классов 300-го уровня или выше?
Как правило, академические консультанты рекомендуют первокурсникам и второкурсникам проявлять осторожность перед зачислением на курсы старших курсов. Как минимум, студенты должны связаться с профессором, чтобы узнать о предварительных требованиях или необходимых знаниях, прежде чем присоединиться к курсу старшего отделения.
Как правило, студенты старших курсов также должны избегать изучения высшей ступени в качестве первого курса академической дисциплины.
Колледжи ожидают, что учащиеся будут проходить курсы старших курсов по своим специальностям. Тем не менее, зачисление в класс старшего дивизиона за пределами вашей специальности может вызвать у вас чувство переутомления или неподготовленности к академическим ожиданиям.
На уровне старшего отделения профессора ожидают, что студенты привнесут в свою курсовую работу предшествующий опыт в этой области. Например, при преподавании истории на 300-м и 400-м уровнях я ожидал, что студенты будут знать, как внимательно анализировать первоисточник, задавать исторические вопросы и писать убедительные статьи, подкрепленные фактами. На всех уроках истории со 100-м и 200-м уровнями основное внимание уделялось обучению этим навыкам.
Колледжи не зря делят классы на старшие и младшие. Уровень класса указывает, какие студенты должны записаться, и ожидания от курса. Студенты, которые обращают внимание на уровень класса, могут настроить себя на успех.
Характерное изображение: Том Вернер / DigitalVision / Getty Images
7 типов курсов колледжа, которые вы можете пройти
Изучите типы курсов колледжа, с которыми студенты чаще всего сталкиваются, включая онлайн-курсы, лабораторные работы и лекции.
Стефани Гродман
Спросите профессора: когда сдавать экзамен в колледже «зачет/незачет»
Хотите узнать о преимуществах и недостатках системы оценивания «зачет/незачет»? Используйте эти советы, чтобы решить, когда вы должны пройти курс или не пройти курс.
Женевьева Карлтон, доктор философии.
Спросите профессора: стоит ли вам бросить занятия?
Когда следует отказаться от занятий, а когда продолжать? Узнайте о последствиях отказа от курса и возможных альтернативах.
Женевьева Карлтон, доктор философии.
BestColleges.com — это сайт, поддерживаемый рекламой. Рекомендуемые или доверенные партнерские программы, а также все результаты поиска, поиска или подбора школ предназначены для школ, которые выплачивают нам компенсацию. Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.
Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.
Сравните варианты школы.
Просмотрите школу, наиболее соответствующую вашим интересам, и сравните их по стоимости обучения, программам, уровню приема и другим факторам, важным для того, чтобы найти ваш колледж.
Руководитель отдела Требования к образованию: Степени, специальности, колледжи
Образование, необходимое для того, чтобы стать начальником отдела, обычно представляет собой степень бакалавра. Начальники подразделений обычно изучают бизнес, менеджмент или политологию. 56% начальников подразделений имеют степень бакалавра, а 24% — степень магистра. Мы нашли их, проанализировав 2,916 начальник отдела возобновляет более детальное изучение темы образования начальника отдела.
Наиболее распространенными колледжами для студентов, стремящихся стать начальником отдела, являются Университет Мэриленда — Колледж-Парк и Университет Вебстера. Мы также выяснили, какие колледжи обеспечивают лучшее общее образование для начальника отдела. Учащиеся могут получить квалификацию начальника отдела в следующих школах:
Мы также выяснили, какие колледжи обеспечивают лучшее общее образование для начальника отдела. Учащиеся могут получить квалификацию начальника отдела в следующих школах:
- University of Pennsylvania
- Северо-западный университет
- Университет Южной Калифорнии
Если вы заинтересованы в получении высшего образования в недорогом колледже для начальников подразделений, Колледж Баруха Городского университета Нью-Йорка — отличный вариант для вас. Если ваши баллы SAT или ACT не так высоки, как вам хотелось бы, вы можете обратиться в Университет Маунт-Сент-Мэри, так как требования к поступающим не слишком избирательны. На другом конце этого спектра находятся Северо-Западный университет, Университет Пенсильвании и Университет Южной Калифорнии.
Для тех, кто предпочитает оставаться в пижаме в течение дня, мы подготовили несколько онлайн-курсов, которые могут помочь в учебе начальника отдела.
Мы подготовили список сертификатов начальника отдела, которые вам следует учитывать. Необходимые сертификаты, которые должны иметь руководители подразделений, — это специалист по управлению программами (PgMP) и специалист по управлению проектами (PMP).
Необходимые сертификаты, которые должны иметь руководители подразделений, — это специалист по управлению программами (PgMP) и специалист по управлению проектами (PMP).
Какое образование нужно получить, чтобы стать начальником отдела?
Наиболее распространенной степенью для руководителей подразделений является степень бакалавра. 56% начальников подразделений получают эту степень. Ближайшее второе место занимает степень магистра с 24%, а затем степень младшего специалиста с 11%.
- Бакалавриат, 56 %
- Магистр, 24 %
- Ассоциированный специалист, 11 %
- Докторантура, 4 %
- Другие степени, 5 %
Большинство начальников отделов, а точнее 25%, занимаются бизнесом. Некоторые другие распространенные специальности для начальника отдела включают специальности по менеджменту и политологии.
- Бизнес, 25%
- Менеджмент, 8%
- Политология, 7%
- Уголовное правосудие, 7%
- Другие специальности, 53%
Проверка работы, которые соответствуют вашему образованию
Средняя школа / GED
Associate
Bachelor’s
Master’s
Докторский докторский.
 колледжи для карьеры начальника отдела в США на основании их резюме. Адвокаты часто получают степень в Университете Мэриленда — Колледж-Парк, Вебстерском университете и Университете Феникса.
колледжи для карьеры начальника отдела в США на основании их резюме. Адвокаты часто получают степень в Университете Мэриленда — Колледж-Парк, Вебстерском университете и Университете Феникса.University of Maryland — College Park
Webster University
University of Phoenix
United States Military Academy
Troy University
Show More
0%
2%
5%
8%
11%
13%
Средняя заработная плата начальника отдела в зависимости от уровня образования
Начальники подразделений со степенью доктора наук зарабатывают больше, чем те, у кого нет, и составляют 202 539 долларов в год. Средний годовой доход руководителей подразделений со степенью магистра составляет 200 227 долларов США.
High School Diploma or Less
Master’s Degree
Bachelor’s Degree
Doctorate Degree
Some College/ Associate Degree
$0
$41,000
$82,000
$123,000
$164,000
$205,000
Salary By Education Уровень
Начальник отдела Уровень образования Заработная плата начальника отдела Диплом средней школы или ниже $110,137 Master’s Degree $200,227 Bachelor’s Degree $144,948 Doctorate Degree $202,539 Some College/ Associate Degree $110,523 10 Best Университеты Для начальников отделов
Во многих случаях высшее образование может означать более высокую зарплату или даже лучшую работу.
 Вот почему мы нашли лучшие колледжи для начальников отделов. Мы составили этот список на основе следующих показателей: уровень приема, уровень удержания, средний заработок работающих студентов, соотношение работающих и неработающих студентов через 10 лет после поступления, средняя стоимость посещения и средний долг выпускников.
Вот почему мы нашли лучшие колледжи для начальников отделов. Мы составили этот список на основе следующих показателей: уровень приема, уровень удержания, средний заработок работающих студентов, соотношение работающих и неработающих студентов через 10 лет после поступления, средняя стоимость посещения и средний долг выпускников.1. Университет Пенсильвании
Филадельфия, Пенсильвания • Частный
в государственном плате
$ 55 584
Включение
10,764
2. Северный университет
366. $54,568
Регистрация
8,451
3. Университет Южной Калифорнии
Лос-Анджелес, Калифорния • Частный
Обучение в штате
$56,225
Регистрация0037
19 548
4. Университет Нью-Йорка
Нью-Йорк, Нью-Йорк • Частный
В государственном обучении
$ 51 828
. Обучение в штате
$18,454
Регистрация
40,108
0037
Enrollment
40,329
7.
 SUNY at Binghamton
SUNY at BinghamtonVestal, NY • Private
In-State Tuition
$9,808
Enrollment
13,990
8. Northeastern University
Boston, MA • Private
Обучение в штате
$51,522
Регистрация
13,760
9. Университет Бентли
Waltham, MA • Частный
Обучение в штате
6 $ 6 6 60036 Enrollment
4,177
10. Lehigh University
Bethlehem, PA • Private
In-State Tuition
$52,930
Enrollment
5,030
20 Best Online Courses for Division Chiefs
Sometimes things are just better when ты можешь оставаться в пижаме весь день. Включая школу. Мы нашли лучшие курсы для руководителей подразделений от Udemy, Coursera, EDX и ed2go, которые помогут вам продвинуться по карьерной лестнице. Вот основные навыки, необходимые для того, чтобы стать начальником отдела:
- Надзор
- Объект
- Аварийная ситуация

Рекламное раскрытие информации
Основы стратегического планирования для управления персоналом
Научитесь сотрудничать с руководителями вашей организации в разработке и реализации стратегического плана…
Подробнее на Udemy
Дипломный курс по управлению персоналом (HRM)
(1007)
Станьте первоклассным специалистом по управлению персоналом — получайте живые проекты, готовые к использованию шаблоны, демонстрации, викторины, статьи, тематические исследования… курсов, помогающих финансовым специалистам достичь высших уровней финансового лидерства…
Подробнее на Udemy
Сертификационный курс по управлению персоналом
Учебная программа соответствует программе управления лучшими школами B: с загружаемыми ресурсами, викторинами, оценками и упражнениями …
Подробнее на Udemy
Введение в управление персоналом
(2,336)
Управление человеческими ресурсами — важная функция любой организации.
 Он включает в себя структурированное и тщательное управление людьми…
Он включает в себя структурированное и тщательное управление людьми…Просмотреть подробности на Udemy
Путь к директору по информационной безопасности — завершающий проектный курс
Конечным назначением менеджера по безопасности является директор по информационной безопасности (или директор по безопасности). старшая исполнительная роль, отвечающая за все операции по кибербезопасности в организации. Но как пройти путь от начального уровня ИТ-специалиста или сотрудника службы безопасности до офиса директора по информационной безопасности и что вам нужно знать, когда вы туда доберетесь? Этот курс исследует путь карьеры и требования, чтобы быть эффективным CISO, а также роли и обязанности положения. В этом курсе слушатель…
Подробнее на Coursera
Управление человеческими ресурсами — комплексный курс по УЧР
Руководство по HR-метрикам, найму, удержанию сотрудников, управлению эффективностью, отношениям с сотрудниками, удовлетворенности, коммуникации.
 ..
..Подробнее на Udemy
Менеджмент
Этот курс познакомит вас с лидерством и управлением кибербезопасностью. Опираясь на отраслевые стандарты, структуры и модели, вы изучите ключевые объективные элементы лидерства в области кибербезопасности. Лидерство и управление кибербезопасностью — это две компетенции высокого уровня, необходимые для успешного управления подразделением кибербезопасности, которое обеспечивает необходимый уровень безопасности, доверия и стабильности (STS), требуемый организацией. Несмотря на то, что лидерство и управление являются необходимыми навыками для …
Подробнее на Coursera
Эффективное управление персоналом
(1,186)
Эффективное управление персоналом…
Подробнее на Udemy
Стратегическое управление понимание того, как фирмы конкурируют, изучая важные аналитические подходы, лежащие в основе бизнес-стратегии. Этот курс покажет вам, как бизнес видит себя в своей «тотальности» и в контексте своего окружения.
 Курс будет преподаваться с точки зрения менеджера или главного исполнительного директора (CEO). Этот курс направлен на то, чтобы вооружить вас хорошим пониманием того, что подразумевает управление фирмой в стратегическом плане? Как…
Курс будет преподаваться с точки зрения менеджера или главного исполнительного директора (CEO). Этот курс направлен на то, чтобы вооружить вас хорошим пониманием того, что подразумевает управление фирмой в стратегическом плане? Как…Подробнее о edX
Обучение управлению проектами
(1,107)
Сертификационное обучение управлению проектами с 4 полными практическими тестами от…
Введение в концепции управления персоналом…
Подробности на Udemy
Ресторанный менеджмент: лучшие практики управления персоналом
Изучите лучшие системы для поиска, развития и удержания лучших сотрудников для управления прибыльным рестораном…
Подробнее о Udemy
Microsoft Project ADVANCED: методы управления проектами 3PDU
MS PROJECT 2016 ADVANCED методы управления проектами, включая уровень предприятия. ПРАКТИЧЕСКОЕ РУКОВОДСТВО от ЛУЧШЕГО ИНСТРУКТОРА №1…
Подробнее о Udemy
Стратегическое планирование рабочей силы: фундаментальное руководство для начинающих
Все, что вам нужно знать, чтобы начать работу.
 ..
..Подробнее о Udemy
Управление проектами Основное обучение
Подробное руководство для новичков, позволяющее успешно изучить управление проектами и легко получить сертификат PMP…
Подробнее на Udemy
Проектирование информационных центров проекта для выполнения программ и проектов
Сложность коммуникации быстро возрастает даже при наличии нескольких программ или проектов члены команды и заинтересованные стороны. Руководители проектов являются «центром» их проектной коммуникации. Руководители программ являются «центром» коммуникации своей организации для достижения стратегических целей. Управление этими сетями необходимо независимо от того, управляете ли вы традиционными программами или проектами. Или гибкие программы и проекты. Руководители программ сталкиваются с двумя дополнительными проблемами. Во-первых, они должны наделить своих руководителей проекта навыками,…
Подробнее о edX
Практический онлайн-курс по HR-аналитике для отдела кадров
От кадровой аналитики и аналитических процессов к человеческому капиталу XL и инструменты интеллектуального анализа данных с открытым исходным кодом и инструменты машинного обучения 6 Назначение данных.
 ..
..Подробнее на Udemy
Программа сертификации специалистов по управлению проектами (PMP)
Ваш путеводитель по Золотому стандарту сертификации по управлению проектами (PMI-PMP) (PMBOK6) (40 PDU)…
Подробнее на Udemy
Управление персоналом (HR) для начинающих
(5,024)
Этот курс представляет собой введение в роль и обязанности отдела кадров (HR)…
1. Специалист по управлению программами (PgMP)
Новейшая аттестат Института управления проектами специально разработана для признания квалификации профессионала, который руководит скоординированным управлением несколькими проектами и обеспечивает окончательный успех программы. Вы сможете воспользоваться многими преимуществами этого нового обозначения. Кандидаты, получившие этот сертификат, будут признаны во всем мире как профессионалы, обладающие знаниями и опытом для принятия и реализации важных решений и достижения стратегических целей, которые улучшают результаты бизнеса.

Новейший сертификат Института управления проектами специально разработан для признания квалификации профессионала, который руководит скоординированным управлением несколькими проектами и обеспечивает окончательный успех программы. Вы сможете воспользоваться многими преимуществами этого нового обозначения. Кандидаты, получившие этот сертификат, будут признаны во всем мире как профессионалы, обладающие знаниями и опытом для принятия и реализации важных решений и достижения стратегических целей, которые улучшают результаты бизнеса.
- Требуется более двух лет образования или обучения после окончания средней школы? Да
- Требуется опыт работы более двух лет? Да
- Требуется устный или письменный экзамен? Да
- Требуется продление? Каждые 3 года
- Начальник отделения
- Вице-президент подразделения
- Начальник отдела операций
- Начальник отдела планирования
Детали
текущим и потенциальным работодателям, что вы продемонстрировали прочную основу знаний, на основе которых вы можете компетентно практиковать управление проектами.
 Чтобы иметь право на получение сертификата PMP, вы должны сначала соответствовать определенным требованиям к образованию и опыту управления проектами и согласиться придерживаться кодекса профессиональной руководить. Последним шагом к тому, чтобы стать PMP, является сдача строгого экзамена с несколькими вариантами ответов, предназначенного для объективной оценки и измерения вашей способности применять знания по управлению проектами в следующих шести областях: инициирование проекта, планирование проекта, выполнение проекта, мониторинг и контроль. проект, закрытие проекта, профессиональная и социальная ответственность. Этот компьютерный экзамен проводится по всему миру с помощью средств перевода на 10 языков.
Чтобы иметь право на получение сертификата PMP, вы должны сначала соответствовать определенным требованиям к образованию и опыту управления проектами и согласиться придерживаться кодекса профессиональной руководить. Последним шагом к тому, чтобы стать PMP, является сдача строгого экзамена с несколькими вариантами ответов, предназначенного для объективной оценки и измерения вашей способности применять знания по управлению проектами в следующих шести областях: инициирование проекта, планирование проекта, выполнение проекта, мониторинг и контроль. проект, закрытие проекта, профессиональная и социальная ответственность. Этот компьютерный экзамен проводится по всему миру с помощью средств перевода на 10 языков.Обозначение PMP после вашего имени сообщает нынешним и потенциальным работодателям, что вы продемонстрировали прочную базу знаний, на основе которой вы можете компетентно практиковать управление проектами. Чтобы иметь право на получение сертификата PMP, вы должны сначала соответствовать определенным требованиям к образованию и опыту управления проектами.
 и соглашаетесь соблюдать кодекс профессионального поведения. Последним шагом к тому, чтобы стать PMP, является сдача строгого экзамена с несколькими вариантами ответов, предназначенного для объективной оценки и измерения вашей способности применять знания по управлению проектами в следующих шести областях: инициирование проекта, планирование проекта, выполнение проекта, мониторинг и контроль. проект, закрытие проекта, профессиональная и социальная ответственность. Этот компьютерный экзамен проводится по всему миру с помощью средств перевода на 10 языков.
и соглашаетесь соблюдать кодекс профессионального поведения. Последним шагом к тому, чтобы стать PMP, является сдача строгого экзамена с несколькими вариантами ответов, предназначенного для объективной оценки и измерения вашей способности применять знания по управлению проектами в следующих шести областях: инициирование проекта, планирование проекта, выполнение проекта, мониторинг и контроль. проект, закрытие проекта, профессиональная и социальная ответственность. Этот компьютерный экзамен проводится по всему миру с помощью средств перевода на 10 языков.- Требуется более двух лет образования или обучения после окончания средней школы? №
- Требуется опыт работы более двух лет? Да
- Требуется устный или письменный экзамен? Да
- Требуется продление? Каждые 3 года
- Начальник отдела
- Директор отдела
- Вице-президент отдела
- Начальник производства
Сертификация по управлению проектами + 2 практических экзамена
Подробнее на Udemy0037
Подробная информация
3.
 Сертифицированный авиационный менеджер (CAM)
Сертифицированный авиационный менеджер (CAM)Программа сертифицированного авиационного менеджера (CAM) NBAA набирает квалифицированных специалистов для руководства летными отделами и компаниями, использующими самолеты бизнес-класса. Присоединяйтесь к числу уважаемых авиационных профессионалов, которые уже были признаны сертифицированными авиационными менеджерами, и подайте заявку на экзамен CAM сегодня.
Программа сертифицированного авиационного менеджера (CAM) NBAA определяет квалифицированных специалистов, которые будут руководить летными отделами и компаниями, использующими самолеты бизнес-класса. Присоединяйтесь к числу уважаемых авиационных профессионалов, которые уже были признаны сертифицированными авиационными менеджерами, и подайте заявку на экзамен CAM сегодня.
- Требуется более двух лет образования или обучения после окончания средней школы? Да
- Требуется опыт работы более двух лет? Да
- Требуется устный или письменный экзамен? Да
- Требуется продление? Каждые 3 года
Сертифицированный авиационный менеджер
Национальная ассоциация деловой авиации
Подробная информация
Топ-10 доступных университетов для руководителей подразделений
эти школы вместо этого.
 После учета стоимости обучения в штате и сборов, средней стоимости посещения, уровня приема, средней чистой цены и среднего заработка через 6 лет мы обнаружили, что это самые доступные школы для руководителей подразделений.
После учета стоимости обучения в штате и сборов, средней стоимости посещения, уровня приема, средней чистой цены и среднего заработка через 6 лет мы обнаружили, что это самые доступные школы для руководителей подразделений.1. Колледж Баруха Городского университета Нью-Йорка
Нью-Йорк, штат Нью-Йорк • Частный
Обучение в штате
7 262 долл. США
Стоимость обучения Стоимость обучения — это ориентировочная годовая стоимость обучения в конкретном колледже или университете. . Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
14 046 долларов
2. Университет Флориды
Гейнсвилл, Флорида • Частный
Обучение в штате
6 381 долларов
Стоимость обучения Стоимость обучения – это ориентировочная годовая стоимость обучения в конкретном колледже или университете. Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
21 034 $
3.
 Университет штата Флорида
Университет штата ФлоридаТаллахасси, Флорида • Частный
Обучение в штате
5 656 $
Стоимость обучения Стоимость обучения – это ориентировочная годовая стоимость обучения в конкретном колледже или университете. Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
21 623 долларов США
4. Университет Бригама Янга
Прово, Юта • Частный
Обучение в штате
5 620 долларов США
Стоимость обучения Стоимость обучения – это ориентировочная годовая стоимость обучения в конкретном колледже или университете. Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
$18,136
5. USF Sarasota-Manatee
Sarasota, FL • Частный
In-State Tuition
$5,587
Стоимость обучения Стоимость обучения в конкретном колледже или университете. Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.

13 043 долларов
6. Университет Южной Флориды
Тампа, Флорида • Частный
Обучение в штате
6 410 долларов
Стоимость обучения Стоимость обучения – это ориентировочная годовая стоимость обучения в конкретном колледже или университете. Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
20 456 долларов США
7. Университет штата Калифорния – Фуллертон
Фуллертон, Калифорния • Частный
Обучение в штате
6 886 долларов США
Стоимость обучения Стоимость обучения – это ориентировочная годовая стоимость обучения в конкретном колледже или университете. Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
17 645 долларов США
8. Международный университет Флориды
Майами, Флорида • Частный
Обучение в штате
6 556 долларов США
Стоимость обучения Стоимость обучения – это ориентировочная годовая стоимость обучения в конкретном колледже или университете.
 Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.$19,434
9. USF Санкт-Петербург
Санкт-Петербург, Флорида • Частный
Обучение в штате
$5,821
Стоимость обучения Стоимость обучения – это расчетная годовая стоимость обучения в конкретном колледже или университете. Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
$19,849
10. SUNY Farmingdale
Farmingdale, NY • Частный
In-State Tuition
$8,306
Стоимость обучения Стоимость обучения в конкретном колледже или университете. Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
$16,091
10 университетов, в которые труднее всего попасть руководителям отделов
Некоторые люди любят вызовы. Что ж, мы предлагаем вам попасть в одну из этих школ. Это будет нелегко. Мы знаем это на основе показателей приема в эти учебные заведения, средних принятых баллов SAT, медианных принятых баллов ACT и среднего заработка студентов через 6 лет после поступления.

1. Северо-Западный университет
Эванстон, Иллинойс • Частный
Уровень приема
8%
SAT Average
1,508
2. University of Pennsylvania
Philadelphia, PA • Private
Admissions Rate
8%
SAT Average
1,492
3. University of Southern California
Los Анхелес, Калифорния • Частный университет
Уровень приема
13%
Средний показатель SAT
1 445
0037
19%
SAT Average
1,466
5. Carnegie Mellon University
Pittsburgh, PA • Private
Admissions Rate
17%
SAT Average
1,507
6. New York University
New Йорк, штат Нью-Йорк • Частный университет
Уровень приема
20%
Средний показатель SAT
1 419
0037
SAT в среднем
1 420
8. Университет Майами
Корал -Гейблс, FL • Частный
Скорость поступления
32%
Средняя
1,365
1,365
1,365
9003 9.
Поступление
22%
Среднее по SAT
1,380
0037
Среднее значение SAT
1,380
10 лучших университетов, в которые легче поступить для начальников отделов
Зачем усложнять себе работу? В эти колледжи вас обязательно примут в кратчайшие сроки. Мы собрали показатели приема, средние баллы SAT, средние баллы ACT и среднюю зарплату студентов через 6 лет после выпуска, чтобы выяснить, в какие школы было легче всего поступить.
1. Университет Маунт-Сент-Мэри
Лос-Анджелес, Калифорния • Частный
Admissions Rate
84%
SAT Average
1,031
2. Barry University
Miami, FL • Private
Admissions Rate
91%
SAT Average
1,006
3. Oklahoma Wesleyan University
Бартлсвилл, Оклахома • Частный
Показатель зачисления
68%
Средний балл SAT
964
4. Университет Северного Техаса в Далласе
Даллас, Техас • Частный
Скорость поступления
83%
SAT в среднем
992
5.
 Университет священных имен
Университет священных именOakland, CA • Private
. The Incarnate Word
Сан-Антонио, Техас • Частный
Уровень зачисления
88%
Средний балл SAT
1044
7. Университет Нотр-Дам-де-Намюр
, Калифорния Бельмонт0037Admissions Rate
82%
SAT Average
983
8. Notre Dame College
Cleveland, OH • Private
Admissions Rate
90%
SAT Average
994
9. Kean University
Union, NJ • Частный
Уровень приема
86%
Средний показатель SAT
991
10. Wayland Baptist University
Plainview, TX 3 • Частный
003798%
Среднее значение SAT
1,003
Обновлено 30 апреля 2021 г.
Академики — UC Berkeley Public Health
Мы готовим различных лидеров для профессиональной и исследовательской карьеры в рамках программ бакалавриата, магистратуры и докторантуры.

Аспиранты
Академические отделы аспирантов
В Berkeley Public Health аспиранты имеют возможность заниматься своими академическими интересами и стать лидерами общественного здравоохранения в одном из шести отделов. Наши подразделения являются междисциплинарными и объединяют преподавателей и студентов из многих областей исследований и направлений. В то же время каждое подразделение предлагает определенные возможности для получения степени, где студенты могут выбрать программу, соответствующую их увлечениям.
Биостатистика
Предлагаемые степени: MA, MPH, PhD
Многие проблемы в области здравоохранения, медицины и биологии решаются путем сбора и изучения соответствующих данных. Разработка и применение методов для лучшего понимания таких данных является основной задачей Группы биостатистики. Программа предлагает обучение теории статистики и биостатистики, компьютерную реализацию аналитических методов и возможности использования этих знаний в области биологических/медицинских исследований.
 Узнайте больше на странице отдела биостатистики.
Узнайте больше на странице отдела биостатистики.Community Health Sciences
Предлагаемые степени: MPH
Мы даем исследователям общественного здравоохранения, клиницистам и практикам более глубокое понимание междисциплинарного и общественного характера общественного здравоохранения. Наши преподаватели сосредотачиваются на том, как биологическая восприимчивость и резистентность работают вместе с социальной, физической и культурной средой, чтобы влиять на возникновение и распространение болезней. Основные направления в рамках этого подразделения: здоровье и социальное поведение; Здоровье матери, ребенка и подростков; и общественное питание. Узнайте больше на странице отдела общественных наук о здоровье.
Науки о гигиене окружающей среды
Предлагаемые степени: MPH, MS, PhD
В состав нашего подразделения входят преподаватели и студенты, находящиеся в авангарде исследований, характеризующих воздействие окружающей среды — индустриализация, урбанизация, последствия изменения климата, микробное и химическое загрязнение вода, воздух и пища — воздействуют на население, особенно на наиболее уязвимых членов общества.
 Узнайте больше на странице отдела наук об окружающей среде.
Узнайте больше на странице отдела наук об окружающей среде.Эпидемиология
Предлагаемые степени: MPH, MS, PhD
Целями эпидемиологических исследований являются выявление причин болезней, продвижение и оценка методов профилактики болезней, а также помощь в планировании и оценке эффективности общественного здравоохранения. программы. Эпидемиологов интересует изучение инфекционных и неинфекционных заболеваний. В последние годы они все больше обращают свое внимание на изучение условий, на которые влияют силы в социальной и физической среде. Узнайте больше на странице отдела эпидемиологии.
Политика и управление в области здравоохранения
Предлагаемые степени: MPH, PhD
Здравоохранение — это быстро развивающаяся область, которая постоянно развивается. С помощью учебной программы, которая охватывает анализ политики, стратегическое управление, информационные технологии, экономику, профилактику заболеваний, право и этику, мы готовим выпускников к руководящим ролям на руководящих должностях в сфере здравоохранения в различных условиях, от оказания медицинской помощи до государственных или некоммерческих агентств.
 Узнайте больше на странице Отдела политики и управления здравоохранением.
Узнайте больше на странице Отдела политики и управления здравоохранением.Инфекционные болезни и вакцинология
Предлагаемые степени: MPH, PhD
Изучение инфекционных заболеваний рассматривает множество аспектов, от молекулярной биологии, экологии и эволюции патогенов до человеческих популяций, где инфекционные агенты передают болезни. Разрабатывая и проводя независимые исследования, наши студенты получают более глубокое и целостное понимание инфекционных заболеваний и иммунологии человека, которое можно применить для разработки диагностики, профилактики, лечения и контроля заболеваний. Узнайте больше на странице отдела инфекционных заболеваний и вакцинологии.
Междисциплинарное отделение
Предлагаемые степени: MPH, DrPH
Общественное здравоохранение Беркли поощряет студентов изучать междисциплинарное образование. С этой целью мы предлагаем уникальные возможности благодаря нашим различным вариантам получения степени: студенты могут настраивать и адаптировать свою учебную программу для выпускников, чтобы она соответствовала их индивидуальным профессиональным потребностям.
 Узнайте больше на странице междисциплинарного подразделения.
Узнайте больше на странице междисциплинарного подразделения.Параллельные степени магистра
Предлагаемые степени: MPH с MBA, MCP, MJ, MPP или MSW
Школа общественного здравоохранения учредила параллельные программы на получение степени с другими школами и факультетами на территории кампуса, которые позволяют студентам воспользоваться уникальными возможностями междисциплинарного обучения, которые предлагает Беркли.
В рамках этих программ учащиеся следуют тщательно разработанному учебному плану, который позволяет им выполнить требования для двух степеней за меньшее время, чем обычно требуется для получения двух степеней по отдельности. Кандидаты на параллельные программы обучения должны быть приняты в обе спонсирующие профессиональные школы.
Узнайте больше о параллельных степенях
Совместные степени магистра с другими учреждениями
Предлагаемые степени: MD/MS, MD/MPH; MPH with Medicine или DPH residency
Berkeley Public Health предлагает совместные программы с Калифорнийским университетом, Сан-Франциско и Стэнфордским университетом, которые дают студентам-медикам и врачам возможность пройти обучение в области общественного здравоохранения в сочетании с их медицинским образованием.

Узнайте больше о совместных дипломах
Public Health Online
Наша 27-месячная онлайн-программа MPH предоставляет полезный образовательный опыт, который дает вам соответствующие уникальные навыки в соответствии с вашим графиком из любой точки мира.
Мы помогаем профессионалам среднего звена продвигаться по карьерной лестнице, одновременно получая степень магистра в области здравоохранения в ведущем университете мира. Наша гибкая программа предназначена для того, чтобы студенты могли расширить свои знания и влияние, сохраняя при этом свой текущий образ жизни.
Дополнительная информация
Бакалавриат Академики
Степени бакалавра и сертификаты
Бакалавр общественного здравоохранения (BA)
Студенты, изучающие общественное здравоохранение, получают степень бакалавра гуманитарных наук. Студенты будут развивать и применять знания из разных дисциплин для укрепления и защиты здоровья населения, уделяя должное внимание принципам прав человека и культурным перспективам, которые изобилуют в нашей многокультурной стране и мире.

Summer Minor in Global Public Health
Summer Minor в программе Global Public Health исследует проблемы, связанные со здоровьем, затрагивающие население в Соединенных Штатах и во всем мире. Студенты проходят курсы, охватывающие ряд дисциплин и методов, имеющих отношение к укреплению и защите здоровья человека, возникающим проблемам со здоровьем и системам здравоохранения. Эту программу также могут пройти студенты, не являющиеся студентами Беркли, чтобы получить сертификат без степени в области глобального общественного здравоохранения.
Благодаря нашим шести подразделениям, различным программам бакалавриата, магистратуры и онлайн-дипломам, а также специальностям, мы предлагаем студентам возможность адаптировать свою исследовательскую и курсовую программу к их индивидуальным карьерным устремлениям.
Найдите наилучшее образование, подходящее для вас Область исследованияСтарениеБиостатистикаОбщинные медицинские наукиСтоматологияОбщественное здравоохранениеНауки об окружающей средеЭпидемиологияПищевое питаниеГлобальное здравоохранениеЗдоровье и социальное поведениеПолитика и управление в области здравоохраненияИнфекционные заболевания, вакцинология и иммунитетМеждисциплинарное здоровье матери, ребенка и подросткаМедицинские наукиМультикультурное здравоохранениеОбщественное здравоохранение Формат питанияГибридный онлайн / в кампусеВ кампусеонлайн
Требования к степени| Отделение бакалавриата
LASAR (академические требования к письмам и естественным наукам) 2022-2023.
Думайте о LASAR как о «кратком руководстве пользователя» для получения научной степени. См. Архив ниже выпуска за предыдущие учебные годы. Он охватывает основные требования и правила, необходимые студентам для получения степени. Для более глубоких погружений учащимся следует обращаться к Общему каталогу .
Требования к получению степени
Требования к получению степени UCSB делятся на четыре основные категории, которые вкратце описаны ниже:
1. Требования к единицам
Вы должны пройти в общей сложности либо 180, либо 184 единицы, включая не менее 60 единиц высшей ступени. .2. Требования к университету
Вы должны выполнить следующее:- Требование к письму начального уровня (ранее Тема A)
- Американская история и институты Требование
- Требование об академическом общежитии
- Требования к среднему баллу
3.
 Требования к общему образованию
Требования к общему образованию Учащиеся должны пройти общеобразовательную программу Колледжа литературы и науки, которая включает Общие требования к предметным областям :
Область A: Чтение и сочинение на английском языке
Область B: Иностранный язык
Направление C: наука, математика и технологии - Текущий год
- ЛАЗАР 2021-22
- ЛАЗАР 2020-21
- ЛАЗАР 2019-20
- ЛАЗАР 2018-19
- ЛАЗАР 2017-18
- ЛАЗАР 2016-17
- ЛАЗАР 2015-16
- ЛАЗАР 2014-15
- ЛАЗАР 2013-14
- ЛАЗАР 2012-13
- ЛАЗАР 2011-12
- ЛАЗАР 2010-11
Студент получает степень магистра экологических исследований и степень юриста (JD) в течение четырех лет. Студенту присуждаются обе степени в один и тот же срок.
Студент получает степень магистра математики с полной кредитной нагрузкой и степень магистра экономики с уменьшенной кредитной нагрузкой. Студенту присуждается степень по математике в определенный срок, а затем он продолжает обучение и получает степень по экономике позднее.
При получении докторской степени в области управления образованием студент также выбирает получение степени магистра в области специального образования. Для получения докторской степени требуется больше времени, и в первую очередь присуждается степень магистра.
Студент получает степень магистра делового администрирования (MBA) и магистра государственного управления (MPA).
 Студенты меняют свое внимание, записываясь на полный рабочий день на курсы, связанные с MBA, в течение одного года и записываясь на полный рабочий день на курсы, связанные с MPA, в следующем году. После выполнения требований по обоим курсам студенту присуждаются обе степени в один и тот же срок.
Студенты меняют свое внимание, записываясь на полный рабочий день на курсы, связанные с MBA, в течение одного года и записываясь на полный рабочий день на курсы, связанные с MPA, в следующем году. После выполнения требований по обоим курсам студенту присуждаются обе степени в один и тот же срок.Получите допуск к обеим программам степени через приложение UO.
Как можно скорее после поступления на обе программы, но не менее чем за три семестра до семестра, в течение которого студент должен получить одну или обе степени (за исключением текущий студенты юридических факультетов ) — встретиться с консультантом факультета в каждом из сотрудничающих подразделений.

Каждый консультант должен одобрить курс обучения и план получения степени, ведущий к одновременной степени. Этот курс обучения установит требования, которые должны быть выполнены для каждого модуля, с явным указанием, какие курсы будут учитываться для получения той или иной степени.
Декларация о параллельных степенях формы должна быть заполнена, распечатана, подписана и отправлена в Отдел последипломного образования, как только студент будет принят на обе программы, но не позднее, чем за три семестра до окончания срока. в котором студент получит одну или обе степени.
Студенты юридического факультета должны подать декларацию о параллельных степенях по форме до срока, на который вы подаете заявку. Вы не будете допущены к программе и не сможете зарегистрироваться на курсы для выпускников, не отправив эту форму. Если вы отправите форму с опозданием, вам необходимо будет подать заявку на следующий семестр, чтобы получить допуск.

Не позднее пятницы 2-й недели срока окончания обучения (для одной или обеих степеней) вы должны подать заявку на выпуск , а завершенный план программы на получение степени должен быть представлен в Отдел последипломного образования.
- Требования к резидентуре
- Одновременное получение степени магистра/юриспруденции
- Одновременное получение степени доктора/магистра
- Получение степени
- 50+ Варианты специальностей и степеней
- 15 : 1 Соотношение студентов и преподавателей
- 50+ Варианты специальностей и степеней
- 15 : 1 Соотношение студентов и преподавателей
Тейлор Джордан проходит стажировку в HudsonAlpha BioTrain
23 сентября 2022 г.Мастер по закупкам и управлению контрактами, утвержденный на весну 2023 г.
22 сентября 2022 г.
2022 Программа «Боннер Лидер»
22 сентября 2022 г.сент. 24
суббота, 24 сентября 2022 г.
Предварительный просмотр штата Афины: дневная сессия
Время события: 9:00–12:00сент.

Направление D: социальные науки
Область E: Культура и мысль
Область F: Arts
Область G: Литература
и Требования к специальным предметной области
Этнерство
Европейские традиции
Количественные отношения
World Coltrers
.
Колледж литературы и науки предлагает четыре степени бакалавра: бакалавр искусств, бакалавр наук, бакалавр изящных искусств и бакалавр музыки. Какую степень — или степени — получают студенты, определяется их специальностью; и требования к степени и количество курсов, необходимых для выполнения этих требований, различаются для каждой степени бакалавра. Ниже приведены ссылки на требования для каждой степени бакалавра:
Ниже приведены ссылки на требования для каждой степени бакалавра:
Контрольный список для получения степени бакалавра гуманитарных наук
Контрольный список для получения степени бакалавра наук
Контрольный список для получения степени бакалавра изящных искусств/бакалавра музыки
Обратите внимание, что курс GE может засчитываться в счет только для одного Общего требования к предметной области (Области A-G). Однако этот курс также может соответствовать одному или нескольким требованиям специальной предметной области. Например, курс истории искусств 6C может соответствовать курсу General Subject Area E или Area F. Он также считается курсом европейских традиций (специальная предметная область) и как курс письма (специальная предметная область). Это означает, что Art History 6C может применяться одновременно к трем требованиям GE.
Списки общеобразовательных курсов
Обратите внимание, что приведенные ниже списки отражают курсы, которые были утверждены для общеобразовательных требований в течение предыдущего учебного года, а не утверждения, сделанные в текущем году. Информация о курсе в GOLD должна включать самые последние изменения.
Информация о курсе в GOLD должна включать самые последние изменения.
В списках ниже показано, как курсы могут перекрываться для выполнения более одного требования.
Общие предметные области A-E
Область A: Английский Чтение и сочинение
Письмо 2, 2E, 2LK
Английский 10, 10AC, 10EM, 10LC; Письмо 50, 50E, 105AA-ZZ, 107AA-ZZ, 109AA—ZZ
Область B: Иностранный язык
2021-22 Область B Список курсов*
Область C: Наука, математика и технологии
2021-22 Список курсов области C* (включая категории IGETC для учащихся с частичной сертификацией IGETC)
Область D Общественные науки
2021-22 Область D Список курсов*
Область E Культура и мысль
2021-22 Область E Список курсов*
Область F: Искусство
2021-22 Область F Список курсов*
7
Область G: Литература2021-22 Область G: Список курсов*
Специальные предметы
Требование по этнической принадлежности
2021-22 Требования к этническим требованиям*
Требования европейских Требования
20211-22 Список*
Требование о количественных отношениях
2021-22 Требования к количественным отношениям Список курсов*
Требование мировых культур
2021-22 Требования мировых культур Список курсов. и институты
и институты
2021-22 Список курсов американской истории и институтов
AHI — это требование всего UC, а не специальное требование общего образования UCSB. Курсы AHI также могут учитываться при выполнении требований по общим и специальным предметам.
_______
*Это списки курсов, соответствующих общеобразовательным требованиям на 2021-22 учебный год, утвержденные Сенатом факультета UCSB. Эти списки могут меняться из года в год: Пожалуйста, обратитесь к Общему каталогу для данного учебного года, чтобы увидеть список за этот год. дополнения будут отражены в ЗОЛОТО. Кроме того, сенат факультета время от времени удаляет курсы из утвержденных списков, но если удаленный курс был одобрен как соответствующий требованиям при поступлении студента в UCSB, он будет продолжать учитываться в требованиях для этого студента.
4 . Основные требования
Информацию об основных требованиях см. в Общем каталоге или обратитесь за консультацией в отдел хостинга.
Еще одним бесценным ресурсом для понимания структуры степени Letters and Science является ежегодная публикация LASAR ( Letters and Science Academic Requirements ), распространяемая среди всех студентов по адресу:
Полные требования к градуировке поясняются в Общем каталоге.
Часто задаваемые вопросы по общему образованию
Я почти выполнил требования Breadth/GE в другом кампусе UC. Могу ли я выполнить оставшиеся требования в UCSB?
Если вы не полностью выполнили требования предыдущей программы UC Breadth/GE до поступления в UCSB, вам необходимо пройти общеобразовательную программу UCSB.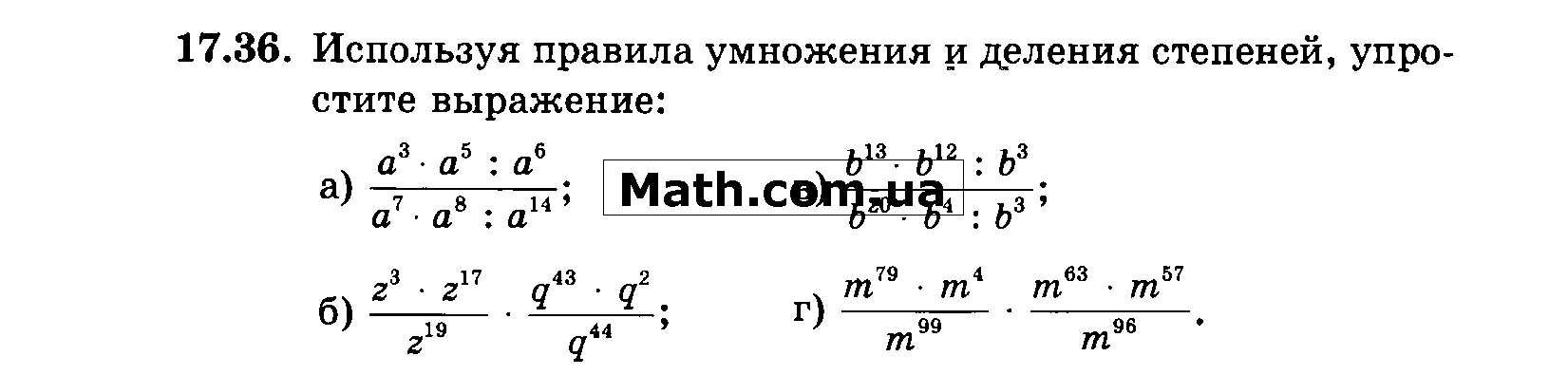 Вы получите кредит общего образования UCSB, где это уместно, за отдельные курсы, пройденные в другой школе, но вам, скорее всего, потребуются дополнительные курсы, чтобы соответствовать требованиям общего образования UCSB.
Вы получите кредит общего образования UCSB, где это уместно, за отдельные курсы, пройденные в другой школе, но вам, скорее всего, потребуются дополнительные курсы, чтобы соответствовать требованиям общего образования UCSB.
Я прошел курс, который, по моему мнению, должен соответствовать требованиям GE, но его нет в списке одобренных курсов. Могу ли я ходатайствовать о кредите GE?
Что касается общих предметных требований, то только курсы, указанные в списках областей от A до G, могут соответствовать этим требованиям. Нет возможности подать апелляцию на получение кредита GE для курсов UCSB, которые не указаны в списках.
Особые требования области (этническая принадлежность, мировые культуры, европейские традиции и количественные отношения) не могут быть удовлетворены путем подачи петиции на курсы UCSB, за единственным исключением требования к письму: до двух курсов, не перечисленных как удовлетворяющих письму Требование по ходатайству может быть применено к шести максимальным требуемым курсам письма.
Я прошел курс, указанный в списках, по двум различным общим предметным областям. Получу ли я кредит за завершение обеих областей?
Хотя некоторые курсы указаны в нескольких списках, отдельные курсы могут охватывать только одну из общих предметных областей. Однако некоторые курсы могут удовлетворять как общей предметной области, так и специальной предметной области.
Может ли курс засчитываться для моей специальности, а также соответствовать общему образованию?
Курс может удовлетворять как требованиям общего образования, так и требованиям вашей основной или предварительной специальности. Однако имейте в виду, что она должна быть принята за буквенную оценку, если она должна быть засчитана в вашу специальность.
Управление параллельными степенями | Отдел последипломного образования
В Орегонском университете термин одновременных ученых степеней используется, когда аспирант принимается и зачисляется на программы двух степеней в любой момент обучения.
Для получения дополнительной информации учащиеся должны прочитать , получающие параллельные ученые степени .
Примеры параллельных степеней выпускников
Шаги для получения параллельной степени магистра
В настоящее время все параллельные программы магистратуры считаются «инициируемыми студентами», а не формализованные программы .
Отдел последипломного обучения призывает всех студентов, которые заинтересованы в получении параллельной степени, связаться с одним или обоими соответствующими академическими подразделениями.
Любой студент, желающий создать параллельную программу получения степени вне формализованного процесса, должен следовать этому процессу:
Плата за обучение
Начиная со срока объявления параллельных степеней, плата за обучение для студентов, получающих параллельные степени, будет оцениваться по ставке, основанной на средней стоимости обучения двух академических единиц.
Об этом четко сообщается в декларации о параллельных степенях формы и на одновременное получение ученых степеней .
Распределение дохода
Если студент одновременно зачислен более чем на одну программу, колледж, в котором находится каждая программа, получит 50% от своей обычной платы за обучение. Если задействовано более двух единиц, будет использоваться пропорциональная формула.
Для параллельных степеней, инициированных студентами, в которых обе специальности проживают в одной школе/колледже, декан этой школы/колледжа несет ответственность за определение потока доходов для программ.
О процессе зачисления
Требуется официальное зачисление через приложение UO.
Порядок приема остается на усмотрение департамента. Тем не менее, факультеты должны иметь справедливую и справедливую практику/политику, установленную для приема студентов, желающих получить второе высшее образование, на свои программы.
Например, факультет может решить, что он не будет принимать студентов вообще, принимать только в течение их текущего годового цикла приема или принимать менее формально, когда есть свободные места.
Департаменты также должны составить список необходимых материалов для приема студентов, желающих получить второе высшее образование.
Студенты должны быть зачислены, имея достаточно времени, чтобы провести не менее двух полных семестров в качестве зачисленных студентов на вторую программу магистратуры.
Это ожидание соответствует действующей политике университета (Отдел последипломного образования) в отношении проживания в магистратуре . Он также устанавливает ожидания в отношении передовой практики консультирования, предоставляя отделам достаточное время и возможность консультировать студентов, получающих вторую степень магистра по своей программе.
Эта политика признает, что получение степени после бакалавриата предполагает больше, чем завершение курсовой работы.
Официальный процесс приема завершится подачей в Отдел заявления о параллельных степенях формы .
См. одновременное получение степени магистра для получения информации о:
Формализация параллельной программы получения степени
Хотя в настоящее время в Орегонском университете нет официальных параллельных программ получения степени, институциональная политика, регулирующая разработку и финансирование параллельных степеней, не препятствует инновационным образовательным возможностям, таким как параллельные степени.
Учитывая важность междисциплинарного обучения и роль параллельных степеней в профессиональном развитии наших студентов, эти правила направлены на создание стимулов для формализации таких программ при сохранении гибкости для инициируемых студентами (неформализованных) программ.
В настоящее время все параллельные программы на получение степени считаются программами, инициируемыми студентами, включая те, которые исторически были популярны среди студентов (например, JD/международные исследования, MBA/MPA).
Дом — Афинский государственный университет
Независимо от того, как вы начали свое образование в колледже, штат Афины является идеальным местом для получения степени . Мы являемся одним из немногих высших учебных заведений в стране.
Подать заявку сегодня
Новости и объявления Карусель
Paving the Way
Кампания по асфальтированию — это совместный проект Афинского государственного университета, Ассоциации выпускников и Управления развития университетов. Приблизительно 10% выручки будет использовано для покрытия расходов, связанных с кампанией, в то время как остаток средств пойдет непосредственно на пользу Ассоциации выпускников, при этом 80% будут выделены на стипендии, а оставшиеся 20% пойдут Ассоциации выпускников без каких-либо ограничений на будущие инициативы. которые приносят пользу учреждению.
Приблизительно 10% выручки будет использовано для покрытия расходов, связанных с кампанией, в то время как остаток средств пойдет непосредственно на пользу Ассоциации выпускников, при этом 80% будут выделены на стипендии, а оставшиеся 20% пойдут Ассоциации выпускников без каких-либо ограничений на будущие инициативы. которые приносят пользу учреждению.
ПРОМЫШИВАЯ ПУТЬ
Истории штата Афины
Хотя нет двух учеников, которые идут по одному и тому же пути к штату Афины, каждый из них ищет соответствующее образование для светлого и уверенного будущего. Узнайте о других афинянах, которые рассказывают о своих историях в Афинском государстве.
Просмотрите новости штата Афины
Готовы принять участие?
Обучение, открытия и развитие не прекращаются после того, как вы покидаете класс. Штат Афины предлагает множество студенческих клубов и организаций, ориентированных на самые разные интересы. Присоединяйтесь и максимально используйте свое время в Афинах!
Присоединяйтесь и максимально используйте свое время в Афинах!
Откройте для себя клубы и организации

 Например, 43 – это “четыре в кубе”.
Например, 43 – это “четыре в кубе”.

 лиц(Скачать-12 kb)
Заявления на регистрацию для юр.лиц(Скачать-11,4 kb)
1. При регистрации новой машины:
1.заявление 2.паспорт […]
лиц(Скачать-12 kb)
Заявления на регистрацию для юр.лиц(Скачать-11,4 kb)
1. При регистрации новой машины:
1.заявление 2.паспорт […] Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […]
Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […] = 10 * 10 * 10 * 10 * 10 = 100000;
= 10 * 10 * 10 * 10 * 10 = 100000;

 колледжи для карьеры начальника отдела в США на основании их резюме. Адвокаты часто получают степень в Университете Мэриленда — Колледж-Парк, Вебстерском университете и Университете Феникса.
колледжи для карьеры начальника отдела в США на основании их резюме. Адвокаты часто получают степень в Университете Мэриленда — Колледж-Парк, Вебстерском университете и Университете Феникса. Вот почему мы нашли лучшие колледжи для начальников отделов. Мы составили этот список на основе следующих показателей: уровень приема, уровень удержания, средний заработок работающих студентов, соотношение работающих и неработающих студентов через 10 лет после поступления, средняя стоимость посещения и средний долг выпускников.
Вот почему мы нашли лучшие колледжи для начальников отделов. Мы составили этот список на основе следующих показателей: уровень приема, уровень удержания, средний заработок работающих студентов, соотношение работающих и неработающих студентов через 10 лет после поступления, средняя стоимость посещения и средний долг выпускников. SUNY at Binghamton
SUNY at Binghamton
 Он включает в себя структурированное и тщательное управление людьми…
Он включает в себя структурированное и тщательное управление людьми… ..
..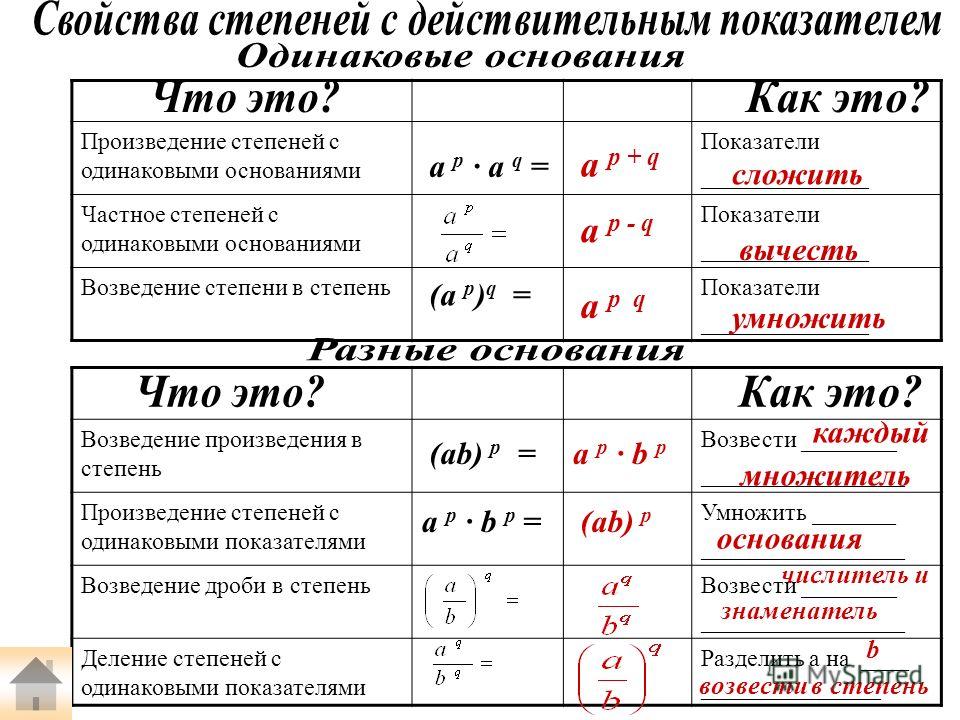 Курс будет преподаваться с точки зрения менеджера или главного исполнительного директора (CEO). Этот курс направлен на то, чтобы вооружить вас хорошим пониманием того, что подразумевает управление фирмой в стратегическом плане? Как…
Курс будет преподаваться с точки зрения менеджера или главного исполнительного директора (CEO). Этот курс направлен на то, чтобы вооружить вас хорошим пониманием того, что подразумевает управление фирмой в стратегическом плане? Как… ..
..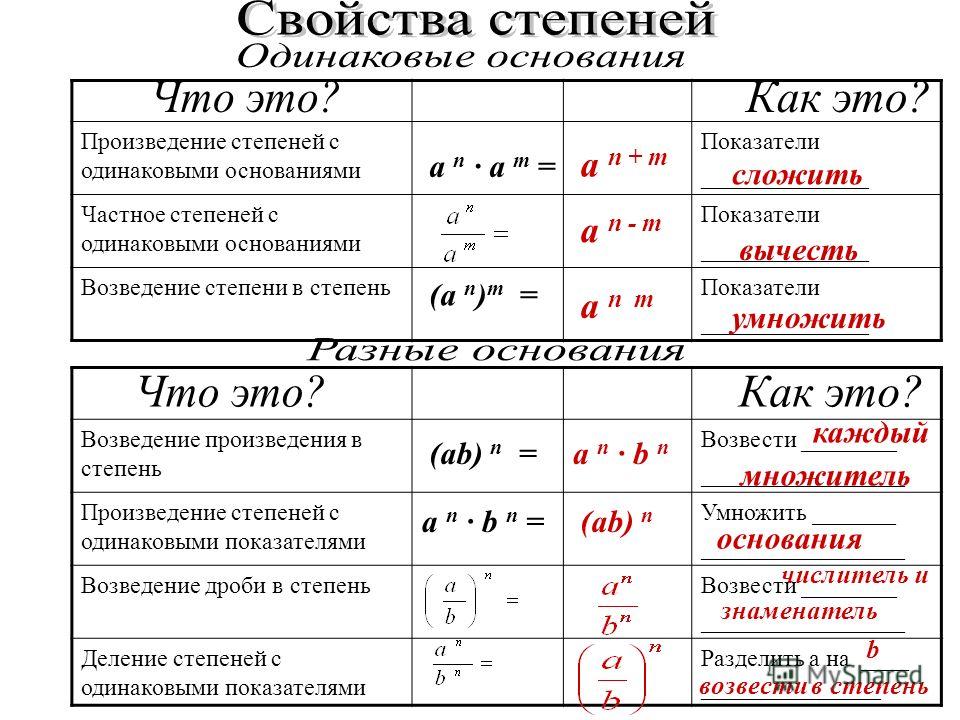 ..
..
 Чтобы иметь право на получение сертификата PMP, вы должны сначала соответствовать определенным требованиям к образованию и опыту управления проектами и согласиться придерживаться кодекса профессиональной руководить. Последним шагом к тому, чтобы стать PMP, является сдача строгого экзамена с несколькими вариантами ответов, предназначенного для объективной оценки и измерения вашей способности применять знания по управлению проектами в следующих шести областях: инициирование проекта, планирование проекта, выполнение проекта, мониторинг и контроль. проект, закрытие проекта, профессиональная и социальная ответственность. Этот компьютерный экзамен проводится по всему миру с помощью средств перевода на 10 языков.
Чтобы иметь право на получение сертификата PMP, вы должны сначала соответствовать определенным требованиям к образованию и опыту управления проектами и согласиться придерживаться кодекса профессиональной руководить. Последним шагом к тому, чтобы стать PMP, является сдача строгого экзамена с несколькими вариантами ответов, предназначенного для объективной оценки и измерения вашей способности применять знания по управлению проектами в следующих шести областях: инициирование проекта, планирование проекта, выполнение проекта, мониторинг и контроль. проект, закрытие проекта, профессиональная и социальная ответственность. Этот компьютерный экзамен проводится по всему миру с помощью средств перевода на 10 языков. и соглашаетесь соблюдать кодекс профессионального поведения. Последним шагом к тому, чтобы стать PMP, является сдача строгого экзамена с несколькими вариантами ответов, предназначенного для объективной оценки и измерения вашей способности применять знания по управлению проектами в следующих шести областях: инициирование проекта, планирование проекта, выполнение проекта, мониторинг и контроль. проект, закрытие проекта, профессиональная и социальная ответственность. Этот компьютерный экзамен проводится по всему миру с помощью средств перевода на 10 языков.
и соглашаетесь соблюдать кодекс профессионального поведения. Последним шагом к тому, чтобы стать PMP, является сдача строгого экзамена с несколькими вариантами ответов, предназначенного для объективной оценки и измерения вашей способности применять знания по управлению проектами в следующих шести областях: инициирование проекта, планирование проекта, выполнение проекта, мониторинг и контроль. проект, закрытие проекта, профессиональная и социальная ответственность. Этот компьютерный экзамен проводится по всему миру с помощью средств перевода на 10 языков. Сертифицированный авиационный менеджер (CAM)
Сертифицированный авиационный менеджер (CAM) После учета стоимости обучения в штате и сборов, средней стоимости посещения, уровня приема, средней чистой цены и среднего заработка через 6 лет мы обнаружили, что это самые доступные школы для руководителей подразделений.
После учета стоимости обучения в штате и сборов, средней стоимости посещения, уровня приема, средней чистой цены и среднего заработка через 6 лет мы обнаружили, что это самые доступные школы для руководителей подразделений. Университет штата Флорида
Университет штата Флорида
 Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.
Он включает в себя обучение и сборы, книги и расходные материалы, а также расходы на проживание.

 Университет священных имен
Университет священных имен
 Узнайте больше на странице отдела биостатистики.
Узнайте больше на странице отдела биостатистики. Узнайте больше на странице отдела наук об окружающей среде.
Узнайте больше на странице отдела наук об окружающей среде. Узнайте больше на странице Отдела политики и управления здравоохранением.
Узнайте больше на странице Отдела политики и управления здравоохранением. Узнайте больше на странице междисциплинарного подразделения.
Узнайте больше на странице междисциплинарного подразделения.


 Требования к общему образованию
Требования к общему образованию  Студенты меняют свое внимание, записываясь на полный рабочий день на курсы, связанные с MBA, в течение одного года и записываясь на полный рабочий день на курсы, связанные с MPA, в следующем году. После выполнения требований по обоим курсам студенту присуждаются обе степени в один и тот же срок.
Студенты меняют свое внимание, записываясь на полный рабочий день на курсы, связанные с MBA, в течение одного года и записываясь на полный рабочий день на курсы, связанные с MPA, в следующем году. После выполнения требований по обоим курсам студенту присуждаются обе степени в один и тот же срок.


