404 — Страница не найдена
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
by/algebra/preobrazovanija-vyrazhenij/svojstva-stepeni-s-naturalnym-pokazatelem/] не найдена.
05.13 
by 2013-2016Свойства степеней с натуральным показателем презентация, доклад
ThePresentationru
- Регистрация |
- Вход
- Загрузить
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Свойства степеней с натуральным показателем, предмет презентации: Математика.
Этот материал содержит 26 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Свойства степеней с натуральным показателем.
Повторяем.
Назовите основание и показатель степени
Выполните возведение в степень:
Представьте числа в виде квадрата или куба числа:
Вычислите:
Умножение степеней
с одинаковыми основаниями
Для любого числа а и произвольных натуральных чисел m и n верно равенство
Правило:
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а
показатели степеней складывают.
Умножение степеней
Представьте произведение в виде степени:
Деление степеней с одинаковыми основаниями
Для любого числа а ≠ 0 и произвольных натуральных чисел m и n , таких что m > n верно равенство
Правило:
При делении степеней с одинаковыми основаниями
основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Деление степеней
Степень числа а ≠ 0 с нулевым показателем
равна единице.
Например:
Выражение 00 не имеет смысла.
Деление степеней
Представьте частное в виде степени:
Назовите показатель степени
Назовите основание степени
Для любых чисел а и в и произвольного натурального числа n верно равенство
Рассмотрим степень
Правило:
Чтобы возвести в степень произведение достаточно возвести в эту степень каждый множитель и результаты перемножить.
Свойство справедливо для степени из произведения трех и более множителей
Свойство справедливо для степеней с нулевым показателем (если основания отличны от нуля)
Замените на произведение степень:
Назовите показатель степени
Назовите основание степени
Для любого числа а и произвольных натуральных чисел n и m верно равенство
Рассмотрим степень
Правило:
При возведении степени в степень основание оставляют тем же, а показатели перемножают.
Свойство справедливо для степеней с нулевым показателем (если основания отличны от нуля)
Выполняя задание по преобразованию выражений, содержащих степени, ученик допустил ошибки:
Какие свойства степени не знает ученик?
Выполняя задание по преобразованию выражений, содержащих степени, ученик допустил ошибки:
Какие свойства степени не знает ученик?
Какие свойства степени не знает ученик?
Выполняя задание по преобразованию выражений, содержащих степени, ученик допустил ошибки:
Какие свойства степени не знает ученик?
Выполняя задание по преобразованию выражений, содержащих степени, ученик допустил ошибки:
Какие свойства степени не знает ученик?
Выполняя задание по преобразованию выражений, содержащих степени, ученик допустил ошибки:
При каком значении k верно равенство?
Вычислите
Сравните выражения.
Ответ обоснуйте
Сравните с нулем значение выражения
Рефлексия
Я знаю…
Я могу …
Я умею…
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.ru?
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Предварительное исчисление по алгебре — Умножение переменных с разными основаниями и разными показателями
спросил
Изменено 6 лет, 11 месяцев назад
Просмотрено 150 раз
$\begingroup$
Я застрял.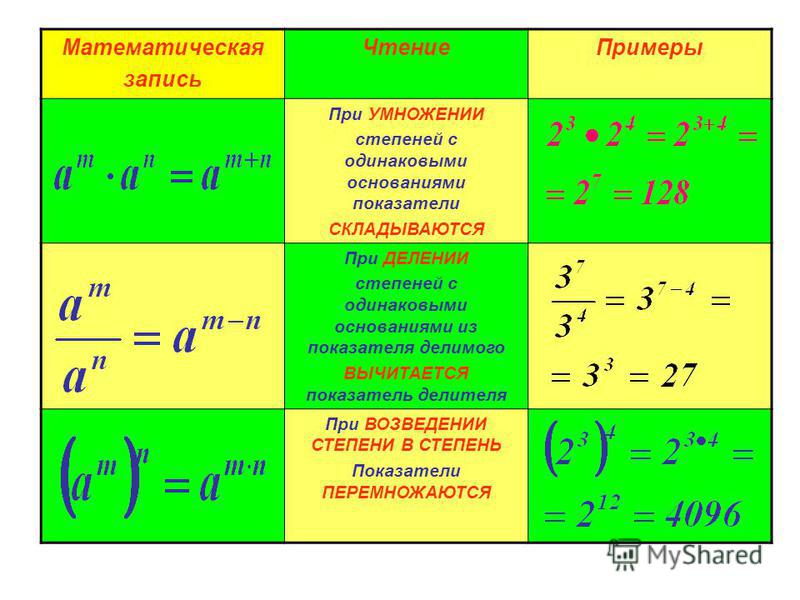
Помощь ребенку с алг II, а в инструкции сказано упростить выражение до одного корня. $$\sqrt{10} \cdot \sqrt[4]{3}$$
Я знаю, как это сделать с той же базой или с той же степенью, но десять в 1/2 умножить на 3 в 1/4? Я просто слишком много думаю об этом? Я не вижу этого. 9b$, когда $a$ и $b$ рациональны — просто запишите показатели степени, используя их наименьший общий знаменатель.
(я начал этот ответ несколько часов назад, прежде чем увидел комментарий @AndreNicolas.)
$\endgroup$
$\begingroup$
Весь фокус в том, чтобы понять, что $\sqrt{10}$ можно переписать как $\sqrt[4]{100}$. Есть по крайней мере два способа установить это соединение:
- Вы можете понять, что $10 = \sqrt{100}$, поэтому $\sqrt{10}=\sqrt{\sqrt{100}}$. 9{1/4} $.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Что делать при умножении показателей степени с разными основаниями? – Gzipwtf.com
Вклад
Диана Монтгомери
Что делать при умножении показателей степени с разными основаниями?
Умножение показателей степени с разными основаниями Сначала перемножьте основания. Затем добавьте показатель степени. Вместо того, чтобы складывать два показателя вместе, оставьте их одинаковыми. Это происходит из-за правила четвертой степени: распределять мощность по каждому основанию при возведении нескольких переменных в степень.
Как вычислить показатели степени с разным основанием?
Чтобы умножать выражения с разными основаниями и одинаковыми степенями, сначала умножаются основания. Математически это можно записать как an × bn = (a × b)n. При перемножении выражений с разными основаниями и разной степенью каждый член оценивается отдельно, а затем перемножается.
Можно ли складывать разные показатели степени с разными основаниями?
Помните, что для сложения или вычитания чисел с показателями степени вы должны сначала убедиться, что основание и показатель степени двух членов, которые вы пытаетесь сложить или вычесть, совпадают. Если они одинаковы, то все, что вам нужно сделать, это сложить их коэффициенты и сохранить одинаковые основание и показатель степени.
При умножении показателей степени с одинаковым основанием складывать показатели степени Верно или неверно?
Схема умножения показателей степени с одинаковым основанием заключается в сохранении основания и сложении показателей степени. Это работает, потому что мы объединяем два термина в один. Каждый термин имеет определенное количество оснований, которые умножаются, и, добавляя показатели степени, вы записываете расширенные основания вместе, используя одно основание и один показатель степени.
Можно ли умножать степени с одинаковым основанием?
Когда вы умножаете два числа или переменные с одинаковым основанием, вы просто складываете показатели степени.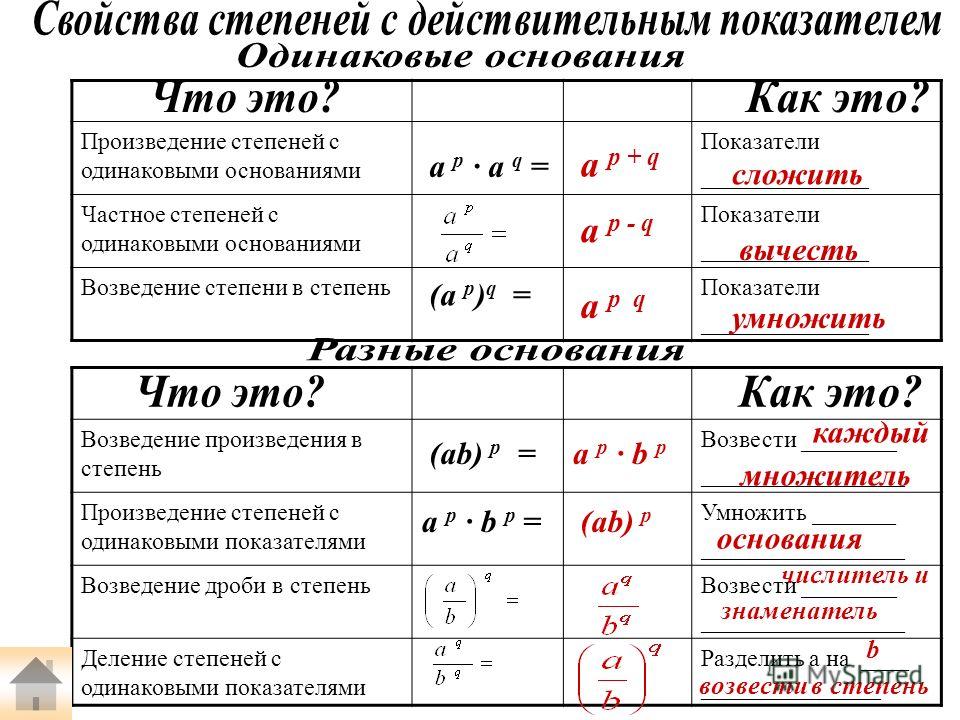
Когда вы умножаете выражения с одним и тем же показателем степени, но с разными основаниями, вы умножаете основания и используете один и тот же показатель степени.
Как складывать степени с одинаковым основанием и разными степенями?
Чтобы добавить показатели степени, и показатели степени, и переменные должны быть одинаковыми. Вы добавляете коэффициенты переменных, оставляя показатели без изменений. Добавляются только термины с одинаковыми переменными и степенями. Это правило также согласуется с умножением и делением показателей.
Когда основание одинаковое, а степень разная при умножении?
Когда вы умножаете степени с одинаковым основанием?
Умножение показателей степени с одинаковым основанием При умножении двух переменных или чисел с одинаковым основанием вы просто складываете показатели степени. Таким образом, x3*x4 = x3+4 = x7.
По какому принципу умножаются степени с одинаковым основанием?
Каков порядок умножения показателей степени с одинаковым основанием? Правило умножения показателей степени с одинаковым основанием называется произведением степенного свойства.
Свойство «Произведение степеней» гласит, что при умножении двух показателей степени на одно и то же основание вы можете сложить показатели степени и сохранить основание.
Как умножать показатели степени с разным основанием и степенью?
Умножение дробей с показателями степени с разными основаниями и показателями: (4/3) 3 ⋅ (1/2) 2 = 2,37 ⋅ 0,25 = 0,5925 Умножение дробей с одинаковыми показателями степени: a n/m ⋅ b n/m = ( a ⋅ б) н/м
Как умножать квадратные корни на экспоненты?
Как умножать квадратные корни на экспоненты? Для показателей с одинаковым основанием мы можем добавить показатели: (√a) n x (√a) m = a (n + m)/2. Пример 9(√5) 2 x (√5) 4 = 5 (2+4)/2 = 5 6/2 = 5 3 = 125; Умножение переменных с показателями; Для показателей с одинаковым основанием мы можем добавить показатели степени: x n * x m = x n + m. Пример 10
Как умножать отрицательные степени?
Умножение отрицательных показателей степени Для показателей степени с одинаковым основанием мы можем сложить показатели степени: a -n ⋅ a -m = a -(n+m) = 1 / a n+m
Что означают показатели степени?
Экспоненты — степени или индексы.