2. Признаки равенства треугольников — Проект по геометрии «Треугольники. Признаки равенства треугольников»
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство: Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1. Так как ∠ А = ∠ А1, то
треугольник ABC можно наложить на треугольник А1В1С1 так,
что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся
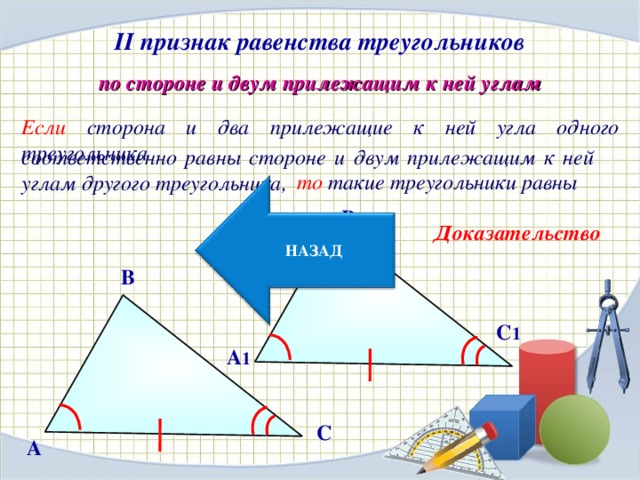
соответственно на лучи А1В1 и A1C1. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Доказательство: Рассмотрим треугольники ABCABC и A1B1C1A1B1C1, у которых AB=A1B1,∠A=∠A1,∠B=∠B1AB=A1B1,∠A=∠A1,∠B=∠B1. Докажем, что △ABC=△A1B1C1△ABC=△A1B1C1. Наложим треугольник ABCABC на треугольник A1B1C1A1B1C1 так, чтобы
вершина AA совместилась с
вершиной AA, сторона ABAB – с равной ей
стороной A1B1A1B1, а вершины CC и C1C1 оказались по одну
сторону от прямой A1B1A1B1. Так как ∠A=∠A1∠A=∠A1 и ∠B=∠B1∠B=∠B1, то по сторона ACAC наложится на луч A1C1A1C1, а сторона BCBC – на луч B1C1B1C1. Поэтому вершина CC – общая точка сторон ACAC и BCBC – окажется как лежащей на луче A1C1A1C1, так и на луче B1C1B1C1 и, следовательно, совместиться с общей точкой этих лучей – вершиной C1C1. Значит, совместятся стороны ACAC и A1C1A1C1, BCBC и B1C1B1C1. Итак треугольники ABCABC и A1B1C1A1B1C1 полностью совместятся. Следовательно, они равны. Третий признак равенства треугольников Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Доказательство: Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, BC = B1C1, CA = C1A1 , и докажем, что эти треугольники равны.Приложим треугольник ABC к треугольнику A1B1C1 так, чтобы вершина A и A1, B и B1совместились, а вершины C и C1 оказались по разные стороны от прямой A1B1 (рис. |
Поскольку АВ = A1B
Геометрия 7-9 класс. Второй и третий признак равенства треугольников — math200.ru
Skip to contentГеометрия 7-9 класс. Второй и третий признак равенства треугольниковadmin2022-12-11T22:49:36+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Второй и третий признак равенства треугольников
Второй признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.Третий признак равенства треугольников: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны.
| Задача 1. Найдите пару равных треугольников и докажите их равенство. | |
| Задача 2. Найдите пару равных треугольников и докажите их равенство. | |
| Задача 3. Найдите пару равных треугольников и докажите их равенство. | |
| Задача 4. Известно, что AD = BF. Найдите пару равных треугольников и докажите их равенство. | |
| Задача 5. Известно, что AD = BC. Найдите пару равных треугольников и докажите их равенство. | |
| Задача 6. Найдите пару равных треугольников и докажите их равенство. | |
| Задача 7. Найдите все пары равных треугольников и докажите их равенство. | |
Задача 8. Известно, что AB = BC, AK = KC, \(\angle \,AKE = \angle \,CKP.\) Докажите, что \(\Delta \,AKE = \Delta \,CKP.\) | |
| Задача 9. Известно, что AB = BC, AM = PC, \(\angle \,AMO = \angle \,OPC.\) Докажите, что \(\Delta \,AMO = \Delta \,OPC.\) | |
| Задача 10. Известно, что AM = MC, AE = DC, \(\angle \,BDA = \angle \,FEC.\) Докажите, что AB = FC. | |
| Задача 11. Найдите все пары равных треугольников и докажите их равенство. | |
| Задача 12. Найдите все пары равных треугольников и докажите их равенство. | |
| Задача 13. Найдите все пары равных треугольников и докажите их равенство. | |
Задача 14. Найдите все пары равных треугольников и докажите их равенство. | |
| Задача 15. Найдите все пары равных треугольников и докажите их равенство. | |
| Задача 16. Найдите все пары равных треугольников и докажите их равенство. | |
| Задача 17. Найдите все пары равных треугольников и докажите их равенство. | |
| Задача 18. Найдите все пары равных треугольников и докажите их равенство. | |
| Задача 19. Найдите все пары равных треугольников и докажите их равенство. | |
Задача 20. Отрезок AB точками P и Q делится на три равные части. Вне отрезка AB по одну сторону от него взяты точки C и D так, что AC = BD и CQ = DP, \(\angle \,DPB + \angle \,CQA = {158^ \circ }. \circ }.\) | |
Реклама
Поддержать нас
Q13 Два смежных угла, образующих линейную пару, находятся в отношении 75. Найдите углы…
Перейти к
- Упражнение 24 (А)
- Упражнение 24(Б)
- Повторное упражнение
- Система счисления (закрепление чувства числа)
- Предварительный расчет
- Числа в Индии и международной системе (со сравнением)
- Место Значение
- Натуральные числа и целые числа (включая шаблоны)
- Отрицательные числа и целые числа
- Номер строки
- HCF и LCM
- Игра с числами
- Наборы
- Соотношение
- Доля (включая словесные задачи)
- Унитарный метод
- Фракции
- Десятичные дроби
- Процент (Процент)
- Представление о скорости, расстоянии и времени
- Основные понятия (алгебра)
- Основные операции (связанные с алгебраическими выражениями)
- Замена (включая использование скобок в качестве группирующих символов)
- Обрамление алгебраических выражений (включая вычисление)
- Простые (линейные) уравнения (включая текстовые задачи)
- Основные понятия (геометрия)
- Углы (с их типами)
- Свойства углов и линий (включая параллельные линии)
- Треугольники (включая типы, свойства и конструкцию)
- четырехугольник
- Полигоны
- Круг
- Повторное упражнение по симметрии (включая построения по симметрии)
- Распознавание твердых тел
- Периметр и площадь плоских фигур
- Обработка данных (включая пиктограмму и гистограмму)
- Среднее и медиана
Главная > Селина Солюшнс Класс 6 Математика > Глава 24 — Углы (с их типами) > Повторное упражнение > Вопрос 14
Вопрос 14 Контрольное упражнение
Q13)
Два смежных угла, образующих линейную пару, относятся как 7:5, найдите углы.
Ответ:
Когда два угла имеют одну и ту же вершину, общую сторону и не пересекаются, говорят, что они смежные. Вершина угла – это точка, в которой лучи сходятся, образуя стороны угла. Когда смежные углы имеют одну и ту же вершину и сторону, они могут быть дополнительными или дополнительными углами.
При пересечении двух прямых в одной точке образуется линейная пара углов. Если углы находятся рядом друг с другом после пересечения двух прямых, они считаются линейными. Сумма углов линейной пары всегда равна 180 градусам.
Решение:
Пусть заданный угол = x
Пусть дополнительный угол данного угла равен y
тогда x+y=90
Но x-3y
3y+ y=90°
3
40=40
y=\frac{90}{4}=22,5°
дополнительный= x=90° -22-5° =67,5°
Расшифровка видео
привет добро пожаловать на домашнее задание сегодня мы собираемся см.
вопрос, который состоит в том, что два дополнительных угла находятся в соотношении семь, чтобы найти найти углы, так что в отношении семи, чтобы найти, мы собираемся найти эти углы, давайте сделаем это, поэтому сначала нам нужно выяснить, что такое дополнительные треугольники среднее дополнительное означает, что сложение этого угла будет 180 градусов, дополнительное сложение двух углов равно 180 градусам, поэтому дано, что это соотношение семь — это бороться с двумя углами и соотношением, поэтому далее мы собираемся найти угол, поэтому, если вы принимаете, что 7x плюс 5x равно 180, ладно, тогда что делать дальше 7x плюс 5x равно 2 лк до 180, так что x равно 180 на 12, то есть 180 на 12, выньте его и сделайте часть деления в грубой работе 180 разделить на 12 12 12. 6 50 12 равно 60, поэтому оно будет в 15 раз, поэтому значение x равно 15, так что теперь поместите это значение x значение в это каждое условие и узнайте каждый угол, поэтому 7 в x это первый прямой угол, поэтому 7 в 15, поэтому ответ будет 1 0 5, а затем другой угол равен 5 в x 5 в 15 15 75 шансов 105 и 75 надеюсь вы понимаете это видео и спасибо за просмотр этого видео
Связанные вопросы
Q1) Объясните, что вы понимаете под: (i) смежными углами? (ii) дополнительными углами? (iii) дополнительными.
..
Q2) Найдите значение «x» для каждой из следующих цифр:
Q3) Найдите количество градусов в углу, который (i) больше прямого угла (ii) в 0,2 раза больше прямого…
Q4) На данном рисунке; AB, CD и EF — прямые. Назовите пару углов, образующих: (i) прямую…
Q5) Найдите дополнение: (i) 210° (ii) 0,4 умножить на 130°
Q6) Найдите дополнение: (i) к 154° (ii) 0,7 умножить на 150°
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 24 (a)
Упражнение 24 (b)
Ревизионное упражнение
Главы
Система чисел (консолидация ощущения числа)
Оценка
Числа в Индии и международная система (с сравнением)
Разрядное значение
Натуральные числа и целые числа (включая шаблоны)
Отрицательные числа и целые числа
Численная линия
HCF и LCM
Игра с числами
Наборы
Соотношение
Пропорция (включая задачи Word)
Сознание.
)
Представление о скорости, расстоянии и времени
Основные понятия (алгебра)
Основные операции (связанные с алгебраическими выражениями)
Подстановка (включая использование скобок в качестве группирующих символов)
Обрамление алгебраических выражений (включая вычисление)
Простые (линейные) уравнения (включая текстовые задачи)
Основные понятия (геометрия)
Углы (с их типами)
Свойства углов и прямых (включая) Треугольники (включая типы, свойства и построение)
Четырехугольник
Многоугольники
Окружность
Повторное упражнение по симметрии (включая построения по симметрии)
Распознавание твердых тел
Периметр и площадь плоских фигур
Обработка данных (включая пиктограммы и гистограммы)
Среднее и медиана
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd.
Все права защищены. на сумму их соответствующих мер.
Смежные углы
Смежные углы — это любые два угла, которые имеют общую сторону, разделяющую два угла, и имеют общую вершину. На рисунке 1 ∠1 и ∠2 — смежные углы.
Рисунок 1 Смежные углы.
Вертикальные уголки
Вертикальные углы образуются, когда две прямые пересекаются и образуют четыре угла. Любые два из этих углов, равные , а не смежных углов называются вертикальными углами. На рисунке 2 линия l и линия м пересекаются в точке Q , образуя ∠1, ∠2, ∠3 и ∠4.
Рисунок 2 Две пары вертикальных углов и четыре пары смежных углов.
- Вертикальные уголки:
- ∠1 и ∠3
- ∠2 и ∠4
- Смежные углы:
- ∠1 и ∠2
- ∠2 и ∠3
- ∠3 и ∠4
- ∠4 и ∠1
Теорема 7: Вертикальные углы равны по мере.
Дополнительные углы
Дополнительными углами являются любые два угла, сумма которых равна 90°. На рисунке 3, поскольку ∠ ABC является прямым углом, м ∠1 + м ∠2 = 90 °, поэтому ∠1 и ∠2 дополняют друг друга.
Рисунок 3 Смежные дополнительные углы.Дополнительные углы не обязательно должны быть смежными. На рисунке 4, поскольку м ∠3 + м ∠4 = 90°, ∠3 и ∠4 являются дополнительными.
Рисунок 4 Несмежные дополнительные углыПример 1: Если ∠5 и ∠6 дополняют друг друга, а м ∠5 = 15°, найдите м ∠6.
Поскольку ∠5 и ∠6 дополняют друг друга,
Теорема 8: Если два угла дополняют один и тот же угол или равные углы, то они равны друг другу.
См. рис. 5 и 6. На рис. 5 ∠ A и ∠ B дополняют друг друга. Кроме того, ∠ C и ∠ B дополняют друг друга.
Теорема 8 говорит вам, что м ∠ A = м ∠ C . На рисунке 6 ∠ A и ∠ B дополняют друг друга. Кроме того, ∠ C и ∠ D являются дополнительными, а m ∠ B = m ∠ D. Теорема 8 теперь говорит вам, что м ∠ A = м ∠ C .
Рисунок 6 Два угла, дополняющих равные углы
Дополнительные уголки
Дополнительный угол — это два угла, сумма которых равна 180°. На рисунке ∠ ABC — прямой угол. Следовательно, 90 256 м 90 257 ∠ 6 + 90 256 м 90 257 ∠ 7 = 180 °, поэтому ∠ 6 и ∠ 7 являются дополнительными.
Рисунок 7 Смежные дополнительные углы.
Теорема 9. Если у двух смежных углов несовпадающие стороны лежат на одной прямой, то они являются дополнительными углами.