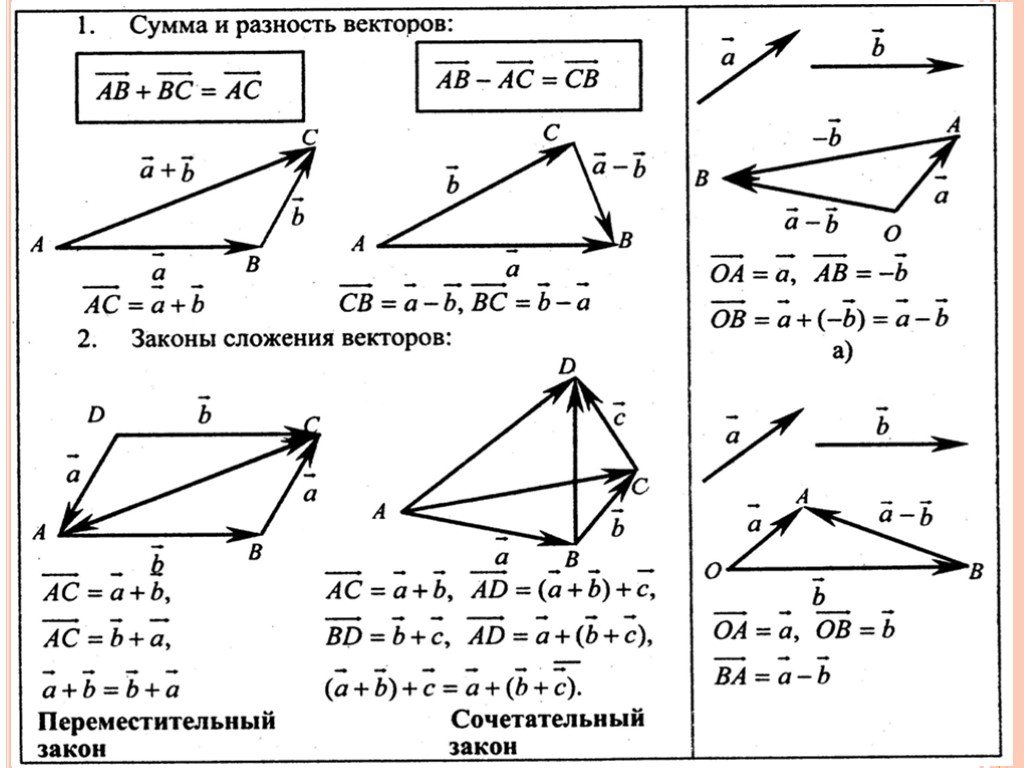
Сума векторів: Сложение и вычитание векторов

Содержание

Додавання і віднімання векторів на площині

Перейти до вмісту

03/04/2022 Ростислав Вектори і операції з ними

Навігація по сторінці.

Правила додавання векторів.
Властивості додавання векторів.
Віднімання векторів.
Додавання і віднімання векторів – розв’язування прикладів.
Блок-схема алгоритму додавання та віднімання векторів.

Нехай і – два довільних вектори. За допомогою паралельного перенесення приведемо вектор до довільної точки , а потім від кінця цього вектора відкладемо вектор .

Сумою цих векторів буде вектор , початок якого збігається з початком вектора , а кінець – із кінцем вектора (правило трикутника).

Для знаходження суми векторів можна також користуватись правилом паралелограма, згідно з яким вектори та приводять до спільного початку (точка ) і будують на цих векторах, як на суміжних сторонах, паралелограм.

Тоді його діагональ, що виходить зі спільної вершини , є сумою векторів .

Зауваження: для обчислення суми векторів використовують правило замикання ламаної (узагальнення правила трикутників). У цьому разі до кінця вектора треба приєднати вектор , до кінця – вектор і так далі. Тоді сумою векторів буде вектор, початок якого співпадає з початком першого вектора , а кінець – із кінцем останнього вектора .

Властивості додавання векторів.

Операція додавання векторів задовільняє наступні алгебраїчні властивості:

сума векторів коммутативна, тобто для будь-яких і ;
сума векторів асоціатівна, тобто для будь-яких векторів , і ;
нульовий вектор є нейтральним щодо операції додавання, тобто для будь-якого вектора ;
сумою протилежних векторів є нуль-вектор, тобто .

Віднімання векторів.

Різницею векторів і є вектор , який в сумі з вектором дає вектор .

Звідси безпосередньо випливає правило віднімання векторів: щоб від вектора відняти вектор , необхідно привести їх до спільного початку (точка ), після чого, з’єднати їх кінці за допомогою вектора , спрямованого у кінець зменшуваного вектора . В результаті отримаємо .

Зазначимо, що користуючись поняттям протилежних векторів, можна сформулювати інше правило віднімання: щоб отримати різницю векторів , потрібно до вектора додати вектор, зворотний вектору , тобто .

За допомогою правила паралелограма можна знаходити як суму, так і різницю векторів та .

Додавання і віднімання векторів – розв’язування прикладів.

Приклад 1: вектори і взаємно перпендикулярні, причому і . Знайти і .

Оскільки задані вектори взаємно перпендикулярні, то паралелограм, побудований на цих векторах, вироджується в прямокутник.

На основі властивості діагоналей прямокутника, а саме сума квадратів діагоналей дорівнює сумі квадратів його сторін, отримаємо:

Розв’язавши останнє рівняння відносно , будемо мати:

Звідси, (як діагоналі прямокутника).

Блок-схема алгоритму додавання та віднімання векторів

Ми в соціальних мережах

віднімання векторівдодавання векторіврізниця векторіврізниця векторів формуласума векторівсума векторів формула

Побудова суми та різниці векторів.

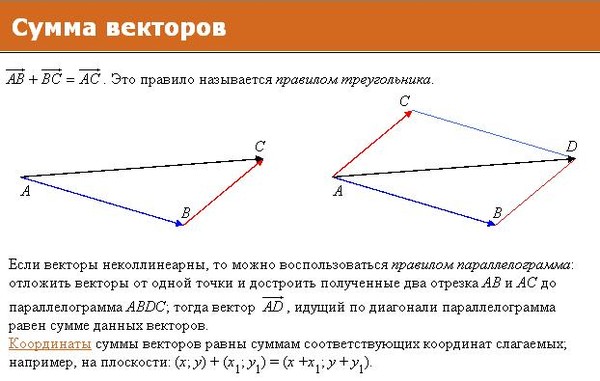Правило трикутника та паралелограма

Для вивчення теми «Вектори» + успішного проходження зовнішнього незалежного тестування нами розв’язані типові тестові завдання. За шпаргалку можете використовувати при побудові векторів наведені далі схеми.

Схема побудови різниці векторів за правилом трикутника та паралелограма

Відповідні формули скалярного добутку векторів, довжини та розрахунку кутів виділені в поясненнях до прикладів червоною рамкою. Для економії часу завантаження сторінки, всюди де йде мова про вектори над ними потрібно писати стрілку , хоча в тексті ми використовували позначення «вектор а». Це зроблено для покращення індексації сторінки та щоб швидше знайти завдання в пошуку, Ви прирозв’язуванні дотримуйтеся правил ().

Приклад 42.28 Установити відповідність між векторами (1–4) та їх координатами (А–Д).

Розв’язування: Знайдемо координати початку та кінця заданих векторів, тоді по них запишемо координати цих векторів:
1. A1(2;6) – початок вектора a,
A2(4;8) – кінець вектора a,
A(4-2;8-6)=(2;2) В.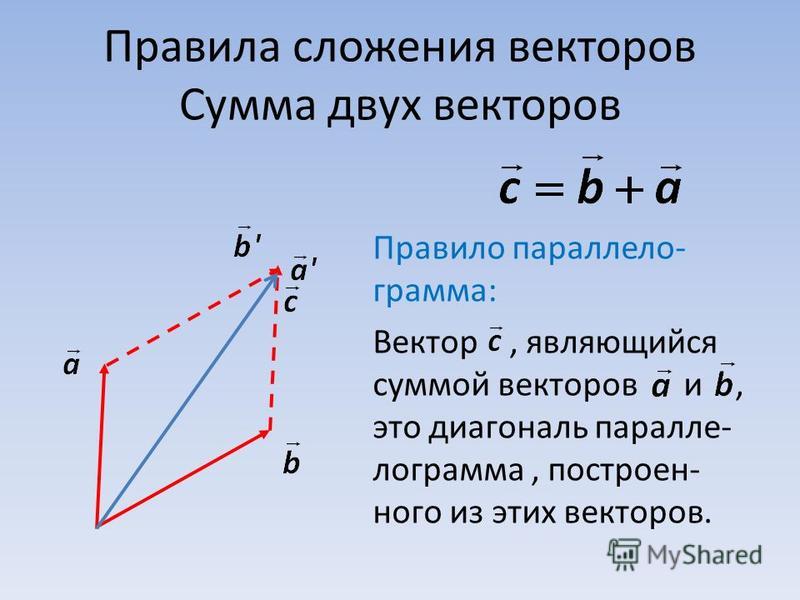

2. B1(5;4) – початок вектора b,
B2(8;5) – кінець вектора b,
B(8-5;5-4)=(3;1) Г.

3. C1(6;6) – початок вектора c,
C2(7;8) – кінець вектора c,
c(7-6;8-6)=(1;2) А.

4. O(0;0) – початок вектора m,
M2(1;3) – кінець вектора m,
M(1-0;3-0)=(1;3) Д.
Отже, маємо 1 – В, 2 – Г, 3 – А, 4 – Д.

Приклад 42.3 Дано вектори a і b. Який з наведених векторів дорівнює різниці a-b?

Розв’язування: Відняти вектор a від вектора b означає, що до вектора a треба додати вектор -b (протилежний за напрямком вектору b).
Додавання робитимемо за правилом трикутника:
від кінця вектора a відкладаємо вектор -b, далі суму векторів отримуємо, з’єднавши початок вектора a з кінцем вектора -b, в результаті отримаємо вектор p, тобто

Відповідь: p – В.

Приклад 42.1 Дано паралелограм ABCD. O – точка перетину діагоналей.

Який з наведених векторів дорівнює сумі BC+OA?

Розв’язування: Паралелограм – чотирикутник, у якого протилежні сторони паралельні та рівні, а діагоналі в точці перетину діляться навпіл. У паралелограма ABCD сторони будемо позначати векторами із заданим напрямком . Звідси слідує, що вектори BC=AD, тобто рівні, бо колінеарні, співнапрямлені та рівні по модулю (довжині). Додавати вектори будемо за правилом трикутника (дивись рисунок б):
від кінця вектора OA відкладаємо вектор AD (він же BC), далі суму векторів отримуємо, з’єднавши початок вектора OA з кінцем вектора BC, в результаті отримаємо вектор OD, тобто OA+BC+OD,
BC+OA=OD.
Відповідь: OD – Г.
Правило трикутника, та як правильно будувати лінійні комбінації векторів Ви повинні поступово вивчити, та пам’ятати, як відкладати вектори,знаходити їх суму та різницю.

Приклад 42.2 Дано вектор a. Який з наведених векторів дорівнює -2/3a?

Розв’язування: Перш за все дамо загальні правила масштабування векторів:
Множення вектора на число λ:
якщо |λ|>1, то вектор розтягнули у λ разів;
якщо |λ|<1, то вектор стиснули у λ разів;
якщо |λ|=1, то модуль (довжина) векторане змінилася;
якщо λ<0, то напрямок вектора a змінили на протилежний.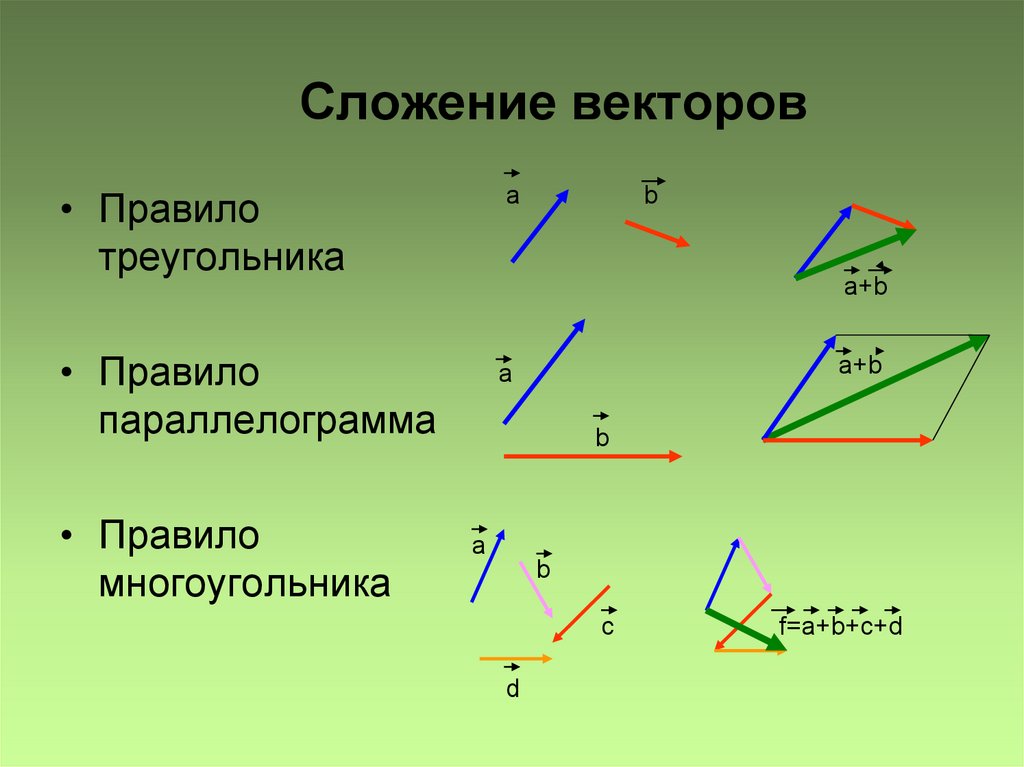

Отже, при множенні вектора на число λ=-2/3 (тут -1< λ <0) вектор -2/3a змінив напрямок і стиснули у 2/3 рази, тобто (кількість клітинок по горизонталі і вертикалі зменшили у 3 рази, а потім збільшили у 2 рази, рисунок В).

Відповідь: m – В.

Приклад 42.4 O – точка перетину медіан трикутника ABC.
Виразити вектор OB через вектори a і c.

Розв’язування: Медіана AK трикутника ABC – відрізок, який виходить з вершини A трикутника і ділить протилежну сторону BC навпіл, тобто BK=KC.
Розглянемо трикутник ABK (рисунок а), у якого сторони є векторами:
BA=a, KB=-c/2 (тут BK=BC/2 і KB=-BK=-BC/2=-c/2).
За правилом трикутника додавання векторів знайдемо вектор AK:
KB+BA=KA, -c/2+a=KA, звідси KA=a-c/2.
Медіани трикутника ABC в точці перетину O діляться у відношенні 2:1, починаючи від вершини. Тобто KA=KO+OA і OA=2KO, звідси AO=2KA/3.
Розглянемо трикутник ABO (рисунок б), у якого сторони є векторами: AB=-a (протилежний до вектора a), OA=2/3•KA (за властивістю перетину медіан ΔABC).
За правилом трикутника додавання векторів знайдемо вектор OB:

Відповідь: -1/3•a-1/3•c – Г.

Приклад 42.23 Дано квадрат ABCD. Який з наведених векторів дорівнює сумі AC+BD?

Розв’язування: У квадрата ABCD сторони і діагоналі будемо векторами із заданим напрямком позначати. Вектор DB паралельно перенесемо так, щоб його початок співпав з кінцем вектора AC, тоді отримаємо йому рівний вектор CB’, тобто DB=CB’ (при паралельному перенесенні напрямок і довжини векторів (їх координати) залишаються незмінними).
Додавати вектори будемо за правилом трикутника (дивись рисунок): від кінця вектора AC відкладаємо вектор DB (він же CB’), далі суму векторів отримуємо, з’єднавши початок вектора AC з кінцем вектора CB, в результаті отримаємо вектор AB’ (він же 2AB, оскільки точка B перейшла в точку B’ на таку ж відстань і напрямок як точку D перенесли в точку C), тобто
AC+CB’=AB’, AC+DB=2AB.
Відповідь: 2AB – А.

Приклад 42.24 Вектор OA лежить на осі Oz прямокутної декартової системи координат у просторі (див. рисунок), і його початок збігається з початком координат.
Визначити координати вектора OA, якщо його довжина дорівнює 3.

Розв’язування: За умовою завдання початок вектора OA збігається з початком координат, тому має координати O(0;0;0). Сам вектор OA лежить на осі Oz, тому його кінець, точка A, також лежить на осі Oz, тобто A(0;0;z) (на осі аплікат Oz абсциса x і ордината y дорівнюють 0).
Оскільки |OA|=3 (за умовою), то |z-0|=3, звідси z=3. Координата z>0 оскільки вектор OA напрямлений в додатному напрямку осі Oz.
Записуємо координати вектора
A(0;0;3).
Відповідь: (0;0;3). – В.

Попереду декілька статей на довжину (модуль) вектора, суми та різниці векторів, обчислення скалярного добутку та кутів між векторами. Готові приклади допоможуть Вам швидко пройти теоретичний матеріал та вивчити формули.

Сложение векторов и матриц

Термин вектор применяется к элементам пространств, для которых определены две операции — сложение и умножение на скаляр. Определение кажется круговым, но на самом деле это не так. Сначала устанавливаются аксиомы векторного пространства для двух операций, определенных для его элементов. Потом, через какое-то время (и мимоходом 🙂 упоминается, что принято называть элементы векторного пространства векторов.

Существенная часть изучения векторных пространств посвящена существованию базисов и представлению векторов в различных базисах. Для данного векторного пространства все базы имеют одинаковую мощность. Когда базы конечны (и, следовательно, имеют одинаковое количество элементов), пространство называется конечномерным, и его элементы можно отождествить с $n-\mbox{tuples}$ $(x_{1}, х_{2},\ldots ,х_{п}).$

Было бы гораздо менее интересно, но все же возможно начать с n -кортежей и определить сложение покомпонентно, как это было сделано для комплексных чисел. При таком определении сразу становится очевидным, что комплексные числа могут быть отождествлены с $2-\mbox{векторами}.$ Покомпонентное сложение имеет очень простую физическую и геометрическую интерпретацию. Если вектор рассматривать как стрелку, выходящую из одной из его конечных точек, то для добавления вектора к вектору нужно сдвигать один вектор до тех пор, пока его начало не совпадет с концом другого вектора. Сумма двух — это вектор, соединяющий их свободные концы — начало одного с концом другого. Это известно как правило параллелограмма. Правило параллелограмма подразумевает, что сложение векторов коммутативно.

Матрицы — это векторы, компоненты которых расположены в прямоугольном массиве, а не в одной строке или столбце. Таким образом, матрица $m\times n$ (читается «$m$ на $n$») представляет собой массив $(a_{ij})$, где $i$ изменяется от $1$ до $m$, тогда как $j$ колеблется от От $1$ до $n.$ Более явно,

$\начать{массив} a_{11} & a_{12} & a_{13} & \ldots & a_{1n}\\ a_{21} & a_{22} & a_{23} & \ldots & a_{2n}\\ a_{31} & a_{32} & a_{33} & \ldots & a_{3n}\\ & \ldots\\ a_{m1} & a_{m2} & a_{m3} & \ldots & a_{mn} \end{массив}$

, который содержит $m$ строк и $n$ столбцов.

Ясно, что если мы снова определим сложение матриц покомпонентно, операция будет и ассоциативной, и коммутативной. Нулевая матрица — это матрица со всеми компонентами $0.$

Определение только векторного и матричного сложения делает несправедливым как векторное, так и матричное пространство. Оба имеют гораздо более глубокие алгебраические структуры. Как я уже упоминал, векторы можно умножать на скаляры. Кроме того, есть скалярных , векторных и тензор товаров. Для матриц у нас есть матричные и тензорные произведения, а также умножение на вектор.

Прямая сумма векторных пространств

Сбор чисел в n-кортежей можно абстрагировать еще одним способом. Пусть это два векторных пространства $X_{1}$ и $X_{2}.$ Тогда мы можем рассмотреть пары элементов $(x_{1},x_{2})$ с первой компонентой из первого пространства и второй со второго. Набор всех таких кортежей известен как прямая сумма пробелов $X_{1}$ и $X_{2}.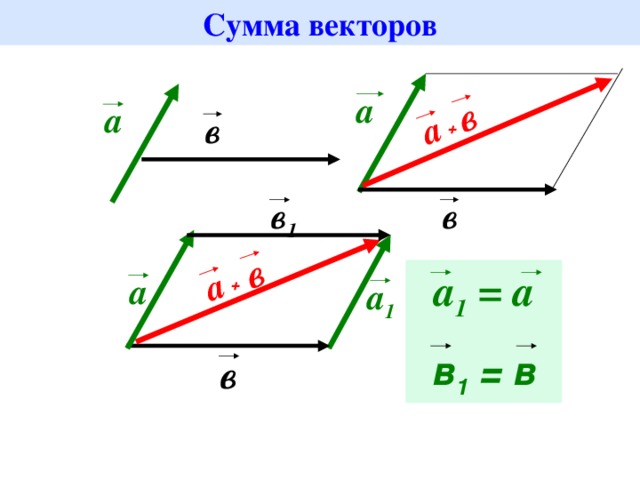

$ Количество пробелов может конечно произвольно. Если мы решим рассматривать кортеж кортежей как один длинный кортеж, полученный путем исключения скобки из «внутренних» кортежей, операция прямой суммы станет ассоциативной. Если, кроме того, мы договоримся идентифицировать векторные пространства, базы которых имеют одинаковую мощность, операция прямой суммы станет также коммутативный. В другом месте мы рассмотрели прямую сумму Булевы алгебры.

Сложение функций

Функция — это соответствие $f$ между элементами пространства $X$ и элементами пространства $Y$ такое, что любому элементу $x$ пространства $X$ соответствует единственный элемент $y$ $Y$, которая обозначается как $y=f(x).$ Если $Y$ является набором чисел, функция называется numeric . Если $Y=\mathbb{R},$ множество всех действительных чисел, функция называется real . Ниже приводится широко используемое сокращение для «функции $f$ от $X$ до $Y$»

$f: X\,\стрелка вправо Y. $

Две функции $f$ и $g$ равны, если они определяют одно и то же соответствие, $f(x) = g(x),$ для всех $x\in X.$ Можно добавлять числовые функции. Например, пусть

$f, g:\,X \rightarrow \mathbb{R}$

— две действительные функции. Затем

$f + g:\,X \стрелка вправо\mathbb{R}$

— это, по определению, другая вещественная функция $(f + g)$ такая, что

$(f + g)(x) = f(x) + g(x).$

Значение суммы равно сумме значений. Заметим, что, вообще говоря, для произвольной функции $f,$ ее значение в одной точке никак не зависит от ее значений в других точках. Сумма функций называется определенной точечно . Благодаря этому некоторые свойства сложения чисел наследуются сложением функций. Коммутативность является одним из примеров:

$(f + g)(x) = f(x) + g(x) = g(x) + f(x) = (g + f)(x)$.

Следовательно,

$f + г = г + f$.

Ассоциативность показана аналогичным образом. Также легко определить $-f$, обратный элемент для $f$.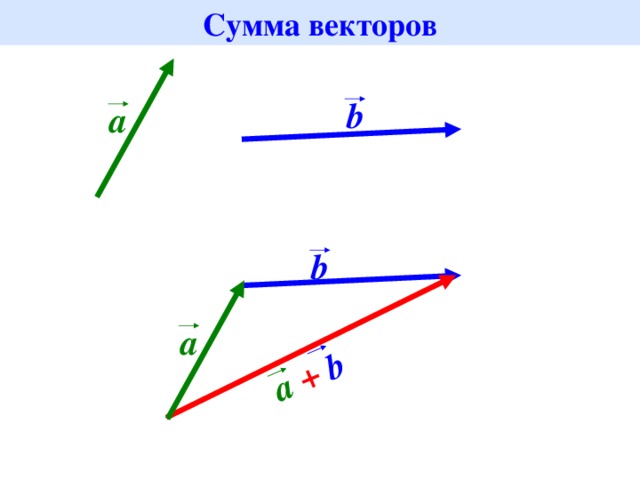 В самом деле, если $(-f)(x) = -f(x),$, то $f + (-f)=0,$, где $0$ — нулевая функция, т. е. функция, принимающая единственное значение $0$ для всех $x:$ $0(x) = 0.$

Стоит отметить, что векторы — это функции, определенные на конечных множествах. Если $\mathbf{f} = (f_{1}, \ldots , f_{n}),$, то

$\mathbf{f}: \{1, \ldots , n\} \rightarrow Y,$

, и мы можем считать $f_{i},$ $i = 1, \ldots , n$ более распространенным в этом контексте, чем $f(i)$. (Существует Java-апплет, который иллюстрирует операции сложения и вычитания функций.)

Стоит отметить, что поточечно и покомпонентно определения на самом деле одинаковы. Действительно, пусть $X = {1, 2, \ldots , n}.$ Тогда функция $f: X \rightarrow \mathbb{R}$ однозначно определяется своими $n$ значениями $f(1), f (2), \ldots , f(n).$ Обозначим их как $f_{1}, f_{2}, \ldots , f_{n}$ и запишем их подряд в виде вектора $ (f_{1}, f_{2}, \ldots , f_{n}).$ Если мы это сделаем, 9{X}.$

Следует также отметить, что функции становятся интересными, когда пространства $X$ и $Y$ являются топологическими. В этом случае можно оговорить, что значения, которые функция принимает в вблизи точек в $X$, равны вблизи друг друга в $Y.$ Функции, которые удовлетворяют этому условию, называются непрерывными . Для непрерывных функций значения $f(x)$ уже не являются независимыми. Сумма двух непрерывных функций снова непрерывна.

Функции

Функциональные обозначения и терминология

Примеры функций
Добавление функций
- Сложение и вычитание функций
Умножение функций
Набор Кантора и функция
Предельные и непрерывные функции
Синус и косинус — непрерывные функции
Состав функций, упражнение

Что можно добавить?

Что такое сложение?
Добавление цепей
Сложение уравнений
Добавление функций
Добавление номеров
Добавление наборов
Добавление форм
Добавление пробелов
Добавление строк
Сложение векторов

Сложение векторов — тригонометрия и генерация однофазного переменного тока для электриков

Перейти к содержимому

Векторы

Пришлось немало подумать, прежде чем мы, наконец, приступили к сложению векторов.

Вот некоторые ключевые моменты:

Векторы содержат величину (результат) и направление (угол).
Каждый вектор можно разбить на координаты X и Y.
Мы должны использовать систему квадрантов для построения координат X и Y.
Обратите внимание на полярность (в каком квадранте она находится?).
Векторы могут быть выражены в полярной форме (результат и угол) или прямоугольной форме (координаты X и Y).
Отталкивайтесь от оси X.
При преобразовании из прямоугольного в полярное чрезвычайно важно обращать внимание на то, в каком квадранте вы находитесь.
- Квадрант 1 — это угол, который вы рассчитываете.
- Квадрант 2 равен 180 минус рассчитанный вами угол.
- Квадрант 3 равен 180 плюс рассчитанный вами угол.
- Квадрант 4 — это либо 360 минус угол, который вы вычисляете, либо поставьте минус перед вычисленным углом.

Хорошо, давайте научимся складывать векторы.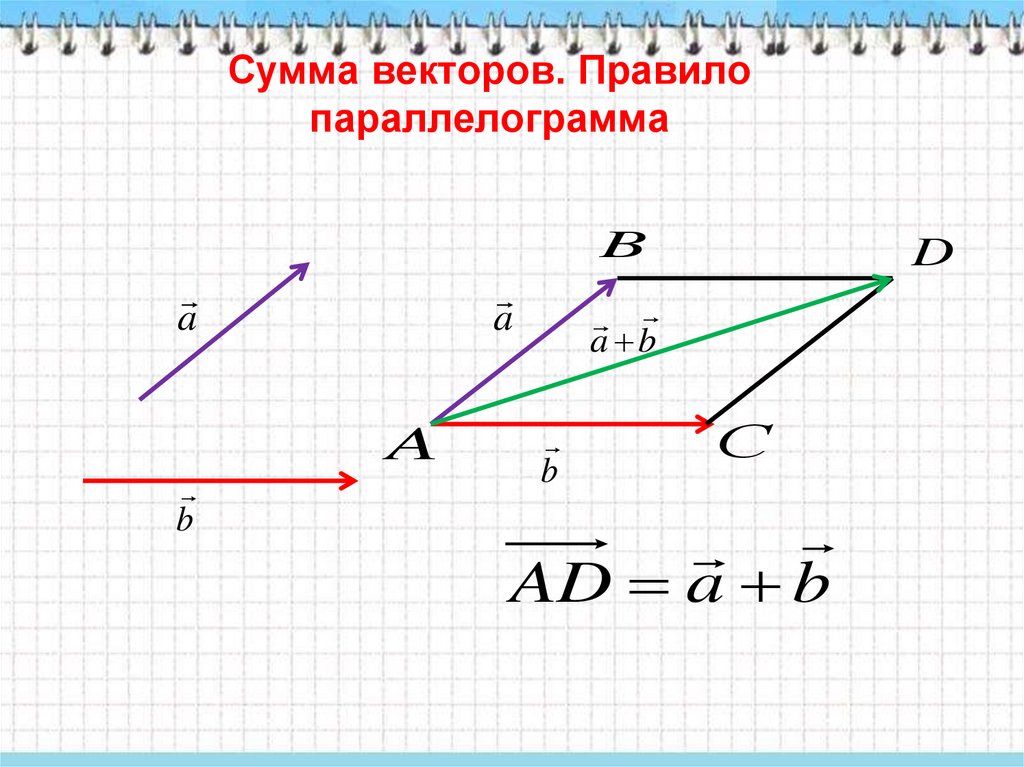

При добавлении векторов мы должны найти точки соприкосновения. Вот почему мы сосредоточимся на координатах X и Y. Каждый вектор можно разбить на координаты X и Y. Это позволяет нам найти точки соприкосновения, поскольку координаты X направлены в одном направлении, а координаты Y — в одном направлении. Давайте посмотрим на пример на рисунке 39..

В этом примере у нас есть один вектор, равный 38 В при 20 градусах, и другой, равный 100 В при 135 градусах.

Рис. 39. Добавление векторов

Первый шаг — нарисовать оси X и Y. (См. рис. 40.) Это поможет нам получить ориентир при определении координат X и Y.

Рисунок 40. Добавление векторов рисует квадрант

Далее мы вычислим X и Y для каждого вектора, как показано на рисунке 41.

Рисунок 41. Добавление векторов, определяющих X и Y

Затем добавьте диаграмму X-Y и введите координаты (Рисунок 42).

Рисунок 42.
No related posts.