Формула — Сумма и разность котангенсов
Формула Сумма и разность котангенсов
Входящие величины
\(\alpha\) — произвольный угол \((рад)\)
\(\beta\) — произвольный угол \((рад)\)
\[\mathrm{ctg}{\alpha} + \mathrm{ctg}{\beta} = \frac{\sin(\alpha + \beta)}{\sin{\alpha} \cdot \sin{\beta}}\]
\[\mathrm{ctg}{\alpha} — \mathrm{ctg}{\beta} = \frac{-\sin(\alpha — \beta)}{\sin{\alpha} \cdot \sin{\beta}}\]
изменить / сообщить об ошибке
связанные материалы
Формула Сумма и разность синусов
Входящие величины
\(\alpha\) — произвольный угол \((рад)\)
\(\beta\) — произвольный угол \((рад)\)
\[\sin{\alpha} + \sin{\beta} = 2 \sin{\frac{\alpha + \beta}{2}} \cos{\frac{\alpha — \beta}{2}}\]
\[\sin{\alpha} — \sin{\beta} = 2 \sin{\frac{\alpha- \beta}{2}} \cos{\frac{\alpha + \beta}{2}}\]
изменить / сообщить об ошибке
Формула Сумма и разность косинусов
Входящие величины
\(\alpha\) — произвольный угол \((рад)\)
\(\beta\) — произвольный угол \((рад)\)
\[\cos{\alpha} + \cos{\beta} = 2 \cos{\frac{\alpha + \beta}{2}} \cos{\frac{\alpha — \beta}{2}}\]
\[\cos{\alpha} — \cos{\beta} = -2 \sin{\frac{\alpha + \beta}{2}} \sin{\frac{\alpha — \beta}{2}}\]
изменить / сообщить об ошибке
Формула Сумма и разность тангенсов
Входящие величины
\(\alpha\) — произвольный угол \((рад)\)
\(\beta\) — произвольный угол \((рад)\)
\[\mathrm{tg}{\alpha} + \mathrm{tg}{\beta} = \frac{\sin(\alpha+ \beta)}{\cos{\alpha} \cos{\beta}}\]
\[\mathrm{tg}{\alpha} — \mathrm{tg}{\beta} = \frac{\sin(\alpha- \beta)}{\cos{\alpha} \cos{\beta}}\]
изменить / сообщить об ошибке
Формулы суммы и разности тригонометрических функций – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Сумма (и разность) тригонометрических функций преобразуется в произведение функций от других аргументов по следующим формулам, которые выводятся из теорем сложения, а также определений тангенса и котангенса.
- Сумма синусов: \(sin \alpha + sin \beta = 2sin \large\frac{{\alpha + \beta }}{2}\normalsize \cdot cos \large\frac{{\alpha — \beta }}{2}\normalsize\).
- Разность синусов: \(sin \alpha — \sin \beta = 2cos \large\frac{{\alpha + \beta }}{2}\normalsize \cdot sin \large\frac{{\alpha — \beta }}{2}\normalsize\).
- Сумма косинусов: \(cos \alpha + cos \beta = 2cos \large\frac{{\alpha + \beta }}{2}\normalsize \cdot cos \large\frac{{\alpha — \beta }}{2}\normalsize\).
- Разность косинусов: \(cos \alpha — cos \beta = -2sin \large\frac{{\alpha + \beta }}{2}\normalsize \cdot sin \large\frac{{\alpha — \beta }}{2}\normalsize\).
- Сумма тангенсов: \(tg\alpha + tg \beta = \large\frac{{sin \left( {\alpha + \beta } \right)}}{{cos \alpha \cdot cos \beta }}\normalsize\).
- Разность тангенсов: \(tg\alpha — tg \beta = \large\frac{{sin \left( {\alpha — \beta } \right)}}{{cos \alpha \cdot cos \beta }}\normalsize\).
- Сумма котангенсов: \(ctg\alpha +ctg \beta = \large\frac{{sin \left( {\beta + \alpha } \right)}}{{sin \alpha \cdot sin \beta }}\normalsize\).
2}\left( {\large\frac{\pi }{4} — \frac{\alpha }{2}\normalsize} \right)\).
2}\left( {\large\frac{\pi }{4} — \frac{\alpha }{2}\normalsize} \right)\).Вопросы
Упростите выражение.
\(\frac{sin\alpha-2sin2\alpha+sin3\alpha}{cos\alpha-2cos2\alpha+cos3\alpha}\)
Упростите.
\(sin52° + sin8° – cos22°\)
Упростите.
\(tg20° + 4sin20°\)
Вычислите.
\(\frac{2cos40°-cos20°}{sin20°}\)
Упростите выражение.
\(cosα + cos2α + cos6α + cos7α\)
Упростите выражение.
\circ) }\) после упрощения будет равно
Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
тригонометрия — Синусы и косинусы суммы и разности тупых углов
Я предполагаю, что «чисто евклидова геометрия» исключает использование комплексных чисел, определения синуса и косинуса рядами Тейлора, методы линейной алгебры, которые позволяют построить несколько Декартовы системы координат на одной плоскости и построение матриц вращения для преобразования координат и т.д. Я даже предполагаю, что вы не хотите видеть явную декартову систему координат, которая исключает обычные определения тригонометрических функций углов вне интервала $[0,\frac\pi2] в виде единичного круга.
Проблема в том, что формулы, которые обычно определяются через прямоугольный треугольник, такие как $\sin(\alpha) = \text{противоположность}/\text{гипотенуза},$, неадекватны даже для определения тригонометрической функции других углов, не говоря уже о выводе для них формул суммы и сложения. Итак, прежде всего вы должны отвлечься от SOHCATOA и решить, что является хорошим определением синуса и косинуса тупого угла.
Имея в виду, что тригонометрические функции предназначены для облегчения вычислений для широкого круга геометрических фигур в целом, неудивительно, что мы определим синус и косинус тупых углов так, чтобы такие теоремы, как синус Правило и правило косинусов по-прежнему верны для тупоугольных треугольников, используя те же самые формулы, что и для остроугольных треугольников, что избавляет нас от необходимости тратить много ненужных усилий на частные случаи этих теорем. Это означает, что синус тупого угла равен синусу дополнительного угла этого угла (который является острым),
тогда как косинус тупого угла есть отрицательное число, равное по величине косинусу добавочного угла (но, очевидно, противоположное по знаку).
Заметим, что если $\alpha$ тупая, то $\alpha = \theta + \frac\pi2$ для некоторого острого угла $\theta,$, а из предыдущего следует, что $\sin(\alpha) = \cos(\theta) = \cos(\alpha — \frac\pi2)$ и $\cos(\alpha) = -\sin(\theta) = -\sin(\alpha — \frac\pi2).$
Вот еще вопрос: как быть с формулами разности, когда разность отрицательна — например , $\sin(\alpha — \beta)$, когда $\beta > \alpha$? Вам даже не нужны тупые углы, чтобы столкнуться с этой проблемой. Но вам нужно знать, что мы решили, чтобы сделать тригонометрические формулы как можно более полезными и свободными от частных случаев, что синус отрицательного угла равен по величине, но противоположен по знаку синусу величины угла, а косинус отрицательного угла есть просто косинус величины угла.
Естественно, из определения прямоугольного треугольника, а также из приведенных выше фактов следует, что как для острых, так и для тупых углов,
$\sin(\alpha) = \cos(\frac\pi2 — \alpha) = \cos(\alpha — \frac\pi2)$ и
$\cos(\alpha) = \sin(\frac\pi2 — \alpha) = -\sin(\alpha — \frac\pi2).
Вооружившись предыдущими фактами, вы можете найти $\sin( \альфа — \бета)$ и $\cos(\alpha — \beta)$ для любых острых и тупых углов $\alpha$ и $\beta,$ просто превратив проблему в проблему, для которой у вас уже есть решение.
Задача 1. Найдите $\sin(\alpha — \beta)$, где $\alpha$ тупое, $\beta$ острое и $\alpha — \beta$ острое.
Пусть $\theta = \alpha — \frac\pi2.$ Тогда $\theta$ острое, $\alpha = \frac\pi2 + \theta,$ и $$\sin(\alpha — \beta) = \sin\left(\frac\pi2 + \theta — \beta\right) = \sin\left(\frac\pi2 — (\beta — \theta)\right) = \cos(\beta — \theta).$$
Если $\beta \geq \theta$, то все три углы $\beta,$ $\theta,$ и
$\beta — \theta$ острые и неотрицательные,
поэтому мы можем полагаться на евклидово доказательство формулы для косинуса
неотрицательная острая разность острых углов, найденная при
Как я могу понять и доказать «формулы суммы и разности» в тригонометрии? Поэтому
\начать{выравнивать}
\cos(\beta — \theta) &= \cos(\beta)\cos(\theta) + \sin(\beta)\sin(\theta) \\
&= \cos(\beta)\cos\left(\alpha — \frac\pi2\right)
+ \sin(\beta)\sin\left(\alpha — \frac\pi2\right) \\
&= \cos(\beta)\cos\left(\frac\pi2 — \alpha\right)
+ \sin(\beta)\left(-\sin\left(\frac\pi2 — \alpha\right)\right) \\
&= \cos(\beta)\sin(\alpha) — \sin(\beta)\cos(\alpha).
\end{выравнивание}
С другой стороны, если $\beta < \theta$, то все три угла
$\beta,$ $\theta,$ и $\beta - \theta$ острые и неотрицательные, поэтому имеем
\начать{выравнивать}
\cos(\beta - \theta) &= \cos(\theta - \beta) \\
&= \cos(\theta)\cos(\beta) + \sin(\theta)\sin(\beta) \\
&= \sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta).
\end{выравнивание}
В любом случае мы приходим к такому выводу: $$\sin(\alpha — \beta) = \sin(\alpha)\cos(\beta) — \cos(\alpha)\sin(\beta).$$
Задача 2. Найти $ \sin(\alpha — \beta)$, где $\alpha$ тупой, $\beta$ острый и $\alpha — \beta$ тупой.
Как и в задаче 1, пусть $\theta = \alpha — \frac\pi2.$ Заметив, что решение проблемы 1 никогда не основывалось на предположении, что $\alpha — \beta$ было острым, мы можем выполнить точно такую же процедуру с теми же результатами. Заключение: $$\sin(\alpha — \beta) = \sin(\alpha)\cos(\beta) — \cos(\alpha)\sin(\beta).$$
Задача 3. Найдите $\sin(\alpha — \beta)$, где $\alpha$ тупое, $\beta$ тупое, а $\alpha — \beta$ острое и неотрицательное.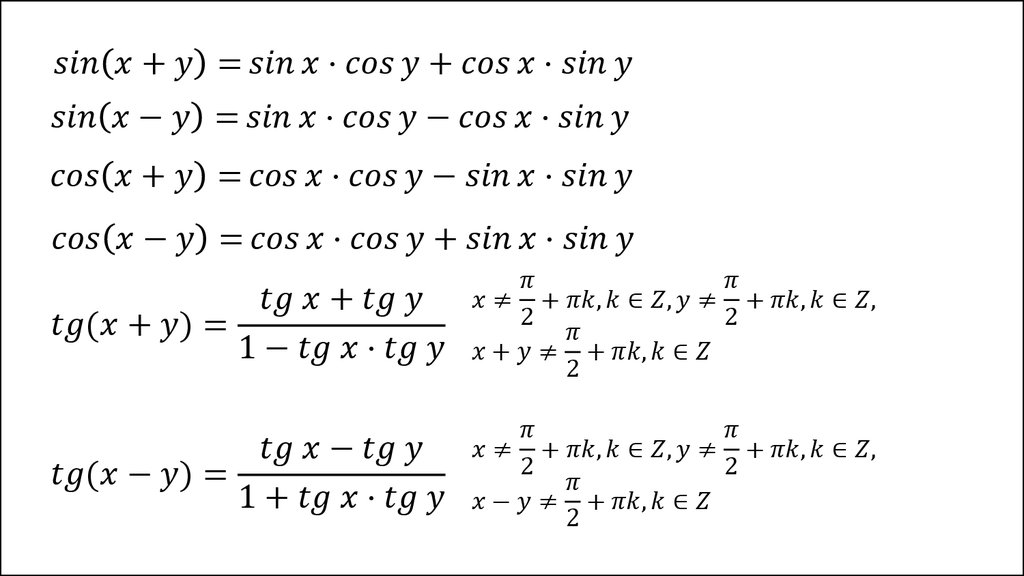
Пусть $\theta = \alpha — \frac\pi2$ и $\phi = \beta — \frac\pi2.$ Тогда $\theta$ и $\phi$ острые, $\alpha = \frac\pi2 + \theta,$ $\beta = \frac\pi2 + \phi,$ и $\alpha — \beta = \frac\pi2 + \theta — \left(\frac\pi2 + \phi\right) = \тета — \фи.$ Тогда из условия задачи следует, что $\theta — \phi$ является острым и неотрицательным. Поэтому $$\sin(\alpha — \beta) = \sin(\theta — \phi)$$ и мы можем положиться на евклидово доказательство формулы синуса неотрицательной острой разности острых углов: \начать{выравнивать} \sin(\theta — \phi) &= \sin(\theta)\cos(\phi) — \cos(\theta)\sin(\phi) \\ &= \sin\left(\alpha — \frac\pi2\right)\cos\left(\beta — \frac\pi2\right) — \cos\left(\alpha — \frac\pi2\right)\sin\left(\beta — \frac\pi2\right)\\ &= -\cos(\alpha)\sin(\beta) — \sin(\alpha)(-\cos(\beta)). \end{выравнивание} Заключение: $$\sin(\alpha — \beta) = \sin(\alpha)\cos(\beta) — \cos(\alpha)\sin(\beta).$$
Задача 4. Найдите $\sin(\alpha + \beta)$, где $\alpha$ острое, $\beta$ острое и $\alpha + \beta$ тупое.
У вас есть доказательство Евклида в разделе Поиск альтернативного доказательства расширения разности углов, но давайте посмотрим, можем ли мы снова полагаться только на доказательства для острых сумм острых углов.
Пусть $\theta = \frac\pi2 — \alpha.$ Тогда $\theta$ острая и неотрицательная, $\alpha = \frac\pi2 — \theta,$ и тот факт, что $\alpha + \beta > \frac\pi2$ (дан как предпосылка постановки задачи) следует, что $\beta > \frac\pi2 — \alpha = \theta,$ откуда следует, что $\beta — \theta$ острая и неотрицательная. Поэтому
$$\sin(\alpha + \beta) = \sin(\pi — (\alpha + \beta)) = \sin\left(\pi — \left(\frac\pi2 — \theta + \beta\right)\right) = \sin\left(\frac\pi2 — (\beta — \theta)\right) = \cos(\beta — \theta).$$
Мы уже нашли, что все три угла $\beta, $$\theta,$ и $\beta — \theta$ острые и неотрицательные, поэтому мы можем полагаться на евклидово доказательство формулы для косинуса неотрицательной острой разности острых углов, и, следовательно,
\начать{выравнивать}
\cos(\beta — \theta) &= \cos(\beta)\cos(\theta) + \sin(\beta)\sin(\theta) \\
&= \cos(\beta)\cos\left(\frac\pi2 — \alpha\right)
+ \sin(\beta)\sin\left(\frac\pi2 — \alpha\right) \\
&= \cos(\beta)\sin(\alpha) + \sin(\beta)\cos(\alpha).
\end{выравнивание}
Заключение: $$\sin(\alpha + \beta) = \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta).$$
гораздо дольше, и это пришлось бы сделать, чтобы доказать все остальные формулы с тупыми углами; мы до сих пор не видели доказательства для $\sin(\alpha + \beta)$, где один из углов тупой, как и сумма, и мы не видели доказанных формул косинуса ни для одного из этих случаев. Но я надеюсь, что общая идея ясна.
Лично я нахожу все эти дела утомительными. Более того, как быть с суммой двух тупых углов? Это рефлекторный угол, который мы еще не рассматривали. (Сумма тупого угла и острого угла в некоторых случаях также является рефлекторным углом.) И теперь, когда мы имеем дело с рефлекторными углами, что произойдет, если мы добавим два из них?
Подход, решающий все подобные проблемы, но при этом использующий евклидову геометрию в качестве основы для доказательств, состоит в следующем.
Во-первых, используйте евклидову геометрию для разработки декартовой системы координат.
В качестве бонуса, построив декартовы координаты таким образом, мы можем построить любую альтернативную декартову систему координат, которую захотим, в той же плоскости.
Используйте декартовы координаты и единичный круг для определения синуса и косинуса угла любой величины, положительной или отрицательной.
Используйте евклидову геометрию (в основном, подобные прямоугольные треугольники), чтобы составить уравнения преобразования координат между системой координат $S$ и системой координат $S’$ с тем же началом, но повернутым на угол $\theta$ от системы $S. $
Используйте этот механизм, чтобы установить формулы для координат точки $P’$
полученное вращением точки $P$ (с заданными координатами)
через угол $\theta$ вокруг начала координат.
Затем, имея в виду, что когда $\theta < 0,$ "угол $\theta$ против часовой стрелки" означает
"угол $\lvert\theta\rvert$ по часовой стрелке",
возьмем точку $(\cos\alpha,\sin\alpha)$ (лежащую на расстоянии $1$ от начала координат вдоль луча под углом $\alpha$ против часовой стрелки от положительной оси $x$),
повернуть его на угол $\beta$ против часовой стрелки,
приходя в точку на расстоянии $1$ от начала координат по лучу под углом
$\alpha + \beta$ от положительной оси $x$,
и прочтите координаты этой точки, чтобы получить формулы для
$\cos(\alpha + \beta)$ и $\sin(\alpha + \beta).
$
Этот подход требует развития большого количества механики, которую мы обычно не изучаем в так называемой «евклидовой геометрии», когда изучаем этот предмет в возрасте около четырнадцати лет (по крайней мере, в типичной математической последовательности в США). но это чрезвычайно полезный набор механик для многих целей, и когда он у вас есть, вы можете решить всех задач на сумму и разность углов для всех знаков и величин углов $\alpha$ и $\ beta$ все одним махом. Я думаю, что это стоит инвестиций.
нелинейная оптимизация — Максимальный минимум суммы двух (или более) косинусов
Задавать вопрос
спросил
Изменено 7 лет, 2 месяца назад
Просмотрено 464 раза
$\begingroup$
Пожалуйста, докажите (или опровергните и дайте правильный ответ):
$$2 =\mathrm{argmax}_{r\geq 1}\min_{x\in \mathbb{R}}\left[\cos\ влево(х\вправо)+\cos\влево(rx\вправо)\вправо] $$
Другими словами, найдите $r \geq 1$, для которого минимум (по $x$) $\cos(x)+\cos(rx)$ является наибольшим.
Или, скорее, докажите, что это $r$ равно 2.
Предыстория: я получаю этот результат при числовом сканировании
Кроме того, это имеет смысл интуитивно, поскольку, рисуя два косинуса и пытаясь выровнять их, это кажется как хорошая конфигурация, чтобы получить высокий минимум
Однако я не могу найти способ доказать это. Также легко показать, что искомые точки не являются седловыми точками функции $f(x,r)=\cos(x)+\cos(rx)$ (единственные точки экстремума находятся на $x=\pi k$ , $r$ целые, и все они являются максимумами), и вместо этого они должны встречаться для значений $r$, для которых вы получаете два равных глобальных минимума. Это звучит как очень странное совпадение в общем случае. Вот почему я чувствую, что должен быть какой-то простой аргумент симметрии, который может решить эту проблему. Я упускаю что-то очевидное (или не столь очевидное)? 9N \cos\left(r_i x\right)\right]$$
Заранее спасибо!
Примечание: Этот вопрос продублирован из math SE, так как ответа я не получил.
- нелинейная оптимизация
- глобальная оптимизация
- тригонометрические суммы
- тригонометрические полиномы
$\endgroup$
2
$\begingroup$
Итак, мы начинаем с рационального $r=\frac{p}{q}$.
1) Произнесите $2\not|p,2\not|q$. Тогда, взяв $x=q\pi$, получим: $$f_r(x)=\cos(x)+\cos(rx)=\cos(q\pi)+\cos(p\pi)=-2$$ поэтому $r$ не является argmax.
2) Допустим, $2$ делит ровно одно из $p,q$. Тогда существует нечетное целое число $k$, которое решает уравнение сравнения: $$kp=q+1 \pmod{2q}$$ берем $x=k\pi$, и имеем: $$f_r(x)=-1+\cos(\frac{kp}{2q}2\pi)=-1+\cos((\frac12+\frac{1}{2q})2\pi)=- 1-\cos(\frac{\pi}{q})$$
Чтобы минимум $f_r$ был больше минимума $f_2$, используя оценки $cos$ вблизи $0$, мы должны иметь $q\le 2$.
3) Допустим, $q=1$, значит, также $2|p$.
Пусть $x=(1+\frac{1}{p})\pi$. Затем:
$$f_r(x)=-\cos(\frac{1}{p}\pi)+\cos((p+1)\pi)=-\cos(\frac{1}{p}\pi) -1$$
, что исключает $p\ge 4$.
4) Наконец, предположим, что $q=2$, значит, также $2\not|p$. Пусть $k=\frac{p-1}{2}$ и $\epsilon=k+1\pmod{2}\in\{0,1\}$. Пусть $x=\frac{k+\epsilon}{2k+1}2\pi$. Затем $$f_r(x)=\cos((1/2+\frac{1-2\epsilon}{4k+2})2\pi)+\cos((k+\epsilon)\pi)=-1- \cos(\frac{1-2\epsilon}{4k+2}2\pi)$$
Это исключает остальные возможные значения. Следовательно, argmax равен $r=2$.
$\endgroup$
0
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.