Формула ⭐ суммы первых n-членов арифметической прогрессии: определение, примеры решения задач
Основные понятия по теме
ОпределениеАрифметической прогрессией называют числовой ряд, каждый член которого равен сумме предыдущего и некого числа d. Число d определяется как разность арифметической прогрессии.
Исходя из определения, арифметическая прогрессия представляет собой последовательность чисел, записанную в форме:
а1, а1 + d, а1 + 2d, …, а1 + (n−1)d, …
В результате в арифметической прогрессии члены, начиная со второго, получают из предшествующего с помощью сложения с неизменным числом d, то есть шагом или разностью прогрессии:
an=an−1+d
Любой n-ый член арифметической прогрессии получается путем вычисления по формуле общего члена:
an=a1+(n−1)d
Арифметическая прогрессия представляет собой монотонный ряд, в котором числа записаны последовательно. Существуют следующие свойства последовательности:
- если d>0, то можно наблюдать возрастание прогрессии;
- если d<0, то прогрессия является убывающей;
- если d=0, последовательность называют стационарной.

Перечисленные свойства арифметической прогрессии являются следствием следующего соотношения:
an+1 −an=d
Формула для вычисления суммы первых членов арифметической прогрессии
Формула 1Формула для вычисления суммы первых n членов для арифметической прогрессии, которая записана в виде Sn=a1+a2+…+an, имеет вид:
Sn=a1+an2·n
Здесь a1 является первым членом арифметической прогрессии, an определяет член последовательности, которому присвоен номер n, количество членов в сумме обозначено, как n.
Формула 2Формула определения суммы первых n членов для арифметической прогрессии через d:
Sn =2a1+d(n-1)2·n
Здесь a1 является первым членом арифметической прогрессии, d обозначает разность прогрессии, количество членов в сумме обозначено, как n.
Примеры решения задач с объяснениями
Задача 1Мастера-отделочники покрывают ограждение, длина которого 630 м, краской. Каждый день норма работы увеличивается на одинаковое количество метров. В первый и последний день было покрашено 140 м ограждения. Нужно вычислить количество рабочих дней.
В первый и последний день было покрашено 140 м ограждения. Нужно вычислить количество рабочих дней.
Решение
Заметим, что в задании речь идет об арифметической прогрессии. Обозначим эту последовательность an. Пусть n определяет рабочие дни. Число an является количеством метров ограждения, которые были покрашены. Тогда:
a1+an=140
Сумма первых n членов:
Sn=630
Запишем формулу сумму n первых членов:
Sn=a1+an2·n
630=1402·n
n=9
Ответ: 9.
Задача 2Ученику задано 315 примеров. Каждый день он решает на одинаковое число примеров больше, чем в предшествующий день. В первый день было решено 11 примеров. На решение всех заданий ушло 9 дней. Необходимо определить количество примеров, которые решил ученик в последний день.
Решение
Запишем данные для арифметической прогрессии an:
a1=11 определяет число примеров, которые были решены в течение первого дня
n=9 общее количество дней
Всего за 9 дней решено следующее число примеров:
S9=315
Определим a9:
S9=a1+a92·9
315=11+a92·9
35=11+a92
70=11+a9
a9=59
Ответ: 59.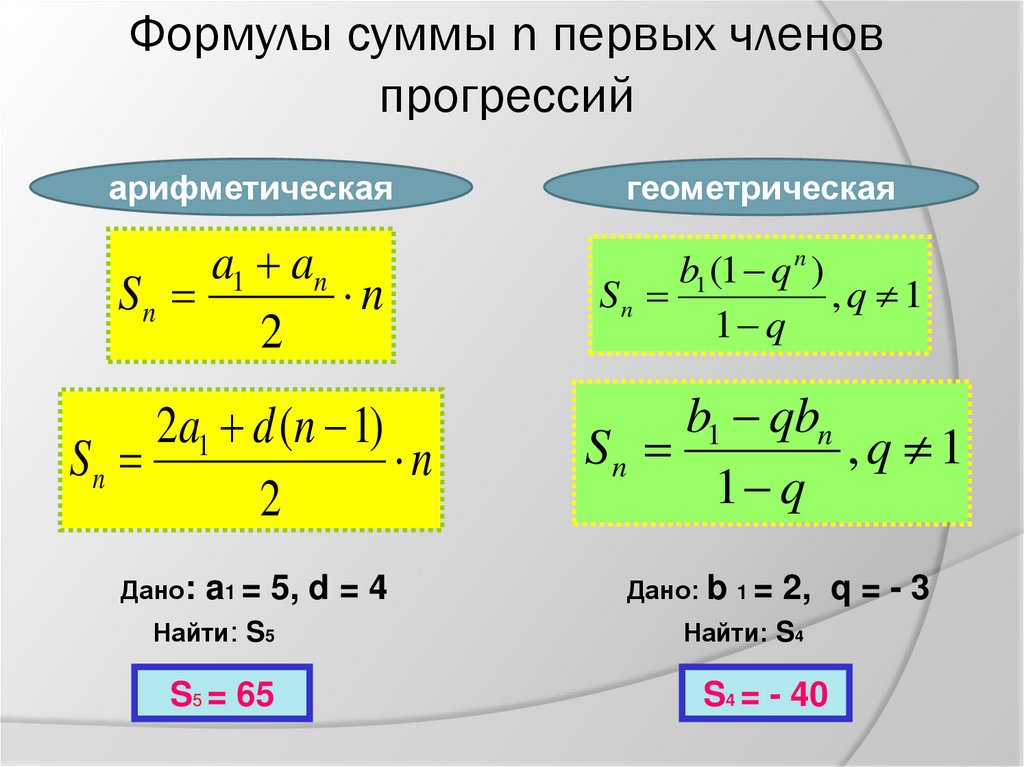
Путешественник построил маршрут из одного населенного пункта в другой. Ежедневно он преодолевает расстояние больше, чем в предшествующий день, на одну и ту же величину. В течение первого дня путешественник прошел путь, равный 9 км. Всего в пути он провел 9 дней. Населенные пункты удалены друг от друга на расстояние 189 км. Требуется найти расстояние, которое путешественник преодолел за пятый день.
Решение
Заметим, что в задаче речь идет об арифметической прогрессии. Запишем известные данные:
a1=9
S9=189
По условию необходимо вычислить a5. Воспользуемся уже знакомой формулой суммы n первых членов:
Sn=a1+an2·n
Получим, что:
S9=a1+a92·9
189=9+a92·9
42=9+a9
a9=33
Вспомним формулу n-го члена арифметической прогрессии:
an=a1+(n-1)d
Вычислим шаг арифметической прогрессии d:
a9=a1+8d
33=9+8d
d=3
В результате:
a5=a1+4d
a5=9+4·3
a5=21
Ответ: 21.
Сумма первых n членов арифметической прогрессии
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Презентация учителя математики
МОУ «Оршинская СОШ»
Калининского района Тверской области
Завьяловой Ольги Юрьевны
по математике
«Сумма первых n членов
арифметической
прогрессии»
(номинация «Мой лучший урок»,
естественно-математический цикл )
«Математика может
последовательность даже в
хаосе».
(Гертруда Стайн)
Дайте определение арифметической
прогрессии;
Числовая последовательность, каждый
член которой, начиная со второго, равен
сумме предыдущего и одного и того же
числа d (разность), называется
арифметической прогрессией
Дана арифметическая прогрессия
2, 6, 10, 14,….
 .
.Найти:
а1= 2
d = 6-2 = 4
Назовите формулу n – го члена
аn а1 п 1 d
а11 = 2+ 10 4 = 42
Из истории математики
С формулой суммы n-первых членов
арифметической прогрессии был связан
эпизод из жизни немецкого математика
Карла Фридриха Гаусса (1777-1855). Когда
ему было 9 лет, учитель, занятый
проверкой учеников других классов, задал
на уроке следующую задачу: «Сосчитать
сумму натуральных чисел от 1 до 100
включительно», надеясь, что это займёт
много времени. Каково же было
удивление учителя, когда один из
учеников (это был Гаусс) через минуту
воскликнул : «Я уже решил…»
Давным-давно сказал
один мудрец
Что прежде надо
Связать начало и
конец
У численного ряда.
a1 an
Sn
n
2
Дано:
Доказать:
÷ а1, а2, а3, а4, ……., аn
a1 an
Sn
n
2
Доказательство:
Сначала докажем, что
а1 + аn = a2+ an-1
a2+ an-1 = а1 + аn
a2 = a1 + d, отсюда a1 = a2 – d,
значит an-1 = an — d
a2+ an-1 = a1 + d + an – d = a1 + an
Аналогично можно доказать, что
a3+ an-2 = а1 + аn
….
 .
.Таким образом
ak+ an-k+1 = а1 + аn
Пусть сумма первых n членов арифметической
прогрессии равна S n тогда:
Sn a1 a2 … an 1 an
или
Sn aп aп 1 … a2 a1
Складывая эти равенства почленно, получим:
2Sn a1 aп а2 ап 1 … an 1 a2 ап а1 .
п
Отсюда имеем формулу
Sn
a1 aп п
2
ЧТД
Сумма первых n членов арифметической
прогрессии равна полусумме крайних
членов, умноженной на число членов.
Sn
a1 aп п
2
Если учесть, что аn а1 п 1 d
2a1 d п 1
Sn
n
2
, то получим:
15. Пример
Найдите сумму первых 20 членоварифметической прогрессии: 1; 3; 5; 7;… .
Sn
a1 aп п
2
а1 = 1
d=2
a20 = 1+ 19 ∙ 2 =39
S20 = (1+39)10 = 400
Ответ: 400
•Дано: а1 = 5, а10 = 23
Найти: S10
•Дано: а1 = -2, d = 1
Найти: S50
•Дано: а1 = 4, а12 = 16
Найти: S12
•Дано: а1 = -1, d = 2
Найти: S40
•Дано: а1 = 5, а10 = 23
Найти: S10
Ответ: 140
•Дано: а1 = 4, а12 = 16
Найти: S12
Ответ: 120
•Дано: а1 = -2, d = 1
Найти: S50
Ответ: 1125
•Дано: а1 = -1, d = 2
Найти: S40
Ответ: 1520
English Русский Правила
Сумма первых n членов арифметического ряда
Горячая математика Если ряд является арифметика сумма первого н термины, обозначаемые С н , есть способы найти его сумму, фактически не добавляя все члены.
Чтобы найти сумму первых
н
члены арифметического ряда используют формулу,
н
члены арифметической прогрессии используют формулу,
С
н
«=»
н
(
а
1
+
а
н
)
2
,
где
н
это количество терминов,
а
1
является первым термином и
а
н
это последний срок.
Сериал 3 + 6 + 9 + 12 + ⋯ + 30 можно выразить как сигма-нотация ∑ н «=» 1 10 3 н . Это выражение читается как сумма 3 н как н идет от 1 к 10
Пример 1:
Найдите сумму первых
20
члены арифметического ряда, если
а
1
«=»
5
и
а
20
«=»
62
.
С 20 «=» 20 ( 5 + 62 ) 2 С 20 «=» 670
Пример 2:
Найдите сумму первых
40
члены арифметической прогрессии
2
,
5
,
8
,
11
,
14
,
⋯
Сначала найдите 40 й срок:
а 40 «=» а 1 + ( н − 1 ) д «=» 2 + 39( 3 ) «=» 119
Затем найдите сумму:
С н «=» н ( а 1 + а н ) 2 С 40 «=» 40 ( 2 + 119) 2 «=» 2420
Пример 3:
Найдите сумму:
∑ к «=» 1 50 ( 3 к + 2 )
Первая находка а 1 и а 50 :
а 1 «=» 3 ( 1 ) + 2 «=» 5 а 20 «=» 3 ( 50 ) + 2 «=» 152
Затем найдите сумму:
С к «=» к ( а 1 + а к ) 2 С 50 «=» 50 ( 5 + 152 ) 2 «=» 3925
1.
 4 Конечный арифметический ряд | Последовательности и ряды
4 Конечный арифметический ряд | Последовательности и рядыАрифметическая последовательность – это последовательность чисел, такая, что разница между любым членом и предыдущим членом — постоянное число, называемое общей разностью (\(d\)):
Когда мы суммируем конечное число членов арифметической последовательности, мы получаем конечный арифметический ряд.
Простая арифметическая последовательность, когда \({a} = 1\) и \(d=1\), которая является последовательностью положительных целых чисел:
Если мы хотим суммировать эту последовательность от \(n=1\) до любого положительного целого числа, например, \(\text{100}\), мы должны написать
Математик Карл Фридрих Гаусс нашел следующее доказательство, когда ему было всего 8 лет. Его учитель
решил дать своему классу задачу, которая отвлекла бы их на весь день, попросив добавить все
числа от \(\text{1}\) до \(\text{100}\). Юный Карл быстро сообразил, как это сделать, и шокировал учителя
с правильным ответом, \(\text{5 050}\).
Эта общая формула полезна, если известен последний член ряда.
Подставим \(l = a + (n-1)d\) в приведенную выше формулу и упростим:
\начать{выравнивать*} S_{n} & = \frac{n}{2}(a + [a + (n-1)d]) \\ \поэтому S_{n} &= \frac{n}{2}[2a + (n-1)d ] \end{align*}\[{S}_{n}= \frac{n}{2} \left[ 2{a} + \left(n-1\right) d \right]\]
или
\[{S}_{n}= \frac{n}{2} (a + l)\] 9{20} \влево[3+7\влево(n-1\вправо)\вправо] \\ & = 3+10+17+24+31+38+45+52 \\ & +59+66+73+80+87+94+101 \\ & +108+115+122+129+136 \\ & = 1390 \конец{выравнивание*}
или, что более разумно, мы могли бы использовать общую формулу для определения арифметического ряда, подставив \({a}=3\), \(d=7\) и \(n=20\):
\начать{выравнивать*} {S}_{n} & = \frac{n}{2}(2a + (n-1)d ) \\ {S}_{20} & = \frac{20}{2} \left[2(3) + 7 \left(20-1\right)\right] \\ & = 1390 \конец{выравнивание*} Этот пример демонстрирует, насколько полезна общая формула для определения арифметического ряда, особенно
когда ряд имеет большое количество членов.
Видео: 286N
Рабочий пример 7: Общая формула суммы арифметической прогрессии
Найдите сумму первых \(\text{30}\) членов арифметического ряда с \(T_{n} = 7n — 5\), используя формула.
Используйте общую формулу, чтобы сгенерировать члены последовательности и записать известные переменные
\начать{выравнивать*} T_{n} &= 7n — 5 \\ \поэтому T_{1} &= 7(1) — 5 \\ &= 2 \\ Т_{2} &= 7(2) — 5 \\ &= 9 \\ Т_{3} &= 7 (3) — 5 \\ &= 16 \конец{выравнивание*}
Это дает последовательность: \(2; 9; 16 \ldots\)
\[а = 2; \quad d = 7; \квадрат n = 30\]
Запишите общую формулу и подставьте известные значения
\начать{выравнивать*} S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ S_{30} &= \frac{30}{2}[2(2) + (30-1)(7)] \\ &= 15(4 + 203) \\ &= 15 (207)\ &= 3105 \конец{выравнивание*}Напишите окончательный ответ
\(S_{30} = 3105\)
temp textРабочий пример 8: Сумма арифметической последовательности, если известны первый и последний члены
Найдите сумму ряда \(-5 -3 -1 + \cdots \cdots + 123\)
Определите тип ряда и запишите известные переменные
\начать{выравнивать*} д &= Т_{2} — Т_{1} \\ &= -3 — (-5) \\ &= 2 \\ д &= Т_{3} — Т_{2} \\ &= -1 — (-3) \\ &= 2 \end{выравнивание*}\[a = -5; \quad d = 2; \quad l = 123\]Определить значение \(n\)
\начать{выравнивать*} T_{n} &= a + (n-1)d \\ \поэтому 123 &= -5 + (n-1)(2) \\ &=-5+2n-2\ \поэтому 130&= 2n \\ \поэтому n &= 65 \end{выравнивание*}Используйте общую формулу, чтобы найти сумму ряда
\начать{выравнивать*} S_{n} &= \frac{n}{2}(a + l) \\ S_{65} &= \frac{65}{2}(-5 + 123) \\ &= \frac{65}{2}(118) \\ &= 3835 \конец{выравнивание*}Напишите окончательный ответ
\(S_{65} = 3835\)
Рабочий пример 9: Нахождение \(n\) по сумме арифметической последовательности
Для заданной арифметической последовательности \(T_{2} = 7\) и \(d = 3\) определите, сколько членов нужно добавить
вместе, чтобы дать сумму \(\text{2 146}\).
Запишите известные переменные
\начать{выравнивать*} д &= Т_{2} — Т_{1} \\ \поэтому 3 &= 7 — а \\ \поэтому &= 4 \end{выравнивание*}\[a = 4 ; \quad d = 3; \quad S_{n} = 2146\]Используйте общую формулу для определения значения \(n\)
\начать{выравнивать*} S_{n} &= \frac{n}{2}(2a + (n-1)d) \\ 2146 &= \frac{n}{2}(2(4) + (n-1)(3)) \\ 4292+5н-4292\ &= (3n + 116)(n — 37) \\ \поэтому n = -\frac{116}{3} &\text{ или } n = 37 \конец{выравнивание*}
, но \(n\) должно быть целым положительным числом, поэтому \(n = 37\).
Мы могли бы решить для \(n\) с помощью квадратичной формулы, но факторизация путем проверки обычно является самый быстрый способ.
Напишите окончательный ответ
\(S_{37} = 2146\)
temp textРабочий пример 10: Нахождение \(n\) по сумме арифметической последовательности
Сумма второго и третьего членов арифметической прогрессии равна нулю, а сумма первых
\(\text{36}\) членов ряда равно \(\text{1 152}\). Найдите первые три члена в
ряд.
Найдите первые три члена в
ряд.
Запишите данную информацию
\начать{выравнивать*} Т_{2} + Т_{3} &= 0 \\ \text{So} \quad (a + d) + (a + 2d) &= 0 \\ \поэтому 2a + 3d &= 0 \ldots \ldots (1) \end{выравнивание*}\begin{выравнивание*} S_{n} &= \frac{n}{2}(2a + (n-1)d) \\ S_{36} &= \frac{36}{2}(2a + (36-1)d ) \\ 1152 &= 18(2а + 35г) \\ \поэтому 64 &= 2a + 35d \ldots \ldots (2) \end{выравнивание*}Решить два уравнения одновременно
\начать{выравнивать*} 2a + 3d &= 0 \ldots \ldots (1) \\ 2a + 35d &= 64 \ldots \ldots (2) \\ \text{Eqn} (2) — (1): \quad 32d &= 64 \\ \поэтому d &= 2 \\ \text{И} 2а + 3(2) &= 0 \\ 2а&=-6\\ \поэтому &= -3 \конец{выравнивание*}Напишите окончательный ответ
Первые три члена ряда:
\начать{выравнивать*} T_{1} &= а = -3 \\ T_{2} &= a + d = -3 + 2 = -1 \\ T_{3} &= а + 2d = -3 + 2(2) = 1 \end{выравнивание*}\[-3 -1 + 1\]
temp textВычисление значения терма по сумме \(n\) термов:
Если первый член ряда равен \(T_{1}\), то \(S_{1} = T_{1}\).
Мы также знаем сумму первых двух членов \(S_{2} = T_{1} + T_{2}\), которые мы переставляем, чтобы сделать \(T_{2}\) предмет уравнения:
\начать{выравнивать*} T_{2} &= S_{2} — T_{1} \\ \text{Заменить} S_{1} &= T_{1} \\ \поэтому T_{2} &= S_{2} — S_{1} \конец{выравнивание*}Точно так же мы можем определить третий и четвертый члены ряда:
\начать{выравнивать*} T_{3} &= S_{3} — S_{2} \\ \text{И } T_{4} &= S_{4} — S_{3} \end{align*}\(T_{n} = S_{n} — S_{n-1}, \text{ for } n \in \{2;3;4; \ldots \}\) и \ (Т_{1} = С_{1}\)
Сумма арифметического ряда 9{k} \влево(-2n\вправо) = — 20\]
\начать{выравнивать*} \влево(-2(1)\вправо) + \влево(-2(2)\вправо) + \влево(-2(3)\вправо) + \ldots + \влево(-2(k)\вправо) «=» -20\\ -2 — 4 — 6 + \ldots -2k & = -20 \конец{выравнивание*}
Это арифметический ряд с \(a = -2\) и \(d = -2\):
\начать{выравнивать*} S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ -20 &= \frac{n}{2}[2(-2) + (n-1)(-2)] \\ -40 &= п [-4 + -2п + 2] \\ -40 &= п [-2п — 2] \\ -40 &= -2n^{2} — 2n \\ 2n^{2} + 2n — 40 &= 0 \\ п^{2} + п — 20 &= 0 \\ (n + 5)(n — 4) &= 0 \\ \поэтому n = -5 &\text{ или } n = 4 \\ \поэтому S_{4} &= -20 \\ \поэтому k &= 4 \конец{выравнивание*} 9{2} + 15н — 850\\ &= (7n + 85)(n — 10) \\ \поэтому n = -\frac{85}{7} &\text{ или } n = 10 \конец{выравнивание*}
, но \(n\) должно быть целым положительным числом, поэтому \(n=10\).
Определите шестой член ряда.
\begin{выравнивание*} {S}_{n} &= \frac{n}{2} \left(7n+15\right) \\ {S}_{1} &= {T}_{1} = а \\ {S}_{1} &= \frac{n}{2} \left(7n+15\right) \\ &= \frac{1}{2} \left(7(1)+15\right) \\ \поэтому &= 11 \\ {S}_{2} &= \frac{2}{2} \left(7(2)+15\right) \\ &= 29\\ \поэтому T_{1} + T_{2} &= 29 \\ \поэтому T_{2} &=29 — 11 \\ \text{И } d &= T_{2} — T_{1} \\ &= 18 — 11\ &= 7 \\ \поэтому T_{n} &= a + (n-1)d \\ &= 11 + (n-1)(7) \\ &=11+7н — 7\ &=7n+4\ \поэтому T_{6} &= 7(6) + 4 \\ &= 46 \end{выравнивание*}
9{\text{th}}\) член ряда равен \(\text{93}\), а сумма первых \(n\) условия: \(\text{975}\).\begin{выравнивание*} д &= 3 \\ {T}_{n} &= a + (n — 1)d \\ 93 &= а + 3(n-1) \\ &= а + 3n — 3 \\ 96 &= а + 3н\ \поэтому а &= 96 — 3n \\ {S}_{n} &= \frac{n}{2}[2a + (n-1)d] \\ \поэтому 975 &= \frac{n}{2}[2(9{2} — 63н + 650\\\ 0 &= (n — 13) (n — 50) \\ \следовательно, n = 13 &\text{ или } n = 50 \end{align*}
Объясните, почему есть два возможных ответа.
Имеется две серии, удовлетворяющие заданным параметрам:
\начать{выравнивать*} д &= 3 \\ а &= 96 — 3н\ \text{Если } n &= 13 \\ а &= 96 — 3(13) \\ &= 57 \\ \поэтому 57 + 60 + 63 + & \ldots + T_{13} = 975\\ \text{Если } n &= 50 \\ а &= 96 — 3(50)\ &=-54\\ \поэтому (-54) + (-51) + (-48) + & \ldots + T_{50} = 975 \конец{выравнивание*}
Третий член арифметической прогрессии равен \(-\text{7}\), а седьмой член равен \(\text{9}\). Определите сумму первых \(\text{51}\) членов последовательности.
\begin{выравнивание*} {T}_{3} &= -7 = a + 2d \ldots \ldots (1) \\ {Т}_{7} &= 9= а + 6d \ldots \ldots (2) \\ \поэтому \text{Вычитание уравнений: } (1) — (2) \quad -7 — (9) &= a + 2d -(a + 6d) \\ -16 &= — 4д\ \поэтому 4 &= d \\ \text{Подставьте обратно в уравнение } (1) \quad a &= -7 -2 (4) \\ \поэтому &= -15 \\ S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ S_{51} &= \frac{51}{2}[2(-15) + (51-1)(4)] \\ &= \frac{51}{2}[-30 + 200] \\ &= (51)(85) \\ \поэтому S_{51}&= 4335 \end{выравнивание*}
Вычислить сумму арифметического ряда \(4+7+10+\cdots +901\).
\begin{выравнивание*} а &= 4 \\ л &= 901 \\ д &= Т_{2} — Т_{1} \\ &= 7 — 4 \\ &= 3 \\ \text{И } T_{n} &= a +(n-1)d \\ &= 4 +(n-1)(3) \\ \поэтому 901 &= 4 + 3n — 3 \\ 900 &= 3н\ \поэтому 300 &= n \\ S_{n} &= \frac{n}{2}[a + l] \\ S_{300} &= \frac{300}{2}[4 + 901 ] \\ &= (150)(905) \\ \поэтому S_{300} &= 135750 \end{align*}
Вычисление без использования калькулятора: \(\dfrac{4 + 8 + 12 + \cdots + 100}{3 + 10 + 17 + \cdots + 101}\)
Рассмотрим числитель: \(4 + 8 + 12 + \ldots + 100\)
\начать{выравнивать*} а &= 4 \\ л &= 100 \\ д &= Т_{2} — Т_{1} \\ &= 8 — 4 \\ &= 4 \\ \text{И } T_{n} &= a +(n-1)d \\ 100 &= 4 +(n-1)(4) \\ 100 &= 4н\ \поэтому 25 &= п \\ S_{n} &= \frac{n}{2}[a + l] \\ S_{25} &= \frac{25}{2}[4 + 100] \\ S_{25} &= (25)(52) \конец{выравнивание*}
Рассмотрим знаменатель: \(3 + 10 + 17 + \ldots + 101\)
\начать{выравнивать*} а &= 3 \\ л &= 101 \\ д &= Т_{2} — Т_{1} \\ &= 10 — 3 \\ &= 7 \\ \text{И } T_{n} &= a +(n-1)d \\ 101 &= 3 +(n-1)(7) \\ 101 &= 3 + 7n — 7\ 105&=7н\ \поэтому 15 &= п \\ S_{n} &= \frac{n}{2}[a + l] \\ S_{15} &= \frac{15}{2}[3 + 101] \\ S_{15} &= (15)(52) \конец{выравнивание*}
Теперь рассмотрим частное двух рядов:
\начать{выравнивать*} \frac{ S_{25} }{ S_{15} } &= \frac{25 \times 52}{15 \times 52} \\ &= \фракция{25}{15} \\ &= \фракция{5}{3} \конец{выравнивание*}
Найдите первый член и общую разность.
\begin{выравнивание*} T_{n} &= a + (n-1)d \\ T_{2} &= a + d \\ -4 &= а + d \ldots \ldots (1) \\ S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ S_{6} &= \frac{6}{2}[2a + (6-1)d] \\ 21 &= 3[2а + 5г] \\ \поэтому 7 &= 2a + 5d \ldots \ldots (2) \\ \text{Ур. } (1) \times 2: \quad -8 &= 2a + 2d \\ \text{Ур. } (2) — 2(1): \quad 7 — (-8) &= (2a + 5d) — (2a + 2d) \\ 15 &= 3д\\ \поэтому 5 &= d \\ \text{И} а &= -4 — 5 \\ &= -9{8}{(7w+8)}\]
Арифметический ряд: \(8 + 15 + 22 + \ldots + 64\)
\начать{выравнивать*} S_{n} &= \frac{n}{2}[2a + (n-1)d]\\ а &= 8 \\ д &= 15 — 8 = 7\ \поэтому S_{9} &= \frac{9}{2}[2(8) + (9-1)(7)]\\ &= \frac{9}{2}[16 + 56]\\ &= \фракция{9}{2}[72]\\ &= (9)(36) \\ &= 324 \конец{выравнивание*} 9{8}{7j+8}\]
Арифметический ряд: \(7 + 14 + 21 + \ldots + 56\)
\начать{выравнивать*} S_{n} &= \frac{n}{2}[2a + (n-1)d]\\ а &= 7 \\ д &= 14 — 7 = 7\ \поэтому S_{8} &= \frac{8}{2}[2(7) + (8-1)(7)]\\ &= 4[14 + 49]\\ &= 4 (63) \ &= 252 \\ \поэтому S_{8} + 8 &= 260 \конец{выравнивание*} \начать{выравнивать*} \text{Или} S_{n} &= \frac{n}{2}[a + l]\\ а &= 7 \\ л&= 56\ \поэтому S_{8} &= \frac{8}{2}[7 + 56]\\ &= 4 (63) \ &= 252 \\ \поэтому S_{8} + 8 &= 260 \конец{выравнивание*} 9{п}{(2 — 3с)} = -330\]
Ряд: \(-1 — 4 — 7 \ldots + (2 — 3n)\)
\начать{выравнивать*} а &= -1 \\ d &= T_{2} — T_{1} = -4 — (-1) = -3 \\ d &= T_{3} — T_{2} = -7 — (-4) = -3 \\ \поэтому &\текст{ это арифметический ряд} \\ \поэтому S_{n} &= \frac{n}{2}[2a + (n-1)d]\\ -330 &= \frac{n}{2}[2(-1) + (n-1)(-3)]\\ — 660 &= п[-2 — 3п + 3] \\ — 660 &= n — 3n^{2} \\ \поэтому 0 &= -3n^{2} + n + 660 \\ 0 &= 3n^{2} — n — 660 \\ 0 &= (3n + 44)(n — 15) \\ \поэтому n = -\frac{44}{3} &\text{ или } n = 15 \конец{выравнивание*} 9{2} — 11(2) \\ &= 20 — 22\ &= -2 \\ &= Т_{1} + Т_{2} \\ \поэтому T _{2} &= S_{2} — S_{1} \\ &= -2 — (-6) \\ &= 4 \\ \поэтому d &= T_{2} — T_{1} \\ &= 4 — (-6) \\ &= 10 \end{align*}
Сумма арифметического ряда равна \(\text{100}\), умноженному на его первый член, а последний член равен
\(\text{9}\) умножить на первый член.

