Свойства бинарных отношений: Национальный исследовательский университет «Высшая школа экономики»

2 3(3) . Свойства бинарных отношений. Рефлексивность, симметричность, транзитивность, иррефлексивность, антисимметричность, интранзитивность.

Декартовым произведением двух множеств А и В является новое множество С, элементами которого являются все пары (a,b), . Порядок в паре очень важен, в общем виде .

Бинарным отношением Т(М) на множестве М называется подмножество , . Довольно часто используется другая, инфексная форма записи бинарного отношения a T b = . Бинарное отношение T(M) называется рефлексивным тогда и только тогда, когда для каждого элемента пара (х,х) принадлежит этому бинарному отношению, т.е. . Для определения этого свойства множество М должно содержать хотя бы один элемент х.

Бинарное отношение T(M) называется иррефлексивным тогда и только тогда, когда для каждого элемента пара (х, х) не принадлежит этому бинарному отношению, т.

е. .

Если бинарное отношение T(M) не обладает ни свойством рефлексивности, ни свойством иррефлексивности, то оно является нерефлексивным.

Cвойство рефлексивности определяется для непустых множеств! В соответствии с этим, бинарное отношение на пустом множестве , является нерефлексивным. Также нерефлексивно пустое бинарное отношение.

Рассмотрим множество M={a,b,c,d}. Ниже приведены примеры рефлексивных, иррефлексивных и нерефлексивных бинарных отношений.

При матричном задании бинарного отношения, отношение рефлексивно, если на главной диагонали стоят единицы. Если на главной диагонали стоят нули, то отношение является иррефлексивным. Если на главной диагонали стоят как «1» так и «0» то отношение нерефлексивно.

Рефлексивно				Иррефлексивно				Нерефлексивно
	a	b	c		a	b	c		a	b	c
a	1	0	0	a	0	0	1	A	1	1	0
b	0	1	1	b	0	0	1	B	1	0	1
c	1	0	1	c	1	1	0	C	0	0	1

Бинарное отношение T(M) называется симметричным тогда и только тогда, когда для каждой пары (х, у) , обратная пара (у, х) также принадлежит этому бинарному отношению, т.

е. . Для определения этого свойства множество М должно содержать хотя бы два различных элемента х и у.

Бинарное отношение T(M) называется антисимметричным тогда и только тогда, когда из того, что следует, что .

Е

3(4)

сли бинарное отношение T(M) не обладает ни свойством симметричности, ни свойством антисимметричности, то оно является несимметричным.

Cвойство симметричности определяется для непустых множеств! В соответствии с этим, бинарные отношения на пустом множестве , так же как на множествах с одним элементом, является несимметричными.

Рассмотрим множество M={a,b,c,d}. На рис.5 приведены примеры рефлексивных, иррефлексивных и нерефлексивных бинарных отношений.

При матричном задании отношения, если отношение симметрично, то матрица отношения симметричная. Если отношение антисимметрично, то .

Свойство транзитивности определяется на трех различных элементах множества М. Бинарное отношение T(M) называется транзитивным тогда и только тогда, когда для каждых двух пар элементов (х, у) и (у ,z), принадлежащих бинарному отношению , пара (x, z) также принадлежит этому бинарному отношению, т.е. . При графическом представлении транзитивного бинарного отношения (рис. 6) можно увидеть спрямление пути длины два (х, у) (у ,z), между двумя элементами, т.е. транзитивное замыкание («транзит») между x и z.

Бинарное отношение T(M) называется интранзитивным тогда и только тогда, когда для каждых двух пар элементов (х, у) и (у ,z), принадлежащих бинарному отношению , пара (x, z) не принадлежит этому бинарному отношению, т. е. . При графическом представлении интранзитивного бинарного отношения (рис. 7) можно увидеть, что ни один имеющийся путей не обладает транзитивным замыканием!

Если бинарное отношение T(M) не обладает ни свойством транзитивности, ни свойством интранзитивности, то оно является нетранзитивным.

Бинарные отношения на пустом множестве , на множествах с одним элементом M1={a} или двумя элементами M2={a,b} является нетранзитивными.

49. Свойства бинарных отношений

Рефлексивность. Пусть отношение b задано на множестве

B. Тогда отношение b называется рефлексивным, если «B Î B Þ B B B, то есть в множестве B любой его элемент находится в отношении b сам с собой.

Противоположным свойству рефлексивности бинарного отношения является свойство антирефлексивности. Оно предполагает, что ни один элемент множества B не находится в отношении b сам с собой.

Очевидно, что бинарное отношение может быть не рефлексивным и не антирефлексивным, если часть элементов множества B находится в отношении b сами с собой, а часть – нет.

Симметричность. Бинарное отношение b на множестве B называется симметричным, если «B, C Î B (B B C Þ C B B), то есть с каждой упорядоченной парой элементов множества B оно содержит и упорядоченную пару с переставленными элементами. Очевидно, что в случае симметричного отношения выполняется равенство b = b–1.

Противоположным свойству симметричности является свойство асимметричности. Бинарное отношение b асимметрично, если «B, C Î B ((B, C) Î b Þ (C, B) Ï b), то есть, если любая упорядоченная пара элементов (B, C) множества B принадлежит отношению b, то пара элементов с переставленными элементами (C, B) этому отношению не принадлежит. Ясно, что асимметричное отношение b не имеет с обратным отношением b–1 ни одной общей пары, что можно записать в виде свойства b Ç b–1 = Æ.

Если бинарное отношение b удовлетворяет более слабому свойству «B, C Î B (B B C & C B B Þ C = B), чем асимметричность, то оно называется антисимметричным. Таким образом, упорядоченная пара элементов с переставленными компонентами может принадлежать исходному бинарному отношению, но только в том случае, когда элементы пары одинаковы.

В любом бинарном отношении g можно выделить симметричную часть бинарного отношения gS = g Ç g–1 и асимметричную часть gA = g \ gS.

Транзитивность. Отношение b на множестве B называется транзитивным, если «B, C, D Î B (B B C & C B D Þ B B D), то есть если оно содержит произведение любых двух примыкающих пар, принадлежащих отношению.

Отметим, что обратное отношение b–1 транзитивного бинарного отношения b транзитивно. Действительно, в транзитивном отношении b для любых двух примыкающих пар (B, C), (C, D) существует и пара элементов (

B, D), принадлежащая этому же отношению. А это означает, что в обратном отношении b–1 любые две примыкающие пары отношения B всегда порождают две примыкающие пары элементов с переставленными компонентами и измененным порядком следования пар: (D, C), (C, B). Таким образом, произведение двух примыкающих пар в отношении b–1 имеет те же элементы, что и произведение примыкающих пар в отношении b, но с измененным порядком следования. Следовательно, отношение b–1 транзитивно и все его упорядоченные пары элементов получены путем перестановки элементов в парах исходного бинарного отношения b, то есть в соответствии с операцией обращения отношений.

Примерами транзитивных отношений являются отношения >, ³, <, £ на множествах целых или действительных чисел.

Линейность. Если для бинарного отношения b на множестве B и любых элементов B и C множества B выполняется условие «B, C Î B Þ B B C È C B B, то отношение называется линейным. Другими словами, если для любой неупорядоченной пары элементов (B, C) множества B выполняется B B C Или C B B, то отношение b является линейным. Примерами линейных отношений являются отношения ³ и £ на множествах целых и действительных чисел.

Ацикличность. Пусть задано бинарное отношение b на множестве B. Последовательность элементов B1, B2, ¼, Bl Î B таких, что B1 b B2 b ¼ b Bl = B1 называется циклом длины L по бинарному отношению b. Минимальное число L, при котором существует такая последовательность элементов, называется минимальной длиной цикла бинарного отношения b. Бинарное отношение называется ацикличным, если ни для какого L > 1 не существует цикла длиной L. В тех случаях, когда необходимо оперировать длинами циклов ацикличных бинарных отношений, минимальную длину цикла принимают равной бесконечности. Граф ацикличного бинарного отношения не имеет циклов (или контуров), то есть последовательностей

B1 R12 B2 R23 B3, ¼, Bl–1 Rl–1, l, Bl rl1 B1,

Где B1, B2, B3, ¼, Bl–1, Bl – последовательность вершин графа, причем все вершины графа различны; L – число вершин графа;

R12, R23, ¼, Rl–1, L, Rl, 1 – последовательность различных направленных ребер графа, причем ребро Rkj (K = 1, 2, ¼, L; J = 2, 3, ¼, L, 1) соединяет вершины K и J и направлено от вершины K к вершине J.

< Предыдущая		Следующая >

26.

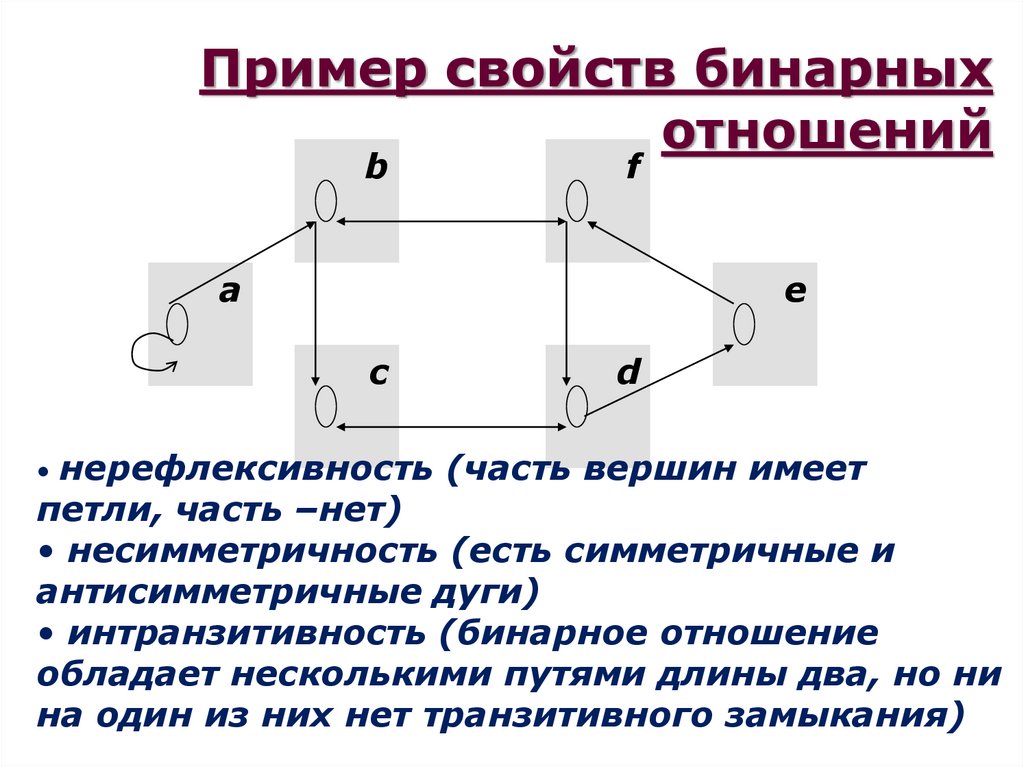Бинарные отношения. Операции над отношениями. Свойства бинарных отношений.

Бинарные отношения.

Свойства предметов окружающего мира, относимые к наборам, состоящим из n предметов, называются n-арными отношениями. (n – любое натуральное число). Т. о., бинарные отношения – свойства предметов, относимые к парам предметов.

Важный момент в задаче принятия решений состоит в изучении (задании) системы предпочтений ЛПР (лицо, принимающее решение). Язык бинарных отношений – язык описания системы предпочтений ЛПР.

Простейшая ситуация, которая позволяет сделать обоснованный выбор из нескольких объектов, возникает, когда задан один «критерий качества», позволяющий сравнить любые два объекта, четко указать, какой из них лучше, и выбрать тот (или те), на котором этот критерий достигает максимального значения. Однако в большинстве реальных ситуаций выделить один такой критерий не удается; более того, часто вообще трудно выделить критерии. Тем не менее, для некоторых пар объектов можно указать, какой из объектов пары лучше (предпочтительнее) другого. В таких случаях говорят, что эти два объекта находятся в бинарном отношении. Понятие бинарного отношения позволяет формализовать операции попарного сравнения. Поэтому они широко используются в теории выбора.

Отношением R на множестве X называется подмножество R множества X×X, т.е. RͼX×X.

Содержательный смысл такого определения состоит в том, что задание подмножества R в множестве X×X определяет, какие пары находятся в отношении R. Если пара <х, у> входит в R, т.е. <х, у> ͼR, то пишут xRy.

Для того чтобы задать отношение R на множестве X, нужно указать все пары <х, у>ͼX×X, которые содержатся в R, т.е. пары <х, у>ͼX², для которых выполняется отношение R. Кроме непосредственного указания всех пар, для которых выполняется отношение R, существуют три основных способа задания отношения: задание отношения матрицей; задание отношения графом; задание отношения сечениями.

Задание матрицей. Пусть X состоит из n элементов, R есть отношение на X. Занумеруем элементы множества X целыми числами от 1 до n. Построим квадратную таблицу размера nхn. Ее i-я строка соответствует i-му элементу множества X, обозначенному через xi, а j-й столбец — элементу xj. На пересечении i-й строки и j-гo столбца ставится единица, если выполнено xi R xj, и нуль — в противном случае. Обозначим элемент, стоящий на пересечении i-й строки и j-гo столбца, через aij. Общее правило задания матрицы отношения R формулируется так: aij (R)=l, если выполнено xi R xj, aij (R)=0, если не выполнено xi R xj (i,j = 1,…,n).

Задание графом. Поставим в соответствие элементам конечного множества X вершины графа x1, …, xn (при некоторой нумерации). Проведем дугу от xi к xj тогда и только тогда, когда выполнено xi R xj (при i=j дуга (xi,xj) превращается в петлю при вершине xi).

Задание сечениями. Рассмотрим отношение R на множестве X. Верхним сечением R+(x) называется множество элементов у таких, что <у, x >ͼR: R+(x) = {уͼX |<у,х >ͼR}; аналогично определяется нижнее сечение: R-(х) = {уͼX |<х,у >ͼR}. Таким образом, множество R-(x) -это множество всех элементов уͼX, с которыми фиксированный элемент хͼX, находится в отношении R. Множество R+(х) — это множество всех элементов уͼX, которые находятся в отношении R с фиксированным элементом xͼX.

Пример:

R={(a,b), (b,b), (b,c), (c,a)}. Для заданного бинарного отношения построить граф, бинарную матрицу и сечения.

Решение.

1 0 0

0 1 1

0 1 0

R+(a)={c} R-(a)={b} R+(b)={a,b} R-(b)={b,c} R+(c)={b} R-(c)={a}

Операции над отношениями.

Так как бинарные отношения являются множествами, то к ним применимы все понятия, которые вводятся для множеств.

1) Включение отношений. Отношение R₁ включено в отношение R₂, (R₁ R₂), если всякая упорядоченная пара элементов, принадлежащая отношению R₁ принадлежит и отношению R₂.

2) Дополнение отношений.

Отношение называется дополнением отношения R, если оно выполняется для тех и только тех пар, для которых не выполняется отношение R. Очевидно, что . В матричной записи:

В графе отношения G( ) присутствуют только те дуги, которые отсутствуют в графе G(R).

3) Обратное отношение.

Обратное отношение R^-1 определяется условием xR^-1yΞyRx.

В матричной записи a_ij(R^-1) = a_ji(R),, т. е. A(R) = A^T(R). Граф отношения G(R^-1) получается из графа отношения G(R) путем замены направления у всех дуг.

4) Пересечение отношений.

Пересечением отношений R₁ и R₂ (обозначается ) называется отношение, определяемое пересечением соответствующих подмножеств из X². В матричной записи

5) Объединение отношений.

Объединением отношений R₁ и R₂ (обозначается ) называется отношение, определяемое объединением соответствующих подмножеств из X². В матричной записи

6) Произведение отношений.

Произведением отношений R₁ и R₂ называется такое отношение , что и Пример 1: R1 — быть братом R2 – быть родителем R1° R2 – брат одного из родителей (быть дядей)

Пример 2: R1={(a,b), (c,c),(b,c)} R2={(b,b), (c,a),(b,a)} R1° R2={(a,b), (a,a),(c,a),(b,a)}

7) Отношение двойственности. Двойственным к R называют отношение =.

Свойства бинарных отношений.

1) Рефлексивность.

Бинарное отношение R на множестве X называется рефлексивным, если каждый элемент множества X находится в отношении R сам с собой.

Если отношение представлено с помощью графа, то рефлексивность этого отношения означает, что в каждой вершине графа обязательно имеется петля; для отношения, заданного с помощью булевой матрицы, его рефлексивность равносильна тому, что по главной диагонали этой матрицы стоят только 1.

2) Антирефлексивность.

Бинарное отношение R, заданное на множестве X, называется антирефлексивным, если ни один элемент из множества X не находится в отношении R с самим собой

Oтношение, не являющееся рефлексивным не обязано быть антирефлексивным. Если отношение представлено с помощью графа, то антирефлексивность этого отношения означает, граф не имеет петель; для отношения, заданного с помощью булевой матрицы, его АР равносильна тому, что по главной диагонали этой матрицы стоят только 0.

3) Симметричность.

Отношение R называют симметричным, когда выполняется условие

В графе симметричного отношения все стрелки двойные, матрица симметричного отношения симметрична относительно главной диагонали. A(R) = A^T(R)

4) Асимметричность. Отношение R называют асимметричным, если В графе асимметричного отношения нет двойных стрелок и петель.

5) Антисимметричность.

Отношение R называют антисимметричным, если . В графе антисимметричного отношения нет двойных стрелок, возможны петли. На языке матриц антисимметричное отношение характеризуется тем, что все элементы матрицы , лежащие вне главной диагонали, равны нулю (матрица получается путем поэлементного перемножения соответствующих элементов.

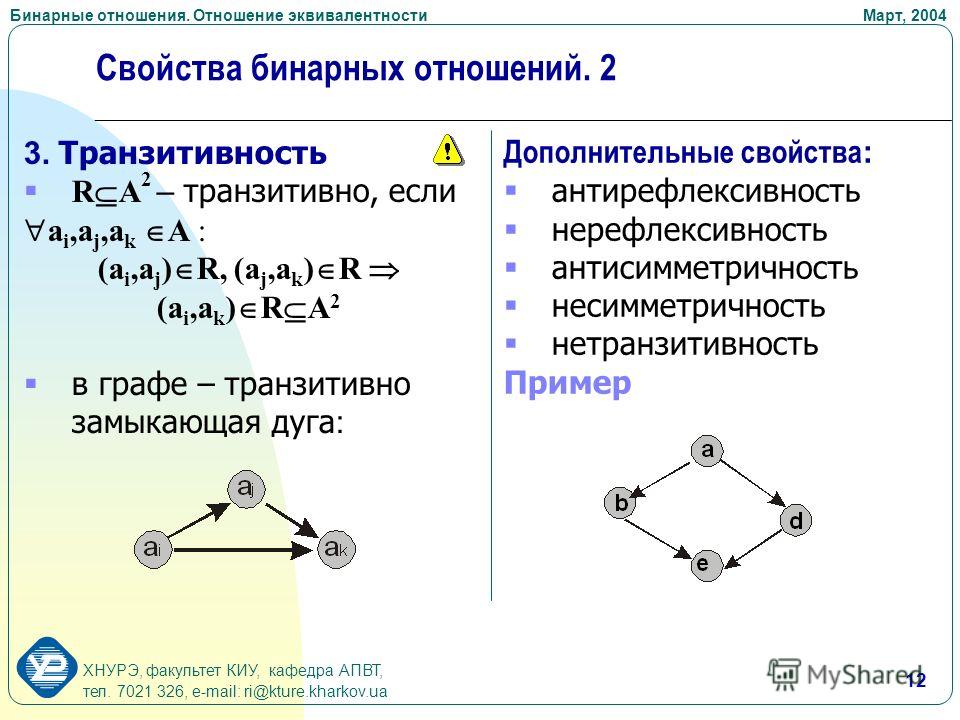
6) Транзитивность.

Отношение R называют транзитивным, если , т.е.

7) Ацикличность.

Отношение R называют ацикличным, если .

Для ацикличного отношения , где

Отношение заказа

Отношение заказа

Связь

Предметы для изучения

• рефлексивное отношение
• иррефлексивное отношение
• симметричное отношение
• антисимметричное отношение
• переходное отношение

Содержимое

Некоторые важные типы бинарных отношений можно охарактеризовать свойствами, которыми они обладают. Здесь мы собираемся изучить некоторые из тех свойств, которыми могут обладать бинарные отношения. Отношения, которые нас здесь интересуют, являются бинарными отношениями на множестве.

Определение (рефлексивное отношение): Отношение R на множестве A называется рефлексивным тогда и только тогда, когда < а, а > Р для каждого элемента из .

Пример 1: Отношение на множестве целых чисел { 1, 2, 3 } есть {< 1, 1 >, < 1, 2 >, < 1, 3 >, < 2, 2 >, < 2, 3 >, < 3, 3 >} и рефлексивно, потому что < 1, 1 >, < 2, 2 >, < 3, 3 > находятся в этом отношении. Собственно говоря на любом наборе чисел также рефлексивно. Сходным образом и = на любом наборе чисел являются рефлексивными. Однако < (или >) на любом наборе чисел не является рефлексивным.

Пример 2: Отношение на множестве подмножеств { 1, 2 } есть { < , > , <, { 1 } >, <, { 2 } > , <, { 1, 2 } > , <{ 1 }, { 1 } >, <{ 1 }, { 1, 2 }>, <{ 2 }, { 2 } >, <{ 2 }, { 1, 2 }>, < { 1, 2 } , { 1, 2 } > }
и он рефлексивный. Фактически отношение на любом наборе множеств рефлексивно.

Определение (иррефлексивное отношение): Отношение R на множестве A называется иррефлексивный тогда и только тогда, когда < а, > Р для каждого элемента из .

Пример 3: Отношение > (или <) на множестве целых чисел { 1, 2, 3 } равно иррефлексивный. На самом деле он иррефлексивен для любого набора чисел.

Пример 4: Отношение {< 1, 1 >, < 1, 2 >, < 1, 3 >, < 2, 3 >, < 3, 3 > } на множестве целых чисел { 1, 2, 3 } не является ни рефлексивным, ни иррефлексивным.

Определение (симметричное отношение): Отношение R на множестве A называется симметричным тогда и только тогда, когда для любых и б в , всякий раз, когда < а, б > р , < б, а > Р .

Пример 5: Отношение = на множестве целых чисел { 1, 2, 3 } равно {< 1, 1 > , < 2, 2 > < 3, 3 > } и он симметричен. Точно так же = на любом наборе чисел симметрично. Однако < (или >), (или же на любом наборе чисел не является симметричным.

Пример 6: Отношение «знакомство с» на множестве людей симметрично.

Определение (антисимметричное отношение): Отношение R на множестве A называется антисимметричный тогда и только тогда, когда для любых a и b в А , всякий раз, когда < а, б > р , а также < б, а > R , a = b должны удерживать. Эквивалентно, R антисимметрично тогда и только тогда, когда когда-либо < а, б > Р и а б , < б, а > Р . Таким образом, в антисимметричном отношении ни одна пара элементов не связана друг с другом.

Пример 7: Отношение < (или > ) на любом наборе чисел антисимметрично. Итак, отношение равенства на любой набор чисел.

Определение (транзитивное отношение): Отношение R на множестве A называется переходный тогда и только тогда, когда для любых a , b и c в А , всякий раз, когда < а, б > р , а также < б, в > Р , < а, в > Р .

Пример 8: Отношение на множестве целых чисел { 1, 2, 3 } есть транзитивно, так как для < 1, 2 > и < 2, 3 > в , < 1, 3 > также в , на < 1, 1 > и < 1, 2 > в , < 1, 2 > также в , и аналогично для остальных. Собственно говоря на любом наборе числа также транзитивно. Сходным образом и = на любом множестве чисел транзитивны.

На следующих рисунках показаны орграфы отношений с различными свойствами.
(а) рефлексивно, антисимметрично, симметрично и транзитивно, но не иррефлексивно.
(b) не является ни рефлексивным, ни иррефлексивным, а также антисимметричным, симметричным и переходный.
(c) иррефлексивно, но не обладает ни одним из остальных четырех свойств.
(d) иррефлексивна и симметрична, но ни одна из трех других.
(e) иррефлексивно, антисимметрично и транзитивно, но ни рефлексивно, ни симметрично.

Проверьте свое понимание свойств двоичных отношений

Укажите, какие из следующих утверждений верны, а какие нет.
Нажмите «Истина» или «Ложь» , затем «Отправить». Есть два блока вопросов.
Далее — Операции над бинарными отношениями

Вернуться к расписанию
Вернуться к оглавлению

Свойства отношений

Свойства отношений

Бинарное отношение R , определенное на множестве A , может иметь следующие свойства:

• Рефлексивность
• Иррефлексивность
• Симметрия
• Антисимметрия
• Асимметрия
• Транзитивность

Далее мы обсудим эти свойства более подробно.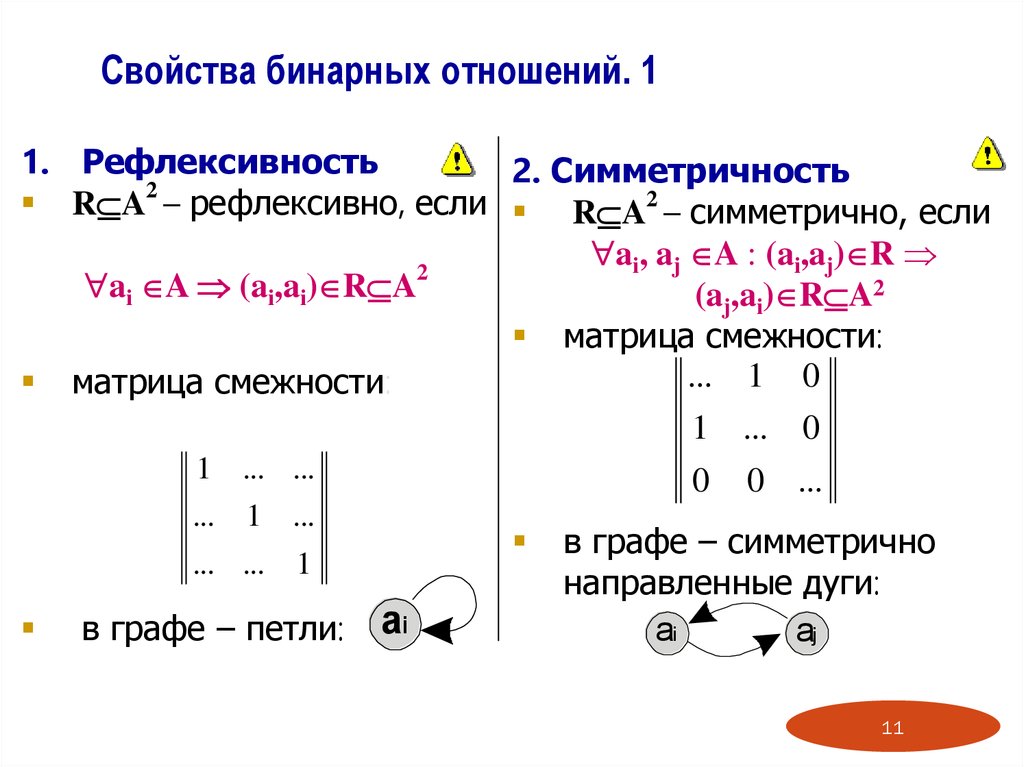

Рефлексивное отношение

Бинарное отношение \(R\) называется рефлексивным тогда и только тогда, когда \(\для всех a \in A,\) \(aRa.\) Итак, отношение \(R\) рефлексивно, если оно связывает каждый элемент \(А\) самому себе.

Примеры рефлексивных отношений:

1. Отношение \(\ge\) («больше или равно») на множестве действительных чисел.
2. Подобие треугольников.
3. Отношение \({R = \left\{ {\left( {1,1} \right),\left( {1,2} \right),}\right.}\) \({\left. {\kern-2pt\left( {2,2} \right),\left( {3,3} \right),\left( {3,1} \right)} \right\}}\) на установить \(A = \left\{ {1,2,3} \right\}.\)

Рис. 1.

Рефлексивные отношения всегда представляются матрицей с \(1\) на главной диагонали. Орграф рефлексивного отношения имеет петлю от каждого узла к самому себе.

Иррефлексивное отношение

Бинарное отношение \(R\) на множестве \(A\) называется иррефлексивным, если \(aRa\) не выполняется ни для какого \(a \in A. \). Это означает, что в \( R\), который связан с самим собой.

Примеров иррефлексивных отношений:

1. Отношение \(\lt\) («меньше чем») на множестве действительных чисел.
2. Отношение одного лица к сыну другого лица.
3. Отношение \({R = \left\{ {\left( {1,2} \right),\left( {2,1} \right),}\right.}\) \({\left. {\kern-2pt\left( {1,3} \right),\left( {2,3} \right),\left( {3,1} \right)} \right\}}\) на установить \(A = \left\{ {1,2,3} \right\}.\)

Рис. 2.

Матрица иррефлексивного отношения имеет все \(0’\text{s}\) на главной диагонали. Ориентированный граф отношения не имеет петель.

Отношение симметрии

Бинарное отношение \(R\) на множестве \(A\) называется симметричным, если для всех \(a,b \in A\) выполняется условие, что если \(aRb\), то \(bRa.\) In Другими словами, относительный порядок компонентов в упорядоченной паре не имеет значения — если бинарное отношение содержит элемент \(\left( {a,b} \right)\), оно также будет включать симметричный элемент \(\ влево( {b,a} \вправо). \)

Примеры симметричных отношений:

1. Отношение \(=\) («равно») на множестве действительных чисел. 9T\) всегда равна исходной матрице \(M.\). В орграфе симметричного отношения для каждого ребра между различными узлами существует ребро в противоположном направлении.

   Антисимметричное отношение

   Бинарное отношение \(R\) на множестве \(A\) называется антисимметричным, если не существует пары различных элементов \(A\), каждый из которых связан \(R\) с другим . Итак, антисимметричное отношение \(R\) может включать обе упорядоченные пары \(\left( {a,b} \right)\) и \(\left( {b,a} \right)\) тогда и только тогда, когда \(а = Ь.\)

   Примеры антисимметричных отношений:

   1. Отношение \(\ge\) («больше или равно») на множестве действительных чисел.
   2. Отношение подмножества \(\subseteq\) на множестве мощностей.
   3. Отношение \({R = \left\{ {\left( {1,1} \right),\left( {2,1} \right),}\right.}\) \({\left. {\kern-2pt\left( {2,3} \right),\left( {3,1} \right),\left( {3,3} \right)} \right\}}\) на установить \(A = \left\{ {1,2,3} \right\}. \)
   Рис. 4.

   В матрице \(M = \left[ {{a_{ij}}} \right]\), представляющей антисимметричное отношение \(R,\), все элементы, симметричные относительно главной диагонали, не равны каждому другое: \({a_{ij}} \ne {a_{ji}}\) for \(i \ne j.\) Орграф антисимметричного отношения может иметь петли, однако соединения между двумя различными вершинами могут идти только через одну путь.

   Асимметричное отношение

   Асимметричное бинарное отношение похоже на антисимметричное отношение. Отличие состоит в том, что асимметричное отношение \(R\) никогда не имеет обоих элементов \(aRb\) и \(bRa\), даже если \(a = b.\)

   Каждое асимметричное отношение также антисимметрично. Обратное неверно. Если антисимметричное отношение содержит элемент вида \(\left( {a,a} \right),\), оно не может быть асимметричным. Таким образом, бинарное отношение \(R\) асимметрично тогда и только тогда, когда оно антисимметрично и иррефлексивно.

   Примеры асимметричных отношений:

   1. Отношение \(\gt\) («больше чем») на множестве действительных чисел.
   2. Семейное отношение «отец».
   3. Отношение \(R = \left\{ {\left( {2,1} \right),\left( {2,3} \right),\left( {3,1} \right)} \right \}\) на множестве \(A = \left\{ {1,2,3} \right\}.\)
   Рис. 5.

   Матрица асимметричного отношения несимметрична относительно главной диагонали и не содержит диагональных элементов. Орграф асимметричного отношения не должен иметь ни петель, ни ребер между различными вершинами в обоих направлениях.

   Переходное отношение

   Бинарное отношение \(R\) на множестве \(A\) называется транзитивным, если для всех \(a,b,c\in A\) верно, что если \(aRb\) и \(bRc,\ ), затем \(aRc.\)

   Это условие должно выполняться для всех троек \(a,b,c\) в наборе. Если существует некоторая тройка \(a,b,c\in A\) такая, что \(\left( {a,b} \right) \in R\) и \(\left( {b,c} \right ) \in R,\), но \(\left( {a,c} \right) \notin R,\), то отношение \(R\) не транзитивно.

   Примеры транзитивных отношений:

   1. Отношение \(\gt\) («больше чем») на множестве действительных чисел.
   2. Отношение «параллельно» на множестве прямых.
   3. Отношение \({R = \left\{ {\left( {1,2} \right),\left( {1,3} \right),}\right.}\) \({\left. {\kern-2pt\left( {2,2} \right),\left( {2,3} \right),\left( {3,3} \right)} \right\}}\) на установить \(A = \left\{ {1,2,3} \right\}.\)
   Рис. 6.

   В матрице \(M = \left[ {{a_{ij}}} \right]\) транзитивного отношения \(R,\) для каждой пары \(\left({i, j}\right)-\) и \(\left({j,k}\right)-\)элементы со значением \(1\) существует \(\left({i,k}\right)- \)элемент со значением \(1.\) Наличие \(1’\text{s}\) на главной диагонали не нарушает транзитивности.

   См. решенные проблемы на стр. 2.

   Страница 1 Страница 2

   2.1: Бинарные отношения — Математика LibreTexts

   1. Последнее обновление

   2. Сохранить как PDF

2. Идентификатор страницы

   7426

Эта страница является черновиком и находится в активной разработке.

• Памини Тангараджа
• Университет Маунт Роял

Определение: бинарное отношение

Пусть \(S\) — непустое множество. Тогда говорят, что любое подмножество \(R\) из \(S \times S\) является отношением над \(S\). Другими словами, отношение — это правило, определенное между двумя элементами в \(S\). Интуитивно, если \(R\) является отношением над \(S\), то утверждение \(a R b\) либо true или false для всех \(a,b\in S\).

Если утверждение \(a R b\) ложно, мы обозначаем это через \( a \not R b\).

Пример \(\PageIndex{1}\):

Пусть \(S=\{1,2,3\}\). Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a

Затем \(1 R 2, 1 R 3, 2 R 3 \) и \( 2 \не R 1\).

Мы можем представить приведенное выше бинарное отношение в виде графа, где вершинами являются элементы S, а есть ребро из \(a\) в \(b\) тогда и только тогда, когда \(a R b\) , для \(a b\in S\).

Ниже приведены некоторые примеры отношений, определенных на \(\mathbb{Z}\).

Пример \(\PageIndex{2}\):

1. Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a < b\), для \(a, b \in \ mathbb{Z}\).
2. Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a >b\), для \(a, b \in \mathbb{Z}\).
3. Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a \leq b\), для \(a, b \in \mathbb{Z}\).
4. Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a \geq b\), для \(a, b \in \mathbb{Z}\).
5. Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a = b\), для \(a, b \in \mathbb{Z}\).

Кратные и делители

Далее мы введем понятие «делит».

Определение: Делитель/Делит

Пусть \(a\) и \(b\) — целые числа. Мы говорим, что \(a\) делит \(b\), обозначается \(a\mid b\), при условии, что у нас есть целое число \(m\), такое что \(b=am\). В этом случае мы также можем сказать следующее:

• \(b\) делится на \(a\)
• \(a\) является коэффициентом \(b\)
• \(a\) является делителем \(b\)
• \(b\) кратно \(a\) 

Если \(a\)  не делится на \(b\), то это  обозначается \(a \not \mid b\).

Пример \(\PageIndex{3}\):

Найти все натуральные числа, делящиеся на \(16.\)

Решение

Кратные \(16. \)

Пример \(\PageIndex{ 4}\):

Найти все натуральные числа делит \(16.\)

Решение

\(1, 2, 4, 8, 16\)

Пример \(\PageIndex{5}\):

\(4 \mid 12\) и \(12 \not\mid 4\)

Далее мы введем понятие «делит» для натуральных чисел.

Определение: Делит  

Пусть \(a\) и \(b\) — положительные целые числа. Мы говорим, что \(a\) делит \(b\), обозначается \(a\mid b\), существует натуральное число \(m\) такое, что \(b=am\).

 

Теорема \(\PageIndex{1}\): Теорема о неравенстве делимости

Если \(a\mid b\), для \(a, b \in \mathbb{Z_+}\), то \(a \ leq b\),

Доказательство

Пусть \(a, b \in \mathbb{Z_+}\) такое, что \(a\mid b\), Так как (a\mid b\), существует натуральное число \(m\) такое, что \ (б = утро \). Поскольку \(m \geq 1\) и \(a\) — натуральное число, \(b=am \geq (a)(1)=a. \)

Обратите внимание, что если \(a\mid b\), для \(a, b \in \mathbb{Z_+}\), то \(a \leq b\), но обратное неверно. Например: \(2 <3\), но \(2 \не\середина 3\).

Пример \(\PageIndex{6}\):

Согласно нашему определению \(0 \mid 0\).

Определение: Четное целое

Целое число является четным при условии, что оно делится на \(2\).

Свойства бинарного отношения:

Определение: рефлексивное

Пусть \(S\) — множество, а \(R\) — бинарное отношение на \(S\). Тогда \(R\) называется рефлексивным, если \( a R a, \forall a \in S.\)

Пример \(\PageIndex{5}\): Визуально

\(\forall a \in S, a R a\).

Мы будем следовать приведенному ниже шаблону, чтобы ответить на вопрос о рефлексивности.

Пример \(\PageIndex{7}\):

Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a < b\), для \(a, b \ в \mathbb{Z}\). Является ли \(R\) рефлексивным?

Пример счетчика:

Выберите \(a=2.\)

Так как \( 2 \not< 2\), \(R\) не рефлексивно.

Пример \(\PageIndex{8}\):

Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a \mid b\), для \(a, b \in \mathbb{Z}\). Является ли \(R\) рефлексивным?

Доказательство:

Пусть \( a \in \mathbb{Z}\). Поскольку \(a=(1) (a)\), \(a \mid a\).

Таким образом, \(R\) рефлексивно. \( \Box\)

Определение: Симметричный

Пусть \(S\) — множество, а \(R\) — бинарное отношение на \(S\). Тогда \(R\) называется симметричным, если верно следующее утверждение: другими словами, \( \для всех a,b \in S, a R b \подразумевает b R a.\)

Пример \(\PageIndex{8}\): Визуально

\(\для всех a,b \in S, a R b \имеет b R a.\) выполняется!

Мы будем следовать приведенному ниже шаблону, чтобы ответить на вопрос о симметричности.

Пример \(\PageIndex{9}\):

Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a < b\), для \(a, b \ в \mathbb{Z}\). Является ли \(R\) симметричным?

Пример счетчика:

\(1<2\), но \(2 \не < 1\).

Пример \(\PageIndex{10}\):

Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a \mid b\), для \(a, b \in \mathbb{Z}\). Является ли \(R\) симметричным?

Пример счетчика:

\(2 \mid 4\), но \(4 \not \mid 2\).

Определение: антисимметричное

Пусть \(S\) — множество, а \(R\) — бинарное отношение на \(S\). Тогда \(R\) называется антисимметричным, если верно следующее утверждение: тогда \(а=б\).

Другими словами, \( \forall a,b \in S\), \( a R b \wedge b R a \подразумевает a=b.\)

Пример \(\PageIndex{11}\): ВИЗУАЛЬНО

\( \для всех a,b \in S\), \( a R b \клин b R a \имеет a=b \)!

Мы будем следовать приведенному ниже шаблону, чтобы ответить на вопрос об антисимметричности.

Пример \(\PageIndex{12}\):

Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a < b\), для \(a, b \ в \mathbb{Z}\). Является ли \(R\) антисимметричным?

Пример \(\PageIndex{13}\):

Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a \mid b\), для \(a, b \in \mathbb{Z_+}\). Является ли \(R\) антисимметричным?

Определение: Транзитив

Пусть \(S\) — множество, а \(R\) — бинарное отношение на \(S\). Тогда \(R\) называется транзитивным, если верно следующее утверждение , то \(aRc\).

Другими словами, \( \для всех a,b,c \in S\), \( a R b \клин b R c \подразумевает a R c\).

Пример \(\PageIndex{14}\): ВИЗУАЛЬНО

\( \forall a,b,c \in S\), \( a R b \wedge b R c \подразумевает a R c\) держит!

Мы будем следовать приведенному ниже шаблону, чтобы ответить на вопрос о транзитивности.

Пример \(\PageIndex{15}\):

Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a < b\), для \(a, b \ в \mathbb{Z}\). Является ли \(R\) транзитивным?

Пример \(\PageIndex{16}\):

Определить \(R\) через \(a R b\) тогда и только тогда, когда \(a \mid b\), для \(a, b \in \mathbb{Z_+}\).

No related posts.