Функция Лапласа | это… Что такое Функция Лапласа?
График функции ошибок
В математике функция ошибок — это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
- .
Дополнительная функция ошибок, обозначаемая (иногда применяется обозначение , определяется через функцию ошибок:
- .
Комплексная функция ошибок, обозначаемая w(x), также определяется через функцию ошибок:
- .
Содержание
|
Свойства
- Функция ошибок нечётна:
- Для любого комплексного x выполняется
где черта обозначает комплексное сопряжение числа x.
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
Это равенство выполняется (и ряд сходится) как для любого вещественного x, так и на всей комплексной плоскости. Последовательность знаменателей образует последовательность A007680 в OEIS.
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
поскольку — сомножитель, превращающий i-й член ряда в (i + 1)-й, считая первым членом x.
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
- Обратная функция ошибок представляет собой ряд
где c0 = 1 и
Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
- [1]
Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Дополнительная функция ошибок
Применение
Если набор случайных чисел подчиняется нормальному распределению со стандартным отклонением σ, то вероятность, что число отклонится от среднего не более чем на a, равна .
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с граничными условиями описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших x полезно асимптотическое разложение для дополнительной функции ошибок:
Хотя для любого конечного x этот ряд расходится, на практике первых нескольких членов достаточно для вычисления с хорошей точностью, в то время как ряд Тейлора сходится очень медленно.
Другое приближение даётся формулой
где
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым Φ(x)
Обратная функция к Φ, известная как нормальная квантильная функция, иногда обозначается и выражается через нормальную функцию ошибок как
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
Обобщённые функции ошибок
График обобщённых функций ошибок En(x):
серая линия:
красная линия:
зелёная линия: E3(x)
синяя линия: E
жёлтая линия: E5(x).
Некоторые авторы обсуждают более общие функции
Примечательными частными случаями являются:
- E0(x) — прямая линия, проходящая через начало координат:
- E2(x) — функция ошибок .
После деления на n! все En с нечётными n выглядят похоже (но не идентично). Все En с чётными n тоже выглядят похоже, но не идентично, после деления на n!. Все обощённые функции ошибок с n > 0 выглядят похоже на полуоси x > 0.
Все En с чётными n тоже выглядят похоже, но не идентично, после деления на n!. Все обощённые функции ошибок с n > 0 выглядят похоже на полуоси x > 0.
На полуоси x > 0 все обобщённые функции могут быть выражены через гамма-функцию:
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
Итерированные интегралы дополнительной функции ошибок
Итерированные интегралы дополнительной функции ошибок определяются как
Их можно разложить в ряд:
откуда следуют свойства симметрии
и
Реализация
В стандартах языков Си и C++ функция ошибок и дополнительная функция ошибок отсутствуют в стандартной библиотеке. Однако в GCC (GNU Compilier Collection) эти функции реализованы как double erf(double x) и double erfc(double x). Функции находятся в заголовочных файлах
Функции находятся в заголовочных файлах math.h или cmath. Там же есть пары функций erff(),erfcf() и erfl(),erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта Boost.
В языке [2]. Класс Erf есть в пакете org.apache.commons.math.special от [3]. Однако эта библиотека не является одной из стандартных библиотек Java 6.
Matlab[4] и
В языке Special проекта scipy [5].
См. также
- Функция Гаусса
Литература
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (См. часть 7)
Внешние ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит… Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Интересное: Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов. Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 4 Если: 1) Число испытаний n велико 2) Оценивается вероятность Р(m1 ,m2 ) попадания числа успехов х в промежуток от m1 до m2. 3) m1 и m2 растут с ростом n 4) вероятность успеха постоянна Тогда выполняется
а (функция Гаусса)
Иначе говоря, Р(m1 ,m2 ) = Ф0(tm2 ) – Ф0(tm1 ), где
— функция Лапласа.
Сделаем отступление и рассмотрим теперь функцию Лапласа отдельно.
Сформулируем свойства функции Лапласа:
1) Функция Лапласа нечетная, т.е. Φ(–t) = –Φ(t) и, соответственно, ее график симметричен относительно начала координат 2) Монотонно возрастающая 3) При х→∞ Φ→1/2, при x→ – ∞ Φ→ –1/2 , причем достаточно быстро: при х=5 Ф = 0,4(9). Поэтому при х >4 функция считается (приблизительно) равной ½ 4) Существуют таблицы значений функции Лапласа, ввиду нечетности функции они составлены только для положительных значений х.
а затем найти по таблице значений функции Лапласа ее значения в этих точках. Графиком функции Лапласа является кривая:
Пример 19.2.2. Игральную кость бросают 800 раз. Какова вероятность того, что число очков, кратное 3, выпадает не менее 280 и не более 294 раз? Здесь Пусть теперь в последовательности наших испытаний n достаточно велико, а p — величина очень малая и успехи редки. Тогда имеет место
Теорема Пуассона. Асимптотическое представление Pn (x) через j(х) тем хуже, чем больше р отличается от ½ , а для случая p=0, q=1 вообще неприменимо. Однако большой круг задач связан именно с отысканием Pn (x) именно при малых значениях р.Для того, чтобы в этом случае теорема Муавра-Лапласа дала небольшую погрешность необходимо очень большое n, Поэтому требуется специальная формула, предназначенная специально для малых р, которая и приводится в теореме Пуассона: Если 1) Число испытаний n велико 2) Мы интересуемся вероятностью Pn (x) числа успехов х в серии из n испытаний 3) р уменьшается с ростом n, т. Тогда выполняется Замечание 19.2.3. Для указанной величины Pn (x) – функции Пуассона — также существуют таблицы. Пример 19.2.3. Вероятность искажения одного символа при передаче сообщения по линии связи равна 0,001. Сообщение считают принятым, если в нем отсутствуют искажения. Найти вероятность того, что будет принято сообщение, состоящее из 20 слов по 100 символов каждое. Предлагаемое сообщение содержит 2000 символов. Предполагая, что символы искажаются независимо, получаем схему Бернулли, в которой n=2000, p=0,001, x=0. λ = np=2. Тогда Р 2000(0) = 0,13534 (0! = 1) Пример 19.2.4. Вероятность попадания в цель при каждом выстреле 0,001. Найти вероятность попадания в цель двумя и более выстрелами, если производится 5000 выстрелов. Искомая вероятность равна 1 — Р 5000(0) — Р 5000(1) »1 – е-5 – 5е-5 » 0,9596
⇐ Предыдущая1234 Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
5.2: Свойства и примеры преобразований Лапласа
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 91073
- Russell Herman
- University of North Carolina Wilmington
ОБЫЧНО ИСПОЛЬЗОВАТЬ преобразования Лапласа, обращаясь к Таблице пар преобразований. Пример таких пар приведен в таблице \(\PageIndex{1}\). Комбинируя некоторые из этих простых преобразований Лапласа со свойствами преобразования Лапласа, как показано в таблице \(\PageIndex{2}\), мы можем иметь дело со многими приложениями преобразования Лапласа. Сначала мы докажем несколько приведенных преобразований Лапласа и покажем, как их можно использовать для получения новых пар преобразований. В следующем разделе мы покажем, как эти преобразования можно использовать для суммирования бесконечных рядов и решения начальных задач для обыкновенных дифференциальных уравнений. 9{-s t} d t \nonumber \]
Пример таких пар приведен в таблице \(\PageIndex{1}\). Комбинируя некоторые из этих простых преобразований Лапласа со свойствами преобразования Лапласа, как показано в таблице \(\PageIndex{2}\), мы можем иметь дело со многими приложениями преобразования Лапласа. Сначала мы докажем несколько приведенных преобразований Лапласа и покажем, как их можно использовать для получения новых пар преобразований. В следующем разделе мы покажем, как эти преобразования можно использовать для суммирования бесконечных рядов и решения начальных задач для обыкновенных дифференциальных уравнений. 9{-s t} d t \nonumber \]
и учитывая, что \(I_{0}=\mathcal{L}[1]=\dfrac{1}{s}\), имеем следующее:
\[ I_{n}=\dfrac{n}{s} I_{n-1}, \quad I_{0}=\dfrac{1}{s} \nonumber \]
Это также то, что называется разностным уравнением . Это разностное уравнение первого порядка с «начальным условием» \(I_{0}\). Следующим шагом является решение этого разностного уравнения. Найти решение этого разностного уравнения первого порядка легко, используя простую итерацию. Обратите внимание, что заменив \(n\) на \(n-1\), мы получим 9{p+1}}\номер \]
Обратите внимание, что заменив \(n\) на \(n-1\), мы получим 9{p+1}}\номер \]
для \(p>-1\).
Теперь мы готовы ввести дополнительные свойства преобразования Лапласа в таблицу \(\PageIndex{2}\). Мы уже обсуждали первое свойство, являющееся следствием линейности интегральных преобразований. Остальные свойства мы докажем в этом и следующем параграфах.
| Свойства преобразования Лапласа 9{\prime}(0) \end{aligned} \label{5.13} \] Мы вернемся к другим свойствам в таблице \(5.3\) после рассмотрения нескольких приложений. Эта страница под названием 5.2: Свойства и примеры преобразований Лапласа распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Расселом Херманом посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.
Свойства преобразования ЛапласаСвойства преобразования Лапласа, а именно, 1. Линейность:Преобразование конечной суммы функций времени представляет собой сумму преобразований Лапласа отдельных функций. Итак, если F 1 (с), F 2 (с), ……..F n (с) являются преобразованиями Лапласа функций времени f 1 (t), f 2 (t), ……….., f n (t) соответственно тогда, Объясните: Найдем преобразование Лапласа суммы из основного определения. Свойство можно дополнительно расширить, если функции времени умножить на константы, т.е. , где 1 ,a 2 ,……..,a n являются константами. 2. Теорема масштабирования: Если K является константой, то преобразование Лапласа функции Kf(t) равно K, умноженному на преобразование Лапласа функции f(t). Это очень легко доказать. Согласно определению, 3. Реальное дифференцирование (дифференцирование во временной области):Еще одним свойством преобразования Лапласа является действительное дифференцирование. Пусть F(s) — преобразование Лапласа функции f(t). Затем где f (0 – ) указывает значение f(t) в момент t = 0 – , т.е. непосредственно перед моментом t = 0 Объясните: Реальное дифференцирование обозначается как Интегрирование правой части по частям, Теорема может быть расширена для производной n th порядка как, значение (n – 1) th производная f(t) при t = 0 – . Это свойство наиболее полезно, поскольку оно преобразует дифференциальные уравнения во временной области в простые алгебраические уравнения вместе с начальными условиями, если таковые имеются. Если F(s) является преобразованием Лапласа f(t), то Объясните: По определению, , Это свойство может быть расширено для кратных интегралов как, 5. Дифференцирование по s:Если F(s) является преобразованием Лапласа f(t), то дифференцирование по s в комплексной частотной области соответствует умножению на t во временной области. Объясните: Из определения преобразования Лапласа, F(s) = ff (t) e’dt Дифференцирование обеих сторон по s, 6. Сложный перевод:Еще одним свойством преобразования Лапласа является комплексный перевод. Если F(s) является преобразованием Лапласа функции f(t), то по свойству комплексного переноса , где a — комплексное число 7. Реальный перевод (теорема о сдвиге): Эта теорема полезна. |

 — КиберПедия
— КиберПедия ..
.. .
. Для того, чтобы воспользоваться табличными значениями функции Лапласа сначала необходимо вычислить значения аргументов
Для того, чтобы воспользоваться табличными значениями функции Лапласа сначала необходимо вычислить значения аргументов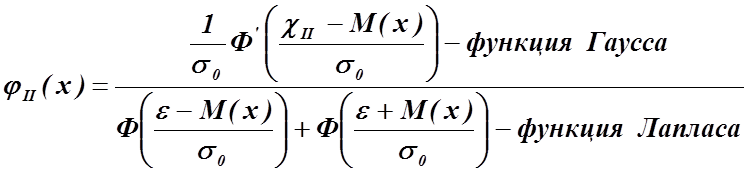 е λ = np – константа(постоянная), т.е, рассматривается случай редких успехов.
е λ = np – константа(постоянная), т.е, рассматривается случай редких успехов. ..
..
 htm
htm