Свойства подобие треугольников: Свойства подобных треугольников, с примерами

Подобие треугольников и пропорциональные отрезки

Теорема 1:

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

 

Доказательство:

Докажем сначала лемму: Если в \(\triangle OBB_1\) через середину \(A\) стороны \(OB\) проведена прямая \(a\parallel BB_1\), то она пересечет сторону \(OB_1\) также в середине.

 

Через точку \(B_1\) проведем \(l\parallel OB\). Пусть \(l\cap a=K\). Тогда \(ABB_1K\) — параллелограмм, следовательно, \(B_1K=AB=OA\) и \(\angle A_1KB_1=\angle ABB_1=\angle OAA_1\). Значит, по второму признаку \(\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\). Лемма доказана.

 

Перейдем к доказательству теоремы. Пусть \(OA=AB=BC\), \(a\parallel b\parallel c\) и нужно доказать, что \(OA_1=A_1B_1=B_1C_1\).

 

Таким образом, по данной лемме \(OA_1=A_1B_1\).

Докажем, что \(A_1B_1=B_1C_1\). Проведем через точку \(B_1\) прямую \(d\parallel OC\), причем пусть \(d\cap a=D_1, d\cap c=D_2\). Тогда \(ABB_1D_1, BCD_2B_1\) — параллелограммы, следовательно, \(D_1B_1=AB=BC=B_1D_2\). Значит, по первому признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2 \Rightarrow A_1B_1=B_1C_1\).

 

Теорема Фалеса:

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

 

Доказательство:

Пусть параллельные прямые \(p\parallel q\parallel r\parallel s\) разбили одну из прямых на отрезки \(a, b, c, d\). Тогда вторую прямую эти прямые должны разбить на отрезки \(ka, kb, kc, kd\) соответственно.

 

Проведем через точку \(A_1\) прямую \(p\parallel OD\) (\(ABB_2A_1\) — параллелограмм, следовательно, \(AB=A_1B_2\)). Тогда \(\triangle OAA_1 \sim \triangle A_1B_1B_2\) по двум углам. Следовательно, \(\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb\).

 

Аналогично проведем через \(B_1\) прямую \(q\parallel OD \Rightarrow \triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) и т.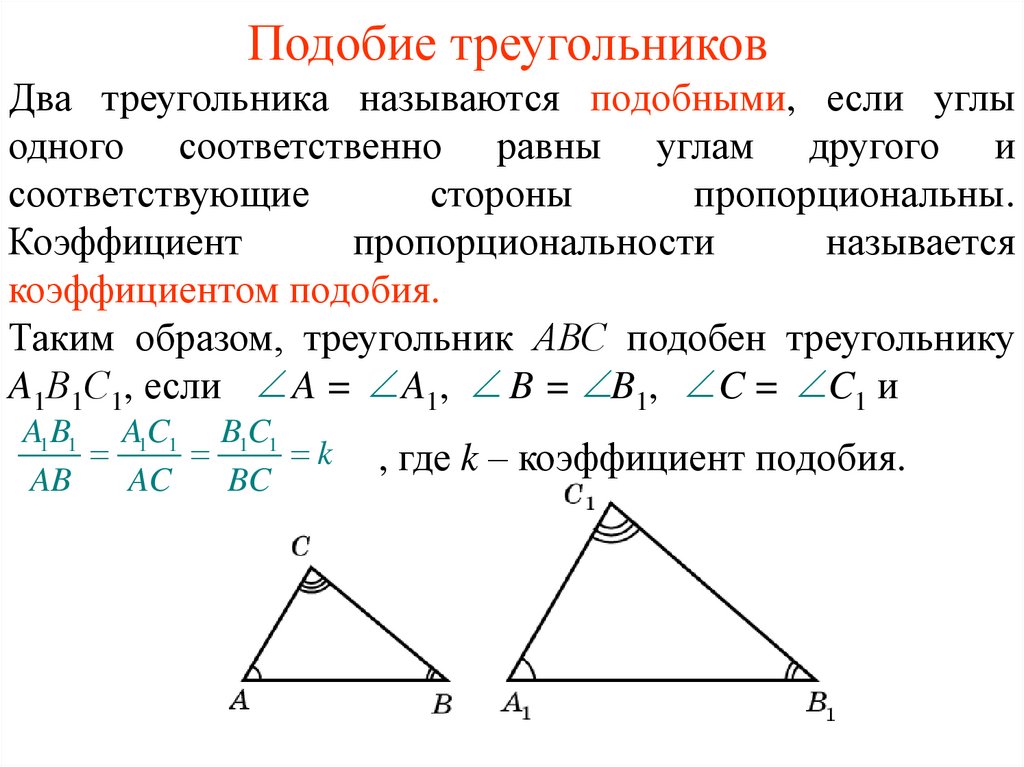 д.

 

Наиболее часто встречающиеся подобия треугольников:

 

Теорема 2.

Средняя линия треугольника отсекает от него подобный ему треугольник.

 

Доказательство:

Т.к. средняя линия — это отрезок, соединяющий середины двух сторон, то \(\dfrac{AB}{A_1B}=\dfrac{CB}{C_1B}=2\).

 

Таким образом, по двум пропорциональным сторонам и углу между ними (\(\angle B\) — общий) \(\triangle A_1BC_1 \sim \triangle ABC\).

 

Теорема 3.

Треугольники, образованные диагоналями трапеции и основаниями, подобны.

 

Доказательство:

Т.к. \(AD\parallel BC \Rightarrow \angle OBC=\angle ODA\). \(\angle BOC=\angle AOD\) как вертикальные. Следовательно, по двум углам \(\triangle BOC\sim \triangle AOD\).

 

Теорема 4.

Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника. \circ-\angle BA_1B_1=\angle BAB_1\).

 

Таким образом, по двум углам (\(\angle O\) — общий) \(\triangle OAB\sim \triangle OA_1B_1\).

 

Теорема 7.

Если к окружности из одной точки проведены касательная и секущая, то:

 

Доказательство:

Т.к. угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними, то \(\angle OKA=\frac12 \buildrel\smile\over{KA}=\angle KBA\).

 

Следовательно, по двум углам (\(\angle O\) — общий) \(\triangle OKA\sim \triangle OKB\).

 

Теорема 8.

Если в окружности две хорды пересекаются, то:

 

Доказательство:

\(\angle A_1AB_1=\angle A_1BB_1\), т.к. опираются на одну и ту же дугу. \(\angle A_1CB=\angle B_1CA\), т.к. они вертикальные. Следовательно, по двум углам \(\triangle A_1BC\sim \triangle B_1C\).

 

Аналогично \(\triangle ABC\sim \triangle A_1B_1C\).

 

Признаки подобия прямоугольных треугольников (тема математики, 5 класс)

4

Средняя оценка: 4

Всего получено оценок: 111.

4

Средняя оценка: 4

Всего получено оценок: 111.

Подобие – это следующее понятие после равенства: как в математике после сложения идет умножение, так в геометрии после равенства треугольников изучают подобие. В реальной жизни подобие помогает, за счет вычислений по тени, определять реальные размеры зданий или высоких сооружений. В задачах на эту тему, благодаря подобию, можно найти значение сторон, воспользовавшись знакомым отношением.

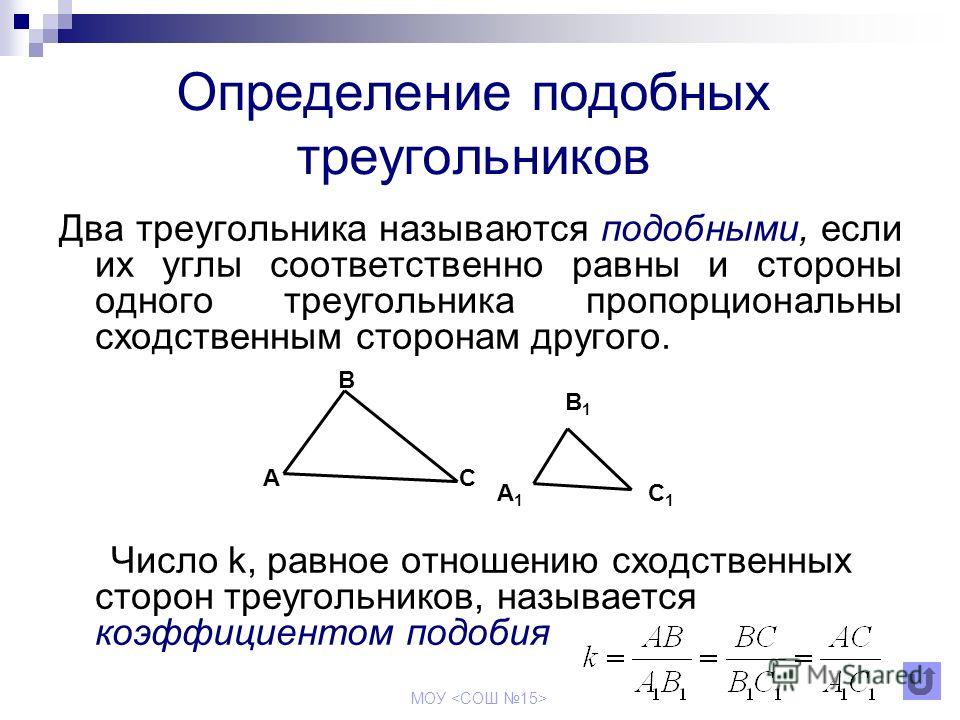
Определения

Подобными называются треугольники, отношение сторон которых соответственно равны. Предположим треугольник АВС равен треугольнику DРН. Это значит, что:

$${АВ\over{DP}}={BC\over{PH}}={AC\over{DH}}=k$$

k это коэффициент подобия.

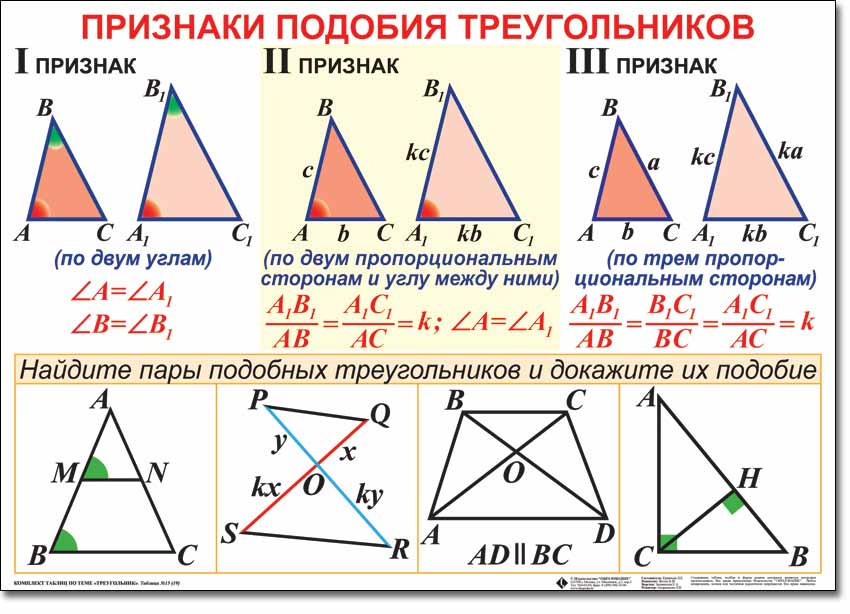
Для обычного треугольника существует три признака подобия. Именно через них доказываются признаки подобия прямоугольных треугольников.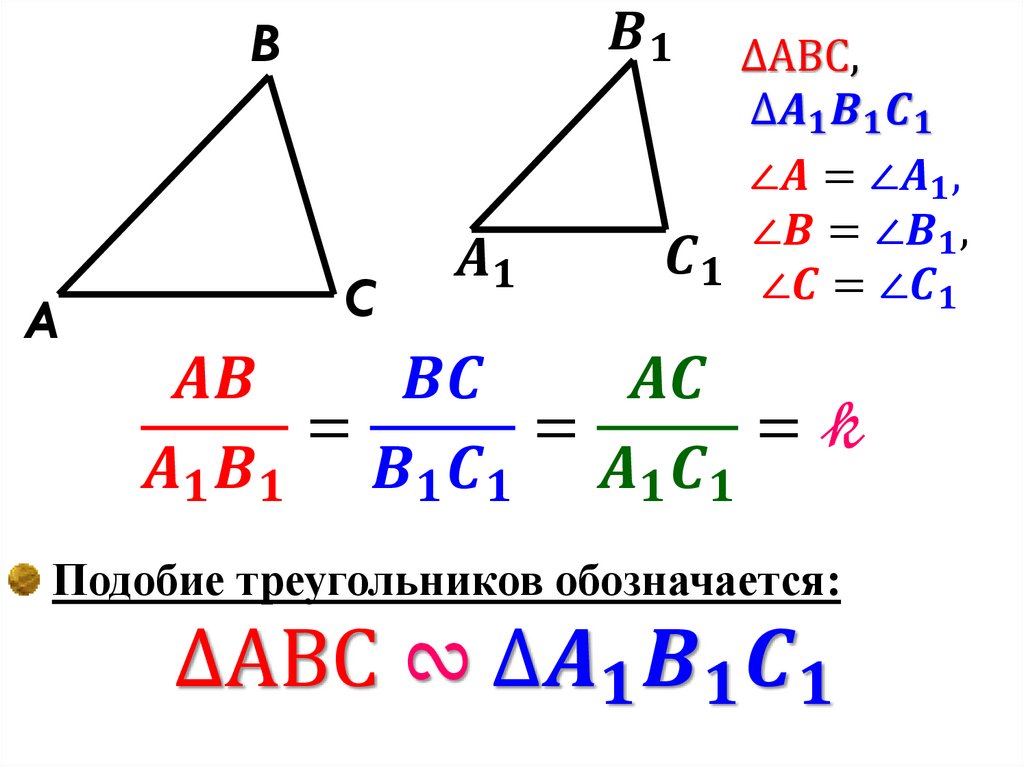

Первый признак подобия: по двум углам. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Рис. 1. Первый признак подобия.

Второй признак: по трем сторонам. Если три стороны одного треугольника пропорциональны соответственным сторонам другого треугольника, то такие треугольники подобны.

Рис. 2. Второй признак подобия.

Третий признак: по двум сторонам и углу. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то такие треугольники подобны.

Рис. 3. Третий признак подобия.

Эти определения необходимо знать, чтобы без проблем разобраться с подобием прямоугольных треугольников.

Признаки подобия прямоугольных треугольников

• Первый признак по острому углу: если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.

Доказать этот признак очень просто. Достаточно вспомнить, что прямоугольным треугольником называется треугольник, который содержит в себе прямой угол. Значит, у двух прямоугольных треугольников, один из углов всегда равен другому. А один из острых углов так же равен соответственному углу в другом треугольнике. Значит, в таких треугольниках есть два равных между собой угла, и треугольники подобны по первому признаку подобия.

• Второй признак: по двум катетам. Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны. Между двумя катетами всегда заключен прямой угол. Значит, у нас имеется две пропорциональные стороны и равные углы между ними. Тогда треугольники подобны по третьему признаку подобия.
• Третий признак: по катету и гипотенузе. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
  Для доказательства признака нужно вспомнить понятие косинуса. Косинус угла это отношения прилежащего катета к гипотенузе.

$$cos(ACB)={BC\over{AC}}$$

$$cos(DHP)={PH\over{DH}}$$

При этом по условию: $${AC\over{DH}}={BC\over{PH}}$$. Из условия выразим ВС и подставим в значение косинуса.

$$ВС=РН*{АC\over{DН}}$$

$$cos(ACB)={BC\over{AC}}={PH*{AC\over{DH}}\over AC}={PH\over{AC}}$$ – то есть косинусы углов равны, оба угла острые, значит и углы равны. Тогда треугольники подобны по двум сторонам и углу между ними.

Что мы узнали?

Мы разобрали понятие подобия, выделили все определения и теоремы, необходимые для доказательства трех признаков подобия прямоугольных треугольников. Мы показали, что эти признаки лишь следствие основных, т.е. эти свойства созданы чтобы упростить и сделать быстрее решение. А это значит, что если вдруг вы забыли признаки для прямоугольного треугольника, то всегда можно воспользоваться общими.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4

Средняя оценка: 4

Всего получено оценок: 111.

---

А какая ваша оценка?

Геометрия: свойства подобных треугольников

Когда мы говорим о сходстве двух вещей, мы пытаемся показать, что наши два объекта во многом похожи. Они не обязательно должны быть взаимозаменяемыми или идентичными, но у них должно быть достаточно общего. Можно подумать, что все треугольники подобны, потому что у них одинаковое количество сторон и одинаковое количество углов. А подобие — это особое отношение только между определенными треугольниками. Чтобы два треугольника были объявлены подобными, они должны удовлетворять определенным критериям угла и длины.

Два треугольника подобны , если все пары соответствующих углов равны и все пары соответствующих сторон пропорциональны. Если мы посмотрим на два треугольника на рис. 13.2, то сможем определить соответствующие углы и различные пропорции, которые должны быть удовлетворены.

Рисунок 13.2 Два подобных треугольника.

Конгруэнтность углов: A ~= R , B ~= S и C ~= T. Используемые пропорциональности: ^AB / _RS = ^BC / _ST = ^AC / _RT и все возможные перестановки с использованием различных свойств пропорций.

Я буду использовать символ ~, чтобы указать, что два треугольника подобны. Если вы пробежитесь по списку, то увидите, что ~ — это отношение эквивалентности, поэтому оно будет иметь рефлексивные, симметричные и транзитивные свойства.

Если вы знаете, что два треугольника подобны, вы можете использовать расширенные пропорции, чтобы узнать больше о треугольниках.

• Пример 5 : Если ABC ~ RST, как показано на рис. 13.3, используйте указанные меры, чтобы найти меры оставшихся сторон и углов каждого из треугольников.

Рисунок 13.3 ABC ~ RST.

• Решение : У вас есть целый список вещей, которые нужно найти: мера третьего угла в ABC ; все три угла RST и длины AC и ST. Поскольку внутренние углы треугольника в сумме составляют 180º, вы можете довольно легко найти мА:
• мА + мВ + мКл = 180º
• мА + 90º + 37º = 180º
• мА = 53º
• Поскольку соответствующие углы равны, вы знаете, что mR = 53º , mS = 90º и mR = 3 . Используя ваши пропорции, вы имеете
• ^AB / _RS = ^BC / _ST = ^AC / _RT
Вы можете подставить известные значения в пропорциональность ST4:
• ³ / ₆ = ⁴ / _ST
• 3(ST) = 24
• ST = 8
• Для определения AC используется вторая половина пропорциональности:
• ³ /5 6 AC ₁₀
• 6(AC) = 30
• AC = 5

Вы будете использовать идею о том, что соответствующие стороны подобных треугольников пропорциональны, так что вы могли бы также ознакомиться с сокращением для этой фразы сейчас— это КПССАТ.

Выдержки из Полное руководство идиота по геометрии © 2004 Дениз Сечеи, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.

Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.

• Геометрия: Большая тройка

Как определить, подобны ли треугольники

Два треугольника подобны, если у них:

• все их углы равны
• соответствующие стороны находятся в одинаковом соотношении

Но нам не нужно знать все три стороны и все три угла… двух-трех из шести обычно достаточно.

Есть три способа определить, подобны ли два треугольника: AA , SAS и SSS :

AA

AA означает «угол, угол» и означает, что у треугольников два угла равны.

Если у двух треугольников два угла равны, то треугольники подобны.

Пример: эти два треугольника подобны:

Если два их угла равны, то должен быть равен и третий угол, потому что сумма углов треугольника всегда составляет 180°.

В этом случае недостающий угол равен 180° − (72° + 35°) = 73°

Таким образом, АА также можно было бы назвать ААА (потому что, когда два угла равны, все три угла должны быть равны).

САС

SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, где:

• соотношение между двумя сторонами такое же, как соотношение между двумя другими сторонами
• и мы также знаем, что прилежащие углы равны.

Если у двух треугольников две пары сторон находятся в одинаковом отношении и прилежащие к ним углы также равны, то такие треугольники подобны.

Пример:

В этом примере мы видим, что:

• одна пара сторон находится в соотношении 21 : 14 = 3 : 2
• другая пара сторон находится в соотношении 15 : 10 = 3 : 2
• между ними имеется согласующий угол 75°

Итак, информации достаточно, чтобы сказать нам, что два треугольника подобны .

Использование тригонометрии

Мы также можем использовать тригонометрию для вычисления двух других сторон, используя закон косинусов:

Продолжение примера

В треугольнике ABC:

• a ² = b ² + c ² — 2bc cos A
• a ² = 21 ² + 15 ² — 2 × 21 × 15 × Cos75°
• a ² = 441 + 225 — 630 × 0,2588…
• a ² = 666 — 163,055…
• a ² = 502,944…
• Итак, а = √502,94 = 22,426…

В треугольнике XYZ:

• x ² = y ² + z ² — 2yz cos X
• x ² = 14 ² + 10 ² — 2 × 14 × 10 × Cos75°
• х ² = 196 + 100 — 280 × 0,2588…
• х ² = 296 — 72,469…
• х ² = 223,530…
• Итак, х = √223,530… = 14,950…

Теперь давайте проверим отношение этих двух сторон:

a : x = 22,426.

No related posts.