Понятие степени. Возведение в степень. Чтение и свойства степеней презентация, доклад
Степени
Понятие степени
Возведение в степень
Чтение степеней
Свойства степеней
Понятие степени
Определение
Компоненты
Чётная и нечётная степень
Степень
Чётная степень
Нечётная степень
Основание
Показатель
Прочитайте слова
основание степени
показатель степени
Прочитайте
Вставьте слова
Назовите компоненты степени
основание степени
показатель степени
Разные показатели
Разные основания
Расскажите об этих степенях
Эти степени имеют одинаковые основания и разные показатели.
Эти степени с одинаковыми основаниями и разными показателями.
Эти степени имеют одинаковые показатели и разные основания.
Эти степени с одинаковыми показателями и разными основаниями
Чётная степень всякого числа есть произведение чётного числа сомножителей.
Нечётная степень всякого числа…
что (1) есть что (1)
есть произведение нечётного числа сомножителей.
Прочитайте
Расскажите о степени
В данном случае степень нечётная, поскольку мы видим произведение нечётного числа сомножителей.
Нечётная степень положительного числа есть ________________ число.
Чётная степень отрицательного числа есть _______________ число.
Нечётная степень отрицательного числа есть _______________ число.
Вставьте слово
положительное
положительное
отрицательное
Возведение в степень
Представление о действии.
Чтение степеней
Возводить/возвести в степень (4)
Возводить в квадрат (4)
Возводить в куб (4)
Возведение в степень (4)
В виде (6) + чего (2)
Представлять/представить число в виде степени
Прочитайте
Прочитайте
Образуйте форму предложного падежа
в квадрате
в кубе
в нулевой степени
в третьей степени
в пятой степени
Чтение степеней
Запомните!
Домашнее задание
Задание 4.
Прочитать и перевести текст.
Написать ответы на вопросы в тетради
Подготовка к тесту по аудированию.
Прочитайте
представлять/представить
представить что (4) в виде чего (2)
8 =
81=
25 =
64 =
0,001=
Представьте числа в виде квадрата или куба
Свойства степеней
Умножение степеней
Деление степеней
Возведение степени в степень
Образуйте по модели
умножение
при
умножении (6)
+
деление
возведение степени в степень
при делении (6)
при возведении (6) степени (2) в степень (4)
Свойства степеней
произведение степеней
частное степеней
степень степени
степень частного
Свойства степеней
основное свойство степени
свойство частного степеней
свойство возведения степени в степень
свойство степени произведения
свойство частного в натуральной степени
Назовите свойство степени
Домашнее задание
Прочитайте образец
а в шестой степени умножить на а в минус третьей степени, умножить на а в минус третьей степени.
Чтобы выполнить действие, используем основное свойство степени. Складываем показатели.
Выполните действия по образцу
(2, 3, 4, 6)
Презентация «Степени»:
свойства степени (названия, ситуации употребления)
Выучите
Скачать презентацию
Цифры с одинаковыми степенями. Степенные выражения (выражения со степенями) и их преобразование. Операции со степенями
Содержание урока
Что такое степень?
Степенью называют произведение из нескольких одинаковых множителей. Например:
2 × 2 × 2
Значение данного выражения равно 8
2 × 2 × 2 = 8
Левую часть этого равенстваможно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
2 3 = 8
Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 5 3 , то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5 .
Число, которое повторяется называют основанием степени . В выражении 5 3 основанием степени является число 5 .
А число, которое надписано над числом 5 называют показателем степени . В выражении 5 3 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
Саму операцию перемножения одинаковых множителей называют возведением в степень .
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень :
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем . Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида a n , которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
Это произведение равно 25
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
Получилась ошибка, поскольку число 5 во второй степени не равно 10.
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 0 0 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 0 0 может иметь смысл.
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1. Возвести число 3 во вторую степень.
Возвести число 3 во вторую степень.
Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
3 2 = 3 × 3 = 9
Пример 2. Возвести число 2 в четвертую степень.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
2 4 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
2 3 =2 × 2 × 2 = 8
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
10 2
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
10 2 = 100
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
10 2 = 10 × 10 = 100
Пример 2 . Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
10 3 = 1000
Пример 3 . Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
10 4 = 10000
Пример 4 . Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
10 1 = 10
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 10 1
10 = 10 1
Пример 2 . Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 10 2
Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 10 2
100 = 10 2
Пример 3 . Представим число 1 000 в виде степени с основанием 10.
1 000 = 10 3
Пример 4 . Представим число 10 000 в виде степени с основанием 10.
10 000 = 10 4
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
(−2) 2 = (−2) × (−2) = 4
Если бы мы не заключили в скобки число −2 , то получилось бы что мы вычисляем выражение −2 2 , которое не равно 4 . Выражение −2² будет равно −4 . Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения .
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −2 2 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −2 2 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
−2 2 = −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2) 2
сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Поэтому в случае вычисления выражения (−2) 2
сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Пример 2 . Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2) 3 = (−2) × (−2) × (−2) = −8
Пример 3 . Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2) 4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3
Покажем это на примере числа −3
В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным .
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным .
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5) 3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4) 4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений
При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.
Пример 1 . Найти значение выражения 2 + 5 2
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 5 2 = 2 + 25 = 27
Пример 10 . Найти значение выражения −6 2 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−6 2 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−6 2 × (−12) = −36 × (−12) = 432
Пример 11 . Найти значение выражения −3 × 2 2
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 2 2 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.
Пример 12 . Найти значение выражения (3 2 + 1 × 3) − 15 + 5
Найти значение выражения (3 2 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3 , затем складываем результаты возведения в степень числа 3 и умножения 1 × 3 . Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
(3 2 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13 . Найти значение выражения 2 × 5 3 + 5 × 2 3
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 5 3 + 5 × 2 3 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (2 3) 2
. В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(2 3) 2 это произведение двух степеней, каждая из которых равна 2 3
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
Получили произведение 2 × 2 × 2 × 2 × 2 × 2 , которое равно 64. Значит значение выражения (2 3) 2 или равно 64
Этот пример можно значительно упростить. Для этого показатели выражения (2 3) 2 можно перемножить и записать это произведение над основанием 2
Получили 2 6 . Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
Данное свойство работает по причине того, что 2 3 это произведение 2 × 2 × 2 , которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 2 6
Вообще, для любого основания a с показателями m и n , выполняется следующее равенство:
(a n ) m = a n × m
Это тождественное преобразование называют возведением степени в степень . Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают» .
Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают» .
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2 . Найти значение выражения (3 2) 2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:
Получили 3 4 . А число 3 в четвёртой степени есть 81
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 2 2 на 3 3 .
2 2 это число 4 , а 3 3 это число 27 . Перемножаем числа 4 и 27 , получаем 108
2 2 × 3 3 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 2 2 на 2 3
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 2 2 и 2 3 . Иными словами, о снование оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 2 5 . Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 2 2 это произведение 2 × 2 , а 2 3 это произведение 2 × 2 × 2 . Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2 . Это произведение представимо в виде 2 5
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени . Его можно прочитать так: «П ри перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают» .
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 2 1 × 2 2 × 2 3 . Основание 2
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1 . Представить в виде степени выражение 5 8 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 5 8 × 25 получилась одна степень.
Число 25 можно представить в виде 5 2 . Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Запишем решение покороче:
Пример 2 . Представить в виде степени выражение 2 9 × 32
Число 32 можно представить в виде 2 5 . Тогда получим выражение 2 9 × 2 5 . Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3 . Вычислите произведение 3 × 3
, используя основное свойство степени.
Вычислите произведение 3 × 3
, используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 3 1 и 3 1
3 1 × 3 1
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
3 1 × 3 1 = 3 2 = 9
Пример 4 . Вычислите произведение 2 × 2 × 3 2 × 3 3 , используя основное свойство степени.
Произведение 2 × 2 заменим на 2 1 × 2 1 , затем на 2 1 + 1 , а затем на 2 2 . Произведение 3 2 × 3 3 заменим на 3 2 + 3 , а затем на 3 5
Пример 5 . Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6 . Выполнить умножение x 2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 7 . Выполнить умножение y 3 y 2 y
Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 8 . Выполнить умножение aa 3 a 2 a 5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 9 . Представить степень 3 8
в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3 , и сумма показателей которых будет равна 8 . Можно использовать любые показатели. Представим степень 3 8 в виде произведения степеней 3 5 и 3 3
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 3 5 × 3 3 можно записать как 3 5 + 3 , откуда 3 8 .
Конечно можно было представить степень 3 8 в виде произведения других степеней. Например, в виде 3 7 × 3 1 , поскольку это произведение тоже равно 3 8
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10 . Представить степень x 12 в виде различных произведений степеней с основаниями x .
Воспользуемся основным свойство степени. Представим x 12 в виде произведений с основаниями x , и сумма показателей которых равна 12
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3 . Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
2 × 3 × 2 × 3
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
2 × 2 × 3 × 3
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2
можно заменить на 2 2
, а произведение 3 × 3
можно заменить на 3 2 .
Тогда выражение 2 × 2 × 3 × 3
обращается в выражение 2 2 × 3 2 .
Произведение 2 × 2
можно заменить на 2 2
, а произведение 3 × 3
можно заменить на 3 2 .
Тогда выражение 2 × 2 × 3 × 3
обращается в выражение 2 2 × 3 2 .
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n , нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Пример 2 . Найти значение выражения (2 × 3 × 4) 2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4 . Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
Пример 3 . Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Пример 4 . Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
(3xyz ) 3
Возведём в третью степень каждый множитель данного произведения:
(3xyz ) 3 = 3 3 x 3 y 3 z 3
Число 3
в третьей степени равно числу 27
. Остальное оставим без изменений:
Остальное оставим без изменений:
(3xyz ) 3 = 3 3 x 3 y 3 z 3 = 27x 3 y 3 z 3
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 5 2 × 3 2 . Возведем каждое число во вторую степень и перемножим полученные результаты:
5 2 × 3 2 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3) 2 . Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
5 2 × 3 2 = (5 × 3) 2 = (15) 2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b ) n = a n × b n , то a n × b n = (a × b) n . То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.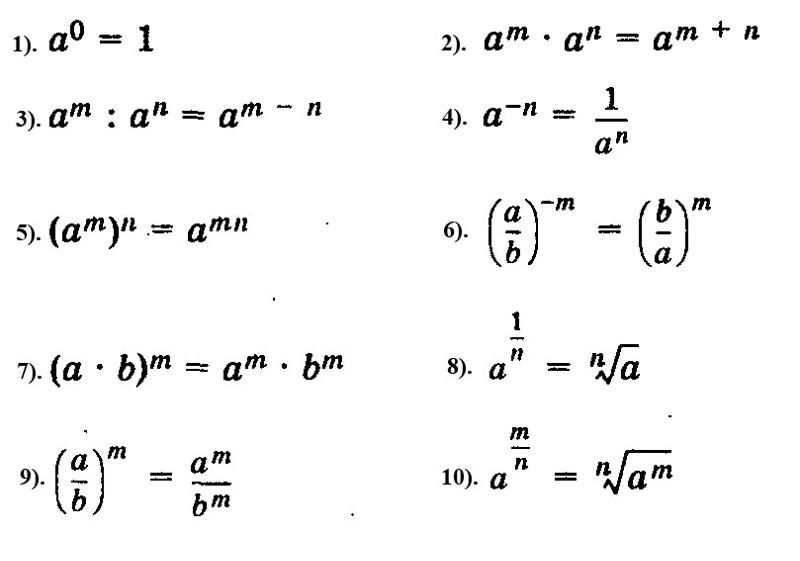
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
(a n ) m = a n × m
К примеру, выражение (2 3) 2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(2 3) 2 = 2 3 × 2 = 2 6
(2 3) 2 = 2 3 × 2 = 2 6 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (2 3) 2 . Выражение в скобках 2 3 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (2 3) 2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2 .
(2 × 2 × 2) 2
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6
Как и раньше получили 2 6 . Значение этой степени равно 64
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (2 2 × 3 2) 3 . Здесь показатели каждого множителя нужно умножить на общий показатель 3 . Далее найти значение каждой степени и вычислить произведение:
(2 2 × 3 2) 3 = 2 2×3 × 3 2×3 = 2 6 × 3 6 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4
изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 2 1 × 4 1
. А это есть возведение степени в степень.
Получается, что множители произведения 2 × 4
изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 2 1 × 4 1
. А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
Пример 2 . Найти значение выражения (3 3) 2
Основание оставляем без изменений, а показатели перемножаем:
Получили 3 6 . Число 3 в шестой степени есть число 729
Пример 3 xy )³
Пример 4 . Выполнить возведение в степень в выражении (abc )⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5 ax ) 3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Пример 6 . Выполнить возведение в степень в выражении (10xy ) 2
Пример 7 . Выполнить возведение в степень в выражении (−5x ) 3
Пример 8 . Выполнить возведение в степень в выражении (−3y ) 4
Выполнить возведение в степень в выражении (−3y ) 4
Пример 9 . Выполнить возведение в степень в выражении (−2abx )⁴
Пример 10 . Упростите выражение x 5 × (x 2) 3
Степень x 5 пока оставим без изменений, а в выражении (x 2) 3 выполним возведение степени в степени:
x 5 × (x 2) 3 = x 5 × x 2 × 3 = x 5 × x 6
Теперь выполним умножение x 5 × x 6 . Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
x 5 × (x 2) 3 = x 5 × x 2× 3 = x 5 × x 6 = x 5 + 6 = x 11
Пример 9 . Найти значение выражения 4 3 × 2 2 , используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 4 3 . Основание у этой степени есть число 4, которое можно представить в виде 2 2 . Тогда исходное выражение примет вид (2 2) 3 × 2 2 . Выполнив возведение степени в степень в выражении (2 2) 3 , мы получим 2 6 . Тогда исходное выражение примет вид 2 6 × 2 2 , вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 4 3 на 2 2 .
Вычислим 4 3 , получим 64 . Вычислим 2 2 , получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 2 3: 2 2
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 2 3: 2 2
равно 2
.
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 2 3: 2 2 . Здесь делимое это 2 3 , а делитель 2 2 .
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 2 3 на 2 2 означает найти такую степень, которая при умножении на делитель 2 2 даст в результате 2 3 . А какую степень можно умножить на 2 2 , чтобы получить 2 3 ? Очевидно, что только степень 2 1 . Из основного свойства степени имеем:
Убедиться, что значение выражения 2 3: 2 2 равно 2 1 можно непосредственно вычислив само выражение 2 3: 2 2 . Для этого сначала найдём значение степени 2 3 , получим 8 . Затем найдём значение степени 2 2 , получим 4 . Разделим 8 на 4, получим 2 или 2 1 , поскольку 2 = 2 1 .
2 3: 2 2 = 8: 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
В этом случае в ответе получится единица.
Например, найдём значение выражения 2 2: 2 2 . Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 2 2: 2 2 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 2 2 и 2 2 равна нулю:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 2 2: 2 2 обычным методом, не используя правило деления степеней, получится единица.
Пример 2 . Найти значение выражения 4 12: 4 10
4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
4 12: 4 10 = 4 12 − 10 = 4 2 = 16
Пример 3 . Представить частное x 3: x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
Показатель делителя равен единице. Для наглядности запишем его:
Пример 4 . Представить частное x 3: x 2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x 3 можно записать как x × x × x , а степень x 2 как x × x . Тогда конструкцию x 3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x . В результате останется один множитель x
Или ещё короче:
Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x 2 . Чтобы сократить дробь на x 2 нужно числитель и знаменатель дроби разделить на x 2
Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Приведённое сокращение можно выполнить короче:
Или ещё короче:
Пример 5 . Выполнить деление x 12 : x 3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x 12 : x 3 запишем в виде . Далее сократим данную дробь на x 3 .
Пример 6 . Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Завершаем пример, вычислив степень 7 2
Пример 7 . Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (2 3) 4
Теперь выполним в числителе умножение степеней с одинаковыми основаниями. 3=8$.
3=8$.
Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n -ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:
Определение 1
1. Главное свойство степени: a m · a n = a m + n
Можно обобщить до: a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .
2. Свойство частного для степеней, имеющих одинаковые основания: a m: a n = a m − n
3. Свойство степени произведения: (a · b) n = a n · b n
Равенство можно расширить до: (a 1 · a 2 · … · a k) n = a 1 n · a 2 n · … · a k n
4. Свойство частного в натуральной степени: (a: b) n = a n: b n
Свойство частного в натуральной степени: (a: b) n = a n: b n
5. Возводим степень в степень: (a m) n = a m · n ,
Можно обобщить до: (((a n 1) n 2) …) n k = a n 1 · n 2 · … · n k
6. Сравниваем степень с нулем:
- если a > 0 , то при любом натуральном n, a n будет больше нуля;
- при a , равном 0 , a n также будет равна нулю;
- при a
- при a
7. Равенство a n
8. Неравенство a m > a n будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.
В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными. Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: a m · a n = a m + n — то же самое, что и a m + n = a m · a n . В таком виде оно часто используется при упрощении выражений.
1. Начнем с основного свойства степени: равенство a m · a n = a m + n будет верным при любых натуральных m и n и действительном a . Как доказать это утверждение?
Как доказать это утверждение?
Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:
Это можно сократить до (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m + n . Таким образом, a m + n , значит, основное свойство степени доказано.
Разберем конкретный пример, подтверждающий это.
Пример 1
Итак, у нас есть две степени с основанием 2 . Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 2 2 · 2 3 = 2 2 + 3 = 2 5 Вычислим значения, чтобы проверить верность этого равенства.
Выполним необходимые математические действия: 2 2 · 2 3 = (2 · 2) · (2 · 2 · 2) = 4 · 8 = 32 и 2 5 = 2 · 2 · 2 · 2 · 2 = 32
В итоге у нас вышло: 2 2 · 2 3 = 2 5 . Свойство доказано.
В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n 1 , n 2 и др. буквой k , мы получим верное равенство:
Если обозначить количество натуральных чисел n 1 , n 2 и др. буквой k , мы получим верное равенство:
a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .
Пример 2
2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство a m: a n = a m − n , которое справедливо при любых натуральным m и n (причем m больше n)) и любом отличном от нуля действительном a .
Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0 n = 0). Условие, чтобы число m обязательно было больше n , нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m , мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:
a m − n · a n = a (m − n) + n = a m
Из него можно вывести: a m − n · a n = a m
Вспомним про связь деления и умножения. Из него следует, что a m − n – частное степеней a m и a n . Это и есть доказательство второго свойства степени.
Пример 3
Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π : π 5: π 2 = π 5 − 3 = π 3
3. Следующим мы разберем свойство степени произведения: (a · b) n = a n · b n при любых действительных a и b и натуральном n .
Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:
Вспомнив свойства умножения, запишем: . Это значит то же самое, что и a n · b n .
Пример 4
2 3 · — 4 2 5 4 = 2 3 4 · — 4 2 5 4
Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:
Введем для числа множителей обозначение k и запишем:
(a 1 · a 2 · … · a k) n = a 1 n · a 2 n · … · a k n
Пример 5
С конкретными числами получим следующее верное равенство: (2 · (- 2 , 3) · a) 7 = 2 7 · (- 2 , 3) 7 · a
4. После этого мы попробуем доказать свойство частного: (a: b) n = a n: b n при любых действительных a и b , если b не равно 0 , а n – натуральное число.
Для доказательства можно использовать предыдущее свойство степени. Если (a: b) n · b n = ((a: b) · b) n = a n , а (a: b) n · b n = a n , то из этого выходит, что (a: b) n есть частное от деления a n на b n .
Пример 6
Подсчитаем пример: 3 1 2: — 0 . 5 3 = 3 1 2 3: (- 0 , 5) 3
Пример 7
Начнем сразу с примера: (5 2) 3 = 5 2 · 3 = 5 6
А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:
Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p , q , r , s , то верно будет:
a p q y s = a p · q · y · s
Пример 8
Добавим конкретики: (((5 , 2) 3) 2) 5 = (5 , 2) 3 · 2 · 5 = (5 , 2) 30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Для начала сравним степень с нулем. Почему a n > 0 при условии, что а больше 0 ?
Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени a n с положительным основанием и натуральным показателем это будет верно.
Пример 9
3 5 > 0 , (0 , 00201) 2 > 0 и 34 9 13 51 > 0
Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.
Пример 10
0 3 = 0 и 0 762 = 0
Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2 · m , где m – натуральное число.
Возьмем для начала случай, когда показатель степени четный, и обозначим его 2 · m , где m – натуральное число.
Вспомним, как правильно умножать отрицательные числа: произведение a · a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда и степень a 2 · m также положительны.
Пример 11
Например, (− 6) 4 > 0 , (− 2 , 2) 12 > 0 и — 2 9 6 > 0
А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2 · m − 1 .
Тогда
Все произведения a · a , согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a , то конечный результат будет отрицателен.
Тогда получим: (− 5) 3
Как это доказать?
a n
Пример 12
Например, верны неравенства: 3 7 (0 , 75) 124
8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Для начала нам нужно убедиться, что a m
Вынесем a n за скобки, после чего наша разность примет вид a n · (a m − n − 1) . Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m − n > 0 , тогда a m − n − 1 –отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
У нас вышло, что a m − a n
Осталось привести доказательство второй части утверждения, сформулированного выше: a m > a справедливо при m > n и a > 1 . Укажем разность и вынесем a n за скобки: (a m − n − 1) .Степень a n при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a > 1 степень a m − n больше единицы. Выходит, a m − a n > 0 и a m > a n , что нам и требовалось доказать.
Пример 13
Пример с конкретными числами: 3 7 > 3 2
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:
Определение 2
1. a m · a n = a m + n
2. a m: a n = a m − n
3. (a · b) n = a n · b n
4. (a: b) n = a n: b n
5. (a m) n = a m · n
6. a n b − n при условии целого положительного n , положительных a и b , a
7. a m n и 0 1 a m > a n .
Если основание степени равно нулю, то записи a m и a n имеют смысл только лишь в случае натуральных и положительных m и n . В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.
Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.
Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (a p) q = a p · q , (a − p) q = a (− p) · q , (a p) − q = a p · (− q) и (a − p) − q = a (− p) · (− q)
Условия: p = 0 или натуральное число; q – аналогично.
Если значения p и q больше 0 , то у нас получится (a p) q = a p · q . Схожее равенство мы уже доказывали раньше. Если p = 0 , то:
(a 0) q = 1 q = 1 a 0 · q = a 0 = 1
Следовательно, (a 0) q = a 0 · q
Для q = 0 все точно так же:
(a p) 0 = 1 a p · 0 = a 0 = 1
Итог: (a p) 0 = a p · 0 .
Если же оба показателя нулевые, то (a 0) 0 = 1 0 = 1 и a 0 · 0 = a 0 = 1 , значит, (a 0) 0 = a 0 · 0 .
Вспомним доказанное выше свойство частного в степени и запишем:
1 a p q = 1 q a p q
Если 1 p = 1 · 1 · … · 1 = 1 и a p q = a p · q , то 1 q a p q = 1 a p · q
Эту запись мы можем преобразовать в силу основных правил умножения в a (− p) · q .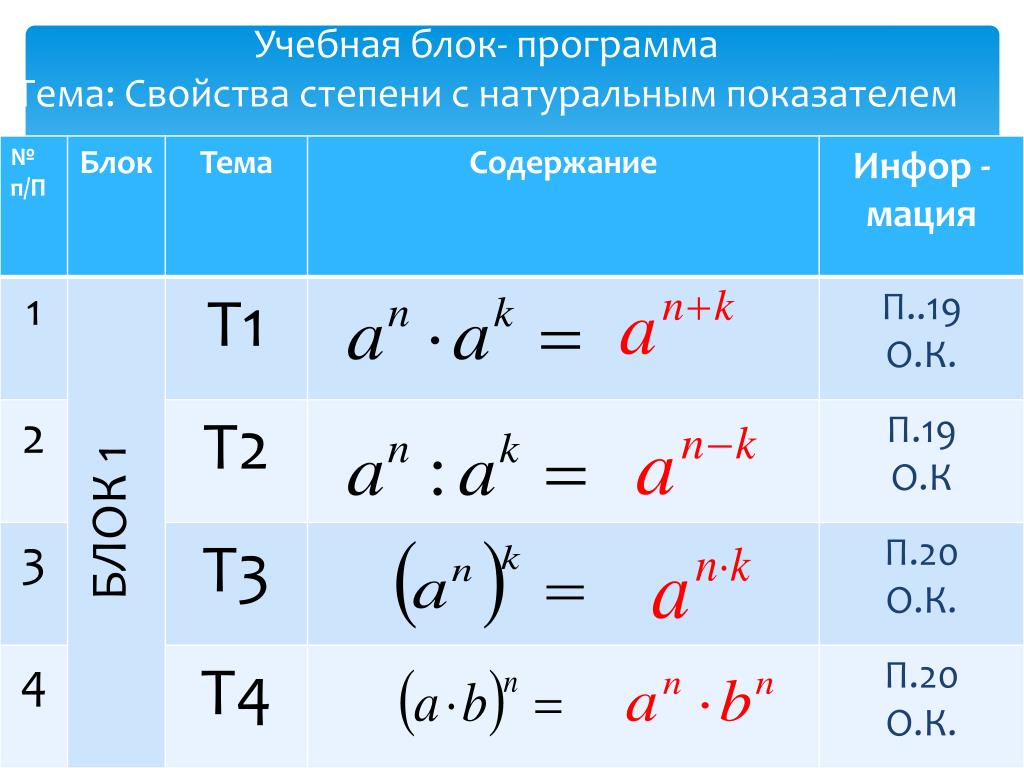
Так же: a p — q = 1 (a p) q = 1 a p · q = a — (p · q) = a p · (- q) .
И (a — p) — q = 1 a p — q = (a p) q = a p · q = a (- p) · (- q)
Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.
Доказательство предпоследнего свойства: вспомним, a − n > b − n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b .
Тогда неравенство можно преобразовать следующим образом:
1 a n > 1 b n
Запишем правую и левую части в виде разности и выполним необходимые преобразования:
1 a n — 1 b n = b n — a n a n · b n
Вспомним, что в условии a меньше b , тогда, согласно определению степени с натуральным показателем: — a n 0 .
a n · b n в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь b n — a n a n · b n , которая в итоге также дает положительный результат. Отсюда 1 a n > 1 b n откуда a − n > b − n , что нам и нужно было доказать.
Отсюда 1 a n > 1 b n откуда a − n > b − n , что нам и нужно было доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Определение 3
1. a m 1 n 1 · a m 2 n 2 = a m 1 n 1 + m 2 n 2 при a > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 (свойство произведения степеней с одинаковыми основаниями).
2. a m 1 n 1: b m 2 n 2 = a m 1 n 1 — m 2 n 2 , если a > 0 (свойство частного).
3. a · b m n = a m n · b m n при a > 0 и b > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 и (или) b ≥ 0 (свойство произведения в дробной степени).
4. a: b m n = a m n: b m n при a > 0 и b > 0 , а если m n > 0 , то при a ≥ 0 и b > 0 (свойство частного в дробной степени).
5. a m 1 n 1 m 2 n 2 = a m 1 n 1 · m 2 n 2 при a > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 (свойство степени в степени).
6. a p 0 ; если p b p (свойство сравнения степеней с равными рациональными показателями).
7. a p q при 0 0 – a p > a q
Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n -ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.
Согласно тому, что из себя представляет степень с дробным показателем, получим:
a m 1 n 1 = a m 1 n 1 и a m 2 n 2 = a m 2 n 2 , следовательно, a m 1 n 1 · a m 2 n 2 = a m 1 n 1 · a m 2 n 2
Свойства корня позволят нам вывести равенства:
a m 1 · m 2 n 1 · n 2 · a m 2 · m 1 n 2 · n 1 = a m 1 · n 2 · a m 2 · n 1 n 1 · n 2
Из этого получаем: a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2
Преобразуем:
a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2
Показатель степени можно записать в виде:
m 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 · n 2 n 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 n 1 + m 2 n 2
Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
a m 1 n 1: a m 2 n 2 = a m 1 n 1: a m 2 n 2 = a m 1 · n 2: a m 2 · n 1 n 1 · n 2 = = a m 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 · n 2 n 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 n 1 — m 2 n 2
Доказательства остальных равенств:
a · b m n = (a · b) m n = a m · b m n = a m n · b m n = a m n · b m n ; (a: b) m n = (a: b) m n = a m: b m n = = a m n: b m n = a m n: b m n ; a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = = a m 1 m 2 n 1 n 2 = a m 1 · m 2 n 1 n 2 = = a m 1 · m 2 n 2 · n 1 = a m 1 · m 2 n 2 · n 1 = a m 1 n 1 · m 2 n 2
Следующее свойство: докажем, что для любых значений a и b больше 0 , если а меньше b , будет выполняться a p b p
Представим рациональное число p как m n . При этом m –целое число, n –натуральное. Тогда условия p 0 будут распространяться на m 0 . При m > 0 и a
Используем свойство корней и выведем: a m n
Учитывая положительность значений a и b , перепишем неравенство как a m n
Таким же образом при m b m , получаем a m n > b m n значит, a m n > b m n и a p > b p .
Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q , p > q при 0 0 будет верно a p > a q .
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m 1 n и m 2 n
Здесь m 1 и m 2 – целые числа, а n – натуральное. Если p > q , то m 1 > m 2 (учитывая правило сравнения дробей). Тогда при 0 1 – неравенство a 1 m > a 2 m .
Их можно переписать в следующем виде:
a m 1 n a m 2 n
Тогда можно сделать преобразования и получить в итоге:
a m 1 n a m 2 n
Подводим итог: при p > q и 0 0 – a p > a q .
Основные свойства степеней с иррациональными показателями
На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a > 0 , b > 0 , показатели p и q – иррациональные числа):
Определение 4
1.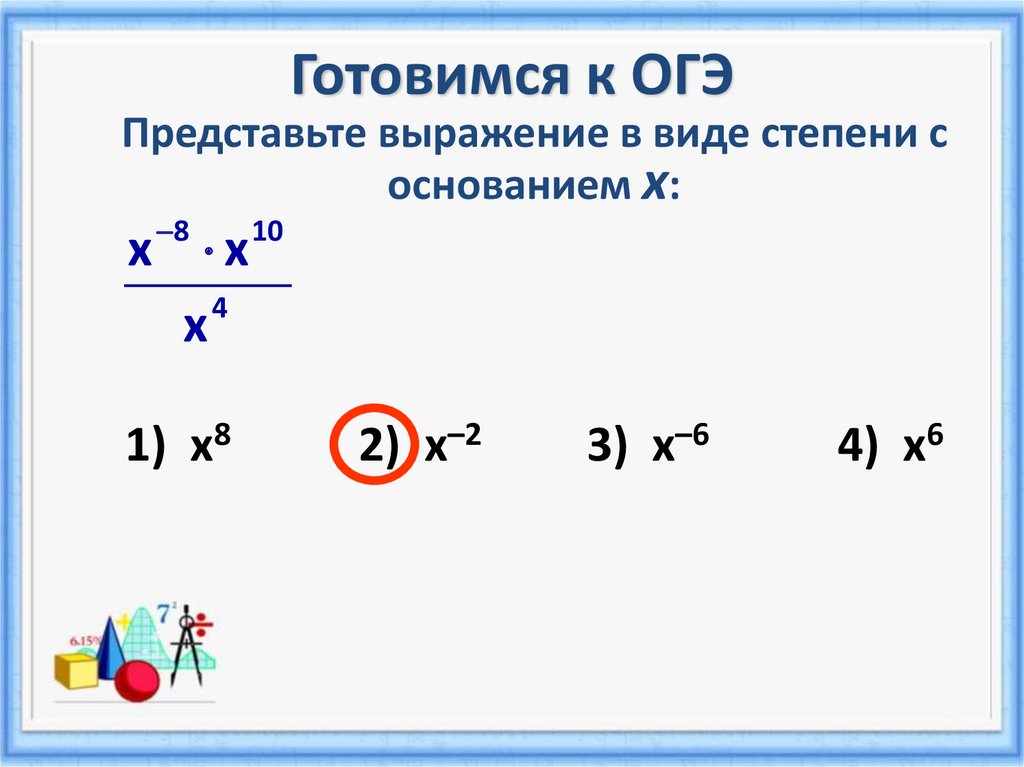 a p · a q = a p + q
a p · a q = a p + q
2. a p: a q = a p − q
3. (a · b) p = a p · b p
4. (a: b) p = a p: b p
5. (a p) q = a p · q
6. a p b p
7. a p 0 , то a p > a q .
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a > 0 обладают теми же свойствами.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел. 3$
3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15 - Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2 - Вычислить.
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.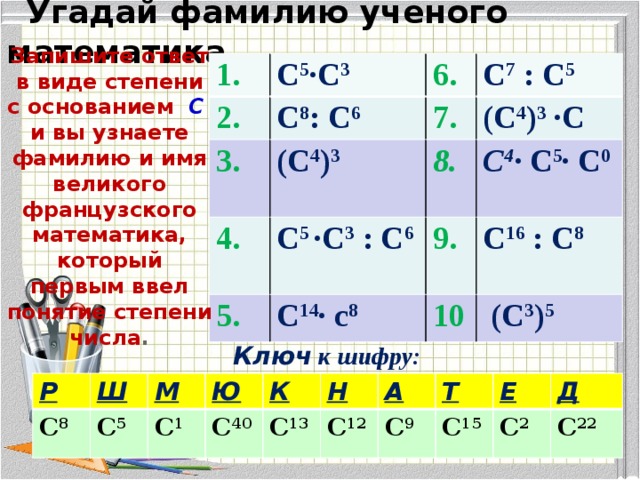
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Как умножать степени
Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?
В алгебре найти произведение степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать степени, на конкретных примерах.
Единицу в показателе степени не пишут, но при умножении степеней — учитывают:
При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:
Умножение степеней с одинаковыми основаниями
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы изучим умножение степеней с одинаковыми основаниями. Вначале вспомним определение степени и сформулируем теорему о справедливости равенства . Затем приведем примеры ее применения на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач.
Тема: Степень с натуральным показателем и ее свойства
Урок: Умножение степеней с одинаковыми основаниями (формула )
1.
 Основные определения
Основные определенияОсновные определения:
n — показатель степени,
— n -ая степень числа.
2. Формулировка теоремы 1
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
По-иному: если а – любое число; n и k натуральные числа, то:
Отсюда правило 1:
3. Разъясняющие задачи
Вывод: частные случаи подтвердили правильность теоремы №1. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
4. Доказательство теоремы 1
Дано число а – любое; числа n и k – натуральные. Доказать:
Доказательство основано на определении степени.
5. Решение примеров с помощью теоремы 1
Пример 1: Представьте в виде степени.
Для решения следующих примеров воспользуемся теоремой 1.
ж)
6. Обобщение теоремы 1
Здесь использовано обобщение:
7.
 Решение примеров с помощью обобщения теоремы 1
Решение примеров с помощью обобщения теоремы 18. Решение различных задач с помощью теоремы 1
Пример 2: Вычислите (можно использовать таблицу основных степеней).
а) (по таблице)
б)
Пример 3: Запишите в виде степени с основанием 2.
а)
Пример 4: Определите знак числа:
, а – отрицательное, так как показатель степени при -13 нечетный.
Пример 5: Замените (·) степенью числа с основанием r:
Имеем , то есть .
9. Подведение итогов
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
1. Школьный помощник (Источник).
1. Представьте в виде степени:
а) б) в) г) д)
3. Запишите в виде степени с основанием 2:
4. Определите знак числа:
а)
5. Замените (·) степенью числа с основанием r:
а) r 4 · (·) = r 15 ; б) (·) · r 5 = r 6
Умножение и деление степеней с одинаковыми показателями
На этом уроке мы изучим умножение степеней с одинаковыми показателями. Сначала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и возведении степень в степень. Затем сформулируем и докажем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью решим ряд типичных задач.
Сначала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и возведении степень в степень. Затем сформулируем и докажем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью решим ряд типичных задач.
Напоминание основных определений и теорем
Здесь a — основание степени,
— n -ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n иk справедливо равенство:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
Теорема 3. Для любого числа а и любых натуральных n иk справедливо равенство:
Все перечисленные теоремы были о степенях с одинаковыми основаниями , на этом уроке будут рассмотрены степени с одинаковыми показателями .
Примеры на умножение степеней с одинаковыми показателями
Рассмотрим следующие примеры:
Распишем выражения по определению степени.
Вывод: из примеров можно заметить, что , но это еще нужно доказать. Сформулируем теорему и докажем ее в общем случае, то есть для любых а и b и любого натурального n.
Формулировка и доказательство теоремы 4
Для любых чисел а и b и любого натурального n справедливо равенство:
Доказательство теоремы 4.
По определению степени:
Итак, мы доказали, что .
Чтобы перемножить степени с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить неизменным.
Формулировка и доказательство теоремы 5
Сформулируем теорему для деления степеней с одинаковыми показателями.
Для любого числа а и b () и любого натурального n справедливо равенство:
Доказательство теоремы 5.
Распишем и по определению степени:
Формулировка теорем словами
Итак, мы доказали, что .
Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.
Решение типичных задач с помощью теоремы 4
Пример 1: Представить в виде произведения степеней.
Для решения следующих примеров воспользуемся теоремой 4.
Для решения следующего примера вспомним формулы:
Обобщение теоремы 4
Обобщение теоремы 4:
Решение примеров с помощью обобщенной теоремы 4
Продолжение решения типичных задач
Пример 2: Запишите в виде степени произведения.
Пример 3: Запишите в виде степени с показателем 2.
Примеры на вычисление
Пример 4: Вычислить самым рациональным способом.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю. М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
2. Школьный помощник (Источник).
1. Представить в виде произведения степеней:
а) ; б) ; в) ; г) ;
2. Запишите в виде степени произведения:
3. Запишите в виде степени с показателем 2:
4. Вычислить самым рациональным способом.
Урок математики по теме «Умножение и деление степеней»
Разделы: Математика
Педагогическая цель :
Задачи :

Деятельностные единицы учения: определение степени с натуральным показателем; компоненты степени; определение частного; сочетательный закон умножения.
I. Организация демонстрации овладение учащимися имеющимися знаниями. (шаг 1)а) Актуализация знаний:
2) Сформулировать определение степени с натуральным показателем.
a n =a a a a … а (n раз)
b k =b b b b a… b (k раз) Обосновать ответ.
II. Организация самооценивания обучаемого степенью владения актуальным опытом. (шаг 2)Тест для самопроверки: (индивидуальная работа в двух вариантах.)
А1) Представьте произведение 7 7 7 7 x x x в виде степени:
А2) Представить в виде произведения степень (-3) 3 х 2
A3) Вычислите: -2 3 2 + 4 5 3
Количество заданий в тесте я подбираю в соответствии с подготовкой уровня класса.
К тесту даю ключ для самопроверки. Критерии: зачёт – не зачёт.
III. Учебно-практическая задача (шаг 3) + шаг 4. (сформулируют свойства сами ученики)
(сформулируют свойства сами ученики) В ходе решения задачи 1) и 2) учащиеся предлагают решение, а я, как учитель, организую класс на нахождение способа для упрощения степеней при умножении с одинаковыми основаниями.
Учитель: придумать способ для упрощения степеней при умножении с одинаковыми основаниями.
На кластере появляется запись:
Формулируется тема урока. Умножение степеней.
Учитель: придумайте правило деления степеней с одинаковыми основаниями.
Рассуждения: каким действием проверяется деление? а 5: а 3 = ? что а 2 а 3 = а 5
Возвращаюсь к схеме – кластер и дополняем запись – ..при делении вычитаем и дописываем тему урока. …и деление степеней.
IV. Сообщение учащимся пределов познания (как минимум и как максимум).
Учитель: задачей минимума на сегодняшний урок является научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимума: применять умножение и деление совместно.
На доске записываем: а m а n = а m+n ; а m: а n = а m-n
V. Организация изучения нового материала. (шаг 5)а) По учебнику: №403 (а, в, д) задания с разными формулировками
№404 (а, д, е) самостоятельная работа, затем организую взаимопроверку, даю ключи.
б) При каком значении m справедливо равенство? а 16 а m = а 32 ; х h х 14 = х 28 ; х 8 (*) = х 14
Задание: придумать аналогичные примеры для деления.
в) № 417(а), №418 (а) Ловушки для учеников : х 3 х n = х 3n ; 3 4 3 2 = 9 6 ; а 16: а 8 = а 2 .
VI. Обобщение изученного, проведение диагностической работы (что побуждает учеников, а не учителя изучать данную тему)(шаг 6)
Диагностическая работа.
Тест (ключи поместить на обратной стороне теста).
Варианты заданий: представьте в виде степени частное х 15: х 3 ; представьте в виде степени произведение (-4) 2 (-4) 5 (-4) 7 ; при каком m справедливо равенство а 16 а m = а 32 ; найдите значение выражения h 0: h 2 при h =0,2; вычислите значение выражения (5 2 5 0) : 5 2 .
Итог урока. Рефлексия. Делю класс на две группы.
Найдите аргументы I группа: в пользу знания свойств степени, а II группа – аргументы, которые будут говорить о том, что можно обойтись без свойств. Все ответы выслушиваем, делаем выводы. На последующих уроках можно предложить статистические данные и назвать рубрику «В голове не укладывается!»
Историческая справка. Какие числа называют числами Ферма.
П.19. №403, №408, №417
Используемая литература:
 Н. Макарычев, Н.Г. Миндюк и др.
Н. Макарычев, Н.Г. Миндюк и др.Свойства степеней, формулировки, доказательства, примеры.
После того как определена степень числа, логично поговорить про свойства степени . В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров.
Навигация по странице.
Свойства степеней с натуральными показателями
По определению степени с натуральным показателем степень a n представляет собой произведение n множителей, каждый из которых равен a . Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел , можно получить и обосновать следующие свойства степени с натуральным показателем :
- если a>0 , то a n >0 для любого натурального n ;
- если a=0 , то a n =0 ;
- если a 2·m >0 , если a 2·m−1 n ;
- если m и n такие натуральные числа, что m>n , то при 0m n , а при a>0 справедливо неравенство a m >a n .

- a m ·a n =a m+n ;
- a m:a n =a m−n ;
- (a·b) n =a n ·b n ;
- (a:b) n =a n:b n ;
- (a m) n =a m·n ;
- если n – целое положительное число, a и b – положительные числа, причем an n и a −n >b −n ;
- если m и n – целые числа, причем m>n , то при 0m n , а при a>1 выполняется неравенство a m >a n .
Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби a m ·a n =a m+n при упрощении выражений часто применяется в виде a m+n =a m ·a n .
Теперь рассмотрим каждое из них подробно.
Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называют основным свойством степени : для любого действительного числа a и любых натуральных чисел m и n справедливо равенство a m ·a n =a m+n .
Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a m ·a n можно записать как произведение . В силу свойств умножения полученное выражение можно записать как , а это произведение есть степень числа a с натуральным показателем m+n , то есть, a m+n . На этом доказательство завершено.
Приведем пример, подтверждающий основное свойство степени. Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3 , по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 ·2 3 =(2·2)·(2·2·2)=4·8=32 и 2 5 =2·2·2·2·2=32 , так как получаются равные значения, то равенство 2 2 ·2 3 =2 5 — верное, и оно подтверждает основное свойство степени.
Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3 , по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 ·2 3 =(2·2)·(2·2·2)=4·8=32 и 2 5 =2·2·2·2·2=32 , так как получаются равные значения, то равенство 2 2 ·2 3 =2 5 — верное, и оно подтверждает основное свойство степени.
Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями. Так для любого количества k натуральных чисел n 1 , n 2 , …, n k справедливо равенство a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k .
Например, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .
Можно переходить к следующему свойству степеней с натуральным показателем – свойству частного степеней с одинаковыми основаниями : для любого отличного от нуля действительного числа a и произвольных натуральных чисел m и n , удовлетворяющих условию m>n , справедливо равенство a m:a n =a m−n .
Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0 n =0 , а при знакомстве с делением мы условились, что на нуль делить нельзя. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n), либо отрицательным числом (что происходит при m m−n ·a n =a (m−n)+n =a m . Из полученного равенства a m−n ·a n =a m и из связи умножения с делением следует, что a m−n является частным степеней a m и a n . Этим доказано свойство частного степеней с одинаковыми основаниями.
Приведем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2 , рассмотренному свойству степени отвечает равенство π 5:π 2 =π 5−3 =π 3 .
Теперь рассмотрим свойство степени произведения : натуральная степень n произведения двух любых действительных чисел a и b равна произведению степеней a n и b n , то есть, (a·b) n =a n ·b n .
Действительно, по определению степени с натуральным показателем имеем . Последнее произведение на основании свойств умножения можно переписать как , что равно a n ·b n .
Приведем пример: .
Данное свойство распространяется на степень произведения трех и большего количества множителей. То есть, свойство натуральной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .
Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .
Следующее свойство представляет собой свойство частного в натуральной степени : частное действительных чисел a и b , b≠0 в натуральной степени n равно частному степеней a n и b n , то есть, (a:b) n =a n:b n .
Доказательство можно провести, используя предыдущее свойство. Так (a:b) n ·b n =((a:b)·b) n =a n , а из равенства (a:b) n ·b n =a n следует, что (a:b) n является частным от деления a n на b n .
Запишем это свойство на примере конкретных чисел: .
Теперь озвучим свойство возведения степени в степень : для любого действительного числа a и любых натуральных чисел m и n степень a m в степени n равна степени числа a с показателем m·n , то есть, (a m) n =a m·n .
Например, (5 2) 3 =5 2·3 =5 6 .
Доказательством свойства степени в степени является следующая цепочка равенств: .
Рассмотренное свойство можно распространить на степень в степени в степени и т.д. Например, для любых натуральных чисел p , q , r и s справедливо равенство . Для большей ясности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .
Осталось остановиться на свойствах сравнения степеней с натуральным показателем.
Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.
Для начала обоснуем, что a n >0 при любом a>0 .
Произведение двух положительных чисел является положительным числом, что следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
Достаточно очевидно, что для любого натурального n при a=0 степень a n есть нуль. Действительно, 0 n =0·0·…·0=0 . К примеру, 0 3 =0 и 0 762 =0 .
Переходим к отрицательным основаниям степени.
Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m , где m — натуральное. Тогда . По правилу умножения отрицательных чисел каждое из произведений вида a·a равно произведению модулей чисел a и a , значит, является положительным числом. Следовательно, положительным будет и произведение и степень a 2·m . Приведем примеры: (−6) 4 >0 , (−2,2) 12 >0 и .
Наконец, когда основание степени a является отрицательным числом, а показатель степени есть нечетное число 2·m−1 , то . Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 17 n n представляет собой произведение левых и правых частей n верных неравенств aсвойств неравенств справедливо и доказываемое неравенство вида a n n . Например, в силу этого свойства справедливы неравенства 3 7 7 и .
Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 17 n n представляет собой произведение левых и правых частей n верных неравенств aсвойств неравенств справедливо и доказываемое неравенство вида a n n . Например, в силу этого свойства справедливы неравенства 3 7 7 и .
Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем его. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями, меньшими единицы, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше. Переходим к доказательству этого свойства.
Докажем, что при m>n и 0m n . Для этого запишем разность a m −a n и сравним ее с нулем. Записанная разность после вынесения a n за скобки примет вид a n ·(a m−n −1) . Полученное произведение отрицательно как произведение положительного числа a n и отрицательного числа a m−n −1 (a n положительна как натуральная степень положительного числа, а разность a m−n −1 отрицательна, так как m−n>0 в силу исходного условия m>n , откуда следует, что при 0m−n меньше единицы). Следовательно, a m −a n m n , что и требовалось доказать. Для примера приведем верное неравенство .
Полученное произведение отрицательно как произведение положительного числа a n и отрицательного числа a m−n −1 (a n положительна как натуральная степень положительного числа, а разность a m−n −1 отрицательна, так как m−n>0 в силу исходного условия m>n , откуда следует, что при 0m−n меньше единицы). Следовательно, a m −a n m n , что и требовалось доказать. Для примера приведем верное неравенство .
Осталось доказать вторую часть свойства. Докажем, что при m>n и a>1 справедливо a m >a n . Разность a m −a n после вынесения a n за скобки принимает вид a n ·(a m−n −1) . Это произведение положительно, так как при a>1 степень a n есть положительное число, и разность a m−n −1 есть положительное число, так как m−n>0 в силу начального условия, и при a>1 степень a m−n больше единицы. Следовательно, a m −a n >0 и a m >a n , что и требовалось доказать. Иллюстрацией этого свойства служит неравенство 3 7 >3 2 .
Свойства степеней с целыми показателями
Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.
Степень с целым отрицательным показателем, а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.
Итак, для любых действительных и отличных от нуля чисел a и b , а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями :
При a=0 степени a m и a n имеют смысл лишь когда и m , и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.
Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.
Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (a p) q =a p·q , (a −p) q =a (−p)·q , (a p) −q =a p·(−q) и (a −p) −q =a (−p)·(−q) . Сделаем это.
Для положительных p и q равенство (a p) q =a p·q доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0·q =a 0 =1 , откуда (a 0) q =a 0·q . Аналогично, если q=0 , то (a p) 0 =1 и a p·0 =a 0 =1 , откуда (a p) 0 =a p·0 . Если же и p=0 и q=0 , то (a 0) 0 =1 0 =1 и a 0·0 =a 0 =1 , откуда (a 0) 0 =a 0·0 .
Теперь докажем, что (a −p) q =a (−p)·q . По определению степени с целым отрицательным показателем , тогда . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению является степенью вида a −(p·q) , которую в силу правил умножения можно записать как a (−p)·q .
Аналогично .
И .
По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.
В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a −n >b −n , которое справедливо для любого целого отрицательного −n и любых положительных a и b , для которых выполняется условие a. Запишем и преобразуем разность левой и правой частей этого неравенства: . Так как по условию an n , следовательно, b n −a n >0 . Произведение a n ·b n тоже положительно как произведение положительных чисел a n и b n . Тогда полученная дробь положительна как частное положительных чисел b n −a n и a n ·b n . Следовательно, откуда a −n >b −n , что и требовалось доказать.
Следовательно, откуда a −n >b −n , что и требовалось доказать.
Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.
Свойства степеней с рациональными показателями
Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:
- свойство произведения степеней с одинаковыми основаниями при a>0 , а если и , то при a≥0 ;
- свойство частного степеней с одинаковыми основаниями при a>0 ;
- свойство произведения в дробной степени при a>0 и b>0 , а если и , то при a≥0 и (или) b≥0 ;
- свойство частного в дробной степени при a>0 и b>0 , а если , то при a≥0 и b>0 ;
- свойство степени в степени при a>0 , а если и , то при a≥0 ;
- свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b , a0 справедливо неравенство a p p , а при p p >b p ;
- свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q .

- a p ·a q =a p+q ;
- a p:a q =a p−q ;
- (a·b) p =a p ·b p ;
- (a:b) p =a p:b p ;
- (a p) q =a p·q ;
- для любых положительных чисел a и b , a0 справедливо неравенство a p p , а при p p >b p ;
- для иррациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q .
Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем доказательства.
По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено.
Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:
По схожим принципам доказываются и остальные равенства:
Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b , a0 справедливо неравенство a p p , а при p p >b p . Запишем рациональное число p как m/n , где m – целое число, а n – натуральное. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При m>0 и am m . Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, a p p .
Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При m>0 и am m . Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, a p p .
Аналогично, при m m >b m , откуда , то есть, и a p >b p .
Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q . Мы всегда можем привести к общему знаменателю рациональные числа p и q , пусть при этом мы получим обыкновенные дроби и , где m 1 и m 2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m 1 >m 2 , что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0m 1 m 2 , а при a>1 – неравенство a m 1 >a m 2 . Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 – неравенство a p >a q .
Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 – неравенство a p >a q .
Свойства степеней с иррациональными показателями
Из того, как определяется степень с иррациональным показателем, можно заключить, что она обладает всеми свойствами степеней с рациональными показателями. Так для любых a>0 , b>0 и иррациональных чисел p и q справедливы следующие свойства степеней с иррациональными показателями :
Отсюда можно сделать вывод, что степени с любыми действительными показателями p и q при a>0 обладают этими же свойствами.
- Алгебра – 10 класс. Тригонометрические уравнения Урок и презентация на тему: «Решение простейших тригонометрических уравнений» Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы […]
- Открыт конкурс на позицию «ПРОДАВЕЦ — КОНСУЛЬТАНТ»: Обязанности: продажа мобильных телефонов и аксессуаров для мобильной связи сервисное обслуживание абонентов Билайн, Теле2, МТС подключение тарифных планов и услуг Билайн и Теле2, МТС консультирование […]
- Параллелепипед формулы Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом. Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником. Любой параллелепипед характеризуется 3 […]
- Общество защиты прав потребителя астана Для того, что бы получить pin-код для доступа к данному документу на нашем сайте, отправьте sms-сообщение с текстом zan на номер Абоненты GSM-операторов (Activ, Kcell, Beeline, NEO, Tele2) отправив SMS на номер, […]
- ПРАВОПИСАНИЕ Н И НН В РАЗНЫХ ЧАСТЯХ РЕЧИ
С.
 Г.ЗЕЛИНСКАЯ
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
Теоретическая зарядка
1. Когда в прилагательных пишется нн? 2. Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […]
Г.ЗЕЛИНСКАЯ
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
Теоретическая зарядка
1. Когда в прилагательных пишется нн? 2. Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […] - Принять закон о Родовых поместьях Принять федеральный закон о безвозмездном выделении каждому желающему гражданину Российской Федерации или семье граждан участка земли для обустройства на нем Родового Поместья на следующих условиях: 1. Участок выделяется для […]
- ИНСПЕКЦИЯ ГОСТЕХНАДЗОРА БРЯНСКОЙ ОБЛАСТИ Квитанция об оплате госпошлины(Скачать-12,2 kb) Заявления на регистрацию для физ.лиц(Скачать-12 kb) Заявления на регистрацию для юр.лиц(Скачать-11,4 kb) 1. При регистрации новой машины: 1.заявление 2.паспорт […]
- Давненько мы не играли турниров 1х1. И пора бы наверное возобновить эту традицию. Пока мы не можем организовать отдельный ладдер и турниры для 1х1 игроков, предлагаем использовать ваши командные профайлы на сайте. Очки за игры в матчах снимать или добавлять […]
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби. 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Как вычитать числа с одинаковыми степенями. Умножение и деление чисел со степенями
Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?
В алгебре найти произведение степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать степени, на конкретных примерах.
Единицу в показателе степени не пишут, но при умножении степеней — учитывают:
При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:
www.algebraclass.ru
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби. 3$
3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
Правила умножения степеней с разным основанием
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,
СТЕПЕННАЯ ФУНКЦИЯ IV
§ 69. Умножение и деление степеней с одинаковыми основаниями
Теорема 1. Чтобы перемножить степени с одинаковыми основаниями, достаточно показатели степеней сложить, а основание оставить прежним , то есть
Доказательство. По определению степени
По определению степени
2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.
Мы рассмотрели произведение двух степеней. На самом же деле доказанное свойство верно для любого числа степеней с одинаковыми основаниями.
Теорема 2. Чтобы разделить степени с одинаковыми основаниями, когда показатель делимого больше показателя делителя, достаточно из показателя делимого вычесть показатель делителя, а основание оставить прежним, то есть при т > п
(a =/= 0)
Доказательство. Напомним, что частным от деления одного числа на другое называется число, которое при умножении на делитель дает делимое. Поэтому доказать формулу , где a =/= 0, это все равно, что доказать формулу
Если т > п , то число т — п будет натуральным; следовательно, по теореме 1
Теорема 2 доказана.
Следует обратить внимание на то, что формула
доказана нами лишь в предположении, что т > п . Поэтому из доказанного пока нельзя делать, например, таких выводов:
Поэтому из доказанного пока нельзя делать, например, таких выводов:
К тому же степени с отрицательными показателями нами еще не рассматривались и мы пока что не знаем, какой смысл можно придать выражению 3 — 2 .
Теорема 3. Чтобы возвести степень в степень, достаточно перемножить показатели, оставив основание степени прежним , то есть
Доказательство. Используя определение степени и теорему 1 этого параграфа, получаем:
что и требовалось доказать.
Например, (2 3) 2 = 2 6 = 64;
518 (Устно.) Определить х из уравнений:
1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;
2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .
519. (У с т н о.) Упростить:
520. (У с т н о.) Упростить:
521. Данные выражения представить в виде степеней с одинаковыми основаниями:
1) 32 и 64; 3) 8 5 и 16 3 ; 5) 4 100 и 32 50 ;
2) -1000 и 100; 4) -27 и -243; 6) 81 75 8 200 и 3 600 4 150 .
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Онлайн-калькулятор возведения в степень
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.
Математически это выглядит следующим образом:
a n = a * a * a * …a n .
Например:
- 2 3 = 2 в третьей степ. = 2 * 2 * 2 = 8;
- 4 2 = 4 в степ. два = 4 * 4 = 16;
- 5 4 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
- 10 5 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000;
- 10 4 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- a n * a m = (a) (n+m) ;
- a n: a m = (a) (n-m) ;
- (a b) m =(a) (b*m) .
Проверим на примерах:
2 3 * 2 2 = 8 * 4 = 32. С другой стороны 2 5 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично: 2 3: 2 2 = 8 / 4 =2. Иначе 2 3-2 = 2 1 =2.
(2 3) 2 = 8 2 = 64. А если по-другому? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.
А как же быть со сложением и вычитанием ? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
- 3 3 + 2 4 = 27 + 16 = 43;
- 5 2 – 3 2 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3) 2 = 2 2 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3) 3 = 8 3 = 512.
Как производить вычисления в более сложных случаях ? Порядок тот же:
- при наличии скобок – начинать нужно с них;
- затем возведение в степень;
- потом выполнять действия умножения, деления;
- после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:
- Корень n-ой степени из числа a в степени m запишется в виде: a m / n .
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b) n = a n * b n .
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?
Исходя из свойств 4 и 5 (смотри пункт выше), получается :
A (- n) = 1 / A n , 5 (-2) = 1 / 5 2 = 1 / 25.
И наоборот:
1 / A (- n) = A n , 1 / 2 (-3) = 2 3 = 8.
А если дробь?
(A / B) (- n) = (B / A) n , (3 / 5) (-2) = (5 / 3) 2 = 25 / 9.
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1…и т. д.
A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3…и т. д.
Кроме того, если (-a) 2 n +2 , n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.
Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: A m / n . Читается как: корень n-ой степени из числа A в степени m.
С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
- А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;
А r 1 ˂ А α ˂ А r 2 , r 1 ˂ r 2 – рациональные числа;
- 0˂А˂1.
В этом случае наоборот: А r 2 ˂ А α ˂ А r 1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
r 1 – в этом случае равно 3;
r 2 – будет равно 4.
Тогда, при А = 1, 1 π = 1.
А = 2, то 2 3 ˂ 2 π ˂ 2 4 , 8 ˂ 2 π ˂ 16.
А = 1/2, то (½) 4 ˂ (½) π ˂ (½) 3 , 1/16 ˂ (½) π ˂ 1/8.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 . a 3 = aa.aaa = aaaaa = a 5 .
a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов. 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Содержание урока
Что такое степень?
Степенью называют произведение из нескольких одинаковых множителей. Например:
2 × 2 × 2
Значение данного выражения равно 8
2 × 2 × 2 = 8
Левую часть этого равенстваможно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
2 3 = 8
Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 5 3 , то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5 .
Число, которое повторяется называют основанием степени . В выражении 5 3 основанием степени является число 5 .
А число, которое надписано над числом 5 называют показателем степени . В выражении 5 3 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
Саму операцию перемножения одинаковых множителей называют возведением в степень .
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень :
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем . Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида a n , которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
Это произведение равно 25
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
Получилась ошибка, поскольку число 5 во второй степени не равно 10.
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 0 0 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 0 0 может иметь смысл.
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1.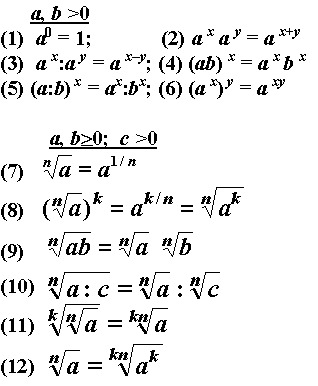 Возвести число 3 во вторую степень.
Возвести число 3 во вторую степень.
Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
3 2 = 3 × 3 = 9
Пример 2. Возвести число 2 в четвертую степень.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
2 4 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
2 3 =2 × 2 × 2 = 8
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
10 2
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
10 2 = 100
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
10 2 = 10 × 10 = 100
Пример 2 . Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
10 3 = 1000
Пример 3 . Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
10 4 = 10000
Пример 4 . Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
10 1 = 10
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 10 1
10 = 10 1
Пример 2 . Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 10 2
Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 10 2
100 = 10 2
Пример 3 . Представим число 1 000 в виде степени с основанием 10.
1 000 = 10 3
Пример 4 . Представим число 10 000 в виде степени с основанием 10.
10 000 = 10 4
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
(−2) 2 = (−2) × (−2) = 4
Если бы мы не заключили в скобки число −2 , то получилось бы что мы вычисляем выражение −2 2 , которое не равно 4 . Выражение −2² будет равно −4 . Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения .
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −2 2 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −2 2 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
−2 2 = −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2) 2
сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Поэтому в случае вычисления выражения (−2) 2
сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Пример 2 . Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2) 3 = (−2) × (−2) × (−2) = −8
Пример 3 . Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2) 4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3
Покажем это на примере числа −3
В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным .
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным .
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5) 3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4) 4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений
При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.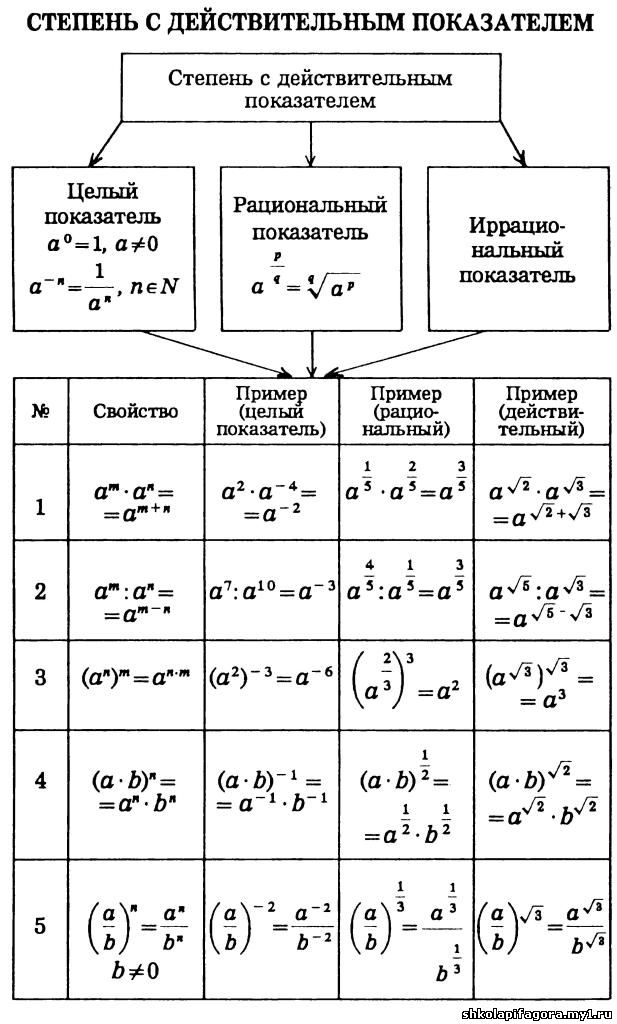
Пример 1 . Найти значение выражения 2 + 5 2
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 5 2 = 2 + 25 = 27
Пример 10 . Найти значение выражения −6 2 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−6 2 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−6 2 × (−12) = −36 × (−12) = 432
Пример 11 . Найти значение выражения −3 × 2 2
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 2 2 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.
Пример 12 . Найти значение выражения (3 2 + 1 × 3) − 15 + 5
Найти значение выражения (3 2 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3 , затем складываем результаты возведения в степень числа 3 и умножения 1 × 3 . Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
(3 2 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13 . Найти значение выражения 2 × 5 3 + 5 × 2 3
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 5 3 + 5 × 2 3 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (2 3) 2
. В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(2 3) 2 это произведение двух степеней, каждая из которых равна 2 3
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
Получили произведение 2 × 2 × 2 × 2 × 2 × 2 , которое равно 64. Значит значение выражения (2 3) 2 или равно 64
Этот пример можно значительно упростить. Для этого показатели выражения (2 3) 2 можно перемножить и записать это произведение над основанием 2
Получили 2 6 . Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
Данное свойство работает по причине того, что 2 3 это произведение 2 × 2 × 2 , которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 2 6
Вообще, для любого основания a с показателями m и n , выполняется следующее равенство:
(a n ) m = a n × m
Это тождественное преобразование называют возведением степени в степень . Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают» .
Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают» .
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2 . Найти значение выражения (3 2) 2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:
Получили 3 4 . А число 3 в четвёртой степени есть 81
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 2 2 на 3 3 .
2 2 это число 4 , а 3 3 это число 27 . Перемножаем числа 4 и 27 , получаем 108
2 2 × 3 3 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 2 2 на 2 3
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 2 2 и 2 3 . Иными словами, о снование оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 2 5 . Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 2 2 это произведение 2 × 2 , а 2 3 это произведение 2 × 2 × 2 . Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2 . Это произведение представимо в виде 2 5
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени . Его можно прочитать так: «П ри перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают» .
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 2 1 × 2 2 × 2 3 . Основание 2
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1 . Представить в виде степени выражение 5 8 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 5 8 × 25 получилась одна степень.
Число 25 можно представить в виде 5 2 . Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Запишем решение покороче:
Пример 2 . Представить в виде степени выражение 2 9 × 32
Число 32 можно представить в виде 2 5 . Тогда получим выражение 2 9 × 2 5 . Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3 . Вычислите произведение 3 × 3
, используя основное свойство степени.
Вычислите произведение 3 × 3
, используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 3 1 и 3 1
3 1 × 3 1
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
3 1 × 3 1 = 3 2 = 9
Пример 4 . Вычислите произведение 2 × 2 × 3 2 × 3 3 , используя основное свойство степени.
Произведение 2 × 2 заменим на 2 1 × 2 1 , затем на 2 1 + 1 , а затем на 2 2 . Произведение 3 2 × 3 3 заменим на 3 2 + 3 , а затем на 3 5
Пример 5 . Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6 . Выполнить умножение x 2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 7 . Выполнить умножение y 3 y 2 y
Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 8 . Выполнить умножение aa 3 a 2 a 5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 9 . Представить степень 3 8
в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3 , и сумма показателей которых будет равна 8 . Можно использовать любые показатели. Представим степень 3 8 в виде произведения степеней 3 5 и 3 3
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 3 5 × 3 3 можно записать как 3 5 + 3 , откуда 3 8 .
Конечно можно было представить степень 3 8 в виде произведения других степеней. Например, в виде 3 7 × 3 1 , поскольку это произведение тоже равно 3 8
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10 . Представить степень x 12 в виде различных произведений степеней с основаниями x .
Воспользуемся основным свойство степени. Представим x 12 в виде произведений с основаниями x , и сумма показателей которых равна 12
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3 . Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
2 × 3 × 2 × 3
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
2 × 2 × 3 × 3
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2
можно заменить на 2 2
, а произведение 3 × 3
можно заменить на 3 2 .
Тогда выражение 2 × 2 × 3 × 3
обращается в выражение 2 2 × 3 2 .
Произведение 2 × 2
можно заменить на 2 2
, а произведение 3 × 3
можно заменить на 3 2 .
Тогда выражение 2 × 2 × 3 × 3
обращается в выражение 2 2 × 3 2 .
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n , нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Пример 2 . Найти значение выражения (2 × 3 × 4) 2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4 . Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
Пример 3 . Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Пример 4 . Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
(3xyz ) 3
Возведём в третью степень каждый множитель данного произведения:
(3xyz ) 3 = 3 3 x 3 y 3 z 3
Число 3
в третьей степени равно числу 27
.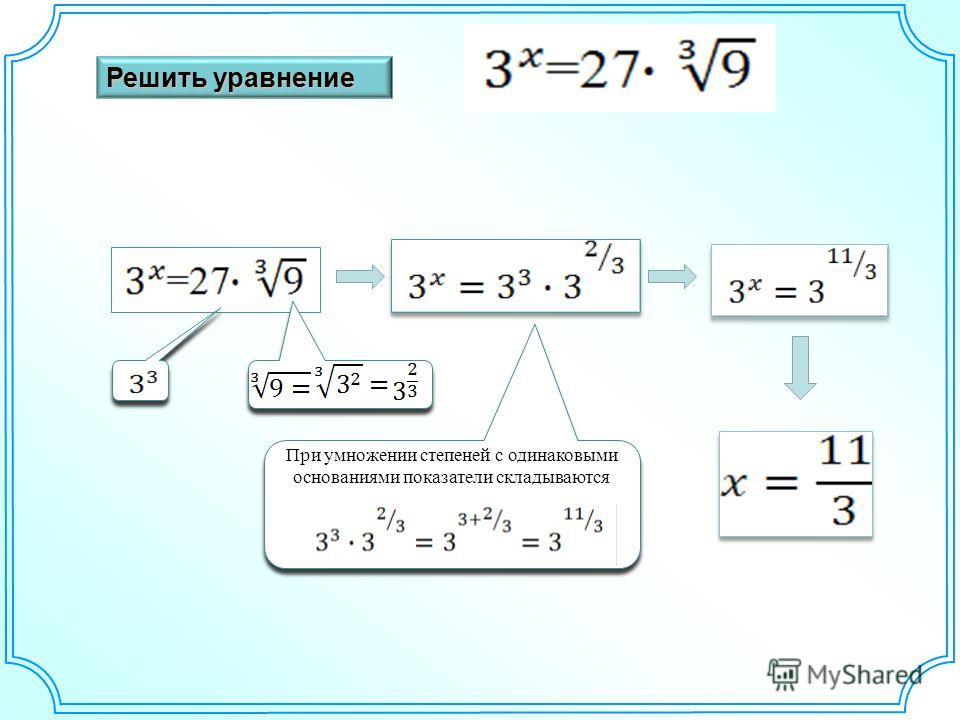 Остальное оставим без изменений:
Остальное оставим без изменений:
(3xyz ) 3 = 3 3 x 3 y 3 z 3 = 27x 3 y 3 z 3
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 5 2 × 3 2 . Возведем каждое число во вторую степень и перемножим полученные результаты:
5 2 × 3 2 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3) 2 . Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
5 2 × 3 2 = (5 × 3) 2 = (15) 2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b ) n = a n × b n , то a n × b n = (a × b) n . То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
(a n ) m = a n × m
К примеру, выражение (2 3) 2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(2 3) 2 = 2 3 × 2 = 2 6
(2 3) 2 = 2 3 × 2 = 2 6 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (2 3) 2 . Выражение в скобках 2 3 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (2 3) 2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2 .
(2 × 2 × 2) 2
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6
Как и раньше получили 2 6 . Значение этой степени равно 64
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (2 2 × 3 2) 3 . Здесь показатели каждого множителя нужно умножить на общий показатель 3 . Далее найти значение каждой степени и вычислить произведение:
(2 2 × 3 2) 3 = 2 2×3 × 3 2×3 = 2 6 × 3 6 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4
изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 2 1 × 4 1
. А это есть возведение степени в степень.
Получается, что множители произведения 2 × 4
изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 2 1 × 4 1
. А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
Пример 2 . Найти значение выражения (3 3) 2
Основание оставляем без изменений, а показатели перемножаем:
Получили 3 6 . Число 3 в шестой степени есть число 729
Пример 3 xy )³
Пример 4 . Выполнить возведение в степень в выражении (abc )⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5 ax ) 3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Пример 6 . Выполнить возведение в степень в выражении (10xy ) 2
Пример 7 . Выполнить возведение в степень в выражении (−5x ) 3
Пример 8 . Выполнить возведение в степень в выражении (−3y ) 4
Выполнить возведение в степень в выражении (−3y ) 4
Пример 9 . Выполнить возведение в степень в выражении (−2abx )⁴
Пример 10 . Упростите выражение x 5 × (x 2) 3
Степень x 5 пока оставим без изменений, а в выражении (x 2) 3 выполним возведение степени в степени:
x 5 × (x 2) 3 = x 5 × x 2 × 3 = x 5 × x 6
Теперь выполним умножение x 5 × x 6 . Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
x 5 × (x 2) 3 = x 5 × x 2× 3 = x 5 × x 6 = x 5 + 6 = x 11
Пример 9 . Найти значение выражения 4 3 × 2 2 , используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 4 3 . Основание у этой степени есть число 4, которое можно представить в виде 2 2 . Тогда исходное выражение примет вид (2 2) 3 × 2 2 . Выполнив возведение степени в степень в выражении (2 2) 3 , мы получим 2 6 . Тогда исходное выражение примет вид 2 6 × 2 2 , вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 4 3 на 2 2 .
Вычислим 4 3 , получим 64 . Вычислим 2 2 , получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 2 3: 2 2
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 2 3: 2 2
равно 2
.
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 2 3: 2 2 . Здесь делимое это 2 3 , а делитель 2 2 .
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 2 3 на 2 2 означает найти такую степень, которая при умножении на делитель 2 2 даст в результате 2 3 . А какую степень можно умножить на 2 2 , чтобы получить 2 3 ? Очевидно, что только степень 2 1 . Из основного свойства степени имеем:
Убедиться, что значение выражения 2 3: 2 2 равно 2 1 можно непосредственно вычислив само выражение 2 3: 2 2 . Для этого сначала найдём значение степени 2 3 , получим 8 . Затем найдём значение степени 2 2 , получим 4 . Разделим 8 на 4, получим 2 или 2 1 , поскольку 2 = 2 1 .
2 3: 2 2 = 8: 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
В этом случае в ответе получится единица.
Например, найдём значение выражения 2 2: 2 2 . Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 2 2: 2 2 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 2 2 и 2 2 равна нулю:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 2 2: 2 2 обычным методом, не используя правило деления степеней, получится единица.
Пример 2 . Найти значение выражения 4 12: 4 10
4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
4 12: 4 10 = 4 12 − 10 = 4 2 = 16
Пример 3 . Представить частное x 3: x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
Показатель делителя равен единице. Для наглядности запишем его:
Пример 4 . Представить частное x 3: x 2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x 3 можно записать как x × x × x , а степень x 2 как x × x . Тогда конструкцию x 3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x . В результате останется один множитель x
Или ещё короче:
Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x 2 . Чтобы сократить дробь на x 2 нужно числитель и знаменатель дроби разделить на x 2
Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Приведённое сокращение можно выполнить короче:
Или ещё короче:
Пример 5 . Выполнить деление x 12 : x 3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x 12 : x 3 запишем в виде . Далее сократим данную дробь на x 3 .
Пример 6 . Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Завершаем пример, вычислив степень 7 2
Пример 7 . Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (2 3) 4
Теперь выполним в числителе умножение степеней с одинаковыми основаниями.
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
Запомните!
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где «a » — любое число, а «m », «n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Важно!
Обратите внимание, что в указанном свойстве речь шла только об умножении
степеней с одинаковыми основаниями . Оно не относится к их сложению.
Оно не относится к их сложению.
Нельзя
заменять сумму
(3 3 + 3 2)
на 3 5
. Это понятно, если
посчитать
(3 3 + 3 2) = (27 + 9) = 36
, а
3 5 = 243
Свойство № 2
Частное степеней
Запомните!
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
= 11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
3 8: t = 3 4
T = 3 8 − 4
Ответ: t = 3 4 = 81Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5 - Пример. Найти значение выражения, используя свойства степени.
= = =
=2 9 + 2 2 5
= 2 11 − 5 = 2 6 = 642 11 2 5 Важно!
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Будьте внимательны!
Свойство № 3
Возведение степени в степеньЗапомните!
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где «a » — любое число, а «m », «n » — любые натуральные числа.
Свойства 4
Степень произведенияЗапомните!
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b) n = a n · b n , где «a », «b » — любые рациональные числа; «n » — любое натуральное число.
- Пример 1.
(6 · a 2 · b 3 · c) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2 - Пример 2.
(−x 2 · y) 6 = ((−1) 6 · x 2 · 6 · y 1 · 6) = x 12 · y 6
Важно!
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000 - Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4Свойства 5
Степень частного (дроби)Запомните!
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где «a », «b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

- Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
- Пример 1.
Умножение и деление степеней с одинаковыми показателями доклад, проект
Умножение
и деление степеней
ГБОУ « Специальная школа интернат г. Грязи»
Подготовила: учитель 1 категории Т.А.Минакова
2016-2017 уч. год
Образовательные:
1) добиться усвоения правил умножения и деления степеней с одинаковыми основаниями;
2) формировать у учащихся навыки умножения и деления степеней с одинаковыми основаниями;
3) закрепить умение решать текстовые задачи разными способами, строить график линейной функции.
Развивающие:
1) развивать логическое мышление;
2) развивать умение самостоятельной работы;
3) расширять кругозор учащихся.
4) развивать умения сравнивать, выявлять закономерности, обобщать
Воспитательные:
1) воспитывать уважение и любовь к природе;
2)ответственность за ее будущее.
3) воспитание ответственного отношения к учебному труду.
Оборудование: презентация, карточки с индивидуальными заданиями,
компьютер, проектор, экран.
Цели:
Начинаем наш урок.
Должен он пойти нам впрок.
Постарайтесь все понять,
Учитесь тайны открывать,
Ответы полные давайте
И на уроке не зевайте.
1. Вычислите:
23 * 32 = … 0,22 – 0,32 = … 52 * 22 = …
72-м, 100 -ш, — 0,05 -у
ШУМ – это загрязнение невидимо для глаз, но его можно услышать.
Его называют “медленный убийца”. Он может привести к потере слуха, снижению памяти, стрессу, преждевременному старению
2.Какие числа надо возвести в квадрат, чтобы получить:
16, 121, 9 , 49
25 81
4-м, 11-г, 3/5-о, 7/9-с
СМОГ – это фотохимический туман – самая страшная форма загрязнения воздуха. Смог представляет собой многокомпонентную смесь газов и аэрозольных частиц. Он вызывает тяжелые заболевания со смертельным исходом. Солнечные лучи превращают газы смога в ядовитые вещества.
3. Представьте в виде степени выражение: (
а7 * а3 ; с * с8; х10 : х2; у6: у
а10 -л, с9 –п х8-ы, у5 -ь.
ПЫЛЬ – в ее составе не только твердые частицы, но и микроскопические паразиты, клещи, бактерии, болезнетворные грибки, поражающие дыхательные пути и вызывающие аллергические заболевания. Ее частицы на своей поверхности удерживают токсические и радиоактивные вещества. Пыль – основной источник попадания в организм страшного яда – диоксина.
Сформулируйте правило умножения степеней с одинаковыми основаниями. Запишите его на доске в виде формулы.
Сформулируйте правило деления степеней с одинаковыми основаниями. Запишите его на доске в виде формулы.
Тренировочные упражнения
№ 418 – на доске и в тетрадях;
№ 411 – в тетрадях с комментированием по цепочке;
№ 419 – на доске и в тетрадях.
Физкультминутка
И на доску посмотрели.
И на доску посмотрели.
Быстро встали, улыбнулись,
Выше-выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали, сели, встали,
И на месте побежали.
А теперь представим, детки,
Будто руки наши – ветки.
Покачаем ими дружно,
Словно ветер дует южный.
Ветер стих. Вздохнули дружно.
Нам урок продолжить нужно.
Подравнялись, тихо сели
И на доску посмотрели.
15(Х +6 ) = 2(8Х+15)
2) 3(Х +7) = 5(4+Х)
1) 15(Х +6 ) = 2(8Х+15) 2) 3(Х +7) = 5(4+Х)
15Х+90=16Х+30 3Х+21 = 20+5Х
15Х-16Х=30 – 90 3Х-5Х = 20-21
-Х = -60 -2Х= -1
Х=60 Х=0, 5
Итак, решив уравнения, мы узнали:
Из одного взрослого дерева можно получить до 60 кг бумаги. На изготовление одного учебника расходуется как минимум 0,5 кг бумаги.
На изготовление одного учебника расходуется как минимум 0,5 кг бумаги.
Сколько деревьев необходимо срубить для того, чтобы обеспечить учебниками учащихся вашего класса, если каждому ученику на учебный год требуется 10 учебников? Сколько деревьев будет срублено на изготовление учебников для всех учеников нашей школы?
Ответ:
0,5 * 10 * 11 = 55 кг на класс, т. е. 1 дерево;
0,5 * 10 * 120 = 600 кг – на школу,
600 : 60 = 10 деревьев на школу.
Итог:
Какой вывод для себя вы сделали, решая эту задачу?
Прежде чем портить учебник, подумай, сколько погибнет деревьев для издательства нового.
Самостоятельная работа
Представить в виде степени
Вариант1 Вариант II
Проверка самостоятельной работы
Взаимопроверка
Подведение итогов урока.
Запомните, ребята, мы – тоже частица живой природы. Заболеет лес или река, и нам будет плохо. Так давайте беречь и любить все живое. Не обижайте ни дерево, ни муравья. Не обижайте друг друга. Когда все добры и вежливы, счастье приходит в нашу жизнь.
Домашнее задание
п. 19( Правила)
№ 412, № 417, № 425.
Дополнительные задания:
№ 425, № 422.
Спасибо
за урок!
Приложение!
«Пусть кто-нибудь попробует вычеркнуть из математики
степени, и он увидит, что без них далеко не уедешь» М.В. Ломоносов
Умножение и деление степеней
Правило умножения степеней
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают
am · an· ak = a (m+n) ·ak = am+n+k
Примеры:
Решаем в парах
а17· а23 =
d4 · d6 =
b4 · b11 =
c12 · c13 =
k3 · k34 =
h42 · h31 =
g24 · g13 =
а40
d10
b15
c25
k37
h53
g37
Найдем частное двух степеней a7 и a3
a ≠ 0
a7 =
a3 ∙
a4
a4 =
a3
a7 :
=
a 7- 3
a7 : a3
a7 : a3 = a 7-3 = a4
Свойство степени
Для любого числа a ≠ 0 и произвольных натуральных чисел m и n, таких, что m > n,
am : an = am-n
am : an = am-n
Правило деления степеней
При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Примеры:
Определение степени с нулевым показателем
При a ≠ 0
Степень числа a, не равного нулю,
с нулевым показателем равна единице.
Проверочная работа
Представить в виде степени:
Вариант I
Вариант II
Найдем частное двух степеней a7 и a3
a7 = a· a ·a ·a ·a ·a ·a
a3 = a ·a ·a
7 раз
3 раза
a7
a3
=
a· a ·a ·a ·a ·a ·a
a· a ·a
=
a4
a7 : a3 = a 7-3 = a4
a ≠ 0
Благодарю за внимание
Действия со степенями | СПАДИЛО
теория по математике 🎲 числа и вычисления
Что такое степень?Степенью числа a с натуральным показателем n называют произведение n одинаковых множителей, каждый из которых равен а. То есть аn=a×a×a×a …..a (а берется n раз). Число а называют основанием, а число n показателем степени. Показатель показывает, сколько раз берется основание как множитель.
То есть аn=a×a×a×a …..a (а берется n раз). Число а называют основанием, а число n показателем степени. Показатель показывает, сколько раз берется основание как множитель.
Пример №1.
- 34=3×3×3×3 число 3 берем 4 раза (показатель 4)
- 213=21×21×21 число 21 берем 3 раза (показатель 3)
Свойства степени (применимы для степеней с одинаковым основанием)
Умножение степенейПри умножении степеней с одинаковым основанием основание оставляют тем же, а показатели складывают:
an× am=an+m
Пример №2.
а2×а8=а2+8=а10
55×53×54=55+3+4=512
Деление степенейПри делении степеней с одинаковым основанием основание оставляют тем же, а показатели вычитают:
an : am=an–m
Пример №3.
с12:с5=с12-5= с7
323:320=323-20= 33
Возведение степени в степеньПри возведении степени в степень основание оставляют тем же, а показатели умножают:
(an)m=an×m
Пример №4.
(с10)2=с20
(63)5=615
Степень произведенияПри возведении в степень произведения разных множителей необходимо возвести в эту степень каждый множитель:
(a×b×c)m=am×bm×cm
Пример №5.
(сmn)5=c5m5n5
(3254)6=312524
Степень дроби (степень частного)При возведении в степень обыкновенной дроби необходимо возвести в данную степень числитель и знаменатель дроби:
Важные правила для работы со степенями
Запомните!- Любое число в нулевой степени равно 1 (а0=1).

- Нуль в любой степени равен нулю (0n=0).
- Свойства степени с натуральным показателем применимы для степени с целым отрицательным показателем.
Пример №6.
с-21× с-2=с-21+(-2)=с-23
х12 : х-2= х12-(-2)=х14
(с-3)5=с-15
Правила для степени с целым отрицательным показателем- Степень с целым отрицательным показателем можно представить в виде обыкновенной дроби, числитель которой равен единице, а знаменатель степени с натуральным показателем.
- Если дана дробь, в знаменателе которой есть степень с целым отрицательным показателем, то ее можно представить в виде степени с натуральным показателем.
- Если дана дробь, в числителе и знаменателе которой есть степень с целым отрицательным показателем, то можно заменить её дробью, содержащей степень с натуральным показателем, просто поменяв числитель и знаменатель местами.

Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.
(3∙3∙4)n4n−2∙32n−1 ..Теперь представим каждый множитель в виде степени:
3n∙3n∙4n4n−2∙32n−1 ..Разложим знаменатель дроби на множители по свойству степеней
3n∙3n∙4n4n∙4−2∙32n∙3−1 ..Теперь можно сократить числитель и знаменатель на 3n и в 4n степени
Получим дробь, которую преобразуем по свойству степеней:
..14−2∙3−1 ..= 42∙311..=16∙3=48
Ответ: 48pазбирался: Даниил Романович | обсудить разбор | оценить
Задание 8OM21R Найти значение выражения(3∙8)737∙85..
В числителе дроби возведем в степень каждый множитель:
(3∙8)737 ∙85. .=37∙8737∙85.
.=37∙8737∙85.
Теперь сократим (выполним деление степеней), сократятся 37 полностью, а при сокращении на 85 по свойству степеней останется 82, возведем 8 во вторую степень, получим 64, т.е.
(3∙8)737 ∙85..=37∙8737∙85..=82=64
Ответ: 64pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1302oНайдите значение выражения:
при a = 13, b = 6,8
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Сокращаем (a-b):
И получаем:
a/2
Подставляем значение a = 13:
13 / 2 = 6,5
Ответ: 6,5pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1301oНайдите значение выражения: (x + 5)2 — x (x- 10) при x = — 1/20
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5)2 – x (x – 10) = x2 + 2 • 5 • x + 25 – x2 + 10x
Затем приведем подобные слагаемые:
x2 + 2 • 5 • x + 25 – x2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24
Ответ: 24pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0807o Найдите значение выражения:Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:
Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0806oНайдите значение выражения:
В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=72 и 100=102. И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем: По аналогии извлекаем и 2-й корень: В итоге получаем:
Ответ: 70,7pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0805oЗначение какого из выражений является рациональным числом?
- √6-3
- √3•√5
- (√5)²
- (√6-3)²
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
1) √6-3
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
2) √3•√5
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
√3•√5 = √(3•5) = √15
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
3) (√5)²
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
(√5)² = 5
Данный вариант ответа нам подходит.
4) (√6-3)²
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0804oКакое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:
16 – 14 = 2
Суммарно наши действия выглядят так:
Ответ: 4pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0801oКакое из данных ниже выражений при любых значениях n равно произведению 121 • 11n ?
- 121n
- 11n+2
- 112n
- 11n+3
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
- при умножении степени складываются
- приделении степени вычитаются
- при возведении степени в степень степени перемножаются
- при извлечении корня степени делятся
Кроме того, для решения необходимо представить 121 как степень 11, а именно это 112.
121 • 11n = 112 • 11n
С учетом правила умножения, складываем степени:
112 • 11n = 11n+2
Следовательно, нам подходит второй ответ.
Ответ: 2pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0606o Найдите значение выражения:–0,3·(–10)4+4·(–10)2–59
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
–0,3·(–10)4+4·(–10)2–59 =
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
= –0,3·10000+4·100–59 =
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Получаем:
= –3000+400–59 =
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
= –2600–59 =
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
= –(2600+59) = –2659
Ответ: -2659pазбирался: Даниил Романович | обсудить разбор | оценить
Алла Василевская | Просмотров: 6.2k | Оценить:
Как найти значение выражения со степенями
Формулировка задачи: Найдите значение выражения (степени, с разными основаниями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 2 (Действия со степенями).
Рассмотрим, как решаются подобные задачи на примере.
Пример задачи 1:
Найдите значение выражения 8 0,76 ∙ 64 0,12 .
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Пример задачи 2:
Найдите значение выражения:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Пример задачи 3:
Найдите значение выражения 35 -4,7 ∙ 7 5,7 : 5 -3,7 .
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Пример задачи 4:
Найдите значение выражения:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Поделитесь статьей с одноклассниками «Найдите значение выражения (степени, с разными основаниями) – как решать».
Есть другой способ решения?
Предложите другой способ решения задачи «Найдите значение выражения (степени, с разными основаниями)». Возможно, он окажется более понятным для кого-нибудь:
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , ( 2 + 1 ) 5 , ( − 0 , 1 ) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , ( a 2 ) 3 . А также степени с нулевым показателем: 5 0 , ( a + 1 ) 0 , 3 + 5 2 − 3 , 2 0 .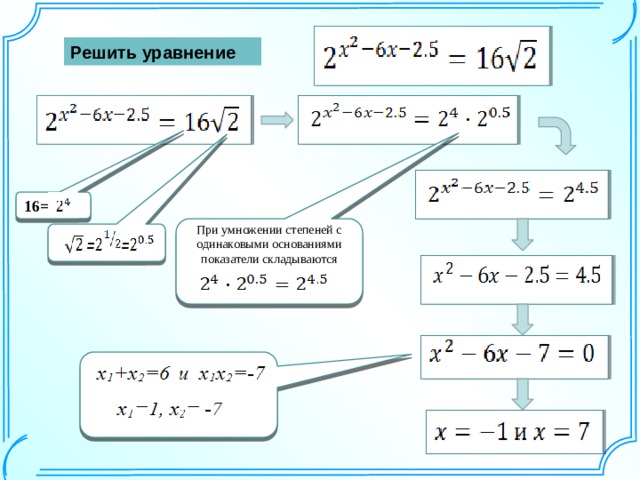 И степени с целыми отрицательными степенями: ( 0 , 5 ) 2 + ( 0 , 5 ) — 2 2 .
И степени с целыми отрицательными степенями: ( 0 , 5 ) 2 + ( 0 , 5 ) — 2 2 .
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .
В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Вычислите значение степенного выражения 2 3 · ( 4 2 − 12 ) .
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · ( 4 2 − 12 ) = 2 3 · ( 16 − 12 ) = 2 3 · 4 .
Имеем 2 3 · ( 4 2 − 12 ) = 2 3 · ( 16 − 12 ) = 2 3 · 4 .
Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.
Ответ: 2 3 · ( 4 2 − 12 ) = 32 .
Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.
Решение
Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:
9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1
Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 и ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) и получить степенное выражение более простого вида a 2 · ( x + 1 ) .
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:
- a r · a s = a r + s ;
- a r : a s = a r − s ;
- ( a · b ) r = a r · b r ;
- ( a : b ) r = a r : b r ;
- ( a r ) s = a r · s .
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Представьте выражение a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 в виде степени с основанием a .
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель ( a 2 ) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a 2 , 5 · a − 6 : a − 5 , 5 = a 2 , 5 − 6 : a − 5 , 5 = a − 3 , 5 : a − 5 , 5 = a − 3 , 5 − ( − 5 , 5 ) = a 2 .
Ответ: a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 = a 2 .
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .
Решение
Если мы применим равенство ( a · b ) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Есть еще один способ провести преобразования:
3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · ( 3 · 7 ) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21
Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21
Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .
Решение
Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени ( a r ) s = a r · s справа налево и получим ( a 0 , 5 ) 3 : a 1 , 5 − a 0 , 5 − 6 = ( a 0 , 5 ) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .
Используем свойство степени в степени ( a r ) s = a r · s справа налево и получим ( a 0 , 5 ) 3 : a 1 , 5 − a 0 , 5 − 6 = ( a 0 , 5 ) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .
Ответ: t 3 − t − 6 .
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2
Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a 0 , 3 :
a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a
б) Обратим внимание на знаменатель:
x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2
Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т. е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2
Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .
Сократите дробь: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .
Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .
30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 )
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4
Ответ: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 ) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .
Решение
Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
x 1 2 — 1 · x 1 2 + 1
x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2
Теперь умножаем дроби:
4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2
Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .
Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1
Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение
Мы можем произвести сокращение дроби на ( x 2 , 7 + 1 ) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .
Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .
Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .
Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение ( x + 1 ) — 0 , 2 3 · x — 1 можно заменить на x 3 · ( x + 1 ) 0 , 2 .
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Представьте выражение x 1 9 · x · x 3 6 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞ ) .
На этом множестве мы имеем право перейти от корней к степеням:
x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6
Используя свойства степеней, упростим полученное степенное выражение.
x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3
Ответ: x 1 9 · x · x 3 6 = x 1 3 .
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .
Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:
5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0
Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .
Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 ( 1 — log 3 5 ) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2 ) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2 ) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
m : a n =—>
| a m |
| a n |
= a m − n , где « a » — любое число, не равное нулю, а « m », « n » — любые натуральные числа такие, что « m > n ».
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2 : 4 4m + 3 = 4 5m + 6 + m + 2 : 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
| 512 · 4 |
| 32 |
=
| 512 · 4 |
| 32 |
=
| 2 9 · 2 2 |
| 2 5 |
=
| 2 9 + 2 |
| 2 5 |
=
| 2 11 |
| 2 5 |
= 2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2 ) на 4 1 . Это понятно, если посчитать (4 3 −4 2 ) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n ) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
- Пример.
(a 4 ) 6 = a 4 · 6 = a 24 - Пример. Представить 3 20 в виде степени с основанием 3 2 .
По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:
Свойства 4
Степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b) n = a n · b n , где « a », « b » — любые рациональные числа; « n » — любое натуральное число.
- Пример 1.
(6 · a 2 · b 3 · c ) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2 - Пример 2.
(−x 2 · y) 6 = ( (−1) 6 · x 2 · 6 · y 1 · 6 ) = x 12 · y 6
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n )= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000 - Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a : b) n = a n : b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
- Пример. Представить выражение в виде частного степеней.
(5 : 3) 12 = 5 12 : 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
10: Полиномы — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 21766
- OpenStax
- OpenStax
Выражения, известные как многочлены, широко используются в алгебре. Применение этих выражений необходимо для многих профессий, включая экономистов, инженеров и ученых. В этой главе мы узнаем, что такое полиномы и как ими манипулировать с помощью основных математических операций.
- 10.1: Сложение и вычитание полиномов
- В этом разделе мы будем работать с полиномами, каждый член которых содержит только одну переменную.
 Степень полинома и степени его членов определяются показателями переменной. Работать с полиномами проще, если вы перечисляете члены в порядке убывания степеней. Когда многочлен записывается таким образом, говорят, что он имеет стандартную форму. Сложение и вычитание полиномов можно рассматривать как просто сложение и вычитание одинаковых членов.
Степень полинома и степени его членов определяются показателями переменной. Работать с полиномами проще, если вы перечисляете члены в порядке убывания степеней. Когда многочлен записывается таким образом, говорят, что он имеет стандартную форму. Сложение и вычитание полиномов можно рассматривать как просто сложение и вычитание одинаковых членов.
- 10.2: Использование свойств умножения показателей степени (часть 1)
- В этом разделе мы начнем работать с переменными выражениями, содержащими показатели степени. Помните, что показатель степени указывает на многократное умножение одной и той же величины. Вы видели, что когда вы комбинируете одинаковые термины путем сложения и вычитания, вам нужно иметь одно и то же основание с одним и тем же показателем степени. Но когда вы умножаете и делите, показатели степени могут быть разными, а иногда и основания тоже могут быть разными. Мы выведем свойства экспонент, ища закономерности в нескольких примерах.

- 10.3: Использование свойств степени умножения (Часть 2)
- Все свойства степени справедливы для любых действительных чисел, но сейчас мы будем использовать только целые степени. Свойство произведения показателей степени позволяет нам умножать выражения с одинаковыми основаниями путем сложения их показателей степени. Свойство степени показателей говорит о том, что для возведения степени в степень необходимо умножить показатели степени. Наконец, свойство показателей степени произведения в степени описывает, как возведение произведения в степень достигается путем возведения каждого множителя в эту степень.
- 10.4: Умножение многочленов (часть 1)
- В этом разделе мы начнем умножать многочлены первой, второй и/или третьей степени. Точно так же, как существуют разные способы представления умножения чисел, существует несколько методов, которые можно использовать для умножения многочлена на другой многочлен.
 Распределительное свойство — это первый метод, с которым вы уже столкнулись и использовали для нахождения произведения любых двух многочленов.
Распределительное свойство — это первый метод, с которым вы уже столкнулись и использовали для нахождения произведения любых двух многочленов.
- 10.5: Умножение многочленов (часть 2)
- Метод FOIL обычно является самым быстрым методом умножения двух двучленов, но он работает только для двучленов. Когда вы умножаете двучлен на двучлен, вы получаете четыре члена. Иногда вы можете комбинировать одинаковые термины, чтобы получить трехчлен, но иногда подобных терминов для объединения нет. Другой метод, который работает для всех полиномов, — это вертикальный метод. Это очень похоже на метод, который вы используете для умножения целых чисел.
- 10.7: Разделение мономов (Часть 2)
- Теперь мы рассмотрели все свойства экспонент.
 Мы будем использовать их для деления мономов. Позже вы будете использовать их для деления многочленов. Когда мы делим одночлены с более чем одной переменной, мы пишем одну дробь для каждой переменной. Как только вы ознакомитесь с процессом и попрактикуетесь в нем шаг за шагом несколько раз, вы сможете упростить дробь за один шаг.
Мы будем использовать их для деления мономов. Позже вы будете использовать их для деления многочленов. Когда мы делим одночлены с более чем одной переменной, мы пишем одну дробь для каждой переменной. Как только вы ознакомитесь с процессом и попрактикуетесь в нем шаг за шагом несколько раз, вы сможете упростить дробь за один шаг.
- 10.8: Целочисленные показатели степени и экспоненциальное представление (Часть 1)
- Отрицательный показатель степени говорит нам переписать выражение, взяв обратное значение основания и затем изменив знак показателя степени. Любое выражение с отрицательными показателями не считается простейшим. Мы будем использовать определение отрицательного показателя и другие свойства показателей, чтобы написать выражение только с положительными показателями.
- 10.9: Целочисленные экспоненты и научная запись (Часть 2)
- Когда число записывается как произведение двух чисел, где первый множитель представляет собой число больше или равное единице, но меньше 10, а второй множитель представляет собой степени 10, записанной в экспоненциальной форме, говорят, что она представлена в научной записи.
 В качестве знака умножения принято использовать ×, хотя мы избегаем использования этого знака в других местах алгебры. Научная нотация — удобный способ записи очень больших или очень маленьких чисел. Он часто используется в науке для облегчения расчетов.
В качестве знака умножения принято использовать ×, хотя мы избегаем использования этого знака в других местах алгебры. Научная нотация — удобный способ записи очень больших или очень маленьких чисел. Он часто используется в науке для облегчения расчетов.
- 10.10: Введение в факторинг полиномов
- Ранее мы перемножали множители, чтобы получить произведение. Теперь мы повернем этот процесс вспять; мы начнем с продукта, а затем разобьем его на факторы. Разбиение продукта на факторы называется факторингом. В Языке алгебры мы разложили числа на множители, чтобы найти наименьшее общее кратное (НОК) двух или более чисел. Теперь мы разложим выражения и найдем наибольший общий делитель двух или более выражений. Метод, который мы используем, аналогичен тому, который мы использовали для поиска LCM.
- 10.11: полиномы (упражнения)
- 10.
 12: Полиномиалы (Суммируют)
12: Полиномиалы (Суммируют)
- 10.
Рисунок 10.1 — Пути рокетов расчеты. (кредит: НАСА, общественное достояние)
Шаблон:HypTestЭта страница под названием 10: Polynomials распространяется по незаявленной лицензии и была создана, изменена и/или курирована OpenStax.
- Вернуться к началу
- Была ли эта статья полезной?
- Тип изделия
- Глава
- Автор
- ОпенСтакс
- Встроить Hypothes.is?
- да
- Показать страницу TOC
- нет
- Теги
- Многочлены
- источник-математика-5018
Сложение степеней с одинаковыми показателями.
 n$. 93=8$.
n$. 93=8$.Степенные формулы используются в процессе сокращения и упрощения сложных выражений, при решении уравнений и неравенств.
Число c равно n -я степень числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием, их показатели складываются:
а м а н = а м + н .
2. При делении степеней с одинаковым основанием вычитаются их показатели:
3. Степень произведения двух и более множителей равна произведению степеней этих множителей:
(abc…) n = a n b n c n …
4. Степень дроби равна равно отношению степеней делимого и делителя:
(a/b) n = a n / b n .
5. Возведение степени в степень умножает показатели степени:
(а м) n = а м н .
Каждая приведенная выше формула верна в направлениях слева направо и наоборот.
Например, . (2 3 5/15)² = 2² 3² 5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень произведения нескольких множителей равен произведению корней этих множителей:
2. Корень отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень достаточно возвести число корня в эту степень:
4. Если увеличить степень корня в n один раз и при этом возвести в n -ю степень подкоренного числа, то значение корня не изменится:
5. Если уменьшаем степень корня н корня одновременно н -й степени от подкоренного числа, тогда значение корня не изменится:
Степень с отрицательным показателем степени. Степень некоторого числа с неположительным (целым) показателем степени определяется как единица, деленная на степень того же числа с показателем степени, равным абсолютному значению неположительного показателя степени:
Формула a m :an = a m — n может использоваться не только для m > n , но и для m n.
Например . а 4:а 7 = а 4 — 7 = а -3 .
Чтобы формула a m :an = a m — n стала справедливой при m=n , необходимо наличие нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем степени равна единице.
Например, . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число a в степень m/n , нужно извлечь корень n th степени m th степени этого числа a .
Сложение и вычитание степеней
Очевидно, что числа со степенями можно складывать так же, как и другие величины , складывая их одно за другим со своими знаками .
Итак, сумма a 3 и b 2 равна a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 равна a 3 — b n + h 5 — d 4.
Коэффициенты одинаковые степени одних и тех же переменных можно складывать или вычитать.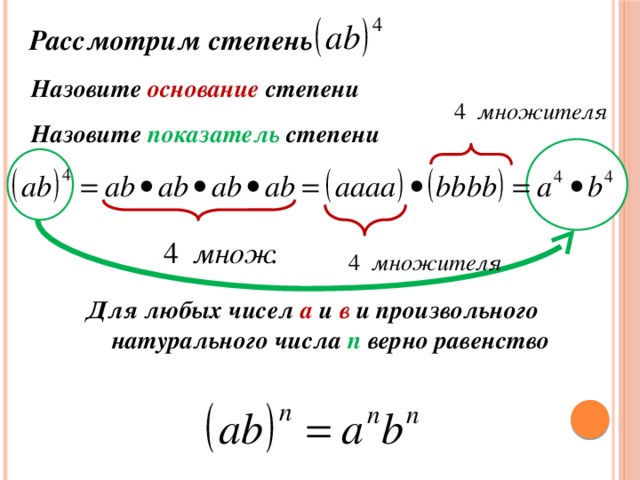
Итак, сумма 2a 2 и 3a 2 равна 5a 2 .
Также очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различные переменные и различные степени идентичные переменные , должны быть добавлены путем добавления их к их знакам.
Итак, сумма 2 и 3 равна сумме 2 + 3 .
Очевидно, что квадрат а и куб а не в два раза больше квадрата а, а в два раза больше куба а.
Сумма a 3 b n и 3a 5 b 6 равна a 3 b n + 3a 5 b 6 .
Вычитание степеней производится так же, как сложение, за исключением того, что знаки вычитаемого должны быть изменены соответствующим образом.
Или:
2а 4 — (-6а 4) = 8а 4
3ч 2 б 6 — 4ч 2 б 6 = -ч 2 б 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Степенное умножение
Числа со степенями можно умножать, как и другие величины, записывая их одно за другим, с или без знак умножения между ними.
Итак, результатом умножения a 3 на b 2 является a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере можно упорядочить, добавив те же самые переменные.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел (переменных) со степенями, мы видим, что если любые два из них перемножить, то в результате получится число (переменная) со степенью, равной сумме степеней слагаемых.
Итак, а 2 .а 3 = аа.ааа = ааааа = а 5 .
Здесь 5 — степень результата умножения, равная 2 + 3, сумма степеней слагаемых.
Итак, an .am m = a m+n .
Для n , a берется в качестве множителя столько раз, сколько раз степень n;
А m , принимается за множитель столько раз, сколько степени m равна;
Поэтому степеней с одинаковыми основаниями можно умножить путем сложения показателей степени.
Итак, а 2 .а 6 = а 2+6 = а 8 . И х 3 .х 2 .х = х 3+2+1 = х 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножить (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: х 4 — у 4.
Умножить (х 3 + х — 5) ⋅ (2х 3 + х + 1).
Это правило также верно для чисел, показатели степени которых — отрицательные .
1. Итак, а -2 .а -3 = а -5 . Это можно записать как (1/аа).(1/ааа) = 1/ааааа.
2. у-н .у-м = у-н-м .
3. а-н .ам = а м-н .
Если a + b умножить на a — b, результатом будет a 2 — b 2: то есть
Результат умножения суммы или разности двух чисел равен сумме или разности их квадратов.
Если сумму и разность двух чисел возвести в квадрат , то результат будет равен сумме или разности этих чисел в четвертой степени.
Итак, (а — у).(а + у) = а 2 — у 2 .
(а 2 — у 2)⋅(а 2 + у 2) = а 4 — у 4 .
(а 4 — у 4)⋅(а 4 + у 4) = а 8 — у 8 .
Деление степеней
Числа со степенями можно разделить, как и другие числа, путем вычитания из делителя или представления их в виде дроби.
Таким образом, a 3 b 2 разделить на b 2 равно a 3 .
Запись 5, деленная на 3, выглядит как $\frac $. Но это равно 2 . В ряду чисел
а+4, а+3, а+2, а+1, 0, а-1, а-2, а-3, а-4.
любое число можно разделить на другое, и показатель степени будет равен разности показателей делимых чисел.
При делении степеней с одинаковым основанием вычитаются их степени. .
Итак, у 3:у 2 = у 3-2 = у 1 . То есть $\frac = y$. 93$
Необходимо очень хорошо освоить умножение и деление степеней, так как такие операции очень широко используются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшить показатели степени в $\frac $ Ответ: $\frac $.
2. Уменьшить показатели в $\frac$. Ответ: $\frac $ или 2x.
3. Привести показатели степени а 2 / 3 и а -3 / а -4 и привести к общему знаменателю.
a 2 .a -4 — это первый числитель -2.
a 3 .a -3 — это a 0 = 1, второй числитель.
a 3 .a -4 есть -1 , общий числитель.
После упрощения: а-2/а-1 и 1/а-1.
4. Привести показатели 2a 4 /5a 3 и 2 /a 4 к общему знаменателю.
Ответ: 2а 3 / 5а 7 и 5а 5 / 5а 7 или 2а 3 / 5а 2 и 5/5а 2.
5. Умножить (а 3 + b)/b 4 на (а — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделить 4/y 3 на 3/y 2 . Ответ: а/у.
степенные свойства
Напоминаем, что в этом уроке мы разбираемся в степенных свойствах с натуральными показателями и нулем. Степени с рациональными показателями и их свойства будут рассмотрены на уроках для 8 класса.
Показатель степени с натуральным показателем имеет несколько важных свойств, позволяющих упростить расчеты в показательных примерах.
Свойство №1
Произведение степеней
При умножении степеней с одним и тем же основанием основание остается неизменным, а показатели степени складываются.
a m a n = a m + n, где «a» — любое число, а «m», «n» — любые натуральные числа.
Это свойство степеней также влияет на произведение трех и более степеней.
- Упростите выражение.
б б 2 б 3 б 4 б 5 = б 1 + 2 + 3 + 4 + 5 = б 15 - Присутствует как степень.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17 - Присутствует как степень.
(0,8) 3 (0,8) 12 = (0,8) 3 + 12 = (0,8) 15 - Запишите частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2 - Рассчитать.
Обратите внимание, что в указанном свойстве речь шла только о умножении степеней с одинаковыми основаниями. . Это не касается их добавления.
Вы не можете заменить сумму (3 3 + 3 2) на 3 5 . Это понятно, если вычислить
(3 3 + 3 2) = (27 + 9) = 36 и 3 5 = 243
Свойство № 2
Частные степени
При делении степеней с одинаковым основанием основание остается неизменным, а из показателя степени делимого вычитается показатель степени делителя.
11 3 — 2 4 2 — 1 = 11 4 = 44
Пример. Решите уравнение. Воспользуемся свойством частичных степеней.
Решите уравнение. Воспользуемся свойством частичных степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Используя свойства №1 и №2, можно легко упростить выражения и выполнять вычисления.
Пример. Упростите выражение.
4 5 м + 6 4 м + 2: 4 4 м + 3 = 4 5 м + 6 + м + 2: 4 4 м + 3 = 4 6 м + 8 − 4 м − 3 = 4 2 м + 5
Пример. Найдите значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что свойство 2 касалось только разделения полномочий по одинаковым основаниям.
Вы не можете заменить разницу (4 3 −4 2) на 4 1 . Это понятно, если вычислить (4 3 −4 2) = (64 − 16) = 48 и 4 1 = 4
Свойство №3
Возведение в степень
При возведении степени в степень основание степени остается не меняется, а показатели умножаются.
(a n)m = a n m, где «а» — любое число, а «m», «n» — любые натуральные числа.
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведения дроби в степень мы остановимся более подробно на следующей странице.
Как умножить силы
Как умножить силы? Какие силы можно умножать, а какие нельзя? Как умножить число на степень?
В алгебре можно найти произведение степеней в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одним и тем же основанием основание должно остаться прежним, а степени должны быть добавлены:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать полномочия, с конкретными примерами.
Единица в показателе степени не пишется, но при умножении степеней учитывают:
При умножении количество степеней может быть любым. Следует помнить, что нельзя ставить знак умножения перед буквой:
В выражениях возведение в степень выполняется первым.
Если вам нужно умножить число на степень, необходимо сначала выполнить возведение в степень, а только потом — умножение:
Умножение степеней с одинаковым основанием
Этот видеоурок доступен по подписке
У вас уже есть подписка ? Прийти
В этом уроке мы научимся умножать степени с одним и тем же основанием. Сначала напомним определение степени и сформулируем теорему о справедливости равенства . Затем приведем примеры его применения к конкретным числам и докажем. Мы также применим теорему для решения различных задач.
Сначала напомним определение степени и сформулируем теорему о справедливости равенства . Затем приведем примеры его применения к конкретным числам и докажем. Мы также применим теорему для решения различных задач.
Topic: Degree with a natural indicator and its properties
Lesson: Multiplying powers with the same bases (formula)
1. Basic definitions
Basic definitions:
n — exponent ,
— n -я степень числа.
2. Утверждение теоремы 1
Теорема 1. Для любого числа a и любых натуральных n и k верно равенство:
Другими словами: если a — любое число; n и k натуральных чисел, тогда:
Отсюда правило 1:
3. Объясняющие задачи
Вывод: частных случаев подтвердили правильность теоремы № 1. Докажем ее в общем случае, то есть для любых и и любые натуральные н и к.
4. Доказательство теоремы 1
Даны числа a — любые; номера н и к- натуральные. Докажите:
Доказательство основано на определении степени.
5. Решение примеров с помощью теоремы 1
Пример 1: Присутствует в виде степени.
Для решения следующих примеров воспользуемся теоремой 1.
и)
6. Обобщение теоремы 1
Вот обобщение:
7. Решение примеров с использованием обобщения теоремы 1
8. Решение различных задач с использованием теоремы 1
Пример 2: Вычислите (можно воспользоваться таблицей основных степеней).
а) (по таблице)
б)
Пример 3: Запишем в виде степени по основанию 2.
а)
Пример 4: Определить знак числа:
Пример 5: Заменить ( ) на степень с основанием r:
Имеем , то есть .
9. Подведение итогов
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и другие. Алгебра 7. 6-е издание. М.: Просветление. 2010
1. Школьный помощник (Источник).
1. Выразить в степени:
a B C D E)
3. Записать в виде степени с основанием 2:
4. Определить знак числа:
a)
5. Заменить ( ) на a степень числа с основанием r:
а) r 4 ( ) = r 15 ; б) ( ) r 5 = r 6
Умножение и деление степеней с одинаковыми показателями
На этом уроке мы будем изучать умножение степеней с одинаковыми показателями. Для начала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и о возведении степени в степень. Затем мы формулируем и доказываем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью мы решим ряд типовых задач.
Напоминание основных определений и теорем
Здесь a — основание степени
— n -я степень числа.
Теорема 1. Для любых чисел a и любых натуральных n и k верно равенство:
При умножении степеней с одним и тем же основанием степени складываются, основание остается неизменным.
Теорема 2. Для любого числа есть и любое натуральное n и k, такие, что n > k верно равенство:
При делении степеней с одинаковым основанием степени вычитаются, а основание остается неизменным.
Теорема 3. Для любых чисел a и любых натуральных n и k верно равенство:
то же самое индикаторы .
Примеры умножения степеней с одинаковыми показателями
Рассмотрим следующие примеры:
Запишем выражения для определения степени.
Вывод: Из примеров видно, что , но это еще нужно доказать. Сформулируем теорему и докажем ее в общем случае, т. е. для любых a и b и любых натуральных n.
Формулировка и доказательство теоремы 4
Для любых чисел a и b и любых натуральных n равенство:
Доказательство Теорема 4 .
По определению степени:
Итак, мы доказали, что .
Для умножения степеней с одинаковым показателем достаточно умножить основания, а показатель степени оставить без изменений.
Формулировка и доказательство теоремы 5
Сформулируем теорему для деления степеней с одинаковыми показателями.
Для любого номера a и b( ) и любое натуральное n равенство верно:
Доказательство Теорема 5 .
Запишем и по определению степени:
Формулировка теорем словами
Итак, мы доказали, что .
Чтобы разделить степени с одинаковыми показателями степени друг на друга, достаточно разделить одно основание на другое, а показатель степени оставить без изменений.
Решение типовых задач с помощью теоремы 4
Пример 1: Выразите в виде произведения степеней.
Для решения следующих примеров воспользуемся теоремой 4.
Для решения следующего примера запомним формулы:
Пример 2: Запишите как степень произведения.
Пример 3: Запишите в виде степени с показателем степени 2.
Примеры расчета
Пример 4: Расчет наиболее рациональным способом.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и другие. Алгебра 7.М.: Образование. 2006
2. Школьный помощник (Источник).
1. Присутствует как произведение полномочий:
а) ; б) ; в) ; ГРАММ) ;
2. Записать как степень произведения:
3. Записать в виде степени с показателем 2:
4. Рассчитать наиболее рациональным способом.
Урок математики на тему «Умножение и деление степеней»
Разделы: Математика
Педагогическая цель :

Задания :
Единиц деятельности доктрины: определение степени с натуральным показателем; компоненты степени; определение частного; Ассоциативный закон умножения.
I. Организация демонстрации освоения студентами имеющихся знаний. (шаг 1)а) Актуализация знаний:
2) Сформулировать определение степени с натуральным показателем.
a n = a a a a … a (n раз)
b k = b b b b a … b (k раз) Обоснуйте свой ответ.
II. Организация самооценки обучаемого по степени владения релевантным опытом. (шаг 2)Самопроверка:(индивидуальная работа в двух вариантах.)
А1) Выразить произведение 7 7 7 7 х х х в степени:
А2) Выразить произведение в степени (-3) 3 х 2
А3) Рассчитать: -2 3 2 + 4 5 3
Количество заданий в тесте подбираю в соответствии с уровнем подготовки класса.
На пробу даю ключ для самопроверки. Критерии: зачет-незачет.
III. Учебно-практическое задание (этап 3) + этап 4. (учащиеся сами формулируют свойства)В ходе решения задач 1) и 2) учащиеся предлагают решение, а я, как учитель, организую занятие по поиску способа упрощения степеней при умножении с одинаковыми основаниями.
Учитель: придумайте способ упростить степени при умножении с одинаковым основанием.
На кластере появляется запись:
Тема урока сформулирована. Умножение сил.
Учитель: придумайте правило деления степеней с одинаковыми основаниями.
Рассуждение: какое действие проверяет деление? а 5: а 3 = ? что а 2 а 3 = а 5
Возвращаюсь к схеме — кластер и дополняю запись — ..при делении убавляю и добавляю тему урока. …и деление степеней.
IV. Сообщение учащимся пределов знаний (как минимума, так и максимума).

Учитель: задача минимум на сегодняшнем уроке научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимум: применить умножение и деление вместе.
Напишите на доске : а м а н = а м + п ; a m: a n = a m-n
V. Организация изучения нового материала. (шаг 5)а) По учебнику: № 403 (а, в, д) задания с разной формулировкой
№ 404 (а, д, е) самостоятельная работа, затем организую взаимную проверку, даю ключи.
б) При каком значении m выполняется равенство? а 16 а м = а 32; х ч х 14 = х 28; х 8 (*) = х 14
Задание: придумать подобные примеры на деление.
в) №417(а), №418(а) Ловушки для учащихся : х 3 х н = х 3н; 3 4 3 2 = 9 6 ; а 16: а 8 = а 2.
VI. Подведение итогов изученного, проведение диагностической работы (которая побуждает к изучению данной темы учащихся, а не преподавателей) (6 этап)
диагностическая работа.
Тест (поместите ключи на обратную сторону теста).
Варианты задания: представить в виде степени частное х 15: х 3; представить в виде степени произведение (-4) 2 (-4) 5 (-4) 7 ; для которого m верно равенство a 16 a m = a 32; найти значение выражения h 0 : h 2 при h = 0,2; вычислить значение выражения (5 2 5 0) : 5 2 .
Подведение итогов урока. Отражение. Я делю класс на две группы.
Найдите аргументы I группы: в пользу знания свойств степени, и II группы — аргументы, которые скажут, что можно обойтись без свойств. Выслушиваем все ответы, делаем выводы. На последующих уроках можно предложить статистические данные и назвать рубрику «В голове не укладывается!»
 Запишите это число, используя степень.
Запишите это число, используя степень.Справочник по истории. Какие числа называются числами Ферма.
стр.19. № 403, № 408, № 417
Б/у книги:
Свойства степеней, формулировки, доказательства, примеры.
После того, как определена степень числа, логично говорить о свойствах степени . В этой статье мы дадим основные свойства степени числа, коснувшись при этом всех возможных показателей степени. Здесь мы приводим доказательства всех свойств степени, а также показываем, как эти свойства применяются при решении примеров.
Навигация по страницам.
Свойства степеней с натуральными показателями
По определению степени с натуральным показателем степени n является произведением n множителей, каждый из которых равен a . Основываясь на этом определении и используя свойства умножения действительных чисел , можно получить и обосновать следующие свойства степени с натуральным показателем :
Основываясь на этом определении и используя свойства умножения действительных чисел , можно получить и обосновать следующие свойства степени с натуральным показателем :
- если a>0 , то an >0 для любого натурального n ;
- если a=0 , то a n =0 ;
- , если a 2 m >0, если a 2 m−1 n;
- если m и n натуральные числа такие, что m>n , то для 0m n и a>0 верно неравенство a m >an .
- а м а н = а м + н;
- a m:an = a m−n ;
- (a b) n = a n b n ;
- (а:б) n =а н:b н ;
- (а м) n = а м n ;
- , если n — натуральное число, a и b — положительные числа и a n n и a−n>b−n ;
- , если m и n целые числа и m>n, то для 0m n и a>1 выполняется неравенство a m >an n.
Сразу отметим, что все записанные равенства равны идентичны при указанных условиях, а их правая и левая части могут быть взаимозаменяемы. Например, основное свойство дроби a m a n = a m + n при упрощении выражения часто используется в виде a m+n = a m a n .
Например, основное свойство дроби a m a n = a m + n при упрощении выражения часто используется в виде a m+n = a m a n .
Теперь давайте подробно рассмотрим каждый из них.
Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называется основным свойством степени : для любого действительного числа а и любых натуральных чисел m и n выполняется равенство a m ·an =am +n верно.
Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a man можно записать в виде произведения . Благодаря свойствам умножения результирующее выражение можно записать в виде , и это произведение является степенью a с натуральным показателем m+n , то есть a m+n . Это завершает доказательство.
Приведем пример, подтверждающий основное свойство степени. Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3, по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 2 3 =(2 2) (2 2 2)=4 8=32 и 2 5 =2 2 2 2 2=32 , так как получаем равные значения, то равенство 2 2 2 3 = 2 5 верно, и это подтверждает основное свойство степени.
Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 2 3 =(2 2) (2 2 2)=4 8=32 и 2 5 =2 2 2 2 2=32 , так как получаем равные значения, то равенство 2 2 2 3 = 2 5 верно, и это подтверждает основное свойство степени.
Основное свойство степени, основанное на свойствах умножения, может быть обобщено на произведение трех или более степеней с одинаковыми основаниями и натуральными показателями. Таким образом, для любого количества k натуральных чисел n 1 , n 2 , …, n k верно равенство an 1 an 2 an k =an 1 +n 2 +…+n k.
Например, (2.1) 3 (2.1) 3 (2.1) 4 (2.1) 7 = (2.1) 3+3+4+7 =(2.1) 17 .
Можно перейти к следующему свойству степеней с натуральным показателем — свойству частичных степеней с одинаковыми основаниями : для любого ненулевого действительного числа a и любых натуральных чисел m и n, удовлетворяющих условию m>n , справедливо равенство a m:an =a m−n.
Прежде чем приводить доказательство этого свойства, обсудим смысл дополнительных условий в утверждении. Условие a≠0 необходимо для того, чтобы избежать деления на ноль, так как 0 n =0, а когда мы знакомились с делением, то договорились, что на ноль делить нельзя. Условие m>n вводится для того, чтобы не выходить за пределы натуральных показателей. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n), либо отрицательным числом (что происходит при m m−n an n =a (m−n) + n = a m Из полученного равенства a m−n an n = a m и соотношения умножения с делением следует, что a m−n является частичной степенью чисел m и an Это доказывает свойство частичных степеней с одинаковыми основаниями.0032
Условие a≠0 необходимо для того, чтобы избежать деления на ноль, так как 0 n =0, а когда мы знакомились с делением, то договорились, что на ноль делить нельзя. Условие m>n вводится для того, чтобы не выходить за пределы натуральных показателей. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n), либо отрицательным числом (что происходит при m m−n an n =a (m−n) + n = a m Из полученного равенства a m−n an n = a m и соотношения умножения с делением следует, что a m−n является частичной степенью чисел m и an Это доказывает свойство частичных степеней с одинаковыми основаниями.0032
Возьмем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2, рассматриваемое свойство степени соответствует равенству π 5: π 2 = π 5−3 = π 3.
Теперь рассмотрим свойство степени произведения : натуральная степень n произведения любых двух действительных чисел a и b равна произведению степеней an и b n , то есть (ab) n = an b n .
Действительно, по определению степени с натуральным показателем имеем . Последнее произведение, исходя из свойств умножения, можно переписать как , что равно a n b n .
Вот пример: .
Это свойство распространяется на степень произведения трех или более множителей. То есть свойство естественной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .
Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .
Следующим свойством является естественное свойство : отношение действительных чисел a и b , b≠0 к натуральной степени n равно отношению степеней an и b n , то есть (a:b) n = а н: б н .
Доказательство можно провести, используя предыдущее свойство. Итак, (a:b) n b n =((a:b) b) n =an , а из равенства (a:b) n b n =an следует, что (a:b) n есть частное числа an на b n .
Напишем это свойство на примере конкретных чисел: .
Теперь озвучим возведение в степень свойства : для любого действительного числа a и любых натуральных чисел m и n степень m в степени n равна степени a с показателем m·n , то есть (a m) п =а м · п .
Например, (5 2) 3 =5 2 3 =5 6 .
Доказательством свойства мощности в степени является следующая цепочка равенств: .
Рассматриваемое свойство может быть расширено до степени внутри степени внутри степени и так далее. Например, для любых натуральных чисел p, q, r и s равенство . Для большей наглядности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .
Осталось остановиться на свойствах сравнения степеней с натуральным показателем.
Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.
Сначала докажем, что a n >0 для любого a>0 .
Произведение двух положительных чисел есть положительное число, как следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого количества положительных чисел также будет положительным числом. А степень а с натуральным показателем n по определению есть произведение n множителей, каждый из которых равен а. Эти рассуждения позволяют нам утверждать, что для любого положительного основания а степень n является положительным числом. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
Эти рассуждения позволяют нам утверждать, что для любого положительного основания а степень n является положительным числом. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
Совершенно очевидно, что для любого натурального n с a=0 степень n равна нулю. Действительно, 0 n =0·0·…·0=0 . Например, 0 3 =0 и 0 762 =0 .
Перейдем к отрицательным основаниям.
Начнем со случая, когда показатель степени — четное число, обозначим его как 2 m , где m — натуральное число. Затем . По правилу умножения отрицательных чисел каждое из произведений вида а равно произведению модулей чисел а и а, а значит, является положительным числом. Следовательно, продукт также будет положительным. и степень а 2 м. Вот примеры: (−6) 4 >0 , (−2,2) 12 >0 и .
Наконец, когда основание a — отрицательное число, а показатель степени — нечетное число 2 m−1, тогда . Все произведения a·a — положительные числа, произведение этих положительных чисел также положительно, и его умножение на оставшееся отрицательное число a дает отрицательное число. В силу этого свойства (−5) 3 17 n n есть произведение левых и правых частей n истинных неравенств a свойств неравенств, доказываемое неравенство имеет вид an n . Например, благодаря этому свойству выполняются неравенства 3 7 7 и .
В силу этого свойства (−5) 3 17 n n есть произведение левых и правых частей n истинных неравенств a свойств неравенств, доказываемое неравенство имеет вид an n . Например, благодаря этому свойству выполняются неравенства 3 7 7 и .
Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями меньше одной, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями больше единицы, больше та степень, показатель которой больше. Перейдем к доказательству этого свойства.
Докажем, что при m>n и 0m n . Для этого запишем разность a m − an и сравним ее с нулем. Записанная разность после вынесения n за скобки примет вид an ·(am−n−1) . Полученное произведение отрицательно как произведение положительного числа n и отрицательного числа a m−n−1 (an положительно как натуральная степень положительного числа, а разность a m−n−1 отрицательна, так как m−n >0 в силу начального условия m>n , откуда следует, что при 0m−n оно меньше единицы). Следовательно, a m − an m n , что и требовалось доказать. Например, приведем правильное неравенство.
Следовательно, a m − an m n , что и требовалось доказать. Например, приведем правильное неравенство.
Осталось доказать вторую часть свойства. Докажем, что для m>n и a>1 истинно a m >an. Разность a m −an после вынесения a n за скобки принимает вид an ·(am−n−1) . Это произведение положительно, так как при a>1 степень n — положительное число, а разность a m−n−1 — положительное число, так как m−n>0 в силу начального условия, а при a>1 степень m−n больше единицы. Следовательно, a m − an > 0 и am > an , что и требовалось доказать. Это свойство иллюстрируется неравенством 3 7 >3 2 .
Свойства степеней с целыми показателями
Поскольку натуральные числа являются натуральными числами, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем абзаце.
Мы определили степень с отрицательным целым показателем, а также степень с нулевым показателем таким образом, что все свойства степеней с натуральными показателями, выраженные равенствами, остаются в силе. Поэтому все эти свойства справедливы как для нулевых показателей, так и для отрицательных показателей, при этом, разумеется, основания степеней отличны от нуля.
Поэтому все эти свойства справедливы как для нулевых показателей, так и для отрицательных показателей, при этом, разумеется, основания степеней отличны от нуля.
Итак, для любых действительных и ненулевых чисел a и b, а также любых целых чисел m и n верны следующие свойства степеней с целыми показателями :
При a=0 степени a m и an имеют смысл только тогда, когда и m, и n являются целыми положительными числами, т. е. натуральными числами. Таким образом, только что написанные свойства справедливы и для случаев, когда a=0, а числа m и n — целые положительные числа.
Доказать каждое из этих свойств несложно, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с вещественными числами. В качестве примера докажем, что свойство мощности выполняется как для положительных, так и для неположительных целых чисел. Для этого нужно показать, что если p равно нулю или натуральному числу, а q равно нулю или натуральному числу, то выполняются равенства (ap) q =ap q , (a − p) q =a (−p) q , (a p ) −q = a p (−q) и (a − p) −q = a (−p) (−q) . Давай сделаем это.
В качестве примера докажем, что свойство мощности выполняется как для положительных, так и для неположительных целых чисел. Для этого нужно показать, что если p равно нулю или натуральному числу, а q равно нулю или натуральному числу, то выполняются равенства (ap) q =ap q , (a − p) q =a (−p) q , (a p ) −q = a p (−q) и (a − p) −q = a (−p) (−q) . Давай сделаем это.
Для положительных p и q равенство (ap) q =a p·q было доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0 q =a 0 =1 , откуда (a 0) q =a 0 q . Аналогично, если q=0 , то (ap) 0 =1 и a p 0 =a 0 =1 , откуда (ap) 0 = a p 0 . Если и p=0, и q=0, то (a 0) 0 =1 0 =1 и a 0 0 =a 0 =1 , откуда (a 0) 0 =a 0 0 .
Теперь докажем, что (a −p) q =a (−p) q . По определению степени с отрицательным целым показателем , то . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению представляет собой степень вида a−(pq) , которая в силу правил умножения может быть записана как a(−p)q .
Аналогично.
И .
По такому же принципу можно доказать и все остальные свойства степени с целым показателем, записанные в виде равенств.
В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a−n >b−n, справедливого для любого отрицательного целого числа −n и любых положительных a и b, для которых выполняется условие a . Запишем и преобразуем разность между левой и правой частями этого неравенства: . Так как по условию n n , следовательно, b n − a n >0 . Произведение a n ·b n также положительно как произведение положительных чисел an и b n . Тогда полученная дробь положительна как частное положительных чисел b n − a n и a n b n . Отсюда следует, что a−n >b−n , что и требовалось доказать.
Последнее свойство степеней с целыми показателями доказывается так же, как и аналогичное свойство степеней с натуральными показателями.
Свойства степеней с рациональными показателями
Мы определили степень с дробным показателем, распространив на нее свойства степени с целым показателем. Другими словами, степени с дробными показателями имеют те же свойства, что и степени с целыми показателями. А именно:
Другими словами, степени с дробными показателями имеют те же свойства, что и степени с целыми показателями. А именно:
- свойство произведения степеней с одинаковым основанием при a>0 , а если и , то и при a≥0 ;
- свойство частичных степеней с теми же основаниями при а>0;
- свойство дробного произведения при a>0 и b>0 , а если и , то при a≥0 и (или) b≥0 ;
- свойство частного в дробной степени при a>0 и b>0 , а если , то при a≥0 и b>0 ;
- свойство степени в степени при a>0 , а если и , то при a≥0 ;
- свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b, a 0 справедливо неравенство a p p , а при pp >b p ;
- свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q p>q при 0p q, а при a>0 неравенство a p >a q .
- а п а д = а п + д ;
- a p:a q = a p−q ;
- (а б) р = а п б р ;
- (а:б) р =а р:б р ;
- (a p) q = a p q ;
- для любых положительных чисел a и b , a 0 справедливо неравенство a p p , а для p p >b p ;
- для иррациональных чисел p и q , p>q для 0p q , а для a>0 неравенство a p >a q .
Доказательство свойств степеней с дробными показателями основано на определении степени с дробным показателем, на свойствах арифметического корня n-й степени и на свойствах степени с целым показателем. Приведем доказательства.
Приведем доказательства.
По определению степени с дробным показателем и , то . Свойства арифметического корня позволяют записать следующие равенства. Далее, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать следующим образом: . Это завершает доказательство.
Второе свойство степеней с дробными показателями доказывается точно так же:
Остальные равенства доказываются по аналогичным принципам:
Перейдем к доказательству следующего свойства. Докажем, что для любых положительных a и b , a 0 справедливо неравенство a p p , а при p p >b p . Мы записываем рациональное число p как m/n , где m — целое число, а n — натуральное число. Условия p 0 в этом случае будут эквивалентны условиям m 0 соответственно. Для m>0 и am m . Из этого неравенства по свойству корней имеем , а так как а и b — положительные числа, то, исходя из определения степени с дробным показателем, полученное неравенство можно переписать в виде , то есть a p p .
Аналогично, когда m m >b m , откуда , то есть и a p >b p .
Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q p>q при 0p q и при a>0 неравенство a p >a q . Мы всегда можем привести рациональные числа p и q к общему знаменателю, получим обыкновенные дроби и , где m 1 и m 2 — целые числа, а n — натуральное число. В этом случае условию p>q будет соответствовать условие m 1 >m 2 , которое следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0m 1 m 2 и при a>1 выполняется неравенство a m 1 >am 2 . Эти неравенства в терминах свойств корней можно переписать соответственно в виде и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 выполняется неравенство a p >a q .
Свойства степеней с иррациональными показателями
Из того, как определяется степень с иррациональным показателем, можно заключить, что она обладает всеми свойствами степеней с рациональным показателем. Таким образом, для любых a>0 , b>0 и иррациональных чисел p и q верны следующие свойства степеней с иррациональными показателями :
Таким образом, для любых a>0 , b>0 и иррациональных чисел p и q верны следующие свойства степеней с иррациональными показателями :
Отсюда можно заключить, что степени с любыми вещественными показателями p и q при а>0 обладают теми же свойствами.
- Алгебра — 10 класс. Тригонометрические уравнения Урок и презентация на тему: «Решение простейших тригонометрических уравнений» Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, предложения! Все материалы […]
- Объявлен конкурс на вакансию «ПРОДАВЕЦ — КОНСУЛЬТАНТ»: Обязанности: продажа мобильных телефонов и аксессуаров для услуг мобильной связи для абонентов Билайн, Теле2, МТС подключение тарифных планов и услуг Билайн и Теле2, МТС консалтинг [… ]
- Параллелепипед формулы Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом.
 Кубоид — это прямоугольный параллелепипед, каждая грань которого представляет собой прямоугольник. Любой параллелепипед характеризуется 3 […]
Кубоид — это прямоугольный параллелепипед, каждая грань которого представляет собой прямоугольник. Любой параллелепипед характеризуется 3 […] - Общество защиты прав потребителей Астана Для того, чтобы получить пин-код для доступа к данному документу на нашем сайте, отправьте SMS-сообщение с текстом zan на номер Абоненты GSM операторов (Activ, Kcell, Beeline, NEO, Tele2) отправив SMS на номер, […]
- ПРАВОПИСАНИЕ Н И НН РАЗНЫМИ ЧАСТЯМИ РЕЧИ 2. Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […]
- Принять закон о родовых поместьях Принять федеральный закон о безвозмездном выделении каждому желающему гражданину Российской Федерации или семье граждан участка земли для устройства на ней Родового Поместья на следующих условиях: 1. Участок предоставляется […]
- ИНСПЕКЦИЯ ГОСТЕХНАДЗОРА ПО БРЯНСКОЙ ОБЛАСТИ Квитанция об оплате государственной пошлины (Скачать-12,2 кб) Заявления о регистрации для физических лиц (Скачать-12 кб) Заявления о регистрации для юридических лиц (Скачать-11,4 кб) 1.
 При регистрации нового машина : 1.заявление 2.паспорт […]
При регистрации нового машина : 1.заявление 2.паспорт […] - Давно мы не играли в турниры 1х1. И пора возобновить эту традицию. Пока мы не сможем организовать отдельный ладдер и турниры для игроков 1 на 1, мы предлагаем использовать профили вашей команды на сайте. Вычитать или добавлять очки за игры в матчах […]
Напоминаем, что в этом уроке мы разбираемся со свойствами степени с натуральными показателями и нулем. Степени с рациональными показателями и их свойства будут рассмотрены на уроках для 8 класса.
Показатель степени с натуральным показателем имеет несколько важных свойств, позволяющих упростить расчеты в показательных примерах.
Свойство №1
Произведение полномочий
Помните!
При умножении степеней с одинаковым основанием основание остается неизменным, а показатели степени складываются.
a m a n = a m + n, где «a» — любое число, а «m», «n» — любые натуральные числа.
Это свойство степеней также влияет на произведение трех и более степеней.
- Упростите выражение.
б б 2 б 3 б 4 б 5 = б 1 + 2 + 3 + 4 + 5 = б 15 - Присутствует как степень.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17 - Присутствует как степень.
(0,8) 3 (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Важно!
Обратите внимание, что в указанном свойстве речь шла только об умножении полномочий с одинаковыми основаниями . Это не касается их добавления.
Вы не можете заменить сумму (3 3 + 3 2) на 3 5 . Это понятно, если вычислить
(3 3 + 3 2) = (27 + 9) = 36 и 3 5 = 243
Свойство #2
Частные степени
Помните!
При делении степеней с одинаковым основанием основание остается неизменным, а из показателя степени делимого вычитается показатель степени делителя.
= 11 3 − 2 4 2 − 1 = 11 4 = 44
3 8: t = 3 4
T = 3 8 − 4
Ответ: t = 3 4 = 81 Используя свойства №1 и №2, можно легко упростить выражения и выполнять вычисления.
- Пример. Упростите выражение.
4 5 м + 6 4 м + 2: 4 4 м + 3 = 4 5 м + 6 + м + 2: 4 4 м + 3 = 4 6 м + 8 − 4 м − 3 = 4 2 м + 5 - Пример. Найдите значение выражения, используя свойства степени.
= знак равно знак равно
=2 9 + 2 2 5
= 2 11 — 5 = 2 6 = 642 11 2 5 Важно!
Обратите внимание, что свойство 2 касалось только разделения полномочий по одинаковым основаниям.
Вы не можете заменить разницу (4 3 −4 2) на 4 1 . Это понятно, если учесть (4 3 −4 2) = (64 − 16) = 48 , и 4 1 = 4
Будьте осторожны!
Свойство №3
Возведение в степеньПомните!
При возведении степени в степень основание степени остается неизменным, а показатели степени умножаются.
(a n)m = a n m, где «a» — любое число, а «m», «n» — любые натуральные числа.
Свойства 4
Степень продуктаПомните!
При возведении произведения в степень каждый из множителей возводится в степень.
 Затем результаты умножаются.
Затем результаты умножаются.(a b) n = a n b n, где «а», «b» — любые рациональные числа; «n» — любое натуральное число.
- Пример 1
(6 a 2 b 3 c) 2 = 6 2 a 2 2 b 3 2 s 1 2 = 36 a 4 b 6 s 2 - Пример 2
(−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6
Важно!
Обратите внимание, что свойство №4, как и другие свойства степеней, применяется и в обратном порядке.
(a n b n)= (a b) nТо есть для умножения степеней с одинаковыми показателями можно умножать основания, а показатель степени оставить без изменений.
- Пример. Рассчитать.
2 4 5 4 = (2 5) 4 = 10 4 = 10 000 - Пример. Рассчитать.
0,5 16 2 16 = (0,5 2) 16 = 1
В более сложных примерах могут быть случаи, когда умножение и деление необходимо выполнять над степенями с разными основаниями и разными показателями степени. В этом случае мы советуем вам сделать следующее.
Например, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 (-0,25) 20 = 4 4 20 (-0,25) 20 = 4 (4 (-0,25)) 20 = 4 (-1) 20 = 4 1 = четыре
Свойства 5
Степень частного (дробей)Помните!
Чтобы возвести частное в степень, можно отдельно возвести делимое и делитель в эту степень и разделить первый результат на второй.
(a:b)n = a n:b n, где «a», «b» — любые рациональные числа, b ≠ 0, n — любое натуральное число.
- Пример. Выразите выражение в виде частичных степеней.
(5:3) 12 = 5 12:3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведения дроби в степень мы остановимся более подробно на следующей странице.
- Пример 1
Ранее мы уже говорили о том, что такое степень числа. У него есть определенные свойства, полезные при решении задач: именно их и все возможные показатели мы и разберем в этой статье. Мы также продемонстрируем на примерах, как их можно доказать и правильно применить на практике.
Напомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n-го числа множителей, каждый из которых равен а. Нам также нужно помнить, как правильно умножать действительные числа. Все это поможет нам сформулировать следующие свойства степени с натуральным показателем:
Нам также нужно помнить, как правильно умножать действительные числа. Все это поможет нам сформулировать следующие свойства степени с натуральным показателем:
Определение 1
1. Основное свойство степени: a man a n = a m + n
Можно обобщить до: an 1 · an 2 · … · an k = a n 1 + n 2 + … + n k .
2. Факторное свойство для степеней с одинаковым основанием: a m: a n = a m − n
3. Свойство степени произведения: (a b) n = a n b n
Равенство можно расширить до: (a 1 a 2 … a k) n = a 1 n a 2 n … a k n
4. Свойство натуральной степени: (a: b) n = a n: b n
5. Возводим степень в степень: (am) n = a m n ,
Можно обобщить до: (((an 1) n 2) …) n k = an 1 n 2 … n k
6. Сравните степень с нулем:
- , если a > 0, то для любого натурального n, n будет больше нуля;
- при равном 0, n также будет равно нулю;
- за
- для
7. Равенство
8. Неравенство a m > an будет верным при условии, что m и n натуральные числа, m больше n и a больше нуля и не меньше единицы.
В результате получилось несколько равенств; если вы выполните все указанные выше условия, то они будут идентичными. Для каждого из равенств, например для основного свойства, можно поменять местами правую и левую части: a m · a n = a m + n — то же, что a m + n = a m · an . В таком виде он часто используется при упрощении выражений.
1. Начнем с основного свойства степени: равенство a m · a n = a m + n будет верным для любых натуральных m и n и вещественного a . Как доказать это утверждение?
Базовое определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим такую запись:
Это можно сократить до (вспомним основные свойства умножения). В результате мы получили степень числа a с натуральным показателем m + n. Таким образом, a m + n , а значит, основное свойство степени доказано.
Давайте рассмотрим конкретный пример, чтобы доказать это.
Пример 1
Итак, у нас есть две степени с основанием 2. Их натуральные показатели равны 2 и 3 соответственно. Получили равенство: 2 2 2 3 = 2 2 + 3 = 2 5 Подсчитаем значения, чтобы проверить правильность этого равенства.
Их натуральные показатели равны 2 и 3 соответственно. Получили равенство: 2 2 2 3 = 2 2 + 3 = 2 5 Подсчитаем значения, чтобы проверить правильность этого равенства.
Проделаем необходимые математические операции: 2 2 2 3 = (2 2) (2 2 2) = 4 8 = 32 и 2 5 = 2 2 2 2 2 = 32
В итоге получили: 2 2 2 3 = 2 5 . Имущество доказано.
Благодаря свойствам умножения мы можем обобщить свойство, сформулировав его в виде трех или более степеней, для которых показатели степени являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n 1, n 2 и т. д. буквой k, то получим правильное равенство:
а п 1 а п 2 … а п k знак равно а п 1 + п 2 + … + п k .
Пример 2
2. Далее нужно доказать следующее свойство, называемое факторным и присущее степеням с одинаковыми основаниями: это равенство a m : an = a m − n , справедливое для любых натуральных m и n (и m больше n)) и любой ненулевой действительный a .
Для начала поясним, что именно означают условия, которые упоминаются в формулировке. Если взять a равным нулю, то в итоге мы получим деление на ноль, чего делать нельзя (ведь 0 n = 0). Условие, что число m должно быть больше n, необходимо для того, чтобы мы могли оставаться в пределах натуральных показателей: вычитая n из m, мы получаем натуральное число. Если условие не выполняется, мы получим отрицательное число или ноль, и снова выйдем за рамки изучения степеней с натуральными показателями.
Если взять a равным нулю, то в итоге мы получим деление на ноль, чего делать нельзя (ведь 0 n = 0). Условие, что число m должно быть больше n, необходимо для того, чтобы мы могли оставаться в пределах натуральных показателей: вычитая n из m, мы получаем натуральное число. Если условие не выполняется, мы получим отрицательное число или ноль, и снова выйдем за рамки изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из изученного ранее напомним основные свойства дробей и сформулируем равенство следующим образом:
a m − n a n = a (m − n) + n = a m
Из него можно вывести: a m − n an n = a m
Вспомним связь между делением и умножением. Отсюда следует, что a m − n есть частное степеней a m и an . Это доказательство свойства второй степени.
Пример 3
Подставить для наглядности в показатели конкретные цифры и обозначить основание степени π: π 5: π 2 = π 5 − 3 = π 3
3. Далее проанализируем свойство степени произведения: (a · b) n = a n · b n для любых вещественных a и b и натурального n .
Согласно основному определению степени с натуральным показателем можно переформулировать равенство следующим образом:
Помня о свойствах умножения, напишем: . Это означает то же самое, что и a n · b n .
Пример 4
2 3 — 4 2 5 4 = 2 3 4 — 4 2 5 4
Если у нас есть три или более множителей, то это свойство применимо и к этому случаю. Введем обозначение k для числа факторов и напишем:
(a 1 a 2 … a k) n = a 1 n a 2 n … a k n
Пример 5
При конкретных числах получаем следующее правильное равенство: (2 (- 2 , 3) a) 7 = 2 7 (- 2 , 3) 7 а
4. После этого попробуем доказать факторное свойство: (a: b) n = a n: b n для любых действительных a и b, если b не равно 0 и n — натуральное число.
Для доказательства мы можем использовать свойство предыдущей степени. Если (a: b) n b n = ((a: b) b) n = a n и (a: b) n b n = an , то отсюда следует, что (a: b) n есть частное от деления an на b n .
Пример 6
Посчитаем пример: 3 1 2: — 0 . 5 3 = 3 1 2 3: (- 0 , 5) 3
5 3 = 3 1 2 3: (- 0 , 5) 3
Пример 7
Начнем сразу с примера: (5 2) 3 = 5 2 3 = 5 6
А теперь составим цепочку из равенства, которые докажут нам правильность равенства:
Если у нас в примере есть степени степеней, то это свойство верно и для них. Если у нас есть любые натуральные числа p, q, r, s, то будет верно:
a p q y s = a p q y s
Пример 8
Добавим уточнений: (((5 , 2) 3) 2) 5 = (5 , 2) 3 2 5 = (5 , 2) 30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, — это свойство сравнения.
Сначала сравним показатель степени с нулем. Почему n > 0 при условии, что а больше 0?
Если мы умножим одно положительное число на другое, мы также получим положительное число. Зная этот факт, можно сказать, что это не зависит от количества множителей — результат умножения любого количества положительных чисел есть положительное число. А что такое степень, как не результат умножения чисел? Тогда для любой степени n с положительным основанием и натуральным показателем это будет верно.
Пример 9
3 5 > 0 , (0 , 00201) 2 > 0 и 34 9 13 51 > 0
Также очевидно, что степень с основанием, равным нулю, сама по себе равна нулю. В какую бы степень мы ни возводили ноль, он таким и останется.
Пример 10
0 3 = 0 и 0 762 = 0
Если основание степени является отрицательным числом, то доказательство немного усложняется, так как важным становится понятие четного/нечетного показателя степени. Начнем со случая, когда показатель степени четен и обозначим его через 2 · m , где m — натуральное число.
Вспомним, как правильно умножать отрицательные числа: произведение а · а равно произведению модулей, а значит, это будет положительное число. Тогда и степень a 2 · m также положительны.
Пример 11
Например, (− 6) 4 > 0 , (− 2 , 2) 12 > 0 и — 2 9 6 > 0
Что, если показатель степени с отрицательным основанием является нечетным числом? Обозначим его 2 · m − 1 .
Тогда
Все произведения a · a , согласно свойствам умножения, положительны, как и их произведение. Но если мы умножим его на единственное оставшееся число a, то конечный результат будет отрицательным.
Но если мы умножим его на единственное оставшееся число a, то конечный результат будет отрицательным.
Тогда получаем: (− 5) 3
Как это доказать?
и
Пример 12
Например, верны неравенства: 3 7 (0 , 75) 124
8. Нам остается доказать последнее свойство: если мы имеем две степени, основания которых одинаковы и положительны, а показатели степени — натуральные числа, то больше та из них, у которой показатель меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями больше единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Сначала нам нужно убедиться, что м
Выносим a n за скобки, после чего наша разность примет вид a n · (am − n − 1) . Его результат будет отрицательным (поскольку результат умножения положительного числа на отрицательное отрицателен). Действительно, по начальным условиям m − n > 0, тогда a m − n − 1 отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
Оказалось, что a m − a n
Осталось доказать вторую часть сформулированного выше утверждения: a m > a верно при m > n и a > 1 . Укажем разницу и вынесем n за скобки: (a m — n — 1) . Степень n больше единицы даст положительный результат; и сама разность тоже окажется положительной в силу начальных условий, а при a > 1 степень a m − n больше единицы. Получается, что a m − an > 0 и am > an , что и требовалось доказать.
Пример 13
Пример с конкретными числами: 3 7 > 3 2
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичными, поскольку положительные целые числа являются натуральными числами, а это означает, что для них справедливы и все доказанные выше равенства. Они подходят и для случаев, когда показатели степени отрицательны или равны нулю (при условии, что основание самой степени не равно нулю).
Таким образом, свойства степеней одинаковы для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей степени m и n (при условии, что они целые). Запишем их кратко в виде формул: : b) n = a n: b n
Запишем их кратко в виде формул: : b) n = a n: b n
5. (am) n = a m n
6. a nb − n с целым положительным числом n, положительными a и b, a
7. а мн и 01 а м > а н .
Если основание степени равно нулю, то записи a m и an имеют смысл только в случае натуральных и положительных m и n. В результате получаем, что приведенные выше формулировки годятся и для случаев со степенью с нулевым основанием, если выполняются все остальные условия.
Доказательства этих свойств в этом случае просты. Нам нужно будет вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с вещественными числами.
Проанализируем свойство степени в степени и докажем, что оно верно как для целых положительных, так и для целых неположительных чисел. Начнем с доказательства равенств (a p) q = a p q , (a − p) q = a (− p) q , (ap) − q = a p (− q) и (a − p) − q = a (− p) (−q)
Условия: p = 0 или натуральное число; д — аналогично.
Если значения p и q больше 0, то получаем (ap p)q = a p · q . Мы уже доказывали подобное равенство ранее. Если р = 0, то:
Мы уже доказывали подобное равенство ранее. Если р = 0, то:
(a 0) q = 1 q = 1 a 0 q = a 0 = 1
Следовательно, (a 0) q = a 0 q
Для q = 0 все точно так же:
(a p) 0 = 1 a p 0 = a 0 = 1
Результат: (ap) 0 = a p 0 .
Если оба индикатора равны нулю, то (a 0) 0 = 1 0 = 1 и a 0 0 = a 0 = 1, тогда (a 0) 0 = a 0 0 .
Вспомним доказанное выше свойство частного в степени и запишем:
1 a p q = 1 q a p q
Если 1 p = 1 1 … 1 = 1 и a p q = a p q , то 1 q a p q = 1 a p q
Мы можем преобразовать это обозначение в силу основных правил умножения в a (− p) · q .
Также: a p — q = 1 (ap) q = 1 a p q = a — (p q) = a p (- q) .
И (a — p) — q = 1 a p — q = (ap) q = a p q = a (- p) (- q)
Остальные свойства степени доказываются аналогично преобразованием существующие неравенства. Подробно на этом останавливаться не будем, укажем лишь на сложные моменты.
Доказательство предпоследнего свойства: напомним, что a − n > b − n верно для любых целых отрицательных значений n и любых положительных a и b при условии, что a меньше b .
Тогда неравенство можно преобразовать следующим образом:
1 a n > 1 b n
Запишем правую и левую части в виде разности и проведем необходимые преобразования:
1 a n — 1 b n = b n — a n a n b n
что в условии a меньше b , то по определению степени с натуральным показателем: — a n 0 .
a n · b n оказывается положительным числом, потому что его множители положительны. В итоге имеем дробь b n — a n an n · b n , что в итоге также дает положительный результат. Отсюда 1 an > 1 b n , откуда a − n > b − n , что и требовалось доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с натуральными показателями.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы обсуждали, что такое степени с рациональными (дробными) показателями. Их свойства такие же, как у степеней с целыми показателями. Запишем:
Определение 3
1. a m 1 n 1 a m 2 n 2 = a m 1 n 1 + m 2 n 2 при a > 0, и если m 1 n 1 > 0 и m 2 n 2 > 0, тогда для a ≥ 0 (степени свойств продукта с той же базой).
2. a m 1 n 1: b m 2 n 2 = a m 1 n 1 — m 2 n 2, если a > 0 (частное свойство).
3. a b m n = a m n b m n при a > 0 и b > 0, а если m 1 n 1 > 0 и m 2 n 2 > 0, то при a ≥ 0 и (или) b ≥ 0 (свойство произведения в дробной степени ).
4. а: b m n = a m n: b m n при a > 0 и b > 0, а если m n > 0, то при a ≥ 0 и b > 0 (свойство частного дробной степени).
5. a m 1 n 1 m 2 n 2 = am 1 n 1 m 2 n 2 при a > 0, а если m 1 n 1 > 0 и m 2 n 2 > 0, то при a ≥ 0 (степень свойство в градусах).
6.ap0; если pb p (свойство сравнения степеней с одинаковыми рациональными показателями).
7.apq at 00 – a p > a q
Для доказательства этих положений нам нужно вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n-й степени и каковы свойства степень с целым показателем. Давайте рассмотрим каждое свойство.
В зависимости от того, что такое степень с дробным показателем степени, получаем:
а м 1 н 1 = ам 1 н 1 и ам 2 н 2 = ам 2 н 2, следовательно, а м 1 н 1 ам м 2 н 2 = ам 1 н 1 ам 2 н 2
Свойства корня позволят вывести равенства:
a m 1 m 2 n 1 n 2 a m 2 m 1 n 2 n 1 = a m 1 n 2 am 2 n 1 n 1 n 2
Отсюда получаем получаем: a m 1 n 2 a m 2 n 1 n 1 n 2 = a m 1 n 2 + m 2 n 1 n 1 n 2
Преобразуем:
a m 1 n 2 a m 2 n 1 n 1 n 2 = a m 1 n 2 + m 2 n 1 n 1 n 2
Показатель степени можно записать как:
m 1 n 2 + m 2 n 1 n 1 n 2 = m 1 n 2 n 1 n 2 + m 2 n 1 n 1 n 2 = m 1 n 1 + m 2 n 2
Это доказательство. Точно так же доказывается и второе свойство. Запишем цепочку равенств:
Точно так же доказывается и второе свойство. Запишем цепочку равенств:
а м 1 п 1: а м 2 п 2 = а м 1 п 1: а м 2 п 2 = а м 1 п 2: а м 2 п 1 п 1 п 2 = = а м 1 п 2 — м 2 п 1 п 1 п 2 = a m 1 n 2 — m 2 n 1 n 1 n 2 = a m 1 n 2 n 1 n 2 — m 2 n 1 n 1 n 2 = a m 1 n 1 — m 2 n 2
Доказательства остальных равенств:
а б м п знак равно (а б) м п знак равно а м б м п знак равно а м п б м п знак равно а м п б м п ; (a: b) m n = (a: b) m n = a m: b m n = = a m n: b m n = a m n: b m n ; а м 1 п 1 м 2 п 2 знак равно а м 1 п 1 м 2 п 2 знак равно а м 1 п 1 м 2 п 2 = = а м 1 м 2 п 1 п 2 = а м 1 м 2 п 1 п 2 = = а м 1 м 2 n 2 n 1 = а м 1 м 2 n 2 n 1 = а м 1 n 1 м 2 n 2
Следующее свойство: докажем, что для любых значений a и b больше 0, если a меньше b, будет выполнено pbp
Представим рациональное число p как m n . В данном случае m — целое число, n — натуральное число. Тогда условия p0 будут распространены на m0. При m > 0 и a
Воспользуемся свойством корней и получим: a m n
Учитывая положительность значений a и b , перепишем неравенство в виде a m n
Таким же образом для mb m получаем a m n > b m n, поэтому a m n > b m n и a p > b p .
Нам осталось доказать последнее свойство. Докажем, что для рациональных чисел p и q p > q для 00 будет верным a p > a q .
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m 1 n и m 2 n
Здесь m 1 и m 2 — целые числа, а n — натуральное число. Если p > q, то m 1 > m 2 (с учетом правила сравнения дробей). Тогда при 01 – неравенство a 1 m > a 2 m .
Их можно переписать в следующем виде:
a m 1 na m 2 n
Тогда можно произвести преобразования и получить в результате:
am 1 na m 2 n
Подытожим: при p > q и 00 – a p > a q .
Основные свойства степеней с иррациональными показателями
Все описанные выше свойства степени с рациональными показателями могут быть распространены на такую степень. Это следует из самого его определения, которое мы дали в одной из предыдущих статей. Кратко сформулируем эти свойства (условия: a > 0, b > 0, показатели p и q — иррациональные числа):
Определение 4
1. a p a q = a p + q
a p a q = a p + q
2. a p: a q = a p − q
3. (a b) p = a p b p
4. (a: b) p = a p: b p
- 2
- Продукт : logloglog (𝑥𝑦) = 𝑥+𝑦,
- Дивизион : logloglog𝑥𝑦 = 𝑥 — 𝑦,
- Powers : loglog. (𝑥)=𝑛𝑥,
- изменение базы : logloglog𝑥=𝑥𝑎.
- Для решения логарифмических уравнений мы использовали законы
Логарифмы:
- Продукт : logloglog (𝑥𝑦) = 𝑥+𝑦,
- Дивизион : logloglog𝑥𝑦 = 𝑥 — 𝑦,
- Powers : loglog (𝑥 𝑥. )=𝑛𝑥,
- изменение основания : logloglog𝑥=𝑥𝑎.
- Если у нас есть логарифм основания 𝑎, мы также можем преобразовать его в логарифм основания 𝑎 с использованием loglog𝑥=1𝑘𝑥.
- Мы также можем поменять местами основание и аргумент логарифма, используя loglog𝑥=1𝑎.
- Мы также можем решать логарифмические уравнения, преобразуя логарифмическую форму 𝑦=𝑥log в экспоненциальной форме 𝑥=𝑎.
- Различные экспоненциальные основания
- Сложение и вычитание
- Решения
- Use the property above to find x : 10 m-n = х; так что 10 5-8 = -3
- Переместить десятичную дробь x раз: (0,0045 x 10 8 )
- Чек: 4,5 x 10 5 = 450 000 ✔; 0,0045 x 10 8 = 450 000 ✔
- Используйте указанное выше свойство, чтобы найти x :10 m-n = x ; 10 6-4 = +2
- Переместить десятичную дробь x раз: (632 x 10 4 )
- Чек: 6,32 x 10 6 = 6 320 000 ✔ ; 632 x 10 4 = 6 320 000 92 285 ✔ 92 286
- Коэффициенты не представляют одинаковые разрядные значения (хотя 2,5 + 4,5 = 7, мы видим, что это не дает нам ничего близкого к правильному ответу 2950).
- Мы не можем складывать части экспоненты вместе, и
- Отсутствуют свойства показателей степени для сложения или вычитания чисел в экспоненциальном представлении
- Изменение Одним из чисел, поэтому оба имеют одинаковую экспоненциальную базу: 4,5 x 10 2 95.

- Задача перезаписи с измененной экспоненциальной базой: (2,5 x 10 3 ) + (0,45 x 10 3 )
- Добавить коэффициенты
- (3,4 x 10 5 ) + (5,68 x 10 8 )
- (5,97 x 10 12 ) — (4,45 x 10 10 )
- (1,07 х 10 -5 ) + (4,98 х 10 -3 )
- (5,70 x 10 -3 ) — (6,24 x 10 -6 )
39 800 x 10 4
0,000 004 9 х 10 9
1450 x 10 -8
0,000 74 х 10 2
(3,4 x 10 5 ) + (5,68 x 10 8 )
(0,0034 х 10 8 ) + (5,68 х 10 8 ) = (5,6834 х 10 8 )
-ИЛИ-
(3,4 х 10 5 ) + (5680 х 10 5 ) = (5,6834 х 10 8 )
(5,97 x 10 12 ) — (4,45 x 10 10 )
(5,97 х 10 12 ) — (0,0445 х 10 12 ) = (5,9255 х 10 12 )
-ИЛИ-
(597 x 10 10 ) — (4,45 x 10 10 ) = 592,55 x 10 10 = (5,9255 x 10 12 )
(1,07 х 10 -5 ) + (4,98 х 10 -3 )
(0,0107 х 10 -3 ) + (4,98 х 10 -3 ) = (4,9907 х 10 -3 )
-ИЛИ-
(1,07 х 10 -5 ) + (498 х 10 -5 ) = 499,07 х 10 -5 ) = (4,9907 х 10 -3 )
(5,70 x 10 -3 ) — (6,24 x 10 -6 )
(5,70 х 10 -3 ) — (0,00624 х 10 -3 ) = (5,69376 х 10 -3 )
-ИЛИ-
(5700 x 10 -6 ) — (6,24 x 10 -6 ) = 5693,76 x 10 -6 = (5,69376 x 10 -3 )
- Упростите выражение.
б б 2 б 3 б 4 б 5 = б 1 + 2 + 3 + 4 + 5 = б 15 - Присутствует как степень.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17 - Присутствует как степень.
(0,8) 3 (0,8) 12 = (0,8) 3 + 12 = (0,8) 15 - Запишите частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2 - Рассчитать.
- , a — отрицательно, потому что показатель степени при -13 нечетный.
Пример 5: Заменить ( ) на степень с основанием r:
Имеем , то есть .
9. Подведение итогов
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и другие. Алгебра 7. 6-е издание. М.: Просветление. 2010
1. Школьный помощник (Источник).
1. Выразить в степени:
a B C D E)
3. Записать в виде степени с основанием 2:
4. Определить знак числа:
a)
5. Заменить ( ) на a степень числа с основанием r:
а) r 4 ( ) = r 15 ; б) ( ) r 5 = r 6
Умножение и деление степеней с одинаковыми показателями
На этом уроке мы будем изучать умножение степеней с одинаковыми показателями.
 Для начала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и о возведении степени в степень. Затем мы формулируем и доказываем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью мы решим ряд типовых задач.
Для начала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и о возведении степени в степень. Затем мы формулируем и доказываем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью мы решим ряд типовых задач. Напоминание основных определений и теорем
Здесь a — основание степени
— n -я степень числа.
Теорема 1. Для любых чисел a и любых натуральных n и k верно равенство:
При умножении степеней с одним и тем же основанием степени складываются, основание остается неизменным.
Теорема 2. Для любого числа есть и любое натуральное n и k, такие, что n > k верно равенство:
При делении степеней с одинаковым основанием степени вычитаются, а основание остается неизменным.
Теорема 3. Для любых чисел a и любых натуральных n и k верно равенство:
то же самое индикаторы .

Примеры умножения степеней с одинаковыми показателями
Рассмотрим следующие примеры:
Запишем выражения для определения степени.
Вывод: Из примеров видно, что , но это еще нужно доказать. Сформулируем теорему и докажем ее в общем случае, т. е. для любых a и b и любых натуральных n.
Формулировка и доказательство теоремы 4
Для любых чисел a и b и любых натуральных n равенство:
Доказательство Теорема 4 .
По определению степени:
Итак, мы доказали, что .
Для умножения степеней с одинаковым показателем достаточно умножить основания, а показатель степени оставить без изменений.
Формулировка и доказательство теоремы 5
Сформулируем теорему для деления степеней с одинаковыми показателями.
Для любого номера a и b( ) и любое натуральное n равенство верно:
Доказательство Теорема 5 .

Запишем и по определению степени:
Формулировка теорем словами
Итак, мы доказали, что .
Чтобы разделить степени с одинаковыми показателями степени друг на друга, достаточно разделить одно основание на другое, а показатель степени оставить без изменений.
Решение типовых задач с помощью теоремы 4
Пример 1: Выразите в виде произведения степеней.
Для решения следующих примеров воспользуемся теоремой 4.
Для решения следующего примера вспомним формулы:
Обобщение теоремы 4
Обобщение теоремы 4: типичные проблемы
Пример 2: Запишите как степень произведения.
Пример 3: Запишите в виде степени с показателем степени 2.
Примеры расчета
Пример 4: Расчет наиболее рациональным способом.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачева М.В., Федорова Н.
 Е. и другие. Алгебра 7.М.: Образование. 2006
Е. и другие. Алгебра 7.М.: Образование. 20062. Школьный помощник (Источник).
1. Присутствует как произведение полномочий:
а) ; б) ; в) ; ГРАММ) ;
2. Записать как степень произведения:
3. Записать в виде степени с показателем 2:
4. Рассчитать наиболее рациональным способом.
Урок математики на тему «Умножение и деление степеней»
Разделы: Математика
Педагогическая цель :
- учащийся научится различать свойства умножения и деления степеней экспонента; применять эти свойства в случае одних и тех же оснований;
- студент будет иметь возможность выполнять преобразования степеней с разными основаниями и сможет выполнять преобразования в комбинированных задачах.
- организовать работу учащихся путем повторения ранее изученного материала;
- обеспечивают уровень воспроизведения путем выполнения упражнений различного типа;
- организовать самооценку обучающихся посредством тестирования.

- вычислить: 2 2 2 3 = ? 3 3 3 2 3 =?
- Упрощение: a 2 a 20 =? б 30 б 10 б 15 = ?
- В среднем человек за свою жизнь съедает 32 10 2 кг огурцов.
- Оса способна совершать беспосадочный перелет на расстояние 3,2 10 2 км.
- При растрескивании стекла трещина распространяется со скоростью около 5 10 3 км/ч.
- За свою жизнь лягушка съедает более 3 тонн комаров. Используя градус, напишите в кг.
- Наиболее плодовитой является океанская рыба — луна (Mola mola), которая за один нерест откладывает до 300 000 000 икринок диаметром около 1,3 мм. Запишите это число, используя степень. VII. Домашнее задание.
- Учебник «Алгебра-7», авторы Ю.Н. Макарычев, Н.Г. Миндюк и др.
- Дидактический материал для 7 класса Л.В. Кузнецова, Л.И. Звавич, С.Б. Суворов.
- Математическая энциклопедия.
- Журнал «Квант».
- основное свойство степени a m ·an n =a m+n , его обобщение an 1 ·an 2 ·…· a n k =an 1 +n 2 +…+n k ;
- свойство частичных степеней с одинаковыми основаниями a m:an =a m−n ;
- свойство степени продукта (a b) n =an b n , его расширение (a 1 a 2 a k) n = a 1 n a 2 n a k n ;
- частное имущество в натуре (a:b) n =an:b n ;
- возведение в степень (a m) n =am n , его обобщение (((an 1) n 2) .
 ..) n k =an 1 ·n 2 ·… n k ;
..) n k =an 1 ·n 2 ·… n k ; - сравнение степени с нулем:
- если a>0 , то an >0 для любого натурального n ;
- если a=0 , то a n =0 ;
- , если a 2 m >0, если a 2 m−1 n;
- если m и n натуральные числа такие, что m>n , то для 0m n и a>0 верно неравенство a m >an .
- а м а н = а м + н;
- а м: а н = а м-п ;
- (a b) n = a n b n ;
- (а:б) n =а н:b н ;
- (а м) n = а м n ;
- , если n — натуральное число, a и b — положительные числа и a n n и a−n>b−n ;
- , если m и n целые числа и m>n, то для 0m n и a>1 выполняется неравенство a m >an n.

Сразу отметим, что все записанные равенства равны идентичны при указанных условиях, а их правая и левая части могут быть взаимозаменяемы. Например, основное свойство дроби a m a n = a m + n при упрощении выражения часто используется в виде a m+n = a m a n .
Теперь давайте подробно рассмотрим каждый из них.
Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называется основным свойством степени : для любого действительного числа а и любых натуральных чисел m и n выполняется равенство a m ·an =am +n верно.
Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a man можно записать в виде произведения .
 Благодаря свойствам умножения результирующее выражение можно записать в виде , и это произведение является степенью a с натуральным показателем m+n , то есть a m+n . Это завершает доказательство.
Благодаря свойствам умножения результирующее выражение можно записать в виде , и это произведение является степенью a с натуральным показателем m+n , то есть a m+n . Это завершает доказательство.Приведем пример, подтверждающий основное свойство степени. Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3, по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 2 3 =(2 2) (2 2 2)=4 8=32 и 2 5 =2 2 2 2 2=32 , так как получаем равные значения, то равенство 2 2 2 3 = 2 5 верно, и это подтверждает основное свойство степени.
Основное свойство степени, основанное на свойствах умножения, может быть обобщено на произведение трех или более степеней с одинаковыми основаниями и натуральными показателями. Таким образом, для любого количества k натуральных чисел n 1 , n 2 , …, n k верно равенство an 1 an 2 an k =an 1 +n 2 +…+n k.

Например, (2.1) 3 (2.1) 3 (2.1) 4 (2.1) 7 = (2.1) 3+3+4+7 =(2.1) 17 .
Можно перейти к следующему свойству степеней с натуральным показателем — свойству частичных степеней с одинаковыми основаниями : для любого ненулевого действительного числа a и любых натуральных чисел m и n, удовлетворяющих условию m>n , справедливо равенство a m:an =a m−n.
Прежде чем приводить доказательство этого свойства, обсудим смысл дополнительных условий в утверждении. Условие a≠0 необходимо для того, чтобы избежать деления на ноль, так как 0 n =0, а когда мы знакомились с делением, то договорились, что на ноль делить нельзя. Условие m>n вводится для того, чтобы не выходить за пределы натуральных показателей. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n), либо отрицательным числом (что происходит при m m−n an n =a (m−n) + n = a m Из полученного равенства a m−n an n = a m и соотношения умножения с делением следует, что a m−n является частичной степенью чисел m и an Это доказывает свойство частичных степеней с одинаковыми основаниями.
 0032
0032Возьмем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2, рассматриваемое свойство степени соответствует равенству π 5: π 2 = π 5−3 = π 3.
Теперь рассмотрим свойство степеней произведения : натуральная степень n произведения любых двух действительных чисел a и b равна произведению степеней an и b n , то есть (ab) n =an b n .
Действительно, по определению степени с натуральным показателем имеем . Последнее произведение, исходя из свойств умножения, можно переписать как , что равно a n b n .
Вот пример: .
Это свойство распространяется на степень произведения трех или более множителей. То есть свойство естественной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .
Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .
Следующим свойством является естественное свойство : отношение действительных чисел a и b , b≠0 к натуральной степени n равно отношению степеней an и b n , то есть (a:b) n = а н: б н .

Доказательство можно провести, используя предыдущее свойство. Итак, (a:b) n b n =((a:b) b) n =an , а из равенства (a:b) n b n =an следует, что (a:b) n есть частное от a n до b n .
Напишем это свойство на примере конкретных чисел: .
Теперь озвучим возведение в степень свойства : для любого действительного числа a и любых натуральных чисел m и n степень m в степени n равна степени a с показателем m·n , то есть (a m) п =а м · п .
Например, (5 2) 3 =5 2 3 =5 6 .
Доказательством свойства мощности в степени является следующая цепочка равенств: .
Рассматриваемое свойство может быть расширено до степени внутри степени внутри степени и так далее. Например, для любых натуральных чисел p, q, r и s равенство . Для большей наглядности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .
Осталось остановиться на свойствах сравнения степеней с натуральным показателем.
Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.

Сначала докажем, что a n >0 для любого a>0 .
Произведение двух положительных чисел есть положительное число, как следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого количества положительных чисел также будет положительным числом. А степень а с натуральным показателем n по определению есть произведение n множителей, каждый из которых равен а. Эти рассуждения позволяют нам утверждать, что для любого положительного основания а степень n является положительным числом. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
Совершенно очевидно, что для любого натурального n с a=0 степень n равна нулю. Действительно, 0 n =0·0·…·0=0 . Например, 0 3 =0 и 0 762 =0 .
Перейдем к отрицательным основаниям.
Начнем со случая, когда показатель степени — четное число, обозначим его как 2 m , где m — натуральное число. Затем . По правилу умножения отрицательных чисел каждое из произведений вида а равно произведению модулей чисел а и а, а значит, является положительным числом.
 Следовательно, продукт также будет положительным. и степень а 2 м. Вот примеры: (−6) 4 >0 , (−2,2) 12 >0 и .
Следовательно, продукт также будет положительным. и степень а 2 м. Вот примеры: (−6) 4 >0 , (−2,2) 12 >0 и .Наконец, когда основание a — отрицательное число, а показатель степени — нечетное число 2 m−1, тогда . Все произведения a·a — положительные числа, произведение этих положительных чисел также положительно, и его умножение на оставшееся отрицательное число a дает отрицательное число. В силу этого свойства (−5) 3 17 n n есть произведение левых и правых частей n истинных неравенств a свойств неравенств, доказываемое неравенство имеет вид an n . Например, благодаря этому свойству выполняются неравенства 3 7 7 и .
Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями меньше одной, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями больше единицы, больше та степень, показатель которой больше.
 Перейдем к доказательству этого свойства.
Перейдем к доказательству этого свойства.Докажем, что при m>n и 0m n . Для этого запишем разность a m − an и сравним ее с нулем. Записанная разность после вынесения n за скобки примет вид an ·(am−n−1) . Полученное произведение отрицательно как произведение положительного числа n и отрицательного числа a m−n−1 (an положительно как натуральная степень положительного числа, а разность a m−n−1 отрицательна, так как m−n >0 в силу начального условия m>n , откуда следует, что при 0m−n оно меньше единицы). Следовательно, a m − an m n , что и требовалось доказать. Например, приведем правильное неравенство.
Осталось доказать вторую часть свойства. Докажем, что для m>n и a>1 истинно a m >an. Разность a m −an после вынесения a n за скобки принимает вид an ·(am−n−1) . Это произведение положительно, так как при a>1 степень n — положительное число, а разность a m−n−1 — положительное число, так как m−n>0 в силу начального условия, а при a>1 степень m−n больше единицы. Следовательно, a m − an > 0 и am > an , что и требовалось доказать.
 Это свойство иллюстрируется неравенством 3 7 >3 2 .
Это свойство иллюстрируется неравенством 3 7 >3 2 .Свойства степеней с целыми показателями
Поскольку натуральные числа являются натуральными числами, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем абзаце.
Мы определили степень с отрицательным целым показателем, а также степень с нулевым показателем, чтобы все свойства степеней с натуральными показателями, выраженные равенствами, оставались в силе. Поэтому все эти свойства справедливы как для нулевых показателей, так и для отрицательных показателей, при этом, разумеется, основания степеней отличны от нуля.
Итак, для любых действительных и ненулевых чисел a и b, а также любых целых чисел m и n верны следующие свойства степеней с целыми показателями :
При a=0 степени a m и an имеют смысл только тогда, когда и m, и n являются целыми положительными числами, т. е. натуральными числами. Таким образом, только что написанные свойства справедливы и для случаев, когда a=0, а числа m и n — целые положительные числа.
Доказать каждое из этих свойств несложно, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с вещественными числами. В качестве примера докажем, что свойство мощности выполняется как для положительных, так и для неположительных целых чисел. Для этого нужно показать, что если p равно нулю или натуральному числу, а q равно нулю или натуральному числу, то выполняются равенства (ap) q =ap q , (a − p) q =a (−p) q , (a p ) −q = a p (−q) и (a − p) −q = a (−p) (−q) . Давай сделаем это.
Для положительных p и q равенство (ap) q =a p·q было доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0 q =a 0 =1 , откуда (a 0) q =a 0 q .
 Аналогично, если q=0 , то (ap) 0 =1 и a p 0 =a 0 =1 , откуда (ap) 0 = a p 0 . Если и p=0, и q=0, то (a 0) 0 =1 0 =1 и a 0 0 =a 0 =1 , откуда (a 0) 0 =a 0 0 .
Аналогично, если q=0 , то (ap) 0 =1 и a p 0 =a 0 =1 , откуда (ap) 0 = a p 0 . Если и p=0, и q=0, то (a 0) 0 =1 0 =1 и a 0 0 =a 0 =1 , откуда (a 0) 0 =a 0 0 .Теперь докажем, что (a −p) q =a (−p) q . По определению степени с отрицательным целым показателем , то . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению представляет собой степень вида a−(pq) , которая в силу правил умножения может быть записана как a(−p)q .
Аналогично.
И .
По такому же принципу можно доказать и все остальные свойства степени с целым показателем, записанные в виде равенств.
В предпоследнем из выписанных свойств стоит остановиться на доказательстве неравенства a −n >b −n , справедливого для любого отрицательного целого числа −n и любых положительных a и b, для которых выполняется условие a . Запишем и преобразуем разность между левой и правой частями этого неравенства: . Так как по условию n n , следовательно, b n − a n >0 .
 Произведение a n ·b n также положительно как произведение положительных чисел an и b n . Тогда полученная дробь положительна как частное положительных чисел b n − a n и a n b n . Отсюда следует, что a−n >b−n , что и требовалось доказать.
Произведение a n ·b n также положительно как произведение положительных чисел an и b n . Тогда полученная дробь положительна как частное положительных чисел b n − a n и a n b n . Отсюда следует, что a−n >b−n , что и требовалось доказать. Последнее свойство степеней с целыми показателями доказывается так же, как и аналогичное свойство степеней с натуральными показателями.
Свойства степеней с рациональными показателями
Мы определили степень с дробным показателем, распространив на нее свойства степени с целым показателем. Другими словами, степени с дробными показателями имеют те же свойства, что и степени с целыми показателями. А именно:
- свойство произведения степеней с одинаковым основанием при a>0 , а если и , то и при a≥0 ;
- свойство частичных степеней с теми же основаниями при а>0;
- свойство дробного произведения при a>0 и b>0 , а если и , то при a≥0 и (или) b≥0 ;
- свойство частного в дробной степени при a>0 и b>0 , а если , то при a≥0 и b>0 ;
- свойство степени в степени при a>0 , а если и , то при a≥0 ;
- свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b, a 0 справедливо неравенство a p p , а при pp >b p ;
- свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q p>q при 0p q, а при a>0 неравенство a p >a q .

- а п а д = а п + д ;
- a p:a q = a p−q ;
- (а б) р = а п б р ;
- (а:б) р =а р:б р ;
- (a p) q = a p q ;
- для любых положительных чисел a и b , a 0 справедливо неравенство a p p , а для p p >b p ;
- для иррациональных чисел p и q , p>q для 0p q , а для a>0 неравенство a p >a q .
Доказательство свойств степеней с дробными показателями основано на определении степени с дробным показателем, на свойствах арифметического корня n-й степени и на свойствах степени с целым показателем. Приведем доказательства.
По определению степени с дробным показателем и , то . Свойства арифметического корня позволяют записать следующие равенства. Далее, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать следующим образом: . Это завершает доказательство.
Второе свойство степеней с дробными показателями доказывается точно так же:
Остальные равенства доказываются по аналогичным принципам:
Перейдем к доказательству следующего свойства. Докажем, что для любых положительных a и b , a 0 справедливо неравенство a p p , а при p p >b p . Мы записываем рациональное число p как m/n , где m — целое число, а n — натуральное число.
 Условия p 0 в этом случае будут эквивалентны условиям m 0 соответственно. Для m>0 и am m . Из этого неравенства по свойству корней имеем , а так как а и b — положительные числа, то, исходя из определения степени с дробным показателем, полученное неравенство можно переписать в виде , то есть a p p .
Условия p 0 в этом случае будут эквивалентны условиям m 0 соответственно. Для m>0 и am m . Из этого неравенства по свойству корней имеем , а так как а и b — положительные числа, то, исходя из определения степени с дробным показателем, полученное неравенство можно переписать в виде , то есть a p p . Аналогично, когда m m >b m , откуда , то есть и a p >b p .
Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q p>q при 0p q и при a>0 неравенство a p >a q . Мы всегда можем привести рациональные числа p и q к общему знаменателю, получим обыкновенные дроби и , где m 1 и m 2 — целые числа, а n — натуральное число. В этом случае условию p>q будет соответствовать условие m 1 >m 2 , которое следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0m 1 m 2 и при a>1 выполняется неравенство a m 1 >am 2 . Эти неравенства в терминах свойств корней можно переписать соответственно в виде и .
 А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 выполняется неравенство a p >a q .
А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 выполняется неравенство a p >a q .Свойства степеней с иррациональными показателями
Из того, как определяется степень с иррациональным показателем, можно заключить, что она обладает всеми свойствами степеней с рациональным показателем. Таким образом, для любых a>0 , b>0 и иррациональных чисел p и q верны следующие свойства степеней с иррациональными показателями :
Отсюда можно заключить, что степени с любыми вещественными показателями p и q при а>0 обладают теми же свойствами.

- Алгебра — 10 класс. Тригонометрические уравнения Урок и презентация на тему: «Решение простейших тригонометрических уравнений» Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, предложения! Все материалы […]
- Объявлен конкурс на вакансию «ПРОДАВЕЦ — КОНСУЛЬТАНТ»: Обязанности: продажа мобильных телефонов и аксессуаров для услуг мобильной связи для абонентов Билайн, Теле2, МТС подключение тарифных планов и услуг Билайн и Теле2, МТС [… ]
- Параллелепипед формулы Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом. Кубоид — это прямоугольный параллелепипед, каждая грань которого представляет собой прямоугольник. Любой параллелепипед характеризуется 3 […]
- Общество защиты прав потребителей Астана Для того, чтобы получить пин-код для доступа к этому документу на нашем сайте, отправьте SMS-сообщение с текстом zan на номер Абоненты GSM операторов (Activ, Kcell, Beeline, NEO, Tele2) отправив SMS на номер, […]
- ПРАВОПИСАНИЕ Н И НН РАЗНЫМИ ЧАСТЯМИ РЕЧИ 2.
 Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […]
Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […] - Принять закон о Родовых Подворьях Принять федеральный закон о безвозмездном выделении земельного участка каждому гражданину Российской Федерации или семья граждан, желающих обустроить на ней Родовое Поместье на следующих условиях: 1. Земельный участок выделяется […]
- ИНСПЕКЦИЯ ГОСТЕХНАДЗОРА ПО БРЯНСКОЙ ОБЛАСТИ Квитанция об оплате государственной пошлины (Скачать-12,2 кб) Заявления о регистрации для физических лиц (Скачать-12 кб) Заявления о регистрации для юридических лиц (Скачать-11,4 кб) 1. При регистрации нового машина : 1.заявление 2.паспорт […]
- Давно мы не играли в турниры 1х1. И пора возобновить эту традицию. Пока мы не сможем организовать отдельный ладдер и турниры для игроков 1 на 1, мы предлагаем использовать профили вашей команды на сайте. Вычитать или добавлять очки за игры в матчах […]
- , если a > 0, то для любого натурального n, n будет больше нуля;
- при равном 0, n также будет равно нулю;
- за
- для
- — натуральное число;
- — целое число;
- — основание степени;
- — показатель степени.
- — натуральное число;
- — целое число;
- даже градусов, — число положительное .
- Отрицательное число увеличено до нечетное градус, — число минус .
- Положительное число в любой степени является положительным числом.
- Ноль в любой степени равен нулю.
- Запомните формулу разности квадратов.
 Отвечать: .
Отвечать: . - Приводим дроби к одному виду: либо обе десятичные, либо обе обыкновенные. Получаем, например: .
- Ничего особенного, применяем обычные свойства степеней:
- Отрицательное число возведено в степень даже , — число положительное .
- Отрицательное число возводится в нечетных градусов, — число отрицательное .

- Положительное число в любой степени является положительным числом.
- Ноль равен любой степени.
- Любое число в нулевой степени равно.
- 2 3 = 2 на третьем шаге. = 2 * 2 * 2 = 8;
- 4 2 = 4 шага. два = 4 * 4 = 16;
- 5 4 = 5 шагов. четыре = 5 * 5 * 5 * 5 = 625;
- 10 5 = 10 в 5 шаге. = 10*10*10*10*10=100000;
- 10 4 = 10 в 4 шаге. = 10 * 10 * 10 * 10 = 10000.
- a n * a m = (a) (n+m) ;
- ан: а м = (а) (н-м) ;
- (а б) м = (а) (б*м) .
- 3 3 + 2 4 = 27 + 16 = 43;
- 5 2 — 3 2 = 25 — 9 = 16
- если есть скобки, начинать нужно с них;
- , затем возведение в степень;
- затем выполнить операции умножения, деления;
- после сложения, вычитания.

- Корень n-й степени из числа a в степень m запишется так: a m/n.
- При возведении дроби в степень: этой процедуре подлежат как числитель, так и его знаменатель.
- При возведении произведения разных чисел в степень выражение будет соответствовать произведению этих чисел в заданную степень. То есть: (a * b) n = a n * b n .
- При возведении числа в отрицательную степень нужно разделить 1 на число на том же шаге, но со знаком «+».
- Если знаменатель дроби стоит в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1 и шагу. 1 = себе.
- А = 1.
 Результат будет равен 1. Так как есть аксиома — 1 равен единице во всех степенях;
Результат будет равен 1. Так как есть аксиома — 1 равен единице во всех степенях; - 0˂А˂1.
- 2
5. (a p) q = a p q
6.apbp
7.ap0 , тогда a p > a q .
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии, что a > 0, обладают одинаковыми свойствами.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl+Enter
Объяснение урока: Логарифмические уравнения с разными основаниями
В этом объяснителе мы научимся решать логарифмические уравнения, включающие логарифмы с разными основаниями.
Давайте сначала вспомним связь между логарифмической и экспоненциальной формами.
Определение: связь между логарифмическим и экспоненциальным Формы
Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма
𝑦=𝑥log эквивалентно экспоненциальной форме
𝑥=𝑎, что позволяет
конвертировать из одной формы в другую, как только мы идентифицируем 𝑎,
𝑥 и 𝑦.
Показательная функция 𝑦=𝑎 – это , обратное логарифмической функции 𝑦=𝑥log. Это означает, что если вы возведете 𝑎 в логарифмическую степень 𝑥 с основанием 𝑎 или если вы сделаете рейз 𝑎 в степени 𝑥 сначала возьми бревно с основанием 𝑎 результата вы получите 𝑥: 𝑎=(𝑎)=𝑥.loglog
Связь между логарифмической и экспоненциальной формами позволяет нам вывести свойства, которым удовлетворяют логарифмические формы, известные как законы логарифмы, которые следуют из законов показателей. Давайте вспомним законы логарифмов.
Определение: законы логарифмов
Предположим, что 𝑥, 𝑦, 𝑎 и 𝑏 — положительные числа с 𝑎,𝑏≠1. Законы логарифмов:
Они будут полезны для решения логарифмических уравнений с разными основаниями,
особенно последний, который позволяет нам преобразовать логарифм по одному основанию в
еще один. Чтобы понять, откуда это взялось, сначала обратите внимание, что
𝑥=𝑎,𝑎=𝑏,логлог
которые непосредственно следуют из того факта, что показатели степени и логарифмы обратны. Если подставить второе выражение в первое, то получим
𝑥=𝑏.loglog
Чтобы понять, откуда это взялось, сначала обратите внимание, что
𝑥=𝑎,𝑎=𝑏,логлог
которые непосредственно следуют из того факта, что показатели степени и логарифмы обратны. Если подставить второе выражение в первое, то получим
𝑥=𝑏.loglog
Используя закон показателей (𝑝)=𝑝, мы можем переписать это как 𝑥=𝑏.loglog⋅
Логарифмируя обе части по основанию 𝑏, находим loglogloglogloglog𝑥=𝑎⋅𝑥𝑥=𝑥𝑎, как требуется. Эта формула вместе с законами логарифмов и эквивалентом экспоненциальная форма позволяет нам решать логарифмические уравнения, включающие логарифмы разные базы. Еще один факт, который будет важен для решения логарифмической уравнения loglog𝑥=𝑦⟺𝑥=𝑦, что непосредственно следует из соотношения между логарифмической и экспоненциальной формы, в частности, из того, что логарифмическая и экспоненциальная функции строго монотонные функции. Мы можем показать это непосредственно, используя законы логарифмы: logloglogloglog𝑥=𝑦𝑥−𝑦=0𝑥𝑦=0.
Преобразовав последнее выражение в экспоненциальную форму, находим
𝑥𝑦=𝑎=1,
и, таким образом, 𝑥=𝑦, как и требовалось.
В качестве примера предположим, что мы хотим найти решения логарифмического уравнения loglog(2𝑥−1)=𝑥.
Сначала мы преобразуем логарифм в левой части в логарифм по основанию 2 используя формулу изменения основания: loglogloglogloglog(2𝑥−1)=(2𝑥−1)4=(2𝑥−1)2=12(2𝑥−1), где мы использовали тот факт, что log𝑎=𝑛 для получить последнюю строку. Таким образом, используя это и законы логарифмов, логарифмическое уравнение становится 12(2𝑥−1)=𝑥(2𝑥−1)=2𝑥(2𝑥−1)=𝑥.loglogloglogloglog
Используя тот факт, что мы установили, если loglog𝑥=𝑦, то 𝑥=𝑦, или приведя к экспоненциальному виду, получим 2𝑥−1=𝑥𝑥−2𝑥+1=0(𝑥−1)=0.
Таким образом, единственное решение логарифмического уравнения loglog(2𝑥−1)=𝑥 равно 𝑥=1.
Теперь давайте рассмотрим несколько примеров, чтобы попрактиковаться и углубить наши знания.
понимание решения логарифмических уравнений. В первом примере имеем
два логарифма по разным основаниям и появляется неизвестное 𝑥
внутри логарифма.
Пример 1. Поиск набора решений логарифмического уравнения по множеству действительных Числа
Найдите набор решений loglog𝑥=4 в ℝ.
Ответ
В этом примере мы хотим определить набор решений конкретного логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри логарифм.
Чтобы решить уравнение, воспользуемся заменой основания формула, logloglog𝑥=𝑥𝑎, и степенной закон, 𝑛𝑥=(𝑥).loglog
Применяя формулу замены основания, мы можем написать правую часть данного логарифмического уравнения, log4, как логарифм по основанию 3, используя 9=3 и журнал𝑎=𝑛: loglogloglogloglog4=49=43=124.
Используя это, данное уравнение становится loglogloglogloglog𝑥=124𝑥=4𝑥=2.
Так как loglog𝑥=𝑥⟺𝑥=𝑥, то 𝑥=2. Таким образом, решение
набор дается
{2}.
Теперь рассмотрим пример, в котором логарифмическое уравнение содержит два логарифма по разным основаниям, в каждом из которых стоит неизвестное.
Пример 2. Поиск набора решений логарифмического уравнения по множеству действительных Числа
Определить множество решений уравнения loglog𝑥+𝑥+3=0 в ℝ.
Ответ
В этом примере мы хотим определить набор решений конкретного логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри два логарифма по разным основаниям.
Чтобы решить уравнение, воспользуемся заменой основания формула, logloglog𝑥=𝑥𝑎, и степенной закон, 𝑛𝑥=(𝑥).loglog
Применяя формулу замены основания, мы можем записать второй член на
левая часть данного логарифмического уравнения,
log𝑥, как логарифм по основанию 3 с использованием
243=3 и log𝑎=𝑛:
logloglogloglogloglog𝑥=𝑥243=𝑥3=15𝑥=𝑥.
Подставляя это в данное логарифмическое уравнение, получаем loglogloglogloglog𝑥+𝑥+3=0𝑥+𝑥+3=02𝑥=−3𝑥=−32.
Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎.
Наконец, преобразование log𝑥=−32 в экспоненциальную форму мы имеем 𝑥=3=13=13×3=13√3.
Таким образом, множество решений 13√3.
В следующем примере мы найдем решение логарифмического уравнения которое содержит сумму трех логарифмов по разным основаниям и неизвестное внутри каждого из логарифмов.
Пример 3. Поиск набора решений логарифмического уравнения по множеству действительных Числа
Найдите набор решений logloglog𝑥+𝑥+𝑥=21 в ℝ.
Ответ
В этом примере мы хотим определить набор решений конкретного
логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри
логарифм.
Чтобы решить уравнение, воспользуемся заменой основания формула, logloglog𝑥=𝑥𝑎, и степенной закон, 𝑛𝑥=(𝑥).loglog
Применяя формулу замены основания, мы можем записать второй член на левая часть данного логарифмического уравнения, log𝑥, как логарифм по основанию 2 с использованием 4=2 и log𝑎=𝑛, loglogloglogloglog𝑥=𝑥4=𝑥2=12𝑥, и аналогично для третьего члена log𝑥, используя 16=2 как loglogloglogloglog𝑥=𝑥16=𝑥2=14𝑥.
Подставляя эти выражения в логарифмическое уравнение, получаем loglogloglogloglogloglog𝑥+𝑥+𝑥=21𝑥+12𝑥+14𝑥=2174𝑥=21𝑥=12.
Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎.
Таким образом, переводя log𝑥=12 в экспоненциальную форму, получаем 𝑥=2=4096.
Следовательно, множество решений
{4096}.
Теперь давайте рассмотрим пример, в котором нам нужно найти решение задачи. логарифмическое уравнение, содержащее сумму обратной трех логарифмы по разным основаниям и неизвестное, появляющееся внутри каждого из логарифмы.
Пример 4. Поиск набора решений логарифмического уравнения по множеству действительных Числа
Найдите набор решений 1𝑥+1𝑥+1𝑥=3logloglog в ℝ.
Ответ
В этом примере мы хотим определить набор решений конкретного логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри три логарифма по разным основаниям.
Чтобы решить уравнение, воспользуемся заменой основания формула, loglogloglogloglog𝑥=𝑥𝑎1𝑥=𝑎𝑥, и степенной закон, 𝑛𝑥=(𝑥).loglog
Применяя формулу замены основания, мы можем записать второй член на
левая часть данного логарифмического уравнения,
1𝑥log в виде логарифма по основанию 2 с использованием
4=2 и log𝑎=𝑛,
1𝑥=4𝑥=2𝑥=2𝑥,логлоглоглоглоглоглог
и аналогично для третьего члена 1𝑥log,
используя 8=2 как
1𝑥=8𝑥=2𝑥=3𝑥. loglogloglogloglog
loglogloglogloglog
Подставляя эти выражения в логарифмическое уравнение, получаем 1𝑥+1𝑥+1𝑥=31𝑥+2𝑥+3𝑥=36𝑥=3𝑥=2.loglogloglogloglogloglog
Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎.
Таким образом, переводя log𝑥=2 в экспоненциальную форму, находим 𝑥=2=4.
Таким образом, множество решений {4}.
В следующем примере мы решим логарифмическое уравнение, содержащее логарифмы по разным основаниям, включая дробное основание, и неизвестное появляется внутри журналов как линейный и квадратичный член.
Пример 5. Решение логарифмических уравнений, использующих законы логарифмов
Найдите набор решений loglog𝑥−𝑥=6 в ℝ.
Ответ
В этом примере мы хотим определить набор решений конкретного
логарифмическое уравнение с разными основаниями и неизвестным, стоящим внутри
два логарифма по разным основаниям.
Чтобы решить уравнение, воспользуемся заменой основания формула, logloglog𝑥=𝑥𝑎, и степенной закон, 𝑛𝑥=(𝑥).loglog
Применяя формулу замены основания, мы можем записать второй член на левая часть данного логарифмического уравнения, log𝑥 в виде логарифма по основанию 3 с использованием 13=3 и журнал𝑎=𝑛: logloglogloglogloglog𝑥=𝑥=𝑥3=−𝑥=−2𝑥.
Наконец, подставляя это выражение в данное логарифмическое уравнение, имеем loglogloglogloglog𝑥−𝑥=6𝑥+2𝑥=63𝑥=6𝑥=2.
Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентно экспоненциальной форме 𝑥=𝑎.
Наконец, преобразуя log𝑥=2 в экспоненциальную форму, мы имеем 𝑥=3=9.
Таким образом, множество решений {9}.
Как мы видели в предыдущих примерах, изменение базового правила для
логарифмы также позволяют нам вычислять выражения вида
log𝑥, переписав этот логарифм по основанию
𝑎 как логарифм по основанию 𝑎 (т. е.
𝑏=𝑎) вместе со степенным законом
loglog(𝑥)=𝑛𝑥 и факт
этот журнал𝑎=𝑘:
loglogloglog𝑥=𝑥𝑎=1𝑘𝑥.
е.
𝑏=𝑎) вместе со степенным законом
loglog(𝑥)=𝑛𝑥 и факт
этот журнал𝑎=𝑘:
loglogloglog𝑥=𝑥𝑎=1𝑘𝑥.
Теперь давайте рассмотрим пример, где у нас есть логарифмическое уравнение который содержит логарифм логарифма с двумя различными основаниями и неизвестное, появляющееся внутри логарифма как квадратное.
Пример 6. Решение логарифмических уравнений с использованием законов логарифмов и Квадратные уравнения
Решить loglog𝑥−8𝑥=1, где 𝑥∈ℝ.
Ответ
В этом примере мы хотим определить решение конкретного логарифмическое уравнение с разными основаниями и неизвестной фигурой внутри логарифм логарифма в виде квадратного уравнения.
Для 𝑥>0 и основания 𝑎>0,
𝑎≠1, показательная форма 𝑦=𝑎
эквивалентна логарифмической форме
𝑥=𝑦log, что позволяет нам конвертировать из одного
форму к другой, как только мы идентифицируем 𝑎, 𝑥,
и 𝑦.
Преобразуя loglog𝑥−8𝑥=1 в экспоненциальную форму, получаем log𝑥−8𝑥=2=2.
Повторяя процесс, получаем 𝑥−8𝑥=3𝑥−8𝑥−9=0(𝑥−9)(𝑥+1)=0,
Следовательно, получаем 𝑥=−1 или 𝑥=9. Набор решений {−1,9}.
До сих пор в примерах, которые мы рассматривали, была неизвестная переменная 𝑥, которую мы должны решить, появляющуюся внутри сам логарифм. Мы также можем найти решения логарифмических уравнений, где неизвестное может появиться в основании логарифма.
В следующем примере рассмотрим логарифмическое уравнение с тройной логарифм по разным основаниям и неизвестное в качестве основания.
Пример 7. Решение логарифмических уравнений над набором действительных чисел
Решить logloglog36=0, где 𝑥∈ℝ.
Ответ
В этом примере мы хотим определить решение конкретного
логарифмическое уравнение с тремя разными основаниями и неизвестной фигурой
как основание логарифма.
Напомним, что для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентна экспоненциальному форма 𝑥=𝑎. Десятичный логарифм без основания указанный имеет основание 10: loglog=.
Переводя logloglog36=0 в экспоненциальную форму, получаем loglog36=10=1.
Повторяя этот процесс для полученного выражения, мы получаем лог36=2=2.
И повторив это еще раз напоследок, получим 𝑥=36.
Таким образом, решения 𝑥=6 или 𝑥=−6, но мы игнорируем второе решение, так как логарифм отрицательного основания (т. е. log36), не определено.
Следовательно, решение логарифмического уравнения равно 𝑥=6.
Теперь давайте рассмотрим пример, где у нас есть логарифмическое уравнение содержащие логарифмы по разным основаниям и неизвестное, находящееся как внутри логарифм и основание того же логарифма.
Пример 8.
 Поиск решения системы экспоненциальных уравнений с логарифмами
над набором действительных чисел
Поиск решения системы экспоненциальных уравнений с логарифмами
над набором действительных чиселНайдите набор решений 𝑥=10logвойти ℝ.
Ответ
В этом примере мы хотим определить решение конкретного логарифмическое уравнение с двумя разными основаниями и неизвестной фигурой внутри и выступает как основание логарифма.
Чтобы решить данное уравнение, воспользуемся степенным законом: 𝑛𝑥=(𝑥).loglog
Применяя это и используя log𝑎=1, мы получаем loglog𝑥=6𝑥=6 а также loglog10=6410=64.
Подставляя их в данное уравнение, получаем 𝑥=64.
Решения таковы: 𝑥=2 и 𝑥=−2; однако мы будем игнорировать второй как логарифм отрицательного числа или с отрицательным основанием не определено. Таким образом, множество решений {2}.
Используя формулу замены основания, мы можем поменять местами аргумент
логарифм и основание. Изменение логарифма
log𝑥 в базу 𝑏=𝑥 и используя
log𝑥=1, имеем
loglogloglog𝑥=𝑥𝑎=1𝑎.
Изменение логарифма
log𝑥 в базу 𝑏=𝑥 и используя
log𝑥=1, имеем
loglogloglog𝑥=𝑥𝑎=1𝑎.
Предположим, мы хотим найти решение loglog5=3; мы хотим определить значения 𝑥, которые удовлетворяют этому логарифмическому уравнению. С log𝑎=1, это упрощается до лог5=1.
Таким образом, преобразуя это в экспоненциальную форму с основанием 𝑥, получаем 𝑥=𝑥=5.
Наконец, давайте рассмотрим пример, когда неизвестное 𝑥, который мы должны решить, появляется как внутри логарифм и как основание другого логарифма.
Пример 9. Поиск решения набора логарифмических уравнений по множеству вещественных Числа
Определить множество решений уравнения loglog𝑥+254=10 в ℝ.
Ответ
В этом примере мы хотим определить решение конкретного
логарифмическое уравнение с двумя разными основаниями и неизвестной фигурой
внутри и выступает как основание логарифма.
Чтобы решить логарифмическое уравнение, воспользуемся изменение базовой формулы: logloglog𝑥=𝑥𝑎.
Если мы используем базу 𝑏=𝑥, эта формула позволяет нам поменять местами аргумент логарифма и основание: loglogloglog𝑥=𝑥𝑎=1𝑎, где мы использовали тот факт, что log𝑥=1. Используя это, данное уравнение становится loglog𝑥+25𝑥=10.
Итак, если мы допустим 𝑦=𝑥log, то мы должны решить 𝑦+251𝑦=10.
Умножение обеих частей этого уравнения на 𝑦 и переставляя, получаем 𝑦−10𝑦+25=0(𝑦−5)=0.
Таким образом, 𝑦=𝑥=5.log
Для 𝑥>0 и основания 𝑎>0, 𝑎≠1, логарифмическая форма 𝑦=𝑥log эквивалентна экспоненциальной форме 𝑥=𝑎.
Таким образом, при преобразовании в экспоненциальную форму имеем 𝑥=4=1024.
Таким образом, множество решений {1024}.
Давайте подытожим то, что было изучено в этом объяснителе.
Ключевые моменты
Экспоненты и полиномы, сложение,… Пошаговое решение математических задач
4.1 Экспоненты и полиномы
В разделе 1.2 мы определили экспоненту как число, указывающее, сколько раз множитель встречается в произведении. На самом деле это определение применимо только к показателям степени натуральных чисел. Отрицательные целые показатели обсуждаются в Приложении I и, наряду с дробными показателями, являются основной темой промежуточной алгебры. В этом разделе мы обсудим значение a° и умножения с алгебраическими терминами, имеющими целые числа. 92+x+10
На самом деле это определение применимо только к показателям степени натуральных чисел. Отрицательные целые показатели обсуждаются в Приложении I и, наряду с дробными показателями, являются основной темой промежуточной алгебры. В этом разделе мы обсудим значение a° и умножения с алгебраическими терминами, имеющими целые числа. 92+x+10
Давайте посмотрим, как наш математический решатель упрощает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
Если выражение содержит более одной пары группирующих (или включающих) символов, таких как круглые скобки ( ), квадратные скобки [ ] или фигурные скобки { ), упростите, удалив самую внутреннюю пару символов первый. Например,
5x-[2x+3(4-x)+1)]-9
=5x-[2x+12-3x+1]-96. Кроме того, мы применили распределительное свойство к таким выражениям, как 5(2x+3)=10x+15. Теперь мы будем использовать обе эти процедуры для умножения многочленов. 2=93+1
2=93+1
Хотя все четыре формулы можно рассматривать как частные случаи метода FOIL, их все же следует запомнить.
Усовершенствованная научная запись: изменение оснований, сложение и вычитание — математические модули Ohlone Biotechnology
Иногда нам нужно взять число в экспоненциальном представлении и изменить его, чтобы оно имело другую экспоненциальную основу. Переписывание числа в экспоненциальном представлении с использованием другой экспоненциальной базы технически «нарушает» правило записи в экспоненциальном представлении: наш коэффициент равен 9.2285 и должны быть больше или равны 1, но меньше 10. Почему и должны быть между этими числами? Потому что это просто обычный способ написать это.
Итак, зачем нам вообще переписывать базы, если мы не придем к стандартной форме научных обозначений?
Во-первых, мы можем использовать это изменение базы для добавления или вычитания чисел в экспоненциальном представлении, как мы рассмотрим во втором разделе этого руководства. Во-вторых, использование другой экспоненциальной базы может упростить визуализацию числа для тех, кто не знаком с научными обозначениями, такими как запись 100 x 10 10 вместо 1,00 x 10 12 .
Во-вторых, использование другой экспоненциальной базы может упростить визуализацию числа для тех, кто не знаком с научными обозначениями, такими как запись 100 x 10 10 вместо 1,00 x 10 12 .
Давайте начнем с изучения изменения основания с 10 8 на 10 5 . Как бы выглядело число 4,5 x 10 5 , если бы мы захотели записать его экспоненциальную базу как 10 8 вместо 10 5 ?
Если вы читали Модуль 1 (Научная нотация), вы, наверное, догадались, что мы будем использовать еще одно свойство показателей степени. Ты прав. Мы будем использовать специальное свойство экспонент, модифицированное под наши нужды:
10 M-N = x
, где M является данным (оригинальным) показателем
и n -новый показатель
SO, что является новым экспонентом
SO, что является новым показателем
11131330 гг. В данном случае 90 130 x – это число, на которое мы переместим десятичную дробь, чтобы получить новое число. Если x отрицательное значение, переместите десятичную дробь влево. Если x положительное значение, сдвиньте десятичную дробь вправо.
В данном случае 90 130 x – это число, на которое мы переместим десятичную дробь, чтобы получить новое число. Если x отрицательное значение, переместите десятичную дробь влево. Если x положительное значение, сдвиньте десятичную дробь вправо.
Пример 1 – Отрицательный «x»
Let’s take another look at writing 4.5 x 10 5 with 10 8 as its exponential base:
4.5 x 10 5 ⇒ x 10 8
Поскольку мы проверили наш ответ на шаге 3, вы можете видеть, что оба ответа эквивалентны.
Совет : Быстро перепроверьте свой ответ с помощью калькулятора. Введите 0,0045 x 10 8 и нажмите клавишу ввода. В зависимости от того, в каком режиме находится ваш калькулятор, он выдаст вам 4,5 x 10 5 или 450 000.
В зависимости от того, в каком режиме находится ваш калькулятор, он выдаст вам 4,5 x 10 5 или 450 000.
Пример 2. Положительный «x»
Давайте попробуем аналогичный пример, где x является положительным, а не отрицательным: запишите 6,32 x 10 6 с 10 4 в качестве экспоненциальной базы.
6,32 x 10 6 ⇒ x 10 4
Всегда проверяйте свои ответы! Проверка поможет вам обнаружить любые ошибки, которые вы могли допустить.
Ниже приведены несколько чисел, которые мы хотим переписать с другим экспоненциальным основанием. Попробуйте решить задачи самостоятельно.
Попробуйте решить задачи самостоятельно.
Проверка на понимание #1: Экспоненциальное представление с различными основаниями
Перепишите следующие числа с их новой экспоненциальной основой (решения для проверки на понимание находятся в конце этого руководства).
Напишите 3,98 x 10 8 с экспоненциальным основанием 10 4 .
Напишите 4,9 x 10 3 с экспоненциальным основанием 10 9 .
Запишите 1,45 x 10 -5 с экспоненциальным основанием 10 -8 .
Запишите 7,4 x 10 -2 с экспоненциальным основанием 10 2 .
Сложение и вычитание чисел в экспоненциальном представлении, к сожалению, не так просто, как умножение и деление чисел, поскольку мы не можем складывать или вычитать коэффициенты, как при умножении/делении.
Давайте посмотрим, что произойдет, если мы попытаемся сложить коэффициенты и части экспоненты:
Мы можем вычислить, что 2500 + 450 = 2950, но если мы рассмотрим те же самые числа, записанные в экспоненте, и попытаемся сложить, используя Те же методы мы делали при умножении и делении, мы получаем
2,500 = 2,5 x 10 3
450 = 4,5 x 10 2
Добавить десятимерные порции и участки. 0200 +4,5 x 10 2
0200 +4,5 x 10 2
≠ 7,0 x 10 5
Что не так с добавлением таким образом? Есть три проблемы:
Нет свойств показателей степени? Вообще? Ничего такого?
До этого момента мы снова и снова использовали свойства показателей степени для решения задач научной записи, включая умножение и деление. Это вот где вся та работа, которую вы проделали, изменяя экспоненциальные основания, вступает в силу.
Давайте еще раз посмотрим на сложение чисел в начале этого раздела, изменив основание экспоненциального выражения из введения:
2,5 x 10 3
+4,5 x 10 2
=
2,5 x 10 3
+0,45 x 10 3
2,95 x 10 3
Важно отметить, что вы НЕ добавляете основания — например, 10 3 + 10 3 6 ≠ 10
4 5 .Потренируйтесь складывать и вычитать числа в экспоненциальном представлении. Хотя здесь в качестве примера мы использовали сложение, принципы вычитания те же.
Проверка понимания #2: сложение и вычитание
Сложите или вычтите следующие числа. Убедитесь, что ваш окончательный ответ представлен в экспоненциальной записи.
Вы заметили, что если вы решили переписать задачу так, чтобы оба числа были в виде числа с большей степенью, это означало, что вам не нужно было менять формат в конце?
Если вам нужна информация об экспоненциальном представлении в целом, а также об умножении и делении в экспоненциальном представлении, ознакомьтесь с Модуль 1 .
Проверка понимания #1: Различные экспоненциальные основания
Проверка понимания #2: сложение и вычитание
формулировок, доказательств, примеров.
 Степень с отрицательным основанием
Степень с отрицательным основаниемПонятие степени по математике вводится уже в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных его формах. Градусы – достаточно сложная тема, требующая запоминания значений и умения правильно и быстро считать. Для более быстрой и качественной работы с математическими степенями придумали свойства степени. Они помогают сократить объем вычислений, в некоторой степени преобразовать огромный пример в одно число. Свойства не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассматриваются основные свойства степени, а также где они применяются.
свойства степени
Мы рассмотрим 12 свойств степени, включая свойства степеней с одинаковым основанием, и приведем пример для каждого свойства. Каждое из этих свойств поможет вам быстрее решать задачи со степенями, а также убережет вас от многочисленных вычислительных ошибок.
1-й объект.
Многие очень часто забывают об этом свойстве, делают ошибки, представляя число в нулевой степени за ноль.
2-й дом.
3-й дом.
Необходимо помнить, что это свойство можно использовать только при умножении чисел, с суммой оно не работает! И нельзя забывать, что это и следующие свойства относятся только к степеням с одним и тем же основанием.
4-й объект.
Если число в знаменателе возведено в отрицательную степень, то при вычитании в скобках берется степень знаменателя для правильной замены знака в дальнейших вычислениях.
Свойство работает только при делении, а не при вычитании!
5-й дом.
6-й объект.
Это свойство можно применять и в обратном порядке. Единица, деленная на число в некоторой степени, является этим числом в отрицательной степени.
7-й объект.
Это свойство нельзя применить к сумме и разности! При возведении суммы или разности в степень используются формулы сокращенного умножения, а не свойства степени.
8 дом.
9 дом.
Это свойство работает для любой дробной степени с числителем равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.
Также это свойство часто используется в обратном порядке. Корень любой степени числа может быть представлен как это число в степени единицы, деленное на степень корня. Это свойство очень полезно в тех случаях, когда корень числа не извлекается.
10-й дом.
Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень возведения этого корня совпадают, то ответ будет подкоренным выражением.
11 дом.
Нужно уметь вовремя увидеть это свойство при его решении, чтобы избавить себя от огромных вычислений.
12-й дом.
Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может потребовать некоторых преобразований и использования других формул. Поэтому для правильного решения недостаточно знать только свойства, нужно практиковаться и подключать остальные математические знания.
Применение степеней и их свойства
Активно используются в алгебре и геометрии. Степени по математике занимают отдельное важное место. С их помощью решают показательные уравнения и неравенства, а также степени часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Экспоненты помогают избежать больших и длинных вычислений, легче уменьшать и вычислять экспоненты. Но для работы с большими степенями, или со степенями больших чисел, нужно знать не только свойства степени, но и грамотно работать с основаниями, уметь их декомпозировать, чтобы облегчить себе задачу. Для удобства следует также знать значение чисел, возведенных в степень. Это сократит ваше время на решение, избавив от необходимости долгих вычислений.
Понятие степени играет особую роль в логарифмах. Так как логарифм, по сути, является степенью числа.
Формулы сокращенного умножения — еще один пример использования степеней. Они не могут использовать свойства степеней, они разлагаются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.
Степени также активно используются в физике и информатике. Все переводы в систему СИ производятся с использованием степеней, и в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие вычисления для преобразования единиц измерения или расчеты задач, так же как и в физике, происходят с использованием свойств степени.
Градусы также очень полезны в астрономии, где редко можно встретить применение свойствам градуса, но сами градусы активно используются для сокращения записи различных величин и расстояний.
Градусы используются и в быту, при расчете площадей, объемов, расстояний.
С помощью степеней записывают очень большие и очень маленькие значения в любой области науки.
показательные уравнения и неравенства
Свойства степени занимают особое место именно в показательных уравнениях и неравенствах. Эти задания очень распространены, как в школьном курсе, так и на экзаменах. Все они решаются путем применения свойств степени. Неизвестное всегда находится в самой степени, поэтому, зная все свойства, решить такое уравнение или неравенство не составит труда.
Все они решаются путем применения свойств степени. Неизвестное всегда находится в самой степени, поэтому, зная все свойства, решить такое уравнение или неравенство не составит труда.
Сложение и вычитание степеней
Очевидно, числа со степенями можно складывать так же, как и другие величины , добавляя их один за другим с их знаками .
Итак, сумма a 3 и b 2 равна a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 равна a 3 — b n + h 5 — d 4.
Коэффициенты одинаковые степени одних и тех же переменных можно складывать или вычитать.
Итак, сумма 2a 2 и 3a 2 равна 5a 2 .
Также очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различные переменные и различные степени идентичные переменные , должны быть добавлены путем сложения их знаков.
Итак, сумма 2 и 3 равна сумме 2 + 3 .
Очевидно, что квадрат а и куб а не в два раза больше квадрата а, а в два раза больше куба а.
Сумма a 3 b n и 3a 5 b 6 равна a 3 b n + 3a 5 b 6 .
Вычитание степеней производится так же, как сложение, за исключением того, что знаки вычитаемого должны быть изменены соответствующим образом.
Или:
2а 4 — (-6а 4) = 8а 4
3ч 2 б 6 — 4ч 2 б 6 = -ч 2 б 6
5(а — з) 6 — 2(а — з) 6 = 3(a — h) 6
Умножение в степени
Числа со степенями можно умножать, как и другие величины, записывая их одно за другим, со знаком умножения между ними или без него.
Итак, результатом умножения a 3 на b 2 является a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере можно упорядочить, добавив те же самые переменные.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел (переменных) со степенями, мы видим, что если любые два из них перемножить, то в результате получится число (переменная) со степенью, равной сумме степеней слагаемых.
Итак, а 2 .а 3 = аа.ааа = ааааа = а 5 .
Здесь 5 — степень результата умножения, равная 2 + 3, сумма степеней слагаемых.
Итак, а н .а м = а м+п .
Для n , a берется в качестве множителя столько раз, сколько раз степень n;
А m , принимается за множитель столько раз, сколько степени m равна;
Поэтому степеней с одинаковыми основаниями можно умножить путем сложения показателей степени.
Итак, а 2 .а 6 = а 2+6 = а 8 . И х 3 .х 2 .х = х 3+2+1 = х 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + ч — у) п+1
Умножить (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: х 4 — у 4.
Умножить (х 3 + х — 5) ⋅ (2х 3 + х + 1).
Это правило также верно для чисел, показатели степени которых — отрицательные .
1. Итак, а -2 .а -3 = а -5 . Это можно записать как (1/аа).(1/ааа) = 1/ааааа.
2. у-н .у-м = у-н-м .
3. а-н .ам = а м-н .
а-н .ам = а м-н .
Если a + b умножить на a — b, результатом будет a 2 — b 2: то есть
Результат умножения суммы или разности двух чисел равен сумме или разности их квадратов.
Если сумму и разность двух чисел возвести в квадрат , то результат будет равен сумме или разности этих чисел в четвертой степени.
Итак, (а — у).(а + у) = а 2 — у 2 .
(а 2 — у 2)⋅(а 2 + у 2) = а 4 — у 4 .
(а 4 — у 4)⋅(а 4 + у 4) = а 8 — у 8 .
Деление степеней
Числа со степенями можно разделить, как и другие числа, путем вычитания из делителя или представления их в виде дроби.
Таким образом, a 3 b 2 разделить на b 2 равно a 3 .
Запись 5, деленная на 3, выглядит как $\frac $. Но это равно 2 . В ряду чисел
а+4, а+3, а+2, а+1, 0, а-1, а-2, а-3, а-4.
любое число можно разделить на другое, и показатель степени будет равен разности показателей делимых чисел.
При делении степеней с одинаковым основанием вычитаются их степени. .
.
Итак, у 3:у 2 = у 3-2 = у 1 . То есть $\frac = y$. 93$
Необходимо очень хорошо освоить умножение и деление степеней, так как такие операции очень широко используются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшить показатели степени в $\frac $ Ответ: $\frac $.
2. Уменьшить показатели в $\frac$. Ответ: $\frac $ или 2x.
3. Привести показатели степени а 2 / 3 и а -3 / а -4 и привести к общему знаменателю.
a 2 .a -4 — это первый числитель -2.
a 3 .a -3 — это a 0 = 1, второй числитель.
a 3 .a -4 есть -1 , общий числитель.
После упрощения: а-2/а-1 и 1/а-1.
4. Привести показатели 2a 4 /5a 3 и 2 /a 4 к общему знаменателю.
Ответ: 2а 3 / 5а 7 и 5а 5 / 5а 7 или 2а 3 / 5а 2 и 5/5а 2.
5. Умножить (а 3 + b)/b 4 на (а — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделить 4/y 3 на 3/y 2 . Ответ: а/у.
Ответ: а/у.
свойства степени
Напоминаем, что в этом уроке мы разбираемся со свойствами степени с натуральными показателями и нулем. Степени с рациональными показателями и их свойства будут рассмотрены на уроках для 8 класса.
Показатель степени с натуральным показателем имеет несколько важных свойств, позволяющих упростить расчеты в показательных примерах.
Свойство №1
Произведение степеней
При умножении степеней с одним и тем же основанием основание остается неизменным, а показатели степени складываются.
a m a n = a m + n, где «a» — любое число, а «m», «n» — любые натуральные числа.
Это свойство степеней также влияет на произведение трех и более степеней.
Обратите внимание, что в указанном свойстве речь шла только о умножении степеней с одинаковыми основаниями. . Это не касается их добавления.
. Это не касается их добавления.
Вы не можете заменить сумму (3 3 + 3 2) на 3 5 . Это понятно, если вычислить
(3 3 + 3 2) = (27 + 9) = 36 и 3 5 = 243
Свойство № 2
Частные степени
При делении степеней с одинаковым основанием основание остается неизменным, а из показателя степени делимого вычитается показатель степени делителя.
11 3 — 2 4 2 — 1 = 11 4 = 44
Пример. Решите уравнение. Воспользуемся свойством частичных степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Используя свойства №1 и №2, можно легко упростить выражения и выполнять вычисления.
Пример. Упростите выражение.
4 5 м + 6 4 м + 2: 4 4 м + 3 = 4 5 м + 6 + м + 2: 4 4 м + 3 = 4 6 м + 8 − 4 м − 3 = 4 2 м + 5
Пример. Найдите значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что свойство 2 касалось только разделения полномочий по одинаковым основаниям.
Вы не можете заменить разницу (4 3 −4 2) на 4 1 . Это понятно, если вычислить (4 3 −4 2) = (64 − 16) = 48 и 4 1 = 4
Свойство №3
Возведение в степень
При возведении степени в степень основание степени остается не меняется, а показатели умножаются.
(a n)m = a n m, где «а» — любое число, а «m», «n» — любые натуральные числа.
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведения дроби в степень мы остановимся более подробно на следующей странице.
Как умножить силы
Как умножить силы? Какие силы можно умножать, а какие нельзя? Как умножить число на степень?
В алгебре можно найти произведение степеней в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одним и тем же основанием основание должно остаться прежним, а степени должны быть добавлены:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать полномочия, с конкретными примерами.
Единица в показателе степени не пишется, но при умножении степеней учитывают:
При умножении количество степеней может быть любым. Следует помнить, что нельзя ставить знак умножения перед буквой:
В выражениях возведение в степень выполняется первым.
Если вам нужно умножить число на степень, необходимо сначала выполнить возведение в степень, а только потом — умножение:
Умножение степеней с одинаковым основанием
Этот видеоурок доступен по подписке
У вас уже есть подписка ? Прийти
В этом уроке мы научимся умножать степени с одним и тем же основанием. Сначала напомним определение степени и сформулируем теорему о справедливости равенства . Затем приведем примеры его применения к конкретным числам и докажем. Мы также применим теорему для решения различных задач.
Topic: Degree with a natural indicator and its properties
Lesson: Multiplying powers with the same bases (formula)
1.
 Basic definitions
Basic definitionsBasic definitions:
n — exponent ,
— n -я степень числа.
2. Утверждение теоремы 1
Теорема 1. Для любого числа a и любых натуральных n и k верно равенство:
Другими словами: если a — любое число; n и k натуральных чисел, тогда:
Отсюда правило 1:
3. Объясняющие задачи
Вывод: частных случаев подтвердили правильность теоремы № 1. Докажем ее в общем случае, то есть для любых и и любые натуральные н и к.
4. Доказательство теоремы 1
Даны числа a — любые; номера н и к- натуральные. Докажите:
Доказательство основано на определении степени.
5. Решение примеров с помощью теоремы 1
Пример 1: Присутствует в виде степени.
Для решения следующих примеров воспользуемся теоремой 1.
и)
6. Обобщение теоремы 1
Вот обобщение:
7. Решение примеров с использованием обобщения теоремы 1
8. Решение различных задач с использованием теоремы 1
Пример 2: Вычислите (можно воспользоваться таблицей основных степеней).
а) (по таблице)
б)
Пример 3: Запишем в виде степени по основанию 2.
а)
Пример 4: Определить знак числа:
Задания :
Единиц деятельности доктрины: определение степени с натуральным показателем; компоненты степени; определение частного; Ассоциативный закон умножения.
I. Организация демонстрации освоения студентами имеющихся знаний. (шаг 1)а) Актуализация знаний:
2) Сформулировать определение степени с натуральным показателем.
a n = a a a a … a (n раз)
b k = b b b b a … b (k раз) Обоснуйте свой ответ.
II. Организация самооценки обучаемого по степени владения релевантным опытом. (шаг 2)Тест для самопроверки: (индивидуальная работа в двух вариантах.)
А1) Выразите произведение 7 7 7 7 х х х в степени:
А2) Выразите произведение в степени (-3) 3 х 2
А3) Рассчитать: -2 3 2 + 4 5 3
Количество заданий в тесте подбираю в соответствии с уровнем подготовки класса.
На пробу даю ключ для самопроверки. Критерии: зачет-незачет.
III. Учебно-практическое задание (этап 3) + этап 4. (учащиеся сами формулируют свойства)
(учащиеся сами формулируют свойства) В ходе решения задач 1) и 2) учащиеся предлагают решение, а я, как учитель, организую занятие по поиску способа упрощения степеней при умножении с одинаковыми основаниями.
Учитель: придумайте способ упростить степени при умножении с одинаковым основанием.
На кластере появляется запись:
Тема урока сформулирована. Умножение сил.
Учитель: придумайте правило деления степеней с одинаковыми основаниями.
Рассуждение: какое действие проверяет деление? а 5: а 3 = ? что а 2 а 3 = а 5
Возвращаюсь к схеме — кластер и дополняю запись — ..при делении убавляю и добавляю тему урока. …и деление степеней.
IV. Сообщение учащимся пределов знаний (как минимума, так и максимума).
Учитель: задача минимум на сегодняшнем уроке научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимум: применить умножение и деление вместе.
Напишите на доске : а м а н = а м + п ; a m: a n = a m-n
V. Организация изучения нового материала. (шаг 5)а) По учебнику: № 403 (а, в, д) задания с разной формулировкой
№ 404 (а, д, е) самостоятельная работа, затем организую взаимную проверку, даю ключи.
б) При каком значении m выполняется равенство? а 16 а м = а 32; х ч х 14 = х 28; х 8 (*) = х 14
Задание: придумать подобные примеры на деление.
в) №417(а), №418(а) Ловушки для учащихся : х 3 х н = х 3н; 3 4 3 2 = 9 6 ; а 16: а 8 = а 2.
VI. Подведение итогов изученного, проведение диагностической работы (которая побуждает к изучению данной темы учащихся, а не преподавателей) (6 этап)
диагностическая работа.
Тест (поместите ключи на обратную сторону теста).
Варианты задания: представить в виде степени частное х 15: х 3; представить в виде степени произведение (-4) 2 (-4) 5 (-4) 7 ; для которого m верно равенство a 16 a m = a 32; найти значение выражения h 0 : h 2 при h = 0,2; вычислить значение выражения (5 2 5 0) : 5 2 .
Подведение итогов урока. Отражение. Я делю класс на две группы.
Найдите аргументы I группы: в пользу знания свойств степени, и II группы — аргументы, которые скажут, что можно обойтись без свойств. Выслушиваем все ответы, делаем выводы. На последующих уроках можно предложить статистические данные и назвать рубрику «В голове не укладывается!»
Ссылка на историю. Какие числа называются числами Ферма.
стр.19. № 403, № 408, № 417
Б/у книги:
Свойства степеней, формулировки, доказательства, примеры.
После определения степени числа логично говорить о свойства степени . В этой статье мы дадим основные свойства степени числа, коснувшись при этом всех возможных показателей степени. Здесь мы приведем доказательства всех свойств степени, а также покажем, как эти свойства применяются при решении примеров.
Навигация по страницам.
Свойства степеней с натуральными показателями
По определению степени с натуральным показателем степень n есть произведение n множителей, каждый из которых равен a . Основываясь на этом определении и используя свойства умножения действительных чисел , можно получить и обосновать следующие свойства степени с натуральным показателем :
Ранее мы уже говорили о том, что такое степень числа. У него есть определенные свойства, полезные при решении задач: именно эти и все возможные показатели мы разберем в этой статье. Мы также продемонстрируем на примерах, как их можно доказать и правильно применить на практике.
У него есть определенные свойства, полезные при решении задач: именно эти и все возможные показатели мы разберем в этой статье. Мы также продемонстрируем на примерах, как их можно доказать и правильно применить на практике.
Напомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n-го числа множителей, каждый из которых равен a. Нам также нужно помнить, как правильно умножать действительные числа. Все это поможет нам сформулировать следующие свойства степени с натуральным показателем:
Определение 1
1. Основное свойство степени: a man a n = a m + n
Можно обобщить до: an 1 · an 2 · … · an k = a n 1 + n 2 + … + n k .
2. Факторное свойство для степеней с одинаковым основанием: a m: a n = a m − n
3. Свойство степени произведения: (a b) n = a n b n
Равенство можно расширить до: (a 1 a 2 … a k) n = a 1 n a 2 n … a k n
4. Свойство натуральной степени: (a: b) n = a n: b n
5. Возводим степень в степень: (am) n = a m n ,
Возводим степень в степень: (am) n = a m n ,
Можно обобщить до: (((an 1) n 2) …) n k = an 1 n 2 … n k
6. Сравните степень с нулем:
7. Равенство
8. Неравенство a m > an будет верным при условии, что m и n натуральные числа, m больше n и a больше нуля и не меньше единицы.
В результате получилось несколько равенств; если вы выполните все указанные выше условия, то они будут идентичными. Для каждого из равенств, например для основного свойства, можно поменять местами правую и левую части: a m · a n = a m + n — то же, что a m + n = a m · an . В таком виде он часто используется при упрощении выражений.
1. Начнем с основного свойства степени: равенство a m · a n = a m + n будет верным для любых натуральных m и n и вещественного a . Как доказать это утверждение?
Базовое определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим такую запись:
Мы получим такую запись:
Это можно сократить до (вспомним основные свойства умножения). В результате мы получили степень числа a с натуральным показателем m + n. Таким образом, a m + n , а значит, основное свойство степени доказано.
Давайте рассмотрим конкретный пример, чтобы доказать это.
Пример 1
Итак, у нас есть две степени с основанием 2. Их натуральные показатели равны 2 и 3 соответственно. Получили равенство: 2 2 2 3 = 2 2 + 3 = 2 5 Подсчитаем значения, чтобы проверить правильность этого равенства.
Проделаем необходимые математические операции: 2 2 2 3 = (2 2) (2 2 2) = 4 8 = 32 и 2 5 = 2 2 2 2 2 = 32
В итоге получили: 2 2 2 3 = 2 5 . Имущество доказано.
Благодаря свойствам умножения мы можем обобщить свойство, сформулировав его в виде трех или более степеней, для которых показатели степени являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n 1, n 2 и т. д. буквой k, то получим правильное равенство:
а п 1 а п 2 … а п k знак равно а п 1 + п 2 + … + п k .
Пример 2
2. Далее нужно доказать следующее свойство, называемое факторным и присущее степеням с одинаковыми основаниями: это равенство a m : an = a m − n , справедливое для любых натуральных m и n (и m больше n)) и любой ненулевой действительный a .
Для начала поясним, что именно означают условия, которые упоминаются в формулировке. Если взять a равным нулю, то в итоге мы получим деление на ноль, чего делать нельзя (ведь 0 n = 0). Условие, что число m должно быть больше n, необходимо для того, чтобы мы могли оставаться в пределах натуральных показателей: вычитая n из m, мы получаем натуральное число. Если условие не выполняется, мы получим отрицательное число или ноль, и снова выйдем за рамки изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из изученного ранее напомним основные свойства дробей и сформулируем равенство следующим образом:
a m − n a n = a (m − n) + n = a m
Из него можно вывести: a m − n an n = a m
Вспомним связь между делением и умножением. Отсюда следует, что a m − n есть частное степеней a m и an . Это доказательство свойства второй степени.
Отсюда следует, что a m − n есть частное степеней a m и an . Это доказательство свойства второй степени.
Пример 3
Подставить для наглядности в показатели конкретные цифры и обозначить основание степени π: π 5: π 2 = π 5 − 3 = π 3
3. Далее проанализируем свойство степени произведения: (a · b) n = a n · b n для любых вещественных a и b и натурального n .
Согласно основному определению степени с натуральным показателем можно переформулировать равенство следующим образом:
Помня о свойствах умножения, напишем: . Это означает то же самое, что и a n · b n .
Пример 4
2 3 — 4 2 5 4 = 2 3 4 — 4 2 5 4
Если у нас есть три или более множителей, то это свойство применимо и к этому случаю. Введем обозначение k для числа факторов и напишем:
(a 1 a 2 … a k) n = a 1 n a 2 n … a k n
Пример 5
При конкретных числах получаем следующее правильное равенство: (2 (- 2 , 3) a) 7 = 2 7 (- 2 , 3) 7 а
4. После этого попробуем доказать факторное свойство: (a: b) n = a n: b n для любых действительных a и b, если b не равно 0 и n — натуральное число.
После этого попробуем доказать факторное свойство: (a: b) n = a n: b n для любых действительных a и b, если b не равно 0 и n — натуральное число.
Для доказательства мы можем использовать свойство предыдущей степени. Если (a: b) n b n = ((a: b) b) n = a n и (a: b) n b n = an , то отсюда следует, что (a: b) n есть частное от деления an на b n .
Пример 6
Посчитаем пример: 3 1 2: — 0 . 5 3 = 3 1 2 3: (- 0 , 5) 3
Пример 7
Начнем сразу с примера: (5 2) 3 = 5 2 3 = 5 6
А теперь составим цепочку из равенства, которые докажут нам правильность равенства:
Если у нас в примере есть степени степеней, то это свойство верно и для них. Если у нас есть любые натуральные числа p, q, r, s, то будет верно:
a p q y s = a p q y s
Пример 8
Добавим уточнений: (((5 , 2) 3) 2) 5 = (5 , 2) 3 2 5 = (5 , 2) 30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, — это свойство сравнения.
Сначала сравним показатель степени с нулем. Почему n > 0 при условии, что а больше 0?
Если мы умножим одно положительное число на другое, мы также получим положительное число. Зная этот факт, можно сказать, что это не зависит от количества множителей — результат умножения любого количества положительных чисел есть положительное число. А что такое степень, как не результат умножения чисел? Тогда для любой степени n с положительным основанием и натуральным показателем это будет верно.
Пример 9
3 5 > 0 , (0 , 00201) 2 > 0 и 34 9 13 51 > 0
Также очевидно, что степень с основанием, равным нулю, сама по себе равна нулю. В какую бы степень мы ни возводили ноль, он таким и останется.
Пример 10
0 3 = 0 и 0 762 = 0
Если основание степени является отрицательным числом, то доказательство немного усложняется, так как важным становится понятие четного/нечетного показателя степени. Начнем со случая, когда показатель степени четен и обозначим его через 2 · m , где m — натуральное число.
Вспомним, как правильно умножать отрицательные числа: произведение а · а равно произведению модулей, а значит, это будет положительное число. Тогда и степень a 2 · m также положительны.
Пример 11
Например, (− 6) 4 > 0 , (− 2 , 2) 12 > 0 и — 2 9 6 > 0
Что, если показатель степени с отрицательным основанием является нечетным числом? Обозначим его 2 · m − 1 .
Тогда
Все произведения a · a , согласно свойствам умножения, положительны, как и их произведение. Но если мы умножим его на единственное оставшееся число a, то конечный результат будет отрицательным.
Тогда получаем: (− 5) 3
Как это доказать?
и
Пример 12
Например, верны неравенства: 3 7 (0 , 75) 124
8. Нам остается доказать последнее свойство: если мы имеем две степени, основания которых одинаковы и положительны, а показатели степени — натуральные числа, то больше та из них, у которой показатель меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями больше единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Сначала нам нужно убедиться, что м
Выносим a n за скобки, после чего наша разность примет вид a n · (am − n − 1) . Его результат будет отрицательным (поскольку результат умножения положительного числа на отрицательное отрицателен). Действительно, по начальным условиям m − n > 0, тогда a m − n − 1 отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
Оказалось, что a m − a n
Осталось доказать вторую часть сформулированного выше утверждения: a m > a верно при m > n и a > 1 . Укажем разницу и вынесем n за скобки: (a m — n — 1) . Степень n больше единицы даст положительный результат; и сама разность тоже окажется положительной в силу начальных условий, а при a > 1 степень a m − n больше единицы. Получается, что a m − an > 0 и am > an , что и требовалось доказать.
Пример 13
Пример с конкретными числами: 3 7 > 3 2
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что положительные целые числа натуральные, а это означает, что все для них справедливы и доказанные выше равенства. Они подходят и для случаев, когда показатели степени отрицательны или равны нулю (при условии, что основание самой степени не равно нулю).
Они подходят и для случаев, когда показатели степени отрицательны или равны нулю (при условии, что основание самой степени не равно нулю).
Таким образом, свойства степеней одинаковы для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей степени m и n (при условии, что они целые). Запишем их кратко в виде формул:
Определение 2
1. a m a n = a m + n
2. a m: a n = a m − n
3. (a b) n = a n b n
4. (a: b) n = a n: b 903 903 903 n 5. (am) n = a m n
6. a nb − n с целым положительным числом n, положительными a и b, a
7. а мн и 01 а м > а н .
Если основание степени равно нулю, то записи a m и an имеют смысл только в случае натуральных и положительных m и n. В результате получаем, что приведенные выше формулировки годятся и для случаев со степенью с нулевым основанием, если выполняются все остальные условия.
Доказательства этих свойств в этом случае просты. Нам нужно будет вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с вещественными числами.
Проанализируем свойство степени в степени и докажем, что оно верно как для целых положительных, так и для целых неположительных чисел. Начнем с доказательства равенств (a p) q = a p q , (a − p) q = a (− p) q , (ap) − q = a p (− q) и (a − p) − q = a (− p) (−q)
Условия: p = 0 или натуральное число; д — аналогично.
Если значения p и q больше 0, то получаем (ap p)q = a p · q . Мы уже доказывали подобное равенство ранее. Если p = 0, то:
(a 0) q = 1 q = 1 a 0 q = a 0 = 1
Следовательно, (a 0) q = a 0 q
При q = 0 все точно так же :
(a p) 0 = 1 a p 0 = a 0 = 1
Результат: (ap) 0 = a p 0 .
Если оба индикатора равны нулю, то (a 0) 0 = 1 0 = 1 и a 0 0 = a 0 = 1, тогда (a 0) 0 = a 0 0 .
Вспомним доказанное выше свойство частного в степени и напишем:
1 a p q = 1 q a p q
Если 1 p = 1 1 … 1 = 1 и a p q = a p q , то 1 q a p q = 1 a p q
Мы можем преобразовать это обозначение в силу основных правил умножения в (− p) · к.
Также: a p — q = 1 (ap) q = 1 a p q = a — (p q) = a p (- q) .
И (a — p) — q = 1 a p — q = (ap) q = a p q = a (- p) (- q)
Остальные свойства степени доказываются аналогично преобразованием существующие неравенства. Подробно на этом останавливаться не будем, укажем лишь на сложные моменты.
Доказательство предпоследнего свойства: напомним, что a − n > b − n верно для любых отрицательных целых значений n и любых положительных a и b при условии, что a меньше b .
Тогда неравенство можно преобразовать следующим образом:
1 a n > 1 b n
Запишем правую и левую части в виде разности и проведем необходимые преобразования:
1 a n — 1 b n = b n — a n a n b n
что в условии a меньше b , то по определению степени с натуральным показателем: — a n 0 .
a n · b n оказывается положительным числом, потому что его множители положительны. В итоге имеем дробь b n — a n an n · b n , что в итоге также дает положительный результат. Отсюда 1 an > 1 b n , откуда a − n > b − n , что и требовалось доказать.
Отсюда 1 an > 1 b n , откуда a − n > b − n , что и требовалось доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с натуральными показателями.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы обсуждали, что такое степени с рациональными (дробными) показателями. Их свойства такие же, как у степеней с целыми показателями. Напишем:
Определение 3
1. a m 1 n 1 a m 2 n 2 = a m 1 n 1 + m 2 n 2 при a > 0, и если m 1 n 1 > 0 и m 2 n 2 > 0, то при a ≥ 0 (степень свойства продукта с тем же основанием).
2. a m 1 n 1: b m 2 n 2 = a m 1 n 1 — m 2 n 2, если a > 0 (частное свойство).
3. a b m n = a m n b m n при a > 0 и b > 0, а если m 1 n 1 > 0 и m 2 n 2 > 0, то при a ≥ 0 и (или) b ≥ 0 (свойство произведения в дробной степени ).
4. а: b m n = a m n: b m n при a > 0 и b > 0, а если m n > 0, то при a ≥ 0 и b > 0 (свойство частного дробной степени).
5. a m 1 n 1 m 2 n 2 = am 1 n 1 m 2 n 2 при a > 0, а если m 1 n 1 > 0 и m 2 n 2 > 0, то при a ≥ 0 (степень свойство в градусах).
a m 1 n 1 m 2 n 2 = am 1 n 1 m 2 n 2 при a > 0, а если m 1 n 1 > 0 и m 2 n 2 > 0, то при a ≥ 0 (степень свойство в градусах).
6.ap0; если pb p (свойство сравнения степеней с одинаковыми рациональными показателями).
7.apq at 00 – a p > a q
Для доказательства этих положений нам нужно вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n-й степени и каковы свойства степень с целым показателем. Давайте рассмотрим каждое свойство.
В зависимости от того, что такое степень с дробным показателем, получаем:
a m 1 n 1 = am 1 n 1 и am 2 n 2 = am 2 n 2, следовательно, a m 1 n 1 a m 2 n 2 = am 1 n 1 a m 2 n 2
Свойства корня позволят вывести равенства:
am 1 m 2 n 1 n 2 a m 2 m 1 n 2 n 1 = a m 1 n 2 a m 2 n 1 n 1 n 2
Отсюда получаем: a m 1 n 2 a m 2 n 1 n 1 n 2 = a m 1 n 2 + m 2 n 1 n 1 n 2
Преобразуем:
a m 1 n 2 a m 2 n 1 n 1 n 2 = а м 1 n 2 + м 2 n 1 n 1 n 2
Показатель степени можно записать как:
m 1 n 2 + m 2 n 1 n 1 n 2 = m 1 n 2 n 1 n 2 + m 2 n 1 n 1 n 2 = m 1 n 1 + m 2 n 2
Это доказательство. Точно так же доказывается и второе свойство. Запишем цепочку равенств:
Точно так же доказывается и второе свойство. Запишем цепочку равенств:
a m 1 n 1: a m 2 n 2 = a m 1 n 1: a m 2 n 2 = a m 1 n 2: a m 2 n 1 n 1 n 2 = = a m 1 n 2 — м 2 п 1 п 1 п 2 = а м 1 п 2 — м 2 п 1 п 1 п 2 = а м 1 п 2 п 1 п 2 — м 2 п 1 п 1 п 2 = а м 1 п 1 — м 2 п 2
Доказательства остальных равенств:
а б м п знак равно (а б) м п знак равно а м б м п знак равно а м п б м п знак равно а м п б м п ; (a: b) m n = (a: b) m n = a m: b m n = = a m n: b m n = a m n: b m n ; а м 1 п 1 м 2 п 2 знак равно а м 1 п 1 м 2 п 2 знак равно а м 1 п 1 м 2 п 2 = = а м 1 м 2 п 1 п 2 = а м 1 м 2 п 1 п 2 = = а м 1 м 2 n 2 n 1 = a m 1 m 2 n 2 n 1 = a m 1 n 1 m 2 n 2
Следующее свойство: докажем, что для любых значений a и b больше 0, если a меньше b , a p будет выполнено bp
Представим рациональное число p как m n . В данном случае m — целое число, n — натуральное число. Тогда условия p0 будут распространены на m0. При m > 0 и a
Воспользуемся свойством корней и получим: a m n
Учитывая положительность значений a и b , перепишем неравенство в виде a m n
Таким же образом для mb m получаем a m n > b m n, поэтому a m n > b m n и a p > b p .
Нам осталось доказать последнее свойство. Докажем, что для рациональных чисел p и q p > q в точке 00 будет верным a p > a q .
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m 1 n и m 2 n
Здесь m 1 и m 2 — целые числа, а n — натуральное число. Если p > q, то m 1 > m 2 (с учетом правила сравнения дробей). Тогда при 01 – неравенство a 1 m > a 2 m .
Их можно переписать в следующем виде:
a m 1 na m 2 n
Тогда можно произвести преобразования и получить в результате:
am 1 na m 2 n
Подытожим: при p > q и 00 – а р > а q .
Основные свойства степеней с иррациональными показателями
Все описанные выше свойства, которыми обладает степень с рациональными показателями, могут быть расширены до такой степени. Это следует из самого его определения, которое мы дали в одной из предыдущих статей. Кратко сформулируем эти свойства (условия: a > 0 , b > 0 , показатели p и q — иррациональные числа):
3. (a b) p = a p b p
(a b) p = a p b p
4. (a: b) p = a p: b p
5. (a p) q = a p q
6.apbp
7.ap0 , тогда a p > a q .
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии, что a > 0, обладают одинаковыми свойствами.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl+Enter
Если не обращать внимания на восьмую степень, что мы здесь видим? Давайте посмотрим на программу 7-го класса. Итак, помните? Это и есть сокращенная формула умножения, а именно на разность квадратов! Получаем:
Внимательно смотрим на знаменатель. Это очень похоже на один из множителей числителя, но что не так? Неправильный порядок терминов. Если бы они были заменены, правило могло бы применяться.
Но как это сделать? Оказывается, это очень просто: здесь нам помогает четная степень знаменателя.
Термины волшебным образом поменялись местами. Это «явление» относится к любому выражению в равной степени: мы можем свободно менять знаки в скобках.
Но важно помнить: все знаки меняются одновременно !
Вернемся к примеру:
И снова по формуле:
целых назовем натуральные числа, их противоположности (то есть взятые со знаком «») и число.
натуральное число , а оно ничем не отличается от натурального, то все выглядит точно так же, как и в предыдущем разделе.
Теперь давайте посмотрим на новые дела. Начнем с показателя, равного .
Любое число в нулевой степени равно единице :
Как всегда, мы спрашиваем себя: почему это так?
Подумайте о силе базы. Возьмем, к примеру, и умножим на:
Итак, мы умножили число на, и получили то же, что и было — . На какое число нужно умножить, чтобы ничего не изменилось? Правильно, на. Означает.
То же самое можно сделать с произвольным числом:
Повторим правило:
Любое число в нулевой степени равно единице.
Но из многих правил есть исключения. И вот оно тоже есть — это число (как основа).
И вот оно тоже есть — это число (как основа).
С одной стороны, он должен быть равен в любой степени — сколько ни умножай ноль сам на себя, все равно получится ноль, это понятно. Но с другой стороны, как и любое число в нулевой степени, оно должно быть равно. Так в чем же правда? Математики решили не вмешиваться и отказались возводить ноль в нулевую степень. То есть теперь мы можем не только делить на ноль, но и возводить в нулевую степень.
Идем дальше. В дополнение к натуральным числам и числам, целые числа включают в себя отрицательные числа. Чтобы понять, что такое отрицательная степень, поступим так же, как и в прошлый раз: умножим какое-нибудь нормальное число на такое же в отрицательной степени:
Отсюда уже легко выразить искомое:
Теперь продолжим полученное правило в произвольной степени:
Итак, сформулируем правило:
Число в отрицательной степени является обратным тому же числу в положительной степени. Но в то же время база не может быть нулевой: (потому что делить нельзя).
Подведем итоги:
I. Выражение в падеже не определено. Если, то.
II. Любое число в нулевой степени равно единице: .
III. Число, не равное нулю в отрицательной степени, является обратным тому же числу в положительной степени: .
Задания для самостоятельного решения:Ну и как обычно примеры для самостоятельного решения:
Разбор задач для самостоятельного решения:Знаю, знаю, цифры страшные, но на экзамене надо быть готовым ко всему! Решите эти примеры или проанализируйте их решение, если вы не смогли его решить, и вы научитесь легко справляться с ними на экзамене!
Продолжим расширять круг чисел, «подходящих» в качестве показателя степени.
Теперь рассмотрим рациональных чисел. Какие числа называются рациональными?
Ответ: все, что можно представить в виде дроби, где и целые числа, причем.
Чтобы понять, что такое «дробная степень» Рассмотрим дробь:
Возведем обе части уравнения в степень:
Теперь вспомним правило «градус в градус» :
Какое число должно быть возведен в степень, чтобы получить?
Эта формулировка является определением корня й степени.
Напомню: корень й степени числа () — это число, которое при возведении в степень равно.
То есть корень й степени есть обратная операция возведения в степень: .
Оказывается, что. Очевидно, этот частный случай можно расширить: .
Теперь добавим числитель: что это? Ответ легко получить с помощью правила возведения в степень:
Но может ли основание быть любым числом? Ведь не из всех чисел можно извлечь корень.
Нет!
Помните правило: любое число, возведенное в четную степень, является положительным числом. То есть из отрицательных чисел нельзя извлекать корни четной степени!
А это значит, что такие числа нельзя возводить в дробную степень с четным знаменателем, то есть выражение не имеет смысла.
Как насчет выражения?
Но тут возникает проблема.
Число может быть представлено в виде других, сокращенных дробей, например, или .
И получается, что он есть, а его нет, и это просто две разные записи одного и того же номера.
Или другой пример: один раз, потом можно записать. Но как только мы напишем индикатор по-другому, опять получим беду: (то есть получили совсем другой результат!).
Чтобы избежать таких парадоксов, рассматривайте только положительный базовый показатель с дробным показателем .
Итак, если:
Примеры:
Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:
5 практических примеровРазбор 5 примеров для обучения
1. Не забываем про обычные свойства степеней:
2. . Тут вспоминаем, что забыли выучить таблицу степеней:
ведь — это или. Решение находится автоматически: .
Ну а теперь — самое сложное. Теперь разберем степень с иррациональным показателем .
Все правила и свойства степеней здесь точно такие же, как и для степеней с рациональным показателем, за исключением
Действительно, по определению иррациональные числа — это числа, которые нельзя представить в виде дроби, где и — целые числа (то есть иррациональными числами являются все действительные числа, кроме рациональных).
При изучении степеней с натуральным, целым и рациональным показателем мы каждый раз составляли некий «образ», «аналогию» или описание в более привычных терминах.
Например, натуральный показатель — это число, умноженное само на себя несколько раз;
… нулевая мощность — это как бы число, умноженное само на себя один раз, то есть оно еще не начало умножаться, а значит, само число еще даже не появилось — поэтому результат есть лишь некая «подготовка числа», а именно числа;
… отрицательный целочисленный показатель степени — как будто произошел некий «обратный процесс», то есть число не умножалось само на себя, а делилось.
Кстати, в науке часто используется степень с комплексным показателем степени, то есть показатель степени не является даже действительным числом.
Но в школе мы не думаем о таких трудностях; у вас будет возможность постичь эти новые концепции в институте.
КУДА, МЫ УВЕРЕНЫ, ВЫ ПОЕДИТЕ! (если научиться решать такие примеры :))
Например:
Решайте сами: Анализ решений: 1. Начнем с уже привычного правила возведения степени в степень степень:
Начнем с уже привычного правила возведения степени в степень степень:
Теперь посмотрите на счет. Он вам ничего не напоминает? Вспоминаем формулу сокращенного умножения разности квадратов:
В данном случае
Получается, что:
Ответ: .
2. Приводим дроби в показателях к одному виду: либо обе десятичные, либо обе обыкновенные. Получаем, например:
Ответ: 16
3. Ничего особенного, применяем обычные свойства степеней:
ПРОДВИНУТЫЙ УРОВЕНЬ
Определение степени
Степень представляет собой выражение вида: , где:
Степень с натуральным показателем (n = 1, 2, 3,…)
Возведение числа в натуральную степень n означает умножение числа на само себя раз:
Степень с целым показателем (0, ±1 , ±2,…)
Если показатель степени равен натуральное число число:
возведение в нулевую степень :
с другой стороны, это любое число в й степени.
Если показатель степени , целое отрицательное число :
(потому что делить нельзя).
Еще раз о нулях: выражение в случае не определено. Если, то.
Примеры:
Степень с рациональным показателем
Примеры:
Свойства степени
Чтобы упростить решение задач, попробуем понять: откуда взялись эти свойства? Докажем их.
Посмотрим: что такое и?
По определению:
Итак, в правой части этого выражения получается следующее произведение:
Но по определению это степень числа с показателем степени, то есть:
К.Э.Д.
Пример : Упростите выражение.
Решение : .
Пример : Упростите выражение.
Решение : Важно отметить, что в нашем правиле обязательно должны иметь одинаковую основу. Поэтому объединяем степени с основанием, но оставляем отдельный множитель:
Еще одно важное замечание: это правило — только для произведений степеней !
Ни при каких обстоятельствах я не должен это писать.
Так же, как и с предыдущим свойством, обратимся к определению степени:
Перестроим так:
Получается, что выражение умножается само на себя один раз, то есть по определению это -я степень числа:
По сути, это можно назвать «брекетингом индикатора». Но вы никогда не сможете сделать это тотально:!
Вспомним формулы сокращенного умножения: сколько раз мы хотели написать? Но это неправда, правда.
Степень с отрицательным основанием.До этого момента мы обсуждали только то, каким должен быть индекс градусов. Но что должно быть основой? В градусах от натуральный индикатор основание может быть любое число .
Действительно, мы можем умножать любые числа друг на друга, будь они положительными, отрицательными или четными. Давайте подумаем, какие знаки (» » или «») будут иметь степени положительных и отрицательных чисел?
Например, число будет положительным или отрицательным? НО? ?
С первым все понятно: сколько бы положительных чисел мы ни перемножали друг с другом, результат будет положительным.
А вот отрицательные немного интереснее. Ведь мы помним простое правило из 6-го класса: «минус на минус дает плюс». То есть или. Но если умножить на (), то получим -.
И так до бесконечности: при каждом последующем умножении знак будет меняться. Вы можете сформулировать эти простые правила:
Определите для себя, какой знак будут иметь следующие выражения:
| 1. | 2. | 3. |
| 4. | 5. | 6. |
Вам удалось? Вот ответы:
1) ; 2) ; 3) ; 4) ; 5) ; 6) .
В первых четырех примерах надеюсь все понятно? Мы просто смотрим на основание и показатель степени и применяем соответствующее правило.
В примере 5) тоже все не так страшно, как кажется: неважно, чему равно основание — степень четная, а значит, результат всегда будет положительным. Ну, за исключением случаев, когда основание равно нулю. База не та? Очевидно, что нет, так как (потому что).
Пример 6) уже не так прост. Здесь нужно выяснить, что меньше: или ? Если вспомнить это, то становится ясно, что, а значит, основание меньше нуля. То есть применяем правило 2: результат будет отрицательным.
И снова используем определение степени:
Все как обычно — записываем определение степени и делим их друг на друга, делим на пары и получаем:
Прежде чем разбирать последнее правило, решим несколько примеров.
Вычислить значения выражений:
Решения :
Если не обращать внимания на восьмую степень, что мы здесь видим? Давайте посмотрим на программу 7-го класса. Итак, помните? Это и есть сокращенная формула умножения, а именно на разность квадратов!
Итак, помните? Это и есть сокращенная формула умножения, а именно на разность квадратов!
Получаем:
Внимательно смотрим на знаменатель. Это очень похоже на один из множителей числителя, но что не так? Неправильный порядок терминов. Если бы они были обратными, можно было бы применить правило 3. Но как это сделать? Оказывается, это очень просто: здесь нам помогает четная степень знаменателя.
Если умножить на, ничего не изменится, верно? Но теперь это выглядит так:
Термины волшебным образом поменялись местами. Это «явление» относится к любому выражению в равной степени: мы можем свободно менять знаки в скобках. Но важно помнить: все знаки меняются одновременно! Его нельзя заменить изменением только одного неугодного нам минуса!
Вернемся к примеру:
И снова формула:
Итак, последнее правило:
Как мы собираемся это доказать? Конечно, как обычно: расширим понятие степени и упростим:
Ну, а теперь раскроем скобки. Сколько букв будет? раз на множители — как это выглядит? Это не что иное, как определение операции умножения : всего получилось множителей. То есть это по определению степень числа с показателем степени:
Сколько букв будет? раз на множители — как это выглядит? Это не что иное, как определение операции умножения : всего получилось множителей. То есть это по определению степень числа с показателем степени:
Пример:
Степень с иррациональным показателем
Помимо информации о степенях для среднего уровня, разберем степень с иррациональным показателем. Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением — ведь по определению иррациональные числа — это числа, которые нельзя представить в виде дроби, где и — целые числа (т.е. , иррациональные числа — это все действительные числа, кроме рациональных).
При изучении степеней с натуральным, целым и рациональным показателем мы каждый раз составляли некий «образ», «аналогию» или описание в более привычных терминах. Например, натуральный показатель — это число, умноженное само на себя несколько раз; число в нулевой степени есть как бы число, умноженное само на себя один раз, т. е. оно еще не начало умножаться, а значит, само число еще даже не появилось — следовательно, результат есть только некая «подготовка номера», именно номера; степень с целым отрицательным показателем – это как бы произошел некий «обратный процесс», то есть число не умножилось само на себя, а поделилось.
е. оно еще не начало умножаться, а значит, само число еще даже не появилось — следовательно, результат есть только некая «подготовка номера», именно номера; степень с целым отрицательным показателем – это как бы произошел некий «обратный процесс», то есть число не умножилось само на себя, а поделилось.
Чрезвычайно сложно представить степень с иррациональным показателем (как трудно представить 4-х мерное пространство). Скорее, это чисто математический объект, созданный математиками для распространения понятия степени на все пространство чисел.
Кстати, в науке часто используется степень с комплексным показателем, то есть показатель степени не является даже действительным числом. Но в школе мы не задумываемся о таких трудностях; у вас будет возможность постичь эти новые концепции в институте.
Итак, что нам делать, если мы видим иррациональный показатель? Мы изо всех сил пытаемся избавиться от него! 🙂
Например:
Решайте сами:
| 1) | 2) | 3) |
Ответы:
РЕЗЮМЕ РАЗДЕЛА И ОСНОВНАЯ ФОРМУЛА
Степенью называется выражение вида: , где:
Степень с целым показателем
степень, показатель степени которого является натуральным числом (т.е. целым и положительным).
Степень с рациональным показателем
степень, показателем которой являются отрицательные и дробные числа.
Степень с иррациональным показателем
показатель степени, показатель которого является бесконечной десятичной дробью или корнем.
Свойства степеней
Свойства степеней.
ТЕПЕРЬ ТЕПЕРЬ ТЕПЕРЬ ТЕПЕРЬ СВЯЩЕННО…
Как вам статья? Дайте мне знать в комментариях ниже, понравилось вам это или нет.
Расскажите нам о своем опыте работы со свойствами питания.
Возможно, у вас есть вопросы. Или предложения.
Пишите в комментариях.
Удачи на экзаменах!
Одной из главных характеристик в алгебре, да и во всей математике, является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше научиться делать самому для развития мозгов.
В этой статье мы рассмотрим наиболее важные вопросы, касающиеся этого определения. А именно, разберемся, что это такое вообще и каковы его основные функции, какие свойства существуют в математике.
Давайте рассмотрим на примерах, как выглядит расчет, каковы основные формулы. Разберем основные виды величин и чем они отличаются от других функций.
Разберем основные виды величин и чем они отличаются от других функций.
Разберемся, как решать различные задачи, используя это значение. Покажем на примерах, как возводить в нулевую степень, иррациональное, отрицательное и т. д.
Онлайн-калькулятор возведения в степень
Что такое степень числа
Что означает выражение «возвести число в степень»?
Степень n числа a равна произведению n раз подряд множителей величины a.
Математически это выглядит так:
ан = а * а * а * …ан .
Например:
Ниже представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже представлены результаты возведения натуральных чисел в положительные степени — «от 1 до 100».
| Ч-ло | 2 класс | 3 класс |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степени
Что характерно для такой математической функции? Рассмотрим основные свойства.
Ученые установили следующие признаков, характерных для всех степеней:
Проверим на примерах:
2 3 * 2 2 = 8 * 4 = 32. С другой стороны 2 5 = 2 * 2 * 2 * 2 * 2 = 32.
Аналогично: 2 3: 2 2 = 8 / 4 = 2. В противном случае 2 3-2 = 2 1 = 2.
(2 3) 2 = 8 2 = 64. А если по-другому? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видите, правила работают.
Но как получить сложением и вычитанием ? Все просто. Сначала выполняется возведение в степень, а только потом сложение и вычитание.
Рассмотрим примеры:
Но в этом случае надо сначала вычислить сложение, так как в скобках стоят действия: (5+3)3=8 3=512.
Как производить вычисления в более сложных случаях ? Порядок тот же:
Существуют специфические свойства, свойственные не всем степеням:
Эти правила важны в отдельных случаях, ниже мы рассмотрим их подробнее.
Степень с отрицательным показателем
Что делать с отрицательной степенью, то есть когда показатель отрицательный?
Исходя из свойств 4 и 5 (см. пункт выше) получается :
пункт выше) получается :
А (- n) = 1 / A n, 5 (-2) = 1/5 2 = 1/25.
И наоборот:
1/A(-n)=An, 1/2(-3)=2 3=8.
А если дробь?
(А/В) (-n) = (В/А)n, (3/5) (-2) = (5/3) 2 = 25/9.
Степень с натуральным показателем
Под ней понимается степень с показателями степени, равными целым числам.
Следует помнить:
A 0 = 1, 1 0 = 1; 2 0 = 1; 3,15 0 = 1; (-4) 0 = 1…и т.д.
А 1 = А, 1 1 = 1; 2 1 = 2; 3 1 = 3… и т.д.
Также, если (-a) 2 n +2 , n=0, 1, 2… то результат будет со знаком «+». Если отрицательное число возвести в нечетную степень, то наоборот.
Им свойственны и общие свойства, и все особенности, описанные выше.
Дробная степень
Этот вид можно записать в виде схемы: А м/н. Читается как: корень n-й степени числа А в степени m.
С дробным показателем можно делать что угодно: уменьшать, разлагать на части, возводить в другую степень и т.д. суть степени с таким показателем, Давайте рассмотрим разные возможные случаи:
А r 1 ˂ А α ˂ А r 2 , r 1 ˂ r 2 — рациональные числа;
В этом случае наоборот: А r 2 ˂ А α ˂ А r 1 при тех же условиях, что и во втором пункте.
Например, показатель степени — это число π. Это рационально.
r 1 — в данном случае он равен 3;
r 2 — будет равно 4.
Тогда для A = 1 1 π = 1,
A = 2, тогда 2 3 ˂ 2 π ˂ 2 4 , 8 ˂ 2 π ˂ 16,
A = 1/2, тогда (½) 4 ˂ (½) π ˂ (½) 3 , 1/16 ˂ (½) π ˂ 1/8.
Такие степени характеризуются всеми математическими операциями и специфическими свойствами, описанными выше.
Заключение
Подведем итоги — для чего эти значения, в чем преимущества таких функций? Конечно, в первую очередь они упрощают жизнь математикам и программистам при решении примеров, так как позволяют минимизировать вычисления, сокращать алгоритмы, систематизировать данные и многое другое.



 Г.ЗЕЛИНСКАЯ
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
Теоретическая зарядка
1. Когда в прилагательных пишется нн? 2. Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […]
Г.ЗЕЛИНСКАЯ
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
Теоретическая зарядка
1. Когда в прилагательных пишется нн? 2. Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […]





 Степень полинома и степени его членов определяются показателями переменной. Работать с полиномами проще, если вы перечисляете члены в порядке убывания степеней. Когда многочлен записывается таким образом, говорят, что он имеет стандартную форму. Сложение и вычитание полиномов можно рассматривать как просто сложение и вычитание одинаковых членов.
Степень полинома и степени его членов определяются показателями переменной. Работать с полиномами проще, если вы перечисляете члены в порядке убывания степеней. Когда многочлен записывается таким образом, говорят, что он имеет стандартную форму. Сложение и вычитание полиномов можно рассматривать как просто сложение и вычитание одинаковых членов.
 Распределительное свойство — это первый метод, с которым вы уже столкнулись и использовали для нахождения произведения любых двух многочленов.
Распределительное свойство — это первый метод, с которым вы уже столкнулись и использовали для нахождения произведения любых двух многочленов. Мы будем использовать их для деления мономов. Позже вы будете использовать их для деления многочленов. Когда мы делим одночлены с более чем одной переменной, мы пишем одну дробь для каждой переменной. Как только вы ознакомитесь с процессом и попрактикуетесь в нем шаг за шагом несколько раз, вы сможете упростить дробь за один шаг.
Мы будем использовать их для деления мономов. Позже вы будете использовать их для деления многочленов. Когда мы делим одночлены с более чем одной переменной, мы пишем одну дробь для каждой переменной. Как только вы ознакомитесь с процессом и попрактикуетесь в нем шаг за шагом несколько раз, вы сможете упростить дробь за один шаг. В качестве знака умножения принято использовать ×, хотя мы избегаем использования этого знака в других местах алгебры. Научная нотация — удобный способ записи очень больших или очень маленьких чисел. Он часто используется в науке для облегчения расчетов.
В качестве знака умножения принято использовать ×, хотя мы избегаем использования этого знака в других местах алгебры. Научная нотация — удобный способ записи очень больших или очень маленьких чисел. Он часто используется в науке для облегчения расчетов. 12: Полиномиалы (Суммируют)
12: Полиномиалы (Суммируют)