Свойства y cos2x: Постройте график функции y=cos2x

Открытый урок по алгебре «Графики функций и их свойства» с презентацией 10 класс | Методическая разработка по алгебре (10 класс) по теме:

Алгебра и начала анализа. 10 класс

Тема: «Графики функций и их свойства»

Цели: 1 .Повторить способы преобразования графиков функций на примере

тригонометрической функции y=cosx.

2.        Учить анализировать, обобщать и систематизировать знания,
определять и объяснять зависимость положения графиков функций от
значений параметров, входящих в уравнение функции.

3.        Через компьютерные графики формировать конструктивные навыки,
показать эстетичность и аккуратность графических работ.

Тип урока: Урок систематизации и обобщение изученного материала.

Методы обучения: методы закрепления знаний, беседа, наглядные методы,

анализ, сравнение, обобщение, учебная работа под руководительством

учителя.

Формы организации познавательной деятельности: наблюдение, применение

информационных технологий.

Оборудование: мультмедийный проектор с экраном и компьютером.

Ход урока.

1.        Организационный этап: приветствие, удобная посадка, тема, задача
урока.

2.        Этап подготовки к активному усвоению знаний.
Учитель: «Многие задания ЕГЭ нельзя решить, не зная свойств
элементарных функций. Наиболее компактным и полным носителем
информации о свойствах функции (т.е. универсальной шпаргалкой) является
что?…. — ее график. Однако запас функций, графики которых вы умеете
строить, пока невелик. Перечислите элементарные функций, графики
которых вы уже умеете строить (y=kx, y=kx+b, у=ах +bx+c, у=к/х, y=sinx,
y=cosx, y=tgx, y=ctgx,).

Но мы, изучая материал функции и их графики и исследуя геометрические сведения о преобразовании фигур, список данных функций можем существенно расширить. Сегодня главная цель нашего урока: на примере графика функции y=cosx повторить все способы преобразования графиков функций, что позволяет не только найти быстро правильный ответ ко многим задачам ЕГЭ типа А и В, но и упростить аргументацию при оформлении решений сложных задач типа С.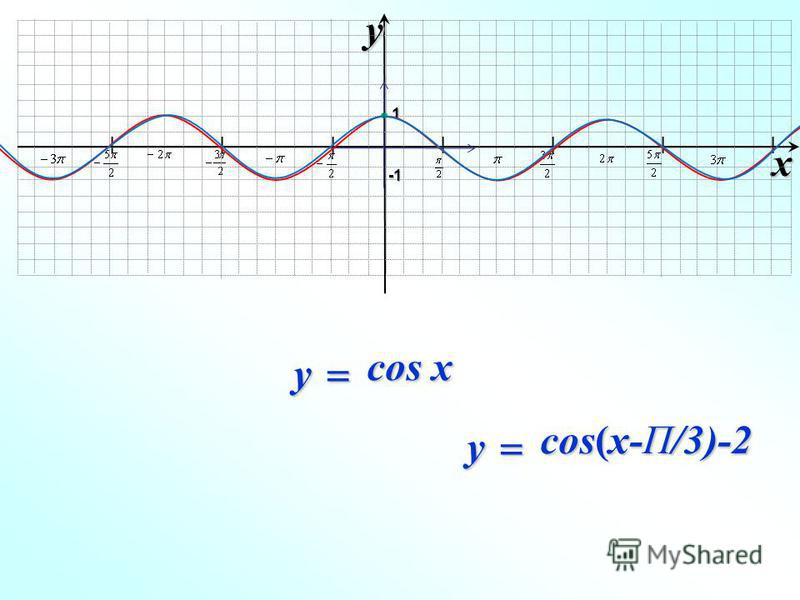 Использование графиков автоматически учитывает область определения функции, невнимание к которой часто приводит к неправильным ответам.

В официальных изданиях федерального института педагогических измерений говорится, что правильно изображенные эскизы графиков сами по себе можно принять в качестве обоснования. А построение графика сложной функции — это и есть цепочка последовательных преобразований графиков. 3. Этап обобщения и систематизация изученного. Внимание на доску: y=f(x) и у=к(х)

I        Внимание на экран: (постепенно появляются графики функции y=cosx,
y=2cosx, y=4cosx)

Итог: Для построения графика функции y=kf(x) надо растянуть график
функции y=f(x) в к раз вдоль оси ординат, при этом всякая точка графика с
координатами (х; f(x))        »(х; kf(x)).

Посмотрим поведение функции если к меняет знак, т.е. к

Вы вод: Чтобы построить y=-4cosx какую надо выполнить цепочку преобразования графика функции y=cosx.

•   Внимание: следующая ситуация — y=f(x), y=f(x-a). Приведите пример таких алгебраических функций: y=V*, y=V* + l Как же получить график функции y=f(x-a) из графика функции f(x). Вывод: если а

II        Внимание на экран: y=cosx y=cos (х-п/3) y=cos(x+n/3)

Итог: График функции y=f(x-a) получается из графика f(x) переносом (вдоль оси абцис), на вектор (а;0) если а>0, то вектор (а;0) направлен в положительном направлении, а при а

III        y=f(x) и y=f(x)+b приведите примеры алгебраически у=х2 ,у=х2+2.

Внимание на экран: y=cosx, y=cosx+2, y=cosx-2.

Итог: Для построения графика функции f(x)+b, где b постоянное число, надо перенести график функции y=f(x) на вектор (0;Ь) вдоль оси ординат. При этом, если Ь>0 , вектор (0;Ь) имеет положительное направление, если Ь

Внимание на экран: следующая ситуация, просмотрите и сделайте вывод!

IV        y=f(x), y=f(kx), y=cosx, y=cos2x, y=cosl/2x.

Итог: При построении графика y=f(kx) происходит вдоль оси ох с
коэффициентом к, при этом любая точка графика y=f(x) с координатами
(x;f(x))        >(kx;f(k))

И еще, если речь идет о тригонометрических функциях, то к в данном случае ведет к изменению периода функции: Т/= Т/|* |, если к- целое, период

уменьшается в к раз, если к — дробное — увеличивается в к раз.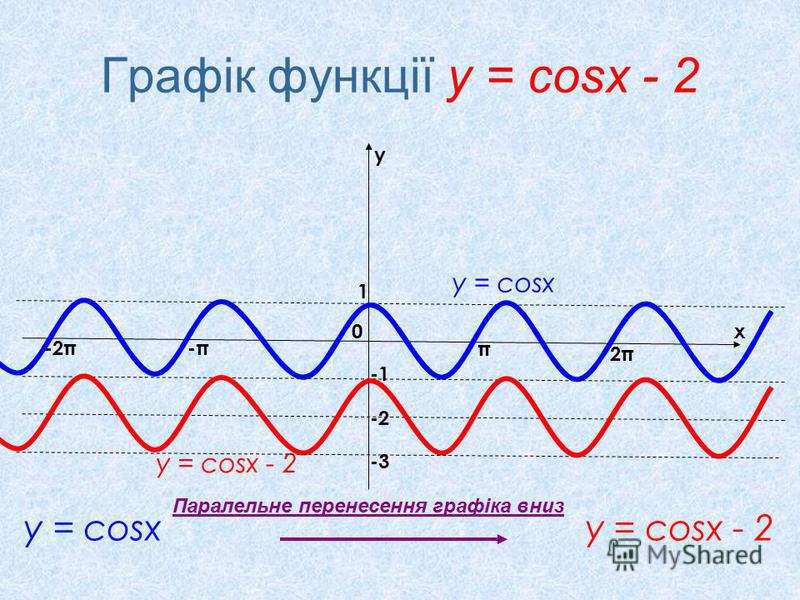 Y=cosx, Т=2П

Y=cos2x, Т/=Т/|2|=2П/2=П

Y=cos 1 /2x, T=T/|1 /2| =2П/- =2П*2=4П

V Внимание на экран:

И последняя ситуация:

y=f(x) и y=A*f(kx-a)+b

y=cosx и у= l/2cos(2x-n/2)-2/

на экране демонстрируется цепочка преобразования графика функции y=cosx

в график функции y=l/2cos(2x- п/2)-2

y=cosx-»y=l/2cosx->y=l/2cos2x-»y= l/2cos(2x-n/2) ->y=l/2cos (2х-п/2)-2

Итог урока: Итак, все преобразования графиков функций, которые вы

увидели с помощью графика функции y=cosx, можно проделать с любой

функцией вида у=А* f(kx-a)+b.

На следующем уроке мы посмотрим с вами, в каких заданиях ЕГЭ это можно

применить.

И еще вопрос: какие из параметров в уравнении функции A,k,a,b- влияют на

область значения функции (ответ: А,Ь)?

Домашнее задание:   подготовиться к диктанту по построению графиков сложных функций. По материалам ЕГЭ.( см. формулировку заданий: найти область значений и область определения функции и добавить – построить график)

Исследование функции с помощью производной

     График  нечетной функции симметричен 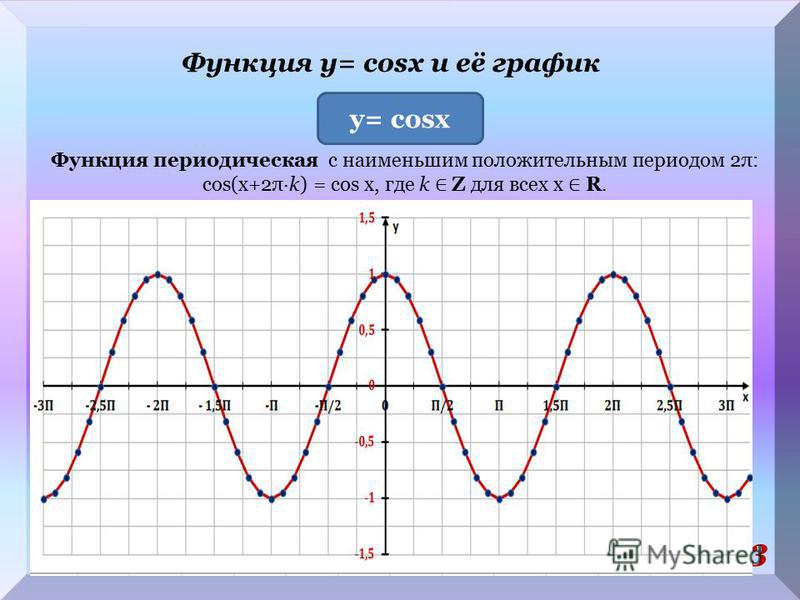относительно начала координат.

      Пример 6. Определить вид функции y=2sin2x.

                  y=2sin2x, D(y)=R

                 y(-x)=2sin2(-x)=-2sin2x=-y(x) – нечетная.

     Пример 7. Определить вид функции y=3x+1/3x.

                 y=3x+1/3x

                 y(-x)=3(-x)+1/3(-x)=-3x-1/3x=-(3x+1/3x)=-y(x) – нечетная. 

     Пример 4.                                                                     Пример 5.

       

     Определение: Функцию f называют периодической с периодом Т≠ 0, если для любого х из области определения значения этой функции в точках х, х-Т и х+Т равны, то есть f(x+T)=f(x)=f(x-T).

     Пример 8. Определить период функции y=cos2x.

                 cos2x=cos2(x+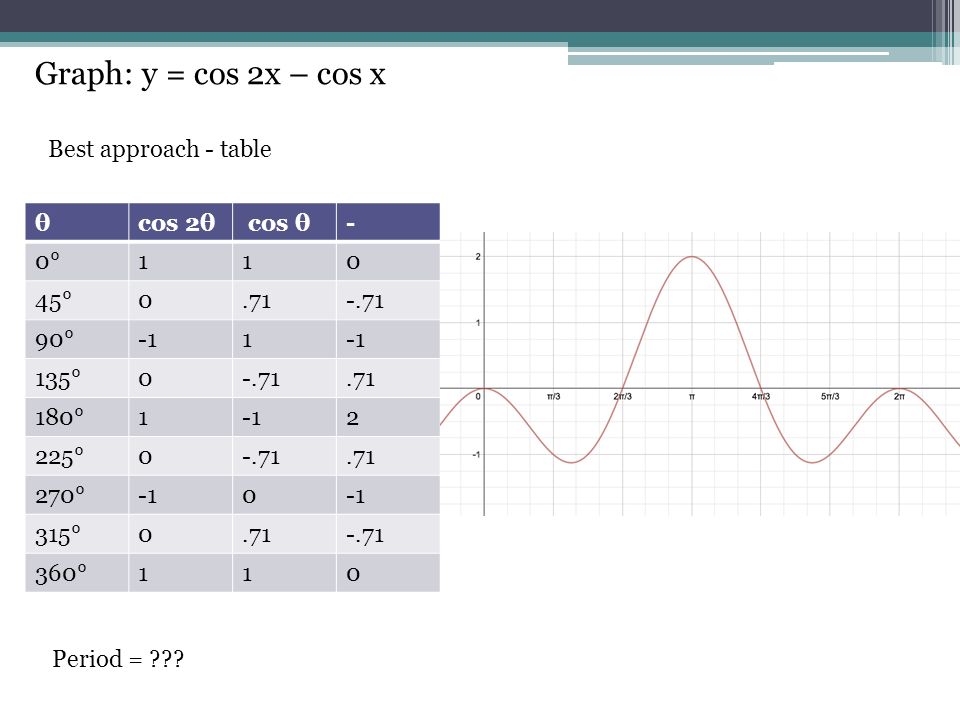T)=cos(2x+2T), где 2T=2π, т. е. Т=π.

     Для построения графика периодической  функции с периодом Т достаточно провести построение на отрезке длиной Т и затем полученный график параллельно  перенести на расстояния nT  вправо и влево вдоль оси Ох.

     Пример 9. Построить график периодической функции f(x)=sin2x.

                 f(x)=sin2x,

                 sin2x=sin2(x+T)=sin(2x+2T), где 2Т=2π, т.е. Т=π.

 

     Также к свойствам функции относятся  возрастание и убывание функции, экстремумы.

     Функция f  возрастает на множестве Р, если для любых х₁ и х₂ из множества Р, таких, что х₂>х₁ , выполнено неравенство f(x₂)>f(x₁).

     Функция  f убывает на множестве Р, если для любых х₁ и х₂ из множества Р, таких, что х₂>х₁ , выполнено неравенство f(x₂)<f(x₁).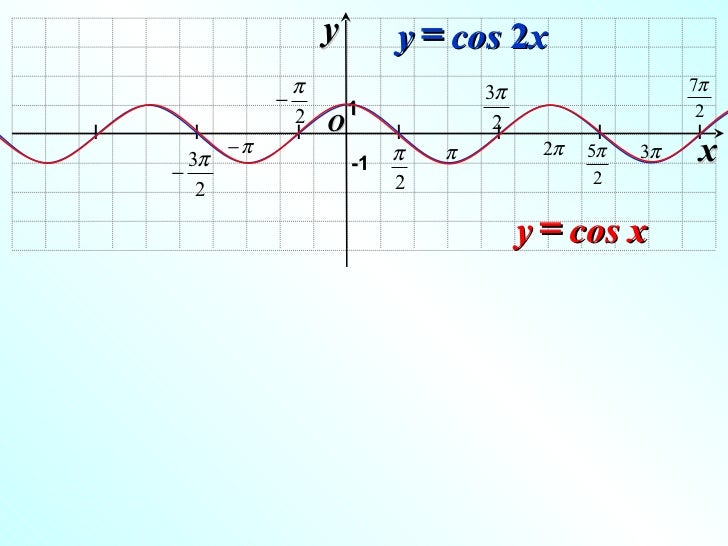

     Иными словами, функция  f называется возрастающей на множестве Р, если большему значению аргумента из этого множества соответствует большее значение  функции. Функция f называется убывающей на множестве Р,  если большему значению аргумента соответствует меньшее значение функции.

     При построении графиков конкретных функций  полезно предварительно найти точки  минимума (x_min) и максимума (x_max).

     Точка х₀ называется точкой максимума функции f , если для всех х из некоторой окрестности х₀ выполнено неравенство f(x) ≤f(x₀).

     Точка х₀ называется точкой минимума функции f , если для всех х из некоторой окрестности х₀ выполнено неравенство f(x)≥ f(x₀).

     Точки минимума и максимума принято  называть точками экстремума.

     Пример 10. Найти точки экстремума, экстремумы функции y=x²+2x, и указать промежутки возрастания и убывания функции.

                 y=x²+2x, D(y)=R

                 y’=(x²+2x)’=2x+2

     y’=0, т.е. 2х+2=0

     2х=-2

     х=-1

Исследуем знак производной справа и слева  от крайней точки.

 
 
 
 
 

                  —     + 

                                  -1

                                 min 

     x=-2, y’=-4+2<0

                  x=0, y’=0+2>0

     Так как производная меняет свой знак  с «-» на «+», то х=-1, это точка  минимума функции.

      Так как функция непрерывна в точке  х=-1, то функция возрастает на        [-1;+∞] и убывает на [-∞;-1].

                     

     Точки экстремума: x_min= -1

     Экстремумы  функции: y_min=y(-1)=1-2= -1

     Исследуя  функцию, нужно знать общую схему  исследования:

1. D(y) – область определения (область изменения переменной х)
2. E(y) – область значения х (область изменения переменной у)
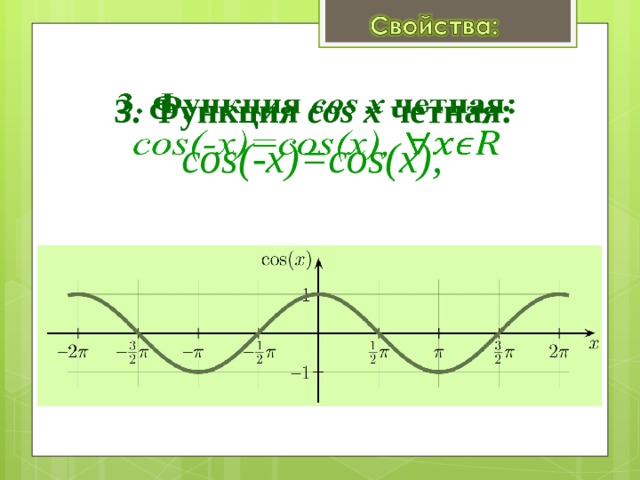
3. Вид функции: четная, нечетная, периодическая или функция общего вида.
4. Точки пересечения графика функции с осями Охи Оу (по возможности).
5. Промежутки знакопостоянства:

6. Промежутки монотонности функции:

а) возрастания;

б) убывания;

7. Точки экстремума (точки минимума и максимума)
8. Экстремумы функции (значение функции в точках минимума и максимума)
9. Дополнительные точки.

Они могут быть взяты для того, чтобы  более точно построить график функции.

     Следует заметить, что экстремумы функции  f не всегда совпадают с наибольшим и наименьшим значением функции.

     Если  строить график функции по каким-либо произвольно выбранным его точкам, соединяя их плавной линией, то даже при очень большом числе случайно выбранных точек может оказаться, что построенный таким образом  график будет сильно отличаться от графика заданной функции.

     Если  при исследовании функции использовать производную и найти так называемые «опорные» точки, т.е. точки разрыва, точки максимума и минимума, промежутки монотонности функции, то даже при небольшом  числе таких «опорных» точек  мы получим правильное  представление о графике функции.

     Прежде  чем обратиться к примерам, приведу  необходимые определения и 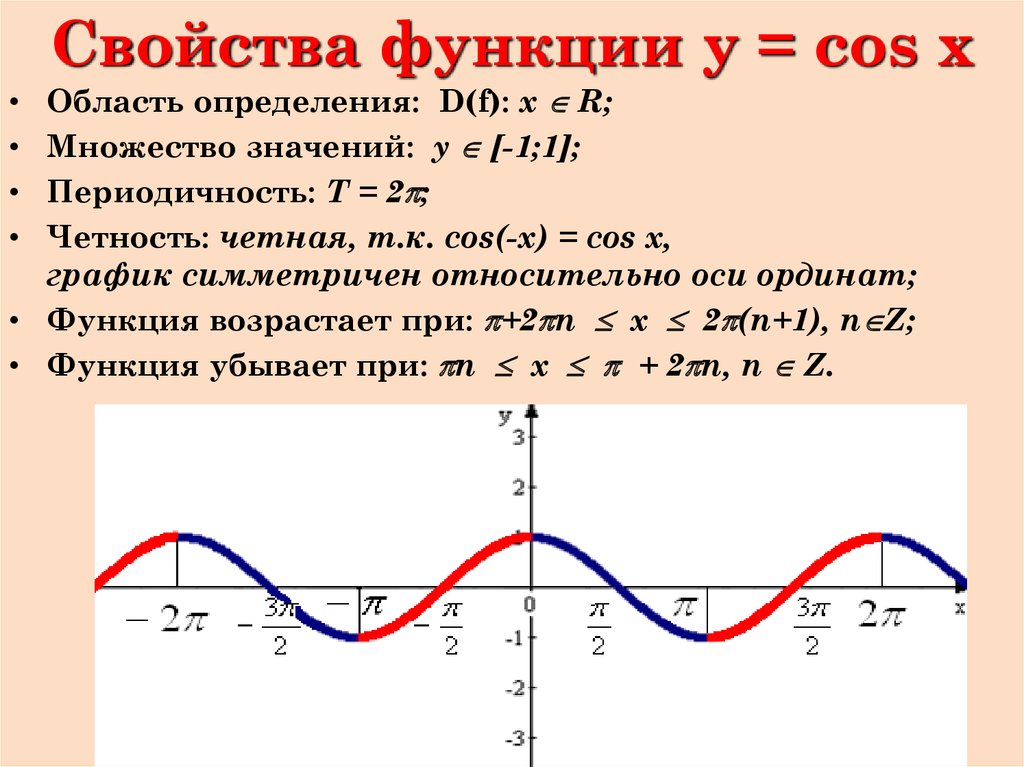теоремы.

     Определение монотонности функции  на интервале Функция y=f(x) называется возрастающей на интервале, если для любых точек х₁ и х₂ этого интервала из  условия х₁<х₂ следует, что f(x₁)<f(x₂). Если же из условия х₁<х₂ следует, что f(x₁)>f(x₂), то функция называется убывающей на этом интервале.

     Достаточный признак монотонности функции в интервале.

Теорема: если функция имеет положительную (отрицательную) производную в каждой точке интервала, то функция возрастает (убывает) на этом интервале.

     Эта теорема в школьных учебниках  принимается без доказательства.

     Геометрическое  истолкование теоремы весьма простое, если вспомнить, что f ’(x)=tgα, α – это угловой коэффициент касательной к графику функции в заданной точке х. Если, например, f ‘ (x)>0 во всех точках некоторого интервала, то касательная к графику с осью абсцисс образуют острые углы, а значит, с ростом х возрастает и f(x). Если же f ‘ (x)<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.

       3.3. Критические точки функции,  максимумы и минимумы.

     Определение точек экстремума функции. Пусть х₀ – внутренняя точка из области определения функции f(x). Тогда, если существует такая δ – окрестность ] x₀— δ, x₀+ δ [ точки х₀, что для всех х из этой окрестности выполняется неравенство f(x)≤f(x₀) (неравенство f(x)≥f(x₀)), точка х₀ называется точкой максимума (точкой минимума) этой функции.

     Точки максимума минимума являются внутренними  точками области определения  функции.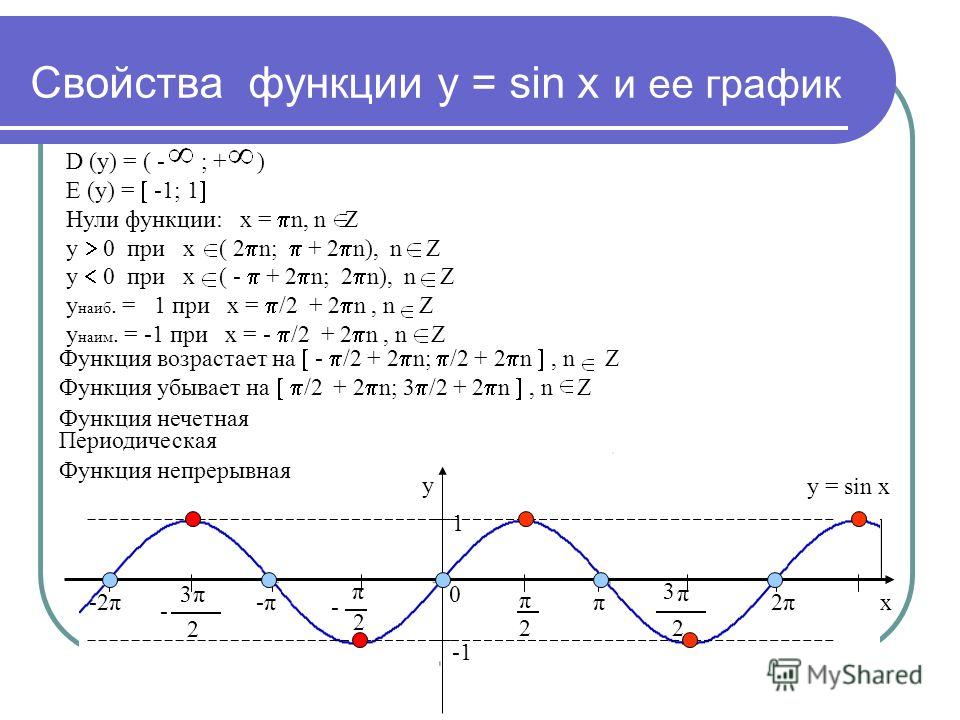

     Необходимый признак существования  экстремума дифференци-руемой функции.

     Теорема Ферма.

     Если  х₀ есть точка экстремума функции f(x) и в этой точке производная существует, то она равна нулю: f ’(x

0)=0.

     Эта теорема не является достаточным  условием существование экстремума дифференцируемой функции: если в некоторой  точке х₀ производная обращается в нуль, то из этого еще не следует, что в точке х₀ функция имеет экстремум.

     Определение критических точек  функции. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называют критическими точками функции.

     Достаточные условия существования  экстремума.

     Теорема 1. Если функция f(x) непрерывна в точке х₀, f ‘(x)>0  на интервале [a, x₀] и f ‘(x)<0  на интервале [x₀, b], то х₀ является точкой максимума функции f(x).

     Теорема 2. Если функция f(x) непрерывна в точке х₀, f ‘(x)<0  на интервале [a, x₀] и f ‘(x)>0  на интервале [x₀, b], то х₀ является точкой минимума функции f(x).

     Для отыскания экстремальных точек  функции нужно найти ее критические  точки и для каждой из них проверить  выполнение достаточных условий  экстремума.

     Правила отыскания наибольшего  и наименьшего  значений функций  в промежутке. Для отыскания наибольшего и наименьшего значений функции, дифференцируемой в некотором промежутке, нужно найти все критические точки, лежащие внутри промежутка, вычислить значения функции в этих точках и на концах промежутка и из всех полученных таким образом значений функции выбрать наибольшее и наименьшее.

     Пример 11. Исследовать функцию y=x³+6x²+9x  и построить график.

           y=x³+6x+9x

1. D(y)=R
2. Определим вид функции:

3. Найдем точки пересечения с осями:

Ox: y=0,

x³+6x²+9x=0

x(x²+6x+9)=0

x=0 или x²+6x+9=0

                D=b²-4ac

                D=36-36=0

x=(-b+D)/2a

x=-6+0/2

x=-3

4. Найдем производную функции:

5. Определим критические точки:

                  x²+4x+3=0

                  D=b²-4ac

                  D=16-12=4

x₁=-1     x₂=-3

Площадь под кривой $y=\left[\sqrt{2+2\cos2x}\right]$

спросил 3 года, 6 месяцев назад

Изменено 3 года, 6 месяцев назад

Просмотрено 189 раз

$\begingroup$

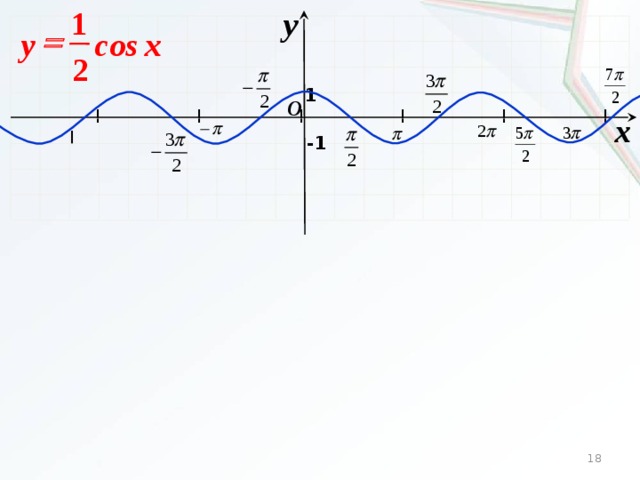
Найдите площадь под кривой $y=[\sqrt{2+2\cos2x}]$ и выше оси $x$, $x\in [-3\pi,6\pi]$, (где $[.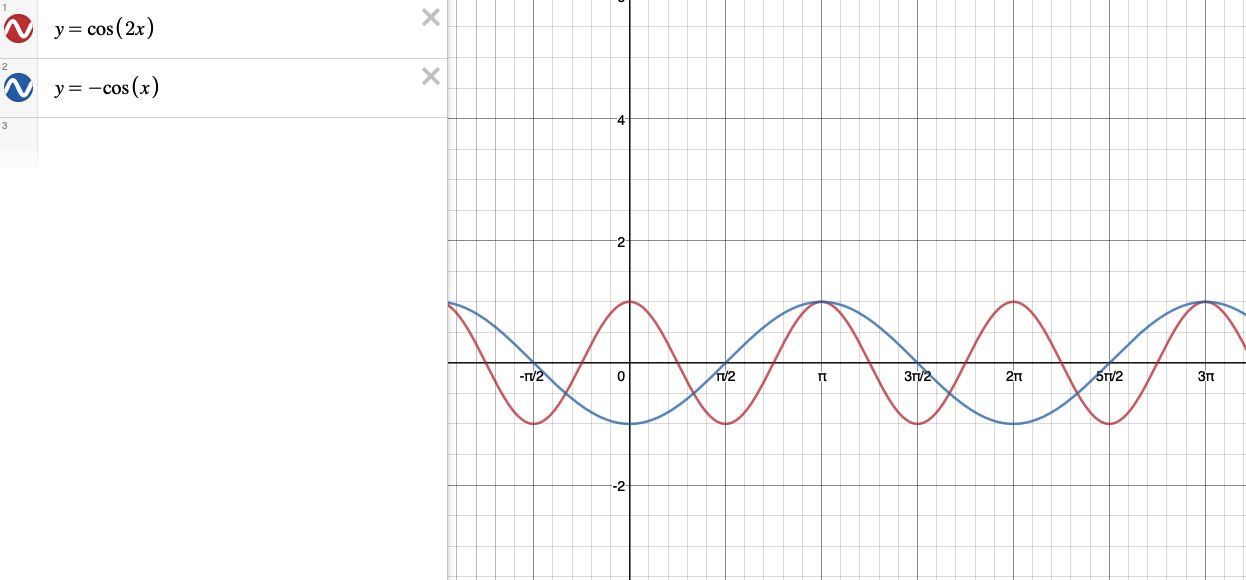 ]$ обозначает функцию наибольшего целого числа). 92x-2}]$$ $$=[|2\cos x|]$$

После этого я не знаю, как это решить и как найти площадь.

$\endgroup$

1

$\begingroup$

$$0\le 2|\cos{x}|\le 2\имплициты [2|\cos{x}|]\in[0,1,2]$$

Функция $[2|\cos {x}|]$ является разрывным для тех значений x, которые делают его равным 2, но это отдельные точки устранимого разрыва, и они не повлияют на свойства интегрирования этой функции. Итак, площадь лежит между значениями $0$ и $1$. Следовательно, нам нужно найти то значение x (просто найдите одно такое значение, остальная часть проблемы будет решена с помощью симметрии и повторения), которое служит пограничной точкой между значениями, которые больше 1, и значениями, которые ниже 1:9{6\pi}ydx$ — это сумма длин интервалов, на которых $y\ge 1$ (т. е. $|\cos x|\ge\frac12$). По отношению к $[-3\pi,\,6\pi]$ дополнением объединения этих интервалов является объединение интервалов, по которым $\cos x$ биектируется из $\pm\frac12$ в $\mp\ 12$. Таких интервалов девять, $\left(k\pi-\frac{8\pi}{3},\,k\pi-\frac{7\pi}{3}\right)$ для целого числа $k$ от $0$ до $8$ включительно. Так как их общая длина $9\times\frac{\pi}{3}=3\pi$, искомый интеграл равен $9\pi-3\pi=6\pi$.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Получение тождеств триггеров с помощью формулы Эйлера

Автор: Джеффри Д.

В этом уроке мы рассмотрим вывод нескольких тригонометрических тождеств, а именно

cos ( x + y ) = cos x cos y 77 907 7 sin y

and

sin ( x + y ) = sin x cos y + sin x cos y

also

cos 2 x = cos ² x – sin ² x

along with

sin 2 x = 2 sin x cos x

and lastly, DeMoivre’s Formula,

(cos x + i sin x ) ⁿ = cos n x + i sin n x

по формуле Эйлера. Чтобы получить хорошее представление о том, что происходит, вам понадобятся предварительные знания о расширении рядов и комплексных числах! Вы можете сначала освежить свои знания по этим предметам.

Расширения степенного ряда

Начнем с изучения степенного расширения функций e ^x , sin x и cos x . Степенной ряд функции обычно получается из ряда Тейлора функции для случая, когда a = 0. Этот случай, когда a = 0, называется рядом Маклорена. Ряд Тейлора:

Случай, когда a = 0, представляет собой ряд Маклорена:

Эти ряды используются для аппроксимации значений функций в определенной точке. Это все, что я скажу об этом. Силовая серия e ^x ; cos x и sin x исходят из их представления серии MacLaurin:

для всех x.

для всех х.

для всех х.

Комплексные числа и

e ^x

Комплексное число — это число вида a + bi , где i — корень уравнения x ² + 1 = 0, а a и b — действительные числа. Заметив это, мы можем использовать и в нашем ряду мощностей и , поскольку это верно для всех x .

для всех х.

Имея в виду, что x ² + 1 = 0 → x = i и т. д. √-1 = i → i ² = -1, i ³ = – i , и т. д. Таким образом, выборочно применяя степени, мы получаем

. have

Now, if we look back at our series representations of cos x and sin x we have

e ^ix = cos x + i sin x

Этот вывод огромен. Он известен как Формула Эйлера . Отсюда мы можем вывести некоторые тригонометрические тождества, а также придумать формулы для общих случаев. Давайте рассмотрим простой вывод сначала:

E ^IX E ^IY = (COS x + I SIN X ) (COS Y + I SIN 7).

Но напомним, что e ^x e ^y = e ^x+y . Следовательно, имеем

E ^{IX + IY} = COS ( x + Y ) + I SIN ( X + Y ) = (COS X + I SIN ) = (COS X + I SIN 777777777) = (COS x + 7 I SIN 7777777) = (COS x + I ) = (COS x + I ) COS Y + I SIN Y )
= COS x COS Y + I SIN X COS Y + I SIN Y CO + I SIN Y COS + I Y .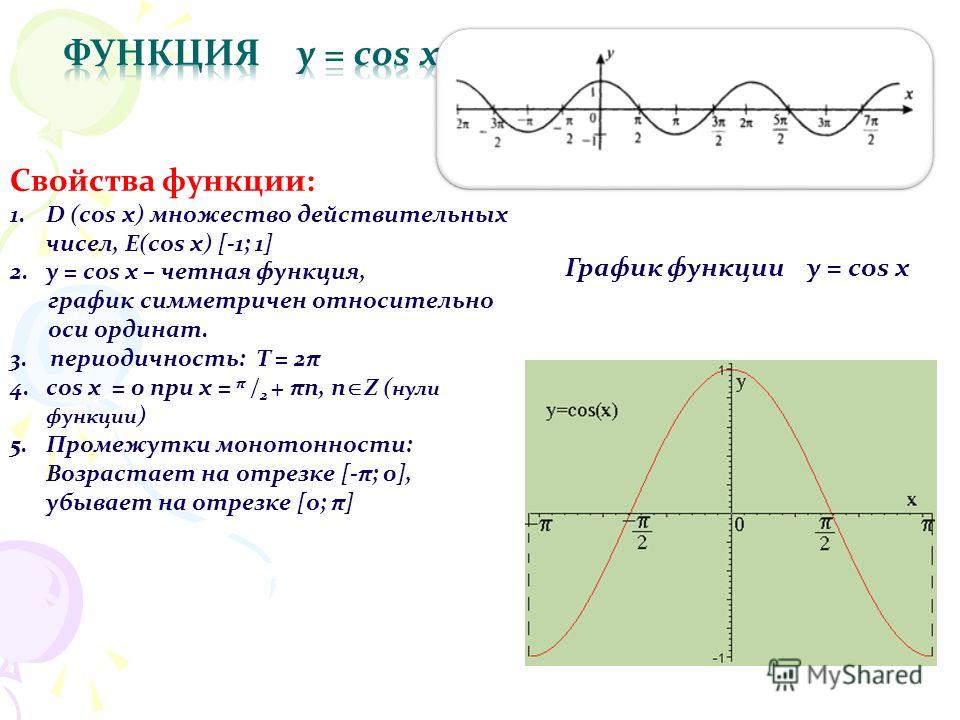 ² sin x sin y

А теперь мы можем изменить это так, чтобы сложная часть и действительная часть были разделены.

и поэтому у нас есть

E ^{IX + IY} = COS ( x + Y ) + I SIN ( x + Y ) = (Cos x + + Y ) = (Cos x + + Y ). SIN X ) (COS Y + I SIN Y )
= COS X COS Y + I SIN X COS Y + I X COS Y + + I I X COS y + + + + I I x .0078 SIN Y COS x + I ² SIN x SIN Y
= (COS x COS Y — SIN x SIN Y Y + ). SIN x COS Y + I SIN Y COS X )

Принимая реальные части и приравниваем их, мы получаем знакомую тригонометрическую сумму:

Cos ( x + Y )) = cos х COS Y — SIN x SIN Y

, а также

SIN ( x + Y ) = SIN X COS Y + SIN Y COS COS Y + SIN Y COS COS Y + SIN Y COS COS Y + SIN Y COS COS Y + SIN Y COS COS Y + SIN Y COS . Теперь предположим, что у нас есть что -то вроде этого:

E ^IX E ^IX = E ^{IX + IX} = E ^I2X = COS ( X + 777777777777 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + 9007 + = COS. я грех( х + х )
= (COS x + I SIN X ) (COS x + I SIN X )
= COS X COS X + 7 = COS X COS X + 777777 7. I COS 78 + 77777777777 7. I COS 7 + 7777777777 7. I COS 7. COS x + I SIN X COS X + I ² SIN X SIN X

Если мы равняем реальные части уравнения

COS 2 7777777777. cos ² x – sin ² х

А также имеем

sin 2 х = 2 sin х cos х

В общем случае мы можем получить формулу для любого кратного угла. Это приводит нас к другой известной формуле, известной как формула Де Муавра. Формулу Де Муавра можно вывести, взяв n -й случай формулы Эйлера.

e ^inx = cos nx + i sin nx

Мы заинтересованы в том, чтобы показать, что

(COS x + I SIN X ) ^N = COS NX + I SIN NX

, что является FRAM78 DEMOULALIV. Очевидно, что это верно для любых n . Мы можем показать, что это верно для всех n , используя индукцию.

(cos x + i sin x ) ^{n +1} = (cos x + i sin x ) ⁿ (cos x + i sin x ) 7 n 0 0 0

= (cos n x + i sin n x )(cos x + i sin x )

Теперь мы можем умножать.

= cos nx cos x + i sin x cos nx + i sin nx cos x + i ² sin nx sin x

.