ОглавлениеВВЕДЕНИЕЧасть первая.  Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. 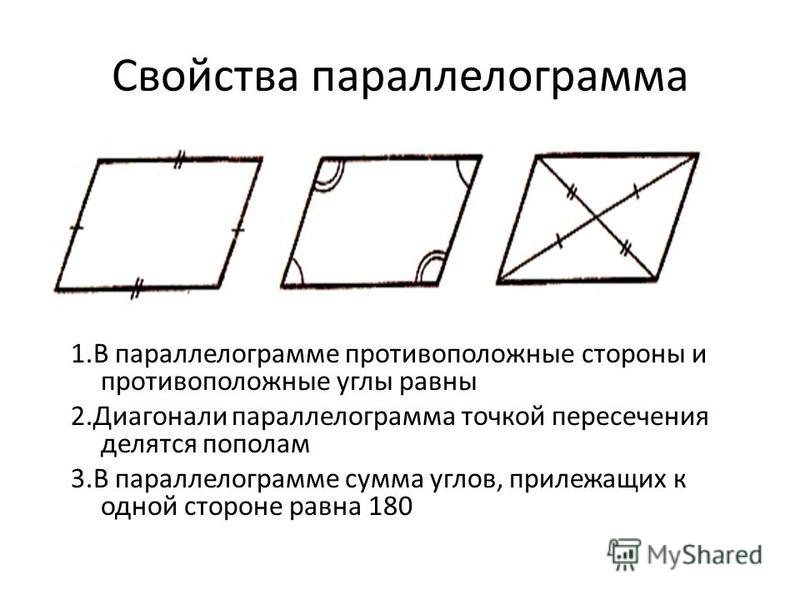 Формула Муавра. Формула Муавра.18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 34. Сложная функция. 35. Обратная функция. 36.  n. n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 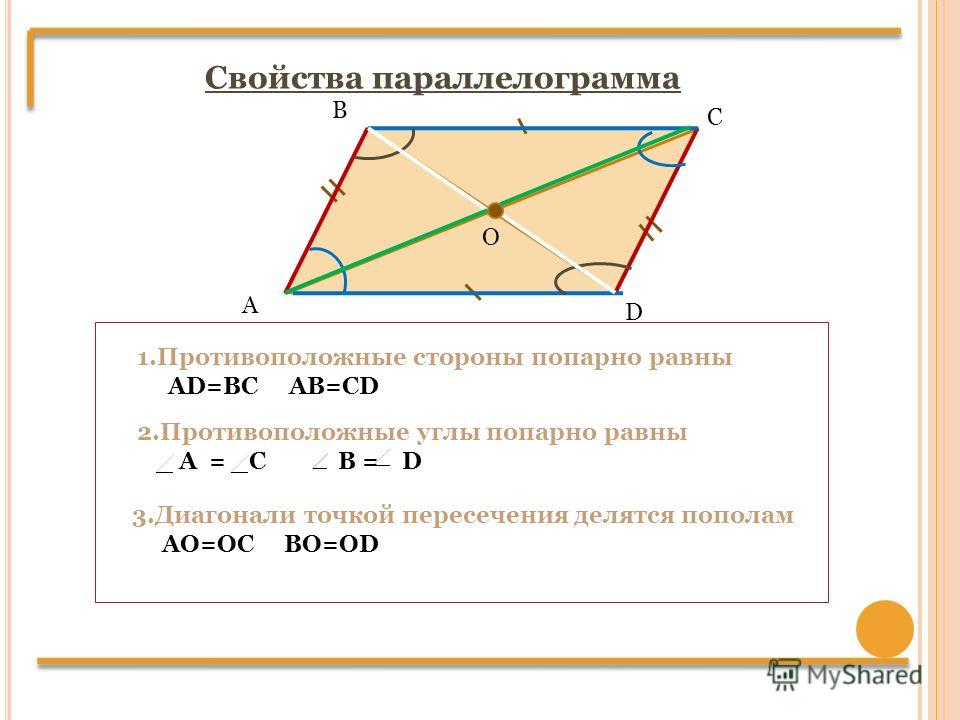 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства. Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 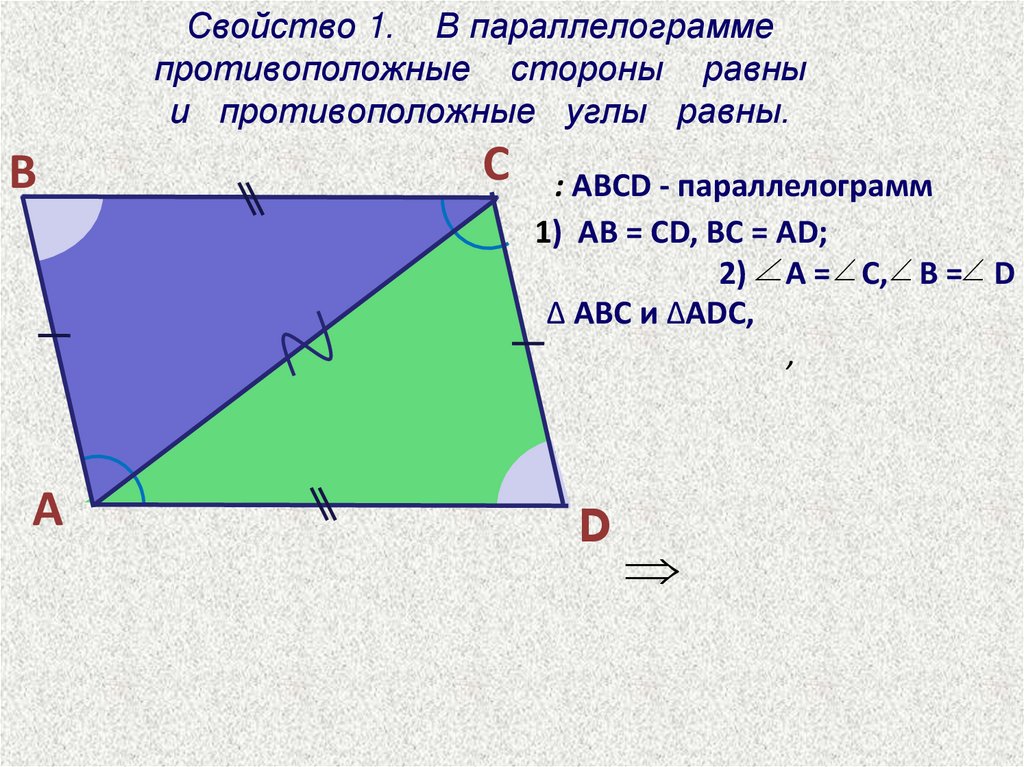 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. 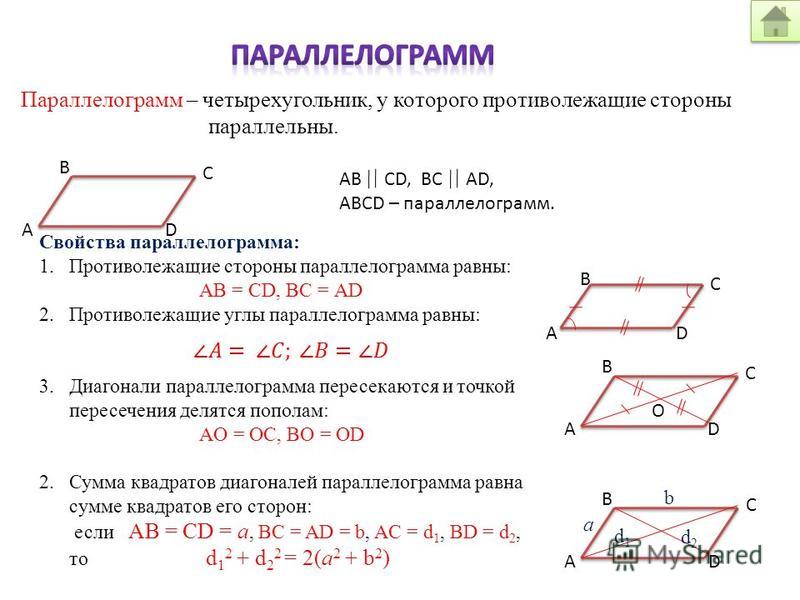 Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 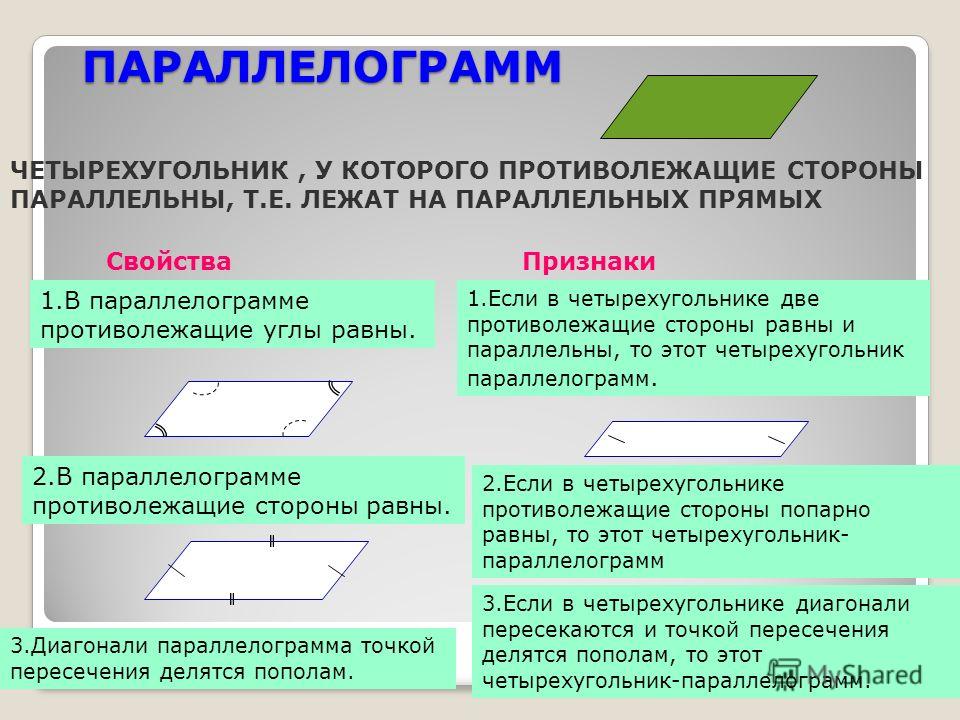 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. 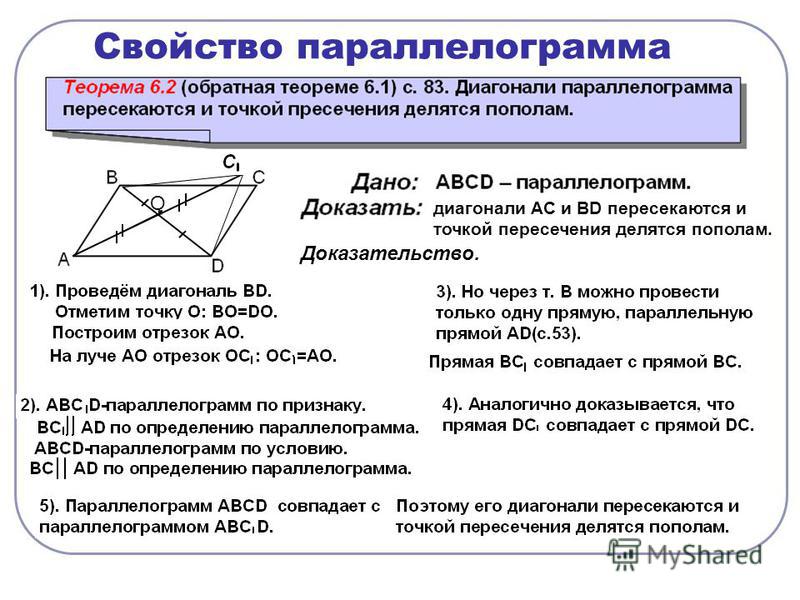 Функция у = arcsin (sin x). Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 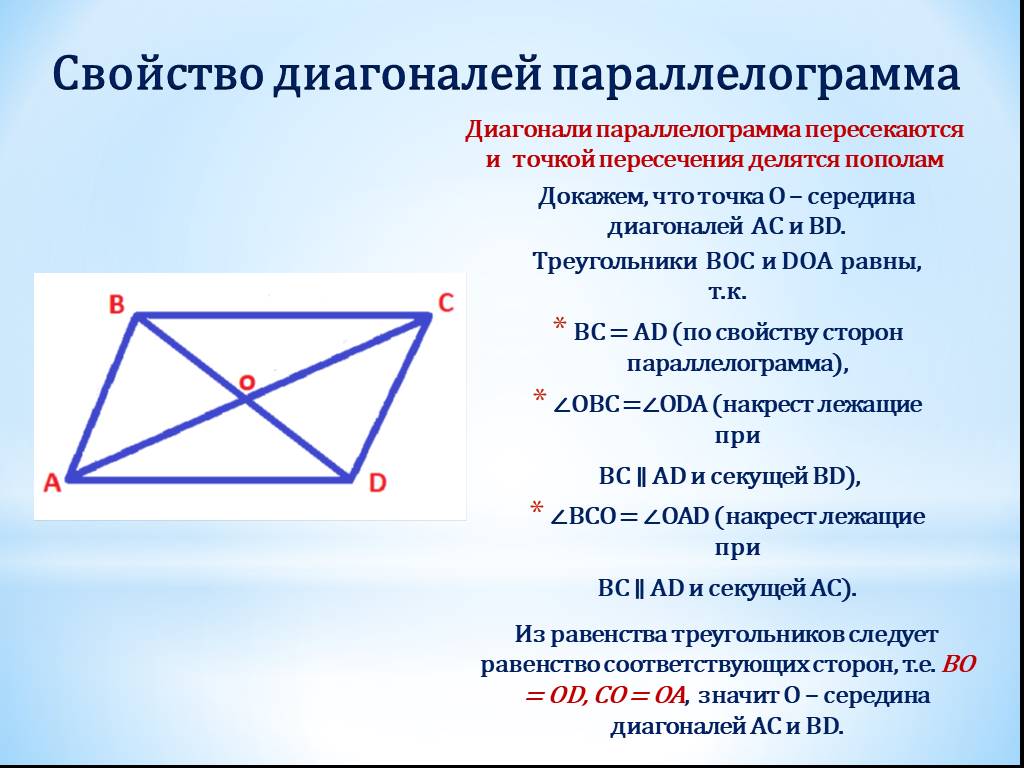 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 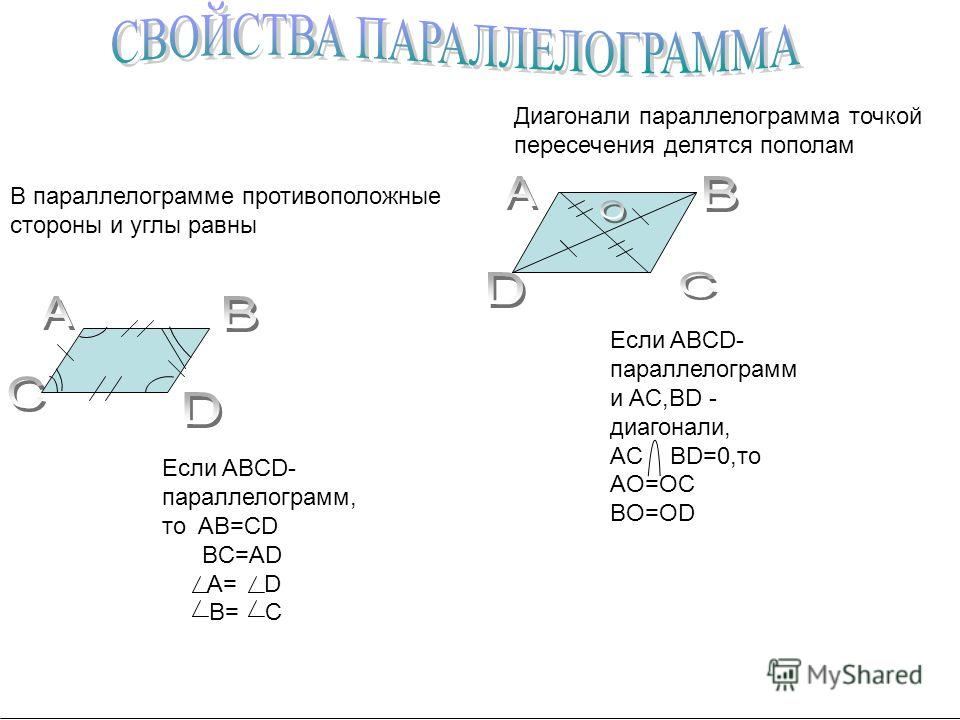 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. 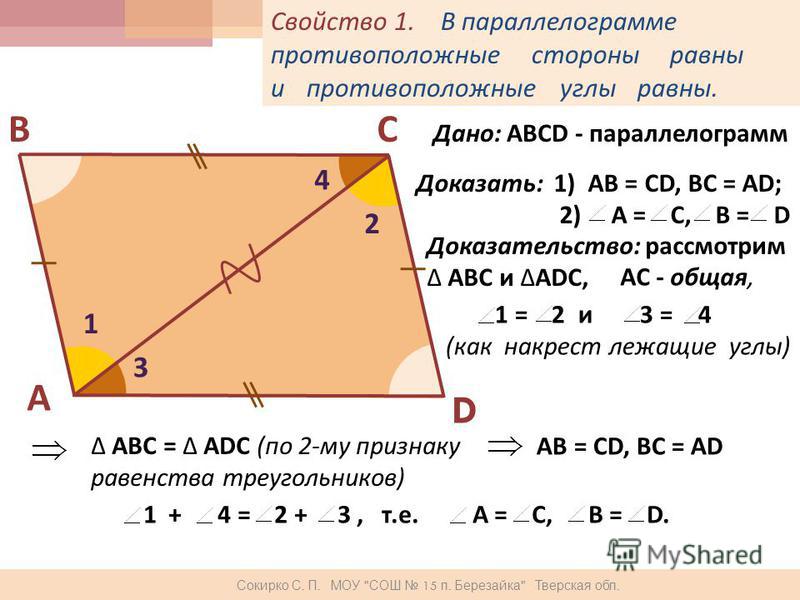 § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора. Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса.  253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
Параллелограмм. Свойства параллелограмма с доказательством — Студопедия
Поделись с друзьями:
Определение. Параллелограмм – это четырёхугольник, противоположные стороны которого попарно параллельны.
Свойство 1. Любая диагональ параллелограмма делит его на два равных треугольника.
Доказательство. По II признаку (накрест лежащие углы и общая сторона).
Теорема доказана.
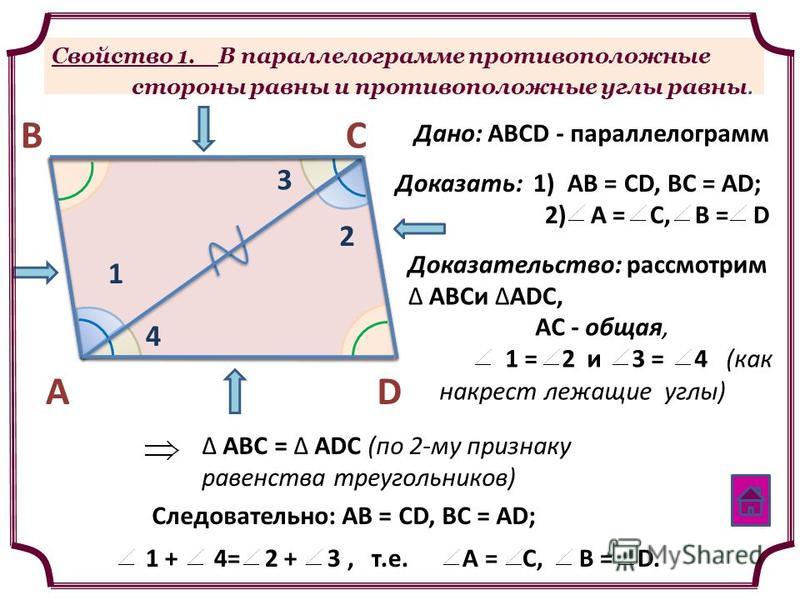
Свойство 2. В параллелограмме противолежащие стороны равны, противолежащие углы равны.
Доказательство.
Аналогично,
Теорема доказана.
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.
Доказательство.
Теорема доказана.
Свойство 4. Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. – вершину – два равнобедренных?-ка).
Доказательство.
Теорема доказана.
Свойство 5. В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.
Доказательство.
Теорема доказана.
Свойство 6. Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.
Доказательство.
Теорема доказана.
Свойство 7. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство.
Теорема доказана.
Построение биссектрисы угла. Свойства биссектрисы угла треугольника.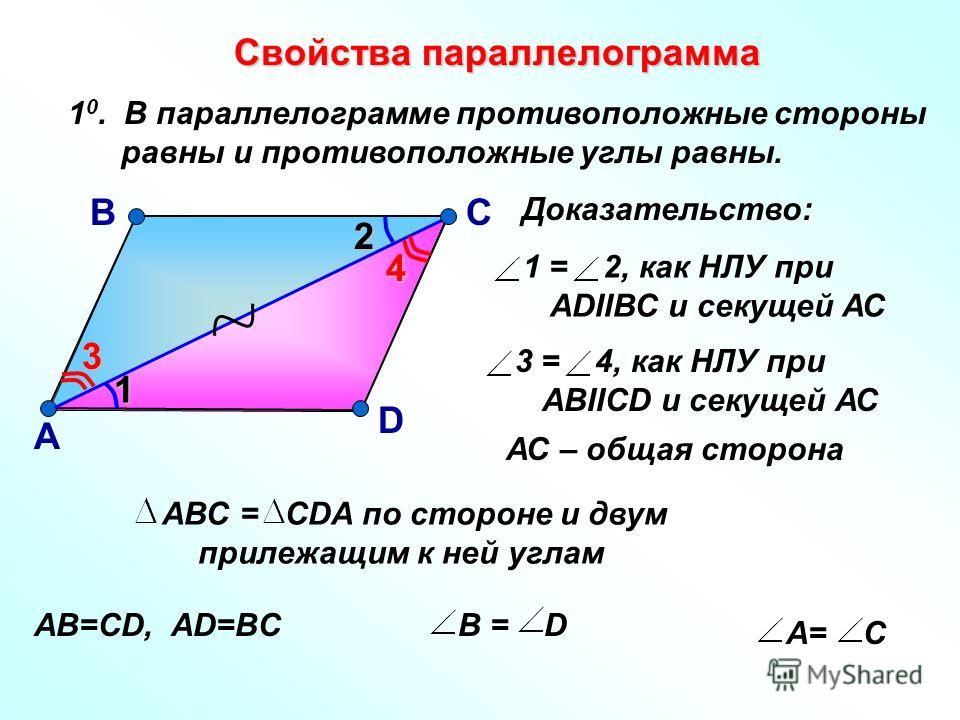
1) Построить произвольный луч DE.
2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.
3) F и G – точки пересечения окружности со сторонами данного угла, H – точка пересечения окружности с построенным лучом
Построить окружность с центром в точке H и радиусом, равным FG.
5) I – точка пересечения окружностей построенного луча.
6) Провести прямую через вершину и I.
IDH – требуемый угол.
(
)
Свойство 1. Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.
Доказательство. Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.
Теорема доказана.
Свойство 2. Биссектриса – ГМТ равноудалённых от прилежащих сторон треугольника.
Свойство 3. Биссектрисы треугольника пересекаются в одной точке, и эта точка – центр вписанной окружности треугольника.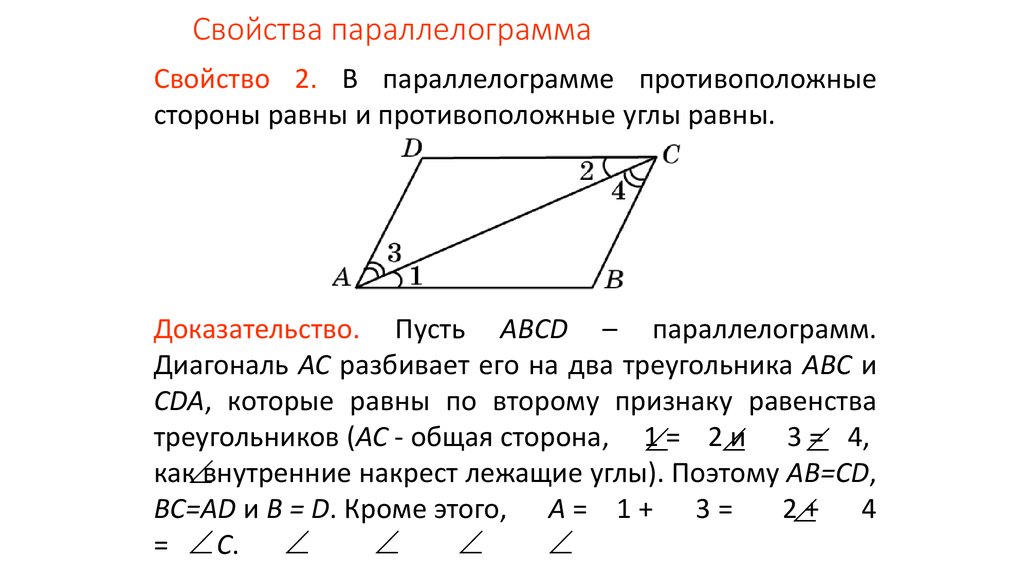 (Из предыдущего свойства)
(Из предыдущего свойства)
Свойство 4. Биссектрисы делятся точкой пересечения в отношении суммы прилежащих сторон к противолежащей стороне, считая от вершины.
Доказательство. Рассмотрим треугольник CBC1:
Теорема доказана.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Геометрия: свойства параллелограммов
Параллелограмм — это четырехугольник, у которого обе пары противоположных сторон параллельны. Параллелограммы обладают многими свойствами, которые легко доказать, используя свойства параллельных прямых. Вы будете иногда использовать диагональ, чтобы разделить параллелограмм на треугольники. Если вы сделаете это осторожно, ваши треугольники будут конгруэнтными, поэтому вы можете использовать CPOCTAC.
Твердые факты
Параллелограмм — это четырехугольник, у которого обе пары противоположных сторон параллельны.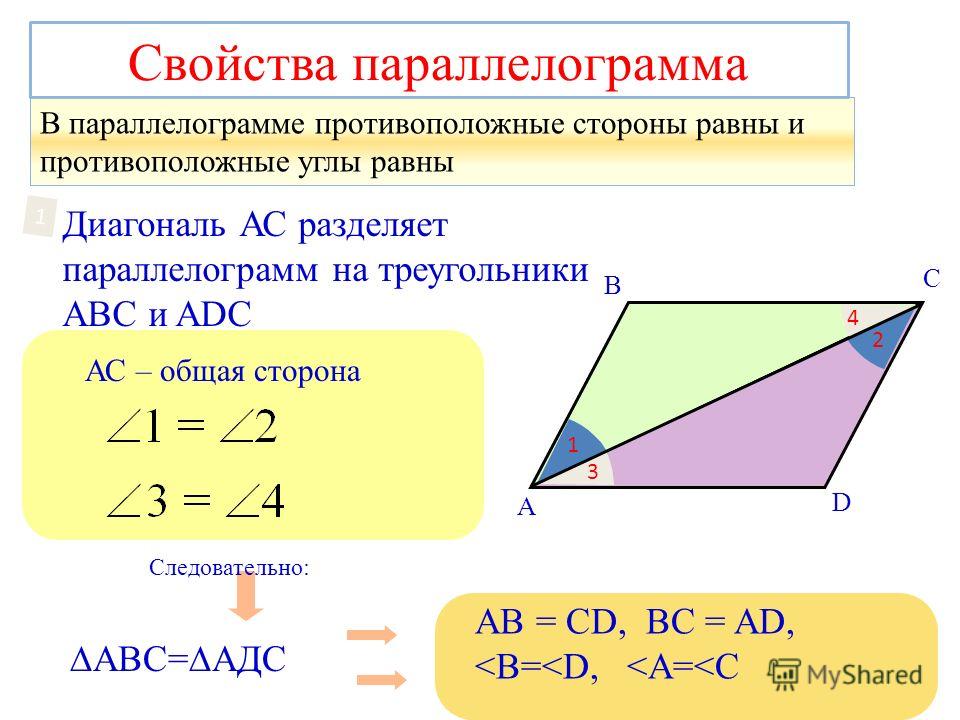
- Теорема 15.5 : Диагональ параллелограмма делит его на два конгруэнтных треугольника.
- Пример 2 : Напишите формальное доказательство теоремы 15.5.
- Решение : Начните со списка того, что вам нужно привести к формальным доказательствам. У нас уже есть формулировка теоремы. На рис. 15.7 показан параллелограмм ABCD с диагональю ¯AC.
Рис. 15.7 Параллелограмм ABCD с диагональю ¯AC.
- Дано: Параллелограмм ABCD с диагональю ¯AC.
- Докажите: ABC ~= CDA.
- Доказательство: Ваш план игры состоит в том, чтобы использовать свойства параллельных прямых, пересеченных секущей, чтобы связать два угла ABC с двумя соответствующими углами в CDA. Поскольку ¯AC ~= ¯AC, вы можете использовать постулат ASA, чтобы показать ABC ~= CDA.
| Утверждения | Причины | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Параллелограмм ABCD имеет диагональ ¯AC | Учитывается | |||||||||||||||||||||||||||||
2. | ¯bc ¯AD CUT с помощью поперечных ¯ac | Определение поперечных | |||||||||||||||||||||||||||||
| 3. | BAC и DCA — Alternate Interior Angles | BAC и DCA — Alternate Interio Angles | BAC и DCA — Alternate Interio Angles | . Теорема 10.20039 | 6. | ACB and DAC are alternate interior angles | Definition of alternate interior angles | ||||||||||||||||||||||||
| 7. | ACB ~= DAC | Theorem 10.2 | |||||||||||||||||||||||||||||
| 8. | ¯AC ~= ¯AC | Рефлексивное свойство ~= | |||||||||||||||||||||||||||||
| 9. | ABC ~= CDA | Постулат ASA |
Эта теорема пригодится при установлении теорем о параллелограммах. Обычный метод включает использование диагонали для разделения параллелограмма на два треугольника с последующим применением CPOCTAC.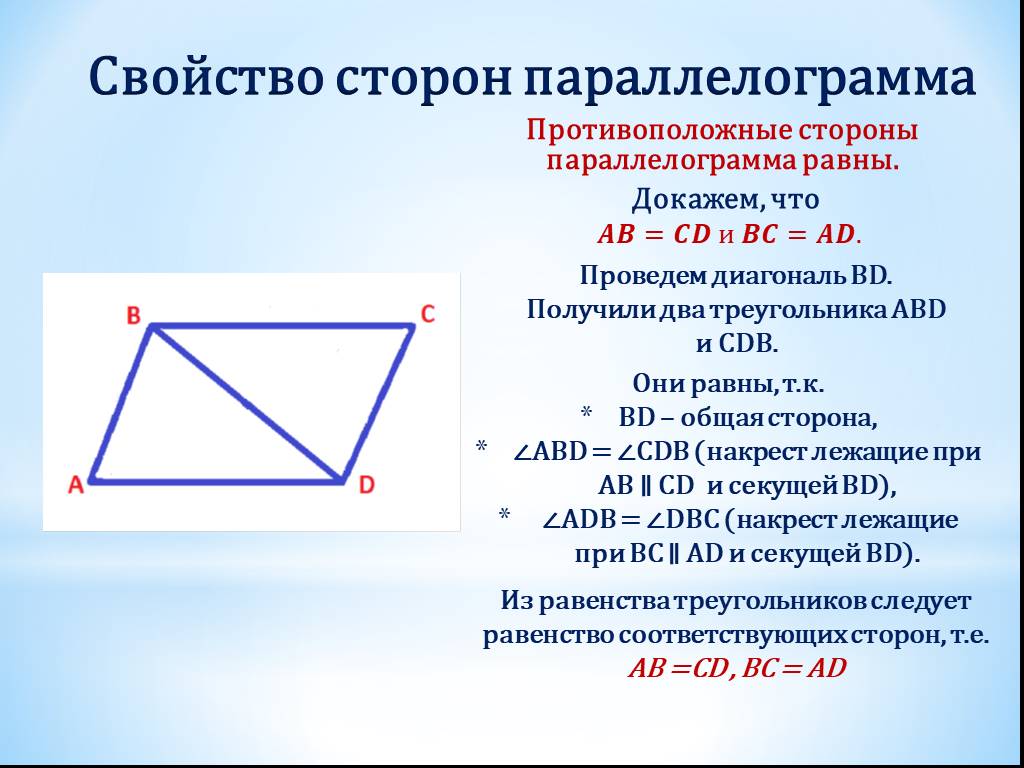 Следующие две теоремы используют эту технику. Я докажу первое, а вы докажите второе.
Следующие две теоремы используют эту технику. Я докажу первое, а вы докажите второе.
- Теорема 15.6 : Противоположные стороны параллелограмма равны.
- Теорема 15.7 : Противоположные углы параллелограмма равны.
- Пример 3 : Напишите доказательство теоремы 15.6 в два столбца.
- Решение : Вы можете воспользоваться информацией, показанной на рис. 15.7. Мы будем иметь дело с параллелограммом ABCD и его диагональю ¯AC. Вы захотите доказать, что ¯BC ~= ¯AD.
| Заявления | Причины | ||
|---|---|---|---|
| 1. | Параллелограмма ABCD имеет диагональный ¯AC | . = ¯AD | CPOCTAC |
Последнее свойство параллелограмма, о котором я упомяну, касается пересечения диагоналей. Получается, что диагонали параллелограмма делят друг друга пополам. Доказательство этого довольно простое, поэтому я проведу вас через план игры и позволю вам сообщить детали.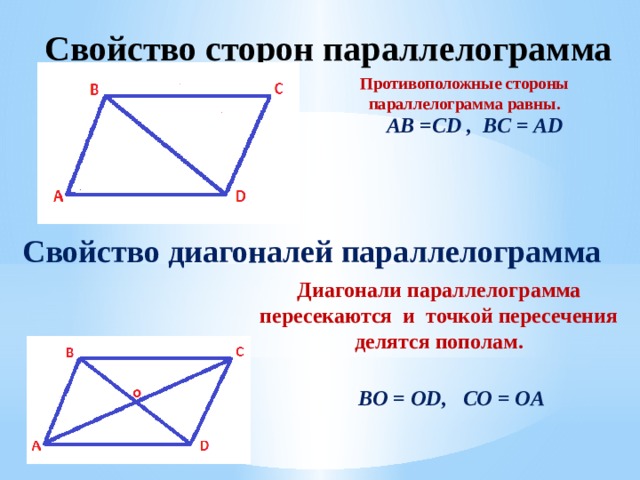
- Теорема 15.8 : Диагонали параллелограмма делят друг друга пополам.
Взгляните на параллелограмм ABCD на рис. 15.8. Диагонали ¯AC и ¯BD пересекаются в точке M. Мы хотим показать, что ¯AM ~= ¯MC. Самый простой способ сделать это — найти два конгруэнтных треугольника и использовать CPOCTAC. Два треугольника, которые мы попытаемся доказать конгруэнтностью, — это AMD и CMB. Поскольку противоположные стороны параллелограмма равны, ¯BC ~= ¯AD. Поскольку вертикальные углы конгруэнтны, AMD ~= ¯CMB. Наконец, у нас есть ¯BC ¯AD, пересеченный секущей ¯AC, и поскольку BCA и CAD являются альтернативными внутренними углами, они конгруэнтны. Используя теорему ААС, мы можем заключить, что AMD ~= CMB. Завершите это с помощью CPOCTAC.
Рисунок 15.8 Параллелограмм ABCD имеет диагонали ¯AC и ¯BD, которые пересекаются в точке M. воспроизведение полностью или частично в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
свойства параллелограмма
Мастер 7 столбов школьного успеха
Улучшить свои оценки и снизить стресс
Стандарт общего ядра: 7.G.6 7 -й класс Матем этот удобный калькулятор, чтобы проверить свою работу.
Рассчитайте следующее:
- Площадь прямоугольника
- Площадь параллелограмма
- Area of a square
- Perimeter of a parallelogram
- Perimeter of a square
- Perimeter of a rectangle
- What is a parallelogram
- Which sides of параллелограмм параллельны?
- Какими свойствами обладают углы параллелограмма?
- Что такое дополнительные углы?
Связанные сайты параллелограммов
Свойства параллелограмма/Math Planet Хорошие картинки, понятные объяснения и видео Кроссворд
Инфографический параллелограмм
Стенограмма
Напротив стороны параллелограмма конгруэнтны (равны длина) |
|
Напротив стороны параллельны |
|
Напротив углы параллелограмма равны |
|
Смежный углы параллелограмма являются дополнительными, что означает, что они равны 180 градусов |
|
Формула площади параллелограмм ш х в основание x высота
Примечание: Высота не сбоку
длина. Высота = площадь/основание или h = а/б |
|
Периметр формула
2(б + с) b = основание s = сторона |
|
Диагональ пересекаются друг с другом на полпути в точке |
|
Что такое параллелограмм?
Углы в параллелограмме
Что такое параллелограмм? Во-первых, параллелограмм — это четырехугольник, а многоугольник — это замкнутая двумерная фигура с четырьмя сторонами.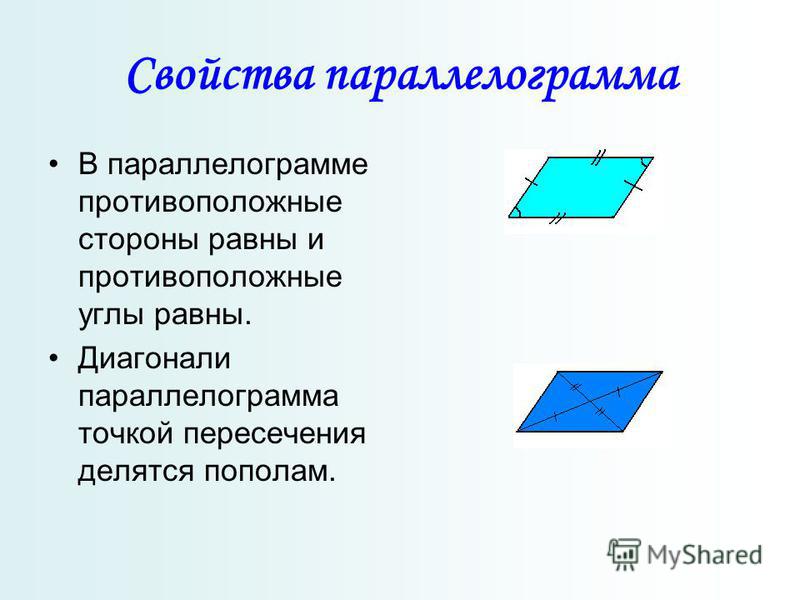 Давайте посмотрим на свойства, которые определяют параллелограмм.
Давайте посмотрим на свойства, которые определяют параллелограмм.
Вы также можете насладиться:
Ромбобы
Диаграмма площади
Определение кайта в геометрии
Семейство четырехсторонности
«A и» B «. дополнительный
Привет Добро пожаловать в MooMooMath. Сегодня мы поговорим о параллелограммах. Прежде чем я перейду к свойствам, давайте посмотрим, где находится параллелограмм в семействе четырехугольников. Параллелограмм — это четырехсторонний многоугольник, что означает, что это четырехугольник, поэтому он находится под большим зонтиком четырехугольников. Итак, мы смотрим на стороны семейства четырехугольников, которые все являются параллелограммами, и под параллелограммами попадают эти другие фигуры, прямоугольник, ромб и квадрат. Давайте посмотрим на свойства просто параллелограмма, у параллелограмма есть несколько свойств. Определение параллелограмма состоит в том, что противоположные стороны AT и MH будут параллельны друг другу, и мы представим это с помощью символа стрелки, а MA и HT также параллельны.

