Книга «Картонка-підказка. Таблиця множення і ділення. Таблиця Піфагора» – , купити за ціною 9.00 на YAKABOO: 9789663141121
Картонка-підказка. Таблиця множення і ділення. Таблиця Піфагора
Паперова книга | Код товару 1332190
Видавництво | Зірка |
| Українська | |
Рік видання | 2021 |
Ілюстрації | Немає ілюстрацій |
Формат | 150х210 мм |
Палітурка | М’яка, Картон |
| Картон | |
| 9789663141121 |
Показати всі характеристики
Усе про книжку
Характеристики
Інші видання
-
Інші мови
Картонка-підказка містить: таблицю множення та ділення, таблицю Піфагора. Вона стане незамінним помічником для учнів початкової (а не рідко й середньої) ланки освіти під час уроків у школі та вдома.
Вона стане незамінним помічником для учнів початкової (а не рідко й середньої) ланки освіти під час уроків у школі та вдома.
Характеристики
Видавництво | Зірка |
| Українська | |
Рік видання | 2021 |
Ілюстрації | Немає ілюстрацій |
Формат | 150х210 мм |
Палітурка | М’яка, Картон |
| Картон | |
| 9789663141121 |
Показати всі характеристики
Характеристики Картонка-підказка. Таблиця множення і ділення. Таблиця Піфагора
Таблиця множення і ділення. Таблиця Піфагора
Видавництво | Зірка |
| Українська | |
Рік видання | 2021 |
Ілюстрації | Немає ілюстрацій |
Формат | 150х210 мм |
Палітурка | М’яка, Картон |
| Картон | |
| 9789663141121 | |
| Паперова |
Таблиця множення.
 Таблиця множення.
Таблиця множення.
Таблиця множення — таблиця, де рядки та стовпчики озаглавлені множниками, а на перетині рядків та стовпчиків таблиці стоять добутки цих множників. Таблиця застосовується для вивчення множення.
Навігація по сторінці: Таблиця множення чисел від 1 до 10 Таблиця множення чисел від 1 до 20
Вправи для перевірки знань таблиці множення!
Завантажити таблицю множення
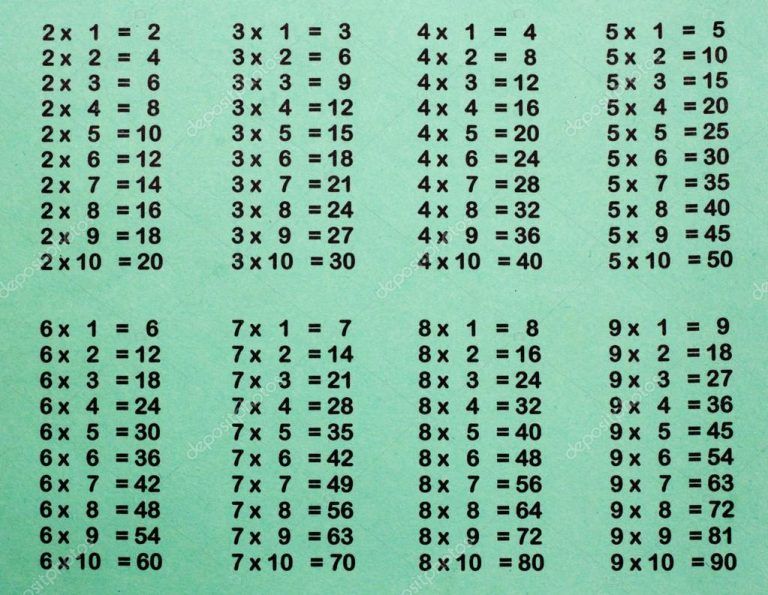
Таблиця множення чисел від 1 до 10
| × 1 | × 2 | × 3 | × 4 | × 5 |
1 × 1 = 1 1 × 2 = 2 1 × 3 = 3 1 × 4 = 4 1 × 5 = 5 1 × 6 = 6 1 × 7 = 7 1 × 8 = 8 1 × 9 = 9 1 × 10 = 10 |
2 × 1 = 2 2 × 2 = 4 2 × 3 = 6 2 × 4 = 8 2 × 5 = 10 2 × 6 = 12 2 × 7 = 14 2 × 8 = 16 2 × 9 = 18 2 × 10 = 20 |
3 × 1 = 3 3 × 2 = 6 3 × 3 = 9 3 × 4 = 12 3 × 5 = 15 3 × 6 = 18 3 × 7 = 21 3 × 8 = 24 3 × 9 = 27 3 × 10 = 30 |
4 × 1 = 4 4 × 2 = 8 4 × 3 = 12 4 × 4 = 16 4 × 5 = 20 4 × 6 = 24 4 × 7 = 28 4 × 8 = 32 4 × 9 = 36 4 × 10 = 40 |
5 × 1 = 5 5 × 2 = 10 5 × 3 = 15 5 × 4 = 20 5 × 5 = 25 5 × 6 = 30 5 × 7 = 35 5 × 8 = 40 5 × 9 = 45 5 × 10 = 50 |
| × 6 | × 7 | × 8 | × 9 | × 10 |
6 × 1 = 6 6 × 2 = 12 6 × 3 = 18 6 × 4 = 24 6 × 5 = 30 6 × 6 = 36 6 × 8 = 48 6 × 9 = 54 6 × 10 = 60 | 7 × 1 = 7 7 × 2 = 14 7 × 3 = 21 7 × 4 = 28 7 × 5 = 35 7 × 6 = 42 7 × 7 = 49 7 × 8 = 56 7 × 9 = 63 7 × 10 = 70 | 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 8 × 6 = 48 8 × 7 = 56 8 × 8 = 64 8 × 9 = 72 8 × 10 = 80 | 9 × 1 = 9 9 × 2 = 18 9 × 3 = 27 9 × 4 = 36 9 × 5 = 45 9 × 6 = 54 9 × 7 = 63 9 × 8 = 72 9 × 9 = 81 9 × 10 = 90 | 10 × 1 = 10 10 × 2 = 20 10 × 3 = 30 10 × 4 = 40 10 × 5 = 50 10 × 6 = 60 10 × 7 = 70 10 × 8 = 80 10 × 9 = 90 10 × 10 = 100 |
Не забудьте перевірити знання таблиці множення вирішуючи вправи! 🙂
Таблиця множення чисел від 1 до 20
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 80 | 85 | 90 | 95 | 100 | |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Таблиця множення a × b Таблиця квадратів a2 Таблиця кубів a3 Таблиця степенів an Таблиця факторіалів a!
Всі таблиці і формули
Підготовка до ДПА по темах.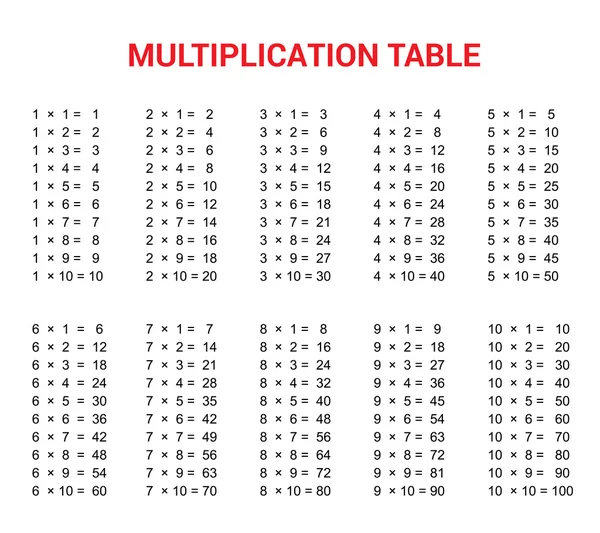
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
Методика вивчення таблиць множення і ділення
Стр 1 из 3Следующая ⇒
Вивчення таблиць множення і відповідних випадків ділення
План
1. Методика вивчення таблиць множення і ділення
2. Вправи на засвоєння таблиць множення і ділення
3. Деякі прийоми навчання табличного множення і ділення
Література
Основна:
1. Богданович М.В., Козак М.В., Король Я.А. Методика викладання математики в початкових класах. — К.: А.С.К., 2001.- § 24.
Додаткова:
2. Богданович М.В. Методика вивчення нумерації та арифметичних дій в початковій школі. — К.: Освіта, 1992.- С. 25 – 34.
3. Вайнтрауб М. Алгоритм побудови таблиці множення // Початкова школа. – 2000. — № 10. – С. 34 – 36.
– 2000. — № 10. – С. 34 – 36.
4. Сарапулова Є. Деякі прийоми навчання табличного множення на 9 // Початкова школа. – 1997. — № 4. – С. 31 – 32.
5. Шпакова В. Про вивчення таблиць арифметичних дій // Початкова школа. – 1997. — № 8. – С. 29 – 31.
Вивчення таблиць множення і відповідних випадків ділення
Методика вивчення таблиць множення і ділення
Математика є важливою складовою частиною шкільної освіти. Аналізуючи програму з цього предмета, ми бачимо, що на вивчення арифметичних дій відводиться майже 63%навчального часу, з них на опрацювання табличних випадків – 26%.
Одним із важливих завдань, що стоять перед вчителем в процесі навчання математики – вироблення міцних обчислювальних навичок.
Усі типи арифметичних дій, які повинні опанувати школярі початкових класів, можна об’єднати у три групи:
1) табличні випадки арифметичних дій;
2) позатабличні випадки арифметичних дій, які виконуються усно;
3) позатабличні випадки арифметичних дій, які виконуються письмово.
Зупинимося на табличних випадках арифметичних дій.
Усі таблиці арифметичних дій можна умовно поділити на такі три групи:
1) таблиці додавання і віднімання в межах 10;
2) таблиці додавання і віднімання з переходом через десяток;
3) таблиці множення і ділення.
Їх опрацювання проходить майже однаково, тому вчителю треба докласти зусиль, щоб діти не втратили інтерес і щоб їхня увага не розпорошувалася. Для цього необхідно вміло добирати різні сюжети для тренувальних вправ, використовувати яскравий наочний матеріал і різні види робіт.
Перші уроки на складання того чи іншого виду таблиць проходить з великою увагою вчителя до самого процесу складання таблиці, до розуміння її суті. Надалі він уже менше звертає на це увагу і працює над закріпленням.
Зупинимося на особливостях роботи над таблицями множення і ділення.
Як відомо, до табличних випадків множення і ділення відносять випадки множення одноцифрових чисел і відповідні їм випадки ділення.
Завдання вивчення теми:
— розкрити способи складання таблиць множення і ділення;
— довести знання табличних випадків множення і ділення до автоматизму.
Складання таблиці множення:
Підготовча робота:
— повторення конкретного змісту множення як додавання однакових доданків;
— визначення значення кожного з множників.
Ознайомлення:
В початковій школі вивчають таблиці множення кожного з чисел (наприклад, таблиця множення числа 2, 3 і т.д., тобто постійним є перший множник. Таблиці множення на кожне з чисел не розглядаються. Вважається, що вивчивши всі таблиці множення кожного з чисел і ознайомившись із переставним законом множення, учні знатимуть всі випадки множення на кожне з чисел).
Всі таблиці множення складають на основі додавання однакових доданків. Приклади на додавання розглядають за таблицями на дошці чи в підручнику; до учнівських зошитів доцільно записати тільки таблицю множення.
Послідовність роботи:
— розгляд прикладів на додавання однакових доданків;
— заміна прикладів на додавання прикладами на множення.
Закріплення:
— завдання, що виконують з безпосереднім використанням таблиці;
— вправи на відтворення таблиці;
— вправи на використання знань табличних результатів;
— складання і розв’язування задач.
Складання таблиці ділення:
Підготовча робота:
— відтворення відповідної таблиці множення;
— повторення зв’язку між діями множення і ділення (складання з одного прикладу на множення двох чи одного прикладів на ділення).
Ознайомлення:
Всі таблиці ділення складають на основі таблиці множення. Таблиця ділення подається в готовому вигляді поруч з відповідною таблицею множення, а учням пропонується пояснити, як складена таблиця ділення, або можна скласти таблицю ділення разом з учнями, пояснюючи кожний випадок ділення з опорою на таблицю множення; до учнівських зошитів доцільно записати тільки таблицю ділення.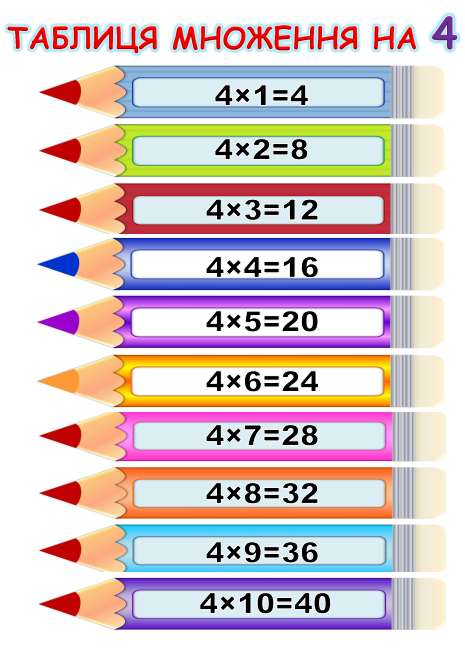
Послідовність роботи:
— розгляд прикладів на множення;
— складання прикладів на ділення на дане число за прикладами на множення.
Закріплення:
— завдання, що виконують з безпосереднім використанням таблиці;
— вправи на відтворення таблиці;
— вправи на використання знань табличних результатів;
— складання і розв’язування задач.
123Следующая ⇒
Поиск по сайту:
Множення та ділення чисел в Excel
Множення та ділення в Excel дуже просто, але потрібно створити просту формулу. Просто пам’ятайте, що всі формули в програмі Excel починаються зі знака рівності (=), і для їх створення можна використовувати рядок формул.
Множення чисел
Скажімо, потрібно дізнатися, скільки пляшок води слід придбати для конференції із клієнтами (загальна кількість учасників × 4 дні × 3 пляшки на день), або вартість транспортних витрат під час службової поїздки (загальна кількість кілометрів × 0,46). Числа можна помножити кількома способами.
Числа можна помножити кількома способами.
Множення чисел у клітинці
Для виконання цього завдання використовується арифметичний оператор * (зірочка).
Наприклад, якщо у клітинку введено таку формулу: =5*10, буде відображено такий результат – 50.
Множення стовпця чисел на константу
Припустимо, що потрібно помножити кожну з комірок у стовпці семи чисел на число, яке міститься в іншій ячейці. У цьому прикладі число, яке потрібно помножити на 3, міститься в клітинці C2.
-
Введіть = a2 * $B $2 у новому стовпці в електронній таблиці (наведений вище приклад використовує стовпець D).
 Обов’язково додайте символ $ до B і до 2 у формулі та натисніть клавішу ENTER.
Обов’язково додайте символ $ до B і до 2 у формулі та натисніть клавішу ENTER.Примітка.: За допомогою символів $ програма Excel вказує на те, що посилання на B2 – «абсолютний», що означає, що під час копіювання формули до іншої клітинки посилання завжди буде до клітинки B2. Якщо ви не використовували символи $ у формулі, і ви перетягнули формулу вниз до розділу клітинці B3, Excel змінить формулу на = a3 * C3, що не працюватиме, тому що немає значення в B3.
-
Перетягніть формулу вниз до інших клітинок у стовпці.
Примітка.: У Excel 2016 для Windows клітинки заповнюються автоматично.
Множення чисел у різних клітинках за допомогою формули
Для множення чисел, клітинок і діапазонів можна використовувати функцію Product .
У функції PRODUCT можна використовувати будь-яке поєднання до 255 чисел або посилань на клітинку. Наприклад, формула = PRODUCT (a2, A4: A15, 12, E3: E5, 150, G4, h5: J6) Перемножує дві окремі клітинки (a2 та G4), два числа (12 і 150) і три діапазони (A4: A15, E3: E5 і h5: J6).
Ділення чисел
Припустімо, ви хочете дізнатися, скільки годин знадобилося, щоб завершити проект (загальний час у програмі Project, що не відповідно до всіх учасників проекту) або фактичні милі за галон для вашої останньої крос-кантрі (загальна кількість миль ÷всього галонів). Існують кілька способів розділення чисел.
Розділення чисел у клітинках
Щоб виконати це завдання, скористайтеся арифметичним оператором / (скісна риска).
Наприклад, якщо ввести = 10/5 у клітинках, у ній відображається 2.
Увага!: Не забудьте ввести знак рівності (=) у клітинках, перш ніж вводити числа та оператор; в іншому разі програма Excel інтерпретує дані, які ви вводите як дату. Наприклад, якщо ввести 7/30, програма Excel може відображати 30-Jul у клітинках. Або, якщо ввести 12/36, програма Excel спочатку перетворить це значення на 12/1/1936 і відобразить 1-Dec у клітинках.
Примітка.: У програмі Excel немає функції розділення .
Розділення чисел за допомогою посилань на кількість комірок
Замість того, щоб вводити числа безпосередньо у формулі, можна використовувати посилання на клітинки, наприклад a2 та a3, щоб посилатися на числа, які потрібно розділити, і поділити за ними.
Приклад.
Приклад буде легше зрозуміти, якщо ви скопіюєте його на чистий аркуш.
Копіювання прикладу
-
Створіть пустий аркуш або книгу.
-
Виділіть приклад у розділі довідки.
Примітка.: Заголовки рядків і стовпців виділяти не потрібно.
Виділення прикладу в довідці
-
Натисніть клавіші Ctrl+C.
org/ListItem»>
-
Щоб переключатися між переглядом результатів і переглядом формул, які повертають результати, натисніть сполучення клавіш CTRL + ‘ (серйозний наголос) або на вкладці формули натисніть кнопку Показати формули .
На аркуші виділіть клітинку A1 і натисніть клавіші Ctrl+V.
|
A |
B |
C |
|
|
1 |
Дані |
Формула |
Опис (результат) |
|
2 |
15000 |
=A2/A3 |
Ділить 15 000 на 12 (1250) |
|
3 |
12 |
Розділення стовпця чисел на константі числа
Припустимо, що потрібно розділити кожну з комірок у стовпці семи чисел на число, яке міститься в іншій ячейці. У цьому прикладі число, яке потрібно розділити, дорівнює 3, що міститься у клітинці C2.
У цьому прикладі число, яке потрібно розділити, дорівнює 3, що міститься у клітинці C2.
|
A |
B |
C |
|
|
1 |
Дані |
Формула |
Константа |
|
2 |
15000 |
= A2/$C $2 |
3 |
|
3 |
12 |
= A3/$C $2 |
|
|
4 |
48 |
= A4/$C $2 |
|
|
5 |
729 |
= A5/$C $2 |
|
|
6 |
1534 |
= A6/$C $2 |
|
|
7 |
288 |
= A7/$C $2 |
|
|
8 |
4306 |
= A8/$C $2 |
Введіть = a2/$C $2 у клітинці B2. Обов’язково додайте символ $ до C і до 2 у формулі.
Перетягніть формулу у клітинці B2 до інших клітинок у стовпці B.
Примітка.: За допомогою символів $ програма Excel вказує на те, що посилання на C2 – «абсолютний», що означає, що під час копіювання формули до іншої, посилання завжди буде у клітинці C2. Якщо у формулі не використано символи $, і ви перетягнули формулу вниз до розділу клітинці B3, Excel змінить формулу на = a3/C3, що не працюватиме, тому що немає значення в C3.
Потрібна додаткова довідка?
Ви завжди можете поставити запитання експерту в спільноті Tech у розділі Excel чи отримати підтримку в спільноті Answers.
Додаткові відомості
Множення стовпця чисел на те саме число
Множення на відсоток
Створення таблиці множення
Оператори обчислень і порядок операцій
Учні початкових класів читатимуть Прохаська і не завчатимуть таблицю множення
З 1 вересня в Україні стартують оновлені навчальні програми для учнів 1-4 класів. Як повідомила міністр освіти України Лілія Гриневич, усі зміни спрямовані на розвантаження програми початкової освіти, щоб «досягнути кращих результатів навчання і при цьому зберегти здоров’я дітей та їхній інтерес до навчання». Велику надію на успіх нової програми покладають й батьки першокласників, пише radiosvoboda.
З 1 вересня 2016 року діти в початкових класах будуть більше спілкуватися та висловлювати свою думку, а не просто зубрити предмети на пам’ять, обіцяють у Міністерстві освіти України.
«В четвер, 4 серпня, колегія МОН затвердила розвантажені і оновлені програми початкової школи. З одного боку, зміни торкнуться приблизно 10% змісту чинних програм, з іншого – ці зміни є реальним переходом до іншої філософії освіти, яка відповідає 21-му століттю і європейському розвитку України: не тиснути на дитину, а заохочувати», – написала у своїй сторінці у «Фейсбук» міністр освіти Лілія Гриневич.
Згодом міністр додала: «Оновлені навчальні програми для 1-4 класів розміщені у відкритому доступі за посиланням. Наступного тижня будуть розміщені орієнтовні вимоги до оцінювання навчальних досягнень учнів та методичні рекомендації до оновлених програм. Вони передбачають зміни підходів до оцінювання та педагогічну свободу вчителя».
Велику надію на успіх нової програми покладають й батьки першокласників.
«Нагадування, що скоро 1 вересня, лякало мене. Досить часто чула нарікання інших батьків, що шкільна програма втомлює дітей та забирає бажання вчитися.
Надіюся, що тепер все ж таки щось зміниться», – розповідає Галина Паращич, мати першокласниці Марічки.
«Відтепер вчитель сам розподілятиме свій час»
Внесли зміни до 13 програм чотирьох класів. Знято розподіл годин за темами. Тобто збільшена свобода вчителя. Тепер він розподілятиме свій час не так, як йому прописує програма, а відповідно до особливостей того класу, в якому він викладає, каже радник міністра освіти Іванна Коберник.
«Раніше, якщо якусь тему діти засвоїли швидше, вчитель мав товкти воду в ступі, бо в нього стільки-то годин не виговорено, або, навпаки, кинути цю тему, не роз’яснивши їм як слід, і перейти до наступної, бо так передбачає програма. Відтепер вчитель сам розподілятиме свій час», – говорить радник міністра.
Маленькі школярі не читатимуть на швидкість
Окрім цього, з усіх програм вилучили застарілу та зайву інформацію. ЇЇ розподілили так, щоб вона була більш зрозумілою для дітей та відповідала їх віковим, фізичним та психологічним особливостям, додає Коберник:
«Саме з цією метою відбувалося оновлення програми – для того, щоб давати дітям ту інформацію, яку вони в цьому віці готові опрацювати».
Маленьким школярам також не доведеться здавати читання на швидкість. Тепер акцент ставитимуть не на темпі, а на розвитку якісного читання. Таким змінам найбільше радіють батьки дітей. Олена Павленко, мама другокласника Сашка, скаржиться, що дитина більше зосереджувалась на прочитанні кількості слів в хвилину, а не на тому, щоб зрозуміти, про ще йдеться в тексті. За словами жінки, це не тільки відбирало в дитини бажання читати, а й знижувало якість прочитаного.
Не вимагатимуть вчити на пам’ять таблиці множення та ділення
Одним із нововведень стало й те, що від учнів 1-2 класів не вимагатимуть вчити на пам’ять таблиці множення та ділення.
«Просто зазубрити таблицю множення не достатньо. Дитина повинна знати, що якщо їй тяжко, вона може додати, згрупувати предмети. В процесі такого практичного засвоєння, вона дійсно вивчить таблицю множення на кінець 3 класу, але при цьому в майбутньому вона зможе множити в голові і двоцифрові, і трицифрові числа», – наголошує Коберник.
37 нових авторів у програмі з літератури
Зміни не обійшли й літератури. Модератори програми спеціально співпрацювали з Національною бібліотекою України імені В. І. Вернадського, а також з експертами дитячих літературних проектів «БараБука», «Казкарка», «Читомо» для того, щоб обрати нових авторів.
Було взято до уваги, що діти найбільше читають та що їм подобається. Загалом в програму додали 37 нових авторів, а вилучили майже 60. Відтепер діти читатимуть твори Марини та Сергія Дяченків, Катерини Бабкіної, Тараса Прохаська та багатьох інших.
Запровадили написання жанру есе в 3 класі
Що ж стосується письма, то тут також відбулися чималі зміни. Тут не тільки забрали такі складні теми, як «Спосіб умовного позначення речень», «Складання речень за поданою графічною схемою», «Умовне позначення слів», а й запровадили написання жанру есе в 3 класі.
Якщо раніше діти понині були написати три види робіт, а саме текст-роздум, текст-міркування і текст-оповідь, то тепер їм надали одну альтернативу. Таким чином у міністерстві планують боротися зі страхом зробити помилку через недотримання структури твору.
Таким чином у міністерстві планують боротися зі страхом зробити помилку через недотримання структури твору.
«Жанр есе – це жанр, мета, якого полягає у висловленні власної думки. Це є найважливішим для розвитку особистості. На переконання наших модераторів, це саме те, чого повинні вчити дітей, а не просто зазубрювати три жанри і думати, як не зробити помилку», – зазначає радник міністра.
Нововведення запроваджувалися на прохання та пропозиції вчителів, які були й основними модераторами оновленої програми. Обговорення змін відбувалося в інтерактивному режимі з можливістю коментування на відкритій платформі.
«Ці зміни вносилися на відкритій платформі EdEra, де було зареєстровано 4000 унікальних, авторизованих користувачів, які залишили понад 8000 коментарів, 90% з цих користувачів – це були вчителі-практики, то ж ми можемо говорити, що відбулися ті зміни, яких давно чекали і прогресивні вчителі, і батьки, і діти», – розповіла Коберник.
Як запевняють у міністерстві, усі пропозиції були взяті до уваги, а користувачі отримали відповідь – врахований чи не врахований їхній коментар.
«Нововведення переносять акцент на результати»
«Ну, звісно, там є запитання, які є неоднозначними, які ще треба обговорювати. Але якщо говорити про внесені зміни, то, на мою думку, вони мають позитивний момент. Нововведення трохи знімають регламентації того, що саме потрібно робити під час занять, і переносять акцент на те, які результати мають бути отримані», – зазначає головний експерт групи «Освіта» Реанімаційного пакету реформ Володимир Бахрушин.
На запитання, як діяти, якщо вчитель відмовляється працювати за оновленою програмою, міністерство радить спершу вирішувати проблему діалогом. Спробувати по-доброму поговорити і попросити навчати за оновленою програмою та критеріями оцінювання. Якщо ж ви бачите, що ніяких змін не відбувається, то в такому випадку потрібно звертатися до директора та органів управління освітою, радять фахівці.
Читайте «Репортер» у Telegram та Instagram – лише якісні новини та цікаві статті у вашому телефоні
Таблиця множення: гра, щоб швидко вивчити дитині
Зміст
- Таблиця множення: як вивчити легко і швидко, не докладаючи особливих зусиль
- Проста таблиця множення: гра щоб швидко вивчити – вихід з положення для багатьох
- Починати слід тільки з початку: як легко вивчити таблицю множення дитині
- Перший етап: одиничка проста, як палиця
- Другий етап: десяточка, майже одиничка, але з нуликом
- Третій етап: таблиця множення на двійку
- Четвертий етап: пятерочка – що може бути простіше
- П’ятий етап: зміна місць множників – запорука гарного і якісного запам’ятовування
- Шостий етап: укладання і повторення – мати будь-якого вчення
- Як дитині вивчити таблицю множення швидко: альтернативні методи і креативний підхід
- Кілька простих порад для батьків
- Вважаємо на пальцях: оригінальний метод множення на дев’ятку
Будь-який батько, раніше чи пізніше, обов’язково зіткнеться з тим, що дитині доведеться докладати колосальних зусиль, щоб вивчити таблицю множення, яка може значно спростити рахунок, а, отже, і життя в подальшому. Насправді це зовсім не просто, хоча у віці восьми-дев’яти років, коли школа пропонує вивчити табличку Піфагора, у хлопців надзвичайно добре розвинена механічна пам’ять. Саме вона і допомагає визубрити напам’ять будь-який текст, таблицю, вірші і так далі. Однак зубріння – це, за визначенням, нудно і не цікаво, і завдання батьків пожвавити цей процес, спростити його, а можливо, навіть і перетворити на веселу і захоплюючу гру. Так як допомогти дитині вивчити таблицю множення і що потрібно зробити для того, щоб вона назавжди відклалася в пам’яті, спливаючи як раз в той момент, коли це вкрай необхідно.
Насправді це зовсім не просто, хоча у віці восьми-дев’яти років, коли школа пропонує вивчити табличку Піфагора, у хлопців надзвичайно добре розвинена механічна пам’ять. Саме вона і допомагає визубрити напам’ять будь-який текст, таблицю, вірші і так далі. Однак зубріння – це, за визначенням, нудно і не цікаво, і завдання батьків пожвавити цей процес, спростити його, а можливо, навіть і перетворити на веселу і захоплюючу гру. Так як допомогти дитині вивчити таблицю множення і що потрібно зробити для того, щоб вона назавжди відклалася в пам’яті, спливаючи як раз в той момент, коли це вкрай необхідно.
Зрозуміло, що насамперед дитина повинна вникнути в суть поставленого завдання, в нашому випадку це множення, тому спершу потрібно пояснити йому, як все відбувається і чому, благо справа, математика – наука точна і всі визначення в ній чіткі і виразні. Причому, коли справа доходить до вивчення таблички множення, значить основи рахунку вже дано і по всій видимості зрозумілі і вивчені.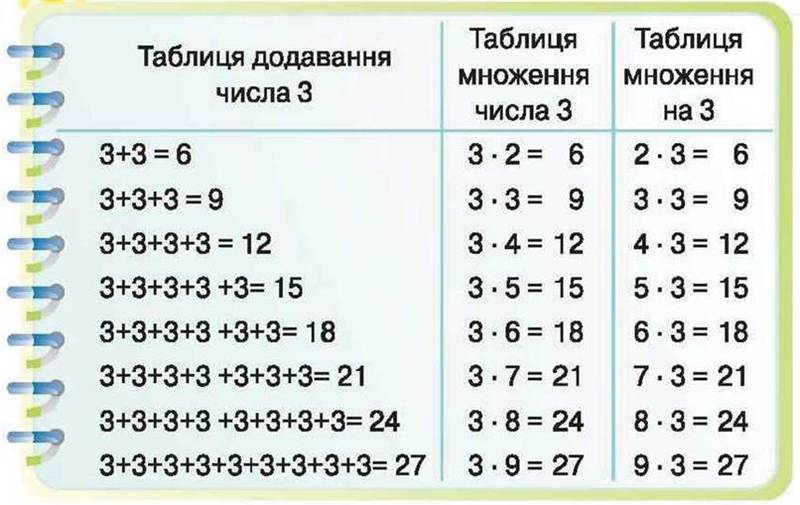 Додавання і віднімання – найпростіші математичні дії, ази, які даються дітям ще в дитячому саду.
Додавання і віднімання – найпростіші математичні дії, ази, які даються дітям ще в дитячому саду.
Потрібно пояснити дитині, що не варто лякатися великий і незрозумілою таблиці, так як по суті, там все зовсім просто. Суть множення – додавання будь-якого числа стільки разів, скільки вказано в завданні. Здається складним навіть вам самим? Давайте спростимо, застосовуючи для цього прості приклади. Для того, щоб 2 помножити на 4, приміром, треба просто скласти двійки чотири рази.
Так все стає набагато простіше, і це розуміння обов’язково допоможе в подальшому. Причому багато дорослі, навіть закінчивши навчання в університеті, продовжують додавати числа в розумі, щоб спростити собі завдання. Крім того, без сумнівів, потрібно дати дитині можливість зрозуміти, як же «працює» та сама таблиця Піфагора, з якою впоратися зможе будь-хто, якщо познають вони ази. Причому нічого складно в використанні такої таблиці, дійсно відкритої геніальним давньогрецьким математиком і філософом Піфагором, зовсім немає: відшукайте число, на перетині стовпчиків цифр, це і буде результат. Приміром, 6 помножити на 8, буде 48 і ніяк інакше.
Приміром, 6 помножити на 8, буде 48 і ніяк інакше.
Проста
таблиця множення: гра щоб швидко вивчити – вихід з положення для багатьохДітки всіх вікових груп просто обожнюють грати, адже саме через гру вони пізнають навколишній світ. Саме тому варто постаратися перетворити такий нудний і рутинний процес, яким і є вивчення таблички множення, цікаву і навіть захоплюючу гру. Гра допоможе не думати про втому, нудьгу, дозволить сприймати навчання дуже весело і приємно. Небажання і лінь відразу відступить на другий план, якщо малюку стане цікаво, і він вникне в процес, даючи все більше і більше правильних відповідей.
Самим популярним і затребуваним пристроєм, що допоможе в ігровій формі допомогти дитині засвоїти табличку множення, є картки, які можна придбати в магазині.
Крім того, подібні картки з математичними діями, причому це може зовсім не тільки множення, але і ділення, простіше простого скачати з інтернету та роздрукувати. Якщо ж справу з цим вже зовсім кисло, то подібні картки можна просто вирізати з паперу і написати на них цифри від руки. Якщо залучити до цього заняття дитини, то швидше за все вийде ще й весела і цікава гра.
Якщо залучити до цього заняття дитини, то швидше за все вийде ще й весела і цікава гра.
Починати слід тільки з початку:
як легко вивчити таблицю множення дитиніКартки, це звичайно ж, справа хороша і цікава, проте вони засновані на простій зубріння, тобто на механічному запам’ятовуванні, а якщо ми бажаємо отримати не робота, який просто тараторить стовпці таблиці множення поспіль, а розуміє суть самої дії, доведеться діяти трохи інакше. Зрозуміло, що починати давати матеріал маленькій дитині потрібно, починаючи з самого простого, тому безперечно краще буде розпланувати вивчення таблички, розділивши весь процес на кілька основних підетапів.
Перший етап: одиничка проста, як палиця
Зрозуміло, що найпростіше – таблиця множення на один, якщо, звичайно, не брати до уваги нуль. Мабуть, варто пояснити, що на нуль не можна множити, ділити ні, це має швидко і просто відкластися в пам’яті, і тоді варто почати, все ж, до одиничці. Намалюйте кілька табличок з прикладами і уточніть, що яке б не було потрібно помножити на один, воно залишиться незмінним. Наприклад:
Наприклад:
Другий етап: десяточка, майже одиничка, але з нуликом
Далі переходимо до ще одного найпростішого дії – множення на десять. Варто обов’язково самому збагнути, а також пояснити і своєму чаду, що множити на десять, це все одно, що на один, тільки в кінці отриманого результату потрібно просто додати нулик. Насправді все досить просто, проте потрібно не забути дати зрозуміти дитині, що тепер він повністю знає всі крайні рядки або стовпці таблички. Причому множення на один і на десять буде для нього відкритою книгою, а далі – більше.
Третій етап: таблиця множення на двійку
Якщо в один день вашій дитині вистачило сил на осмислення подібних завдань, а весела гра в картки підтверджує засвоєні знання, можна продовжувати, повільно переходячи від простого до складного. Проте досвідчені фахівці-педагоги рекомендують давати малюкові відпочинок, тому такі заняття варто перенести на наступний день, коли він встане з новими силами.
Найчастіше, множення на пару дається всім школярам і навіть дошкільнятам досить легко і просто, так як на насправді, все дійсно елементарно.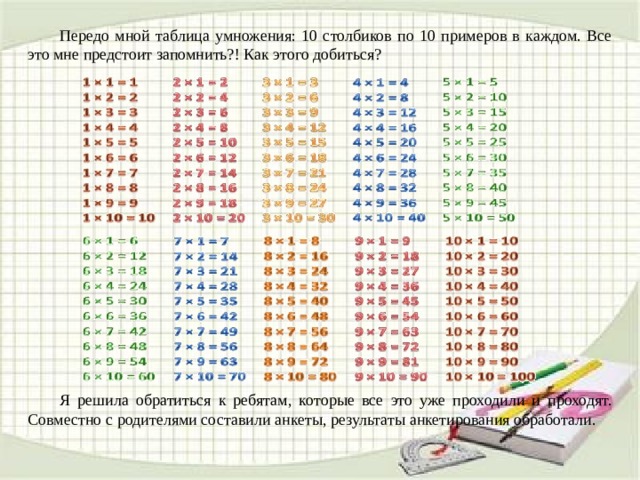 Помножити на два, значить додати число сама до себе, тобто скласти два числа запропонованих. Причому, коли виникає необхідність вчити таблицю множення, простий рахунок, як, наприклад, додавання, вже дитяте має бути відомо, от нехай і складає, тим більше, що з невеликими числами це досить просто. Далі доведеться запам’ятовувати механічно, тобто табличку на три, чотири, шість, сім і так далі краще постаратися вивчити напам’ять, так буде простіше і швидше.
Помножити на два, значить додати число сама до себе, тобто скласти два числа запропонованих. Причому, коли виникає необхідність вчити таблицю множення, простий рахунок, як, наприклад, додавання, вже дитяте має бути відомо, от нехай і складає, тим більше, що з невеликими числами це досить просто. Далі доведеться запам’ятовувати механічно, тобто табличку на три, чотири, шість, сім і так далі краще постаратися вивчити напам’ять, так буде простіше і швидше.
Четвертий етап: пятерочка – що може бути простіше
Наступним етапом варто засвоїти табличку множення на п’ять, що також буде не складніше, ніж горезвісна двійка. Просто додавати п’ять до результату, якщо вчити послідовно. Зрозуміло, що спочатку буде трохи не зрозуміло, але з часом все проясниться і найпростіше пояснювати на дрібниці, додаючи до певної суми по п’ять копійок, або ж віднімаючи, при поділі, але це вже окрема тема для розмови.
П’ятий етап: зміна місць множників – запорука гарного і якісного запам’ятовування
Вивчити напам’ять можна що завгодно, і виконати такий трюк більшості дітей зовсім не складе ніякої праці. Однак зубріння, як вже зазначалося, перший ворог розуміння, тому варто дати дитині усвідомлених правил, одне з яких чітко говорить, що від зміни місць множників результат абсолютно не зміниться.
Однак зубріння, як вже зазначалося, перший ворог розуміння, тому варто дати дитині усвідомлених правил, одне з яких чітко говорить, що від зміни місць множників результат абсолютно не зміниться.
Шостий етап: укладання і повторення – мати будь-якого вчення
Наостанок варто сказати, що вся табличка Піфагора зазвичай дається дітям досить просто і вивчити її досконально не складе для більшості з шибеників ніякої праці. Однак є і нюанси, які варто врахувати, даючи малюкові такий складний матеріал. В першу чергу, варто розуміти, що чим частіше ви згадуєте про табличці в реальному житті, наприклад, рахуючи скільки млинців потрібно спекти, щоб вся сім’я поснідала, і так далі. Тобто повторюйте стовпці таблички з порядком та розкид постійно, нагадуючи дитині, що це весело і цікаво, а головне – просто.
Крім усього іншого є в таблиці множення позиції, які особливо складні для запам’ятовування, причому навіть багато дорослих примудряються плутатися в результатах навіть давно закінчили школу і два університети. Вивчити їх доведеться настільки чітко, щоб прокинувшись вночі, ви могли «оттараторить» результат, навіть не встигнувши задуматися, чому і дитину потрібно обов’язково навчити.
Вивчити їх доведеться настільки чітко, щоб прокинувшись вночі, ви могли «оттараторить» результат, навіть не встигнувши задуматися, чому і дитину потрібно обов’язково навчити.
Важливо
Процес вивчення таблиці множення – справа зовсім не просте і не варто дивуватися, якщо це займе у вас і вашого малюка досить багато часу. Головне в цій справі – це терпіння, а також грунтовність. Не потрібно чекати, поки вчителька в школі сама все розтлумачить, а ви просто будете ходити поруч, всі в білому і піддакувати, розберіться спершу самі, тим більше, що нічого складного в цьому немає. Причому, крім традиційного методу простого заучування є і кілька простих порад, а також оригінальний спосіб, який допоможе помножити будь-яке число на дев’ять, навіть зовсім не пам’ятаючи, що ж там було у таблиці Піфагора.
Кілька простих порад для батьків
- Ніколи, ні в якому разі і ні за яких обставин не підвищуйте голос під час навчання.
 Навчання для малюка не повинна перетворитися на важку, рабську службу. Нехай це буде весела гра, яку можна легко відкласти на потім, зайнявшись чим-небудь іншим.
Навчання для малюка не повинна перетворитися на важку, рабську службу. Нехай це буде весела гра, яку можна легко відкласти на потім, зайнявшись чим-небудь іншим. - Постійно повторюйте весь пройдений матеріал, у тому числі і табличку множення. Причому можна і в реальному житті застосовувати нові навички. Приміром, питайте свою дочку, скільки цукерок потрібно купити, щоб роздати шести дівчаткам по три, або ж скільки коліс у трьох автомобілів, при обліку запасних. Дитині має бути цікаво, а ніяк не нудно.
- Легко йдіть на поводу у малюка, припиняючи заняття у будь-який момент, проте наполегливо і часто давайте йому приклади множення в реальному житті. Чим більше дитина буде бачити практичної вигоди від такого рахунку, тим швидше і простіше буде йти процес запам’ятовування.
Вважаємо на пальцях: оригінальний метод множення на дев’ятку
Навчитися такому «пальчикових» методом рахунку зовсім не складно. Для цього потрібні тільки власні руки малюка, які потрібно покласти перед собою долонями вниз. Вважати пальці потрібно буде зліва направо, як і прийнято.
Вважати пальці потрібно буде зліва направо, як і прийнято.
- Отже, якщо потрібно помножити дев’ятку на сім, потрібно відрахувати сім пальців зліва, і загнути той, на якому зупинився рахунок.
- Далі все просто. Порахувавши всі пальці, які не загнуті зліва від сьомого. Це і буде число десятків у відповіді.
- Інші пальці, які знаходяться праворуч від того, що ви вже загнули, і будуть одиницями відповіді.
Поділитися:
Умножение бумажных тарелок
Автор: Лия | 23 декабря 2020 г.
Разбавьте свою программу умножения к Новому году тремя увлекательными математическими заданиями, которые дети могут выполнять с помощью бумажных тарелок! Эти веселые занятия без беспорядка помогут малышам попрактиковаться в основных фактах умножения. Читайте дальше, чтобы узнать, как вы и ваши ученики можете умножить математические навыки с помощью умножения бумажных тарелок!
Почему умножение бумажных тарелок? Мы любим математические игры, которые легко подготовить и в которые весело играть! Следующие упражнения на умножение бумажных тарелок настолько просты, но они дают детям как тактильный, так и визуальный способ концептуализировать факты умножения. В дополнение к нескольким бумажным тарелкам вам понадобится несколько предметов повседневного обихода, которые вы легко найдете в своем классе или дома. Ниже мы выделим материалы, необходимые для каждого занятия.
В дополнение к нескольким бумажным тарелкам вам понадобится несколько предметов повседневного обихода, которые вы легко найдете в своем классе или дома. Ниже мы выделим материалы, необходимые для каждого занятия.
Обязательно отметьте @superteacherworksheets в социальных сетях, если вы и ваши ученики попробуете какое-либо из этих заданий по умножению бумажных тарелок! Нам нравится видеть, как творчески вы и ваш класс адаптируете идеи и занятия, которые мы представляем в нашем блоге, к вашей собственной учебной среде!
Вращение таблицы умножения
Вот забавное математическое задание, которое поможет вам придать творческий смысл таблице умножения. В дополнение к две бумажные тарелки , убедитесь, что у вас есть ножницы , маркер , линейка , карандаш и латунная застежка для бумаги под рукой для этого задания. Вот что нужно сделать:
Сначала напишите на одной из бумажных тарелок таблицу умножения, которую вы хотите попрактиковать, например, таблицу умножения на 5.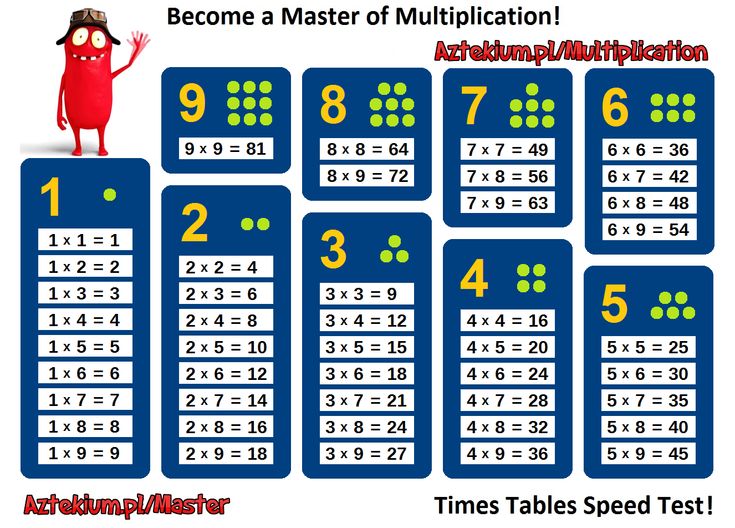 Запишите частичный математический факт слева от центра бумажной тарелки, 5 x … как мы сделали на фотографии ниже:
Запишите частичный математический факт слева от центра бумажной тарелки, 5 x … как мы сделали на фотографии ниже:
Пропустите достаточно места, чтобы разместить второе число в математическом факте, и напишите знак равенства и знак вопроса, = ?, как здесь:
Теперь обратите внимание на вторую бумажную тарелку. Разделите бумажную тарелку на двенадцать равных частей с помощью линейки и карандаша.
Используйте маркер, чтобы пометить внутренние разделы цифрами от 1 до 12. Пометьте внешние разделы ответом на каждый факт умножения, если он умножается на число, которое вы используете в своей таблице умножения. Например, поскольку 5 x 1 = 5, вы должны написать цифру 5 на внешней части бумажной тарелки, а цифру 1 — на внутренней.
Когда вы закончите, ваша опорная плита должна выглядеть так:
Затем положите первую бумажную тарелку поверх опорной плиты. Пока не скрепляйте их вместе. Соедините частичное уравнение, которое вы написали на верхней пластине, с числами на нижней. Когда вы уверены, что ваши числа выровнены, нарисуйте прямоугольник, где должен появиться второй множитель факта умножения. Вырежьте коробку ножницами. Также вырежьте две ручки по краю тарелки, которые можно отогнуть, чтобы открыть ответы:
Когда вы уверены, что ваши числа выровнены, нарисуйте прямоугольник, где должен появиться второй множитель факта умножения. Вырежьте коробку ножницами. Также вырежьте две ручки по краю тарелки, которые можно отогнуть, чтобы открыть ответы:
Чтобы максимизировать практику умножения и способствовать групповому обучению, вы можете назначить разные таблицы умножения разным детям. Как только каждый ребенок составит свою таблицу умножения и попрактикуется с ней, он или она может поменяться местами с другими детьми, чтобы попрактиковаться в разных таблицах умножения.
Раскрытие фактов об умножении
Это действие по умножению похоже на приведенную выше вращающуюся таблицу умножения, но без элемента «вращения». Вам все равно понадобится две бумажные тарелки , ножницы , маркер , линейка и карандаш , но вместо латунной скрепки для бумаги для создания прялки мы выберем немного клея , чтобы прочно удерживать пластины на месте.
Сначала наклейте на одну из бумажных тарелок таблицу умножения, которую вы хотите попрактиковать, например, таблицу умножения на 2. Затем маркером напишите 12 фактов умножения по краю бумажной тарелки, например: 2 x 1 = ; 2 х 2 = ; 2 х 3 = ; 2 х 4 = ; 2 х 5 = ; 2 х 6 = ; 2 х 7 = ; 2 х 8 = ; 2 х 9знак равно 2 х 10 = ; 2 х 11 = ; и 2 х 12 = . Вырежьте маленькие ручки между каждым математическим фактом, которые вы можете свернуть, чтобы открыть ответы.
Затем разделите вторую бумажную тарелку на двенадцать равных частей с помощью линейки и карандаша. Напишите ответ на каждый из математических фактов, которые вы написали на краю первой тарелки и на краю второй тарелки, по одному в каждой из двенадцати секций, чтобы они были расположены на одинаковом расстоянии друг от друга.
Наконец, сопоставьте факты умножения на верхней пластине с соответствующими ответами на нижней пластине. Как только вы убедитесь, что пластины выровнены правильно, соедините их вместе с помощью небольшого количества клея или скотча.
Теперь учащиеся могут практиковаться в умножении, раскрывая каждый ответ, работая по кругу!
Сеть фактов об умножении
Сплетите сеть умножения с помощью этого увлекательного математического задания, для которого потребуется одна бумажная тарелка , маркер , линейка и карандаш .
Опять же, вы захотите пометить свою бумажную тарелку таблицей умножения, которую хотите попрактиковать, скажем, таблицей умножения на 7. Затем разделите бумажную тарелку на двенадцать равных частей с помощью линейки и карандаша. Вы можете пройтись по этим линиям маркером, чтобы сделать их толще. Также нарисуйте круг на внутренней стороне тарелки:
Теперь пометьте части внутреннего круга цифрами от 1 до 12.
На этом этапе дети могут умножать число в центре круга на каждое число от 1 до 12, записывая ответ на каждый факт умножения. во внешней части соответствующего кусочка круга:
Совет. Вы можете попросить детей написать свои ответы на стикерах и приклеить их по краю тарелки, чтобы вы могли повторно использовать тарелки для дополнительной практики!
Какое из этих упражнений на умножение бумажных тарелок вы и ваши ученики попробуете? Дайте нам знать в разделе комментариев ниже!
Если вы ищете забавные задания по умножению для самых маленьких, ознакомьтесь с набором «Рабочие листы для супер-учителей» «Базовая коллекция умножения» . Вы найдете задания для печати, игры на умножение, викторины, карточки, математические загадочные картинки и многое другое!
Вы найдете задания для печати, игры на умножение, викторины, карточки, математические загадочные картинки и многое другое!
Вам также может понравиться:
Fidget Spinner Факты!
Математические карточные игры
Соревнование по математическим шашкам!
Комментарии
Оставить комментарий
Спасибо! Ваш комментарий отправлен.
Умножение и деление
Перейти к содержимому Перейти к навигацииВойти Завести аккаунт
Отследить заказ Обслуживание клиентов Наша компания Способы делать покупки Колодец желаний
Связаться со службой поддержки
1-877-867-1920
С понедельника по пятницу с 9:00 до 17:00 по восточному поясному времени.
Свяжитесь с нами по электронной почте
Доступность
- Дом
- Магазин по темам
- Математика
- Умножение и деление
Новый
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Новый
Добавлено в Колодец желаний
Нет в наличии
Нет в наличии
Добавлено в список желаний
Нет в наличии
Нет в наличии
Добавлено в список желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец Желаний
Доступ
Распродажа
(5. 0)
0)
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Добавлено в Колодец желаний
Новый
Добавлено в ваш колодец желаний
Положитесь на инструменты от Really Good Stuff, которые помогут учащимся освоить умножение и деление.
Четыре основные операции арифметики тесно связаны друг с другом. В то время как сложение и вычитание считаются первым шагом, умножение и деление требуют немного больше работы. Понятия преподаются с использованием основы сложения и вычитания, но также используется множество методов запоминания, чтобы запомнить основные вычисления.
Наша команда по разработке продукции Really Good Stuff состоит из учителей, которые помогали учащимся овладеть этими важными навыками, которые служат основой практически для всего, что они будут делать по математике в своей образовательной карьере и за ее пределами.
Наши обучающие материалы по умножению и делению охватывают всю гамму. Разработанные учителями, они помогают напомнить учащимся о важных понятиях и эффективно учить, не говоря ни слова.
Множество вариантов
Наша коллекция учебных пособий выходит далеко за рамки таблицы умножения и деления. Наши продукты с привлекательным оформлением и стилем включают в себя:
- Игры и головоломки. Эти увлекательные занятия укрепляют стандарты учебной программы в увлекательной игровой форме, уменьшая рутинную работу с рабочими листами.
- Таблицы умножения. Эти важные инструменты помогают учащимся запоминать значения и понимать отношения между числами, а также сложные понятия, такие как квадраты и квадратные корни.
- Мультипликационные плакаты: важные для понимания дробей и множителей в будущем, эти плакаты ярко окрашены и легко читаются.
- Наборы для успешного обучения, которые разбивают уроки на веселые и целенаправленные занятия.

- Флэш-карточки, которые позволяют учащимся тренировать друг друга.
- Математические лайфхаки, которые показывают отличные советы и приемы для определения определенных значений.
Все они были разработаны с учетом текущих стандартов учебной программы, поэтому ваши ученики будут готовы к тестированию в конце года и другим целям. Эти математические инструменты, изготовленные из прочных материалов, год за годом будут помогать учащимся, не снимая большие суммы денег с вашего банковского счета.
Рекомендуется для вас
Предложение о бесплатной доставке действительно онлайн только при минимальном заказе 39 долларов США. Максимальная экономия $500. Используйте промокод SHIP39 при оформлении заказа. Бесплатная доставка распространяется только на стандартную наземную доставку в пределах 48 континентальных штатов США. Товары со значком грузовика на странице товара не допускаются. Не действует на предыдущие заказы. Можно комбинировать с другими избранными купонами или акциями. Действительно только при минимальном заказе на сумму 39 долларов США, после применения других скидок и рекламных акций, а также без учета налогов и стоимости доставки. Предложение заканчивается 31.05.20.
Действительно только при минимальном заказе на сумму 39 долларов США, после применения других скидок и рекламных акций, а также без учета налогов и стоимости доставки. Предложение заканчивается 31.05.20.
Действителен онлайн до 31.05.20, 23:59 по восточному поясному времени. Введите код купона FLAT5 во время оформления заказа, чтобы воспользоваться предложением. Заказы должны быть отправлены на один адрес в пределах Соединенных Штатов. Только стандартная доставка. Исключает товары с ограничениями по доставке. Не использовать в сочетании с любыми другими предложениями или скидками. Не может быть использован для предыдущих покупок или товаров, изготовленных по индивидуальному заказу. Не подлежит перепродаже или использованию в коммерческих целях. Акция не суммируется с другими кодами купонов. Действует только на товары в наличии. Нет денежной стоимости. Недействительно там, где это запрещено. Возможны ограничения и изменения без предварительного уведомления.
Этот значок грузовика означает, что этот предмет требует особого обращения и/или доставки. Этот продукт не подлежит бесплатной или ускоренной доставке. В некоторых случаях товар может быть отправлен напрямую от производителя. Пожалуйста, нажмите здесь, чтобы увидеть наш раздел доставки для получения дополнительной информации.
Этот продукт не подлежит бесплатной или ускоренной доставке. В некоторых случаях товар может быть отправлен напрямую от производителя. Пожалуйста, нажмите здесь, чтобы увидеть наш раздел доставки для получения дополнительной информации.
Закрыть
Обязательная математическая деревянная игрушка Умножение и деление на бусины для детей младшего возраста Дошкольное обучение Обучающие интерактивные игрушки для детей от PersonalhomeD
Обязательная математическая деревянная игрушка Умножение и деление на бусины для раннего детства | Магазин FashionSpotПерсональный дом44,15 $
44,15 $
Купить в WalmartПерсональный дом44,15 $
Эта игрушка развивает у детей сосредоточенное, точное и независимое отношение к работе. позволяет вашему ребенку научиться умножению и делению основного вычислительного метода. Великолепные учебные пособия для дошкольных детских садов, укрепляющие концепцию … Магазин Thefashionspot предлагает вам отличные предложения на множество товаров PersonalhomeD Educational & STEM, включая математику, деревянные игрушки, умножение и деление, пластины для дошкольного обучения, развивающие интерактивные игрушки для детей.
Аналогичные продукты
Персонал.
Двухсторонняя доска для обучения математике, рисование, написание, деревянные блоки с цифрами, детская развивающая игрушка; двухсторонняя доска для обучения математике, деревянные блоки с цифрами, детская игрушка
Walmart
Buy Now на Walmart
Personalhomed
$ 37,83
3IN1 ДЕТИ ДЕРЕВОДНЫЕ ДЕРЕВОЕ ИГРА
КУПИТЬ СЕЙЧАС В Walmart
PersonalhomeD
$11,70
PersonalhomeD Безликая кукла Креативные подарки Cute Love Украшения для дома Украшения Декор Цилиндр Винтажные настольные фигурки Детское украшение
Walmart
BUY NOW ON Walmart
PersonalhomeD
$21.32
PersonalhomeD Dancing Doll Lovely Big Eyes Toy Education Toys Cactus Convenient Sing Very Cute Early Childhood For Children Ornament
Walmart
BUY NOW ON Walmart
PersonalhomeD
$12,43
Моделирование милый звук внимание пушистый цыпленок плюшевый цыпленок дети дети звуковая игрушка подарок
Walmart
Купить сейчас на Walmart
Personalhomed
$ 30,87
Длинные ноги милые кроличьи кукла детские мягкие плюшевые игрушки для детей спящего кроличь
18,83 $
Ежик Животное Плюшевые мягкие игрушки Кукла Подушка Мягкий домашний декор День рождения Рождественский подарок
Walmart
КУПИТЬ СЕЙЧАС В Walmart
PersonalhomeD
$13.
 15
15Большой милый светодиодный мишка панда, светящаяся в темноте, мягкая кукла, красочный мигающий свет, медвежонок, объятие, плюшевая детская игрушка в подарок; Walmart
PersonalhomeD
$20,11
Украшения для окон Украшения для кукол Декоративные куклы Ремесла Детские игрушки «сделай сам» для Хэллоуина Розовый Красный Подарок на День святого Валентина
Walmart
Buy Now на Walmart
Подробнее образовательное и стебель от Walmart
Scienceek
$ 25,53
Scienceek Magnetic Levitator Плавание классическое анти-грифта. PEMOTYST
21,68 $
PEMOTYST 15 шт. Прозрачные спиннеры Математические игры для сухого стирания с радужной стрелкой Спиннеры для обучения и игр для вечеринок
Walmart
КУПИТЬ СЕЙЧАС В Walmart
Золотая игрушка
63,92 $
Золотой игрушечный телескоп для детей Набор включает 3 увеличительные линзы, диагональное зеркало и подставку для штатива.
 Игрушка для мальчиков и девочек
Игрушка для мальчиков и девочекWalmart
КУПИТЬ В Walmart
BToBackyard
46,05 $
19 шт.0003
Walmart
Buy Now на Walmart
Mgaxyff
$ 28,12
Mgaxyff Kids Walmart Numbers Matching Toy Kids Learning Count Toy Toy Count Toy
Buy No On Bound Count Toy
Buy No On Bound Count Toy
9000
Buy No On Learning Count Toy
.
Музей естествознания
9,99 $
Музей естествознания Жуткий ползучий фонарик и проектор с 24-цветными изображениями жуков — игрушка-ствол
Walmart
КУПИТЬ СЕЙЧАС В Walmart
Amerteer
9,99 $
Amerteer Разберите игрушки динозавров — набор строительных игрушек Красочный динозавр Пасхальное яйцо Декоратор с отверткой Инструмент Строительная инженерия Игровой набор STEM Обучение для детей Мальчики Девочки от 3 лет
Walmart
90 NOW Walmart
MindWare
$29,95
Mindware Imagination Magnets~
Walmart
КУПИТЬ НА Walmart Generic
9013ric 9 00130Shulemin
$ 9,90 9000 3
Shulemin Word Wood Lobging Loban Loban Loban Loban Loban Loban Loban Loban Loban Loban Lopc
Walmart
КУПИТЬ В Walmart
0003
$ 46,48
Деревянные арабские цифры Sudoku Teaching Math Board Plate Toy
Walmart
Купить сейчас на Walmart
Другие продукты для обучения и естественных наук
Carson
29,99 $
Carson Optigami Educational Kids Science Kit Stem Diy Картонный микроскоп для детей (OG-100)
Amazon
Buy Now Amazon
Top Trumps
$ 32.
 00
00Top Tops Card Card Card Card Card Card Card Card Card Card Card Card Card Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Game Card Card Card Card (002708)
3
66
КУПИТЬ СЕЙЧАС НА Amazon
Think Fun
47,68 $
ThinkFun Rush Hour Junior Traffic Jam Логическая игра и игрушка STEM для мальчиков и девочек в возрасте от 5 лет и Chocolate Fix — отмеченная наградами логическая игра и игрушка STEM для детей в возрасте 8 лет и до
Amazon
КУПИТЬ НА Amazon
Nickelodeon
32,52 $
Magformers Paw Patrol 25 шт.
КУПИТЬ НА Amazon
Smartivity
$12,53 $24,99
Smartivity Rover Bot Обучающая игрушка STEM для детей от 6 лет и старше
Amazon
КУПИТЬ НА Amazon
Osmo
94,84 $ 149,98 $
Osmo — Genius Starter Kit & Monster Game для iPad — Возраст 5–12 — Математика, правописание, творчество и базовые обучающие монстры для iPad — 6 игр (iPad
Amazon
КУПИТЬ НА Amazon
Magformers
78,53 $
Tileblox Rainbow 104pc Set Магнитные строительные блоки, набор обучающих магнитных плиток, набор игрушек STEM на магнитной конструкции
Amazon
BUY NOW ON Amazon
Magformers
$80.
 99$143.99
99$143.99Magformers Challenger Set (112-pieces) Deluxe Magnetic Building Blocks, Educational Magnetic Tiles Kit , Magnetic Construction shapes STEM Toy Set — 63077
Amazon
КУПИТЬ СЕЙЧАС НА Amazon
Sassy
$6,99 $10,99
Sassy Rain Shower Bath Ball STEM Игрушка для ванны, от 6 месяцев
Amazon
КУПИТЬ НА Amazon
NATIONAL GEOGRAPHIC
34,99 $
Потрясающий химический набор NATIONAL GEOGRAPHIC — мега-научный набор с более чем 15 простыми экспериментами, созданием вулкана, запуском ракеты, созданием шипучих реакций и многим другим, игрушкой STEM, эксклюзивным научным набором Amazon3
Amazon
КУПИТЬ СЕЙЧАС НА Amazon
В нашем магазине
Выбрать тарелку | NZ Maths
Цель
Это числовое задание 2-го уровня из серии «Разберись». Это относится к этапу 5 системы нумерации.
Цели достижения
NA2-1: используйте простые аддитивные стратегии с целыми числами и дробями.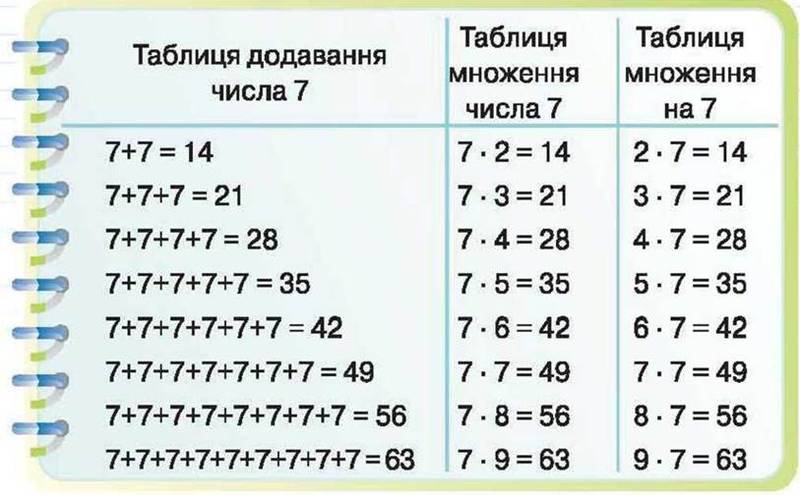
Разработка АО и другие учебные ресурсы
Действия учащихся
Нажмите на изображение, чтобы увеличить его. Нажмите еще раз, чтобы закрыть. Скачать PDF (439 КБ)
Конкретные результаты обучения
Использование фактов сложения и вычитания
Использование умственных стратегий для сложения чисел
Описание математики
Ссылки на числовую структуру
Используйте эти упражнения, чтобы:
• помочь учащимся, которые начинают использовать ранние аддитивные стратегии (этап 5), стать уверенными на этом этапе в областях сложения, вычитания, умножения и деления
• развить учащихся ‘ знание основных фактов к этапу 6.
Необходимые материалы
Одноклассник
FIO, уровни 2–3, чувство чисел и алгебраическое мышление, книга вторая, «Выбери тарелку», страницы 8–10
Копи-мастер таблицы
Упражнение
Эта интересная вычислительная игра будет полезна в качестве постоянного занятия по поддержанию здоровья как в школе, так и за ее пределами. Действия используют контекст номерного знака, чтобы поощрить различные стратегии расчета. Они также побуждают учащихся сравнивать влияние на большие и маленькие цифры сложения, вычитания, умножения и деления. Затем учащиеся имеют возможность обобщить влияние этих операций на задействованные числа.
Действия используют контекст номерного знака, чтобы поощрить различные стратегии расчета. Они также побуждают учащихся сравнивать влияние на большие и маленькие цифры сложения, вычитания, умножения и деления. Затем учащиеся имеют возможность обобщить влияние этих операций на задействованные числа.
Первое задание
Некоторые учащиеся смогут выполнить это задание самостоятельно, но убедитесь, что они понимают структуру игры. Они могут захотеть обсудить, выигрывает ли самый высокий или самый низкий балл. Проверьте, понимают ли они, что буквы на табличках не важны.
Вместе с обучающей группой убедитесь, что учащиеся заметили, что и Джессика, и Калеб получили одинаковый результат для первого номерного знака, несмотря на то, что Калеб умножал и делил, а Джессика складывала и вычитала.
Вопрос 1 заставляет учащихся сосредоточиться на изучении эффектов различных стратегий, которые используют Калеб и Джессика. Используйте такие вопросы, как:
Какая стратегия, как вы ожидаете, будет чаще всего получать наибольшее число?
Всегда ли на тарелке будет одинаковое количество нечетных и четных чисел?
Есть ли стратегия, которая лучше подходит для номерного знака с большим количеством цифр, которые являются большими числами?
Нечетных цифр больше, чем четных. Будет ли это иметь значение? (Нет. Это больше зависит от того, являются ли цифры старшими или младшими.)
Будет ли это иметь значение? (Нет. Это больше зависит от того, являются ли цифры старшими или младшими.)
В вопросе 2 учащиеся, вероятно, будут вычислять нечетные и четные числа отдельно, а затем объединять их. Калеб умножает все нечетные числа на 2, поэтому он может либо умножить каждое по отдельности, а затем сложить их вместе, либо сначала сложить их все, а затем умножить на 2. У него также есть два варианта для четных цифр, но на этот раз он будет делить на 2.
Модель для записи каждой из этих двух стратегий на планшете ZQ4731 для Калеба может быть:
Другая модель:
Вопрос 3 предназначен для подробного сравнения каждого набора правил. Предложите учащимся разработать диаграмму, которую они могут использовать для изучения влияния правил на каждую цифру. Например:
Общий выигрыш: Джессика получит на 2 больше, чем Калеб, поэтому она должна выигрывать чаще, если правило гласит, что побеждает тот, кто набрал наибольшее количество очков.
Второе задание
Стратегии, которые будут работать в новой игре с номерными знаками, могут включать чередование наибольшей и наименьшей суммы в качестве выигрышного сценария. Учащиеся должны сосредоточиться на стратегиях своих игр, в которых шансы на победу у обоих участников будут близки к равным. Например, предложите учащимся изучить сценарий, в котором один игрок прибавляет 1 к нечетным числам и вычитает 1 из четных чисел, а другой игрок удваивает нечетные числа и делит пополам четные числа. Таблица для этого правила будет:
Несмотря на то, что +1, – 1 игрок выигрывает в 3 из 9 и проигрывает в 4 из 9, влияние различий больше для x 2, ÷ 2 игрока (+20 по сравнению с +6 для + 1, — 1 игрок).
Правило, предложенное в ответах на вопрос 2, состоит в том, чтобы изменить вычисления для нечетных и четных чисел, что даст обоим игрокам одинаковые шансы на победу. Если учащиеся воспользуются подходом с диаграммой, предложенным там или выше, они смогут быстро увидеть, являются ли предложенные ими правила справедливыми для каждого игрока.
Хорошей темой для обсуждения является тот факт, что даже «справедливое» правило, такое как в «Ответах», не является гарантией успеха. Например, это правило, примененное к номерным знакам Калеба и Джессики, дает Калебу разницу +28. В конце концов, все зависит от диапазона цифр в используемых номерных знаках.
Добавочный номер
Используя правило, данное в ответах, предложите учащимся составить таблицу, чтобы изучить влияние вычислений на каждое число и обсудить результаты.
Другая игра с номерными знаками состоит в том, чтобы попытаться использовать все числа, чтобы достичь целевого числа, скажем, 10. Игроки могут использовать числа только один раз и могут комбинировать их, используя любую операцию. Например, в WZ7283 8 – 3 = 5, затем 7 + 5 = 12 и, наконец, 12 – 2 = 10,9.0003
Ответы на задание
Первое задание
1. Нет. Объяснения могут отличаться. Калеб часто получает больше, чем Джессика, когда удваивает нечетные числа (например, для 9 на номерном знаке, таком как TS9696, Калеб наберет 2 x 9 = 18, а Джессика наберет 9 + 5 = 14).
Но Калеб должен разделить пополам четные числа (например, 6 = 3), тогда как Джессика вычитает только 2 (например, 6 – 2 = 4). Таким образом, с TS9696 Калеб набрал бы 18 + 18 + 3 + 3 = 42, а Джессика набрала бы 14 + 14 + 4 + 4 = 36.
2. а. Джессика имеет самый высокий общий балл. Таблица может выглядеть так:
Один из способов подсчета ZQ4731:
b. Методы будут разными. Возможные способы включают в себя:
Калеб: Сложите нечетные числа и удвойте это количество, затем сложите четные числа
и уменьшите это количество пополам. Сложите две новые суммы, чтобы получить окончательную сумму.
Джессика: Сложите нечетные числа, затем подсчитайте количество нечетных цифр и умножьте это на 5. Затем сложите обе суммы вместе, чтобы получить общую сумму шансов. Сложите четные числа, подсчитайте количество четных цифр и умножьте это на 2, затем вычтите это из общего числа четных. Сложите новые суммы шансов и четных, чтобы получить окончательную сумму.
Чтобы определить победителя, сложите положительную разницу в баллах. (Например, в
(Например, в
таблице ответов на вопрос 2а положительные разности Калеба составляют в сумме 6, а Джессики — 18, поэтому Джессика выигрывает с результатом 12.)
3. a. Калеб обычно получает более высокие баллы за номерные знаки, у которых хотя бы на 1 нечетная цифра выше 5, а четные цифры меньше (если они есть).
б. Джессика обычно набирает больше очков за номерные знаки, которые имеют 2 или более старших четных цифр и более низкие нечетные цифры (если они есть).
с. Калеб набирает больше очков, когда он удваивает 7 или 9, чем Джессика, когда она просто прибавляет 5. Джессика набирает больше, когда вычитает 2 из 6 или 8, чем Калеб, когда он делит их пополам.
д. 5 и 4
Занятие второе
1. Практическая деятельность. Ответы будут различаться.
2. Правила будут различаться. Правило, которое дает обоим игрокам одинаковые шансы на победу, гласит: один игрок может умножать нечетные числа на 3 и четные числа на 2, а другой игрок может прибавлять 10 к нечетным числам и прибавлять 5 к четным числам.
Вы можете показать это на графике:
Обратите внимание, что хотя это дает обоим игрокам одинаковые шансы на победу, фактический победитель все же зависит от используемых номерных знаков. Например, за номерные знаки Калеба и Джессики в Упражнении 1 Калеб набрал бы 506 баллов, а Джессика — 480, то есть разница в 26 баллов.
Вложения
Добавить в план
Второй уровень
4 простых шага с визуальными моделями
Введение: умножение и деление дробейКрепкие существа – дроби!
Дроби считаются одним из самых сложных математических понятий для маленьких детей, потому что они имеют иные обозначения, чем целые числа. Это абстрактное понятие, которое побуждает маленьких рок-звезд работать лучше.
Операции с дробями усложняют задачу, так как детям становится трудно понять, что означают эти операции, и поэтому их визуализация может привести к лучшему пониманию концепции. Умножение и деление дробей может противоречить уже существующему пониманию умножения и деления целых чисел.
Умножение и деление дробей может противоречить уже существующему пониманию умножения и деления целых чисел.
Например, умножение двух целых чисел всегда приводит к большему произведению, но это не относится к умножению дробей.
Точно так же при делении двух целых чисел частное обычно меньше делимого, но это не относится к делению дробей.
Деление дробей отличается от деления двух целых чиселИз-за отсутствия надлежащего понимания этих понятий даже среди учителей ученики с трудом понимают дроби. Это также вызывает путаницу и неправильные представления среди них.
Цель этой статьи — предложить увлекательные методы, которые помогут детям визуализировать понятия умножения и деления. Кроме того, мы также попытаемся облегчить понимание процедур, связанных с умножением и делением дробей, с помощью простой методики, включающей всего 4 шага.
Читайте дальше и сделайте изучение дробей легким и приятным!
Содержание- Глоссарий
- Необходимые знания
- Введение в умножение дробей
- Первый шаг в умножение дробей: визуальное моделирование
- Умножение дробей: 4 простых шага
- Анализ: умножение дробей в сравнении с умножением целых чисел
- Деление дробей: 4 простых шага
- Резюме
- Часто задаваемые вопросы (FAQ)
- Дробь – Часть целого числа, записанная в виде a/b
- Знаменатель – Нижнее число дроби
- Числитель – Верхнее число дроби 1 9013 Единица дроби — Дробь с числителем 1
- Целое число — Счетные числа (0, 1, 2, 3, 4…)
- Эквивалентная дробь — Дробь, имеющая такое же значение, что и другая дробь
- Упрощение – Упрощение дроби
- Правильная дробь – Дробь со значением меньше 1 (числитель < знаменатель)
- Неправильная дробь – Дробь со значением больше 1 (числитель > знаменатель)
- Смешанное число – Способ записи неправильной дроби с использованием целого числа и правильной дроби
- Делитель – Число, на которое нужно разделить другое число
- Делимое – Число, которое нужно разделить
- Частное – Результат деления одного числа на другое Необходимые знания
- Понимание умножения и деления целых чисел
- Понимание дробей и их визуальных моделей
- Представление целых чисел в виде дробей
- эквивалентные фракции
- Упрощающие фракции в их самую низкую форму
- Преобразование неправильной фракции в смешанное число и наоборот
- Добавление фракций
.
Введение: умножение дробей
Прежде чем приступить к умножению дробей, необходимо усвоить концептуальное понимание умножения дробей. Дети должны уметь визуализировать умножение и должны знать, что означает умножение дроби на целое число или дробь.
Совет: Начните с моделирования умножения или деления, используя только целые числа. Затем вы можете перейти к дробным числам. Таким образом, существующие знания детей об умножении или делении целых чисел будут обновлены, и они смогут связать их с построением моделей умножения или деления дробей.
Начнем с умножения дробей.
Первый шаг к умножению дробей: моделированиеИспользование визуальных моделей в качестве учебного пособия делает процесс преподавания и обучения более эффективным, увлекательным и интерактивным. Это ориентированный на учащихся подход, который помогает детям визуализировать ключевые математические концепции, что в дальнейшем помогает им глубже понять концепцию на корневом уровне.

Для учителей визуальные модели могут вызвать обсуждение математических идей и отношений с ранее известными понятиями. Это помогает им лучше понять, как учащиеся понимают концепцию.
По этой причине обучение умножению дробей сначала с помощью моделей, а затем переход к стандартным процедурам было бы идеальным подходом.
Начнем с того, что умножение дробей может принимать 3 разные формы.
Level 1A : Whole × Fraction
Level 1B: Fraction × Whole
Level 2 : Fraction × Fraction
Please note: We will not be taking up mixed numbers as a отдельный случай, потому что это тоже дроби, записанные в другой форме. Чтобы помочь своим детям узнать о смешанных числах и неправильных дробях с помощью веселых игр, вы можете зарегистрироваться здесь!
Уровень 1A: Целое × Дробь
Пример 1: Тим использовал ¼ тыквы, чтобы испечь один тыквенный пирог.

Он испек 3 пирога. Давайте узнаем, сколько всего тыкв он использовал.
Так как он использовал одну четверть тыквы 3 раза , его выражение умножения будет 3 × ¼
3 раза 1/4 равно 3/4Итак,
7 =3
3/4
Итак, Тим использовал три четверти тыквы, чтобы испечь 3 пирога.
Пример 2: Если бы Тиму нужно было испечь 5 пирогов, сколько тыкв ему понадобилось бы?
5 умножить на 1/4 равно 5/45 × ¼ = 5/4
Итак, Тиму понадобится 1 целая тыква и четверть куска, чтобы испечь 5 пирогов.
Уровень 1B: Дробь × Целое
Визуализация модели Дробь × Целое может быть очень сложной для детей.
Начнем с того, что первое число в предложении умножения обозначает количество групп или количество повторений чего-либо.
 Но, в Дробь × Целое Сценарий , как мы формируем группы в дробном числе?
Но, в Дробь × Целое Сценарий , как мы формируем группы в дробном числе?Пример: ¼ × 8
Мы можем описать это выражение простыми словами как одна четвертая от восьми . Математически слово «из» означает умножение.
Давайте нарисуем модель для этого выражения.
Шаг 1 :
Шаг 1 – Умножение дроби с целым числомШаг 2:
Шаг 2 – Умножение дроби с целым числомSO, ¼ × 8 = 2
Пример 1: ¾ × 8
Это означает: Три-четверть из восьми
Пример 1-Умножение фракции с целым номером. Так, ,
. × 8 = 6Давайте попробуем еще несколько примеров.
Пример 2: Джейми приготовил 4 стакана сока из 3 лаймов. Найдите количество плодов лайма, которые он использовал для каждого стакана сока.

Это означает, что он использовал четверть 3 лайма для приготовления одного стакана сока.
Математическое выражение, которое необходимо решить для этого примера: ¼ × 3
Предположим, что три лайма — это A, B и C.
Пример 2. Умножение дробей с целыми числами Одна четвертая часть всех времен на каждой тарелкеКаждая тарелка представляет собой одну четвертую или четверть всей партии, то есть 3 лайма.
Сколько четвертей в одной тарелке? Три четверти
Итак, ¼ × 3 = ¾
Джейми использовал ¾ лайма на один стакан сока.
Пример 3: Узнайте, сколько лаймов Джейми использовал для 3 стаканов сока.
Это значит, что нам нужно узнать, сколько составляет три четверти от 3 лаймов .
Математическое выражение, которое нужно решить для этой ситуации: ¾ × 3
Выяснение, сколько лаймов используется для 3 стаканов сокаКаждая тарелка представляет одну четвертую или четверть всей партии, т.
 е. 3 лайма. Итак, три тарелки будут представлять три четверти.
е. 3 лайма. Итак, три тарелки будут представлять три четверти.Сколько четвертей в 3 тарелках? Девять четвертых
Резюме последнего примераИтак, ¾ × 3 = 9/4
Джейми использовал 9/4 сока лайма в 909.
Что означает дробь x целое?Похожие чтения: Лучшие платформы онлайн-обучения, набирающие популярность в наши дни
Уровень 2: Дробь × Дробь
Умножение дроби на дробь также является сложной формой, и учащимся довольно сложно понять применение умножения двух дробей.
Теперь мы можем помочь им визуализировать эту концепцию с помощью этого увлекательного и простого занятия по складыванию бумаги.
Пример 1: Визуализируйте и решите: ⅓ × ½
В общем случае это выражение будет означать одну треть половины . Вы можете помочь своему ребенку смоделировать этот сценарий, используя лист бумаги.

Попросите вашего маленького ученика выполнить следующие простые шаги:
- Возьмите прямоугольный лист бумаги и сложите его пополам.
- Затем сложите половинку на 3 равные части.
- Раскрасьте одну из сложенных сторон, чтобы показать одну треть половины.
- Откройте лист обратно.
- Определите, какую часть целого представляет заштрихованная часть.
⅓ × ½ = ⅙
ДОЛЖЕН ПОПРОБОВАТЬ БОЛЬШЕ!
Предложите детям попробовать умножить разные дроби, используя один и тот же метод.
Давайте рассмотрим еще несколько примеров:
Следующие модели следуют тому же принципу, что и в приведенном выше упражнении по складыванию бумаги. Упомянутый принцип заключается в моделировании двух фракций в одной модели.
Пример 2: Сколько будет ¼ × ½?
Представляет четверть половины.
Пример 2 – Умножение дроби на дробьСовет по умножению дроби на дробь
Пример 3: 5/7 × ¾
Пример 3. Умножение дроби на дробьПример 4: 1/3 × 1⅗
Пример 4. Умножение дроби на дробьПосле нескольких примеров вы можете предложить своему ребенку непосредственно нарисовать комбинированную модель.
Нарисуйте модель умножения двух дробей, выполнив следующие шаги:
- Нарисуйте большой прямоугольник.
- Разделите его на столько равных горизонтальных полос, сколько знаменатель первой дроби. Заштрихуйте части, чтобы представить первую фракцию.
- Далее эту же модель разделите на столько равных вертикальных полос, сколько знаменатель второй дроби. Заштрихуйте части, чтобы представить вторую фракцию.
- Определите перекрывающуюся часть в модели. Представленная дробь является произведением двух дробей.
Попросите детей наблюдать за произведениями, полученными из моделей, а также скажите им, какое правило соблюдается при умножении дробей.
Мы можем помочь им понять процесс с помощью этих 4 простых шагов умножения дробей.
- Запишите оба числа в виде дроби.
- Умножьте числители. Произведение является новым числителем.
- Умножьте знаменатели. Продукт является новым знаменателем.
- Перепишите ответ в форме наименьшего или смешанного числа.
Посмотрите несколько примеров.
Пример 1:
Пример 1 – Этапы умножения дробейExample 2:
Example 2 – Steps of multiplying fractionsExample 3:
Example 3 – Steps of multiplying fractions Analysis : Multiplying Fractions versus Whole Number Multiplication
Question : Do мы всегда получаем большее произведение при умножении двух чисел?Обратите внимание на следующие задачи на умножение.
6 × 4 = 24
2 × 9 = 18
3 × 1 = 3
5 × 7 = 35
10 × 8 = 80
19 × 1 = 19
8 × 0 = 0
7 × 11 = 77
16 × 2 = 32
Вы думаете, что и то же самое вопрос актуален и для умножения с дробями?Ответ на это: « иногда ».

Давайте рассмотрим несколько случаев, чтобы лучше их понять.
Случай 1: Когда одно из множимых равно 0
Произведение также будет равно нулю независимо от другой дроби.¼ × 0 = 0/4 = 0
⅗ × 0 = 0/5 = 0
7/2 × 0 = 0/2 = 0
6. одно из множимых меньше 1
Произведение будет меньше, чем другая дробь.3/4 × 7/3 = 21/12 = 7/4 (< 7/3)
1/4 × 7/8 = 7/32 (< 7/8)
3/4 × 1/9 = 1/12 (< 1/9)
Случай 3: Когда одно из множимых является дробью, эквивалентной 1
Произведение будет таким же, как и другое число.
1 × 7/8 = 7/8
6/6 × 9/5= 54/30= 9/5 5
Случай 4: Когда одно из множимых является дробью больше 1
Произведение будет больше, чем другая дробь .

8/3 × 2/5= 16/15 (> 2/5)
6/10 × 9/5= 54/50= 27/25 (> 6/10)
9/6 × 1/7= 9/42= 3/14 (> 1/7)
Случай 5: Когда оба множимых являются дробями больше 1
Произведение будет больше обеих дробей.
8/3 × 3/2 = 4 (> 8/3, 3/2)
6/4 × 5/2 = 30/8 (> 6/4, 5/2)
Похожие материалы: Различные типы графических органайзеров для учителей и учащихся
Деление дробей в реальной жизни: Введение
В повседневной жизни мы сталкиваемся с ситуациями, когда мы применяем концепцию деления дробей. Разделение на дроби можно сделать интересным, а концепцию можно полностью внедрить в сознание детей, если им будет предложено решать сценарии из реальной жизни.Это поможет детям визуализировать и понять деление на дроби.
Пример: Предположим, у вас есть 3 яблока, каждое из которых разрезано пополам.
 На сколько человек вы сможете раздать эти 3 яблока, если каждому достанется по половинке?
На сколько человек вы сможете раздать эти 3 яблока, если каждому достанется по половинке?Давайте представим эту ситуацию и решим ее. В конце концов, одно яблоко в день избавит вас от математической хандры!
Разделение трех яблок между 6 людьмиЗадачу можно расширить, изменив дробь.
Например, что, если вы решите дать каждому человеку по четверти? Сколько человек можно обслужить сейчас?
Понимание дробного деленияПонимание дробного деленияИли что, если вы решите дать каждому человеку три четверти? Сколько человек можно обслужить сейчас?
Концептуальное понимание деления на дроби Концептуальное понимание деления на дроби
Понимание проблемы и последующее ее моделирование является важным шагом в любом сценарии решения проблем с делением на дроби. Предложите учащимся попытаться визуализировать сценарий, а затем найти его решение.Рисуй и решай!
Группа друзей купила пиццу. Они поровну поделили пиццу и съели ее.

Попробуйте определить, сколько было друзей, если у каждого из них было:
Первый шаг к разделению.9 Как и в случае с умножением, когда учащиеся научатся моделировать задачи на деление дробей, найти ответ будет проще простого.one-eighth of the pizza two-eighth of the pizza 8 friends 4 friends SO, 1 ÷ ⅛ = 8 SO, 1 ÷ 2/8 = 4 Поэтому и для деления дробей предлагается подход от визуального к незрительному методу. Для студентов такой подход более правдоподобен, так как закладывает прочную концептуальную основу.
Давайте рассмотрим несколько примеров.
Целое число ÷ дробьПример 1:
Пример 1. Деление целых чисел на дроби
Деление целых чисел на дробиПример 2.
Пример 2. Деление целых чисел на дробиДополнительная литература: Наиболее важные математические символы, необходимые учащимся для решения задач
6 2 Подсказка: . Когда делитель является дробным числом, полезно описать операторы деления как «Сколько групп (делителя) можно составить из (делимого)?» или «Сколько групп (делителя) существует. в (дивиденд)». Эти описания помогают детям легче визуализировать ситуацию. Дробь ÷ Целое Деление дроби на целые числа Дробь ÷ Дробь Деление дроби на дробь Смешанное число ÷ Дробь Деление смешанных чисел на дроби6 Остаток
Пример 1
Пример 1 – Разделение дроби с остаткомПример 2:
Пример 2 – Деление дроби с остатком Некоторые распространенные трудности при делении дробей- Учащиеся часто пытаются понять разницу между делением на 2 и делением на ½.

Следующие модели помогут им легко увидеть разницу.
Проблемы с делением дробей Проблемы с делением дробей- Учащимся часто трудно понять, что деление дробей не всегда приводит к уменьшению частного.
Крайне важно, чтобы мы поощряли детей наблюдать за частными, полученными из моделей, и рассказывать им, какое правило следует при умножении дробей. Выполнение таких действий с ними может помочь в развитии навыков логического вывода и рассуждения.Помогите им освоить процедуру деления дробей за 4 простых шага.
- Переверните дробь делителя.
- Изменить знак с ÷ на ×
- Умножение дробей.
- Упрощение.
Понимание дробей и операций с ними станет намного проще, когда дети приобретут навыки визуализации задачи и знания того, что нужно вычислить. Но чтобы обрести такую уверенность, им нужно попрактиковаться в большом количестве математических задач. Необходимо, чтобы они смоделировали проблему, а затем решили ее.
Но чтобы обрести такую уверенность, им нужно попрактиковаться в большом количестве математических задач. Необходимо, чтобы они смоделировали проблему, а затем решили ее.Вы можете обратиться к этим рабочим листам на SplashLearn, которые легко загрузить и распечатать, чтобы помочь вашему ребенку лучше понять умножение дробей.
Подводя итог- Для более глубокого понимания концепции обязательно создайте для детей среду, благоприятную для экспериментального обучения.
- Вы можете использовать предыдущие и существующие знания ваших детей об умножении и делении целых чисел, чтобы получить новые знания об умножении и делении дробей.
- Поощряйте детей визуализировать проблемы и моделировать их. Сделайте так, чтобы они чувствовали себя комфортно, задавая вопросы.
- Крайне важно меньше сосредотачиваться на правильном ответе и больше на рассуждениях и мыслительном процессе ребенка.
- Как родитель, свяжите математические задачи с ситуациями из реальной жизни и приведите примеры из повседневной деятельности.

Упростите дроби с помощью SplashLearn
Благодаря интерактивным играм и наградам, которые помогут вашему ребенку повысить уверенность в себе и повысить его баллы, вы сможете сделать обучение легким и беспроблемным. Присоединяйтесь к нашему сообществу из 40+ миллионов бесстрашных учеников уже сегодня!Зарегистрируйтесь бесплатно!
Часто задаваемые вопросы (FAQ)
Q1 – Как шаг за шагом умножать дроби?
- Запишите оба числа в виде дроби.
- Умножьте числители.
- Умножьте знаменатели.
- Упростите или перепишите ответ в форме смешанного числа.
Q2 – Как делить дроби шаг за шагом?
- Переверните дробь делителя.
- Изменить знак с ÷ на ×.
- Умножьте дроби.
- Упрощение.
Q3. Как определить, будет ли произведение умножения на дробь большим или меньшим?
Сравните числитель и знаменатель дроби, чтобы проверить, будет ли произведение больше или меньше числа, на которое они умножаются.

Большее произведение → Числитель > Знаменатель. Примеры: 3/2, 4/3, 8/5 и так далее.
Меньший продукт → Числитель < знаменатель. Примеры: 3/4, 4/7, 5/9 и так далее.
Умножение – Элементарная математика
Как с картинкой, так и с выражениями, это не что иное, как чудо, что 4 × 3 = 3 × 4. Дети, конечно, могут переставлять объекты, сгруппированные как 3 + 3 + 3 + 3, чтобы показать эквивалентность 4 + 4 + 4, но требует перестановки и не является «очевидной».
Но если одно и то же печенье разложить на подносе рядами и столбцами, то совершенно очевидно, что как бы мы ни держали поднос, количество печенья одинаково. Даже если у нас есть предпочтения в отношении того, как мы обозначаем первые две картинки ниже (настаивая, например, на том, что одна имеет размер 4 × 3, а другая — 3 × 4, чего математики не делают), у нас нет способа сделать такое изображение. задание для последнего лотка. 4 × 3 просто равно 3 × 4, хотя обозначения не совпадают.

Если мы описываем картинку «три тарелки, по четыре печенья на каждой», используя повторяющееся выражение сложения, то 4 + 4 + 4 более «естественно» использовать, чем 3 + 3 + 3 + 3. Но если мы опишем эту картинку с помощью выражение умножения, 3 × 4 и 4 × 3 одинаково правильно; нет математически предпочтительного порядка записи выражений умножения.[1].
Для младших школьников полезно и возможно развить представление об умножении, которое выдержит переход от целых чисел к дробям и десятичным дробям. Конечно, также полезно увидеть, как умножение может упростить вычисление, которое в противном случае потребовало бы повторного сложения, но оно не должно быть первичным образом умножения и, по этой причине, предпочтительно не его первым образом.
В Подумай о математике! умножение связано прежде всего с рядами и пересечениями, а довольно рано связано с «сочетаниями» (в том числе и простыми парами) вещей: улицами и проспектами, гласными и согласными в двухбуквенных словах и т.
 д. Идея повторного сложения также представлена, но позже, как пример другой задачи, которую решает умножение.
д. Идея повторного сложения также представлена, но позже, как пример другой задачи, которую решает умножение.Учитывая количество строк и столбцов в прямоугольном массиве, умножение сообщает нам, сколько элементов в массиве, не заставляя нас считать их один за другим или многократно добавлять (или пропускать счет) элементы в каждой строке или столбце. Когда элементы в строках и столбцах представляют собой квадраты, выровненные из стороны в сторону, умножение подсчитывает эти квадраты и, следовательно, дает нам площадь прямоугольника. Это изображение отлично работает даже для дробей и объясняет алгоритм умножения дробей.
Если прямоугольник размером три на четыре разместить «на уровне» в одну сторону, он будет состоять из 3 строк и 4 столбцов ; если мы повернем его на 90 градусов, строки станут столбцами, а столбцы станут строками, поэтому он будет иметь 4 строки и 3 столбца . Если он держится под наклоном, нет правила, указывающего, какие строки называть, а какие столбцы, но в любом случае это не имеет значения; количество квадратов внутри него одинаково.
 Также не имеет значения, в каком порядке мы обозначаем ширину и длину прямоугольника: 3 × 4 и 4 × 3 обозначают один и тот же прямоугольник, независимо от того, как прямоугольник держат. Два выражения, 3 × 4 и 4 × 3, называют одно и то же число. Комбинации: сколько возможных блоков можно составить ровно из трех цветов и четырех форм? (Предположим, что каждый блок одного цвета и все блоки одного размера.) Вопросы такого рода предполагают другой образ (и использование) умножения.
Также не имеет значения, в каком порядке мы обозначаем ширину и длину прямоугольника: 3 × 4 и 4 × 3 обозначают один и тот же прямоугольник, независимо от того, как прямоугольник держат. Два выражения, 3 × 4 и 4 × 3, называют одно и то же число. Комбинации: сколько возможных блоков можно составить ровно из трех цветов и четырех форм? (Предположим, что каждый блок одного цвета и все блоки одного размера.) Вопросы такого рода предполагают другой образ (и использование) умножения.На самом деле умножение подходит для любой ситуации, в которой элементы одного набора соединяются по порядку с элементами другого набора. Здесь элементы одного набора являются началами «слов», а элементы другого набора — окончаниями.
Намек на связь с алгоритмом умножения.
См. статью об умножении и делении для полной разработки алгоритма многоразрядного умножения, показывающего, как он является точной записью показанных здесь моделей пересечения/площади.

В отличие от сложения, которое объединяет только одинаковые количества (сотни с сотнями, единицы с единицами), умножение дает все пары (3 × 7, 3 × 40, 3 × 200, 80 × 7, 80 × 40, 80 × 200)
Для целей выполнения многозначного умножения изображение «пересечения», показанное выше, неудобно, поскольку оно рассеивает частичные произведения таким образом, что это создает неудобства для конечного шага сложения. . Для понимания того, как организовать вычисления, удобнее использовать табличное представление комбинаций, а также знакомит с моделью массива/площади.
Такой взгляд на многозначное умножение лежит в основе ведического умножения в Индии. Это может быть увлекательной культурной побочной темой для учащихся, которые научились умножать многозначные числа.
Массивы и таблица умножения
В начале второго класса дети могут решать такие задачи и получать удовольствие от них.
Вот две красные буквы и три синие буквы: A, I, S, N, T .
 Сколько двухбуквенных слов вы можете составить, начиная с красной буквы и заканчивая синей буквой?
Сколько двухбуквенных слов вы можете составить, начиная с красной буквы и заканчивая синей буквой?Сколько двухблочных башен именно такой формы можно построить из этих блоков?
Вот два примера: . Сколько других вы можете сделать?Дети могут проводить эксперименты, создавая актуальные комбинации, а также изобретать собственную систему записи этих комбинаций. В случае двухбуквенных слов достаточно просто написать слова. Что касается башен, дети могут нарисовать их или указать сочетания цветов более абстрактным способом. Когда количество вариантов достаточно мало, как в случае с двухбуквенными словами, второклассники быстро находят все варианты.
Пересечения как модель для составления организованного списка
Когда число возможностей больше, как в задаче о блочной башне, дети склонны пропускать комбинации или дублировать их, если только они не систематизированы.
Вот один из способов визуализировать пары в этих двух экспериментах. Каждое пересечение представляет собой комбинацию. Сам символ × связан с изображением пересечения, пересечением линий.
Каждое пересечение представляет собой комбинацию. Сам символ × связан с изображением пересечения, пересечением линий.
Дети могут «водить» пальцем вдоль «улицы А» и «проспекта Н» и обозначить светофор на этом перекрестке «ан». например, top. Когда второклассники впервые проводят эти эксперименты, они учатся составлять систематические списки, а не умножать. Но мы видим, к чему это ведет: пересечения сами по себе перечисляют комбинации, которые ищут дети, и помогают им понять, как организовать эти списки; количество пересечений можно найти путем умножения, и дети получают предварительный просмотр этих идей умножения.Таблицы как модель для составления упорядоченного списка
Таблицы одинаково хороши для представления комбинаций и организации задачи их перечисления. Ячейки внутри таблицы (старательно избегая путаницы с ячейками «заголовка» над каждым столбцом и слева от каждой строки) снова показывают, как умножение отвечает на вопрос «сколько пар можно составить?»
Математика широко использует обе структуры — таблицы и пересекающиеся линии.

Умножение часто представляется в виде массивов смежных квадратов — «модель площади» умножения — или массивов точек или других мелких объектов. Первые визуально больше похожи на внутренности столов; последние визуально больше похожи на пересечения. Якорь
Построение основных фактов
Первые шаги
Когда мы видим одинаковые тройки чисел — 3, 5, 15; 4, 3, 12; 2, 5, 10; 6, 4, 24 — всплывающие в разных контекстах, они начинают казаться знакомыми еще до каких-либо сознательных усилий по их запоминанию. На самом деле, сфокусированные, преднамеренные усилия, которые кажутся необходимыми для некоторых троек (например, 7, 8, 56), могут быть связаны именно с тем, что существует так мало естественных контекстов, в которых эти тройки иначе появляются. Многие внешкольные занятия помогают построить таблицу умножения на 5: опыт определения времени в минутах на часах, обращения с монетами, наблюдения за своими руками. Следующие идеи представляют несколько контекстов для одних и тех же основных фактов, чтобы разнообразить практику (чтобы она оставалась интересной и создавала богатое разнообразие образов), чтобы к тому времени, когда дети пытаются запомнить факты умножения, они уже были хорошо знакомы с наиболее распространенными.
 те, что знают их «на холодную», а количество оставшихся фактов, требующих заучивания, совсем невелико (всего пятнадцать!).
те, что знают их «на холодную», а количество оставшихся фактов, требующих заучивания, совсем невелико (всего пятнадцать!).Удвоение и деление пополам
В первом классе дети учатся удваивать ([[арифметика в уме|в уме]) все целые числа до 12. Второклассники практикуют эти основные удвоения, используя их, наряду с развитием своих представлений о разрядном значении , удваивать (мысленно) целые числа до 50. В этих классах дети также учатся находить половину четных чисел, получающихся в результате такого удвоения.
Малые массивы
В Подумай о математике! , вторая половина второго класса дает учащимся большой опыт работы с небольшими массивами, из которых они могут запоминать небольшие факты умножения. В одном из упражнений учитель может поднять такой массив и спросить: «Сколько строк? Сколько столбцов? Сколько маленьких квадратиков?»
Учащиеся, которые еще не умеют правильно складывать, могут использовать сложение или пропускать счет, чтобы определить количество квадратов.
 Связь размеров массива — количества строк и столбцов — с количеством маленьких квадратов устанавливает факт умножения.
Связь размеров массива — количества строк и столбцов — с количеством маленьких квадратов устанавливает факт умножения.Затем учитель может держать тот же массив в этой ориентации и задавать те же вопросы.
Строки и столбцы меняются местами, но количество квадратов остается прежним.
Преподаватель может устроить из этого веселую игру, изменяя набор поддерживаемых массивов (2×3, 3×3, 4×5 и т. д., но не более 5 строк или столбцов, потому что большие числа слишком сложны). узнавать без утомительного подсчета), и учащиеся довольно быстро запоминают, сколько квадратов в этих знакомых прямоугольниках.
Тот факт, что прямоугольник, расположенный горизонтально или вертикально, имеет одинаковое количество маленьких квадратов внутри, дает наглядное представление о том, почему умножение является коммутативным.
Пересекающиеся вертикальные и горизонтальные линии дают еще один образ для умножения — 2 вертикальные линии пересекают 3 горизонтальные линии в 6 пересечениях — и еще один контекст для репетиции фактов. Они могут рисовать их или играть с прозрачными картами, сначала пытаясь предсказать количество пересечений, а затем перекрывая прозрачные пленки, чтобы непосредственно подсчитать их предсказания. С картами с прорезями в них тоже интересно играть. Дети выбирают пару и, как и в случае с диапозитивами, пытаются изобразить количество пересечений, прежде чем они начнут экспериментировать, кладя одну карточку поверх другой, чтобы убедиться, что их предсказание было верным. Если карту с 2 вертикальными слотами положить поверх карты с 5 горизонтальными слотами, мы сможем видеть сквозь двойной слой только на 10 пересечениях.
Они могут рисовать их или играть с прозрачными картами, сначала пытаясь предсказать количество пересечений, а затем перекрывая прозрачные пленки, чтобы непосредственно подсчитать их предсказания. С картами с прорезями в них тоже интересно играть. Дети выбирают пару и, как и в случае с диапозитивами, пытаются изобразить количество пересечений, прежде чем они начнут экспериментировать, кладя одну карточку поверх другой, чтобы убедиться, что их предсказание было верным. Если карту с 2 вертикальными слотами положить поверх карты с 5 горизонтальными слотами, мы сможем видеть сквозь двойной слой только на 10 пересечениях.Пересечения для разъяснения умножения на 0 и 1. «Представьте себе крошечный городок с тремя дорогами, идущими с востока на запад…» Проведите пальцем по воздуху горизонтально, чтобы объяснить, что означает «восток-запад». Затем «нарисуйте» еще две дороги с востока на запад прямо в воздухе, чтобы дети могли представить их в уме. Позже вы или ребенок нарисуете их на доске.
 «…и только одна дорога, идущая с севера на юг».
«…и только одна дорога, идущая с севера на юг».В воздухе укажите пальцем дорогу с севера на юг.
«Давайте нарисуем карту этого крошечного городка. Вот дороги с востока на запад.
Нарисуйте неправильную границу города, а в ней нарисуйте три параллельные горизонтальные линии, идущие от одной стороны города к другой (и слегка выходящие за границу города, чтобы указать, что они продолжают идти в соседние районы).
«На карте дороги выглядят как три горизонтальные линии. Кто хотел бы нарисовать дорогу с севера на юг?»
Можно снова указать направление пальцем в воздухе, но не прямо на карте. Пригласите кого-нибудь порисовать.
«Город поставил светофор на каждом перекрестке (укажите на перекрестки). Сколько там светофоров?»
Играйте с изображением.
«А что, если бы город построил еще одну дорогу с востока на запад? Сколько пересечений получится?»
Умножение любого числа на 1 дает это число; умножение любого числа на 0 дает 0.
 Дети, которых учат этим просто правилам для запоминания, без некоторого понимания часто искажают правила, путая их друг с другом. (Что дает 1 умножение числа на 1 или число?) Изображение крошечного городка помогает понять, почему 1 умножение на любое число дает это число. (При наличии только одной вертикальной линии количество пересечений будет таким же, как и количество горизонтальных линий.)
Дети, которых учат этим просто правилам для запоминания, без некоторого понимания часто искажают правила, путая их друг с другом. (Что дает 1 умножение числа на 1 или число?) Изображение крошечного городка помогает понять, почему 1 умножение на любое число дает это число. (При наличии только одной вертикальной линии количество пересечений будет таким же, как и количество горизонтальных линий.)
Карты с 0-5 слотами также могут быть особенно полезны. Когда карта с одним вертикальным слотом помещается поверх карты с тремя горизонтальными слотами, три пересечения появляются как единственные «окна» через пару карт. Изменение того, какая карта находится сверху или какая вертикальная, а какая горизонтальная, не имеет значения. Если одна карта имеет один слот, количество пересечений будет соответствовать количеству слотов на другой карте, когда они наложены друг на друга (и другие слоты перпендикулярны одному слоту). Изображение слота особенно ясно показывает, почему умножение на 0 всегда дает 0.
Этот урок дает прекрасную возможность использовать слова горизонтальный и вертикальный в контексте и связать их использование в качестве направлений на картах с востоком, западом, севером и югом как направлениями на земле. (См. «Горизонтальный» и «Вертикальный», чтобы узнать о распространенных заблуждениях относительно идей, которые представляют эти слова.)
Построение таблицы умножения
Учащийся проект для второго класса: Учащиеся используют сетку, которая организована как таблица умножения, но не имеет строки или столбец для нуля. Используя лист бумаги в форме буквы L, они выбирают часть сетки; в правом нижнем углу выделения они пишут количество захваченных квадратов (что равно площади прямоугольника, если каждый маленький квадрат представляет собой одну квадратную единицу площади).
Обратите внимание, что число вверху, ближайшее к синей границе, дает ширину зеленого прямоугольника, количество столбцов квадратов; число слева, ближайшее к синей границе, дает высоту зеленого прямоугольника и количество строк в нем.

Если мы переместим границу прямо на один шаг вниз, мы добавим новую строку без изменения количества квадратов в строке.
Таким образом, скажем, что 6 (количество квадратов в предыдущем прямоугольнике, 2×3) плюс 3 (количество квадратов в новом ряду) равно 9(количество квадратов в новом прямоугольнике). Другой способ описать новый прямоугольник — 3×3. Итак, 2×3 + 3 = 3×3.
Этот прямоугольник имеет одинаковую ширину и высоту, так что это квадрат. Поэтому число в углу (количество крошечных квадратов внутри него) называется квадратным числом.
Ход по диагонали — один шаг «на юг» и один шаг «на восток» (или один шаг вниз и один шаг вправо) — дает еще одно квадратное число.
Два шага по диагонали на юго-восток дают еще один квадратный номер.
Интересно, если начать с квадратного числа (в данном случае 16) и сделать один шаг на северо-восток
или юго-запад
полученное число ровно на 1 меньше квадратного числа, с которого вы начали.
 Этот пример показывает, что прямоугольник 3×5 содержит на один квадрат меньше, чем прямоугольник 4×4. См. статью о разнице квадратов, чтобы узнать больше об этом интригующем шаблоне и еще одном особенно эффективном способе для студентов практиковать факты, развивая новые и полезные математические идеи.
Этот пример показывает, что прямоугольник 3×5 содержит на один квадрат меньше, чем прямоугольник 4×4. См. статью о разнице квадратов, чтобы узнать больше об этом интригующем шаблоне и еще одном особенно эффективном способе для студентов практиковать факты, развивая новые и полезные математические идеи.Симметрия таблицы умножения
Подсчет квадратов в прямоугольниках позволяет понять, почему 3×4 = 4×3. Оба способа описания этого прямоугольника . И даже если мы решим зарезервировать одну из этих нотаций для , а другую нотацию для , они все равно будут равны.
Поскольку умножение коммутативно, т. е. 2×6 = 6×2, 3×5 = 5×3 и т. д., таблица умножения симметрична по диагонали северо-запад-юго-восток. Эта диагональ, желтая на этих иллюстрациях, содержит квадратные числа.
Избавившись от отвлекающих цифр и стрелок, мы видим три области: диагональ с квадратными цифрами, зеленую область с другими товарами и белую область с теми же номерами, что и в зеленой области.

Это очень хорошая новость для всех, кто пытается запомнить факты умножения! (См. Сколько фактов нужно выучить? ниже.)
Умножение на 10 и 100
Строится: 7 стержней - это 70 маленьких кубиков
Умножение на 5 и 50
Дети, которые могут умножить на 10 и взять половину, могут затем использовать эти навыки, чтобы умножить на 5. Например, 7×5 — это половина 7×10, то есть 35. В конечном счете, 7 × 5 следует просто распознавать сам по себе — один из «основных фактов», — но двухэтапная процедура (умножение на 10 и затем взятие половины результата) также полезно знать, и хорошая связь, чтобы установить с 5-кратные факты. Точно так же, зная, что 50 — это половина 100, мы можем видеть, что 50 семерок — это половина 100 семерок, поэтому 50 × 7 — это половина 100 × 7: мы можем умножить любое число на 50, умножив его на 100, а затем взяв половину. Дети, хорошо усвоившие это, могут легко умножить в уме 18×5, подумав «половину от 180». Поскольку умножение и деление можно выполнять в любом порядке с одинаковым результатом, мы можем сначала взять половину (от 18), а затем умножить на 10.


 Обов’язково додайте символ $ до B і до 2 у формулі та натисніть клавішу ENTER.
Обов’язково додайте символ $ до B і до 2 у формулі та натисніть клавішу ENTER. Надіюся, що тепер все ж таки щось зміниться», – розповідає Галина Паращич, мати першокласниці Марічки.
Надіюся, що тепер все ж таки щось зміниться», – розповідає Галина Паращич, мати першокласниці Марічки.

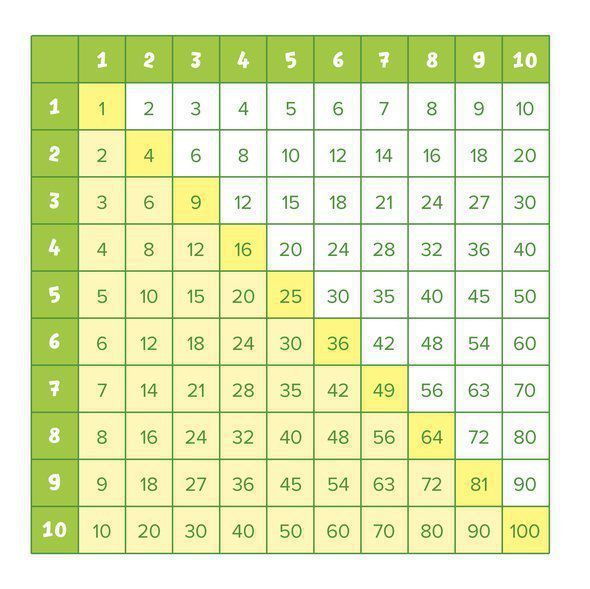
 Навчання для малюка не повинна перетворитися на важку, рабську службу. Нехай це буде весела гра, яку можна легко відкласти на потім, зайнявшись чим-небудь іншим.
Навчання для малюка не повинна перетворитися на важку, рабську службу. Нехай це буде весела гра, яку можна легко відкласти на потім, зайнявшись чим-небудь іншим.
 15
15 Игрушка для мальчиков и девочек
Игрушка для мальчиков и девочек 00
00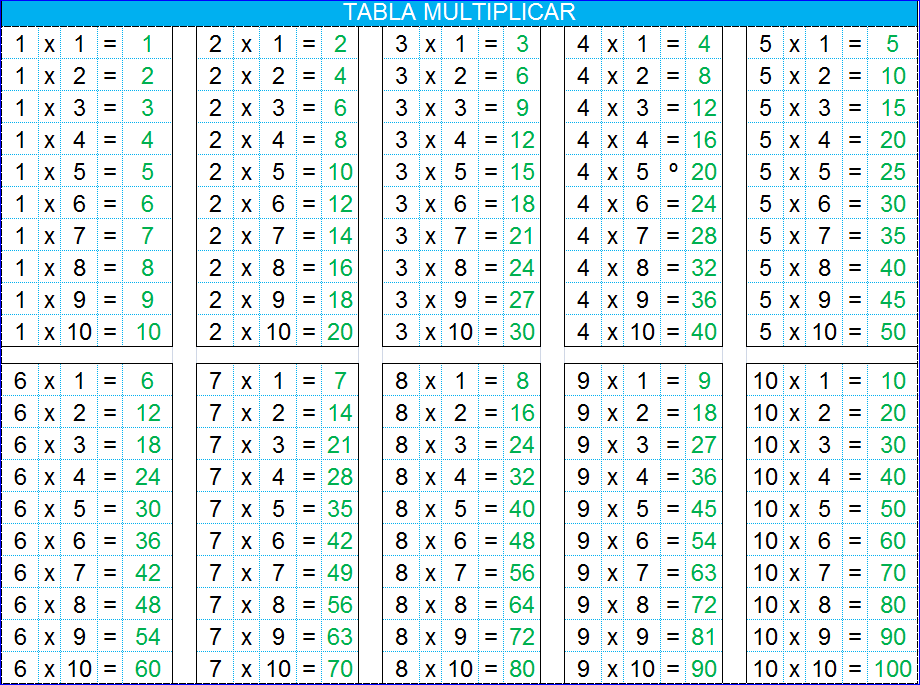 99$143.99
99$143.99