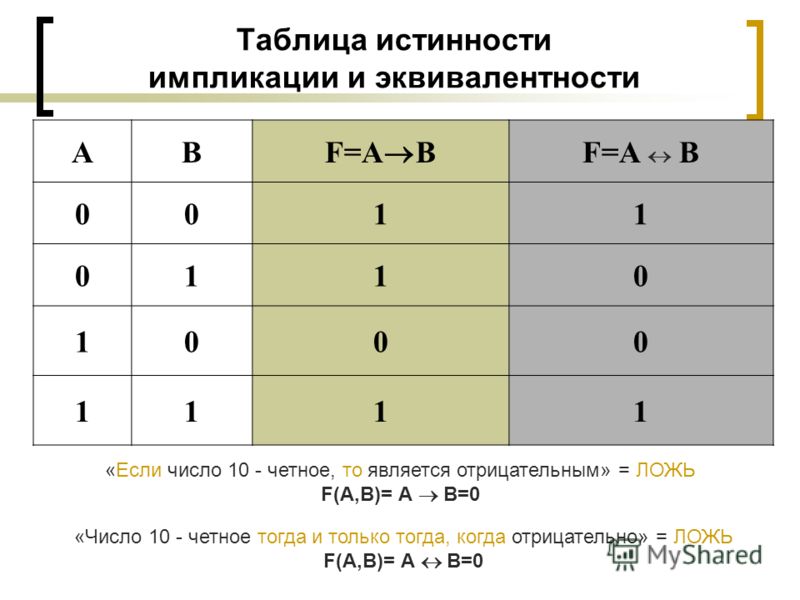
Эквивалентность | Введение в математическую логику
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
У современной математики есть собственный формальный язык. С его помощью мы сводим сложные высказывания к формальностям — то есть переводим рассуждения и мысли в плоскость математики. Так мы лучше понимаем мысли других людей, точнее высказываем свои рассуждения и учимся рассуждать логически.
В этом уроке мы продолжим изучать формальный язык логики высказываний. Мы разберем отношения эквивалентности и научимся определять высказывания, которые равнозначны по смыслу. Так мы сможем экономить время и заранее понимать, какие высказывания можно посчитать истинными или ложными без дополнительных рассуждений.
Логическая эквивалентность
Возьмем для примера такое предложение:
Если Вася получит прибавку к зарплате, то он пойдет в театр
С точки зрения логики в этом высказывании есть и такой смысл:
Если Вася не пошел в театр, значит он не получил прибавку к зарплате
Эти высказывания логически эквивалентны — одно можно заменить на другое без потери смысла.
В этом и заключается логическая эквивалентность — два выражения считаются эквивалентными, если они имеют одинаковое истинностное значение во всех случаях.
Как эквивалентность помогает доказывать
Основная польза эквивалентности в том, что она помогает доказывать математические результаты. Допустим, мы знаем, что . Попробуем это доказать.
Можно заменить выражение на другое эквивалентное выражение , которое также будет равно .
Как видите, значение составной пропозиции не изменилось. Значит, эквивалентность помогла нам доказать первоначальное высказывание — .
Как эквивалентность помогает рассуждать
Кроме доказательств, эквивалентность используется и в рассуждениях. Она помогает осмыслить предложение и отнести его к одной из трех категорий в таблице истинности.
Таблица истинности — это разбиение логической функции путем перечисления всех возможных значений, которые может принимать функция.
Такая таблица обычно содержит несколько строк и столбцов. В верхней строке представлены логические переменные и комбинации, которые по возрастанию сложности приводят к конечной функции.
В логической функции есть три основные операции:
НЕ (Инверсия или отрицание, обозначается как ¬)
ИЛИ (Дизъюнкция или сложение, обозначается как )
И (Конъюнкция или умножение, обозначается как )
Значениям функций обычно присваивается логический ноль (ложь) или логическая единица (истина).
Таблица истинности выглядит так:
¬ | ¬ | ¬ | |
Тавтология | Противоречие | Случайность | Случайность |
Рассмотрим ее подробнее:
Тавтология ( ) — высказывание, которое всегда истинно независимо от того, истинны ли значения переменных внутри него.
По таблице вся колонка истинна
Противоречие или абсурд ( ) — высказывание, которое всегда ложно
Случайность — составное предложение, которое не является ни тавтологией, ни противоречием.
Тавтологии и противоречия помогают доказывать и проверять математические аргументы, а также объяснить пропозициональные эквивалентности — утверждения, которые равны в логическом аргументе. В этом случае самый простой способ — создать таблицу истинности и посмотреть, идентичны столбцы.
По такой таблице мы можем проверить, эквивалентны ли высказывания a и b.
Иногда в математике полезно заменить одно утверждение другим, но эквивалентным. Возьмем такой пример:
Если четное, то — это целое число
Эквивалентное утверждение звучит так:
Если не целое число, то — это нечетное число
Первое высказывание имело вид «Если
, то
», а второе — «Если не
, то не
».
Законы логической эквивалентности (Законы Моргана)
Ниже приведен список важных законов эквивалентности — также их называют законами алгебры высказываний. На протяжение всего курса мы будем использовать такие законы:
Эквивалентность | Закон | То же, что равенство в булевой алгебре |
Законы тождества | Высказывание с определенным значением (истина или ложь) сохраняет свою первоначальную форму | |
Законы доминирования | : Если в выражении первое И ложно, то все выражение И будет ложным | |
Законы тавтологии | Высказывание принимает только истинные значения в любом случае | |
¬ ¬ | Закон двойного отрицания | Два отрицания эквивалентны отсутствию отрицания |
Законы коммутативности | Результат операции над двумя высказываниями не зависит от того, в каком порядке берутся эти высказывания |
Применим некоторые из этих законов на практике.
Возьмем для примера составное предложение:
Я обедаю в ресторане и иду на танцы
Используем законы де Моргана — они связывают с помощью отрицания конъюнкцию и дизъюнкцию. Можно выразить отрицание так:
Я не буду есть в ресторане или не пойду танцевать
Обратите внимание, что мы отрицаем оба простых предложения и заменили «и» на «или».
В качестве еще одного примера рассмотрим следующее утверждение:
Неверно, что Глеб — доктор, а Вася — инженер
Это переводится на математический язык как:
¬ доктор инженер
Эквивалентное утверждение будет иметь вид:
¬ доктор инженер ¬доктор ¬инженер
Следовательно, мы можем сказать, что Глеб — доктор, а Вася — не инженер.
Приведенные выше примеры можно легко решить с помощью таблицы истинности. Но это можно сделать только для предложения с небольшим числом переменных — здесь их всего две.
Чем больше переменных, тем менее практично использовать метод таблицы истинности.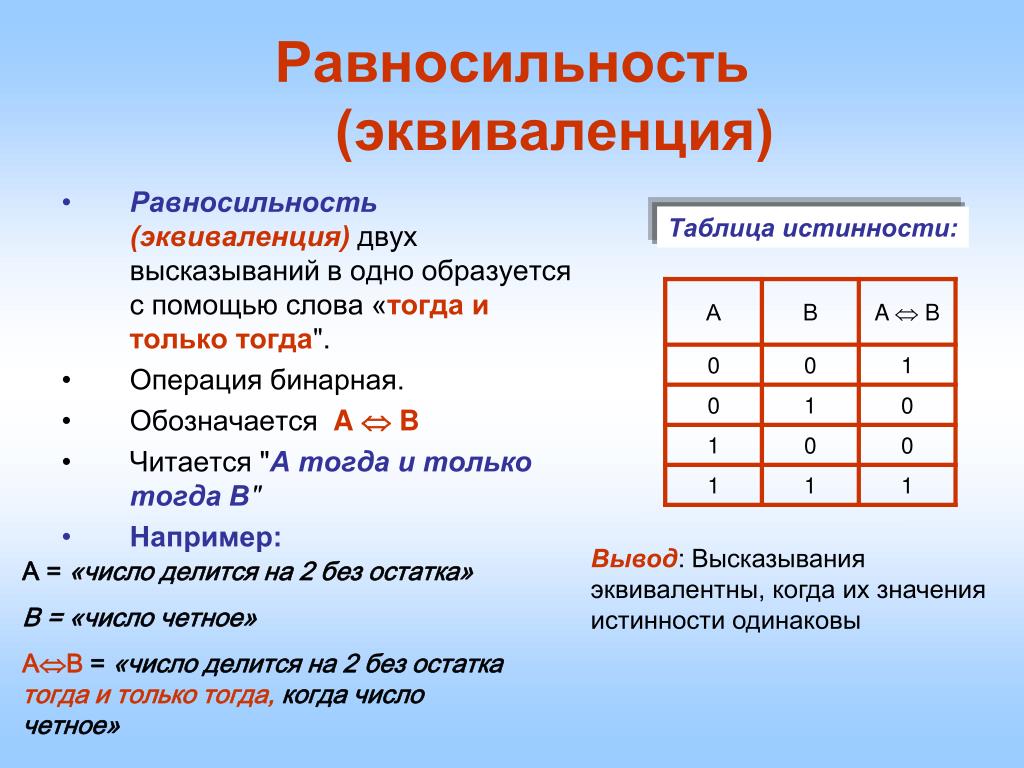
Для пропозиции с 20 переменными необходимо оценить
строк в таблице истинности. Человеку будет сложно справиться с такой задачей, но можно упростить процесс и воспользоваться компьютером.
Но если переменных будет больше 1000, вычисление на компьютере будет очень долгим.
А еще бывают случаи, когда можно не строить таблицу истинности — вместо этого можно указать причину, по которой два высказывания логически эквивалентны. При этом мы преобразуем левую часть высказывания, чтобы она соответствовала правой части, и приводим причины каждого преобразования. Как в примере выше:
Высказывание: Если четное, то — целое число
И его эквивалент: Если не целое число, то не четное
При этом преобразование справедливо для любого
Открыть доступ
Курсы программирования для новичков и опытных разработчиков. Начните обучение бесплатно
- 130 курсов, 2000+ часов теории
- 1000 практических заданий в браузере
- 360 000 студентов
Электронная почта *
Отправляя форму, вы принимаете «Соглашение об обработке персональных данных» и условия «Оферты», а также соглашаетесь с «Условиями использования»
Наши выпускники работают в компаниях:
Эквивалентность светодиодных лампочек.
Научитесь выбирать лучшее, чтобы сэкономитьНаверняка вы слышали о светодиодных лампах и их снижении потребления электроэнергии. Технологии развиваются все больше и больше, и мы должны научиться экономить как на потреблении энергии, так и на выбросах, которые мы производим в атмосфере, используя эту энергию. Это нормально быть немного дезориентированным вначале, когда мы решаем переделать лампочки в нашем доме на светодиоды. Оба Лампа накаливания поскольку низкое потребление не приводит к экономии, и мы должны хорошо знать
В этой статье мы собираемся подробно объяснить эквивалентность светодиодных ламп по сравнению с другими лампами, и мы дадим вам несколько советов, чтобы вы могли больше сэкономить на счете.
Индекс
- 1 Поменяйте старые лампочки на светодиоды
- 2 Эквивалентность светодиодных ламп обычным
- 3 Эффективность освещения
- 4 Таблица эквивалентностей
Поменяйте старые лампочки на светодиоды
Когда мы видим счет за электроэнергию в месяцы наибольшего потребления, мы бросаем руки на голову.
И дело в том, что только в освещении дома мы упускаем большую щепотку. Просто с Поменяв в доме лампочки, мы сильно сэкономим. Это правда, что поначалу они, как правило, стоят дороже, чем лампы накаливания или лампы с низким потреблением энергии. Но в этом разница в качестве.В то время как обычная лампа накаливания тратит большую часть своей энергии на тепло, Светодиоды способны работать при низких температурах. Попробуйте прикоснуться к исправной лампочке и вы увидите, насколько она холодная, а обычные у вас перегорели. Если мы хотим оптимизировать потребление энергии, необходимо изменить среду освещения в доме. Покупка всех лампочек, которые у нас есть из дома, прямо к светодиодам, поначалу может быть дорогостоящим (хотя здесь у вас есть предложения получить их дешевле). Поскольку обычные лампочки имеют более короткий срок службы, вы просто
Светодиодные лампы имеют лучшее качество и позволяют значительно экономить электроэнергию.
Это приносит нам огромную пользу, поскольку мы можем использовать эту экономию энергии для других целей. Однако когда дело доходит до замены лампочек, мы сталкиваемся с дилеммой ватт. Мы должны знать, какие светодиодные лампы эквивалентны другим.
Мощность от одной лампы к другой была изменена, и теперь мы должны знать, какая из ламп эквивалентна, чтобы снизить потребление. Было бы бесполезно менять светодиодную лампу для экономии денег, если мы покупаем ее с большей мощностью, чем необходимо.
Эквивалентность светодиодных ламп обычным
Первое и главное, что вам следует знать, это то, что светоотдача этих новых лампочек не измеряется в ваттах. Это новая мера под названием Люмены или люмен. Эта мера пытается сказать нам количество света, излучаемого лампочкой для практических целей. Чем больше люменов у лампы, тем больше света она нам дает. Это имеет большое значение по сравнению с мощностью обычных ламп на весь срок службы.
Поскольку светодиодные лампы требуют меньше энергии, им требуется меньше энергии для освещения того же пространства.
Это самые эффективные и экологичные лампы, существующие на сегодняшний день. Более того, имеет то преимущество, что не содержит загрязняющих элементов при производстве, например, ртуть или другие токсичные и радиоактивные материалы.
Экономия достигается благодаря тому, что нет необходимости генерировать плазменные мосты или нагревать ртуть, как в случае с неоном. Он просто сразу включается и не тратит лишнюю энергию.
Эквивалентность лампы не следует воспринимать всерьез. Даже зная систему измерения ватт, важно иметь в качестве ориентира, что единицы измерения не совпадают. У каждого производителя есть ряд характеристик, которые они придают продукту, которые будут различаться по количеству и качеству светового излучения. Имейте в виду, что
В случае светодиодов ватты указывают только на состояние потребления при работе лампы накаливания, но не на количество излучаемого света.
Эффективность освещения
Единица измерения люмен связана с количеством света, излучаемого лампой, и электроэнергия потребляется, что измеряется в ваттах. Еще один параметр, который учитывается при установлении эквивалентности с другими лампами, — это яркость. Около люмен на квадратный метр, излучаемый рассматриваемой лампочкой. Обычно он будет варьироваться в зависимости от высоты, на которой он установлен, и размера области, которую мы хотим осветить.
С помощью светодиодной лампы с 5 Вт, мы можем достичь такого же количества освещения, что и обычная лампа мощностью около 35-40 Вт. Таким образом, потребляемая электрическая мощность и, в конце концов, стоимость, которую мы производим, на 85% меньше, чем у обычных лампочек.
Таблица эквивалентностей
Это можно лучше представить в таблице, в которой собраны приблизительные значения различных типов лампочек, их мощность и способность к свечению. Эквивалентность можно проверить практически со всеми типами ламп, от ламп накаливания до галогенных, натриевых и т.
Д. Светодиодные лампы мощностью 7 Вт эквивалентны обычным галогенным лампам мощностью 60 Вт.
Если мы умножим эту экономию на количество лампочек, которые есть в доме, и время, в которое они включены, то экономия будет действительно эффективной. Кроме того, они не выделяют лишнего тепла (что очень ценно летом) и имеют гораздо более длительный срок службы.
Здесь мы оставляем вам таблицу со всеми наиболее важными эквивалентами, где вы можете сравнить, сколько ватт светодиодной лампы по сравнению с другими и наоборот. Таким образом, вы сможете добиться оптимального освещения в доме, сэкономив как можно больше.
Я надеюсь, что эта информация поможет вам составить самые ясные идеи по этой теме.
benzo.org.uk : Таблица эквивалентности бензодиазепинов
benzo.org.uk : Таблица эквивалентности бензодиазепинов« назад · www.benzo.org.uk »
ТАБЛИЦА ЭКВИВАЛЕНТНОСТИ БЕНЗОДИАЗЕПИНА
(Таблица эквивалентности бензодиазепинов)Пересмотрено в апреле 2007 г.
Эта таблица эквивалентности бензодиазепинов основана на обширных исследованиях и клиническом опыте профессора С. Хизер Эштон, доктора медицинских наук, FRCP, почетного профессора клинической психофармакологии в Университете Ньюкасл-апон-Тайн, Англия. Источники: Информационный бюллетень NRHA по наркотикам, 19 апреля.85 и «Бензодиазепины: как они работают и как вывести» (Руководство Эштона), 2002 г. Приведены приблизительные дозы, эквивалентные 10 мг диазепама (валиума).
Для обсуждения периодов полураспада и эквивалентности см. также документ часто задаваемых вопросов по бензо.
Бензодиазепины 1 Период полувыведения (ч) 2
[активный метаболит]Приблизительно Эквивалент
Пероральные дозы (мг) 3Рыночная цель 4 Алпразолам
(ксанакс, ксанор, тафил)6-12 0,5 и Бромазепам
(Лексотан, Лексомил)10-20 5-6 и Хлордиазепоксид
(либриум)5-30 [36-200] 25 и Клобазам
(Фризиум) 512-60 20 а,е Клоназепам
(клонопин, ривотрил) 518-50 0,5 а,е Клоразепат
(транксен)[36-200] 15 и Диазепам
(валиум)20-100 [36-200] 10 и Эстазолам
(ПроСом, Нукталон)10-24 1-2 ч Флунитразепам
(рогипнол)18-26 [36-200] 1 ч Флуразепам
(Далмане)[40-250] 15-30 ч Галазепам
(Паксипам)[30-100] 20 и Кетазолам
(Анксон)30-100 [36-200] 15-30 и Лопразолам
(Дормонокт)6-12 1-2 ч Лоразепам
(Ативан, Теместа, Тавор)10-20 1 и Лорметазепам
(ноктамид)10-12 1-2 ч Медазепам
(Нобриум)36-200 10 и Нитразепам
(Могадон)15-38 10 ч Нордазепам
(Нордаз, Калмдей)36-200 10 и Оксазепам
(Серакс, Серенид,
Серепакс, Сереста)4-15 20 и Празепам
(Centrax, Lysanxia)[36-200] 10-20 и Квазепам (Дорал) 25-100 20 ч Темазепам
(Ресторил, Нормисон,
Эугипнос)8-22 20 ч Триазолам
(Хальцион)2 0,5 ч Небензодиазепины
с аналогичным действием 1 , 6Залеплон
(Соната)2 20 ч Золпидем
(Амбиен, Стильнокт, Стильнокс)2 20 ч Зопиклон
(Зимоване, Имоване)5-6 15 ч Эзопиклон
(Люнеста)6
(9 у пожилых)3 ч
Все эти препараты рекомендуются только для краткосрочного применения (максимум 2-4 недели).
Период полувыведения: время, необходимое для снижения концентрации в крови до половины пикового значения после однократного приема. Период полувыведения активного метаболита указан в квадратных скобках. Это время может значительно различаться у разных людей.
Эти эквиваленты не совпадают с эквивалентами, используемыми некоторыми авторами. Они основаны на клиническом опыте перехода на диазепам в начале программ отмены, но могут различаться у разных людей.
Рыночная цель: Хотя все бензодиазепины имеют схожие действия, они обычно продаются как анксиолитики (а), снотворные (з) или противосудорожные средства (д).
В Великобритании клобазам (Фризиум) и клоназепам (Ривотрил) лицензированы для использования только в качестве противоэпилептических средств.
Эти препараты химически отличаются от бензодиазепинов, но оказывают такое же воздействие на организм и действуют по тем же механизмам.
Руководство Эштона · Главная страница профессора Эштона
« назад · наверх · www.benzo.org.uk »
См. Руководство 1988 года.
| | Длина | |||||||||||||
| 1 дюйм = | 2.540 | сантиметры | | 1 миллиметр = | 0,03937 | дюймы | ||||||||
| 1 фут = | 30.4878 | сантиметры | | 1 сантиметр = | 0,3937 | дюймы | ||||||||
| 1 ярд = | 0,9144028 | метров | | 1 метр = | 3. 281 | ноги | ||||||||
| 1 миля = | 1.6093419 | километр | | 1 километр = | 0,621372 | мили | ||||||||
| | Зона | |||||||||||||
| 1 кв. дюйм = | 6.4516 | кв. сантиметры | | 1 кв. сантиметр = | 0,1550 | кв. дюймы | ||||||||
| 1 кв. фут = | 0,0929 | кв метров | | 1 кв. метр = | 1.195986 | кв. ярдов | ||||||||
| 1 кв. ярд = | 0,83613 | кв метров | | 1 кв. км = | 0,386101 | кв миль | ||||||||
| 1 кв. миля = | 2,589999 | кв км | | 1 га = | 2.471044 | акры | ||||||||
| 1 акр = | 0,404687 | гектаров | | |||||||||||
| | Масса (вес) | |||||||||||||
| 1 зерно = | 0,05 сомнения = | 0,016667 драм = | 0,00208 унции | | 1 унция = | 28. 3495 | грамм | | 1 грамм = | 0,03527396 | унции | |||
| 1 фунт = 16 унций = | 0,4535924 | килограммы | | 1 килограмм = | 2.2046223 | фунтов стерлингов | ||||||||
| 1 короткая тонна = | 0,892857 | метрическая тонна | | 1 метрическая тонна = | 1.1200 | короткие тонны | | 1 длинная тонна = | 1. 01605 | метрических тонн | ||||
| | Объем | |||||||||||||
| 1 чайная ложка = | 5 | миллилитры | | 1 миллилитр = | 0,0338147 | жидкие унции | ||||||||
| 1 столовая ложка = | 15 | миллилитры | | 1 литр = | 2.11342 | пинты = | 1000 кубических сантиметров | |||||||
| 1 жидкая унция = | 30 | миллилитры | | 1 литр = | 1,05671 кварт = | 0,264178 галлона | 1 галлон = | 3. 785332 | литра = | 231 куб. дюйм | ||||
| 1 чашка = | 0,23658 | литры | | 1 пинта = | 0,473167 | литры | | 1 кубический метр = | 35.3144 | кубические футы = | 1.30794 | кубические ярды | ||
| 1 кубический фут = | 0,0283170 | кубические метры | 1 кубический ярд = | 0,764559 | кубические метры | | ||||||||
| | Температура | |||||||||||||
| по Фаренгейту | Вычтите 32, затем умножьте на 5/9. | |||||||||||||