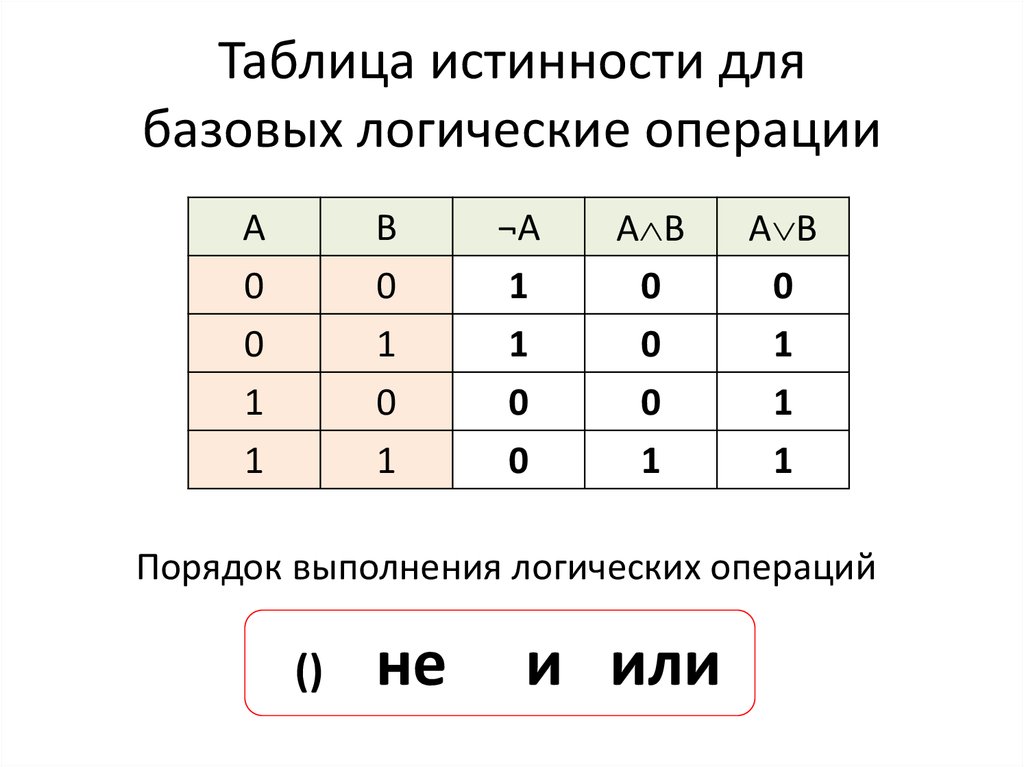
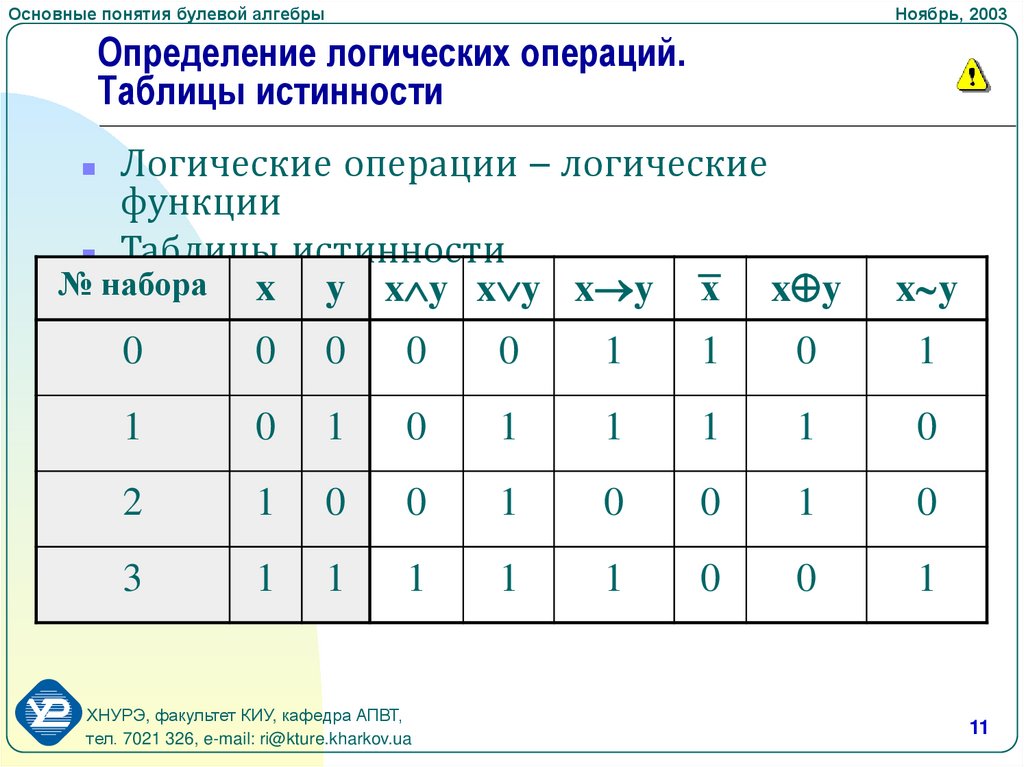
Что такое таблица истинности? Таблица, описывающая логическую функцию, называется таблицей истинности. В таблице истинности перечислены все возможные наборы входных переменных. В последнем столбце таблицы истинности выводится число, соответствующее значению функции, по которой строилась данная таблица истинности.
Рассмотрим пример: Допустим, у нас есть две булевых переменных x1 и x2. От этих переменных зависит логическая функция f(x1,x2) Для примера возьмем f(x1,x2)=x1∧x2∨x1. Так как x1, x2 булевы, то они принимают значния 0 или Все возможные варианты входных переменных x1 и x2 можно представить в таблице:
Подставим значения переменных x1 и x2 в каждой строчке в функцию f(x1,x2). f(0,0)= 0∧0∨0=0 f(0,1)= 0∧1∨0=0 f(1,0)= 1∧0∨1=1 f(1,1)= 1∧1∨1=1
Получившиеся значения запишем в последний столбец нашей таблицы:
Мы получили таблицу истинности функции f(x1,x2)=x1∧x2∨x1.
На нашем сайте вы можете построить таблицу истинности online. Для этого вам всего лишь нужно ввести функцию в поле и нажать вычислить.
Таблицы истинности основных булевых функций:
Бинарные функции
| |||||||||||||||||||||||||||||||
Построение таблиц истинности логических выражений
Похожие презентации:
Пиксельная картинка
Информационная безопасность. Методы защиты информации
Электронная цифровая подпись (ЭЦП)
Этапы доказательной медицины в работе с Pico.
Первый этап
История развития компьютерной техники
От печатной книги до интернет-книги
Краткая инструкция по CIS – 10 шагов
Информационные технологии в медицине
Информационные войны
Моя будущая профессия. Программист
Практическая работа №3
«Построение таблиц истинности
логических выражений»
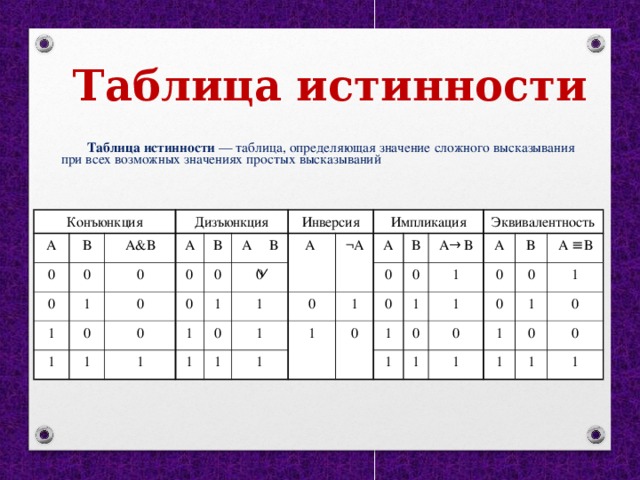
Основные логические операции
Название логической
операции
Обозначение
Инверсия
«¯»
Конъюнкция
«&»
Дизъюнкция
«V»
Логические операции
Инверсия − это логическая операция, которая преобразует исходное высказывание
в новое, значение которого противоположно исходному.
А=0
инверсия
Ā=1
А=1
инверсия
Ā=0
A
Ā
0
1
1
0
Логические операции
Конъюнкция − это логическая операция, которая объединяет два высказывания в
одно новое, которое будет являться истинным тогда и только тогда, когда оба
исходных высказывания истинны.
А−
А=1
А−
А=0
A
B
A&B
0
0
0
0
1
0
1
0
0
1
1
1
Дизъюнкция − это логическая операция, которая объединяет два высказывания в
одно новое, которое будет являться ложным тогда и только тогда, когда ложны оба
исходных высказывания.
А−
А=1
А−
А=0
A
B
AVB
0
0
0
0
1
1
1
0
1
1
1
1
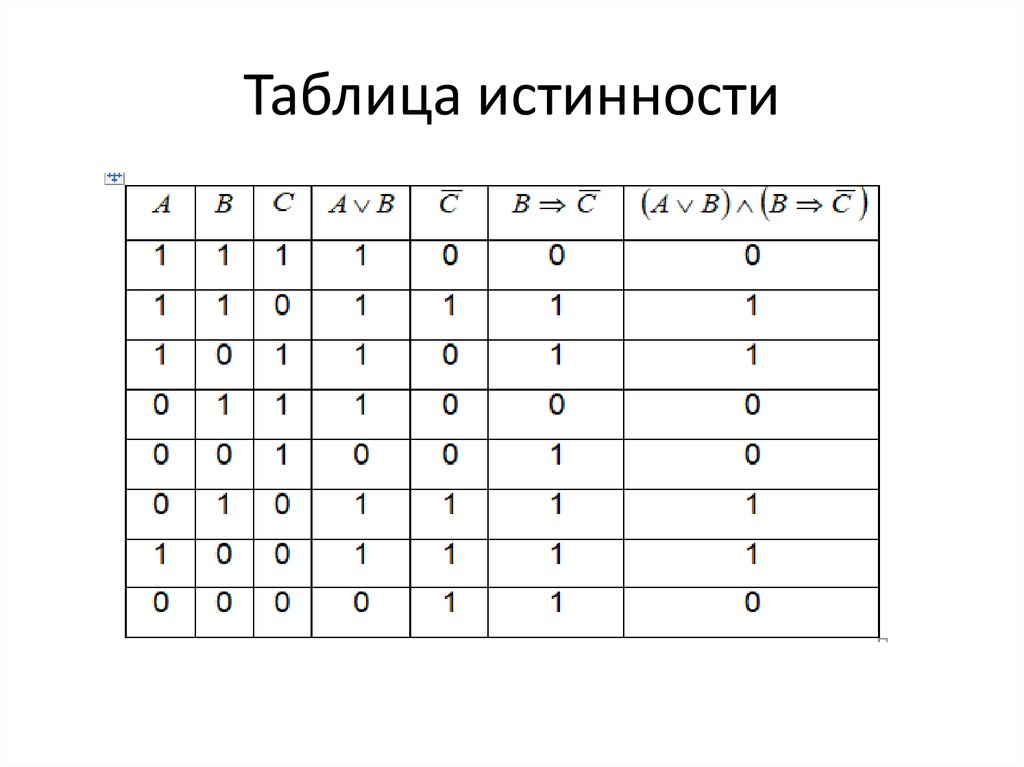
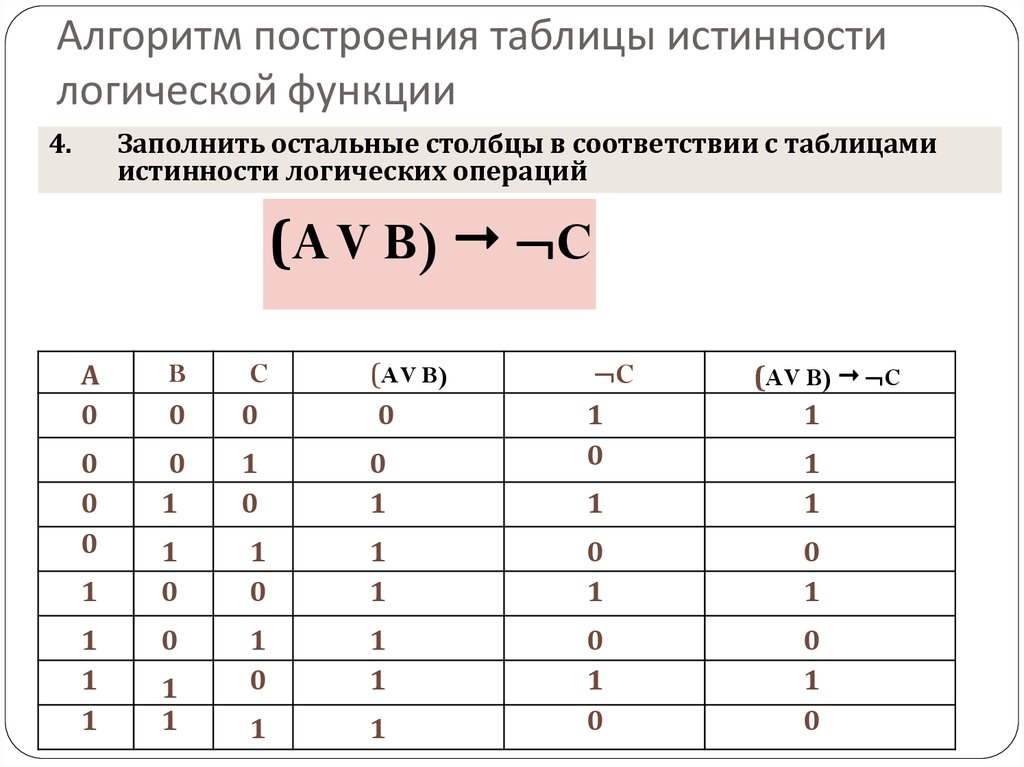
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
2.
Подсчитать общее число логических операций в
выражении.
3.
Установить последовательность логических
операций с учётом скобок и приоритетов.
4.
Определить число столбцов в таблице: число
переменных + число операций.
5.
Заполнить шапку таблицы, включив в неё
переменные и операции в соответствии с
последовательностью.
6.
Определить число строк в таблице (не считая
шапку таблицы): m = 2n.
7.
Выписать наборы входных переменных с учётом
того, что они представляют собой ряд целых nразрядных двоичных чисел от 0 до 2n — 1.
А B C
AVB
(A V B) & C
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
(А V B) & C
n=3
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
(А V B) & C
2.
Подсчитать общее число логических операций в
выражении.
Количество логических
операций: 2
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
(А V B) & C
2.
Подсчитать общее число логических операций в
выражении.
1.
Операции в скобках.
Установить последовательность логических
операций с учётом скобок и приоритетов.
2.
Инверсия.
3.
Конъюнкция.
4.
3.
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
(А V B) & C
2.
Подсчитать общее число логических операций в
выражении.
Количество столбцов: 5.
3.
Установить последовательность логических
операций с учётом скобок и приоритетов.
4.
Определить число столбцов в таблице: число
переменных + число операций.
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
2.
Подсчитать общее число логических операций в
выражении.
3.
Установить последовательность логических
операций с учётом скобок и приоритетов.
4.
Определить число столбцов в таблице: число
переменных + число операций.
5.
Заполнить шапку таблицы, включив в неё
переменные и операции в соответствии с
последовательностью.
А B C
AVB
(A V B) & C
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
2.
Подсчитать общее число логических операций в
выражении.
3.
Установить последовательность логических
операций с учётом скобок и приоритетов.
4.
Определить число столбцов в таблице: число
переменных + число операций.
5.
Заполнить шапку таблицы, включив в неё
переменные и операции в соответствии с
последовательностью.
6.
Определить число строк в таблице (не считая
шапку таблицы): m = 2n.
А B C
n=3
m = 23 = 8
AVB
(A V B) & C
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
2.
Подсчитать общее число логических операций в
выражении.
3.
Установить последовательность логических
4.
Определить число столбцов в таблице: число
переменных + число операций.
5.
Заполнить шапку таблицы, включив в неё
переменные и операции в соответствии с
последовательностью.
6.
Определить число строк в таблице (не считая
шапку таблицы): m = 2n.
А B C
AVB
(A V B) & C
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
2.
Подсчитать общее число логических операций в
выражении.
3.
Установить последовательность логических
операций с учётом скобок и приоритетов.
4.
Определить число столбцов в таблице: число
переменных + число операций.
5.
Заполнить шапку таблицы, включив в неё
переменные и операции в соответствии с
последовательностью.
6.
Определить число строк в таблице (не считая
шапку таблицы): m = 2n.
7.
Выписать наборы входных переменных с учётом
того, что они представляют собой ряд целых nразрядных двоичных чисел от 0 до 2n — 1.
А B C
AVB
(A V B) & C
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
А B C
2.
Подсчитать общее число логических операций в
выражении.
0
0
0
3.
Установить последовательность логических
операций с учётом скобок и приоритетов.
0
0
1
0
1
0
Определить число столбцов в таблице: число
переменных + число операций.
0
1
1
1
0
0
Заполнить шапку таблицы, включив в неё
переменные и операции в соответствии с
последовательностью.
1
0
1
1
1
0
6.
Определить число строк в таблице (не считая
шапку таблицы): m = 2n.
1
1
1
7.
Выписать наборы входных переменных с учётом
того, что они представляют собой ряд целых nразрядных двоичных чисел от 0 до 2n — 1.
4.
5.
AVB
(A V B) & C
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
А B C
2.
Подсчитать общее число логических операций в
выражении.
0
0
0
3.
Установить последовательность логических
операций с учётом скобок и приоритетов.
0
0
1
0
1
0
Определить число столбцов в таблице: число
переменных + число операций.
0
1
1
1
0
0
Заполнить шапку таблицы, включив в неё
переменные и операции в соответствии с
последовательностью.
1
0
1
1
1
0
6.
Определить число строк в таблице (не считая
шапку таблицы): m = 2n.
1
1
1
7.
Выписать наборы входных переменных с учётом
того, что они представляют собой ряд целых nразрядных двоичных чисел от 0 до 2n — 1.
4.
5.
8.
AVB
(A V B) & C
Провести заполнение
таблицы по столбцам.
План построения таблицы истинности
1.
Посчитать n – число переменных в выражении.
А B C
2.
Подсчитать общее число логических операций в
выражении.
0
0
3.
Установить последовательность логических
операций с учётом скобок и приоритетов.
0
AVB
(A V B) & C
0
0
0
0
1
0
0
0
1
0
1
0
Определить число столбцов в таблице: число
переменных + число операций.
0
1
1
1
1
1
0
0
1
0
Заполнить шапку таблицы, включив в неё
переменные и операции в соответствии с
последовательностью.
1
0
1
1
1
1
1
0
1
0
6.
Определить число строк в таблице (не считая
шапку таблицы): m = 2n.
1
1
1
1
1
7.
Выписать наборы входных переменных с учётом
того, что они представляют собой ряд целых nразрядных двоичных чисел от 0 до 2n — 1.
4.
5.
8.
Провести заполнение
таблицы по столбцам.
Задание. Составить таблицу истинности следующих выражений:
1.
2.
3.
4.
5.
(неA)&B
A v B&C
(неА) v B&(неC)
(неА) & B&C
Не(неА V не(В&С))
на оценку «3»
на оценку «4»
на оценку «5»
English Русский Правила
Что делает утверждение последовательным или непоследовательным?
FutureLearn использует куки-файлы для повышения удобства использования веб-сайта. Все файлы cookie, кроме строго необходимых, в настоящее время отключены для этого браузера. Включите JavaScript, чтобы применить настройки файлов cookie для всех необязательных файлов cookie. Вы можете ознакомиться с политикой FutureLearn в отношении файлов cookie здесь.
Определение того, когда наборы утверждений согласуются, а когда они противоречивы, важно для выработки того, чему верить
© University of York
Набор утверждений является непротиворечивым тогда и только тогда, когда все утверждения в наборе могут быть истинными вместе.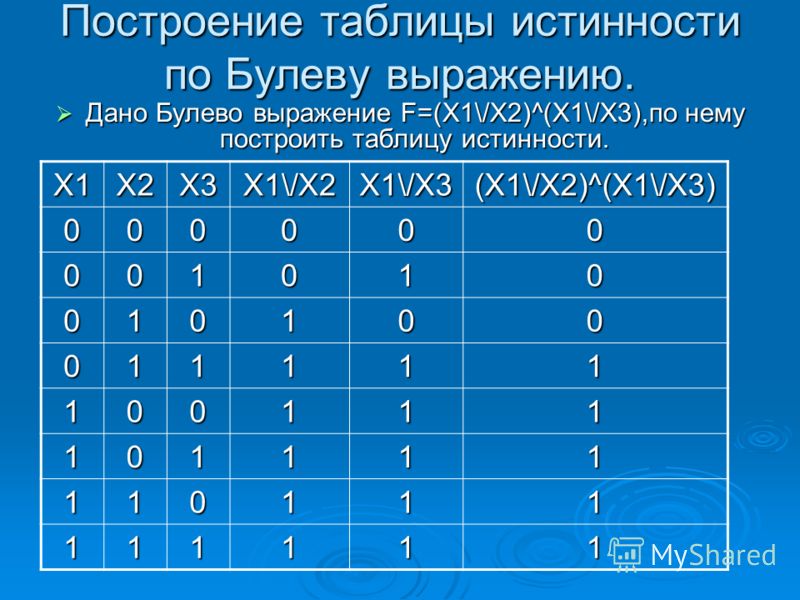
Набор утверждений является несовместимым тогда и только тогда, когда невозможно, чтобы все утверждения в наборе были истинными вместе.
Определение того, когда наборы утверждений непротиворечивы, а когда они непротиворечивы, очевидно, важно для выработки того, во что верить. Если мы обнаружим, что некоторые из утверждений, которые мы считаем, несостоятельны, тогда что-то должно дать сбой.
Не имеет смысла верить им всем, потому что они никак не могут быть правдой. Мы, по крайней мере, хотим, чтобы вещи, в которые мы верим, были последовательными.
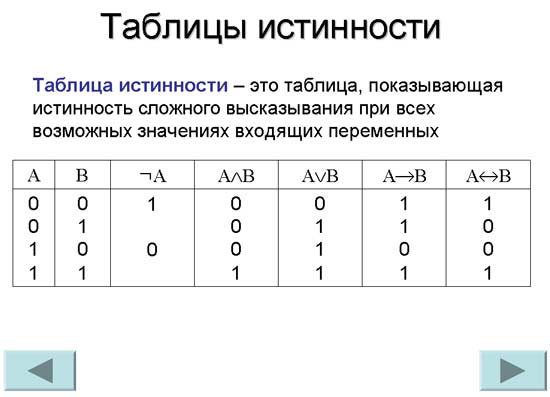
Таблицы истинности
Мы можем проверить непротиворечивость и непротиворечивость на основе пропозициональной логической формы (непротиворечивый/непротиворечивый PL), используя таблицы истинности. Мы строим таблицу истинности для предложений в наборе, а затем проверяем, существует ли хотя бы одна строка , в которой все предложения истинны. Если есть, набор является PL-непротиворечивым; если нет, это несовместимо с PL.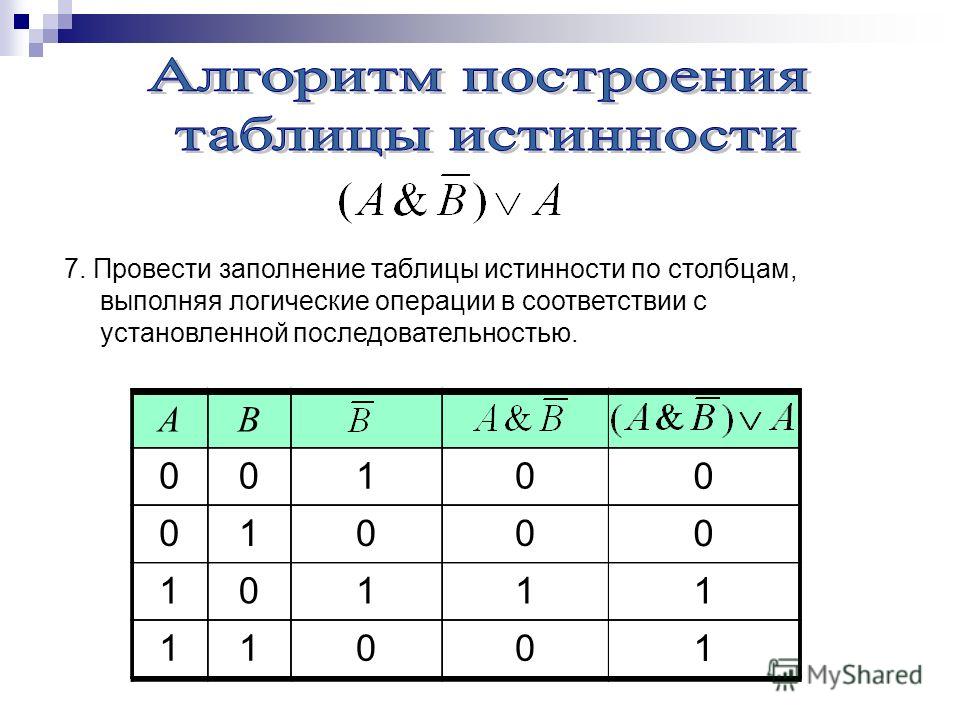
Посмотрите на таблицу истинности для предложений ‘(P ⋁ ~Q)’ и ‘(~P ⋁ Q)’ ниже:
Рисунок 1. Пример таблицы истинности, показывающей непротиворечивостьПредложения являются PL непротиворечивыми . Существует по крайней мере одна строка, в которой они оба верны. На самом деле, их два: они оба истинны, когда оба «P» и «Q» истинны (первая строка), и они также оба истинны, когда оба «P» и «Q» ложны (последний ряд). .
Теперь посмотрим на таблицу истинности предложений ‘~(P ⋁ Q)’, ‘~P’, ‘Q’:
Рисунок 2. Пример таблицы истинности, показывающей несоответствиеОтсюда видно, что эти три предложения (PL) несовместимы . Нет строки, в которой (нет возможной ситуации в какой) все три предложения верны.
© Йоркский университет
Эта статья из бесплатного онлайн-ресурса
Логика: язык истины
Создано
Присоединяйся сейчас
Наша цель — изменить доступ к образованию.
Мы предлагаем широкий выбор курсов от ведущих университетов и учреждений культуры со всего мира. Они предоставляются поэтапно и доступны на мобильных устройствах, планшетах и компьютерах, поэтому вы можете приспособить обучение к своей жизни.
Мы считаем, что обучение должно быть приятным, социальным опытом, поэтому наши курсы дают возможность обсудить то, что вы изучаете, с другими, помогая вам делать новые открытия и формировать новые идеи.
Вы можете разблокировать новые возможности с неограниченным доступом к сотням коротких онлайн-курсов в течение года, подписавшись на наш безлимитный пакет. Развивайте свои знания в ведущих университетах и организациях.
Узнайте больше о том, как FutureLearn меняет доступ к образованию
Представляем таблицы истинности
FutureLearn использует куки-файлы для повышения удобства пользования веб-сайтом. Все файлы cookie, кроме строго необходимых, в настоящее время отключены для этого браузера.
Включите JavaScript, чтобы применить настройки файлов cookie для всех необязательных файлов cookie. Вы можете ознакомиться с политикой FutureLearn в отношении файлов cookie здесь.
На этом шаге мы увидим, как составить таблицу истинности и использовать ее для определения значения и логических возможностей связного предложения.
© University of York
Есть способ обойти проблему, которую мы только что отметили. Есть изящный прием, который позволит нам зафиксировать определение значения и логической силы «&» без использования «и» — прием, который также окажется полезным во многих других отношениях. Мы можем выразить наше определение значения и логических возможностей «&», используя таблица истинности .
Обратите внимание, что наша попытка определить значение ‘&’ в ясном смысле касается истины: то, что мы сказали о его значении, относится к условиям истинности предложений и придаточных предложений, которые построен с его помощью.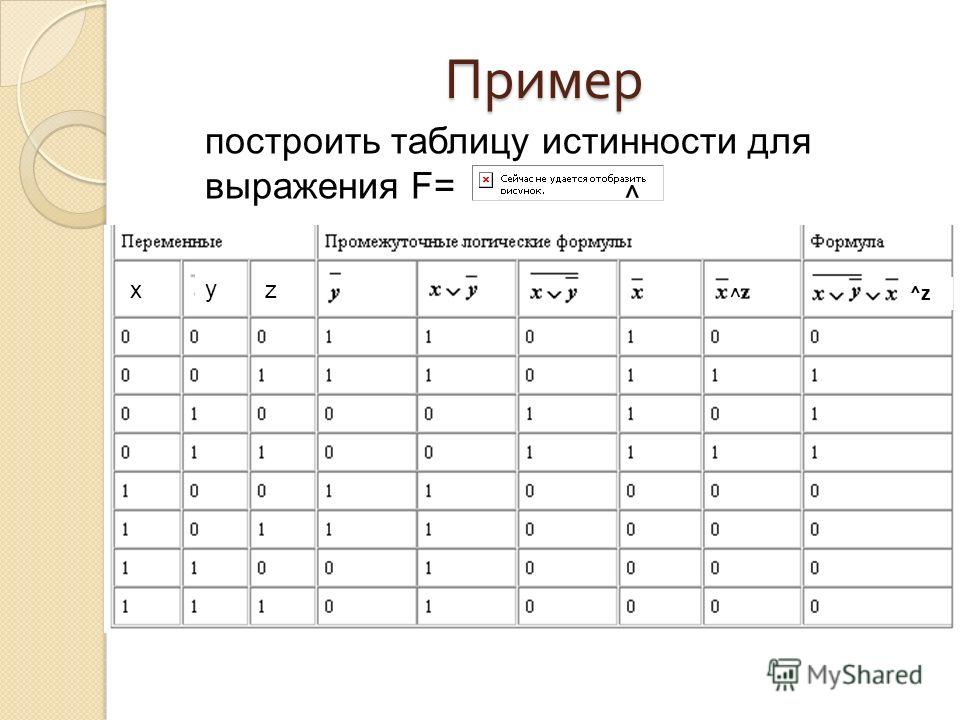
Что мы пытались сделать, так это указать, как истинность или ложность предложения с амперсандом фиксируется значениями истинности вставленных предложений. Мы можем сделать это чисто и успешно, используя таблицу следующим образом.
Амперсанд — двуместная связка: нам нужно вставить в нее два предложения, чтобы получилось новое предложение. Теперь подумайте о том, как могут обстоять дела с истинностными значениями двух предложений.
Если у нас есть только одно предложение — скажем, «П», — то оно будет либо истинным, либо ложным. (Здесь, как и везде, мы будем использовать заглавные латинские буквы в качестве заменителей или сокращений отдельных предложений.) Но теперь предположим, что мы возьмем другое предложение — «Q». В случаях, когда «P» верно, ситуации делятся на два типа: ситуации, в которых «Q» также верно, и ситуации, в которых «Q» ложно. Мы можем выразить это в виде таблицы:
| Р | Q | |
|---|---|---|
| Т | Т | |
| Т | Ф |
Каждая строка таблицы соответствует определенной ситуации.
Первая строка соответствует таким ситуациям: «P» — правда; «К», правда. Вторая строка для таких ситуаций: «P», правда; «К», ложь.
Но, конечно, мы также должны учитывать ситуации, в которых «P» ложно. И они также будут делиться на ситуации, в которых «Q» верно, и ситуации, в которых «Q» ложно. Это дает нам следующее:
| Р | Q | |
|---|---|---|
| Т | Т | |
| Т | Ф | |
| Ф | Т | |
| Ф | Ф |
Обратите внимание, что это дает нам все способы, которыми могут обстоять дела с истинностными значениями наших двух предложений: «P», «Q». Любая ситуация подпадает под один из этих четырех видов.
Следующий шаг показывает, как мы можем использовать подобную таблицу, чтобы указать значение связки, такой как амперсанд. (Примечание: в видео, которое открывает шаг, используется термин « основное предложение ».