Таблица координатных прямых: Координатная прямая (числовая прямая), координатный луч

Координатная прямая (числовая прямая), координатный луч

Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.

Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.

Координатный луч

Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.

Определение 1

Луч — это геометрическая фигура, которая имеет начало отсчета координатного луча и направление движения. Прямую обычно изображают горизонтально, указывая направление направо.

На примере мы видим, что O является началом луча.

Пример 1

Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.  

Пример 2

Определение 2

Единичный отрезок — это расстояние от 0 до точки, выбранной для измерения.

Пример 3

От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку. 

Благодаря манипуляциям, которые мы проделали с лучом, он стал координатным. Подпишите штрихи натуральными числами в последовательности от 1 — например, 2, 3, 4, 5… 

Пример 4

Определение 3

Координатный луч – это шкала, которая может длиться до бесконечности.

Зачастую его изображают лучом с началом в точке O, и откладывают единственный единичный отрезок. Пример указан на рисунке.

Пример 5

 Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.

Пример 6

Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.

Координатная прямая

Принцип изображения координатной прямой практически не отличается от изображения луча.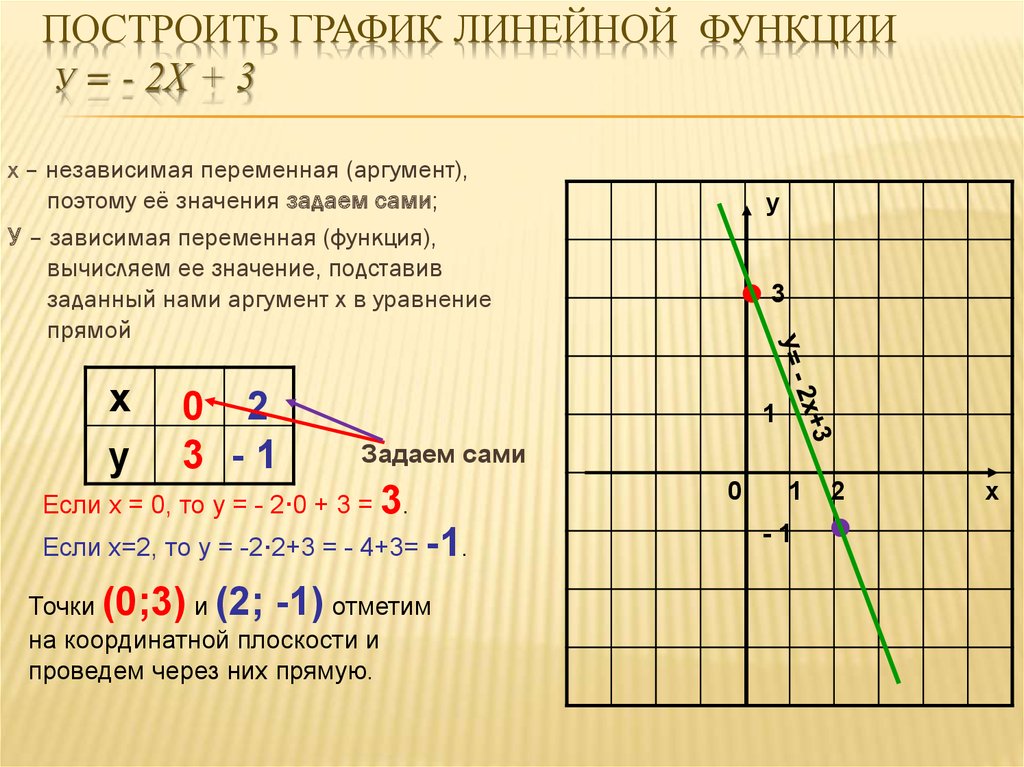 Все просто — прочертите луч и дополните до прямой, придав положительное направление, которое указывается стрелочкой.

Пример 7

Проведите луч в противоположную сторону, дополнив его до прямой 

Пример 8

Отложите единичные отрезки по примеру, указанному выше

С левой стороны запишите натуральные числа 1, 2, 3, 4, 5… с противоположным знаком. Обратите внимание на пример.

Пример 9

Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.

Пример 10

Определение 4

Координатная прямая – это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Соответствие между точками координатной прямой и действительными числами

Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.

Определение 5

Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.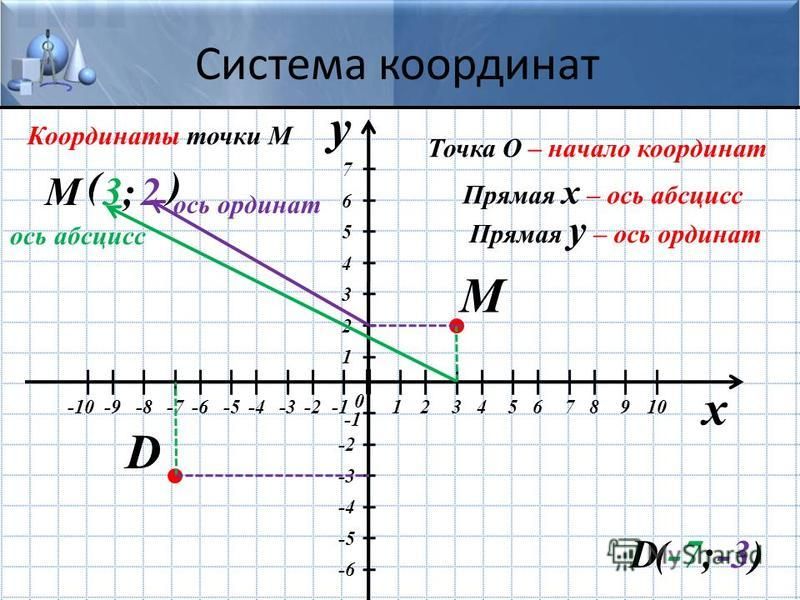

Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.

Пример 11

Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.

Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.

Отмеченные отрезки помогут нам отыскать на координатной прямой необходимую точку. Это могут быть как целые, так и дробные числа.

Однако на прямой существуют точки, которые очень сложно найти с помощью единичных отрезков. Этим точкам соответствуют десятичные дроби. Для того, чтобы искать подобную точку, придётся откладывать единичный отрезок, десятую, сотую, тысячную, десятитысячную и другие его доли. Одной точке координатной прямой отвечает иррациональное число π(=3,141592…).

Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.

Определение 6

Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.

Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении.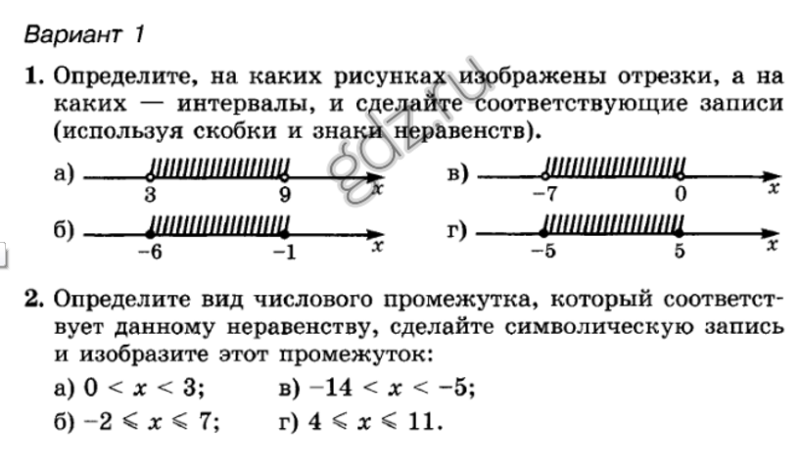

Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.

Согласно правилу,

Определение 7

Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.

Благодаря этому утверждению координатную прямую зачастую определяют как числовую.

Следует отметить, что знак, стоящий перед числом, зависит от размещения точки на прямой. Точкам, лежащим правее начала отсчета, соответствуют положительные числа, а точкам, лежащим левее, — отрицательные.

Координаты точек на координатной прямой

Определение 8

Число, соответствующее точке на координатной прямой, называется координатой этой точки.

Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.

Перед тем, как завершить статью, следует упомянуть о принятых обозначениях координаты точки. Координату принято записывать в круглых скобках справа от буквы, которой обозначена точка. Например, если точка M имеет координату – 6, то можно записать как M(-6) , а запись вида M(53+7) значит, что координатой является 53+7

Координатная прямая — что это, определение и ответ

Координатная прямая – это прямая, имеющая направление, начало отсчета и заданный масштаб.

Начало координат соответствует координате \(= 0\), а положительное направление указано стрелочкой.

Единичный отрезок – это расстояние между соседними делениями на координатной прямой. Единичный отрезок показывает масштаб координатной прямой.

ТОЧКА НА КООРДИНАТНОЙ ПРЯМОЙ:

1. Любая точка, соответствующая числу на координатной прямой, имеет координату, равную этому числу.

Например:

Точка А соответствует числу 2. В таком случае говорят, что существует точка А с координатой 2 или записывают её как А(2). Если точка не обозначается буквой, можно сказать, что существует точка 2.

2. На координатной прямой можно отмечать не только целые числа, но и дробные.

Например:

Теперь координата точки В\(\left( — \frac{3}{4} \right)\) дробная и отрицательная:

С помощью координатной прямой удобно сравнивать числа. Любое число справа будет больше, чем число слева.

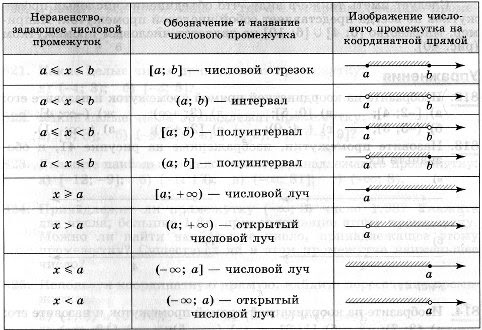
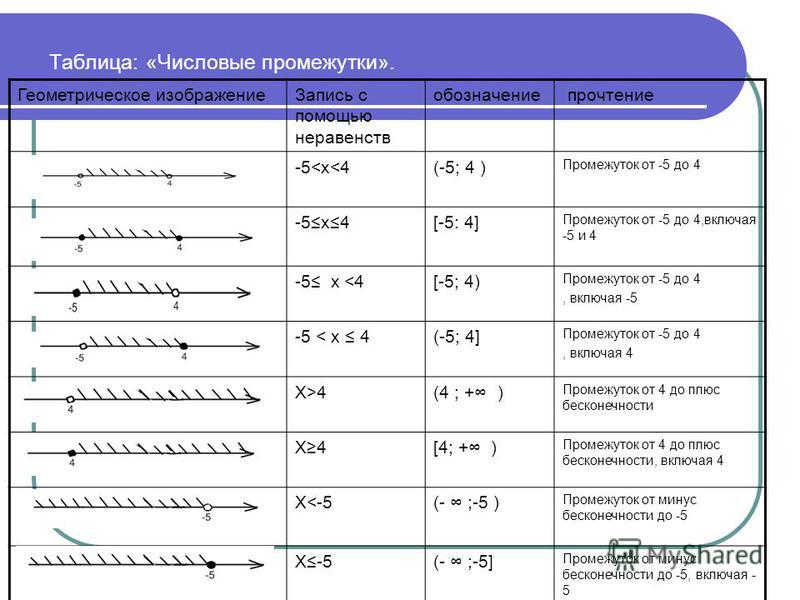
ПРОМЕЖУТКИ НА КООРДИНАТНОЙ ПРЯМОЙ:

На координатной прямой можно отмечать сразу совокупность точек, входящие в тот или иной промежуток.

Числовой промежуток – это множества чисел, обозначенные на координатной прямой с помощью луча, интервала или отрезка.

Луч – это открытый числовой промежуток с помощью которого обозначается множество чисел больше или меньше какого-то числа.

Например:

Отметим на координатной прямой все значения \(x > 2\):

Само число 2 не может быть больше себя же, поэтому точка, которой отмечается эта координата остается пустой или выколотой. Такой точке соответствует круглая скобка.

Таким образом любое число на закрашенной области соответствует заданному неравенству, а обозначить его можно как

\(x \in (2; + \infty)\)

Закрытый луч – это луч на координатной прямой, точка начала которого входит в заданный промежуток

Например:

Отметим на координатной прямой все значения \(x \leq 2\):

Число 2 равно самому себе, поэтому точка 2 входит в заданный промежуток. Такая точка закрашивается и называется вколотой. Такой точке соответствует квадратная скобка. Промежуток обозначается как

\(x \in (–\infty;\left. \ 2 \right\rbrack\).

Отрезок – числовой промежуток, который имеют ограничения с двух сторон, при этом точки, ограничивающие отрезок, в него входят.

Например:

Отметим на координатной прямой все значения \(- 3 \leq x \leq 1\):

Точки -3 и 1 входят в этот промежуток и являются вколотыми. Все числа, обозначенные на координатной прямой, удовлетворяют неравенству. Такой промежуток обозначается как

\(x \in \left\lbrack — 3;1 \right\rbrack\)

Интервал – числовой промежуток, который имеют ограничения с двух сторон. Разница с отрезком заключается в том, что граничные точки НЕ входят в интервал. В интервал входит все, что между этими точками.

Например:

Отметим на координатной прямой все значения \(- 3 < x < 1\):

Поменялись только точки, но описывается уже совсем другая математическая ситуация.

\(x \in ( — 3;1)\)

Полуинтервал – числовой промежуток, одна граница которого в него входит, а вторая нет. При чем не важно с какой стороны находится пустая точка.

Например:

Отметим на координатной прямой все значения \(0 < x \leq 2\):

Точки такого полуинтервала будут вколоты и выколоты в соответствии с условием: 0 не входит в полуинтервал – точка выколота, 2 – входит в интервал – точка вколота.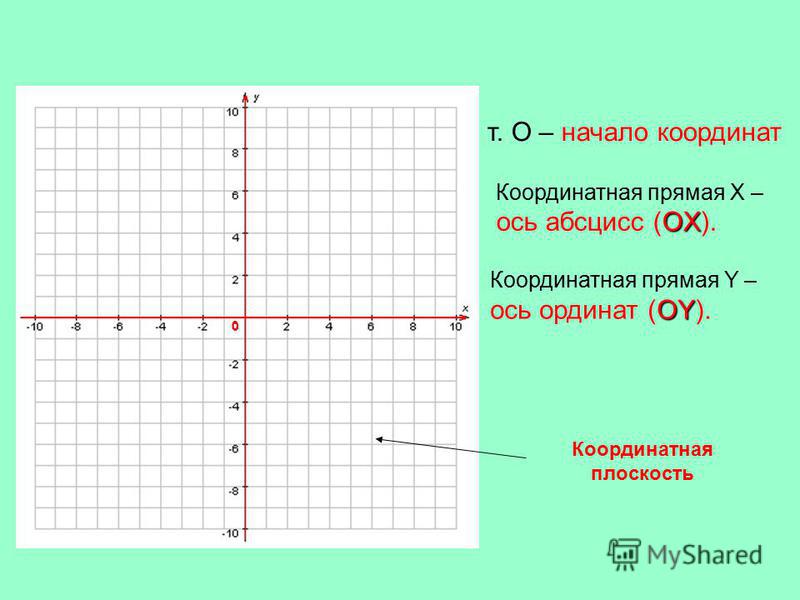 Тогда полуинтервал записывается так:

\(x \in (0;\left. \ 2 \right\rbrack\)

Координатная таблица по 2-точечной линии (защита)—ArcGIS Pro

В этом разделе

1. Сводка
2. Использование
3. Параметры
4. Окружающая среда
5. Информация о лицензировании

   5

   Сводка

   Создает двухточечные линейные объекты из координат, хранящихся в таблице.

   Параметры

   Метка	Объяснение	Тип данных
   Таблица ввода	Таблица, содержащая исходные координаты.	Табличное представление
   Класс выходных линий	Класс пространственных объектов, содержащий выходные линейные объекты.	Класс объектов
   Начальное поле X (долгота, UTM, MGRS, USNG, GARS, GEOREF)	Поле в таблице ввода, содержащее начальный x или координаты долготы.	Поле
   Конец X Поле (долгота, UTM, MGRS, USNG, GARS, GEOREF)	Поле в таблице ввода, содержащее конечные координаты x или долготы.	Поле
   Формат ввода координат	Задает формат координат точки. Десятичные градусы — одно поле — координаты будут отформатированы в виде пары координат в десятичных градусах, хранящихся в одном поле с координатами, разделенными пробелом, запятой или косой чертой. Десятичные градусы — два поля — координаты будут отформатированы в паре координат в десятичных градусах, сохраненной в двух полях таблицы. Это значение по умолчанию. Градусы и десятичные минуты — одно поле — координаты будут отформатированы в виде пар координат в градусах и десятичных минутах, хранящихся в одном поле таблицы с координатами, разделенными пробелом, запятой или косой чертой. Градусы и десятичные минуты — два поля — координаты будут отформатированы в паре координат градусов и десятичных минут, сохраненной в двух полях таблицы. Градусы, минуты и секунды — одно поле — координаты будут отформатированы в виде пар координат в градусах, минутах и ​​секундах, хранящихся в одном поле таблицы с координатами, разделенными пробелом, запятой или косой чертой. Градусы, минуты и секунды — два поля — координаты будут отформатированы в виде пар координат в градусах, минутах и ​​секундах, хранящихся в двух полях таблицы. Система отсчета глобальной области — координаты будут отформатированы в системе отсчета глобальной области. Всемирная географическая справочная система — координаты будут отформатированы в Мировой географической справочной системе. Универсальные поперечные каналы Меркатора — координаты будут отформатированы в универсальных поперечных каналах Меркатора. Универсальные поперечные зоны Меркатора — координаты будут отформатированы в универсальных поперечных координатных зонах Меркатора. Национальная сетка США — координаты будут отформатированы в национальной сетке США. Система отсчета военной сетки — координаты будут отформатированы в системе отсчета военной сетки.	Строка
   Начальное поле Y (широта) (Необязательно)	Поле в таблице ввода, содержащее начальные координаты y или широты. Параметр Начальное поле Y (широта) используется, когда для параметра Формат входных координат установлено значение Десятичные градусы — два поля, градусы и десятичные минуты — два поля или градусы, минуты и секунды — два поля.	Поле
   Конец Y Поле (широта) (Необязательно)	Поле в таблице ввода, содержащее конечные координаты y или широты. Параметр Конечное поле Y (широта) используется, когда параметр Входной формат координат имеет значение Десятичные градусы — два поля, градусы и десятичные минуты — два поля или градусы, минуты и секунды — два поля.	Поле
   Тип строки (дополнительно)	Указывает тип выходной строки. Геодезическая линия — будет использоваться кратчайшее расстояние между любыми двумя точками на сфероидальной поверхности Земли (эллипсоид). Это значение по умолчанию. Линия большого круга — будет использоваться линия на сфероиде (эллипсоиде), определяемая пересечением плоскости, проходящей через центр сфероида. Линия румба — будет использоваться линия постоянного пеленга или азимута. Нормальное сечение — будет использоваться нормальная плоскость к эллипсоидальной поверхности Земли, содержащая начальную и конечную точки.	Строка
   Выходная система координат (Необязательно)	Пространственная привязка выходного класса объектов. По умолчанию используется GCS_WGS_1984.	Пространственная привязка

    arcpy.defense.CoordinateTableTo2PointLine(in_table, out_feature_class, start_x_or_lon_field, end_x_or_lon_field, in_coordinate_format, {start_y_or_lat_field}, {end_y_or_lat_field_}system}, {end_y_or_lat_field_}system}, {end_y_or_lat_field_}system},0191 
    
    
    
    Имя 
    
    Объяснение 
    
    Тип данных 
    
    
    
    
    
    in_table 
    
    
    
    Таблица, содержащая исходные координаты.  
    
    
    Табличное представление 
    
    
    
    
    out_feature_class 
    
    
   
    
    Класс пространственных объектов, содержащий выходные линейные объекты. 
    
    
    Класс объектов 
    
    
    
    
    start_x_or_lon_field 
    
    
    
    Поле во входной таблице, содержащее начальный x или координаты долготы. 
    
    
    Поле 
    
    
    
    
    end_x_or_lon_field 
    
    
   
    
    Поле в таблице ввода, содержащее конечные координаты x или долготы. 
    
    
    Поле 
    
    
    
    
    in_coordinate_format 
    
    
    
    Задает формат координат точки.  
    
    
    DD_1 — координаты будут отформатированы в виде пары координат в десятичных градусах, хранящихся в одном поле с координатами, разделенными пробелом, запятой или косой чертой. 
    
    DD_2 — координаты будут отформатированы в паре координат в десятичных градусах, хранящихся в двух полях таблицы. Это значение по умолчанию. 
    
    DDM_1 — координаты будут отформатированы в виде пар координат в градусах и десятичных минутах, хранящихся в одном поле таблицы с координатами, разделенными пробелом, запятой или косой чертой. 
    
    DDM_2 — координаты будут отформатированы в паре координат градусов и десятичных минут, хранящихся в двух полях таблицы. 
    
    DMS_1 — координаты будут отформатированы в виде пар координат в градусах, минутах и ​​секундах, хранящихся в одном поле таблицы с координатами, разделенными пробелом, запятой или косой чертой. 
    
    DMS_2 — координаты будут отформатированы в паре координат градусов, минут и секунд, сохраненной в двух полях таблицы.  
    
    GARS — координаты будут отформатированы в глобальной системе координат. 
    
    GEOREF— Координаты будут отформатированы в World Geographic Reference System. 
    
    UTM_BANDS — координаты будут отформатированы в универсальных поперечных координатах Меркатора. 
    
    UTM_ZONES — координаты будут отформатированы в универсальных поперечных координатных зонах Меркатора. 
    
    USNG — координаты будут отформатированы в национальной системе координат США. 
    
    MGRS — координаты будут отформатированы в военной системе координат. 
    
    
    
    Строка 
    
    
    
    
    start_y_or_lat_field 
    
    (Необязательно) 
    
    
    
    Поле во входной таблице, содержащее начальные координаты y или широты.  
    
    Параметр start_y_or_lat_field используется, когда параметр in_coordinate_format имеет значение DD_2, DDM_2 или DMS_2. 
    
    
    Поле 
    
    
    
    
    end_y_or_lat_field 
    
    (Необязательно) 
    
    
    
    Поле во входной таблице, содержащее конечные координаты y или широты. 
    
    Параметр end_y_or_lat_field используется, когда параметр in_coordinate_format имеет значение DD_2, DDM_2 или DMS_2. 
    
    
    Поле 
    
    
    
    
    line_type 
    
    (Необязательно) 
    
    
    
    Указывает тип выходной строки. 
    
    
    GEODESIC — будет использоваться кратчайшее расстояние между любыми двумя точками на сфероидальной поверхности Земли (эллипсоид). Это значение по умолчанию.  
    
    GREAT_CIRCLE — будет использоваться линия на сфероиде (эллипсоиде), определяемая пересечением плоскости, проходящей через центр сфероида. 
    
    RHUMB_LINE — будет использоваться линия постоянного направления или азимута. 
    
    NORMAL_SECTION — будет использоваться нормальная плоскость к эллипсоидальной поверхности земли, содержащая начальную и конечную точки. 
    
    
    
    Строка 
    
    
    
    
    система координат 
    
    (Необязательно) 
    
    
    
    Пространственная привязка выходного класса пространственных объектов. По умолчанию используется GCS_WGS_1984. 
    
    
    Пространственная привязка 
    
    
     
    Пример кода 
     CoordinateTableTo2PointLine пример 1 (окно Python)
    
    Следующий оконный сценарий Python демонстрирует, как использовать функцию CoordinateTableTo2PointLine.  
    
    импорт аркпи
   arcpy.env.workspace = r"C:/Data.gdb"
   arcpy.CoordinateTableTo2PointLine_defense(r"C:/CSV/Tableto2PointLine.csv",
                                             "Выходные линии", "POINT_X", "POINT_X2",
                                             "DD_2", "POINT_Y", "POINT_Y2") 
   CoordinateTableTo2PointLine, пример 2 (автономный скрипт)
    Создайте линейные объекты из таблицы и уплотните линии.
    # Описание: Уплотнение линейных объектов, созданных из табличных данных
   # Импорт системных модулей
   импортировать аркпи
   # Установить параметры среды
   arcpy.env.workspace = "C:/Data.gdb"
   arcpy.env.overwriteOutput = Истина
   # Создаем линии
   input_table = r"C:/CSV/TableTo2PointLine.csv"
   result_line = "Таблица в 2 точки"
   arcpy.CoordinateTableTo2PointLine_defense (входная_таблица, результирующая_строка, "POINT_X",
                                             "POINT_X2", "DD_2", "POINT_Y",
                                             "POINT_Y2")
   # Уплотнение линий
   arcpy.Densify_edit(result_line, "DISTANCE", "2 километра") 
    Environments 
    Output Coordinate System, Geographic Transformations, Current Workspace, Scratch Workspace
    Licensing information 
    Basic: Yes
    Standard: Yes
    Advanced: Yes
    Related topics 
    Отзыв по этой теме?
    Математика, Графики с упорядоченными парами (координатами), Урок 2 
    Расмус - Математика, Графики с упорядоченными парами (координатами), Урок 2    
    
      2004 Расмус Эхф  
     Заказываемые пары 
    
     
    Печать
    Графики с упорядоченными парами
   (координаты)
     Урок 2. 
     Линейные уравнения 
    Уравнения, имеющие форму y = ax + b , где a и
   б являются
   известные значения, называются линейными уравнениями, потому что их координаты лежат на прямой линии. Не менее 2 точек
   нужны для рисования линии. Это хорошая идея, чтобы построить
   не менее 3 баллов при построении графика линейного уравнения.
    Таблица значений: если у вас есть линейное уравнение с двумя переменными, вы можете составить таблицу значений. Вот пример
   линейное уравнение:  y = x + 1 Соотношение
   между переменными должны оставаться одинаковыми, но вы можете выбрать значения для x
   и вычислить соответствующие значения
   для тебя  .
     Таблица значений для
   у = х + 1 
      
    
    Примечание. Вы можете решить, сколько
   значения, которые вы хотите рассчитать. Но помните, что вы всегда должны находить значения
   минимум на 3 балла. Если 3 точки не лежат на прямой, вы
   ошиблись в своих расчетах.
      График для уравнения: y
   = х + 1  
    Стрелка
   отмечает точку (3,4), которая является одной из
   координаты найдены в таблице значений. Другая точка - (0,1), которая является точкой
   где линия пересекает ось Y. Когда вы нанесете 2 точки на сетку, вы
   можно соединить их, чтобы нарисовать график линейного уравнения.
     Параболы 
    Уравнение, имеющее вид  
    где а и
   б являются
   известных значений, представляет собой уравнение параболы.
    Вам нужно несколько точек, чтобы нарисовать
   график параболы.
     Пример. Вам предоставляется
   уравнение
    Вычислить несколько значений y
   для x от -5 до + 5.
    Составьте таблицу значений (см. выше).
     Таблица значений для 
      
    Обратите внимание, что некоторые значения y
   повторил.
   No related posts.