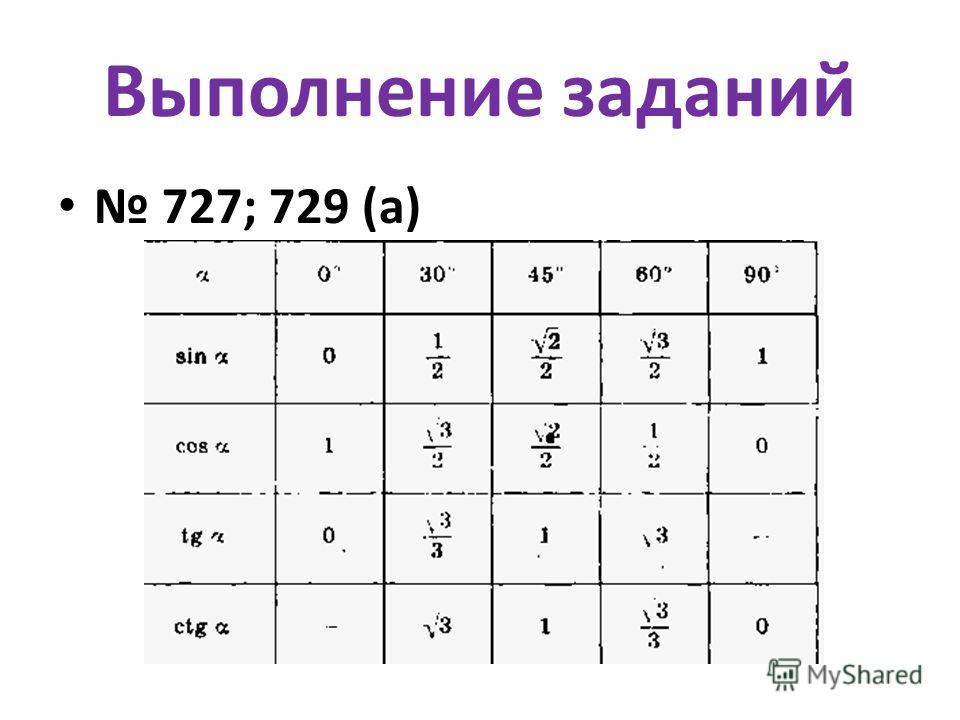
Как определить значения синуса, косинуса, тангенса и котангенса
Определение значения синуса, косинуса, тангенса и котангенса
Определение
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
Процесс работы и расчета функций данного вида, очень непростой. Решение задач и уравнение, очень часто вызывают сложности. Поэтому, со временем, были созданы и разработаны несколько видов решений, чтобы облегчить жизнь математика и всем представителям технических наук. Преобразовывая тригонометрические формулы, необходимо руководствоваться следующими правилами:
- Нельзя продумывать весь процесс решения от начала до самого конца сразу.
 Нужно определиться с основными задачами и данными.
Нужно определиться с основными задачами и данными. - Весь пример, подвергать упрощению или преобразования постепенно;
- Разрешается применять все преобразования и действия, связанные с алгеброй, а именно: вынести значение за пределы скобок. сократить значение и многое другое:
\[ \sin x=\frac{a}{c} ; \cos x=\frac{b}{c} ; \operatorname{tg} x=\frac{\sin x}{\cos x} ; \operatorname{ctg}=\frac{1}{\operatorname{tg} x}=\frac{\sin x}{\cos x} \]
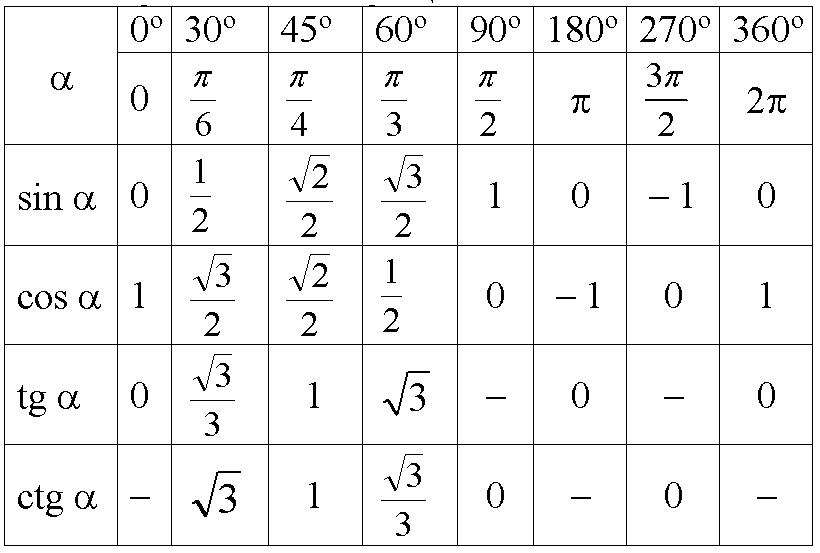
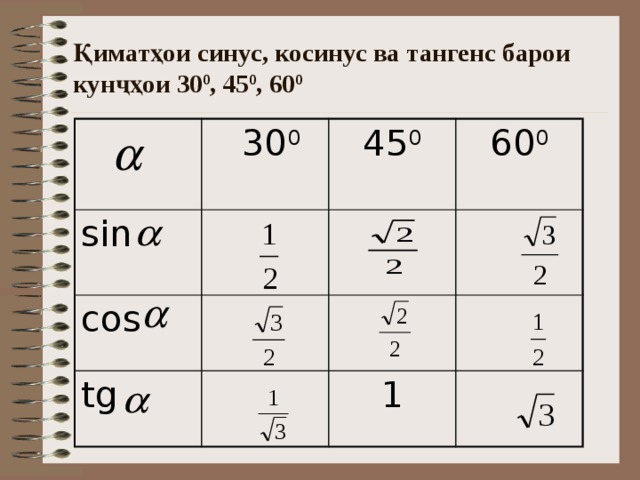
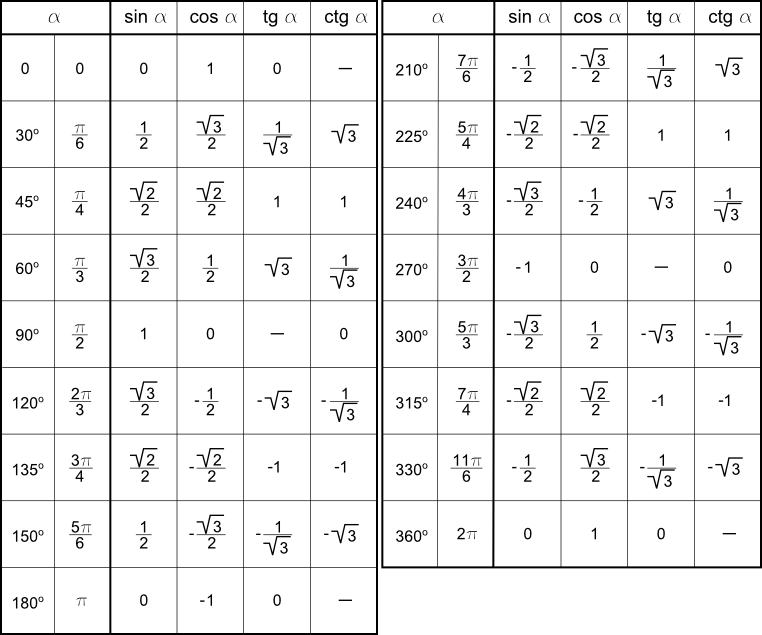
Зная основные определения тригонометрических функций, можно определить их угловые значения. Для углов от нуля до трехсот шестидесяти градусов, вычислим данные и запишем их в виде таблицы.
Значения вышеупомянутых математических функций, в частности в разделе геометрия, вычисляются как соотношения длин прямоугольного треугольника.
Углы геометрической фигуры имеют соответствующие значения в градусах. Используя основные определения математики, а именно тригонометрии можно определить нужные нам данные.
Определим основные значения
1. {\circ}
\]
{\circ}
\]Для перечисленных выше угловых значений по законам математики и всех технических наук в целом, значения не определяются
Мы произвели основные расчеты. Определили результаты угловых значений.
Мы определились с основными угловыми значениями функций. Следующим шагом будет их сведение в таблицу.
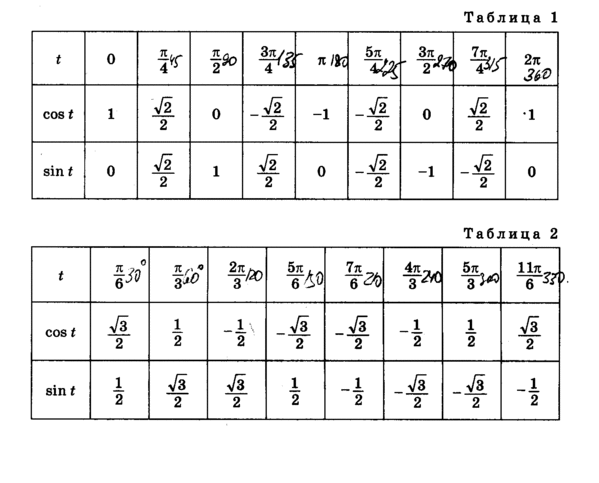
Таблица1. Основные значения функций косинус, синус, тангенс и котангенс, для угловых значений и радиан
Продолжение таблицы 1Продолжение таблицы 1Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более лучшего восприятия. Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
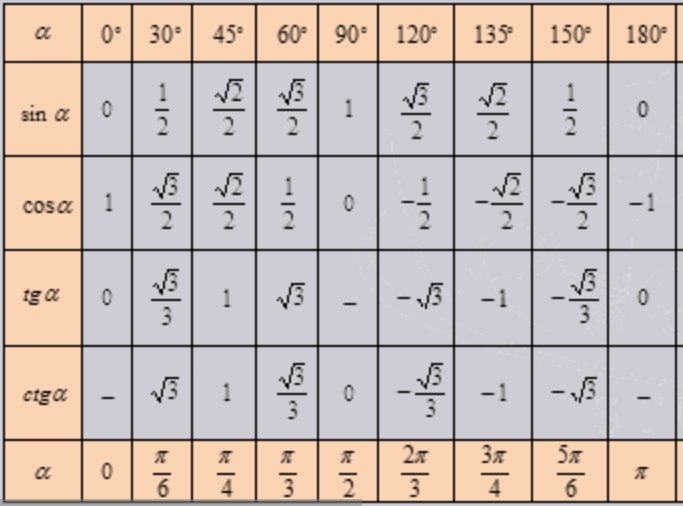
Таблица 2. Нестандартные углы функций косинус, синус, тангенс и котангенс в тригонометрии
В данной таблице приведены значения углов, которые считаются нестандартными, также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
Значение заданной функции берется из таблицы.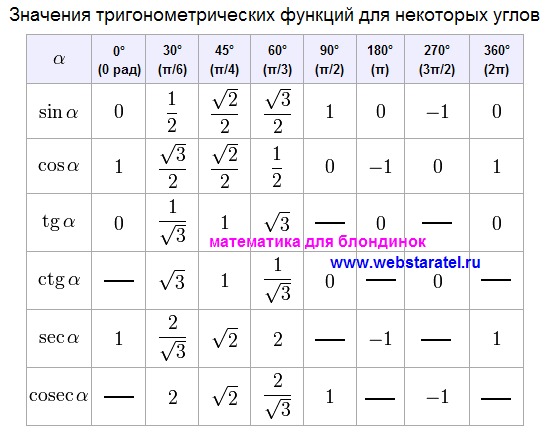 {\circ}.\]
{\circ}.\]
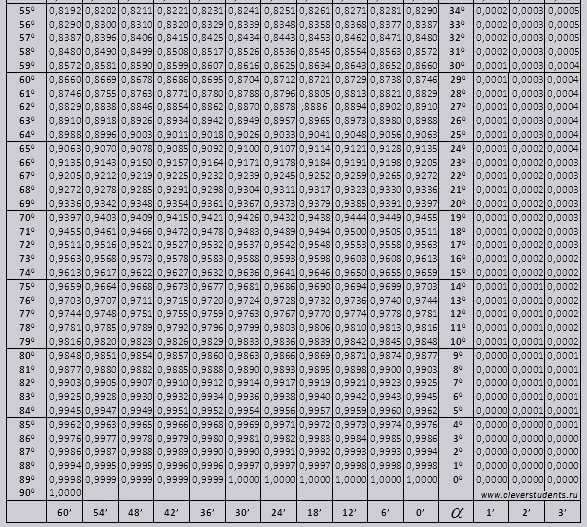
Таблица Брадиса для решения основных задач по тригонометрии
Первое упоминание о таблице, датируется 20-ми годами прошлого века. Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис. Созданная Брадисом таблица, позволяет определить значения тригонометрических функций, с большой точностью, а именно до четырех знаков. На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения. Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме. В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.

Можно определить точность углового значения до минуты. Существуют также таблицы, где есть семизначные значения.
Для того чтобы составить таблицы следует пользовался методом разложения функций (либо метод разложения на степень в ряд)
Примеры решения задач
Пример 1:
Необходимо определить синус угла 18 ° 44 ‘.
По таблице значений определяем данные синуса 18 ° 42 ‘. Далее используем поправку, равную две минуты. Плюсуем ее и заданные минуты: 18 ° 44 ‘ − 18 ° 42 ‘ = 2 ‘
Нужное значение равняется — 0,0006.
Узнав все необходимые значения, находим окончательное решение:
sin 18 ° 44 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 2:
Условие задачи, заключается в необходимости вычислить угол функции синус 76 ° 12. В таблице находим столбец с название угол и ищем 76 градусов и строку со значением 12. Далее, исходя из найденных ячеек, находим значение угла — 0,2284.
Ответ: синус 76 ° 12 =0,2284.
Пример 3:
Нужно найти значение синус 16 градусов 32 минут.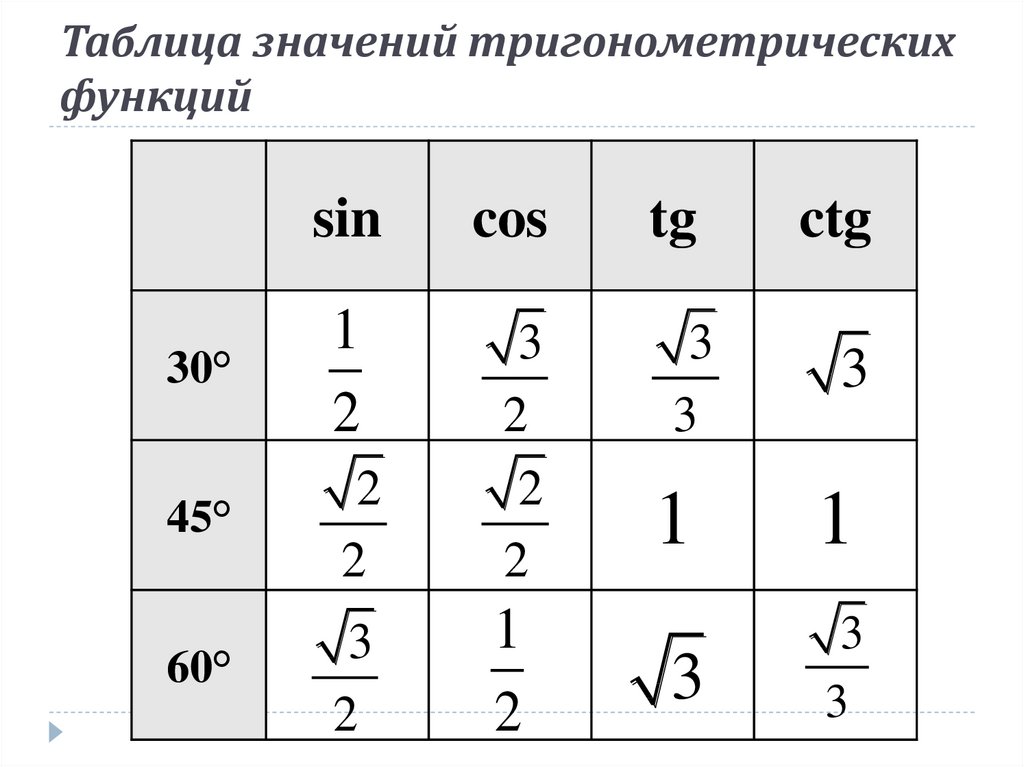 Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть
Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть
sin 16 ° 32 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 4:
Нужно найти значение синус 22 градусов 10 минут. Чтобы посчитать значение 22 ° 12, в таблице найдем значение необходимого угла, наиболее подходящее заданному. Это sin16 30 =0.3778. Так как 22 ° 10= 22 ° 12+2, то тогда выбираем поправку равную двум и видим, что нужный нам градус равный 22 ° имеет значение 0,0005. Далее записываем:
sin 22 ° 10 ‘ = (22 12-2) =0. 3778 + 0. 0005 = 0. 3773
Пример 5:
Нужно найти значение косинус 50 градусов 33 минут. Для того, чтобы посчитать значение 53 31 в таблице найдем значение нужного угла, наиболее близкого к искомому со знаком минус. Это косинус 50 33 =0. 6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:
6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:
косинус 50 ° 33 ‘ = (50 30-3) =0. 6361 +(- 0. 0007) = 0. 6454
Пример 6:
Нужно найти tg 35 градусов 6 минут. В таблице значений функции, в столбце найдем значение 35 градусов, а в строке 6 минут. Определяем нужное значение по таблице равное 0,7028.
Пример 7:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102.
Пример 8:
Нужно найти значение косинус для 49° 33 минут.
Для того чтобы вычислить значение 49° 31. В таблице найдем значение угла, наиболее близкого по значению к заданному, но только с отрицательным знаком минус. Это косинус 49° 31/ =0.6361 Так как 49° 31/=50 30+3, из этого следует, что поправка равняется трем. Значение 49 градусов равно 0,0007, поэтому: косинус 49° 33 ‘ = ( 49° 31-3) =0 .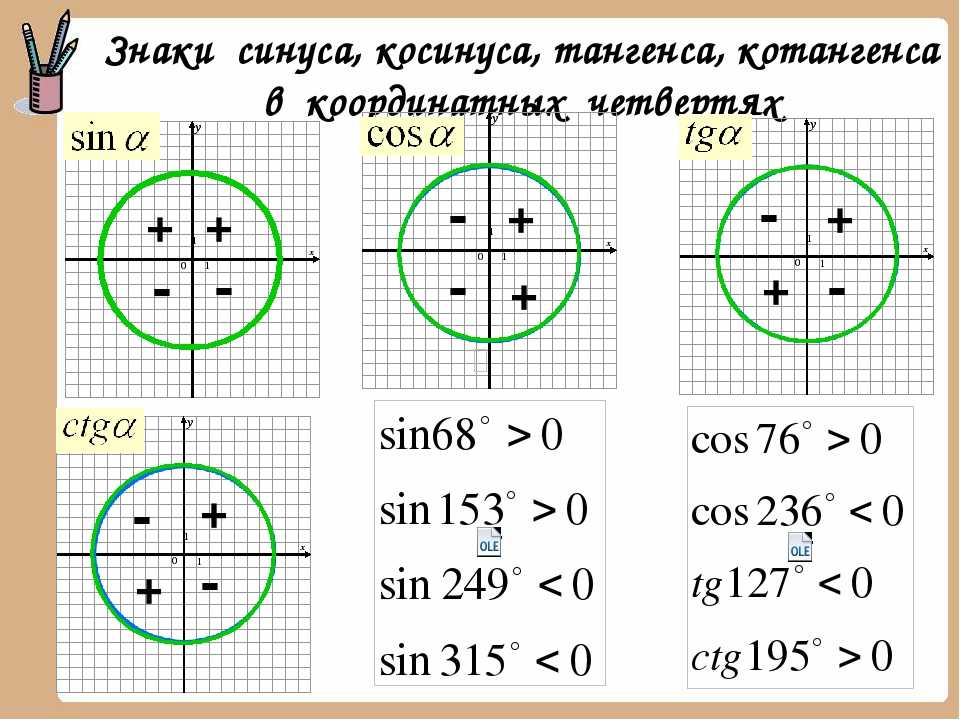 6361 +(- 0 . 0007) = 0,6454
6361 +(- 0 . 0007) = 0,6454
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Основные способы, которые помогут заполнить таблицу функций
1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec).
2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение \[\frac{\sqrt{x}}{2}\] и подставляем числовые значения, то есть величины углов.
Для наглядности все прописанные действия, можно разобрать на конкретном примере.
Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении \[\frac{\sqrt{x}}{2}\] записываем значение угла.
Получаем следующую запись: \[\frac{\sqrt{x}}{2}=\frac{0}{2}=0\]. Затем, проводим те же операции для заполнения оставшихся пустых строк.
\[ \frac{\sqrt{1}}{2}=\frac{1}{2} ; \frac{\sqrt{2}}{2}=\frac{(\sqrt{2 \cdot 2})}{(2 \cdot \sqrt{2})}=\frac{2}{2 \cdot \sqrt{2}}=\frac{1}{\sqrt{2}} ; \frac{\sqrt{3}}{2} \frac{\sqrt{4}}{2}=\frac{2}{2}=1 \]
Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.
3. Действие: Продолжаем считать таблицу. {\circ}=\frac{1}{\frac{1}{2}}=2\]
{\circ}=\frac{1}{\frac{1}{2}}=2\]
Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.
\[\text { Таким же методом заполняются оставшиеся строки таблицы. Так } \text { как } \operatorname{ctg}=\frac{1}{t g}, \text { в свою очередь } \operatorname{ctg}=\frac{\cos }{\sin }\]
Вычисление данных при помощи фигуры — прямоугольный треугольник
Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.
Вычисление при помощи длин сторон треугольника происходит следующим образом:
- обозначается катет;
- сторона возле угла;
- сторона напротив угла с прямым значением.
 {\circ}=\frac{4}{6}=0,67\]
{\circ}=\frac{4}{6}=0,67\]Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.
В процессе решения задачи, это придется применять постоянно.
Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.
Косеканс находится \[\operatorname{cosec}=\frac{1}{\sin }\] следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету \[\mathrm{sec}=\frac{1}{\cos }\].
Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8. Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.
При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.
Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд.
 Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.Вычисление значений углов по окружности
Самый простой и понятный способ для вычисления углов и радиан.
Для этого вычерчиваем окружность с радиусом R. Он в свою очередь, равен единичному значению. Центр окружности равен центру системы координат. От положительной оси считаем углы, по часовой стрелке, выполняющей движении против хода. Точка, имеющая координаты 1;0 равняется угловому значению ноль. если координаты -1;0, тогда угол равен 90 градусов. Точка, находящаяся на окружности, соответствует углу от нуля до 360 градусов. Так как окружность является единичной, значения углов для синуса и косинуса находятся в пределах от -1 до 1:
Определяются знаки функций, также по окружности. если угловое значение более 360 градусов, делается два оборота по часовой стрелке и плюсуется еще дополнительно 12 минут.

\[ \cos (\alpha+360 \cdot n)=\sin \alpha ;\] \[ \sin (\alpha+360 \cdot n)=\sin \alpha / \]
Значения тангенсов и котангенсов, можно вычислить аналогично, по окружности. Однако легче посчитать по формулам, уже известных данных.
\[ \operatorname{tg} \alpha=\frac{\sin \alpha}{\cos \alpha} ; \operatorname{ctg} \alpha=\frac{\cos \alpha}{\sin \alpha} \]
Функции cos sin. Что такое синус и косинус
Здоровье
Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».
См. также полезные материалы:
Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая.
 Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.Синус пи, косинус пи, тангенс пи и других углов в радианах
Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.
Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.
Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 .

Примеры :
1. Синус пи .
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.2. Косинус пи .
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
значение угла α
(градусов)значение угла α
в радианах(через число пи)
sin
(синус)cos
(косинус)tg
(тангенс)ctg
(котангенс)sec
(секанс)cosec
(косеканс)0 0 0 1 0 — 1 — 15 π/12 2 — √3 2 + √3 30 π/6 1/2 √3/2 1/√3 √3 2/√3 2 45 π/4 √2/2 √2/2 1 1 √2 √2 60 π/3 √3/2 1/2 √3 1/√3 2 2/√3 75 5π/12 2 + √3 2 — √3 90 π/2 1 0 — 0 — 1 105 7π/12 — √3 — 2 120 2π/3 √3/2 -1/2 -√3 -√3/3 135 3π/4 √2/2 -√2/2 -1 -1 -√2 √2 150 5π/6 1/2 -√3/2 -√3/3 -√3 180 π 0 -1 0 — -1 — 210 7π/6 -1/2 -√3/2 √3/3 √3 240 4π/3 -√3/2 -1/2 √3 √3/3 270 3π/2 -1 0 — 0 — -1 360 2π 0 1 0 — 1 — Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения.
 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов
0, 15, 30, 45, 60, 90 … 360 градусов
(цифровые значения «как по таблицам Брадиса»)значение угла α (градусов) значение угла α в радианах sin (синус) cos (косинус) tg (тангенс) ctg (котангенс) 0 0 15 0,2588
0,9659
0,2679
30 0,5000
0,5774
45 0,7071
0,7660
60 0,8660
0,5000
1,7321
7π/18
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате .

Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами .
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x» , что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе.
 Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BCИ просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.

cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Я не буду убеждать вас не писать шпаргалки. Пишите! В том числе, и шпаргалки по тригонометрии. Позже я планирую объяснить, зачем нужны шпаргалки и чем шпаргалки полезны. А здесь — информация, как не учить, но запомнить некоторые тригонометрические формулы. Итак — тригонометрия без шпаргалки!Используем ассоциации для запоминания.
1. Формулы сложения:
косинусы всегда «ходят парами»: косинус-косинус, синус-синус. И еще: косинусы — «неадекватны». Им «все не так», поэтому они знаки меняют: «-» на «+», и наоборот.
Синусы — «смешиваются» : синус-косинус, косинус-синус.
2. Формулы суммы и разности:
косинусы всегда «ходят парами».
 Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.Синусы — «смешиваются» :
3. Формулы преобразования произведения в сумму и разность.
Когда мы получаем пару косинусов? Когда складываем косинусы. Поэтому
Когда мы получаем пару синусов? При вычитании косинусов. Отсюда:
«Смешение» получаем как при сложении, так и при вычитании синусов. Что приятнее: складывать или вычитать? Правильно, складывать. И для формулы берут сложение:
В первой и в третьей формуле в скобках — сумма. От перестановки мест слагаемых сумма не меняется. Принципиален порядок только для второй формулы. Но, чтобы не путаться, для простоты запоминания мы во всех трех формулах в первых скобках берем разность
а во вторых — сумму
Шпаргалки в кармане дают спокойствие: если забыл формулу, можно списать. А дают уверенность: если воспользоваться шпаргалкой не удастся, формулы можно легко вспомнить.

Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов (или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .

Отметим на оси ординат точку с ординатой :
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату . Эти точки соответствуют углам поворота на и радиан:
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , .
 (2)
(2)Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем (то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем (то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3.
 Решим уравнение
Решим уравнениеЛиния тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
4. Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.

Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение :
ОСОБЫЕ РЕШЕНИЯ:
Отметим на окружности точки, ордината которых равна 0:
Отметим на окружности единственную точку, ордината которой равна 1:
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
Отметим на окружности точки, абсцисса которых равна 0:
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:Отметим на окружности единственную точку, абсцисса которой равна -1:
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
Разделим обе части равенства на 3:
Ответ:
2.

Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать .
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье.
 Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений .
 Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл.
 Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Таблицы синусов Диаграмма угла от 0° до 90°
Расчет математических чисел онлайн, формулы, Расчет алгебры онлайн, формулы, Матричный расчет, формулы, Цифровой расчет, Статистические расчеты
Таблицы синусов Таблица углов от 0° до 90°
Тригонометрические онлайн-таблицы
От 0° до 15° от 16° до 31° от 32° до 45° sin(0°) = 0 sin(16°) = 0,275637 sin(32°) = 0,529919 sin(1°) = 0,017452 sin(17°) = 0,292372 sin(33°) = 0,544639 sin(2°) = 0,034899 sin(18°) = 0,309017 sin(34°) = 0,559193 sin(3°) = 0,052336 sin(19°) = 0,325568 sin(35°) = 0,573576 sin(4°) = 0,069756 sin(20°) = 0,34202 sin(36°) = 0,587785 sin(5°) = 0,087156 sin(21°) = 0,358368 sin(37°) = 0,601815 sin(6°) = 0,104528 sin(22°) = 0,374607 sin(38°) = 0,615661 sin(7°) = 0,121869 sin(23°) = 0,390731 sin(39°) = 0,62932 sin(8°) = 0,139173 sin(24°) = 0,406737 sin(40°) = 0,642788 sin(9°) = 0,156434 sin(25°) = 0,422618 sin(41°) = 0,656059 sin(10°) = 0,173648 sin(26°) = 0,438371 sin(42°) = 0,669131 sin(11°) = 0,190809 sin(27°) = 0,45399 sin(43°) = 0,681998 sin(12°) = 0,207912 sin(28°) = 0,469472 sin(44°) = 0,694658 sin(13°) = 0,224951 sin(29°) = 0,48481 sin(45°) = 0,707107 sin(14°) = 0,241922 sin(30°) = 0,5 sin(15°) = 0,258819 sin(31°) = 0,515038 46° до 60° от 61° до 75° от 76° до 90° sin(46°) = 0,71934 sin(61°) = 0,87462 sin(76°) = 0,970296 sin(47°) = 0,731354 sin(62°) = 0,882948 sin(77°) = 0,97437 sin(48°) = 0,743145 sin(63°) = 0,891007 sin(78°) = 0,978148 sin(49°) = 0,75471 sin(64°) = 0,898794 sin(79°) = 0,981627 sin(50°) = 0,766044 sin(65°) = 0,906308 sin(80°) = 0,984808 sin(51°) = 0,777146 sin(66°) = 0,913545 sin(81°) = 0,987688 sin(52°) = 0,788011 sin(67°) = 0,920505 sin(82°) = 0,9 sin(53°) = 0,798636 sin(68°) = 0,927184 sin(83°) = 0,992546 sin(54°) = 0,809017 sin(69°) = 0,93358 sin(84°) = 0,994522 sin(55°) = 0,819152 sin(70°) = 0,939693 sin(85°) = 0,996195 sin(56°) = 0,829038 sin(71°) = 0,945519 sin(86°) = 0,997564 sin(57°) = 0,838671 sin(72°) = 0,951057 sin(87°) = 0,99863 sin(58°) = 0,848048 sin(73°) = 0,956305 sin(88°) = 0,999391 sin(59°) = 0,857167 sin(74°) = 0,961262 sin(89°) = 0,999848 sin(60°) = 0,866025 sin(75°) = 0,965926 sin(90°) = 1 Работает на mymathtables.
 com
com
Другие тригонометрические страницыТаблица котангенсов от 0° до 90°
Таблица котангенсов от 91° до 180°
Таблица котангенсов от 181° до 170° 6 Котангенс 3
9003 0°Таблица касательной от 0° до 90°
Таблица касательной от 91° до 180°
Таблица касательной от 181° до 270°
Таблица касательной от 271° до 360°
Рекомендуемые страницыТаблица синусов от 0° до 90°
Таблица синусов от 91° до 180° Таблица с 01° до 180°
2
9 70°Таблица синуса от 271° до 360°
Таблица косинуса от 0° до 90°
Таблица косинуса от 91° до 180°
Таблица косинуса от 181° до 270°
Таблица косинуса от 271° до 360°
Математические таблицы умноженияМатематическая таблица умножения для учащихся в простейшей форме.
Уловки и стратегии по таблице умножения
Самопроверка таблицы умножения
Математические символы и терминология
Рабочие листы таблицы умножения
Популярные математические диаграммы
Изучение типов математических чисел
9000 Таблица умножения Неограниченное количество Генератор таблицОдин щелчок Таблица умножения Генератор ответов
Интерактивный генератор викторин по таблице умножения
Таблица сотен
Другие таблицы
Что такое синус в математике?
Синус — тригонометрическая функция угла.
 Синус угла определяется в контексте прямоугольного треугольника: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника (деленное на нее). (так называемая гипотенуза).
Синус угла определяется в контексте прямоугольного треугольника: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника (деленное на нее). (так называемая гипотенуза).Что такое значение синуса 0°?
= 0
Что такое значение синуса 30°?
= 0,5
Значение синуса 90°?
= 1
Таблица синусов в радианах
Вычисление тригонометрических функций
Вычисление тригонометрических функцийЭто совершенно необязательная страница. Нет необходимости знать, как вычислять триггерные функции и их обратные, чтобы использовать их. Тем не менее, многих интересует, как вычислялись значения этих функций до и после изобретения калькуляторов и компьютеров. Если вам интересно, то читайте дальше. В противном случае переходите к следующему разделу о косых треугольниках.
До компьютеров: таблицы
Птолемей (100–178) создал одну из первых таблиц для тригонометрии в своей работе, Альмагест, , и он включил математику, необходимую для разработки этой таблицы. Это была таблица хорд (обсуждавшаяся ранее) для каждой дуги от 1/2° до 180° с интервалами в 1/2°. Также он объяснил, как интерполировать между заданными углами.
Это была таблица хорд (обсуждавшаяся ранее) для каждой дуги от 1/2° до 180° с интервалами в 1/2°. Также он объяснил, как интерполировать между заданными углами.Вместо того, чтобы повторять то, что он сделал для аккордов, давайте посмотрим, как создавать таблицы для синусов и косинусов, используя его методы. Во-первых, на основе теоремы Пифагора и подобных треугольников можно напрямую вычислять синусы и косинусы определенных углов. В частности, вы можете напрямую найти синусы и косинусы для углов 30°, 45° и 60°, как описано в разделе о косинусах. Птолемей знал еще два угла, которые можно построить, а именно 36° и 72°. Эти углы были построены Евклидом в предложении IV.10 его Элементы. Подобно Птолемею, мы можем использовать эту конструкцию для вычисления триггерных функций для этих углов. На данный момент мы можем вычислить триггерные функции для углов 30°, 36°, 45°, 60° и 72°, и, конечно же, мы знаем значения для 0° и 90°.
Имейте в виду, что если известен синус угла θ , то известен и косинус дополнительного угла 90° – θ ; аналогично, если вы знаете косинус угла θ , то вы знаете синус дополнительного угла 90° – θ :
Таким образом, у вас также есть триггерные функции для 18° и 54°.

Далее вы можете использовать формулы половинного угла для синусов и косинусов, чтобы вычислить значения половины угла, если вы знаете значения угла. Если θ — это угол между 0° и 180°, то
Используя их, из значений 18°, 30° и 54° можно найти значения 27°, 15° и 9° и, следовательно, их дополнения 63°, 75° и 81°.
С помощью формул суммы и разности
Вы можете найти синус и косинус для 3° (от 30° до 27°), а затем заполнить таблицы для синуса и косинуса для углов от 0° до 90° с шагом 3°.
Опять же, используя формулы половинного угла, вы можете создать таблицу с шагом 1,5° (то есть 1° 30′), затем 0,75° (что составляет 45′) или даже 0,375° (что составляет 22′ 30′). «). Но как получить таблицу с приращением в 1°? Птолемей признал, что не существует евклидовой конструкции, позволяющей разделить угол в 3° на три части, чтобы получить угол в 1°, но поскольку функция синуса почти линейна для малых углов, вы можете аппроксимировать sin 1°, просто интерполируя треть пути между значениями sin 0,75° и sin 1,5°.
 С помощью этого шага мы можем построить таблицы триггеров для триггерных функций с шагом 1°.
С помощью этого шага мы можем построить таблицы триггеров для триггерных функций с шагом 1°.Лучшие триггерные таблицы создавались веками. Например, Улугбек (15 век) построил таблицы синусов и тангенсов для каждой угловой минуты с точностью до девяти знаков!
Улугбек (1394–1449) Обсерватория Улугбека, Самарканд, Узбекистан Между прочим, если у вас есть таблица синусов, вы можете прочитать ее в обратном порядке, чтобы вычислить арксинус, поэтому для обоих нужна только одна таблица.
После компьютеров: силовая серия
Хотя компьютеры и калькуляторы могут просто хранить триггерные таблицы в своей памяти, они также могут напрямую вычислять триггерные функции, что они обычно и делают.
В конце 17 века Ньютон и другие математики разработали степенные ряды. Степенной ряд подобен многочлену неограниченной степени. Для различных триггерных функций эти математики нашли степенные ряды. Вот степенные ряды для синуса и косинуса (где x — это угол, измеренный в радианах):
Три точки … означают, что выражение должно продолжаться бесконечно, добавляя новый термин, затем вычитая термин и т. д. Восклицательный знак ! следует читать как «факториал», и это означает, что вы перемножаете целые числа от 1 до заданного числа. Например, 5!, «факториал пяти», равно 1 умножить на 2 умножить на 3 умножить на 4 умножить на 5, что равно 120, и, следовательно, 6! = 720.
Эти степенные ряды имеют бесконечно много членов, но они так быстро становятся маленькими, что только первые несколько членов дают большой вклад.
Предположим, вы хотите вычислить синус 45°, с точностью до некоторого числа разрядов, используя этот степенной ряд.
 Сначала преобразуйте 45° в радианы, чтобы получить π /4, что равно 0,78539816 в восьми разрядах. Затем вычислить значение
Сначала преобразуйте 45° в радианы, чтобы получить π /4, что равно 0,78539816 в восьми разрядах. Затем вычислить значение- 0,78539816 0,78539816 3 /3! + 0,78539816 5 0,78539816 7 /7! +…
- 0,78539816 =
0,78539816
0,70465265 = 0,78539816 0,78539816 3 /3!
0,70714304 = 0,78539816 0,78539816 3 /3! + 0,78539816 5 /5!
0,70710647 = 0,78539816 0,78539816 3 /3! + 0,78539816 5 /5! 0,78539816 7 /7!
0,70710678 = 0,78539816 0,78539816 3 /3! + 0,78539816 5 /5! 0,78539816 7 /7! + 0,78539816 9 /9!

 Нужно определиться с основными задачами и данными.
Нужно определиться с основными задачами и данными.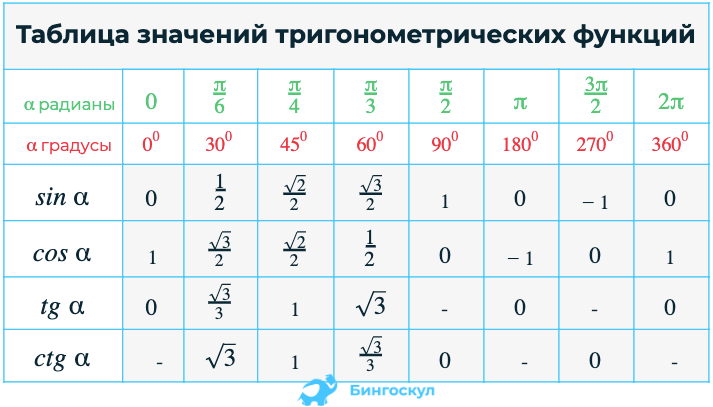
 {\circ}=\frac{4}{6}=0,67\]
{\circ}=\frac{4}{6}=0,67\]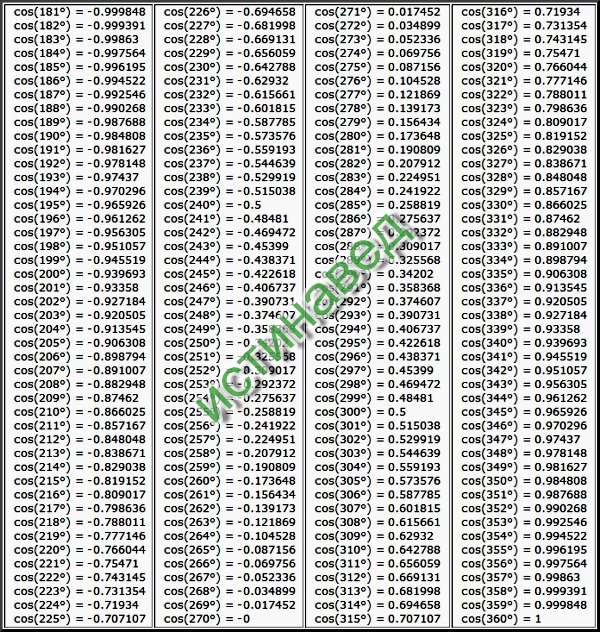 Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
 Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.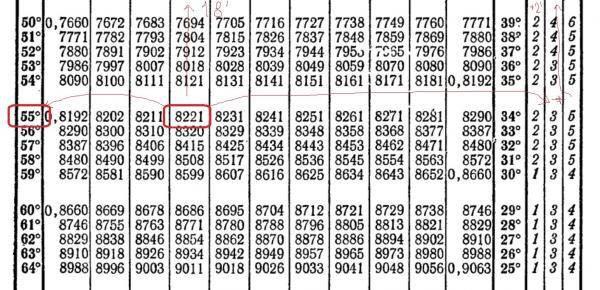
 Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC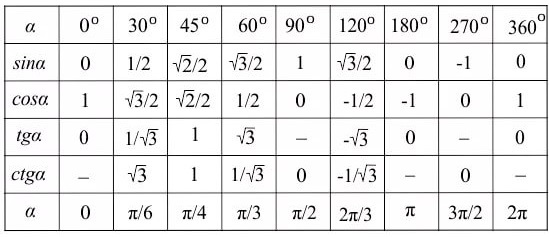
 Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.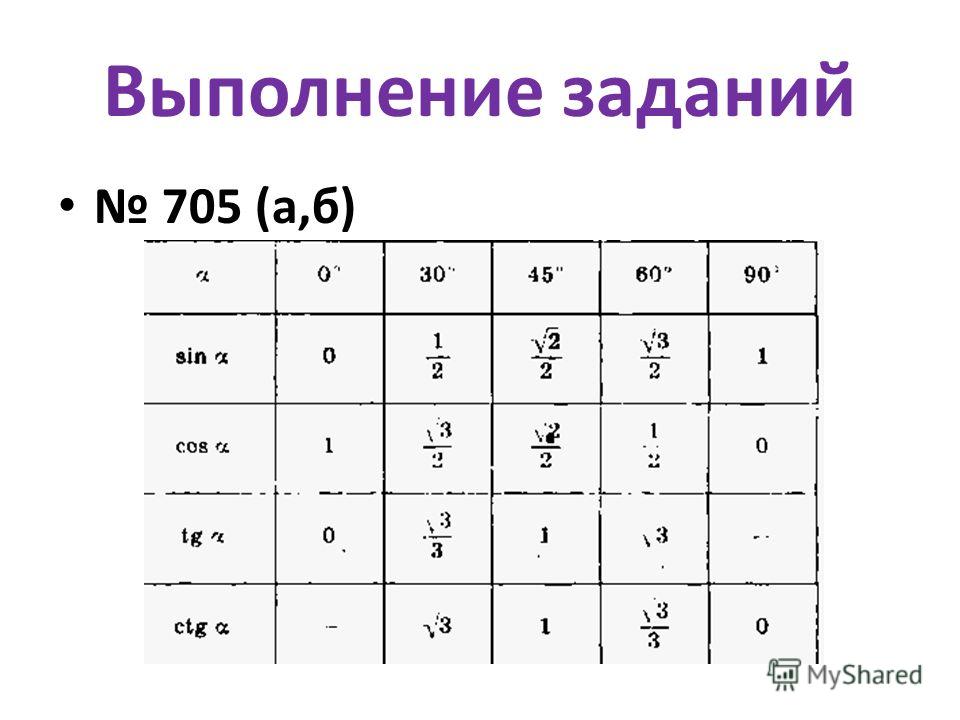

 (2)
(2) Решим уравнение
Решим уравнение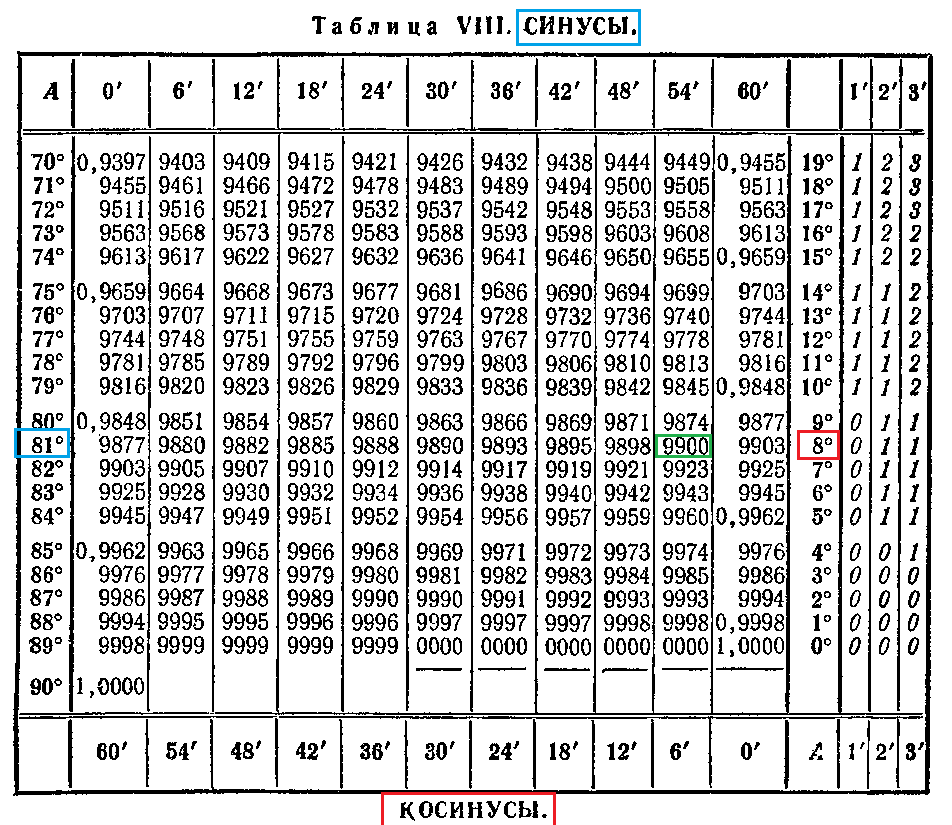
 Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения. Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое . com
com Синус угла определяется в контексте прямоугольного треугольника: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника (деленное на нее). (так называемая гипотенуза).
Синус угла определяется в контексте прямоугольного треугольника: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника (деленное на нее). (так называемая гипотенуза). Это была таблица хорд (обсуждавшаяся ранее) для каждой дуги от 1/2° до 180° с интервалами в 1/2°. Также он объяснил, как интерполировать между заданными углами.
Это была таблица хорд (обсуждавшаяся ранее) для каждой дуги от 1/2° до 180° с интервалами в 1/2°. Также он объяснил, как интерполировать между заданными углами.
 С помощью этого шага мы можем построить таблицы триггеров для триггерных функций с шагом 1°.
С помощью этого шага мы можем построить таблицы триггеров для триггерных функций с шагом 1°.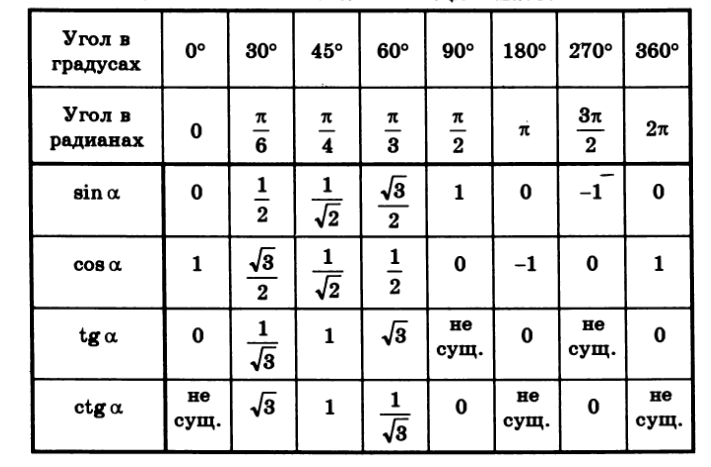
 Сначала преобразуйте 45° в радианы, чтобы получить π /4, что равно 0,78539816 в восьми разрядах. Затем вычислить значение
Сначала преобразуйте 45° в радианы, чтобы получить π /4, что равно 0,78539816 в восьми разрядах. Затем вычислить значение