Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/». См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
Синус 0 6 сколько косинус — Сборка-Доработка
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.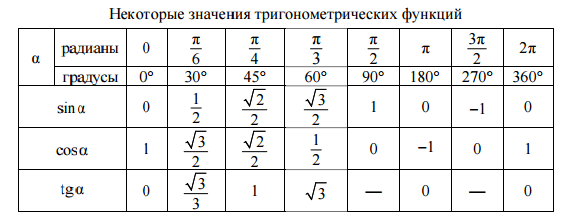 1564 1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0. 5878 5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.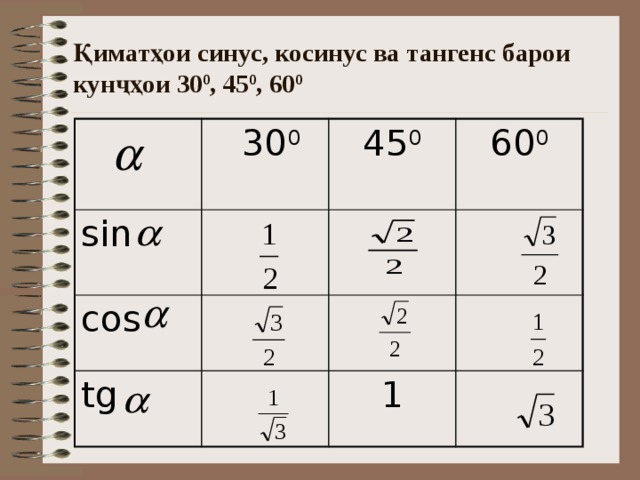 891 891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.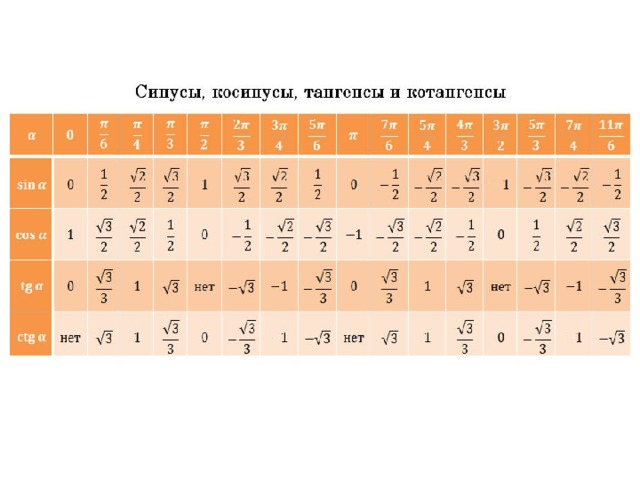 9998 9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.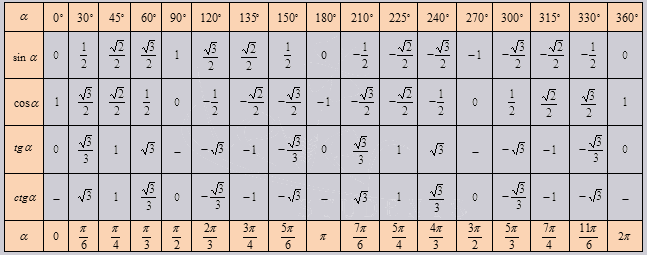 891 891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0. 6018 6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.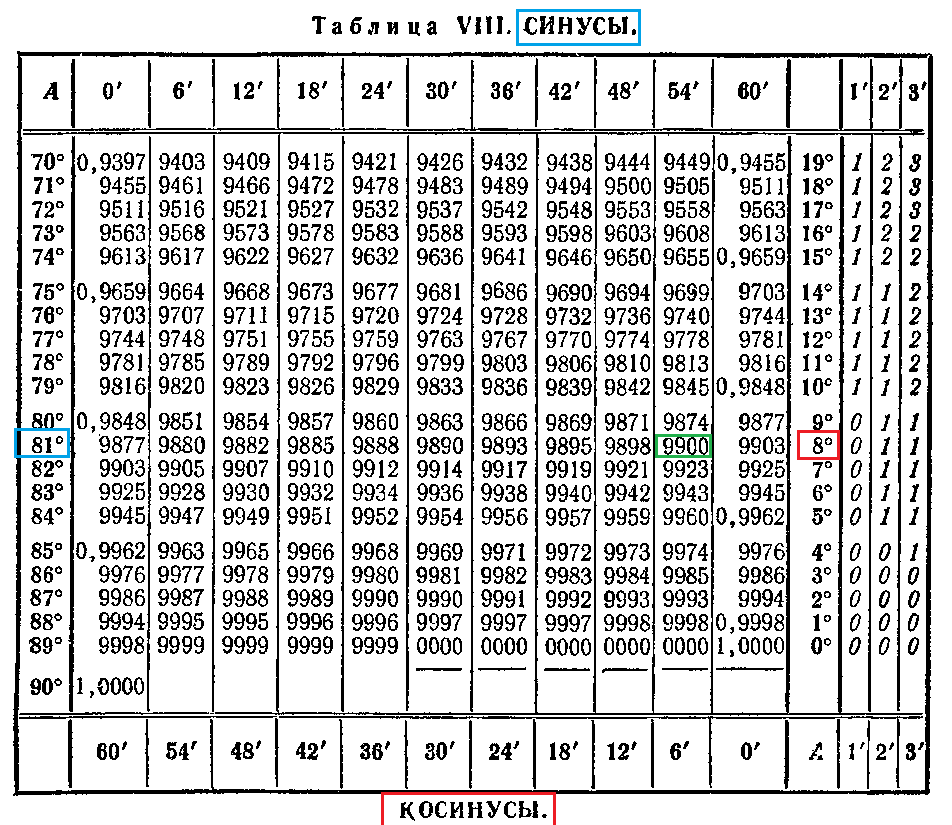 1908 1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.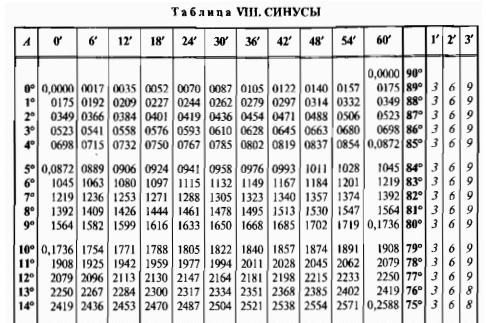 2079 2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.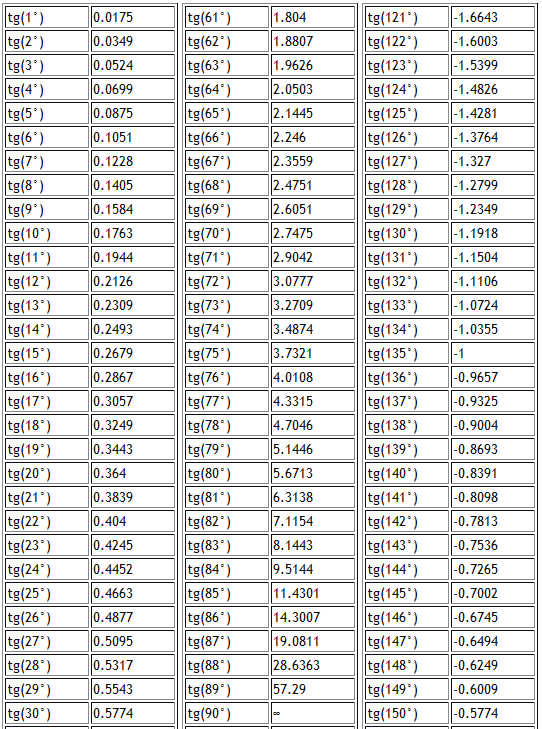 6157 6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0. 8988 8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.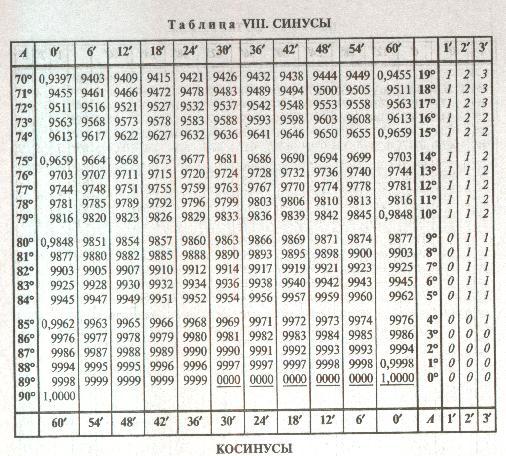 9998 9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0. 891 891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.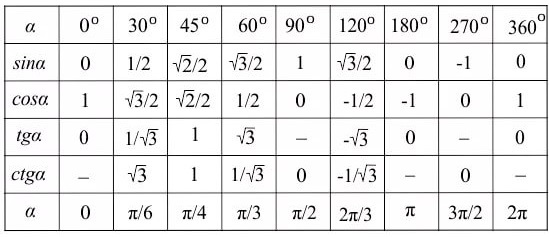 6018 6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0. 1908 1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.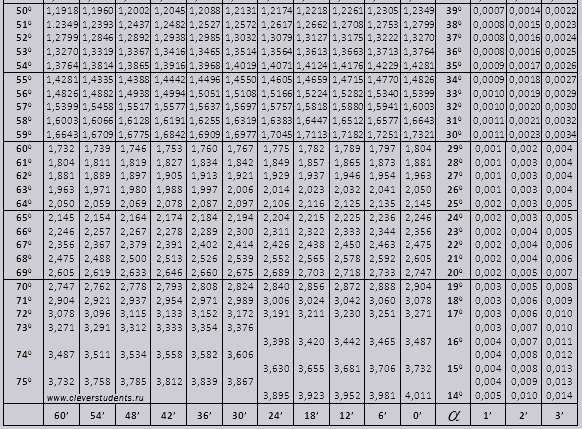
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Калькулятор поможет рассчитать точные значения тригонометрических функций sin, cos, tg и ctg для различных значений углов в градусах или радианах.
На данной странице таблица Брадиса, которая дает значение sin, cos, tg, ctg любого острого угла, содержащего целое число градусов и десятых долей градуса. Для нахождения значения угла берется число на пересечении строки, которое соответствует числу градусов и столбца, которое соответствует числу минут. Например, sin 70°30′ = 0.9426.
Таблица косинусов — это записанные в таблицу посчитанные значения косинусов углов от 0° до 360°. Используя таблицу косинусов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение косинуса от нужного Вам угла, достаточно найти его в таблице или вычислить с помощью калькулятора.
Таблица градусов в тригонометрии. Cинус, косинус, тангенс и котангенс
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.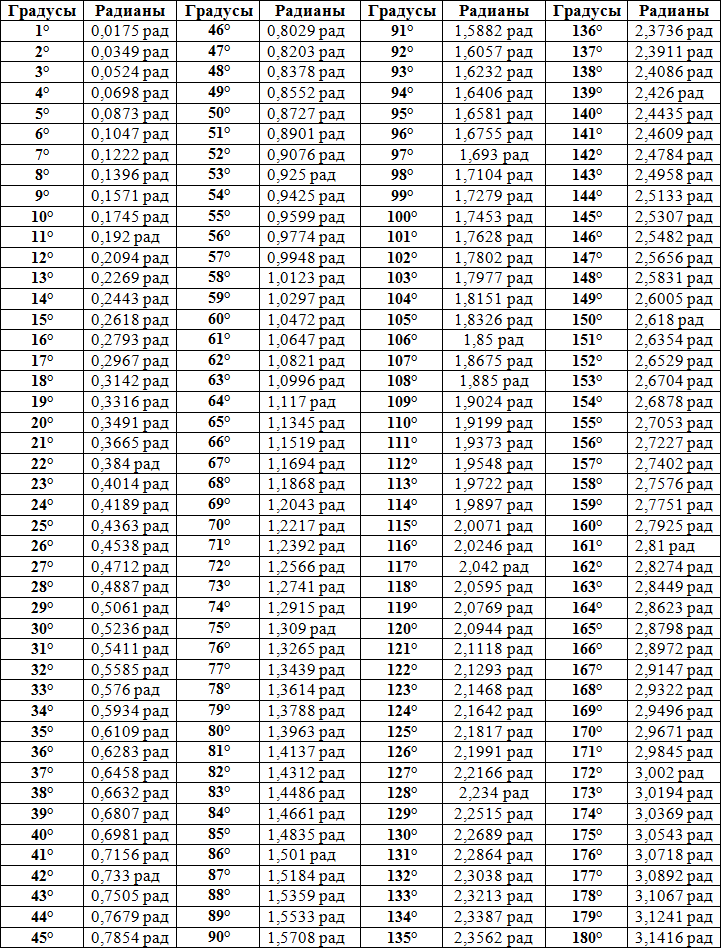
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»
Вот этот вывод:
Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое.
Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Почему почти? Об этом ниже.
Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов. )
Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)
И зачем тогда этот урок?! — спросите вы.
А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё . На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов.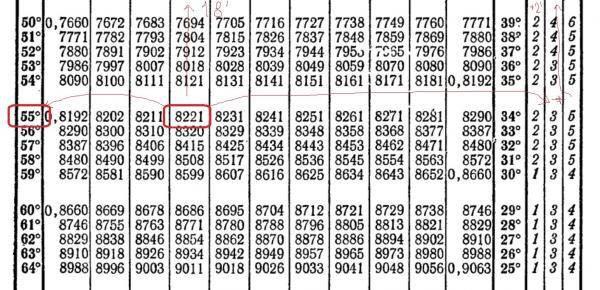 .. Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
.. Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется…)
Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу . Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов. )
)
Итак, начнём. Для начала разобьём все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группа углов из семнадцати особых . Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:
Угол х(в градусах) | 0 | 90 | 180 | 270 | 360 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | 0 | -1 | 0 |
cos x | 1 | 0 | -1 | 0 | 1 |
tg x | 0 | не сущ.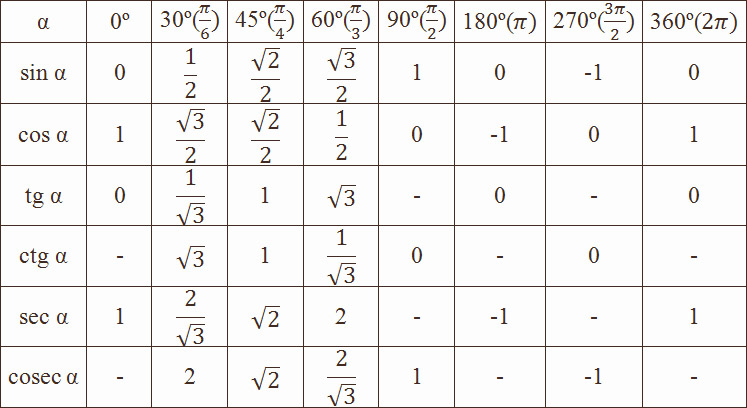 | 0 | не сущ. | 0 |
ctg x | не сущ. | 0 | не сущ. | 0 | не сущ. |
Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов.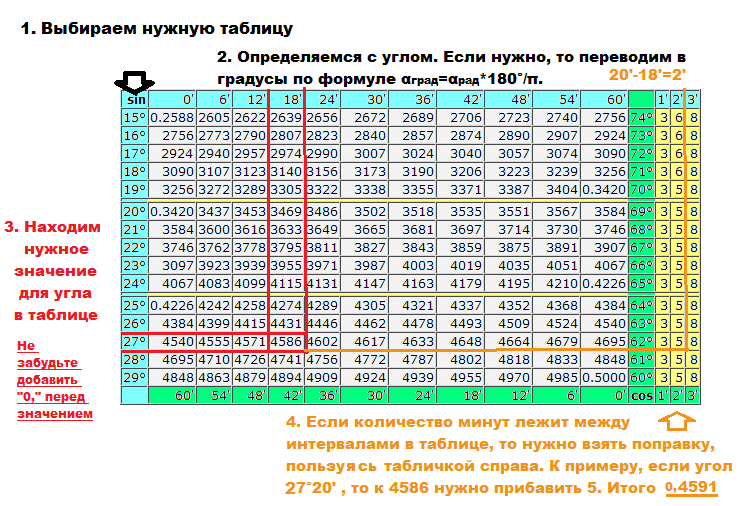 Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Вот и всё.
Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество…) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол
вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол
Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.
Итак, с пятью углами из семнадцати — разобрались.
Вторая группа углов.

Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
Угол х(в градусах) | 0 | 30 | 45 | 60 | 90 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | |||
cos x | 1 | 0 | |||
tg x | 0 | 1 | не сущ. | ||
ctg x | не сущ. | 1 | 0 |
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же. Для углов 20, 50, 80 так бы не получилось…
Для углов 20, 50, 80 так бы не получилось…
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?
С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.
Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:
и многие другие, вы должны знать всё .
Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память.
И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах. Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. Школьная таблица синусов.
Для тригонометрической функции косинус в таблице приведены значения для следующих углов: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 в градусной мере, что соответствует cos 0 пи, cos пи на 6, cos пи на 4, cos пи на 3, cos пи на 2, cos пи, cos 3 пи на 2, cos 2 пи в радианной мере углов. Школьная таблица косинусов.
Тригонометрическая таблица для тригонометрической функции тангенс приводит значения для следующих углов: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 в градусной мере, что соответствует tg 0 пи, tg пи/6, tg пи/4, tg пи/3, tg пи, tg 2 пи в радианной мере углов. Следующие значения тригонометрических функций тангенса не определены tg 90, tg 270, tg пи/2, tg 3 пи/2 и считаются равными бесконечности.
Для тригонометрической функции котангенс в тригонометрической таблице даны значения следующих углов: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 в градусной мере, что соответствует ctg пи/6, ctg пи/4, ctg пи/3, tg пи/2, tg 3 пи/2 в радианной мере углов. Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.
Значения тригонометрических функций секанс и косеканс приведены для таких же углов в градусах и радианах, что и синус, косинус, тангенс, котангенс.
В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.
Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.
Еще три монстра тригонометрии. Первый — это тангенс 1,5 полутора градусов или пи деленное на 120. Второй — косинус пи деленное на 240, пи/240. Самый длинный — косинус пи деленное на 17, пи/17.
Тригонометрический круг значений функций синус и косинус наглядно представляет знаки синуса и косинуса в зависимости от величины угла. Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.
Эта тригонометрическая таблица представляет значения синуса, косинуса, тангенса и котангенса для углов от 0 нуля до 90 девяносто градусов с интервалом через один градус. Для первых сорока пяти градусов названия тригонометрических функций необходимо смотреть в верхней части таблицы. В первом столбце указаны градусы, значения синусов, косинусов, тангенсов и котангенсов записаны в следующих четырех столбцах.
Для углов от сорока пяти градусов до девяноста градусов названия тригонометрических функций записаны в нижней части таблицы. В последнем столбце указаны градусы, значения косинусов, синусов, котангенсов и тангенсов записаны в предыдущих четырех столбцах. Следует быть внимательными, поскольку в нижней части тригонометрической таблицы названия тригонометрических функций отличаются от названий в верхней части таблицы. Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.
Знаки тригонометрических функций представлены на рисунке выше. Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Тригонометрические функции синус, тангенс и котангенс являются нечетными функциями. Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.
В таблице значений для тригонометрической функции синус приведены значения для следующих углов
ДокументОтдельной странице находятся формулы приведения тригонометрических функций . В таблице значений для тригонометрической функции синус приведены значения для следующих углов : sin 0, sin 30, sin 45 .
 ..
..Предлагаемый математический аппарат является полным аналогом комплексного исчисления для n-мерных гиперкомплексных чисел с любым числом степеней свободы n и предназначен для математического моделирования нелинейных
Документ… функции равно функции изображения. Из этой теоремы следует , что для нахождения координат U, V достаточно вычислить функцию … геометрии; полинарные функции (многомерные аналоги двухмерных тригонометрических функций ), их свойства, таблицы и применение; …
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол . С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье).
 Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
Данные функции часто появляются при решении дифференциальных и функциональных уравнений.2. К тригонометрическим функциям относятся следующие 6 функций: синус , косинус , тангенс ,котангенс , секанс и косеканс . Для каждой из указанных функций существует обратная тригонометрическая функция.
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга . На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠07.
 Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠08. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠09. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠010. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.11. График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤112. График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤113. График функции тангенс
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞14. График функции котангенс
y=cotx, область определения: x∈R,x≠kπ, область значений: −∞15. График функции секанс
y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪∪}
Таблица синусов — Мир в таблицах
Главная » Математика
Автор admin На чтение 6 мин Просмотров 222 Опубликовано
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Содержание
Таблица синусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| sin α | 0 | 12 | √22 | √32 | 1 | 0 | -1 | 0 |
Таблица синусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°
| Угол х (в градусах) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π |
| sin x | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 |
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0.  017452 017452sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.  694658 694658sin(45°) = 0.707107 | sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.  997564 997564sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 | sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.  798636 798636sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 | sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.  207912 207912sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.  406737 406737sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 | sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.  891007 891007sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 | sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.  978148 978148sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 | sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.  62932 62932sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
Скачать таблицы синусов (правой кнопкой — сохранить изображение)
Таблица косинусов 30 45 60
В математике выделяют шесть тригонометрических функций, из которых четыре (синус, косинус, тангенс и котангенс) являются основными и еще две (секанс и косеканс) применяются довольно редко. Исходя из данного положения, косинус можно определить как одну из основных тригонометрических функций, выражающих отношение прилежащего катета в прямоугольном треугольнике к гипотенузе этого треугольника. Косинус угла x обозначается как cos x. Величина косинуса угла зависит от длины отрезков, образующих стороны прямоугольного треугольника и от его размера.
Исходя из данного положения, косинус можно определить как одну из основных тригонометрических функций, выражающих отношение прилежащего катета в прямоугольном треугольнике к гипотенузе этого треугольника. Косинус угла x обозначается как cos x. Величина косинуса угла зависит от длины отрезков, образующих стороны прямоугольного треугольника и от его размера.
Как использовать калькулятор, чтобы найти тривиальные отношения и углы?
Отношение сторон треугольника равно. Из треугольника получаем соотношения следующим образом. Сочетая две таблицы, мы получаем. Поиск коэффициентов триггера и углов с помощью вашего калькулятора. Используйте калькулятор, чтобы найти значение функции. Определите θ в десятичных градусах, 0 ° ≤ θ ≤ 90 °.
Определение значений тригонометрических функций в калькуляторе. Мы также можем инвертировать тригонометрические функции для решения правого треугольника. Попробуйте приведенные примеры или введите свою собственную проблему и проверьте свой ответ с пошаговыми объяснениями. Синус, косинус и касательные значения для определенных значительных углов. Геометрический смысл тригонометрических отношений в гониометрической сфере. Отношения между тригонометрическими отношениями.
Синус, косинус и касательные значения для определенных значительных углов. Геометрический смысл тригонометрических отношений в гониометрической сфере. Отношения между тригонометрическими отношениями.
Чему равен косинус и синус 30 градусов
Косинус угла в 30 градусов получится, если корень из трех разделить на два. Вычисляя данное отношение, получаем значение косинуса равное 0,866. Синус угла в 30 градусов равен одной второй или 0,5.
Чему равен косинус и синус 60 градусов
Косинус угла в 60 градусов равен синусу угла 30 градусов, то есть одной второй (1111/2) или 0,5. Синус того же угла косинусу угла в 30 градусов, то есть корень из трех делим на 2 и получаем число 0,866.
Разрешение треугольников: теоремы синуса и косинуса. Тригонометрическими отношениями правого треугольника являются следующие функции: функция синус, косинус, касательная, косекантная, секущая и котангенс. Все они могут пониматься как отношения между сторонами правого треугольника.
Гониометрическая окружность — это единица, которая имеет единицу в качестве радиуса. Для гониометрической окружности можно дать очень интуитивный смысл всем тригонометрическим отношениям. Посмотрим на следующий рисунок. Тригонометрические упражнения решены.
Для гониометрической окружности можно дать очень интуитивный смысл всем тригонометрическим отношениям. Посмотрим на следующий рисунок. Тригонометрические упражнения решены.
Чему равен косинус и синус 45 градусов
Косинус 45 градусов получается путем деления корня из двух на два или единицы на корень из двух. Следовательно, косинус угла в 45 градусов равен 0,7071. Синус угла в 45 градусов равен косинусу угла в 45 градусов и также выражается как корень из двух, разделенный на два, или единица, разделенная на корень из двух. Числовое значение также 0,7071.
Разрешение треугольника: теоремы синуса и косинуса. Будьте следующим треугольником. Он не должен быть прямоугольником! Проверяются следующие два выражения, известные как теорема синуса и теорема о косинусах. Расчет тригонометрических соотношений. Прямыми тригонометрическими отношениями являются синус, косинус и касательная, а также обратный косекант, секущий и котангенс.
Мы собираемся связать все их с грудью, которые они дают нам. Секант является обратным косинусу. Вычислите прямые отношения α и β Решение. Прямыми тригонометрическими отношениями являются синус, косинус и касательная. Найти тригонометрические отношения следующих углов.
Секант является обратным косинусу. Вычислите прямые отношения α и β Решение. Прямыми тригонометрическими отношениями являются синус, косинус и касательная. Найти тригонометрические отношения следующих углов.
Чему равен косинус и синус 90 градусов
Косинус угла в 90 градусов равен нулю (0), а синус того же угла равен 1.
Чему равен косинус и синус 120 градусов
Косинус 120 градусов равен -0,5 (минус пять десятых), синус того же угла равен 0,866.
Чему равен косинус и синус 0 градусов
Косинус 0 градусов равен 1, а синус 0 градусов равен 0 (нулю).
135º Решение: угол 135º находится во втором квадранте. Угол, который мы должны обрабатывать, составляет -200º. Решение. Мы выведем его, используя фундаментальное соотношение. Остальные тригонометрические отношения получены немедленно. Поскольку α находится в третьем квадранте, сигнал отрицательный.
Демонстрация тригонометрических равенств. Как мы только что видели, выполняется равенство. Мы пришли, чтобы получить сторону В данного выражения, тогда было показано, что равенство истинно. Наконец, мы изучаем каждый из этих двух случаев. Мы будем использовать следующие отношения.
Наконец, мы изучаем каждый из этих двух случаев. Мы будем использовать следующие отношения.
Чему равен косинус и синус 135 градусов
Косинус 135 градусов равен -0,7071 (отрицательное значение), а синус того же угла равен 0,7071 (положительное значение).
Чему равен косинус и синус 150 градусов
Косинус угла в 150 градусов равен -0,866 (отрицательное значение), а синус того же угла равен 0,5 (пять десятых).
Теорема косинусов
Теорема косинусов для общего случая формулируется следующим образом: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника, минус удвоенное произведение этих сторон на косинус угла (х) между ними, что эквивалентно выражению: a 2 = b 2 + c 2 х 2 b c cos х, где а, b, с – это стороны треугольника. Для вычисления стороны прямоугольного треугольника достаточно воспользоваться теоремой Пифагора, из которой вытекает теорема косинусов. Для гипотенузы прямоугольного треугольника теорема формулируется следующим образом: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Мы пытаемся выразить косинус как функцию синуса, возведя квадрат в два члена уравнения: 2. Мы используем формулу синуса суммы двух углов в левой части уравнения. Вычислите высоту дерева, которое на расстоянии 10 м просматривается под углом 30 °. Из каждого из них мы получим тригонометрическое уравнение.
Найти высоту горы 45º. В дальнейшем мы рассматриваем тригонометрические функции, определяемые с помощью степени как меры углов. Следовательно, р будет общим простым множителем а и Ь, противоречием. Они становятся сколь угодно большими. О нерациональности некоторых тригонометрических функций. Математическая ассоциация Америки, математические монографии Каруса.
Производная косинуса
Производная косинуса равна синусу с противоположным знаком (то есть производная cos x равна -sin x).
Вводный урок по тригонометрии был представлен в предыдущей презентации. Школьники ознакомились с понятиями синус, косинус и тангенс, как они обозначаются, как их находить. Рассматривался острый угол некоторого прямоугольного треугольника. Также, они ознакомились с основным тригонометрическим тождеством, что составляет основу для многочисленных формул, с которыми ученики ознакомятся несколько позже.
Также, они ознакомились с основным тригонометрическим тождеством, что составляет основу для многочисленных формул, с которыми ученики ознакомятся несколько позже.
Тригонометрия — это отрасль математики, которая состоит из изучения прямоугольных треугольников — в частности, соотношений сторон прямоугольных треугольников. Триг-функции просто возвращают отношение некоторых двух сторон треугольника, заданного одним углом; или угол, заданный отношением двух сторон. Точка тригонометрии должна быть способна быстро связывать углы с длинами сторон и наоборот, иначе выполнять сложные вычисления. Например, выяснение нового положения спрайта после того, как он переместился на некоторое расстояние, если его направление невозможно без тригонометрии.
Данный урок предлагает рассмотреть определенные углы: 45, 30 и 60 градусов. Необходимо найти их синус, косинус и тангенс. Все эти три угла являются острыми. Подразумевается, что мы работаем с прямоугольными треугольниками, как и в предыдущем уроке.
В принципе, тригонометрия является ярлыком для нахождения отношений, которые могут быть теоретически измерены. Это мощный инструмент и имеет приложения во всех видах полей. Тригонометрия имеет дело с углами и направлениями. Чем шире угол, тем больше его измерение. Ниже приведено описание всех углов до 360 °. Углы, превышающие 360 градусов, являются котерминальными для меньших, то есть они лежат в одном направлении относительно начала координат и имеют тот же результат.
Обратите внимание, как угол увеличивается при вращении влево. Вращение угла вправо уменьшает его. Угол 180 °, 0 ° и любой из их котерминальных углов изображают геометрическую фигуру, прямую линию. Направления скреста инициируют аналог вместо тригонометрического стиля, поэтому он несовместим с тригонометрией. Вот функции быстрого преобразования между ними.
слайды 1-2 (Тема презентации «Значение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов», пример)
Первый слайд презентации «Значение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов» продемонстрирует учащимся некоторый прямоугольный треугольник, острый угол которого равен 30 градусов. Зная о том, что один из углов является прямым, можем легко вычислить значение третьего угла. Сумма всех углов любого треугольника составляет 180 градусов. Об этом свойстве ученики восьмого класса уже должны знать. Итак, для того, чтобы найти третий неизвестный угол, необходимо отнять от 180и градусов 120 градусов, что составляет сумму остальных двух сторон. Третий неизвестный угол равен 60 градусов. Это отмечено на чертеже.
Зная о том, что один из углов является прямым, можем легко вычислить значение третьего угла. Сумма всех углов любого треугольника составляет 180 градусов. Об этом свойстве ученики восьмого класса уже должны знать. Итак, для того, чтобы найти третий неизвестный угол, необходимо отнять от 180и градусов 120 градусов, что составляет сумму остальных двух сторон. Третий неизвестный угол равен 60 градусов. Это отмечено на чертеже.
В тригонометрии угол образуется между двумя линиями: начальным лучом и терминальным лучом. Это потому, что математики предпочитают это так — это стандарт, который используется для определения тригонометрических значений. Другая линия называется терминальным лучом, который может вращаться вокруг начала координат. Тригонометрия имеет дело с отношениями между начальной и конечной линиями. Пример этого показан на следующем изображении.
Сначала это может показаться запутанным, но концепция очень проста. Угол формируется как поворот между двумя линиями или сегментами. На следующем рисунке показано увеличение угла. Обратите внимание на приведенные ниже изображения, терминальная линия останавливается и не продолжается вечно. Это относится к сценарию расстояния между двумя точками. Например, предположим, что начало координатной плоскости является объектом. В этом случае конец стороны терминала является другим объектом, а линия представляет собой расстояние между этими двумя объектами или математически «точками».
На следующем рисунке показано увеличение угла. Обратите внимание на приведенные ниже изображения, терминальная линия останавливается и не продолжается вечно. Это относится к сценарию расстояния между двумя точками. Например, предположим, что начало координатной плоскости является объектом. В этом случае конец стороны терминала является другим объектом, а линия представляет собой расстояние между этими двумя объектами или математически «точками».
Автор отмечает, что отношение катетов прямоугольного треугольника ABС равно одной второй. Откуда автор получил такое число? Дело в том, что катет, который лежит напротив угла 30 градусов, что можно увидеть на рисунке, равняется половине гипотенузы данного треугольника. Это является одним из важных свойств прямоугольных треугольников. Данное отношение является синусом угла 30 градусов. Таким образом, синус угла 30 градусов найден.
Терминальная сторона всегда будет известна как гипотенуза с точки зрения геометрии и тригонометрии. Где задействованы треугольники? Учитывайте двумерную координатную плоскость. Пара значений х и у, используемых для определения положения точки, называется упорядоченной парой.
Пара значений х и у, используемых для определения положения точки, называется упорядоченной парой.
Тригонометрия касается отношения упорядоченных пар. Если любые две упорядоченные пары имеют три связанные линии, которые образуют треугольник, если этот треугольник состоит из прямого угла, то отношение сторон треугольника зависит и зависит от угла, образованного между начальной стороной и гипотенузой.
слайды 3-4 (пример, таблица синусов, косинусов, тангенсов)
Данное отношение является также и косинусом для угла прилежащего к катету, то есть для угла 60 градусов. Далее, исходя из информации, которая была получена на предыдущем уроке, можно посчитать оставшийся тангенс, поделив найденный синус определенного угла на найденный косинус того же угла.
Существуют три основные триггерные функции. Чтобы определить их, мы используем следующие имена для сторон. Имена изменяются в зависимости от угла, который вы считаете.
- Синус — это противоположный ÷ гипотенуза.

- Косинус — это смежный œ гипотенуза.
- Тангенс — противоположный ÷ смежный.
Существуют также три незначительные триггерные функции.
Использование тригонометрических функций: пример
- Секант является обратным косинусом.
- Косакант — это обратная сторона синуса.
- Котангенс является обратным касательной.
Взаимная величина любого значения просто равна 1, деленной на значение. Чтобы моделировать параболический путь скалы, нам нужно разбить наклонную скорость на горизонтальную и вертикальную скорость, а затем переместить спрайт по этим значениям в соответствующих направлениях повторно. Чтобы разделить значения, мы используем тригонометрию. Теперь противоположная сторона должна быть вертикальной, а смежная сторона должна быть горизонтальной.
Следующий слайд аналогичным образом исследует синус, косинус и тангенс угла 45 градусов. Для начала находится третий неизвестный угол. Выясняется, что углы при гипотенузе равны, то есть треугольник, помимо того, что является прямоугольным, еще и равнобедренный. По теореме Пифагора выразим гипотенузу через катеты. Так как они равны, как выяснилось, то можно заменить один катет другим и получить простое произведение числа 2 на квадрат одного из катетов. Далее, автор избавляется от иррациональности и выражает катет. Таким образом, находятся два катета. Далее, пользуясь изученными формулами можно найти и синус, и косинус, и тангенс угла 45 градусов.
Выясняется, что углы при гипотенузе равны, то есть треугольник, помимо того, что является прямоугольным, еще и равнобедренный. По теореме Пифагора выразим гипотенузу через катеты. Так как они равны, как выяснилось, то можно заменить один катет другим и получить простое произведение числа 2 на квадрат одного из катетов. Далее, автор избавляется от иррациональности и выражает катет. Таким образом, находятся два катета. Далее, пользуясь изученными формулами можно найти и синус, и косинус, и тангенс угла 45 градусов.
Затем мы умножим его на гипотенузу. Вам рекомендуется попытаться каждый из них узнать больше о тригонометрии. Одна из великих особенностей тригонометрических функций состоит в том, что они все циклические, что означает, что они продолжают повторяться. Таким образом, вы можете получить сложные движения, которые повторяются бесконечно без особых проблем.
Предсказание положения спрайта после того, как он перемещается на некоторое расстояние в определенном направлении — это простое применение синуса и косинуса. Одно интересное использование этого состоит в том, чтобы заставить спрайт двигаться перпендикулярно направлению, в котором он находится, или перемещаться по кругу, не меняя его направления. Перемещенное расстояние можно рассчитать с помощью более сложной тригонометрии.
. Углы более 90 градусов также имеют триггерные функции.
Одно интересное использование этого состоит в том, чтобы заставить спрайт двигаться перпендикулярно направлению, в котором он находится, или перемещаться по кругу, не меняя его направления. Перемещенное расстояние можно рассчитать с помощью более сложной тригонометрии.
. Углы более 90 градусов также имеют триггерные функции.
На последнем слайде приводятся данные значения в виде таблицы. Желательно, чтобы школьники записали таблицу себе с тетради. Можно сказать, она является аналогом таблицы умножения, только тригонометрическая. Желательно, чтобы школьники знали о том, откуда появились данные значения и запомнили таблицы.
Синусы, косинусы и их родственники | Тригонометрия: очень краткое введение
Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаКнигиЖурналы Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
CITE
Van Brummelen, Glen,
‘Sines, Cosines и их родственников’
,
Тригонометрия: очень короткое введение
, очень короткие вступления
(
Oxford,
202020;
онлайн-издание,
Oxford Academic
, 23 января 2020 г.
), https://doi.org/10.1093/actrade/9780198814313.003.0002,
, по состоянию на 30 сентября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаКнигиЖурналы Термин поиска на микросайте
Advanced Search
Abstract
Раздел «Синусы, косинусы и их родственники» начинается с определения основных тригонометрических функций — синуса, косинуса и тангенса — и объяснения их использования. Эти функции представляют собой геометрические величины, определяемые с помощью отношений противоположной, смежной и гипотенузной сторон прямоугольного треугольника. Менее распространенными функциями являются функции косеканса, секанса и котангенса. Обсуждается история именования тригонометрических функций наряду с объяснением еще более малоизвестных функций: аверсного синуса, аверсного косинуса, экссеканса и экссеканса. Развернутый синус часто использовался в практических приложениях, таких как астрономия, навигация и геодезия. Наконец, рассматриваются обратные тригонометрические функции и графики тригонометрических функций.
Эти функции представляют собой геометрические величины, определяемые с помощью отношений противоположной, смежной и гипотенузной сторон прямоугольного треугольника. Менее распространенными функциями являются функции косеканса, секанса и котангенса. Обсуждается история именования тригонометрических функций наряду с объяснением еще более малоизвестных функций: аверсного синуса, аверсного косинуса, экссеканса и экссеканса. Развернутый синус часто использовался в практических приложениях, таких как астрономия, навигация и геодезия. Наконец, рассматриваются обратные тригонометрические функции и графики тригонометрических функций.
Ключевые слова: аналитическая геометрия, угол, Архимед, Декарт, окружность, координаты, циклоида, Рене Декарт, Региомонтан, касательная
Предмет
Чистая математика
Серия
Очень краткое введение
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Войти через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
таблиц синус-косинусоидальных триггеров
таблиц синус-косинусоидальных триггеровТаблицы синуса и косинуса
для углов в градусах
Для синуса прочтите первые 6 столбцов.
Для косинуса прочтите последние 6 столбцов.
| Угол | Угол +.0 | Угол +.2 | Угол +.4 | Угол +.6 | Угол +0,8 | Угол +1,185 | +0,8 | Угол +1,10185 | +0,8 | +1,10185 | +0,8 | +1,0185 | .0184 0.0000 | 0.0035 | 0.0070 | 0.0105 | 0.0140 | 0.0175 | 89 | |
| 1 | 0.0175 | 0.0209 | 0.0244 | 0.0279 | 0.0314 | 0. 0349 0349 | 88 | |||||||||||||
| 2 | 0,0349 | 0,0384 | 0,0419 | 0,0454 | 0,0488 | 0,0523 | 871 | |||||||||||||
| 3 | 0.0523 | 0.0558 | 0.0593 | 0.0628 | 0.0663 | 0.0698 | 86 | |||||||||||||
| 4 | 0.0698 | 0.0732 | 0.0767 | 0.0802 | 0.0837 | 0.0872 | 85 | |||||||||||||
| 5 | 0,0872 | 0,0906 | 0,0941 | 0,0976 | 0,1814 0,1840185 | 0.1045 | 84 | |||||||||||||
| 6 | 0.1045 | 0.1080 | 0.1115 | 0.1149 | 0.1184 | 0.1219 | 83 | |||||||||||||
| 7 | 0.1219 | 0.1253 | 0.1288 | 0.1323 | 0,1357 | 0,1392 | 82 | |||||||||||||
| 8 | 0,1392 | 0,1426 | 0,1484 0,14840184 0. 1495 1495 | 0.1530 | 0.1564 | 81 | ||||||||||||||
| 9 | 0.1564 | 0.1599 | 0.1633 | 0.1668 | 0.1702 | 0.1736 | 80 | |||||||||||||
| 10 | 0.1736 | 0.1771 | 0,1805 | 0,1840 | 0,1874 | 0,1908 | 79 | |||||||||||||
| 11 | 0,1908 | 0.1942 | 0.1977 | 0.2011 | 0.2045 | 0.2079 | 78 | |||||||||||||
| 12 | 0.2079 | 0.2113 | 0.2147 | 0.2181 | 0.2215 | 0.2250 | 77 | |||||||||||||
| 13 | 0,2250 | 0,2284 | 0,2317 | 0,2351 | 0,2385 | 0,2419 | 79 | 0.2419 | 0.2453 | 0.2487 | 0.2521 | 0. 2554 2554 | 0.2588 | 75 | ||||||
| 15 | 0.2588 | 0.2622 | 0.2656 | 0.2689 | 0.2723 | 0.2756 | 74 | |||||||||||||
| 16 | 0,2756 | 0,2790 | 0,2823 | 0,2857 | 0,2890 | 0,219824 | 73 | |||||||||||||
| 17 | 0.2924 | 0.2957 | 0.2990 | 0.3024 | 0.3057 | 0.3090 | 72 | |||||||||||||
| 18 | 0.3090 | 0.3123 | 0.3156 | 0.3190 | 0.3223 | 0,3256 | 71 | |||||||||||||
| 19 | 0,3256 | 0,3289 | 0,3352 | 0.3387 | 0.3420 | 70 | ||||||||||||||
| 20 | 0.3420 | 0.3453 | 0.3486 | 0.3518 | 0.3551 | 0.3584 | 69 | |||||||||||||
| 21 | 0. 3584 3584 | 0.3616 | 0.3649 | 0,3681 | 0,3714 | 0,3746 | 68 | |||||||||||||
| 22 | 0,3746 | 0,37460.3811 | 0.3843 | 0.3875 | 0.3907 | 67 | ||||||||||||||
| 23 | 0.3907 | 0.3939 | 0.3971 | 0.4003 | 0.4035 | 0.4067 | 66 | |||||||||||||
| 24 | 0.4067 | 0,4099 | 0,4131 | 0,4163 | 0,4195 | 0,4226 | 65 | 251980185 | 0.4226 | 0.4258 | 0.4289 | 0.4321 | 0.4352 | 0.4384 | 64 | |||||
| 26 | 0.4384 | 0.4415 | 0.4446 | 0.4478 | 0.4509 | 0.4540 | 63 | |||||||||||||
| 27 | 0,4540 | 0,4571 | 0,4602 | 0,4633 | 0,4664 | 0,4869584 62 | ||||||||||||||
| 28 | 0. 4695 4695 | 0.4726 | 0.4756 | 0.4787 | 0.4818 | 0.4848 | 61 | |||||||||||||
| 29 | 0.4848 | 0.4879 | 0.4909 | 0.4939 | 0.4970 | 0,5000 | 60 | |||||||||||||
| 30 | 0,5000 | 0,5030 | 0,5060 | 0,51090 | 0.5120 | 0.5150 | 59 | |||||||||||||
| 31 | 0.5150 | 0.5180 | 0.5210 | 0.5240 | 0.5270 | 0.5299 | 58 | |||||||||||||
| 32 | 0.5299 | 0.5329 | 0.5358 | 0,5388 | 0,5417 | 0,5446 | 57 | |||||||||||||
| 33 | 0,5446 | 0,51859 | 0.5505 | 0.5534 | 0.5563 | 0.5592 | 56 | |||||||||||||
| 34 | 0.5592 | 0. 5621 5621 | 0.5650 | 0.5678 | 0.5707 | 0.5736 | 55 | |||||||||||||
| 35 | 0.5736 | 0,5764 | 0,5793 | 0,5821 | 0,5850 | 0,5878 | 54 | |||||||||||||
| 89 | 0.5878 | 0.5906 | 0.5934 | 0.5962 | 0.5990 | 0.6018 | 53 | |||||||||||||
| 37 | 0.6018 | 0.6046 | 0.6074 | 0.6101 | 0.6129 | 0.6157 | 52 | |||||||||||||
| 38 | 0,6157 | 0,6184 | 0,6211 | 0,6239 | 0,6266 | 0,6293 | 5 10188||||||||||||||
| 39 | 0.6293 | 0.6320 | 0.6347 | 0.6374 | 0.6401 | 0.6428 | 50 | |||||||||||||
| 40 | 0.6428 | 0.6455 | 0. 6481 6481 | 0.6508 | 0.6534 | 0.6561 | 49 | |||||||||||||
| 41 | 0,6561 | 0,6587 | 0,6613 | 0,6639 | 0,6639 | 0,65870185 | 0.6691 | 48 | ||||||||||||
| 42 | 0.6691 | 0.6717 | 0.6743 | 0.6769 | 0.6794 | 0.6820 | 47 | |||||||||||||
| 43 | 0.6820 | 0.6845 | 0.6871 | 0.6896 | 0,6921 | 0,6947 | 46 | |||||||||||||
| 44 | 0,6947 | 0,6972 | 0,6972 | 0,69720185 | 0.7022 | 0.7046 | 0.7071 | 45 | ||||||||||||
| 45 | 0.7071 | 0.7096 | 0.7120 | 0.7145 | 0.7169 | 0.7193 | 44 | |||||||||||||
| 46 | 0.7193 | 0. 7218 7218 | 0,7242 | 0,7266 | 0,7290 | 0,7314 | 43 | |||||||||||||
| 47 | 0.7337 | 0.7361 | 0.7385 | 0.7408 | 0.7431 | 42 | ||||||||||||||
| 48 | 0.7431 | 0.7455 | 0.7478 | 0.7501 | 0.7524 | 0.7547 | 41 | |||||||||||||
| 49 | 0,7547 | 0,7570 | 0,7593 | 0,7615 | 0,7638 | 0,7660 | 40 | 0183 | 50 | 0.7660 | 0.7683 | 0.7705 | 0.7727 | 0.7749 | 0.7771 | 39 | ||||
| 51 | 0.7771 | 0.7793 | 0.7815 | 0.7837 | 0.7859 | 0.7880 | 38 | |||||||||||||
| 52 | 0,7880 | 0,7902 | 0,7923 | 0,7944 | 0,7965 | 6 | 37 | |||||||||||||
| 53 | 0. 7986 7986 | 0.8007 | 0.8028 | 0.8049 | 0.8070 | 0.8090 | 36 | |||||||||||||
| 54 | 0.8090 | 0.8111 | 0.8131 | 0.8151 | 0.8171 | 0,8192 | 35 | |||||||||||||
| 55 | 0,8192 | 0,8211 | 0,8231 | 90.01850.8271 | 0.8290 | 34 | ||||||||||||||
| 56 | 0.8290 | 0.8310 | 0.8329 | 0.8348 | 0.8368 | 0.8387 | 33 | |||||||||||||
| 57 | 0.8387 | 0.8406 | 0.8425 | 0,8443 | 0,8462 | 0,8480 | 32 | |||||||||||||
| 58 | 0,8480 | 4 0.01850.8517 | 0.8536 | 0.8554 | 0.8572 | 31 | ||||||||||||||
| 59 | 0.8572 | 0.8590 | 0. 8607 8607 | 0.8625 | 0.8643 | 0.8660 | 30 | |||||||||||||
| 60 | 0.8660 | 0,8678 | 0,8695 | 0,8712 | 0,8729 | 0,8746 | 29 | 6 185 | 0.8746 | 0.8763 | 0.8780 | 0.8796 | 0.8813 | 0.8829 | 28 | |||||
| 62 | 0.8829 | 0.8846 | 0.8862 | 0.8878 | 0.8894 | 0.8910 | 27 | |||||||||||||
| 63 | 0,8910 | 0,8926 | 0,8942 | 0,8957 | 0,8973 | 0,88985 | 80184 26 | |||||||||||||
| 64 | 0.8988 | 0.9003 | 0.9018 | 0.9033 | 0.9048 | 0.9063 | 25 | |||||||||||||
| 65 | 0.9063 | 0.9078 | 0.9092 | 0. 9107 9107 | 0.9121 | 0,9135 | 24 | |||||||||||||
| 66 | 0,9135 | 0,9150 | 0,9164 | 0, | 0.9191 | 0.9205 | 23 | |||||||||||||
| 67 | 0.9205 | 0.9219 | 0.9232 | 0.9245 | 0.9259 | 0.9272 | 22 | |||||||||||||
| 68 | 0.9272 | 0.9285 | 0.9298 | 0,9311 | 0,9323 | 0,9336 | 21 | |||||||||||||
| 69 | 0,9336 | 0, | 0.9361 | 0.9373 | 0.9385 | 0.9397 | 20 | |||||||||||||
| 70 | 0.9397 | 0.9409 | 0.9421 | 0.9432 | 0.9444 | 0.9455 | 19 | |||||||||||||
| 71 | 0.9455 | 0,9466 | 0,9478 | 0,9489 | 0,9500 | 0,9511 | 18 | |||||||||||||
0. 9511 9511 | 0.9521 | 0.9532 | 0.9542 | 0.9553 | 0.9563 | 17 | ||||||||||||||
| 73 | 0.9563 | 0.9573 | 0.9583 | 0.9593 | 0.9603 | 0.9613 | 16 | |||||||||||||
| 74 | 0,9613 | 0,9622 | 0,9632 | 0,9641 | 0,9650 | 0,9659 | 1||||||||||||||
| 75 | 0.9659 | 0.9668 | 0.9677 | 0.9686 | 0.9694 | 0.9703 | 14 | |||||||||||||
| 76 | 0.9703 | 0.9711 | 0.9720 | 0.9728 | 0.9736 | 0.9744 | 13 | |||||||||||||
| 77 | 0,9744 | 0,9751 | 0,9759 | 0,9767 | 0.9781 | 12 | ||||||||||||||
| 78 | 0.9781 | 0. 9789 9789 | 0.9796 | 0.9803 | 0.9810 | 0.9816 | 11 | |||||||||||||
| 79 | 0.9816 | 0.9823 | 0.9829 | 0.9836 | 0,9842 | 0,9848 | 10 | |||||||||||||
| 80 | 0,9848 | 0,9854 | 0 9.0185 | 0.9866 | 0.9871 | 0.9877 | 9 | |||||||||||||
| 81 | 0.9877 | 0.9882 | 0.9888 | 0.9893 | 0.9898 | 0.9903 | 8 | |||||||||||||
| 82 | 0.9903 | 0.9907 | 0,9912 | 0,9917 | 0,9921 | 0,9925 | 7 | |||||||||||||
| 83 | 0,9925 | 70184 0.9930 | 0.9934 | 0.9938 | 0.9942 | 0.9945 | 6 | |||||||||||||
| 84 | 0.9945 | 0.9949 | 0. 9952 9952 | 0.9956 | 0.9959 | 0.9962 | 5 | |||||||||||||
| 85 | 0,9962 | 0,9965 | 0,9968 | 0,9971 | 0,9973 | 0,9976 | 4 | 300184 86 | 0.9976 | 0.9978 | 0.9980 | 0.9982 | 0.9984 | 0.9986 | 3 | |||||
| 87 | 0.9986 | 0.9988 | 0.9990 | 0.9991 | 0.9993 | 0.9994 | 2 | |||||||||||||
| 88 | 0,9994 | 0,9995 | 0,9996 | 0,9997 | 0,9998 | 0,81 | ||||||||||||||
| 89 | 0.9998 | 0.9999 | 0.9999 | 1.0000 | 1.0000 | 1.0000 | 0 | |||||||||||||
| 90 | 1.0000 | 1.0000 | 1.0000 | |||||||||||||||||
| Угол+1 | Угол+. 8 8 | Угол+.6 | Угол+.4 | Угол+.2 | угол+.0 | косинус |
© 2006, Агнес Аццолино www.mathnstuff.com/math/spoken/here/2class/330/sincost.htm |
16. Тригонометрическая таблица|Chip One Stop
- TOP
- Инженерные ссылки
- Тригонометрическая таблица
Он показывает значение от 0 до 90 градусов для синуса (синуса и синуса), косинус(cos и косинус), тангенс(tan и тангенс), косеканс(cos и косеканс), секанс(сек и секанс) и котангенс(котангенс и котангенс).
| θ゜ | θрад | sinθ | г. , потому что , потому что | г.tanθ | косекθ | сек | детская кроваткаθ |
|---|---|---|---|---|---|---|---|
0 | 0,0000 | 0 | 1.0000 | 0 | ∞ | 1.0000 | ∞ |
1 | 0,0175 | 0,0175 | 0,9998 | 0,0175 | 57. | 1.0002 | 57.3008 |
2 | 0,0349 | 0,0349 | 0,9994 | 0,0349 | 28.6533 | 1.0006 | 28. |
3 | 0,0524 | 0,0523 | 0,9986 | 0,0524 | 19.1058 | 1.0014 | 19.0811 |
4 | 0,0698 | 0,0698 | 0,9976 | 0,0699 | 14. | 1.0024 | 14.3013 |
5 | 0,0873 | 0,0872 | 0,9962 | 0,0875 | 11.4732 | 1.0038 | 11. |
6 | 0,1047 | 0,1045 | 0,9945 | 0,1051 | 9,5666 | 1.0055 | 9.5143 |
7 | 0,1222 | 0,1219 | 0,9925 | 0,1228 | 8. | 1,0075 | 8.1446 |
8 | 0,1396 | 0,1392 | 0,9903 | 0,1405 | 7.1855 | 1.0098 | 7. |
9 | 0,1571 | 0,1564 | 0,9877 | 0,1584 | 6.3926 | 1.0125 | 6.3137 |
10 | 0,1745 | 0,1737 | 0,9848 | 0,1763 | 5. | 1.0154 | 5.6714 |
11 | 0,1920 | 0,1908 | 0,9816 | 0,1944 | 5.2408 | 1.0187 | 5. |
12 | 0,2094 | 0,2079 | 0,9781 | 0,2126 | 4.8098 | 1.0223 | 4.7046 |
13 | 0,2269 | 0,2250 | 0,9744 | 0,2309 | 4. | 1.0263 | 4.3315 |
14 | 0,2444 | 0,2419 | 0,9703 | 0,2493 | 4.1336 | 1.0306 | 4. |
15 | 0,2618 | 0,2588 | 0,9659 | 0,2679 | 3,8637 | 1.0353 | 3,7320 |
16 | 0,2793 | 0,2756 | 0,9613 | 0,2867 | 3,6279 | 1. | 3.4874 |
17 | 0,2967 | 0,2924 | 0,9563 | 0,3057 | 3.4203 | 1.0457 | 3.2708 |
18 | 0,3142 | 0,3090 | 0,9511 | 0,3249 | 3. | 1.0515 | 3.0777 |
19 | 0,3316 | 0,3256 | 0,9455 | 0,3443 | 3.0715 | 1.0576 | 2. |
20 | 0,3491 | 0,3420 | 0,9397 | 0,3640 | 2,9238 | 1.0642 | 2,7474 |
21 | 0,3665 | 0,3584 | 0,9336 | 0,3839 | 2. | 1.0711 | 2,6051 |
22 | 0,3840 | 0,3746 | 0,9272 | 0,4040 | 2,6694 | 1.0785 | 2. |
23 | 0,4014 | 0,3907 | 0,9205 | 0,4245 | 2,5593 | 1.0864 | 2,3558 |
24 | 0,4189 | 0,4067 | 0,9135 | 0,4452 | 2,4586 | 1. | 2.2460 |
25 | 0,4363 | 0,4226 | 0,9063 | 0,4663 | 2,3662 | 1.1034 | 2.1445 |
26 | 0,4538 | 0,4384 | 0,8988 | 0,4877 | 2. | 1.1126 | 2.0503 |
27 | 0,4712 | 0,4540 | 0,8910 | 0,5095 | 2.2027 | 1.1223 | 1,9626 |
28 | 0,4887 | 0,4695 | 0,8829 | 0,5317 | 2. | 1.1326 | 1.8807 |
29 | 0,5062 | 0,4848 | 0,8746 | 0,5543 | 2,0627 | 1.1434 | 1. |
30 | 0,5236 | 0,5000 | 0,8660 | 0,5774 | 2.0000 | 1.1547 | 1.7320 |
31 | 0,5411 | 0,5150 | 0,8572 | 0,6009 | 1. | 1.1666 | 1,6643 |
32 | 0,5585 | 0,5299 | 0,8480 | 0,6249 | 1.8871 | 1.1792 | 1. |
33 | 0,5760 | 0,5446 | 0,8387 | 0,6494 | 1,8361 | 1.1924 | 1,5399 |
34 | 0,5934 | 0,5592 | 0,8290 | 0,6745 | 1,7883 | 1. | 1.4826 |
35 | 0,6109 | 0,5736 | 0,8191 | 0,7002 | 1,7434 | 1.2208 | 1.4281 |
36 | 0,6283 | 0,5878 | 0,8090 | 0,7265 | 1. | 1.2361 | 1.3764 |
37 | 0,6458 | 0,6018 | 0,7986 | 0,7536 | 1,6616 | 1.2521 | 1. |
38 | 0,6632 | 0,6157 | 0,7880 | 0,7813 | 1,6243 | 1.2690 | 1.2799 |
39 | 0,6807 | 0,6293 | 0,7771 | 0,8098 | 1,5890 | 1,2868 | 1. |
40 | 0,6981 | 0,6428 | 0,7660 | 0,8391 | 1,5557 | 1.3054 | 1.1918 |
41 | 0,7156 | 0,6561 | 0,7547 | 0,8693 | 1,5243 | 1. | 1.1504 |
42 | 0,7330 | 0,6691 | 0,7431 | 0,9004 | 1.4945 | 1.3456 | 1.1106 |
43 | 0,7505 | 0,6820 | 0,7314 | 0,9325 | 1. | 1,3673 | 1.0724 |
44 | 0,7679 | 0,6947 | 0,7193 | 0,9657 | 1.4396 | 1.3902 | 1. |
45 | 0,7854 | 0,7071 | 0,7071 | 1.0000 | 1.4142 | 1.4142 | 1.0000 |
46 | 0,8029 | 0,7193 | 0,6947 | 1. | 1.3902 | 1.4396 | 0,9657 |
47 | 0,8203 | 0,7314 | 0,6820 | 1.0724 | 1,3673 | 1. | 0,9325 |
48 | 0,8378 | 0,7431 | 0,6691 | 1.1106 | 1.3456 | 1.4945 | 0,9004 |
49 | 0,8552 | 0,7547 | 0,6561 | 1. | 1.3250 | 1,5243 | 0,8693 |
50 | 0,8727 | 0,7660 | 0,6428 | 1.1917 | 1.3054 | 1,5557 | 0,8391 |
51 | 0,8901 | 0,7771 | 0,6293 | 1. | 1,2868 | 1,5890 | 0,8098 |
52 | 0,9076 | 0,7880 | 0,6156 | 1.2800 | 1.2690 | 1,6243 | 0,7812 |
53 | 0,9250 | 0,7986 | 0,6018 | 1. | 1.2521 | 1,6616 | 0,7536 |
54 | 0,9245 | 0,8090 | 0,5878 | 1.3764 | 1.2361 | 1. | 0,7265 |
55 | 0,9599 | 0,8192 | 0,5736 | 1.4281 | 1.2208 | 1,7434 | 0,7002 |
56 | 0,9774 | 0,8290 | 0,5592 | 1. | 1.2062 | 1,7883 | 0,6745 |
57 | 0,9948 | 0,8387 | 0,5446 | 1,5399 | 1.1924 | 1,8361 | 0,6494 |
58 | 1. | 0,8480 | 0,5299 | 1.6003 | 1.1792 | 1.8871 | 0,6249 |
59 | 1.0297 | 0,8572 | 0,5150 | 1,6643 | 1. | 1.9416 | 0,6009 |
60 | 1.0472 | 0,8660 | 0,5000 | 1.7321 | 1.1547 | 2.0000 | 0,5773 |
61 | 1,0647 | 0,8746 | 0,4848 | 1. | 1.1434 | 2,0627 | 0,5543 |
62 | 1.0821 | 0,8829 | 0,4695 | 1.8807 | 1.1326 | 2. | 0,5317 |
63 | 1.0996 | 0,8910 | 0,4540 | 1,9626 | 1.1223 | 2.2027 | 0,5095 |
64 | 1. | 0,8988 | 0,4384 | 2.0503 | 1.1126 | 2.2812 | 0,4877 |
65 | 1.1345 | 0,9063 | 0,4226 | 2. | 1.1034 | 2,3664 | 0,4663 |
66 | 1.1519 | 0,9135 | 0,4067 | 2.2461 | 1.0946 | 2,4586 | 0,4452 |
67 | 1. | 0,9205 | 0,3907 | 2,3560 | 1.0863 | 2,5595 | 0,4244 |
68 | 1.1868 | 0,9272 | 0,3746 | 2. | 1.0785 | 2,6694 | 0,4040 |
69 | 1.2043 | 0,9336 | 0,3584 | 2,6051 | 1.0711 | 2. | 0,3839 |
70 | 1.2217 | 0,9397 | 0,3420 | 2,7475 | 1.0642 | 2,9238 | 0,3640 |
71 | 1. | 0,9455 | 0,3256 | 2.9042 | 1.0576 | 3.0715 | 0,3443 |
72 | 1,2566 | 0,9511 | 0,3090 | 3. | 1.0515 | 3.2361 | 0,3249 |
73 | 1.2741 | 0,9563 | 0,2924 | 3.2710 | 1.0457 | 3. | 0,3057 |
74 | 1.2915 | 0,9613 | 0,2756 | 3.4874 | 1.0403 | 3,6279 | 0,2867 |
75 | 1. | 0,9659 | 0,2588 | 3,7321 | 1.0353 | 3,8637 | 0,2679 |
76 | 1.3265 | 0,9703 | 0,2419 | 4. | 1.0306 | 4.1336 | 0,2493 |
77 | 1,3439 | 0,9744 | 0,2250 | 4.3314 | 1.0263 | 4. | 0,2309 |
78 | 1.3614 | 0,9781 | 0,2079 | 4.7047 | 1.0223 | 4.8098 | 0,2126 |
79 | 1,3788 | 0,9816 | 0,1908 | 5. | 1.0187 | 5.2408 | 0,1944 |
80 | 1,3963 | 0,9848 | 0,1737 | 5.6712 | 1.0154 | 5. | 0,1763 |
81 | 1.4137 | 0,9877 | 0,1564 | 6.3139 | 1.0125 | 6.3926 | 0,1584 |
82 | 1. | 0,9903 | 0,1392 | 7.1154 | 1.0098 | 7.1853 | 0,1405 |
83 | 1.4486 | 0,9925 | 0,1219 | 8. | 1.0075 | 8.2053 | 0,1228 |
84 | 1.4661 | 0,9945 | 0,1045 | 9.5147 | 1,0055 | 9,5671 | 0,1051 |
85 | 1,4835 | 0,9962 | 0,0872 | 11. | 1.0038 | 11.4737 | 0,0875 |
86 | 1.5010 | 0,9976 | 0,0698 | 14.3000 | 1.0024 | 14. | 0,0699 |
87 | 1,5184 | 0,9986 | 0,0523 | 19.0824 | 1.0014 | 19.1086 | 0,0524 |
88 | 1,5359 | 0,9994 | 0,0349 | 28. | 1.0006 | 28.6539 | 0,0349 |
89 | 1,5533 | 0,9998 | 0,0175 | 57.2800 | 1.0002 | 57. | 0,0175 |
90 | 1.5708 | 1.0000 | 0 | ∞ | 1.0000 | ∞ | 0 |
Таблица синусов и косинусов в радианах.
 Тригонометрические функции
Тригонометрические функцииТригонометрия как наука зародилась на Древнем Востоке. Первые тригонометрические соотношения были разработаны астрономами для создания точного календаря и ориентирования по звездам. Эти расчеты относятся к сферической тригонометрии, а в школьном курсе изучают отношения сторон и углов плоского треугольника.
Тригонометрия — раздел математики, изучающий свойства тригонометрических функций и отношения между сторонами и углами треугольников.
В период расцвета культуры и науки в I тысячелетии нашей эры знания распространились с Древнего Востока в Грецию. Но главные открытия тригонометрии — заслуга мужчин Арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений синусов, тангенсов и котангенсов. Понятие синуса и косинуса ввели индийские ученые. Много внимания уделено тригонометрии в трудах таких великих деятелей древности, как Евклид, Архимед и Эратосфен.
Основные тригонометрические величины
Основными тригонометрическими функциями числового аргумента являются синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синус, косинус, тангенс и котангенс.
Формулы для расчета значений этих величин основаны на теореме Пифагора. Школьникам оно более известно в формулировке: «Пифагорейские штаны, равные во всех направлениях», так как доказательство приведено на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы расчета этих величин для угла А и проследим связь тригонометрических функций:
Как видите, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы c, а катет b как cos A*c, то получим следующие формулы для тангенса и котангенса:
тригонометрическая окружность
Графически соотношение указанных величин можно представить следующим образом:
Окружность в данном случае представляет все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от угла. Например, sin α будет со знаком «+», если α принадлежит I и II четвертям окружности, то есть находится в диапазоне от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательной величиной.
Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от угла. Например, sin α будет со знаком «+», если α принадлежит I и II четвертям окружности, то есть находится в диапазоне от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательной величиной.
Попробуем построить тригонометрические таблицы для конкретных углов и выяснить значение величин.
Значения α, равные 30°, 45°, 60°, 90°, 180° и так далее, называются частными случаями. Значения тригонометрических функций для них рассчитываются и представляются в виде специальных таблиц.
Эти ракурсы выбраны не случайно. Обозначение π в таблицах относится к радианам. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Это значение было введено для того, чтобы установить универсальное отношение; при расчете в радианах фактическая длина радиуса в см значения не имеет.
Углы в таблицах для тригонометрических функций соответствуют значениям в радианах:
Итак, нетрудно догадаться, что 2π — это полный круг или 360°.
Свойства тригонометрических функций: синус и косинус
Для того чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо нарисовать их функции. Это можно сделать в виде кривой, расположенной в двумерной системе координат.
Рассмотрим сравнительную таблицу свойств синусоиды и косинуса:
| синусоида | косинусоид |
|---|---|
| y = sin x | y = cos x |
| ОДЗ[-1; один] | ОДЗ [-1; один] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т.е. нечетная функция | cos (-x) = cos x, т.е. функция четная |
| функция периодическая, наименьший период 2π | |
| sin x › 0, где x принадлежит четвертям I и II или от 0° до 180° (2πk, π + 2πk) | cos x › 0, где x принадлежит четвертям I и IV или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, где x принадлежит четвертям III и IV или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, где x принадлежит четвертям II и III или из 90 ° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на интервале [- π/2 + 2πk, π/2 + 2πk] | возрастает на интервале [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить, является функция четной или нет, очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси ОХ. Если знаки одинаковые, функция четная; в противном случае это странно.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси ОХ. Если знаки одинаковые, функция четная; в противном случае это странно.
Введение радиан и перечисление основных свойств синусоиды и косинуса позволяют вывести следующую закономерность:
Проверить правильность формулы очень легко. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно выполнить, просмотрев таблицы или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса существенно отличаются от синусоиды и косинуса. Значения tg и ctg обратны друг другу.
- Y = tgx.
- Тангенс стремится к значениям y при x = π/2 + πk, но никогда их не достигает.
- Наименьший положительный период тангеноида равен π.
- Tg(-x)=-tgx, т. е. функция нечетная.
- Tg x = 0, для x = πk.

- Функция увеличивается.
- Tg x › 0, для x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, для x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоида ниже по тексту.
Основные свойства котангенсоида:
- Y = ctgx.
- В отличие от функций синуса и косинуса, в тангеноиде Y может принимать значения множества всех действительных чисел.
- Котангенсоид стремится к значениям y при x = πk, но никогда их не достигает.
- Наименьший положительный период котангенсоида равен π.
- Ctg(-x)=-ctgx, т. е. функция нечетная.
- Ctg x = 0, для x = π/2 + πk.
- Функция уменьшается.
- Ctg x › 0, для x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, для x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Fix
ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Таблица значений тригонометрических функций составляется для углов 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им углов в радианах. Из тригонометрических функций в таблице указаны синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записываются в виде дроби с сохранением знаков извлечения квадратного корня из чисел, что очень часто помогает сократить сложные математические выражения. Для тангенса и котангенса значения некоторых углов определить невозможно. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций ставится прочерк. Принято считать, что тангенс и котангенс таких углов равны бесконечности. На отдельной странице приведены формулы приведения тригонометрических функций.
Из тригонометрических функций в таблице указаны синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записываются в виде дроби с сохранением знаков извлечения квадратного корня из чисел, что очень часто помогает сократить сложные математические выражения. Для тангенса и котангенса значения некоторых углов определить невозможно. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций ставится прочерк. Принято считать, что тангенс и котангенс таких углов равны бесконечности. На отдельной странице приведены формулы приведения тригонометрических функций.
В таблице значений тригонометрической функции синуса приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусная мера, которая соответствует sin 0 pi, sin pi/6, sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi в радианной мере углов. Школьная таблица синусов.
Для функции тригонометрического косинуса в таблице приведены значения для следующих углов: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 в градусах, что соответствует cos 0 pi, cos pi к 6, cos pi к 4, cos pi к 3, cos pi к 2, cos pi, cos 3 pi к 2, cos 2 pi в радианах углов. Школьная таблица косинусов.
Тригонометрическая таблица для тангенса тригонометрической функции дает значения для следующих углов: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 в градусной мере, что соответствует tg 0 pi, tg pi / 6, tg pi / 4, tg pi/3, tg pi, tg 2 pi в радианной мере углов. Следующие значения тригонометрических функций тангенса не определены тг 90, tg 270, tg pi/2, tg 3 pi/2 и считаются равными бесконечности.
Для котангенса тригонометрической функции в тригонометрической таблице даны следующие углы: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 в градусах, что соответствует ctg pi/6, ctg pi/4, ctg pi / 3, tg pi / 2, tg 3 pi/2 в радианной мере углов. Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi и считаются равными бесконечности.
Значения тригонометрических функций секанса и косеканса даны для тех же углов в градусах и радианах, что и синус, косинус, тангенс, котангенс.
В таблице значений тригонометрических функций нестандартных углов приведены значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градуса и в радианы пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражаются через дроби и квадратные корни для упрощения приведения дробей в школьных примерах.
Еще три монстра тригонометрии. Первый — это тангенс 1,5 с половиной градуса, или число пи, деленное на 120. Второе — это косинус числа пи, деленное на 240, пи/240. Самый длинный — это косинус числа пи, деленного на 17, пи/17.
Тригонометрический круг значений функций синуса и косинуса наглядно представляет знаки синуса и косинуса в зависимости от величины угла. Специально для блондинок значения косинуса подчеркнуты зеленой черточкой, чтобы меньше путаться. Также очень наглядно представлен перевод градусов в радианы, когда радианы выражаются через число пи.
Также очень наглядно представлен перевод градусов в радианы, когда радианы выражаются через число пи.
В этой тригонометрической таблице представлены значения синуса, косинуса, тангенса и котангенса для углов от 0 ноль до 90 девяносто градусов с интервалом в один градус. Для первых сорока пяти степеней названия тригонометрических функций надо смотреть вверху таблицы. Первый столбец содержит градусы, в следующих четырех столбцах записываются значения синусов, косинусов, тангенсов и котангенсов.
Для углов от сорока пяти градусов до девяноста градусов названия тригонометрических функций записываются внизу таблицы. Последний столбец содержит градусы, в предыдущих четырех столбцах записываются значения косинусов, синусов, котангенсов и тангенсов. Следует быть осторожным, так как названия тригонометрических функций в нижней части тригонометрической таблицы отличаются от названий в верхней части таблицы. Синусы и косинусы меняются местами, как тангенс и котангенс. Это связано с симметрией значений тригонометрических функций.
Знаки тригонометрических функций показаны на рисунке выше. Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синуса от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов, или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательный тангенс и котангенс равны 9От 0 до 180 градусов и от 270 до 360 градусов, или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Тригонометрические функции синуса, тангенса и котангенса являются нечетными функциями. Значения этих функций для отрицательных углов будут отрицательными. Косинус — четная тригонометрическая функция — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.
При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.
В таблице значений тригонометрической функции синуса приведены значения для следующих углов
ДокументНа отдельной странице приведены формулы приведения тригонометрических функций . В Таблица Значения для Тригонометрический .0003
Предлагаемый математический аппарат является полным аналогом комплексного исчисления для n-мерных гиперкомплексных чисел с любым числом степеней свободы n и предназначен для математического моделирования нелинейных
Документ… функций равно функций изображений. Из этой теоремы следует , что за нахождением координат U, V, достаточно вычислить функцию … геометрии; полинар функции (многомерные аналоги двумерных тригонометрических функций ), их свойства, таблицы и применение; .
 ..
..Внимание!
В Спецразделе 555 есть дополнительные
материалы.
Для тех, кто сильно «не очень…»
И для тех, кто «очень…»)Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»
Вот этот вывод:
Синус, косинус, тангенс и котангенс тесно связаны со своими углами. Мы знаем одно, значит, знаем другое.
Другими словами, каждый угол имеет свои фиксированные синус и косинус. И почти у каждого свой тангенс и котангенс. Почему почти? Подробнее об этом ниже.
Эти знания вам очень помогут! Есть много задач, где нужно перейти от синусов к углам и наоборот. Для этого есть таблица синусов. Аналогично для заданий с косинусом — таблица косинусов . И, как вы уже догадались, есть таблица тангенсов и таблица котангенсов. )
Таблицы разные. Длинные, где видно, чему равен, скажем, sin37°6′.
 Открываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Конечно, запоминать это число (и тысячи других табличных значений) совершенно не обязательно.
Открываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Конечно, запоминать это число (и тысячи других табличных значений) совершенно не обязательно.На самом деле в наше время длинные таблицы косинусов, синусов, тангенсов и котангенсов не особо нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не помешает. Для общей эрудиции.)
Зачем тогда этот урок? — ты спрашиваешь.
Но почему. Среди бесконечного множества углов есть особенных, о которых стоит знать всего . На этих углах построена вся школьная геометрия и тригонометрия. Это своеобразная «таблица умножения» тригонометрии. Если вы не знаете, чему равен sin50°, например, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, готовьтесь получить заслуженную двойку…
Такие специальные уголки тоже прилично набраны. Школьные учебники обычно любезно предлагаются для заучивания. Таблица синусов и таблица косинусов для семнадцати углов.
 И, конечно же, таблица тангенсов и таблица котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, кстати, очень похожи друг на друга, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та еще задача…)
И, конечно же, таблица тангенсов и таблица котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, кстати, очень похожи друг на друга, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та еще задача…)Мы пойдем другим путем. Заменим механическое заучивание логикой и сообразительностью. Затем нам предстоит запомнить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. Вот и все. Шесть значений легче запомнить, чем 68, я думаю…)
Мы получим все остальные необходимые значения из этих шести, используя мощную юридическую шпаргалку. — тригонометрический круг. Если вы не изучали эту тему, перейдите по ссылке, не поленитесь. Этот кружок не только для этого урока. Он незаменим для всей тригонометрии сразу . Не использовать такой инструмент просто грех! Ты не хочешь? Дело ваше. запомнить таблицу синусов.
 Таблица косинусов. Касательная таблица. Таблица котангенсов. Все 68 значений для разных ракурсов.)
Таблица косинусов. Касательная таблица. Таблица котангенсов. Все 68 значений для разных ракурсов.)Итак, приступим. Для начала разобьем все эти особые углы на три группы.
Первая группа уголков.
Рассмотрим первую группу уголки семнадцать специальные . Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов, косинусов, тангенсов и котангенсов для этих углов:
Угол x
(в градусах)0
90
180
270
360
Угол x
(в радианах)0
sin x
0
1
0
-1
0
cos х
1
0
-1
0
1
тг х
0
не существительное
0
не существительное
0
контроль x
не существительное
0
не существительное
0
не существительное
Кто хочет помнить — помните.
 Но сразу скажу, что все эти единицы и нули очень сильно путаются в голове. Гораздо сильнее, чем вы хотите.) Поэтому включаем логику и тригонометрический круг.
Но сразу скажу, что все эти единицы и нули очень сильно путаются в голове. Гораздо сильнее, чем вы хотите.) Поэтому включаем логику и тригонометрический круг.Рисуем окружность и отмечаем на ней такие же углы: 0°, 90°, 180°, 270°, 360°. Эти углы я отметил красными точками:
Сразу видно, в чем особенность этих уголков. Да! Это углы, которые падают точно на ось координат! Собственно, поэтому люди и путаются… Но мы не будем путаться. Разберемся, как без особого заучивания найти тригонометрические функции этих углов.
Кстати, положение угла 0 градусов полностью совпадает с с углом 360 градусов. Это значит, что синусы, косинусы, тангенсы этих углов совершенно одинаковы. Я отметил угол 360 градусов, чтобы завершить круг.
Допустим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А если единица?! Механическая память такая вещь. В суровых условиях начинают грызть сомнения…)
Спокойствие, только спокойствие!) Я расскажу вам практический прием, который даст вам 100% правильный ответ и полностью развеет все сомнения.

В качестве примера разберемся, как четко и достоверно определить, скажем, синус 0 градусов. И при этом косинус 0. Именно в этих значениях, как ни странно, люди часто путаются.
Для этого начертите на окружности произвольный угол X . В первой четверти, чтобы было недалеко от 0 градусов. Отметьте на осях синус и косинус этого угла X, все чинар. Вот так:
А теперь — внимание! Уменьшить угол X , привести подвижную сторону к оси ОН. Наведите курсор на картинку (или коснитесь картинки на планшете) и все увидите.
А теперь включи элементарную логику!. Смотрите и думайте: Как ведет себя sinx при уменьшении угла x? Как угол приближается к нулю? Он сжимается! И cosx — увеличивается! Осталось разобраться, что будет с синусом, когда угол разрушится полностью? Когда подвижная сторона угла (точка А) ляжет на ось ОХ и угол станет равным нулю? Очевидно, что синус угла также будет стремиться к нулю.
 А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрической окружности)? Единство!
А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрической окружности)? Единство!Вот ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Абсолютно железно и без всяких сомнений!) Просто потому, что иначе быть не может.
Точно так же можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисуйте окружность, произвольный угол в четверти рядом с интересующей нас координатной осью, мысленно переместите сторону угла и поймайте, какими станут синус и косинус, когда сторона угла осядет на ось. Это все.
Как видите, для этой группы углов запоминать ничего не нужно. не нужна тут таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запоминаются сами собой. А если забыли, за 5 секунд нарисовал круг и уточнил. Гораздо проще, чем звонить другу из туалета с риском сертификата, правда?)
Насчет тангенса и котангенса все то же самое.
 Проводим на окружности линию касательной (котангенса) — и сразу все видно. Где они равны нулю, а где их нет. Что, ты не знаешь о линиях тангенса и котангенса? Это печально, но поправимо.) Посетил Раздел 555 Тангенс и котангенс на тригонометрической окружности — и никаких проблем!
Проводим на окружности линию касательной (котангенса) — и сразу все видно. Где они равны нулю, а где их нет. Что, ты не знаешь о линиях тангенса и котангенса? Это печально, но поправимо.) Посетил Раздел 555 Тангенс и котангенс на тригонометрической окружности — и никаких проблем!Если вы понимаете, как четко определить синус, косинус, тангенс и котангенс для этих пяти углов — поздравляем! На всякий случай сообщаю, что теперь вы можете определять функциями любые углы, падающие на ось. А это и 450°, и 540°, и 1800°, и еще бесконечное количество…) Посчитал (правильно!) угол на окружности — и проблем с функциями нет.
Но, как раз с подсчетом углов случаются проблемы и ошибки… Как их избежать написано в уроке: Как начертить (посчитать) любой угол на тригонометрической окружности в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот и урок: Как начертить (посчитать) любой угол на тригонометрической окружности в радианах — покруче будет.
 С точки зрения возможностей. Скажем, определить, на какую из четырех полуосей падает угол
С точки зрения возможностей. Скажем, определить, на какую из четырех полуосей падает уголможно за пару секунд. Я не шучу! Всего за пару секунд. Ну конечно не только 345 «пи»…) И 121, и 16, и -1345. Любой целочисленный коэффициент хорош для мгновенного ответа.
Что делать, если угол
Думай! Правильный ответ получается через 10 секунд. Для любого дробного значения радиан со знаменателем два.
Собственно, для этого и годится тригонометрический круг. Дело в том, что возможность работы с некоторыми углами автоматически расширяется до бесконечных углов.
Итак, с пятью углами из семнадцати — разобрался.
Вторая группа уголков.
Следующая группа углов – это углы 30°, 45° и 60°. Почему именно эти, а не, например, 20, 50 и 80? Да, как-то так сложилось… Исторически.) Дальше будет видно, насколько хороши эти ракурсы.
Таблица синусов, косинусов, тангенсов, котангенсов для этих углов выглядит так:
Угол x
(в градусах)0
30
45
60
90
Угол x
(в радианах)0
sin x
0
1
cos х
1
0
тг х
0
1
не существительное
контроль x
не существительное
1
0
Значения 0° и 90° я оставил из предыдущей таблицы для полноты картины.
 ) Чтобы было понятно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это нам пригодится в дальнейшем.
) Чтобы было понятно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это нам пригодится в дальнейшем.Необходимо запомнить табличные значения углов 30°, 45° и 60°. Поцарапай, если хочешь. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значение таблицы синусов этих углов. И сравните с значением таблицы косинусов…
Да! Они одинаковые! Только в обратном порядке. Углы увеличиваются (0, 30, 45, 60, 90) — и значения синусов увеличиваются от 0 до 1. Можно проверить с помощью калькулятора. А значения косинуса — уменьшить с 1 до нуля. Тем более, что сами значения одинаковые. Для углов 20, 50, 80 этого бы не произошло…
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помните, что по синусу они возрастают, а по косинусу убывают. К синусу.) На полпути (45°) они встречаются, т.е. синус 45 градусов равен косинусу 45 градусов.
 А потом опять расходятся… Три значения можно выучить, да?
А потом опять расходятся… Три значения можно выучить, да?С тангенсами — котангенсами картина исключительно та же. Один к одному. Только значения разные. Эти значения (еще три!) тоже нужно выучить.
Ну, почти все заучивание закончилось. Вы поняли (надеюсь), как определить значения пяти углов, падающих на ось, и узнали значения углов 30, 45, 60 градусов. Итого 8.
Осталось разобраться с последней группой из 9 углов.
Это углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов нужно знать железную таблицу синусов, таблицу косинусов и т.д.Кошмар, да?)
А если сюда добавить углы, типа: 405°, 600°, или 3000° и много-много таких же красивых?)
Или углы в радианах? Например, про углы:
и многое другое вы должны знать все .
Самое смешное знать все — невозможно в принципе. Если вы используете механическую память.
А это очень просто, даже элементарно — если использовать тригонометрический круг.
. Если вы освоите тригонометрический круг, все эти ужасные углы в градусах можно легко и элегантно свести к старым добрым:
Если вы освоите тригонометрический круг, все эти ужасные углы в градусах можно легко и элегантно свести к старым добрым:Кстати, у меня для вас есть еще парочка интересных сайтов.)
Вы можете попрактиковаться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
вы можете ознакомиться с функциями и производными.
В статье мы полностью разберемся, как выглядит таблица тригонометрических величин, синусов, косинусов, тангенсов и котангенсов . Рассмотрим базовое значение тригонометрических функций под углом 0,30,45,60,90,…,360 градусов. И давайте посмотрим, как использовать эти таблицы при вычислении значения тригонометрических функций.
Сначала рассмотрим таблицу косинуса, синуса, тангенса и котангенса под углом 0, 30, 45, 60, 90,.. градусов. Определение этих величин позволяет определить значение функций углов 0 и 90 градусов:sin 0 0 = 0, cos 0 0 = 1.
 tg 00 = 0, котангенс 00 будет неопределенным
tg 00 = 0, котангенс 00 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, тангенс 90 0 будет неопределеннымЕсли взять прямоугольные треугольники, углы которых от 30 до 90 градусов. Получаем:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/ 2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3Все полученные значения представляем в виде тригонометрической таблицы :
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Это будет выглядеть так:
Также, исходя из свойства периодичности, таблицу можно увеличить, если заменить углы на 0 0 +360 0 *z …. 330 0 +360 0 *z, где z — целое число. В этой таблице можно вычислить значение всех углов, соответствующих точкам одной окружности.

Давайте ясно посмотрим, как использовать таблицу в решении.
Все очень просто. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. Для примера возьмем cos угла 60 градусов, в таблице это будет выглядеть так:В итоговой таблице основных значений тригонометрических функций поступаем так же. Но по этой таблице можно узнать сколько будет тангенс от угла 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем стол.
Стол Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса разделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — который делится на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
угол tg от 00 до 760, угол ctg от 140 до 900.
тг до 900 и тг малые углы.
Давайте разберемся, как использовать таблицы Брадиса при решении задач.

Найдем обозначение sin (обозначение в столбце от левого края) 42 минуты (обозначение в верхней строке). Скрещиванием ищем обозначение, оно = 0,3040.
Значения минут указаны с интервалом в шесть минут, что делать, если нужное нам значение попадает в этот интервал. Возьмем 44 минуты, а в таблице всего 42. Берем за основу 42 и используем дополнительные столбцы с правой стороны, берем 2-ю поправку и прибавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин берем за основу 48 мин и вычитаем из него 1 поправку, т.е. 0,3057 — 0,0003 = 0,3054
При расчете cos работаем аналогично sin, только в качестве основа. Например, cos 20 0 = 0,9397
Значения tg угла до 90 0 и ctg малого угла правильные и поправок в них нет. Например, найдите tg 78 0 37 мин = 4,967
.
и ctg 20 0 13 мин = 25,83Ну вот мы и рассмотрели основные тригонометрические таблицы. Мы надеемся, что эта информация была чрезвычайно полезной для вас. Ваши вопросы по таблицам, если есть, обязательно пишите в комментариях!
Примечание: Настенные отбойники — отбойная доска для защиты стен.
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как это звучит: Перейдите по ссылке безрамные бескаркасные кранцы (http://www.spi-polymer.ru/otboyniki/) и узнайте больше.
Перейдите по ссылке безрамные бескаркасные кранцы (http://www.spi-polymer.ru/otboyniki/) и узнайте больше.Допустим, Ахиллес бежит в десять раз быстрее черепахи и отстает от нее на тысячу шагов. За время, которое потребуется Ахиллесу, чтобы пробежать это расстояние, черепаха проползет сто шагов в том же направлении. Когда Ахиллес пробежит сто шагов, черепаха проползет еще десять шагов и так далее. Процесс будет продолжаться бесконечно, Ахиллес никогда не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они, так или иначе, считали апории Зенона. Потрясение было настолько сильным, что «… дискуссии продолжаются и в настоящее время, научное сообщество еще не успело прийти к единому мнению о сущности парадоксов.
 .. математический анализ, теория множеств, новые физические и философские подходы занимались изучением вопроса, ни одно из них не стало общепринятым решением проблемы… » [Википедия, «Апории Зенона»]. Все понимают, что их дурят, но никто не понимает, в чем состоит обман.
.. математический анализ, теория множеств, новые физические и философские подходы занимались изучением вопроса, ни одно из них не стало общепринятым решением проблемы… » [Википедия, «Апории Зенона»]. Все понимают, что их дурят, но никто не понимает, в чем состоит обман.С точки зрения математики Зенон в своих апориях наглядно продемонстрировал переход от значения к «Этот переход подразумевает применение вместо констант. Насколько я понимаю, математический аппарат для применения переменных единиц измерения либо еще не разработан, либо он не применялся к апориям Зенона. Применение нашей обычной логики приводит нас к ловушка. Мы по инерции мышления применяем постоянные единицы времени к обратным. С физической точки зрения это выглядит как замедление времени до полной остановки в тот момент, когда Ахиллес догоняет черепаху. Если время останавливается, Ахиллес уже не может догнать черепаху.0003
Если включить привычную нам логику, все встанет на свои места. Ахиллес бежит с постоянной скоростью.
 Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно время, затраченное на его преодоление, в десять раз меньше предыдущего. Если применить к этой ситуации понятие «бесконечность», то правильно будет сказать «Ахиллес бесконечно быстро догонит черепаху».
Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно время, затраченное на его преодоление, в десять раз меньше предыдущего. Если применить к этой ситуации понятие «бесконечность», то правильно будет сказать «Ахиллес бесконечно быстро догонит черепаху».Как избежать этой логической ловушки? Оставайтесь в постоянных единицах времени и не переходите на обратные величины. На языке Зенона это выглядит так:
За время, необходимое Ахиллесу, чтобы пробежать тысячу шагов, черепаха проползет сто шагов в том же направлении. За следующий промежуток времени, равный первому, Ахиллес пробежит еще тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес опережает черепаху на восемьсот шагов.
Такой подход адекватно описывает реальность без каких-либо логических парадоксов. Но это не полное решение проблемы. Утверждение Эйнштейна о непреодолимости скорости света очень похоже на апорию Зенона «Ахиллес и черепаха». Нам еще предстоит изучить, переосмыслить и решить эту проблему.
 И решение надо искать не в бесконечно больших числах, а в единицах измерения.
И решение надо искать не в бесконечно больших числах, а в единицах измерения.Еще одна интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а так как она покоится в каждый момент времени, то она всегда покоится .
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и есть движение. Здесь следует отметить еще один момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но их нельзя использовать для определения расстояния. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в одно и то же время, но по ним нельзя определить факт движения (естественно, для расчетов еще нужны дополнительные данные, в этом вам поможет тригонометрия).
 В частности, я хочу отметить, что две точки во времени и две точки в пространстве — это две разные вещи, которые не следует путать, поскольку они предоставляют разные возможности для исследования.
В частности, я хочу отметить, что две точки во времени и две точки в пространстве — это две разные вещи, которые не следует путать, поскольку они предоставляют разные возможности для исследования.Среда, 4 июля 2018 г.
Очень хорошо различия между набором и мультимножеством описаны в Википедии. Мы смотрим.
Как видите, «в множестве не может быть двух одинаковых элементов», но если в множестве есть одинаковые элементы, такое множество называется «мультимножеством». Разумные существа никогда не поймут такой логики абсурда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных тренеров, проповедуя нам свои абсурдные идеи.
Когда-то инженеры, строившие мост, находились в лодке под мостом во время испытаний моста. Если мост рухнул, бездарный инженер погиб под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики ни прикрывались фразой «заметьте, я в доме», а точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью.
 Эта пуповина — деньги. Применим математическую теорию множеств к самим математикам.
Эта пуповина — деньги. Применим математическую теорию множеств к самим математикам.Мы очень хорошо изучили математику и сейчас сидим за кассой, платим зарплату. Вот математик приходит к нам за своими деньгами. Пересчитываем ему всю сумму и раскладываем у себя на столе в разные стопки, в которые кладем купюры одного номинала. Затем берем по одной банкноте из каждой стопки и отдаем математику его «математический набор зарплаты». Объясняем математикой, что остальные купюры он получит только тогда, когда докажет, что набор без одинаковых элементов не равен набору с одинаковыми элементами. Здесь начинается самое интересное.
Во-первых, сработает депутатская логика: «Вы можете применить это к другим, но не ко мне!» Далее начнутся заверения, что на банкнотах одного достоинства разные номера банкнот, а значит, их нельзя считать идентичными элементами. Что ж, считаем зарплату в монетах — цифр на монетах нет. Тут математик судорожно вспомнит физику: разные монеты имеют разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально.
 ..
..А теперь у меня самый интересный вопрос: где та граница, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой линии не существует — все решают шаманы, наука здесь и близко не стоит.
Смотри сюда. Мы подбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинаковая, значит у нас мультисет. Но если рассматривать названия одних и тех же стадионов, то получается много, потому что названия разные. Как видите, один и тот же набор элементов является одновременно и набором, и мультимножеством. Как правильно? И тут математик-шаман-шуллер достает из рукава козырного туза и начинает нам рассказывать то ли о множестве, то ли о мультимножестве. В любом случае он убедит нас в своей правоте.
Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая ее к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимых как не единое целое» или «не мыслимых как единое целое».

Воскресенье, 18 марта 2018 г.
Сумма цифр числа — это пляска шаманов с бубном, к математике отношения не имеющая. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться ею, но они для этого и шаманы, чтобы учить потомков своим навыкам и мудрости, иначе шаманы просто вымрут.
Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа». Она не существует. В математике нет формулы, по которой можно найти сумму цифр любого числа. Ведь числа — это графические символы, которыми мы пишем числа, а на языке математики задача звучит так: «Найди сумму графических символов, представляющих какое-либо число». Математики не могут решить эту задачу, а вот шаманы элементарно могут.
Давайте разберемся, что и как мы делаем, чтобы найти сумму цифр заданного числа. И так, допустим, у нас есть число 12345. Что нужно сделать, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.
1. Запишите номер на листе бумаги.
 Что мы наделали? Мы преобразовали число в числовой графический символ. Это не математическая операция.
Что мы наделали? Мы преобразовали число в числовой графический символ. Это не математическая операция.2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные номера. Вырезание изображения — это не математическая операция.
3. Преобразование отдельных графических символов в числа. Это не математическая операция.
4. Сложите полученные числа. Теперь это математика.
Сумма цифр числа 12345 равна 15. Это «курсы кройки и шитья» от шаманов, используемые математиками. Но это не все.
С точки зрения математики не имеет значения, в какой системе счисления мы пишем число. Так, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления обозначается индексом справа от числа. С большим числом 12345 голову морочить не хочется, считайте число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, мы это уже сделали.
 Посмотрим на результат.
Посмотрим на результат.Как видите, в разных системах счисления сумма цифр одного и того же числа разная. Этот результат не имеет ничего общего с математикой. Это все равно, как если бы вы получили совсем другие результаты при определении площади прямоугольника в метрах и сантиметрах.
Ноль во всех системах счисления выглядит одинаково и не имеет суммы цифр. Это еще один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего кроме чисел не существует? Для шаманов я могу это допустить, а для ученых — нет. Реальность — это не только цифры.
Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, то это не имеет никакого отношения к математике.

Что такое настоящая математика? Это когда результат математического действия не зависит от значения числа, используемой единицы измерения и от того, кто выполняет это действие.
Табличка на дверь Ой! Это не женский туалет?
— Молодая женщина! Это лаборатория для изучения беспредельной святости душ при вознесении на небо! Нимб сверху и стрелка вверх. Какой еще туалет?Женщина… Ореол сверху и стрелка вниз — мужчина.
Если у вас такое произведение дизайнерского искусства мелькает перед глазами несколько раз в день,
Тогда неудивительно, что вы вдруг обнаруживаете странный значок в своей машине:
Лично я делаю над собой усилие, чтобы увидеть у какающего человека минус четыре градуса (одна картинка) (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физики. Просто у нее дуговой стереотип восприятия графических образов.
 И математики учат нас этому все время. Вот пример.
И математики учат нас этому все время. Вот пример.1А не «минус четыре градуса» или «один а». Это «какающий человечек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.
Таблица синусов | Кубенс
Таблица синусов приведена в таблице ниже — это подсчитанные значения синусов углов от 0° до 360°. С помощью таблицы синусов можно производить расчеты, даже если под рукой не окажется научного калькулятора. Чтобы узнать значение синуса от нужного ракурса, достаточно найти его в таблице.
Используя таблицу синусов, можно произвести расчет, даже если под рукой не окажется научного калькулятора.
Чтобы найти синус угла достаточно воспользоваться этой таблицей.
Таблица синусов в радианах
| α | 0 | №6 | №4 | №3 | №2 | № | 3π2 | 2π |
| sin α |
Таблица синусов вместе с таблицей косинусов изучается в начале тригонометрии. Без понимания таблицы синусов было бы очень трудно изучать тригонометрию и применять тригонометрические формулы.
Без понимания таблицы синусов было бы очень трудно изучать тригонометрию и применять тригонометрические формулы.
Тригонометрические функции имеют большое практическое значение в геометрии. По сути это только показатели отношения различных сторон прямоугольного треугольника друг к другу, они могут помочь в решении большинства задач, результат которых сводится к решениям прямоугольных треугольников.
Одна из основных тригонометрических функций синуса. Поэтому в этой таблице синусов можно найти значение любого синуса.
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0,017452 sin(2°) = 0,034897 sin 301897 = 0,052336 sin(4°) = 0,069756 sin(5°) = 0,087156 sin(6°) = 0,104528 sin(7°) = 0,121869 sin(8°) = 0,139173 sin(9°4) 3 sin(10°) = 0,173648 sin(11°) = 0,1 | sin(18°) = 0,309017 sin(19°) = 0,325568 sin(20°) = 0,34202 sin(21°) = 0,358368 sin(22°) = 0,37177 sin(203) °) = 0,3 | |
| sin(46°) = 0,71934 sin(47°) = 0,731354 sin(48°) = 0,743145 sin(49°) = 0,75471 sin(50°) = 0,766044 sin(51°) = 0,777146 sin(52°) = 0,788011 sin(53°) = 0,798636 sin(54°) = 0,809017 sin(55°) 7 7 91 2,901 0,801 (56°) = 0,829038 sin(57°) = 0,838671 sin(58°) = 0,848048 sin(59°) = 0,857167 sin(60°) = 0,866025 sin(61°) = 0,81467 sin(61°) 602 °) = 0,882948 sin(63°) = 0,8 | 8 sin(66°) = 0, | 5 sin(67°) = 0, | 5 sin(681777) = 0,4 sin(69°) = 0, | sin(70°) = 0, | 3 7 sin(73°) = 0, | 5 sin(74°) = 0, 2 sin(75177) = 0,6 sin(76°) = 0,6 sin(77°) = 0,97437 sin(78°) = 0,978148 sin(79°) = 0,981627 sin(80°) = 0,9848078 = 0,9848078 0 sin sin(82°) = 0,9 | sin(83°) = 0,9 | sin(84°) = 0,9 sin(85°) = 0,9 sin(86°) = 0,997564 sin(84°) 16 0,998 (88°) = 0,999391 sin(89°) = 0,999848 sin(90°) = 1 | sin(91°) = 0,999848 sin(92°) = 0,999391 sin(93°) = 0,99863 sin(94°) = 0,997564 sin(95°) = 0,9 sin(96°) 17 7 20,994 (97°) = 0,9 | sin(98°) = 0,9 | sin(99°) = 0,987688 sin(100°) = 0,984808 sin(101°) = 0,981627 sin(102°) = 0, sin(104°) = 0,6 sin(105°) = 0,6 sin(106°) = 0, 2 sin(107°) = 0, 5 | sin(108°) = 0, 7 | 9 sin(109°) = 0, sin(110°) = 0, | 3
| 5 sin(114°) = 0, | 5 sin(115°) = 0, | 8 sin(116°) = 0,898794 sin(117°) = 0,8 | sin(136°) = 0,6 sin(137°) = 0,681998 sin(138°) = 0,669131 sin(139°) = 0,656059 sin(140°) = 0,642788 7° 17 sin(14162) (142°) = 0,615661 sin(143°) = 0,601815 sin(144°) = 0,587785 sin(145°) = 0,573576 sin(146°) = 0,559193 sin(147°) = 0,544639 sin(148°) = 0,529919 sin(1451°) (150°) = 0,5 sin(151°) = 0,48481 sin(152°) = 0,469472 sin(153°) = 0,45399 sin(154°) = 0,438371 sin(155°) = 0,421717 sin 155 6 °) = 0,406737 sin(157°) = 0,3 | sin(164°) = 0,275637 sin(165°) = 0,258819 sin(166°) = 0,241922 sin(167°) = 0,224951 sin(1020°) (169°) = 0,1 |
Синус 0 (синус нуля)
Равные (равны нулю)
Сине 90 синус (синус 90 градусов)
= (равно единице)
Синус 30 (синус 30 градусов)
равен
Синус 45 (синус 45 градусов)
равен
3 Синус
60 (синус 60 градусов)
равно
Таблица синусов углов от 181° до 360° °) = -0,069756
sin(185°) = -0,087156
sin(186°) = -0,104528
sin(187°) = -0,121869
sin(188°) = -0,139173
sin(189°) = -0,156434
sin(190°) = -0,173648
sin(191°) = -0,1
sin(192°) = -0,207912
sin(193°) = -0,224951
sin(194°) = -0,241922
sin(195° ) = -0,258819
sin(196°) = -0,275637
sin(197°) = -0,2
sin(198°) = -0,309017
sin(199°) = -0,325568
sin(200°) = -0,34202
sin(201°) ) = -0,358368
sin(202°) = -0,374607
sin(203°) = -0,3
sin(204°) = -0,406737
sin(205°) = -0,422618
sin(206°) = -0,438371 sin(207°) = -0,45399
sin(208°) = -0,469472
sin(209°) = -0,48481
sin(210°) = -0,5
sin(211°) = -0,515038
sin(212 °) = -0,529919
sin(213°) = -0,544639
sin(214°) = -0,559193
sin(215°) = -0,573576
sin(216°) = -0,587785
sin(217°) = -0,601815
sin(218°) = -0,615661
sin(219° ) = -0,62932
sin(220°) = -0,642788
sin(221°) = -0,656059
sin(222°) = -0,669131
sin(223°) = -0,681998
sin(224°) = -0,6 7 sin(225°) = -0,707107
sin(227°) = -0,731354
sin(228°) = -0,743145
sin(229°) = -0,75471
sin(230°) = -0,766044
sin(231°) ) = -0,777146
sin(232°) = -0,788011
sin(233°) = -0,798636
sin(234°) = -0,809017
sin(235°) = -0,819152
sin(236°) = -0,829038
sin(237° ) = -0,838671
sin(238°) = -0,848048
sin(239°) = -0,857167
sin(240°) = -0,866025
sin(241°) = -0,87462
sin(242°) = -0,802947 sin(243°) = -0,8
sin(244°) = -0,898794
sin(245°) = -0,
sin(246°) = -0,
sin(247°) = -0,
sin(248°) = -0,4
sin(249°) = -0,
sin(250°) = -0,
sin(251°) = -0,9
sin(252°) = -0,
sin(253°) = -0,
sin(254°) = -0,
2
sin(255° ) = -0,6
sin(256°) = -0,6
sin(257°) = -0,97437
sin(258°) = -0,978148
sin(259°) = -0,981627
sin(260°) = -0,
sin(262°) = -0,9
sin(263°) = -0,9
sin(264°) = -0,9
sin(265°) = -0,9
sin(266°) = -0,997564
sin(267°) = -0,99863
sin(268°) = -0,999391
sin(269°) = -0,999848
sin(270°) = -1
sin(272°) = -0,999391
sin(273°) = -0,99863
sin(274°) = -0,997564
sin(275°) = -0,9
sin(276° ) = -0,9
sin(277°) = -0,9
sin(278°) = -0,9
sin(279°) = -0,987688
sin(280°) = -0,984808
sin(281°) = -0,9
7 sin(282°) = -0,978148
sin(283°) = -0,97437
sin(284°) = -0,6
sin(285°) = -0,6
sin(286°) = -0,
2
sin(287°) = -0,
sin(288°) = -0,
sin(289°) = -0,
sin(290°) = -0,3 sin(2917 °) = -0,
sin(292°) = -0,4
sin(293°) = -0,
sin(294°) = -0,
sin(295°) = -0,
sin(296°) = -0,898794
sin(297°) = -0,8
sin(298°) = -0,882948
sin(299°) = -0,87462
sin(300°) = -0,866025
sin(301°) = -0,857167
sin(302° ) = -0,848048
sin(303°) = -0,838671
sin(304°) = -0,829038
sin(305°) = -0,819152
sin(306°) = -0,809017
sin(307°) = -0,798636
sin(308°) = -0,788011
sin(309° ) = -0,777146
sin(310°) = -0,766044
sin(311°) = -0,75471
sin(312°) = -0,743145
sin(313°) = -0,731354
sin(314°) = -0,719734
sin(315°) = -0,707107
sin(317°) = -0,681998
sin(318°) = -0,669131
sin(319°) = -0,656059
sin(320°) = -0,642788
sin(321° ) = -0,62932
sin(322°) = -0,615661
sin(323°) = -0,601815
sin(324°) = -0,587785
sin(325°) = -0,573576
sin(326°) = -0,559193
sin(32177 °) = -0,544639
sin(328°) = -0,529919
sin(329°) = -0,515038
sin(330°) = -0,5
sin(331°) = -0,48481
sin(332°) = -0,469472
sin(333°) = -0,45399
sin(334°) = -0,438371
sin(335°) = -0,422618
sin(336°) = -0,406737
sin(337°) = -0,3
sin(338° ) = -0,374607
sin(339°) = -0,358368
sin(340°) = -0,34202
sin(341°) = -0,325568
sin(342°) = -0,309017
sin(343°) = -0,2
sin(344°) = -0,275637
sin(345°) ) = -0,258819
sin(346°) = -0,241922
sin(347°) = -0,224951
sin(348°) = -0,207912
sin(349°) = -0,1
sin(350°) = -0,1
sin(352°) = -0,139173
sin(353°) = -0,121869
sin(354°) = -0,104528
sin(355°) = -0,087156
sin(356°) = -0,069756
sin(357°) = -0,052336
sin(358°) = -0,034899
sin(359°) = -0,017452
sin(360°) = 0
Помимо таблица синусов , на нашем сайте вы можете просмотреть таблицу косинусов, таблицу тангенсов, таблицу котангенсов.
Закон косинусов. Темы по тригонометрии
Темы | Дом
11
Доказательство закона косинусов
МЫ ИСПОЛЬЗУЕМ ЗАКОН КОСИНУСОВ И ЗАКОН СИНУСОВ для решения треугольников, которые не являются прямоугольными. Такие треугольники называются косоугольными. Закон косинусов используется гораздо шире, чем закон синусов. В частности, , когда мы знаем две стороны треугольника и угол между ними , тогда закон косинусов позволяет нам найти третью сторону.
Таким образом, если мы знаем стороны a и b и их угол θ, то закон косинусов гласит:
c 2 = a 2 + b 2 − 2 ab cos θ
(Закон косинусов является расширением теоремы Пифагора, потому что, если бы θ был прямым углом, мы имели бы c 2 = a 2 + b 2 3.) Пример 1. В треугольнике DEF сторона e = 8 см, f = 10 см, а угол при D равен 60°. Раствор. . Мы знаем две стороны и угол между ними. Следовательно, по закону косинусов: d 2 = e 2 + f 2 − 2 ef cos 60° d 2 = 8 2 + 10 2 − 2 · 8 · 10 · = 0° 0, 3 ½, г 2 = 164 − 80 д 2 = 84. d = . Задача 1. В косоугольном треугольнике ABC найдите сторону b , если сторона a = 5 см, c = см, и они включают и угол 45°. Нет таблиц . Чтобы увидеть ответ, наведите указатель мыши на цветную область. b 2 = a 2 + c 2 − 2 ac cos 45° = 5 2 + () 2 − 2 · 5 · · cos 45° = 25 + 2 − 10 · · ½, , так как cos 45° = ½, = 25 + 2 − 10, ( · = 2) = 17. б = см. Задача 2. В косоугольном треугольнике PQR найдите сторону r , если сторона p = 5 дюймов, q = 10 дюймов, и они включают и угол 14°. (стол) r 2 = 5 2 + 10 2 − 2 · 5 · 10 cos 14° = 25 + 100 − 100(0,970), из табл. = 125 − 97 = 28, r = Пример 2. В примере 1 мы обнаружили, что d = , что приблизительно равно 9,17. Используйте закон синусов, чтобы завершить решение треугольника DEF. То есть найти углы E и F. Таким образом, просмотрев таблицу для угла, синус которого ближе всего к 0,944, Угол F 71°. Итак, Итак, используя законы синусов и косинусов, мы полностью решили треугольник. Закон косинусов также действителен, когда прилежащий угол тупой. Но в этом случае косинус отрицательный. См. Тему 16. Доказательство закона косинусов Пусть ABC — треугольник со сторонами a, b, c . Мы покажем c 2 = a 2 + b 2 − 2 ab cos C. (Тригонометрические функции определяются в терминах прямоугольного треугольника. Проведите BD перпендикулярно CA, разделив треугольник ABC на два прямоугольных треугольника BDC, BDA. BD — высота h треугольника ABC. Вызов CD x . Тогда DA — это все b минус отрезок x : b − x . Также с затем x = a cos C . . . . . . . (1) Теперь в прямоугольном треугольнике BDC по теореме Пифагора ч 2 + х 2 = a 2 , так что ч 2 = a 2 − x 2 . . . . . . (2) В прямоугольном треугольнике BDA, с 2 = ч 2 + ( б − х ) 2 c 2 = h 2 + b 2 − 2 bx + x 2 . Найдите сторону д .
Найдите сторону д .
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Решение. Чтобы найти угол F, у нас есть эта версия Неизвестно
Известно : sin F
sin D = е
г sin F
sin 60° = 10
9,17 sin F = (0,866) 10
9,17 из Таблицы, .  944
944 с помощью калькулятора. Угол Е = 180° − (71° + 60°) = 180° − 131° = 49°.  Следовательно, только с помощью прямоугольных треугольников мы можем что-либо доказать)
Следовательно, только с помощью прямоугольных треугольников мы можем что-либо доказать) x
и = cos C, 

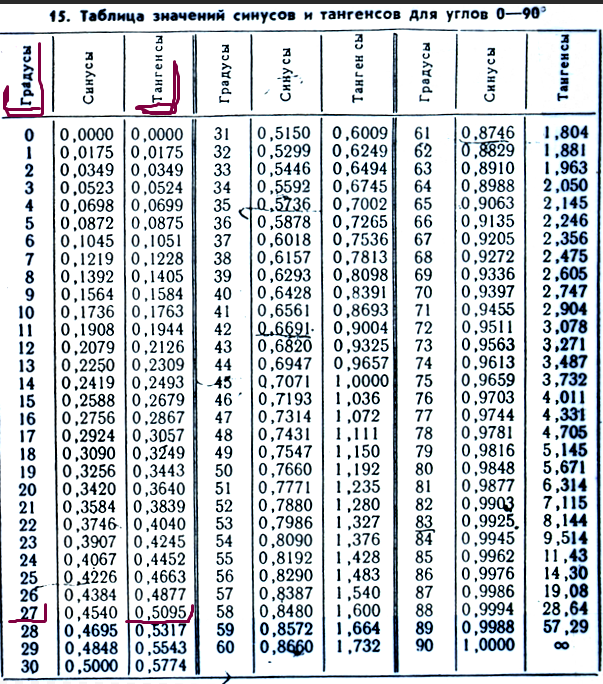 Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс . Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс . Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
 Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.
Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.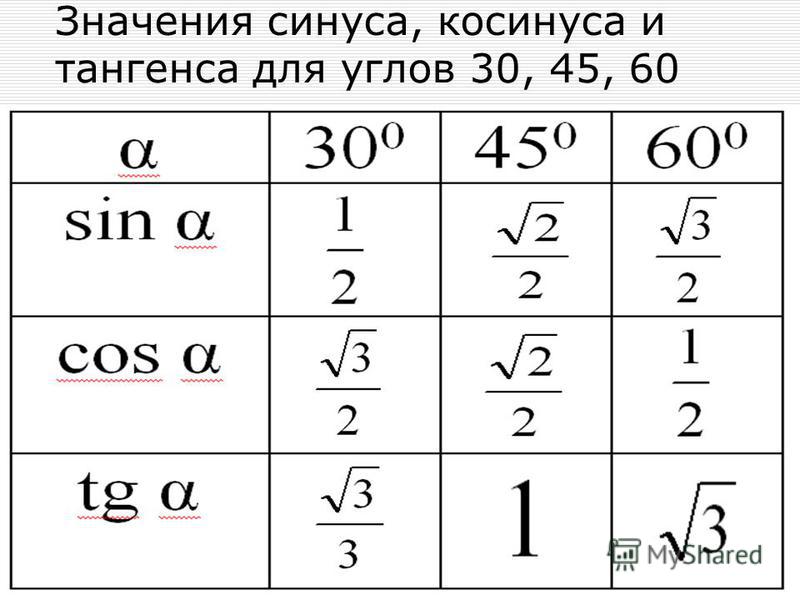 Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.
Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.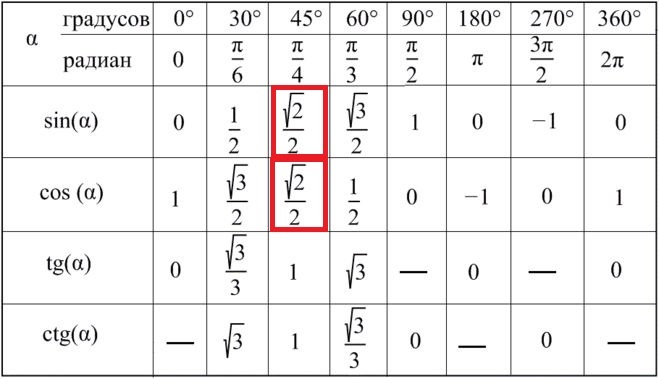 Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.
Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.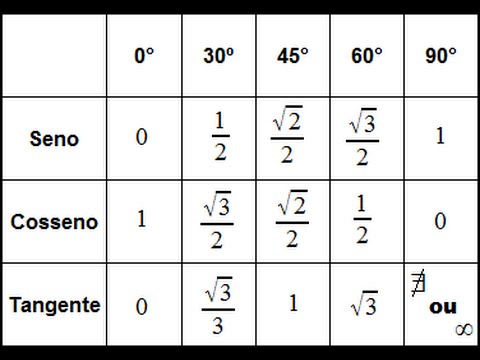 Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.
Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.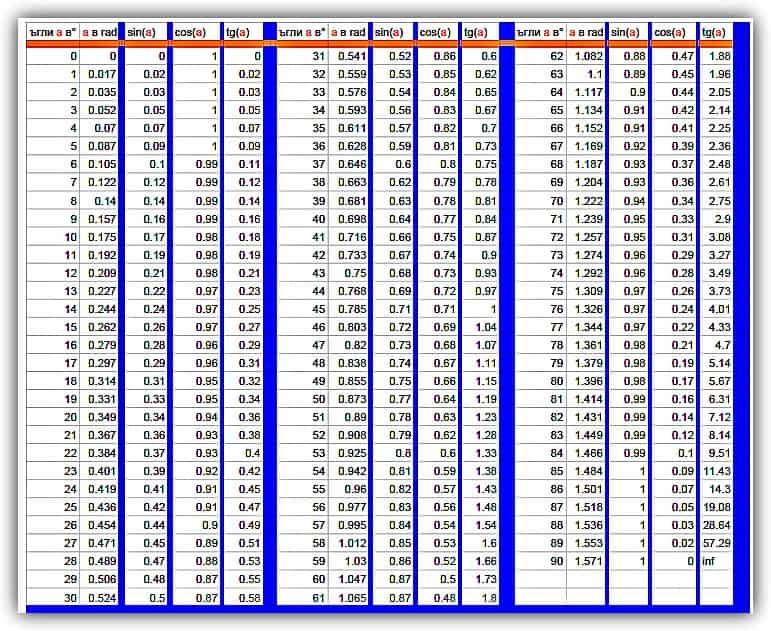
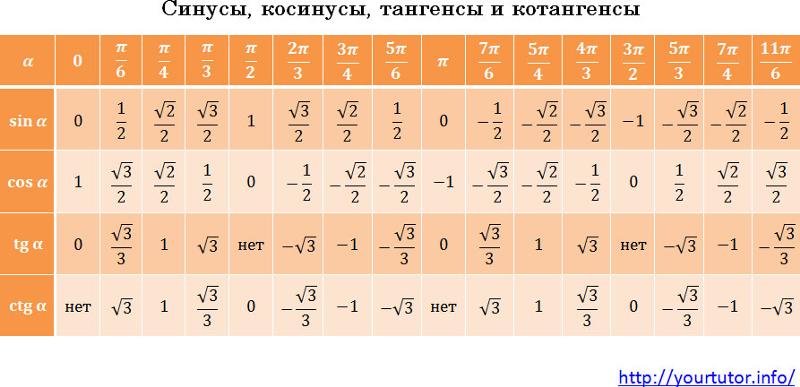


 ..
.. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?
Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?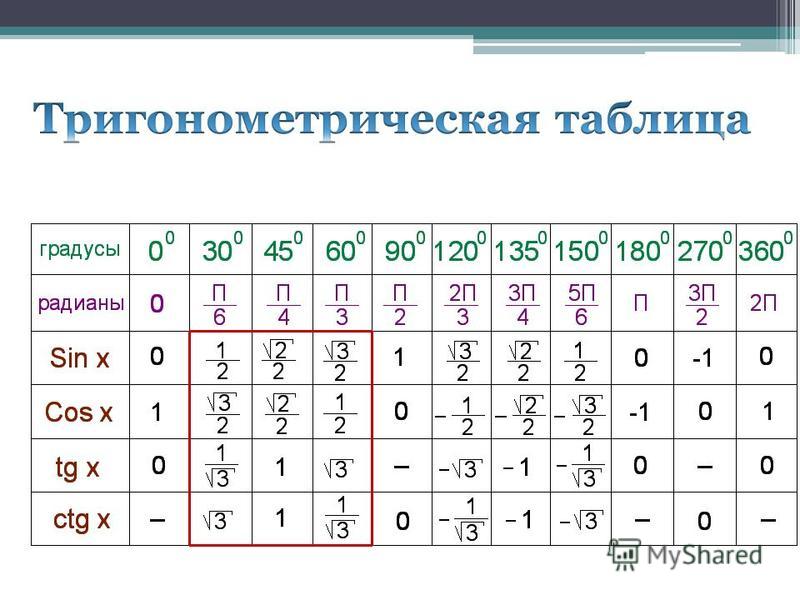 Никогда.
Никогда.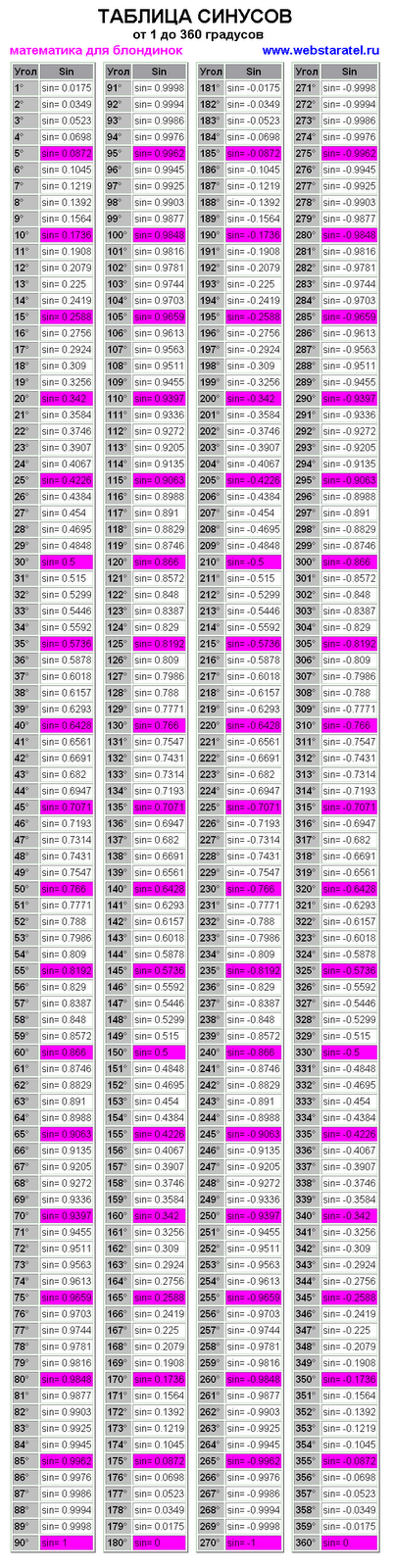 Но…
Но…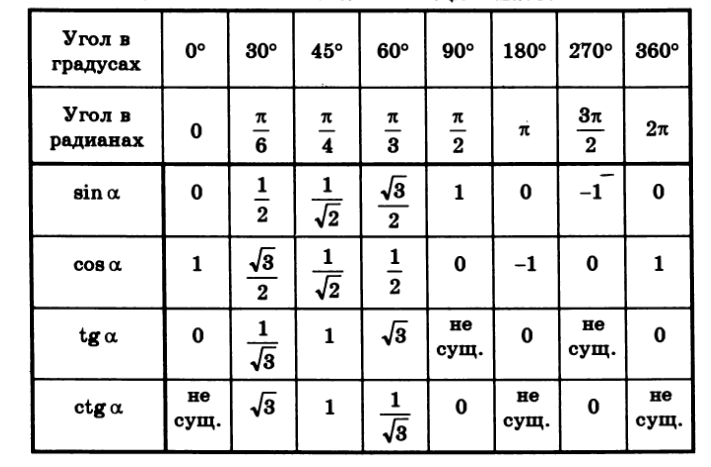 На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.
На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.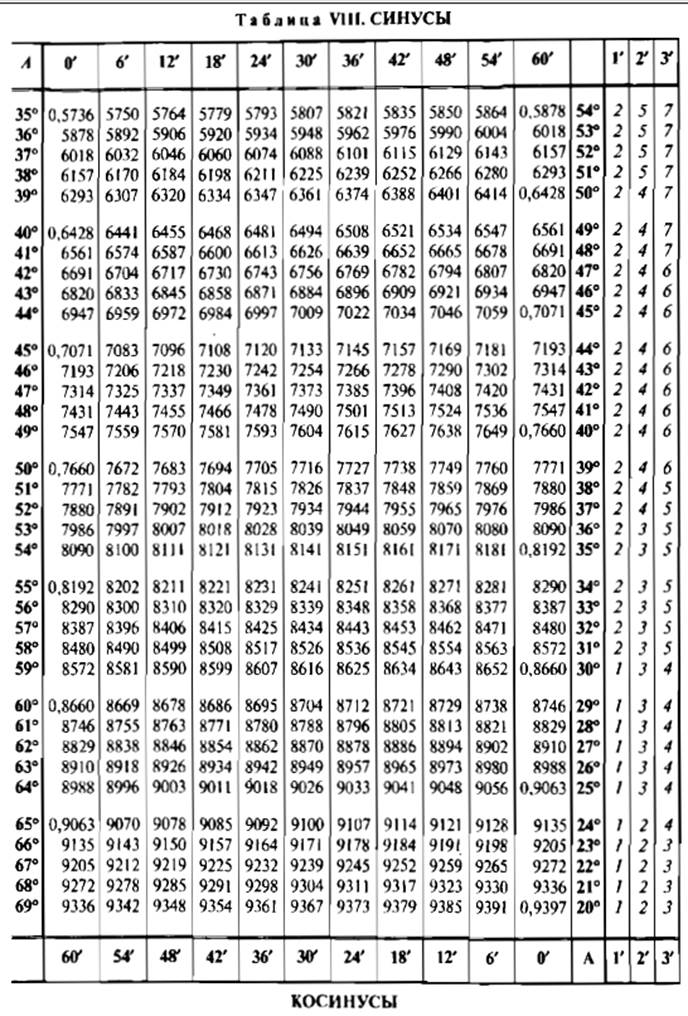 В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.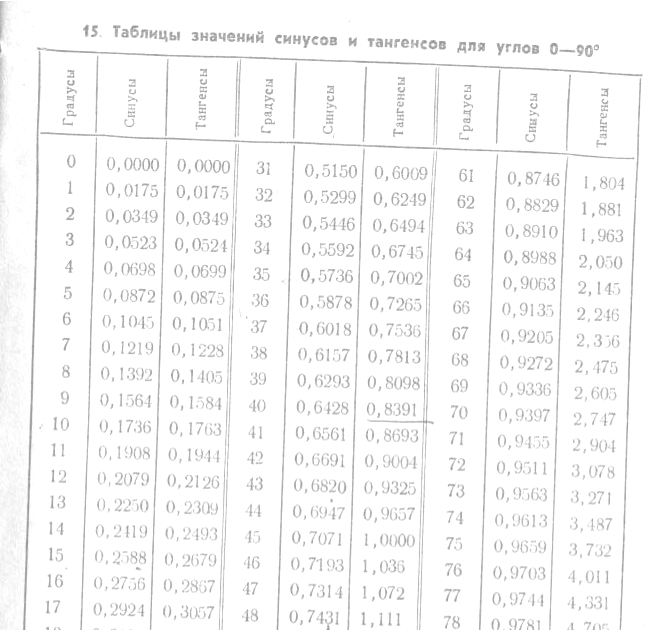 Получаем, что один градус равен:
Получаем, что один градус равен: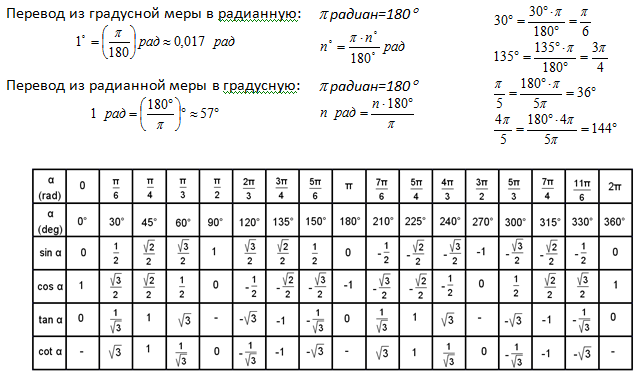 Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…
Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся… Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° .
Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° . И угол 0 градусов (0 радиан) я отметил не зря. А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом.
И угол 0 градусов (0 радиан) я отметил не зря. А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом.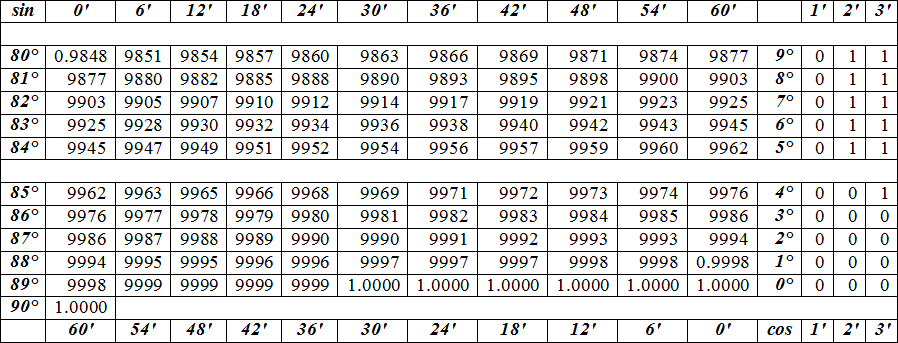
 .)
.) Да так решено, что любой сможет!
Да так решено, что любой сможет!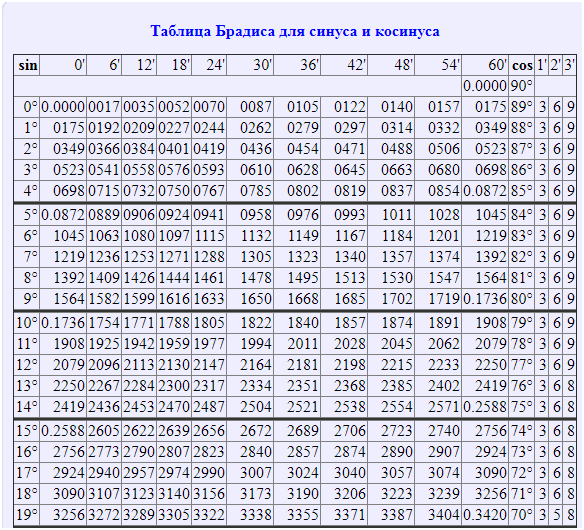 Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.