Таблица локальная лапласа: таблицы функций Лапласа, вероятностей распределения Пуассона

интегральная, локальная, таблицы, примеры задач

Содержание:

• Личность Пьер-Симона Лапласа
• Интегральная теорема Муавра-Лапласа
• Локальная теорема Муавра-Лапласа
• Таблицы
• Примеры решения задач

Содержание

• Личность Пьер-Симона Лапласа
• Интегральная теорема Муавра-Лапласа
• Локальная теорема Муавра-Лапласа
• Таблицы
• Примеры решения задач

Личность Пьер-Симона Лапласа

Пьер-Симон Лаплас известен в качестве ученого из Франции, который изучал и добился высоких результатов в таких научных областях, как математика, механика, физика, астрономия. Популярность исследователю принести труды в области небесной механики, анализ дифференциальных математических соотношений. Лаплас являлся одним из авторов вероятностной теории.

Сложно переоценить заслуги ученого в математических и астрономических дисциплинах. Благодаря исследованиям великого научного деятеля, были качественно доработаны практически все направления перечисленных областей. Пьер-Симон Лаплас состоял во Французском Географическом обществе, шести научных академиях и королевских организациях, в числе которых Академия Петербурга (1802 г). Исследователь заслужено был удостоен звания величайшего ученого Франции. С этим перечнем великих научных деятелей можно ознакомиться при посещении Эйфелевой башни в Париже.

Интегральная теорема Муавра-Лапласа

В процессе разбора теоремы для наглядности приведем простой пример. Предположим, что имеется тысяча деталей. Пусть усредненная концентрация бракованных товаров, которыми нельзя пользоваться, составляет 10%. При этом некорректно сделать вывод о наличии 100 единиц брака в рассматриваемой основной партии, так как записанный процент является средним. Возможно, что некачественных деталей всего 101, 98 или другое число. Вычислить, каковы шансы найти в партии ровно 100 изделий с браком, можно с помощью теоремы Муавра-Лапласа в интегральном виде. Данный подход значительно упрощает и сокращает расчеты.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Если число опытов равно n, то шансы на успешный результат в интервале от \({K}_{1}\) до \({K}_{2}\) определены таким соотношением: \({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\)

В данном случае функцию F, которая включена в запись выражения, называют функцией Муавра-Лапласа. Ее расчет построен по такому принципу: \(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)

 

Примечание 1

Заметим, что в процессе вычислений вероятнее всего возникнут сложности с интегрированием.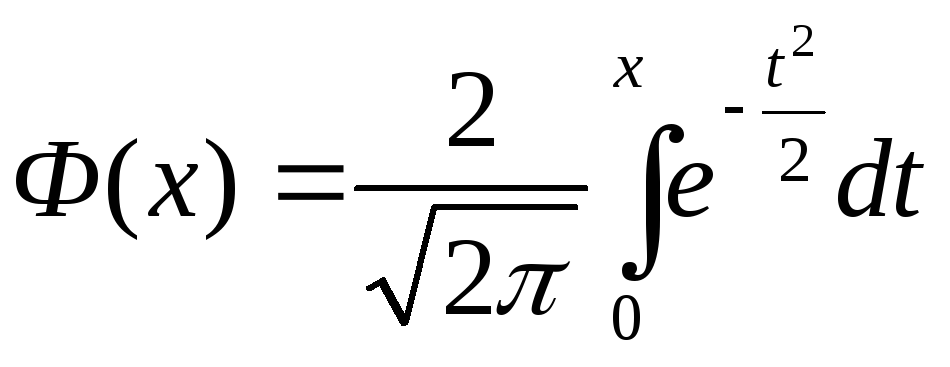 {2}}{2}}\right)\)

Таблицы

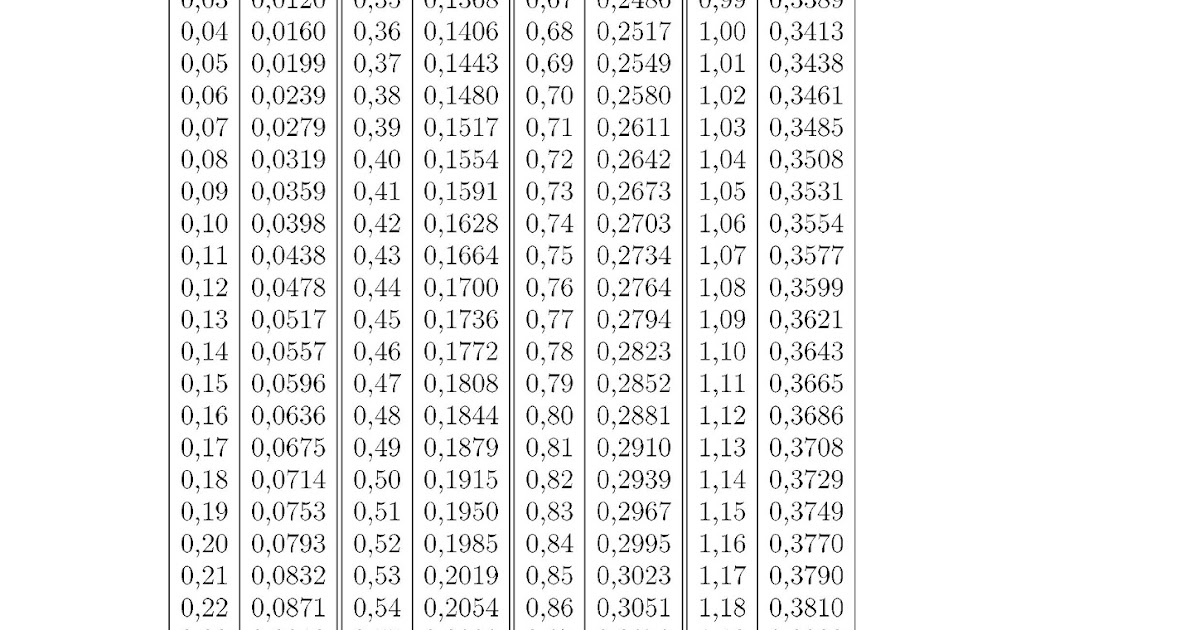
Таблица значений локальной функции Лапласа:

 

 

 

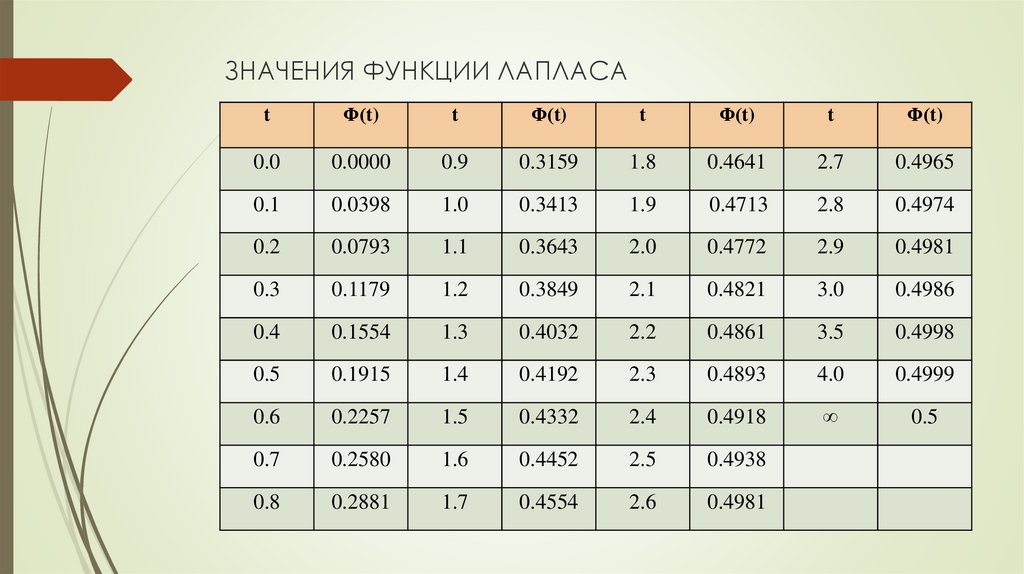
Таблица значений интегральной функции Лапласа:

 

 

Примеры решения задач

Задача 1

Около 5% учащихся вуза ходят в очках. Требуется проанализировать группу из 200 людей, из которых как минимум 10% в очках. Необходимо определить, какова вероятность собрать аудиторию с таким условиями.

Решение

Заметим, что в данном случае целесообразно воспользоваться теоремой Муавра-Лапласа в интегральной форме, то есть:

\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\)

Здесь также целесообразно воспользоваться следующим соотношением, с которым мы уже успели познакомиться в начале темы:

\(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)

Запишем условия задачи, чтобы было удобно выполнять подстановку числовых значений величин в записанную ранее формулу:

n=200

p=0,05

1-0,05=0,95

Далее определим значение \(\sqrt{npq}\):

\(\sqrt{npq}=\sqrt{200\cdot 0,05\cdot 0,95}=\sqrt{9,5}\approx 3,08\)

Затем вычислим, чему равно np:

\(np=200\cdot 0,05=10\)

Путем подстановки продолжим расчет:

\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{200-10}{3,08} \right)-F\left( \frac{20-10}{3,08} \right)= F\left( 61,7 \right)-F\left( 3,25 \right)\)

\(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)

\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx 0,5-0,49942=0,00058=5,8\cdot {{10}^{-4}}\)

Ответ: \(5,8\cdot {{10}^{-4}}\)

Задача 2

Театральный зал вместимостью в тысячу человек оснащен парой входов, которые доступны без исключения всем зрителям. Каждый вход расположен около гардероба. Нужно вычислить количество вешалок в любом из гардеробов, чтобы с вероятностью в 0,99 каждый человек имел возможность оставить верхнюю одежду.

Решение

Запишем данные из условия задачи:

n=1000

\(p=\frac{1}{2}\)

\(q=1-\frac{1}{2}=\frac{1}{2}\)

Воспользуемся рассмотренными ранее формулами и выполним соответствующие вычисления:

\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)=0,99\)

Заметим, что при определении интервала значений событий напрашивается следующий вывод:

\({{K}_{1}}=0\)

В таком случае необходимо вычислить, чему соответствует \({K}_{2}\). Обратимся к формулировке теоремы Муавра-Лапласса:

\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\)

Отметим, что в данном случае справедливым является следующее равенство:

\(np=1000\cdot \frac{1}{2}=500\)

В результате:

\(\sqrt{npq}=\sqrt{1000\cdot \frac{1}{2}\cdot \frac{1}{2}}=\sqrt{250}=5\sqrt{10}=15,8\)

Путем подстановки численных значений, которые были определены ранее, учитывая, что \({K}_{1}=0\), получим следующее соотношение:

\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-500}{15,8} \right)-F\left( \frac{0-500}{15,8} \right)=0,99\)

Рассчитаем значение функции по доказательству:

\(F\left( \frac{-500}{15,8} \right)=-F\left( 31,6 \right)=0,5\)

Таким образом:

\(F\left( \frac{{{K}_{2}}-500}{15,8} \right)+0,5=0,99\)

\(F\left( \frac{{{K}_{2}}-500}{15,8} \right)=+0,49\)

С помощью табличной формы определим близкие к 0,49 значения функции. Таковым соответствуют точки 2,32 и 2,34. Выполним вычисления:

\(F\left( 2,32 \right)=0,48983\)

\(F\left( 2,34 \right)=0,49036\)

\(\frac{{{K}_{2}}-500}{15,8}=2,33\)

\({{K}_{2}}-500=2,33\cdot 15,8\)

\({{K}_{2}}-500=36,8\)

\({{K}_{2}}\approx 536,8=537\)

Ответ: 537.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Поиск по содержимому

Локальная и интегральная теоремы Лапласа

Если же при достаточно большом n условия формулы Пуассона не выполняются, следует обратиться к локальной теореме Муавра-Лапласа ^[1].

Для ее формулировки понадобится следующее

Определение

Функция называется функцией Гаусса.

Функцию Гаусса в табличном виде можно найти в любом справочнике и учебнике, имеющих отношение к теории вероятностей и математической статистике ^[2]. Но для того, чтобы пользоваться ее таблицей, нужно знать следующие

Свойства функции Гаусса

1. Функция является четной, то есть

ϕ(−x) = ϕ(x)                                                        

 2. Если ^[3]

x → ∞, то ϕ(x) → 0.                                                

Теорема

Локальная теорема Муавра-Лапласа Если в схеме n независимых испытаний событие A наступает в каждом из них с вероятностью p, где 0 < p < 1, а n → ∞, то вероятность того, что событие A наступит k раз, где .

[1] де Муавр Абрахам (фр. и англ. Abraham de Moivre, 1667-1754) − английский математик. Основные работы в математическом анализе и теории вероятности. Член Лондонского королевского общества, Парижской и Берлинской академий наук.

де Лаплас Пьер-Симон, (фр. de Laplace Pierre-Simon, 1749-1827) − маркиз, французский математик, механик, физик и астроном; известен работами в области небесной механики, дифференциальных уравнений, один из создателей теории вероятностей.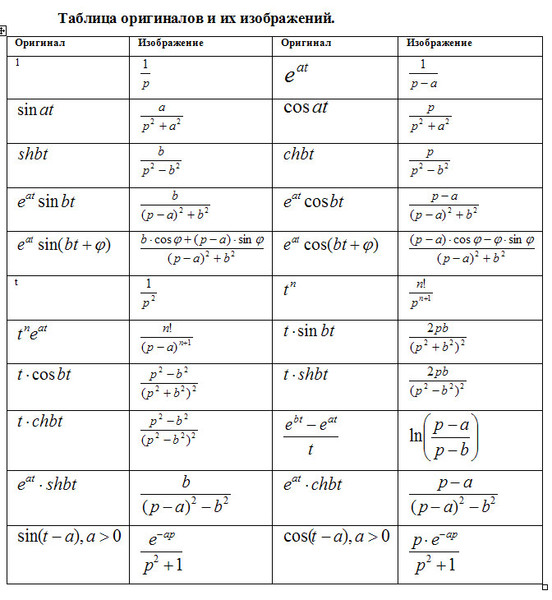 Иностранный член шести академий наук и королевского общества.

2 Как видно из таблицы значений функции Гаусса, при x ≥ 4 ϕ(x) практически равна нулю.

(Здесь, как и ранее, q = 1 − p.) В практических расч¨етах используют приближ¨енную формулу, которая называется локальной формулой Лапласа:

P_n(k) ^∼= √1   ϕ(x), где x = k√− np (q = 1 − p). 

Замечание

Следует заметить, что чем ближе значения вероятностей p и q к 0,5, тем точнее формула. А при p, близких к 0 или 1 локальная теорема Муавра-Лапласа дает большую погрешность, если сравнивать с результатами, полученным с помощью формулы Бернулли.

Являясь «конкурентом» формулы Пуассона, локальная теорема применяется обычно при npq > 10.

Задача

В честь праздника состоялся массовый забег на дистанцию 10 км. В забеге приняли участие 250 человек. Обычно в забегах такого типа из каждых десяти участников 8 доходят до финиша. Какова вероятность того, что до финиша добежали 200 человек?

Решение

Так как вероятность добежать финиша для каждого участника есть число постоянное, то перед нами схема Бернулли при большом числе испытаний. В силу того, что p = 0,8 > 0,1, вероятность можно вычислить с помощью локальной формулы Лапласа.

Определим q = 1 − 0,8 ⇒ q = 0,2. По условию n = 250, а k = 200. Следовательно, аргумент функции Гаусса .

Из таблицы значений функции Гаусса или с помощью калькулятора находим ϕ(0) = 0,3989.

Таким образом, .

вероятность того, что 200 человек добежали до финиша, равна 0,063.

Поэтому,

Далее возникает вопрос, как определять вероятность того, что в схеме независимых испытаний событие A наступает k раз, при этом значения k ∈ [k₁; k₂]?

Если n не велико, а число значений, попавших в диапазон мало, то, используя несовместность событий «k = k₁», «k = k₁ + 1», …, «k = k₂», можно там, где применимы формулы Бернулли и Пуассона, воспользоваться ими.

Там же, где это невозможно, обращаются к интегральной теореме Лапласа. Прежде, чем ее сформулировать, рассмотрим следующее

Определение

Функция

называется интегральной функцией Лапласа.

Точно также, как и функцию Гаусса, интегральную функцию Лапласа можно найти в табличном виде в любом справочнике и учебнике, имеющих отношение к теории вероятностей и математической статистике ^[1]. Но для того, чтобы пользоваться таблицей функции, нужно знать следующие Свойства интегральной функции Лапласа

Функция является нечетной, то есть

Φ(−x) = −Φ(x)

Если ^[2]

x → ∞, то Φ(x) → 0,5.

Теорема

Интегральная теорема Лапласа Если в схеме n независимых испытаний событие A наступает в каждом из них с вероятностью p, где 0 < p < 1, а n → ∞, то вероятность того, что событие A наступит от k₁ до k₂ раз

P(k₁; k₂) = lim (Φ(x₂) − Φ(x₁)), где. n→∞

(Здесь, как и ранее, q = 1 − p.)

На практике используют приближенную формулу:

k − np

P_n(k₁; k₂) = Φ(x₂) − Φ(x₁), где x , x  ,

(q = 1 − p).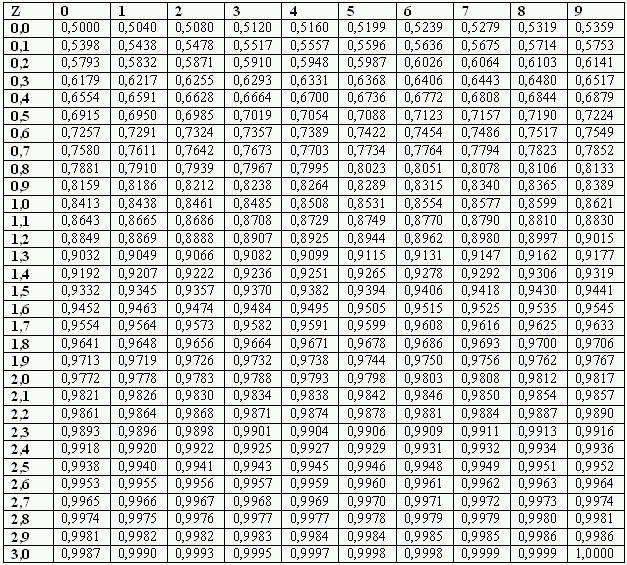

Задача

В условиях задачи определить вероятность того, что до финиша добежали от 180 до 210 человек.

Решение

Как и задача, эта задача посвящена схеме Бернулли. Правда, воспользоваться локальной формулой Лапласа, определяя для каждого k от 180 до 210 вероятность проблематично. Поэтому

 

Как видно из таблицы значений интегральной функции Лапласа, при x ≥ 4 Φ(x) практически равна 0,5.

воспользуемся интегральной формулой Лапласа. Зная, что n = 250; p = 0,8; q = 0,2; k₁ = 180, а k₂ = 210, вычислим соответствующие значения аргумента для интегральной функции Лапласа.;

Подставляя найденные значения аргумента в формулу, воспользуемся таблицей значений интегральной функции Лапласа:

Φ(1,1581)−Φ(−3,162) = Φ(1,1581)+Φ(3,162) = 0,3761+0,4993 = 0,8754.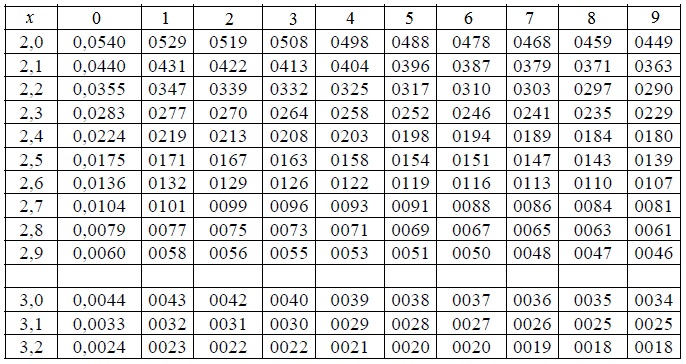

вероятность того, что до финиша добежали от 180 до 210 человек, равна 0,8754.

Следовательно,

Вероятность отклонения относительной частоты события от постоянной вероятности в независимых испытаниях

Теорема

Если в схеме n независимых испытаний событие A наступает в каждом из них с вероятностью p, где относительная частота события A, то для любого заданного числа ε > 0

(Здесь, как и ранее, q = 1 − p.)

Д о к а з а т е л ь с т в о

 Преобразуем неравенство, «подогнав» его под условия интегральной теоремы Лапласа. Раскрывая модуль, получим двойное неравенство

m −ε <      − p < ε, n

Затем, умножим все части неравенства на n:

−εn < m − np < εn. √

Далее, разделим все части неравенства на npq:

Сократив числитель и знаменатель левой и правой дробей на  n:,

введем обозначения:

Что и требовалось доказать.

Задача

Вероятность появления события в каждом из независимых испытаний равна 0,5. Сколько нужно провести испытаний n, чтобы с вероятностью γ = 0,7698 можно было ожидать, что относительная частота появления события ε отклонится от его вероятности по абсолютной величине не более чем на 0,02.

Решение

Согласно условию задачи p = 0,5, q = 0,5. То есть, мы имеем дело со схемой независимых испытаний. Согласно теореме.

По условию задачи .

То есть,

Согласно таблицам функции Лапласа Φ(x) = 0,3849, если x = 1,2. Таким образом,

для выполнения условий задачи нужно провести 900 испытаний.

Следовательно,

Задача

Вероятность выхода устройства из строя во время проведения эксперимента, целью которого является определение надежности устройства в работе, равна 0,2.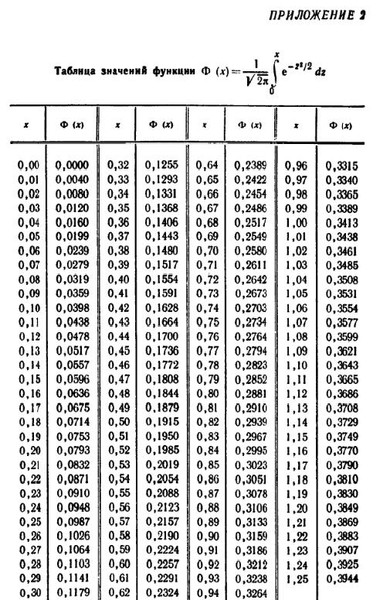 Было проверено 625 устройств. Чему равна вероятность, того, что абсолютная величина отклонения относительной частоты выхода из строя устройств от вероятности p=0,2 не превысит 0,02?

Решение

По условию задачи n = 625, p = 0,2, ε = 0,02.

Так как q = 1−p, то q = 0,8. Тогда аргумент функции Лапласа в теореме

Из таблиц интегральной функции Лапласа следует, что Φ(1,25) = 0,3944.

Поэтому, искомая вероятность

вероятность, того, что абсолютная величина отклонения относительной частоты выхода из строя устройств от вероятности p=0,2 не превысит 0,02 приблизительно равна 0,7888.

Что такое преобразование Лапласа?

Преобразование Лапласа — полезный инструмент для работы с линейными системами, описываемыми ОДУ. Как упоминалось в другом ответе, преобразование Лапласа определено для более широкого класса функций, чем родственное преобразование Фурье.

‘Большое дело’ заключается в том, что дифференциальный оператор (‘$\frac{d}{dt}$’ или ‘$\frac{d}{dx}$’) преобразуется в умножение на ‘$s$’, поэтому дифференциальные уравнения становятся алгебраическими уравнениями. Другими словами, свертка во временной или пространственной области становится умножением в s-области. Другой, часто негласный, «большой вопрос» заключается в том, что преобразование в некотором смысле уникально (например, если преобразования двух непрерывных функций согласуются, то и функции согласуются в исходной области). Таким образом, если вы можете решить проблему в домене s, то в некотором смысле вы решили ее и в исходном домене. Существует формула для инверсии, хотя для инверсии обычно используются таблицы. Однако формула обращения показывает, как проявляются полюса преобразованных функций во временной или пространственной области.

Существует несколько разновидностей преобразования Лапласа; для инженерных приложений наиболее распространенным является одностороннее преобразование (поведение при $t<0$ не имеет значения). {p_n t}$ (кратности нулей и полюсов $\hat{f}$ несколько усложняют эту упрощенную точку зрения). Итак, подумайте о частотах (т.е. полюсах и нулях) как о характеристиках структуры $\hat{f}$. 92}$ терм «вносит» два полюса (при $s = \pm i \omega_n$), лежащие на мнимой оси, в $\hat{x}$. Итак, мы ожидаем (по крайней мере) поведения, включающего $t \mapsto \sin \omega_n t$ и $t \mapsto \cos \omega_n t$.

Если мы возьмем $f = 0$, вы увидите (имеется в виду просмотр таблицы преобразований), что начальные условия преобразуются в функцию времени вида $x(t) = x(0) \cos \omega_n t + \frac{x'(0)}{\omega_n} \sin \omega_n t$. Итак, в этой конкретной задаче начальные условия «остаются» навсегда. 9{i \omega_n t}$. Обратите внимание, что ответ в этом случае не ограничен, даже если вход ограничен. Член ‘$t$’ возникает из-за полюса кратности 2 в точке $s = i \omega_n$.

Вычислительное четверное преобразование Лапласа для решения уравнений в частных производных

Прикладная математика Том 05 № 21 (2014 г. ), идентификатор статьи: 52117, 10 страниц
10.4236/am.2014.521314

Вычислительное четверное преобразование Лапласа для решения дифференциальных уравнений в частных производных

HAMOUD UR REHMAN ¹ , MUZAMMAL IFTIKHAR ¹ , SHOAIB SAILEEM ¹ , Muhammad Younis ² , Абдул Муд ³

9002 ¹ Департамент Mathed of Mathemed of Mathemed of Mathed of Mathemed of Mathemed of Mathemed of Mathemed of Mathed of Mathed of Mathed of Mathed of Mathed of Mathed of Mathed of Mathed of Mathed of Mathed of Mathed. Пакистан

² Центр бакалавриата Университета Пенджаба, Лахор, Пакистан

³ Кампус Air University Multan, Мултан, Пакистан

Электронная почта: [email protected], [email protected]. pk, [email protected], [email protected], [email protected]

Авторские права © 2014 принадлежат авторам и Scientific Research Publishing Inc.

Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Поступила в редакцию 11 октября 2014 г.; пересмотрено 2 ноября 2014 г.; принята 16 ноября 2014 г.

АННОТАЦИЯ

В этой статье мы предложили новые результаты по четверному преобразованию Лапласа и доказали некоторые свойства, связанные с четверным преобразованием Лапласа. Мы также разработали несколько приложений, основанных на этих результатах, и решали однородные, а также неоднородные уравнения в частных производных с четырьмя переменными. Эффективность четверного преобразования Лапласа очень обнадеживает на конкретных примерах. Также представлена ​​элементарная таблица четверного преобразования Лапласа.

Ключевые слова:

Четверное преобразование Лапласа, точное решение, свертка, уравнение в частных производных, однородные и неоднородные задачи

описывающих физические явления. Для нахождения решений дифференциальных уравнений можно использовать ряд методов (например, приближенный и точный).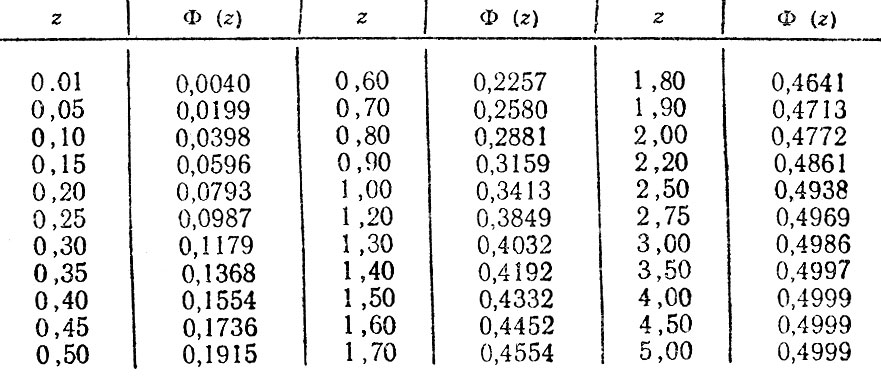

В большинстве случаев может быть сложно решить эти уравнения аналитически. Такие уравнения обычно решаются с помощью интегральных преобразований, таких как преобразования Лапласа и Фурье, а ценность преобразований Лапласа и Фурье заключается в их способности преобразовывать дифференциальные уравнения в алгебраические уравнения, что позволяет систематически и просто находить решение. Численные методы могут дать приближенные решения, а не аналитические решения задач [1] . Ряд аспектов этих методов изучался в [2][3].

Преобразование Лапласа эффективно используется для решения линейных и нелинейных обыкновенных дифференциальных уравнений и уравнений в частных производных и широко используется в электротехнике. Преобразование Лапласа сводит линейное дифференциальное уравнение к алгебраическому уравнению, которое можно решить по правилам алгебры. Затем исходное дифференциальное уравнение можно решить, применив обратное преобразование Лапласа. Хевисайд впервые предложил схему без использования преобразования Лапласа (см.

[4] и ссылки в ней).

Eltayeb и Kiliçman [5] применили двойное преобразование Лапласа, чтобы найти решение общих линейных телеграфных уравнений и интегро-дифференциальных уравнений в частных производных. Дахия и Наджафаи [6] установили новые теоремы для вычисления преобразований Лапласа n-мерного пространства и рассмотрели применение этих теорем к ряду часто используемых специальных функций, и, наконец, авторы решили одномерное волновое уравнение, включающее специальные функции, используя двумерные преобразования Лапласа. Агили и Могаддам [7] представили новую теорему и следствие о многомерных преобразованиях Лапласа. На основе этих результатов авторы разработали некоторые приложения. Киличман и Эльтайеб [8] обсудили взаимосвязь между преобразованиями Сумуду и Лапласа, а также провели некоторое сравнение решений. Авторы привели несколько контрпримеров. Шенигель и Региуа [9] исследовал решение трехмерного уравнения диффузии с нелокальным условием методом разложения Адомиана. Атангана [4] ввел тройное преобразование Лапласа.

Автор обсудил некоторые свойства и теоремы о тройном преобразовании Лапласа. Более того, автор использовал оператор для решения какого-то дифференциального уравнения третьего порядка.

Целью этой статьи является обсуждение некоторых свойств и теорем о четверном преобразовании Лапласа и предоставление хорошей стратегии решения дифференциальных уравнений в частных производных четвертого порядка в области техники и физики с помощью четверного преобразования Лапласа.

Прежде всего, напомним следующие определения.

Двойное преобразование Лапласа непрерывной функции можно определить [5] [10] как

(1.1)

, где x, y > 0 и p, q — переменные Лапласа.

Обратное двойное преобразование Лапласа определяется как

(1.2)

Тройное преобразование Лапласа [4] непрерывной функции может быть определено как

(1.3)

где x, y, z > 0 и p, q, r — переменные Лапласа.

Обратное тройное преобразование Лапласа определяется как

(1. 4)

В следующем разделе представлены определения четверного преобразования Лапласа, его обратного преобразования и некоторых его свойств.

2. Определения и свойства

Прежде чем перейти к основной части статьи, мы определим некоторые обозначения и термины, которые останутся стандартными.

Четверное преобразование Лапласа: Пусть f — непрерывная функция четырех переменных, тогда четверное преобразование Лапласа определяется равенством

(2.1)

где w, x, y, z > 0, а p, q, r, s — переменные Лапласа.

Следует отметить, что оператор четверного преобразования Лапласа является линейным.

(2.2)

Теперь, если четверное преобразование Лапласа известно, его обратное значение определяется как преобразование для частной производной первого порядка функции четырех переменных

(2.4)

2) Четверное преобразование Лапласа для частной производной второго порядка функции четырех переменных производная функции четырех переменных

(2. 8)

(2.9)

Единственность и существование четверного преобразования Лапласа обсуждается в следующем разделе.

3. Единственность и существование четверного преобразования Лапласа

Рассмотрим непрерывную функцию на интервале. Кроме того, предположим, что имеет экспоненциальный порядок, т. е. существуют такие константы, которые удовлетворяют следующему условию условие (3.1). Следующая теорема объясняет единственность.

Теорема 1. Пусть и определено – непрерывные функции, определенные для w, x, y, z ≥ 0 и имеющие преобразования Лапласа, и соответственно. Если , то.

Доказательство Если достаточно велики. Тогда из определения четверного обратного преобразования Лапласа имеем

(3.3)

Используя гипотезу, выражение (3.3) можно записать в виде

(3.4)

, что завершает доказательство.

4. Теорема свертки для четверного преобразования Лапласа

В этом разделе мы дадим некоторые определения свертки для функций и сформулируем теорему свертки для четверного преобразования Лапласа.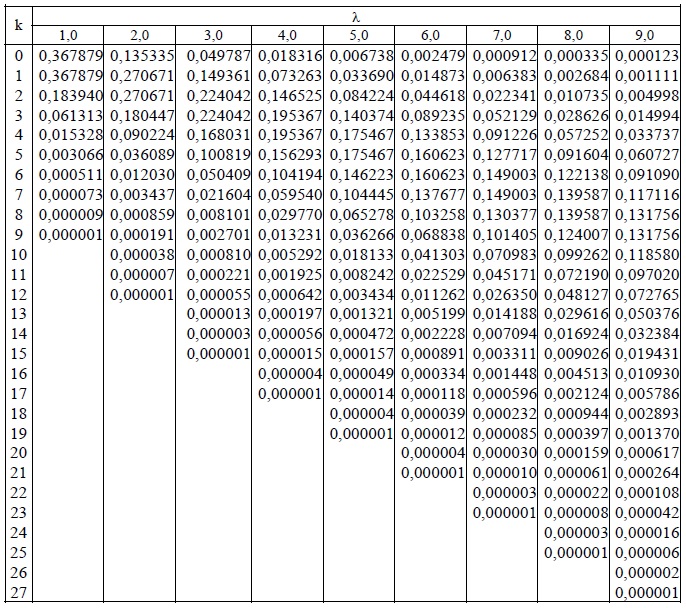

Рассмотрим функции , и.

Свертка функций и может быть определена как

(4.1)

Свертка функций и может быть определена как

(4.2)

Аналогично, свертка функций, и может быть определена как

Теорема 2. (Теорема о свертке) Если

(4.3)

(4.4)

(4.5)

сходятся в точке и если

(4.6)

, то абсолютно сходится выражение

(4.7)

есть преобразование Лапласа функции

(4.8)

и интеграл

(4.9)

сходится в точке, см. доказательство в [11] .

5. Свойства четверного преобразования Лапласа

В этом разделе представлены некоторые свойства четверного преобразования Лапласа. уравнения (5.1) можно решить как

(5.2)

Внутренний интеграл по z в уравнении (5.2) может быть решен после соответствующей замены как

(5.3)

Уравнение (5.2) принимает вид к y в уравнении (5.4) можно решить после соответствующей замены как

(5. 5)

. После подстановки значения из уравнения (5.5) в уравнение (5.4) мы можем получить

(5.6)

. , соответственно дважды проинтегрировав уравнение (5.6), можно получить требуемый результат Уравнение (5.1).

Свойство (2)

(5.7)

Доказательство: По определению (2.1) четверного преобразования Лапласа правая часть (5.7) может быть решена как

(5.8)

Внутренний интеграл по z может решить после соответствующей подстановки как

(5.9)

Аналогично, интегрируя уравнение (5.9) по y, x, w после соответствующей подстановки, можно получить искомый результат Уравнение (5.7).

Недвижимость (3)

(5.10)

Доказательство: По определению (2.1) четверного преобразования Лапласа левая часть (5.10) решается как

(5.11)

Внутренний интеграл по z решается по частям и дает

(5.12)

Уравнение (5.11) принимает вид

Аналогично, интегрируя уравнение (5.13) соответственно по y, x, w, мы можем получить требуемый результат Уравнение (5.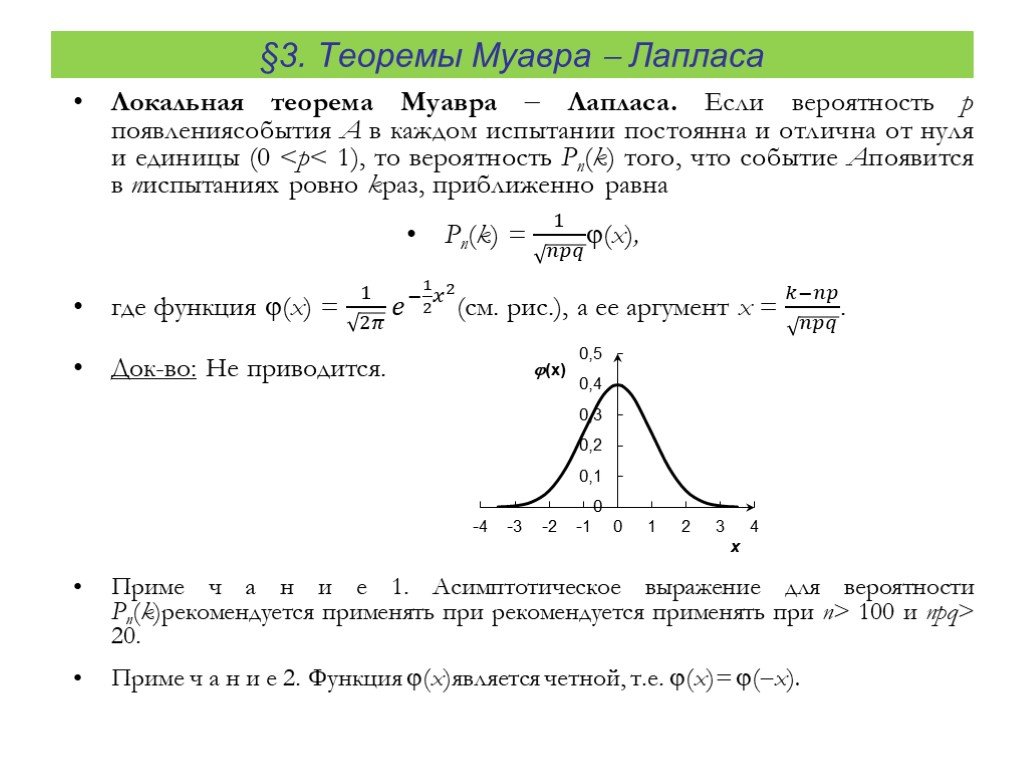 10).

Теорема 3. Функция, непрерывная на и удовлетворяющая условию роста (3.1), может быть восстановлена ​​только как

(5.13)

Для проверки эффективности теоремы рассмотрим следующий пример.

Позвольте, для которого преобразование Лапласа легко найти как применение логарифма и правила Лопиталя к предыдущему выражению дает

(5.15)

6. Численные примеры

Чтобы проиллюстрировать применимость и эффективность нашего метода, в этом разделе построено несколько примеров.

Пример 4.1. Рассмотрим следующее уравнение в частных производных четвертого порядка:

. Применение четверного преобразования Лапласа к обеим частям уравнения (6.1) дает

(6.1)

, где

(6.2)

После подстановки значения уравнение (6.1) становится

(6.3)

Применение четверного обратного преобразования Лапласа к (6.3)

(6.4)

Пример 4.2. Рассмотрим следующие уравнения трехмерной диффузии [9]

Применение четверного преобразования Лапласа к обеим частям уравнения (6.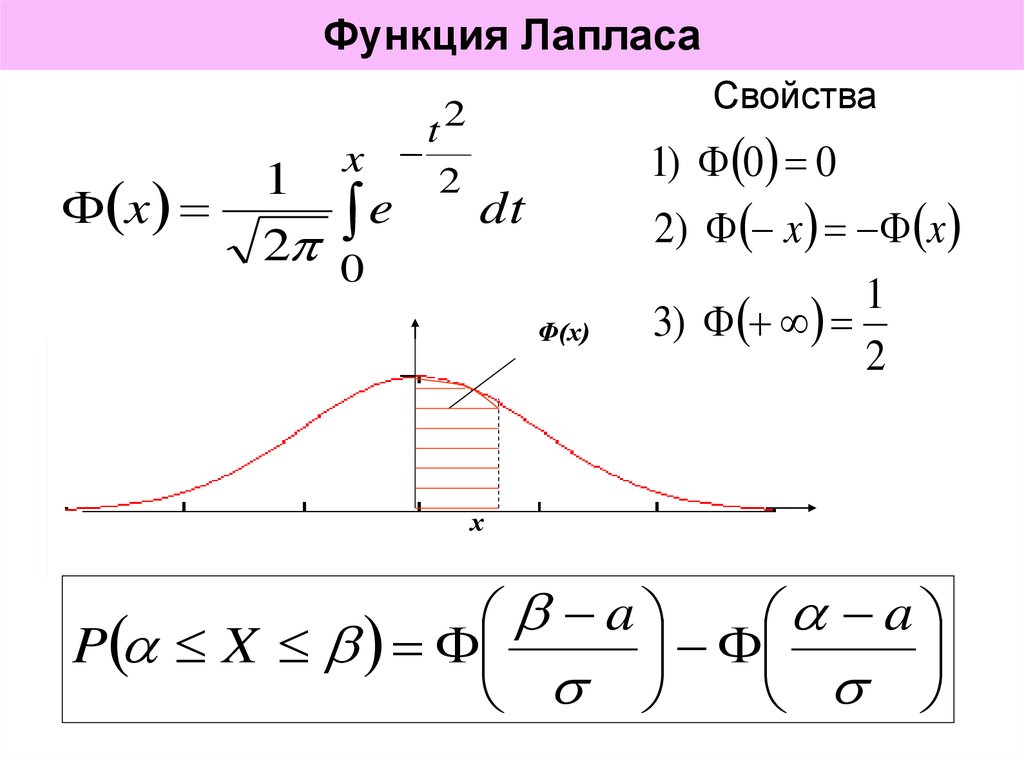 5) дает Уравнение (6.5) принимает вид

(6.7)

Применение четверного обратного преобразования Лапласа к (6.7)

(6.8)

Пример 4.3. Рассмотрим следующее неоднородное дифференциальное уравнение в частных производных четвертого порядка

Применение четверного преобразования Лапласа к обеим частям уравнения (6.9) дает

(6.9)

, где

(6.10)

Применение четверного обратного преобразования к (11)

(6.12)

Пример 4.4. Рассмотрим следующее уравнение неоднородной трехмерной диффузии0003

(6,13)

, где

(6,14)

После замены значения уравнение (6,13) становится

(6,15)

, применяя обратное преобразование квадрупов на (6,15)

(6,16)

7. Заключение

В этой статье мы расширяем работу [4] [5] на четверное преобразование Лапласа. Существование и единственность четверного преобразования также обсуждаются в этой работе. Также представлены некоторые свойства, теоремы с использованием нового четверного преобразования Лапласа и таблица, в которой четверное преобразование Лапласа применяется к некоторым функциям.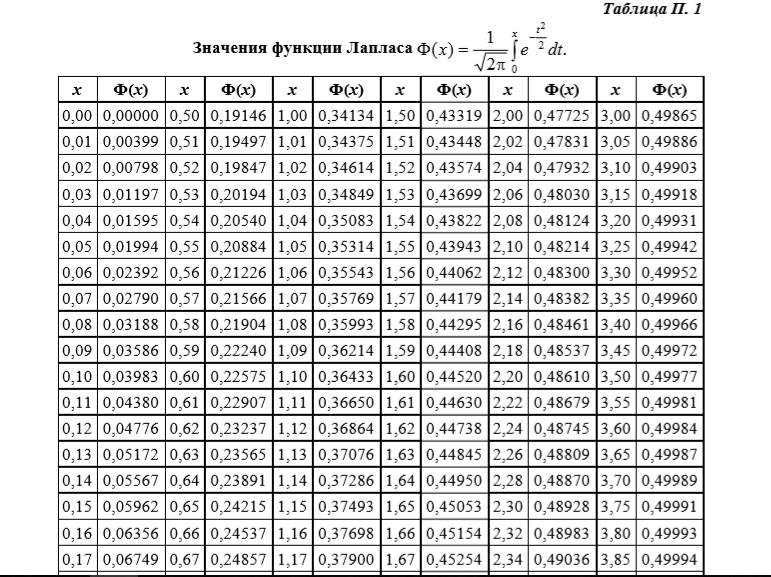 Анализируется, что предложенный нами метод хорошо подходит для использования в дифференциальном уравнении в частных производных с четырьмя переменными. Таким образом, настоящий метод является точным и надежным методом для дифференциальных уравнений в частных производных.

Ссылки

1. Kurnaz, A. and Oturanç, G. (2005) Метод N-мерного дифференциального преобразования для решения уравнений в частных производных. Международный журнал компьютерной математики, 167, 369-380. http://dx.doi.org/10.1080/0020716042000301725
2. Эванс, Д.Дж., Эргу, М. и Булут, Х. (2003) Вариационный итерационный метод — разновидность нелинейного аналитического метода: некоторые примеры. Международный журнал компьютерной математики, 80, 1189-1198. http://dx.doi.org/10.1080/00207160310001597161
3. Inc, М. и Эванс, Д.Дж. (2004) Эффективный подход к приближенным решениям краевых задач восьмого порядка. Международный журнал компьютерной математики, 81, 685-692. http://dx.doi.org/10.1080/0020716031000120809
4. Атангана, А. (2013) Заметка о тройном преобразовании Лапласа и его приложениях к некоторым дифференциальным уравнениям третьего порядка. Abstract and Applied Analysis, 2013 г., идентификатор статьи: 769102. http://dx.doi.org/10.1155/2013/769102
5. Эльтайеб, Х. и Киличман, А. (2013) Заметка о двойном преобразовании Лапласа и телеграфных уравнениях . Реферативный и прикладной анализ, 2013, № статьи: 932578. http://dx.doi.org/10.1155/2013/932578
6. Дахия Р.С. и Сабери-Наджаф, Дж. (1999) Теоремы о N-мерных преобразованиях Лапласа и их приложениях. 15-я ежегодная конференция прикладной математики, Univ. Центральной Оклахомы, Электронный журнал дифференциальных уравнений, 02, 61-74.
7. Агили, А. и Могаддам, Б.С. (2008) Пары преобразования Лапласа n-мерного измерения и линейные дифференциальные уравнения в частных производных второго порядка с постоянными коэффициентами. Анналы Mathematicae et Informaticae, 35, 3–10.
8. Киличман, А. и Эльтайеб, Х. (2012) Некоторые замечания о преобразованиях Сумуду и Лапласа и приложениях к дифференциальным уравнениям.

   No related posts.