Таблица производных и интегралов
Таблица производных. Табличные производные.
Производная степенной функции
Производная степенной функции
Производная экспоненциальной функции
Производная экспоненты
Производная сложной экспоненциальной функции
Производная экспоненциальной функции
Производная логарифмической функции
Производная натурального логарифма
Производная натурального логарифма функции
Производная синуса
Производная косинуса
Производная косеканса
Производная секанса
Производная арксинуса
Производная арккосинуса
Производная арксинуса
Производная арккосинуса
Производная тангенса
Производная котангенса
Производная арктангенса
Производная арккотангенса
Производная арктангенса
Производная арккотангенса
Производная арксеканса
Производная арккосеканса
Производная арксеканса
Производная арккосеканса
Производная гиперболического синуса
Производная гиперболического косинуса
Производная гиперболического тангенса
Производная гиперболического котангенса
Производная гиперболического секанса
Производная гиперболического косеканса
Таблица
первообразных («интегралов»). Табличные неопределенные интегралы.
(Простейшие интегралы и интегралы с
параметром).
Табличные неопределенные интегралы.
(Простейшие интегралы и интегралы с
параметром).
Интеграл степенной функции.
Интеграл степенной функции.
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
Интеграл экспоненциальной функции.
Интеграл экспоненты, где a-постоянное число.
Интеграл сложной экспоненциальной функции.
Интеграл экспоненциальной функции.
Интеграл, равняющийся натуральному логорифму.
Интеграл : «Длинный логарифм».
Интеграл : «Длинный логарифм».
Интеграл : «Высокий логарифм».
Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму.
Интеграл : «Высокий логарифм».
Интеграл
косинуса.
Интеграл синуса.
Интеграл, равный тангенсу.
Интеграл, равный котангенсу.
Интеграл, равный как арксинусу, так и арккосинусу
Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл, равный как арксинусу, так и арккосинусу.
Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл равный косекансу.
Интеграл, равный секансу.
Интеграл, равный арксекансу.
Интеграл, равный арккосекансу.
Интеграл, равный арксекансу.
Интеграл, равный арксекансу.
Интеграл, равный гиперболическому синусу.
Интеграл, равный гиперболическому косинусу.
Интеграл, равный гиперболическому тангенсу.
Интеграл, равный гиперболическому котангенсу.
Интеграл,
равный гиперболическому тангенсу.
Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому секансу.
Интеграл, равный гиперболическому косекансу.
Таблица производных — Таблица производных и интегралов
Таблица производных — Таблица производных и интегралов — n1.docТаблица производных и интегралов
Скачать все файлы (203.5 kb.)
Доступные файлы (1):
| n1.doc | 204kb. | 01.02.2014 15:34 | скачать |
n1.doc
Таблица производных
Простая функция | Сложная функция | |
| 1 | | |
| 2 | | |
| 3 | | |
| 4 | | |
| 5 | | |
| 6 | | |
| 7 | | |
| 8 | | |
| 9 | | |
| 10 | | |
| 11 | | |
| 12 | | |
| 13 | | |
| 14 | | |
| 15 | | |
Правила дифференцирования
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
Таблица интегралов
| 1 | | 8 | |
| 2 | | 9 | |
| 3 | | 10 | |
| 4 | | 11 | |
| 5 | | 12 | |
| 6 | | 13 | |
| 7 | | 14 | |
Таблица дифференциалов
| 1 | | 6 | |
| 2 | | 7 | |
| 3 | | 8 | |
| 4 | | 9 | |
| 5 | | 10 | |
Свойства неопределенного интеграла
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
© perviydoc. ru
ru
При копировании укажите ссылку.
обратиться к администрации
World Web Math: сводка исчисления
World Web Math: сводка исчисления Исчисление состоит из двух основных частей: дифференциального исчисления и интегрального исчисления. исчисление. Дифференциальное исчисление изучает производную и интегральное исчисление изучает (сюрприз!) интеграл. Производная и интеграл связаны тем, что они оба определяются через понятие предела: они являются операциями, обратными друг друга (факт, иногда известный как основная теорема исчисления): и они оба являются фундаментальными для большей части современной науки, как мы знаю это.Производные
Предел функции f ( x ) как x приближается к a равно b , если для каждой желаемой близости к b можно найти небольшой интервал вокруг (но не включая) и , которые достигают этой близости, когда нанесен на карту f . Пределы дают нам прочную математическую основу для изучения как бесконечное и бесконечное.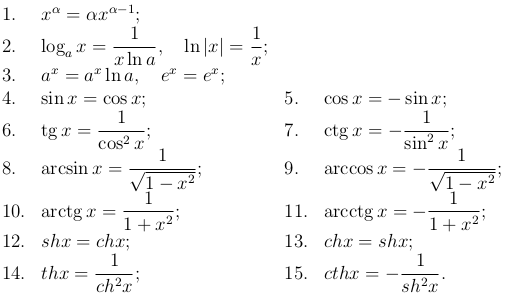 Они также легко обрабатываются алгебраически:
где в последнем уравнении c
Они также легко обрабатываются алгебраически:
где в последнем уравнении c Важно помнить, что
вовсе не зависит от f (а) — на самом деле f (a) часто не определяется. В счастливом случай, когда мы говорим, что f есть непрерывное в a . Это также иногда полезно говорить об односторонней (левой или правой) пределы, где нас интересуют только значения x это меньше или больше a .Производная от ф ( х ) при x = a (или f´ ( a )) определяется как
везде, где существует предел. Производная имеет много интерпретаций и приложений, включая скорость (где f дает положение как функция времени), мгновенная скорость изменения или наклон касательной к графику f . С использованием алгебраические свойства пределов, вы можете доказать эти чрезвычайно важные алгебраические свойства производные: Эти правила, например, позволяют вычислить производную любого рациональная (= отношение двух многочленов) функция.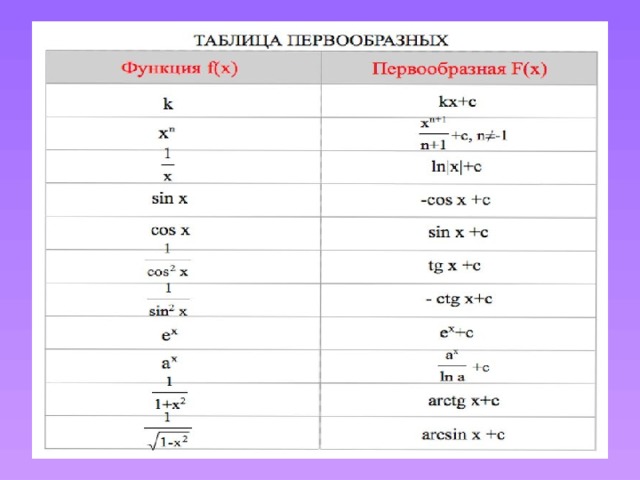 Цепное правило, в частности, имеет
много приложений. Во-первых, если у вас есть две обратные функции ф и g , то есть если f ( g ( x )) =  x , то цепное правило подразумевает, что f´ ( г ) =
1/ g´ ( x ).
Цепное правило, в частности, имеет
много приложений. Во-первых, если у вас есть две обратные функции ф и g , то есть если f ( g ( x )) =  x , то цепное правило подразумевает, что f´ ( г ) =
1/ g´ ( x ).Кроме того, если у вас есть неявное определенная функция между x и y x 2 — 2 x у + у 2 = 1, то вы можете выполнить неявное дифференцирование (в основном, просто взяв производную от всего по оба x и y добавляются к dx s и dy s указать какой) получить 2 x dx
 Примечание
что в этом случае любая производная будет через оба х и у .
Примечание
что в этом случае любая производная будет через оба х и у .Вам могут быть интересны производные вашего любимого тригонометрические функции. Что ж,
Эти два факта в сочетании с приведенными выше правилами позволяют легко вычислить производные остальных тригонометрических функций и их инверсии. Производные гиперболического функции аналогичны, за исключением того, что Многие физические применения производных сводятся к поиску решений к дифференциальным уравнениям: уравнения, связывающие функцию и ее производные. Например, и синус, и косинус удовлетворяют дифференциальное уравнение ф ´´( х ) = — f ( x ), который моделирует идеальные маятники, пружины, и другие примеры простого гармонического движения. Уравнение f ´( x ) = k f ( x ) возникает при моделировании роста населения и радиоактивного распада и решается функцией f ( x ) = e kx , куда называется постоянной Эйлера и определяется как уникальное действительное число e , такое что ( e x )´ = e x . Обратная сторона
экспоненциальная функция e x функция натурального логарифма
log( x ), обладающий множеством полезных и интересных свойств,
включая:
Обратная сторона
экспоненциальная функция e x функция натурального логарифма
log( x ), обладающий множеством полезных и интересных свойств,
включая:- log( ab ) = log a + log b
[Таким образом логарифмы превратить умножения в в дополнениях было то, почему журнальные таблицы (и их аналоговые кузены, логарифмические линейки) использовались для выполнения длинных умножений до того, как появились компьютеры.] - лог( a/b ) = лог а — лог б
- e (log x ) = x и log e x = x
- бревно x a = a бревно x
- a x = e ( x log a )
- (log( x ))´ = 1/ x
- журнал 1 = 0
Тесно связана с натуральным логарифмом
логарифм по основанию b , (log b x ), которые можно определить
как лог( x )/лог( б ).

Наконец, производные можно использовать для построения графиков функций. Первый, они дают вам наклон графика в точке, что полезно. Во-вторых, точки, в которых наклон графика горизонтален. ( f ´( x ) = 0) особенно важно, потому что это единственные точки, в которых относительная может иметь место минимум или максимум (в дифференцируемой функции). Эти точки, где f ´( x )) = 0 называется критическими точками . Чтобы определить, является ли критическим точка является минимумом или максимумом, или, в более общем смысле, для определения вогнутость функции, можно использовать вторые производные; f ´´( x ) f´´( x ) > 0 означает относительный минимум /вогнутость вверх. Наконец, принимая предел как x переходит в положительную или отрицательную бесконечность дает информацию об асимпотическом поведении функции. К этому концу, производные могут помочь вам с некоторыми трудными ограничениями: Правило Лопиталя, если lim
 Доказательство правила Лопиталя основано на теореме о среднем значении:
для любой функции f ( x ) дифференцируется между и и b , между c есть некоторая точка a и b такие, что производная ф на c такой же, как средний наклон между и и б :
Доказательство правила Лопиталя основано на теореме о среднем значении:
для любой функции f ( x ) дифференцируется между и и b , между c есть некоторая точка a и b такие, что производная ф на c такой же, как средний наклон между и и б :Интегралы
Интеграл f ( x ) от до b по отношению к x отмечается как и дает площадь под графиком f и выше интервал [ a , b ]. Формально его можно определить как Риман сумма: предел площадей прямоугольных приближений к площади поскольку приближения становятся все лучше и лучше.Как было сказано ранее, интегрирование и дифференцирование обратны. операции. Точнее, основная теорема исчисления утверждает что
В более общем случае, используя правило цепочки, Зная эти факты, мы теперь знаем огромное количество интегралов: просто переверните стороны любой таблицы производных. Вот некоторые
дополнительные сведения об интегралах:
Для c константа,
Вот некоторые
дополнительные сведения об интегралах:
Для c константа,
Интеграл положительной непрерывной функции от до до б с b > a больше нуля. Интеграл от a до b от f ( x )- г ( x ), с f ( x ) > г ( x ) в интервал [ a , b ] дает площадь между f ( x ) и g ( x ).Если этих свойств недостаточно для решения вашего интеграла, и если вы не могу найти его ни в одной таблице, то вот еще несколько трюков торговля:
- Замена («обратная» цепному правилу):
- Интеграция по частям («invserse» правила продукта):
- Частичные дроби: любая рациональная функция со знаменателем
который можно разбить
в сумму дробей вида
где А , В , С , Д и E — константы (конечно, не те константы в
две формы) могут быть (более) легко интегрированы.

- Численное приближение. Это может не дать вам точного ответ, но аппроксимируя площадь под ф ( х ) с прямоугольниками, трапециями или даже более сложными формами может дать вам значение близкое к интегралу, когда никакой другой метод не будет работать. Для краткое объяснение использования приложения, доступного для MIT студенты, см. Определенные Интегралы в Maple, часть Использование Maple для предметов ESG, используемых как часть предмета MIT 18.01A на ESG.
 Наконец,
площадь поверхности, образованной вращением графика f ( x ) между x =a и х =b о
ось x может быть найдена интегралом
Иногда вам может понадобиться взять интеграл по неограниченному интервалу.
например, от 1 до бесконечности, или взять интеграл от функции, которая
в некоторых точках не определено (например, 1/ x 1/2 ).
Это несобственные интегралы, и их можно найти, взяв предел
интеграл по интервалу, который либо растет к бесконечности, либо
к точкам, где функция не определена.
Наконец,
площадь поверхности, образованной вращением графика f ( x ) между x =a и х =b о
ось x может быть найдена интегралом
Иногда вам может понадобиться взять интеграл по неограниченному интервалу.
например, от 1 до бесконечности, или взять интеграл от функции, которая
в некоторых точках не определено (например, 1/ x 1/2 ).
Это несобственные интегралы, и их можно найти, взяв предел
интеграл по интервалу, который либо растет к бесконечности, либо
к точкам, где функция не определена.Страница индекса исчисления | Вернуться на страницу категорий World Web Math
[email protected] Последнее изменение 10 января 2000 г.
Таблица интегралов — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14727
Для этого курса необходимо показать всю работу, чтобы получить большинство этих интегральных форм. Из приведенных ниже формул интегрирования только те, которые можно применить без дополнительной работы, это #1 – 10, 15 – 17, а также 49 и 50.
Из приведенных ниже формул интегрирования только те, которые можно применить без дополнительной работы, это #1 – 10, 15 – 17, а также 49 и 50.
Все остальные могут быть полезны для проверки ваших окончательных ответов, но их нельзя использовать для пропуска необходимой работы, чтобы показать, что вы понимаете, как использовать методы интеграции, изучаемые в этом курсе. 9{n−2}u\,du\)
34. \(\quad \displaystyle ∫\sin au\sin bu\,du=\frac{\sin (a−b)u}{2(a−b )}−\frac{\sin (a+b)u}{2(a+b)}+C\)
35. \(\quad \displaystyle ∫\cos au\cos bu\,du=\frac {\ sin (a-b) u} {2 (a-b)} + \ frac {\ sin (a + b) u} {2 (a + b)} + C \)
36. \(\ quad \ displaystyle ∫ \ sin au \ cos bu \, du = — \ frac {\ cos (a-b) u} {2 (a-b)} — \ frac {\ cos (a + b) u} {2 (a+b)}+C\)
37. \(\quad \displaystyle ∫u\sin u\,du=\sin u−u\cos u+C\)
38. \(\quad \ стиль отображения ∫u\cos u\,du=\cos u+u\sin u+C\) 92}[(n+1)\ln u−1]+C\)
48. \(\quad \displaystyle ∫\frac{1}{u\ln u}\,du=\ln |\ln u |+C\)
Гиперболические интегралы
49.


 Доказательство правила Лопиталя основано на теореме о среднем значении:
для любой функции f ( x ) дифференцируется между и и b , между c есть некоторая точка a и b такие, что производная ф на c такой же, как средний наклон между и и б :
Доказательство правила Лопиталя основано на теореме о среднем значении:
для любой функции f ( x ) дифференцируется между и и b , между c есть некоторая точка a и b такие, что производная ф на c такой же, как средний наклон между и и б : Вот некоторые
дополнительные сведения об интегралах:
Для c константа,
Вот некоторые
дополнительные сведения об интегралах:
Для c константа, 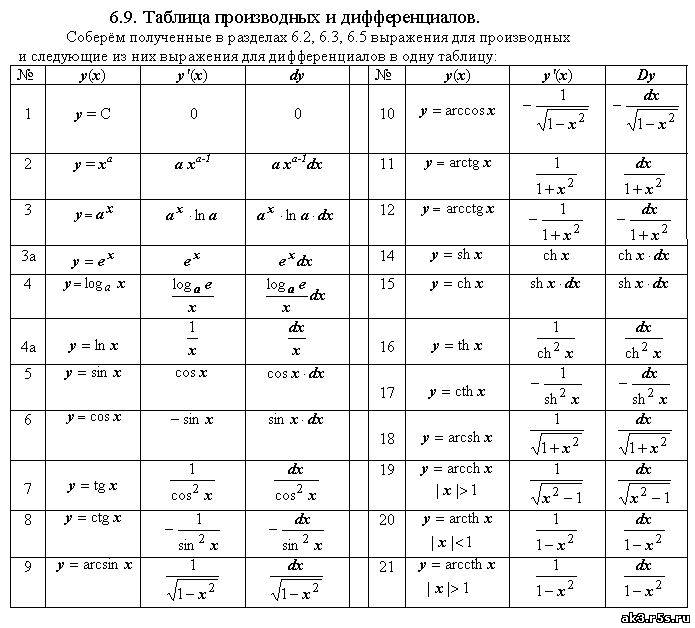
 Наконец,
площадь поверхности, образованной вращением графика f ( x ) между x =a и х =b о
ось x может быть найдена интегралом
Иногда вам может понадобиться взять интеграл по неограниченному интервалу.
например, от 1 до бесконечности, или взять интеграл от функции, которая
в некоторых точках не определено (например, 1/ x 1/2 ).
Это несобственные интегралы, и их можно найти, взяв предел
интеграл по интервалу, который либо растет к бесконечности, либо
к точкам, где функция не определена.
Наконец,
площадь поверхности, образованной вращением графика f ( x ) между x =a и х =b о
ось x может быть найдена интегралом
Иногда вам может понадобиться взять интеграл по неограниченному интервалу.
например, от 1 до бесконечности, или взять интеграл от функции, которая
в некоторых точках не определено (например, 1/ x 1/2 ).
Это несобственные интегралы, и их можно найти, взяв предел
интеграл по интервалу, который либо растет к бесконечности, либо
к точкам, где функция не определена.