Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 11.12.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Читать статью можно без ограничений. Однако для копирования и использования текста нужно зарегистрироваться в экосистеме Автор24.
Это бесплатно.
Однако для копирования и использования текста нужно зарегистрироваться в экосистеме Автор24.
Это бесплатно.
775 экспертов, которые помогали студентам с темой
«Особенности управления распределительными центрами в деятельности розничной торговой организации»
право и юриспруденция …
право и юриспруденция
Обратиться за помощью
作业有问题吗?
Author24 会帮助你!
中文客服帮你下单
关注我们的微信公众号
获得中文服务
Елена Борисовна Калюжная.
Таблица производных сложных функций //
Образовательный портал «Справочник». — Дата последнего обновления статьи: 11. 12.2021.
— URL https://spravochnick.ru/matematika/proizvodnaya_i_differencial/tablica_proizvodnyh_slozhnyh_funkciy/
(дата обращения: 03.10.2022).
12.2021.
— URL https://spravochnick.ru/matematika/proizvodnaya_i_differencial/tablica_proizvodnyh_slozhnyh_funkciy/
(дата обращения: 03.10.2022).
Добавлено в буфер обмена
Как находить производные сложных функций. Производная сложной функции
На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.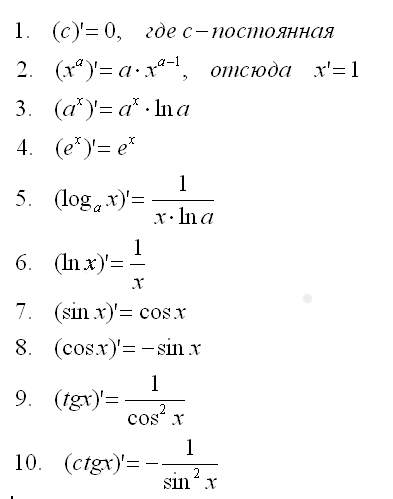
Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
Разбираемся. Прежде всего, обратим внимание на запись . Здесь у нас две функции – и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию я буду называть внешней функцией , а функцию – внутренней (или вложенной) функцией .
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.
Для того, чтобы прояснить ситуацию, рассмотрим:
Пример 1
Найти производную функции
Под синусом у нас находится не просто буква «икс», а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочлен является внутренней функцией (вложением), а – внешней функцией.
Первый шаг , который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней .
В случае простых примеров вроде понятно, что под синус вложен многочлен . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому многочлен и будет внутренней функцией :
Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции .
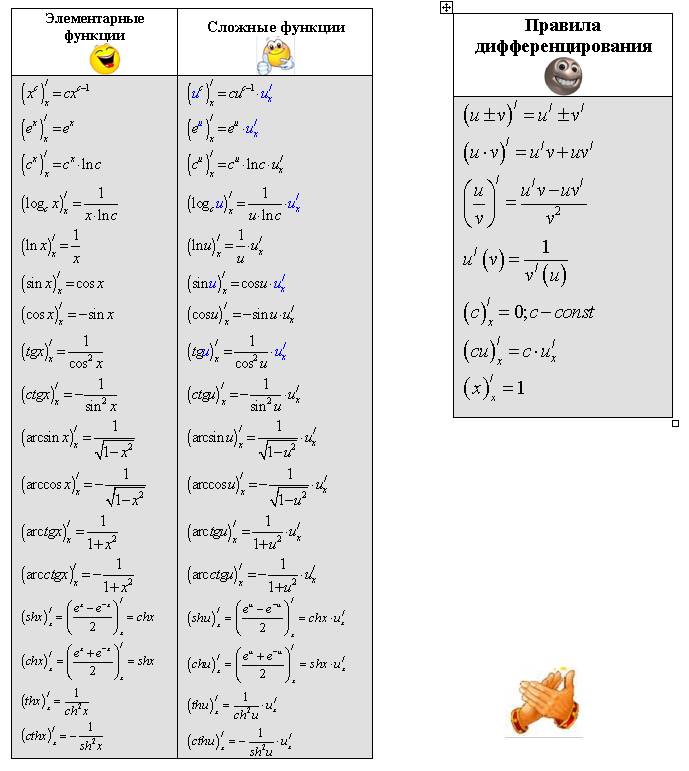
Начинаем решать. С урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:
Сначала находим производную внешней функции (синуса), смотрим на таблицу производных элементарных функций и замечаем, что . Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением , в данном случае:
Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем .
Ну и совершенно очевидно, что
Результат применения формулы в чистовом оформлении выглядит так:
Постоянный множитель обычно выносят в начало выражения:
Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.
Пример 2
Найти производную функции
Пример 3
Найти производную функции
Как всегда записываем:
Разбираемся, где у нас внешняя функция, а где внутренняя.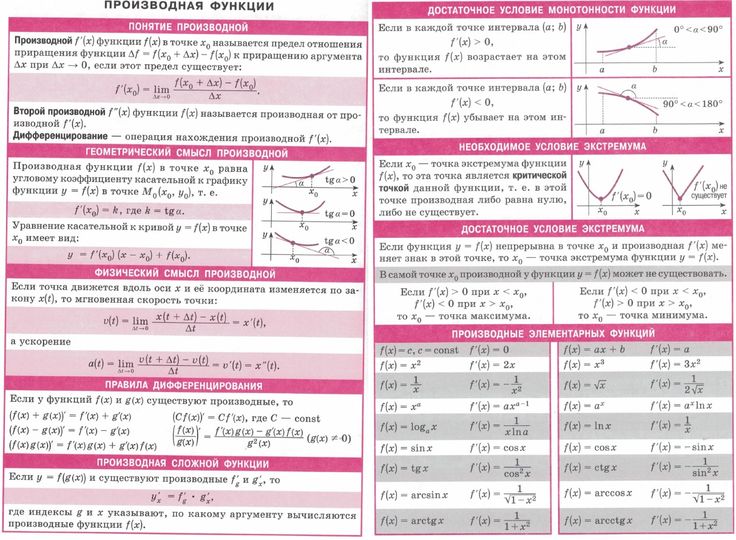 Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция:
Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения . Таким образом, результат применения правила дифференцирования сложной функции следующий:
Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функция у нас не меняется:
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:
Пример 4
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).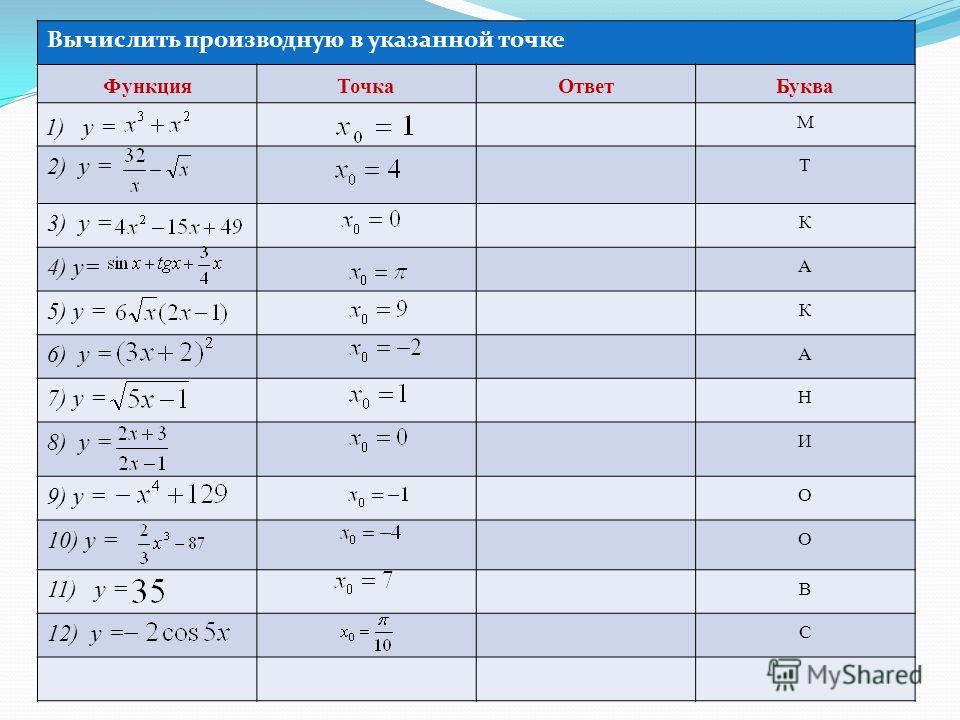
Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?
Пример 5
а) Найти производную функции
б) Найти производную функции
Пример 6
Найти производную функции
Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :
Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:
Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Пример 7
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного , но такое решение будет выглядеть как извращение забавно. Вот характерный пример:
Пример 8
Найти производную функции
Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :
Находим производную внутренней функции, косинус сбрасываем обратно вниз:
Готово.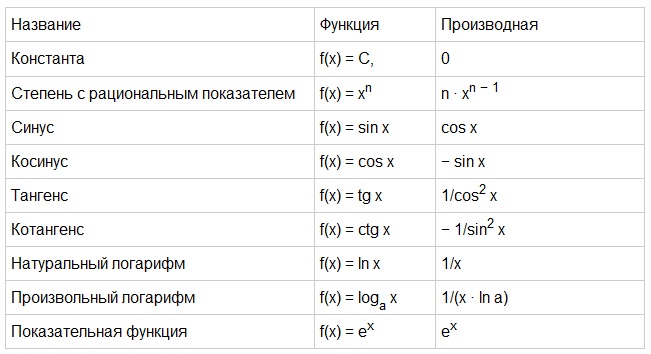 В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
Пример 9
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрешки, одна в другую, вложены сразу 3, а то и 4-5 функций.
Пример 10
Найти производную функции
Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?
Сначала нужно найти , значит, арксинус – самое глубокое вложение:
Затем этот арксинус единицы следует возвести в квадрат :
И, наконец, семерку возводим в степень :
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.
Начинаем решать
Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: Единственное отличие – вместо «икс» у нас сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий:
Под штрихом у нас снова сложная функция! Но она уже проще. Легко убедиться, что внутренняя функция – арксинус, внешняя функция – степень. Согласно правилу дифференцирования сложной функции сначала нужно взять производную от степени.
И теорему о производной сложной функции, формулировка которой такова:
Пусть 1) функция $u=\varphi (x)$ имеет в некоторой точке $x_0$ производную $u_{x}»=\varphi»(x_0)$, 2) функция $y=f(u)$ имеет в соответствующей точке $u_0=\varphi (x_0)$ производную $y_{u}»=f»(u)$. Тогда сложная функция $y=f\left(\varphi (x) \right)$ в упомянутой точке также будет иметь производную, равную произведению производных функций $f(u)$ и $\varphi (x)$:
$$ \left(f(\varphi (x))\right)»=f_{u}»\left(\varphi (x_0) \right)\cdot \varphi»(x_0) $$
или, в более короткой записи: $y_{x}»=y_{u}»\cdot u_{x}»$. {\frac{1}{2}}}=\frac{1}{\sqrt{u}}$, то равенство (4.2) можно переписать в таком виде:
{\frac{1}{2}}}=\frac{1}{\sqrt{u}}$, то равенство (4.2) можно переписать в таком виде:
$$ (\sqrt{u})»=\frac{1}{2}\cdot \frac{1}{\sqrt{u}}\cdot u»=\frac{1}{2\sqrt{u}}\cdot u» $$
Полученное равенство $(\sqrt{u})»=\frac{1}{2\sqrt{u}}\cdot u»$ и есть формула №4 таблицы производных. Как видите, формулы №3 и №4 таблицы производных получаются из формулы №2 подстановкой соответствующего значения $\alpha$.
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y». Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых
существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых
существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f»(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f»(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет
производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f»(x) \), т.е.
\(\Delta y \approx f»(x) \cdot \Delta x \).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально»
приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х. 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. 2} $$
2} $$
Функции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y = sin x — (2 — 3) · a r c t g x x 5 7 x 10 — 17 x 3 + x — 11 , то ее нельзя считать сложной в отличие от y = sin 2 x .
Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.
Yandex.RTB R-A-339285-1
Основные определения
Определение 1
Сложной функцией считается такая функция, у которой аргумент также является функцией.
Обозначается это таким образом: f (g (x)) . Имеем, что функция g (x) считается аргументом f (g (x)) .
Определение 2
Если есть функция f и является функцией котангенса, тогда g (x) = ln x – это функция натурального логарифма. Получаем, что сложная функция f (g (x)) запишется как arctg(lnx). Или функция f , являющаяся функцией возведенной в 4 степень, где g (x) = x 2 + 2 x — 3 считается целой рациональной функцией, получаем, что f (g (x)) = (x 2 + 2 x — 3) 4 .
Или функция f , являющаяся функцией возведенной в 4 степень, где g (x) = x 2 + 2 x — 3 считается целой рациональной функцией, получаем, что f (g (x)) = (x 2 + 2 x — 3) 4 .
Очевидно, что g (x) может быть сложной. Из примера y = sin 2 x + 1 x 3 — 5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y = f (f 1 (f 2 (x))) . Откуда имеем, что f – это функция синуса, а f 1 — функция, располагаемая под квадратным корнем, f 2 (x) = 2 x + 1 x 3 — 5 — дробная рациональная функция.
Определение 3
Степень вложенности определено любым натуральным числом и записывается как y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .
Определение 4
Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида
(f (g (x))) » = f » (g (x)) · g » (x)
Примеры
Пример 1
Найти производную сложной функции вида y = (2 x + 1) 2 .
Решение
По условию видно, что f является функцией возведения в квадрат, а g (x) = 2 x + 1 считается линейной функцией.
Применим формулу производной для сложной функции и запишем:
f » (g (x)) = ((g (x)) 2) » = 2 · (g (x)) 2 — 1 = 2 · g (x) = 2 · (2 x + 1) ; g » (x) = (2 x + 1) » = (2 x) » + 1 » = 2 · x » + 0 = 2 · 1 · x 1 — 1 = 2 ⇒ (f (g (x))) » = f » (g (x)) · g » (x) = 2 · (2 x + 1) · 2 = 8 x + 4
Необходимо найти производную с упрощенным исходным видом функции. Получаем:
y = (2 x + 1) 2 = 4 x 2 + 4 x + 1
Отсюда имеем, что
y » = (4 x 2 + 4 x + 1) » = (4 x 2) » + (4 x) » + 1 » = 4 · (x 2) » + 4 · (x) » + 0 = = 4 · 2 · x 2 — 1 + 4 · 1 · x 1 — 1 = 8 x + 4
Результаты совпали.
При решении задач такого вида важно понимать, где будет располагаться функция вида f и g (x) .
Пример 2
Следует найти производные сложных функций вида y = sin 2 x и y = sin x 2 .
Решение
Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g (x) – функцией синуса. Тогда получим, что
Тогда получим, что
y » = (sin 2 x) » = 2 · sin 2 — 1 x · (sin x) » = 2 · sin x · cos x
Вторая запись показывает, что f является функцией синуса, а g (x) = x 2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как
y » = (sin x 2) » = cos (x 2) · (x 2) » = cos (x 2) · 2 · x 2 — 1 = 2 · x · cos (x 2)
Формула для производной y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) запишется как y » = f » (f 1 (f 2 (f 3 (. . . (f n (x)))))) · f 1 » (f 2 (f 3 (. . . (f n (x))))) · · f 2 » (f 3 (. . . (f n (x)))) · . . . · f n » (x)
Пример 3
Найти производную функции y = sin (ln 3 a r c t g (2 x)) .
Решение
Данный пример показывает сложность записи и определения расположения функций. Тогда y = f (f 1 (f 2 (f 3 (f 4 (x))))) обозначим, где f , f 1 , f 2 , f 3 , f 4 (x) является функцией синуса, функцией возведения в 3 степень, функцией с логарифмом и основанием е, функцией арктангенса и линейной.
Из формулы определения сложной функции имеем, что
y » = f » (f 1 (f 2 (f 3 (f 4 (x))))) · f 1 » (f 2 (f 3 (f 4 (x)))) · · f 2 » (f 3 (f 4 (x))) · f 3 » (f 4 (x)) · f 4 » (x)
Получаем, что следует найти
- f » (f 1 (f 2 (f 3 (f 4 (x))))) в качестве производной синуса по таблице производных, тогда f » (f 1 (f 2 (f 3 (f 4 (x))))) = cos (ln 3 a r c t g (2 x)) .

- f 1 » (f 2 (f 3 (f 4 (x)))) в качестве производной степенной функции, тогда f 1 » (f 2 (f 3 (f 4 (x)))) = 3 · ln 3 — 1 a r c t g (2 x) = 3 · ln 2 a r c t g (2 x) .
- f 2 » (f 3 (f 4 (x))) в качестве производной логарифмической, тогда f 2 » (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
- f 3 » (f 4 (x)) в качестве производной арктангенса, тогда f 3 » (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2 .
- При нахождении производной f 4 (x) = 2 x произвести вынесение 2 за знак производной с применением формулы производной степенной функции с показателем, который равняется 1 , тогда f 4 » (x) = (2 x) » = 2 · x » = 2 · 1 · x 1 — 1 = 2 .
Производим объединение промежуточных результатов и получаем, что
y » = f » (f 1 (f 2 (f 3 (f 4 (x))))) · f 1 » (f 2 (f 3 (f 4 (x)))) · · f 2 » (f 3 (f 4 (x))) · f 3 » (f 4 (x)) · f 4 » (x) = = cos (ln 3 a r c t g (2 x)) · 3 · ln 2 a r c t g (2 x) · 1 a r c t g (2 x) · 1 1 + 4 x 2 · 2 = = 6 · cos (ln 3 a r c t g (2 x)) · ln 2 a r c t g (2 x) a r c t g (2 x) · (1 + 4 x 2)
Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.
Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.
Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.
Пример 4
Необходимо рассмотреть на приведении подобного примера. Если имеется функция вида y = t g 2 x + 3 t g x + 1 , тогда ее можно рассмотреть в качестве сложной вида g (x) = t g x , f (g) = g 2 + 3 g + 1 . Очевидно, что необходимо применение формулы для сложной производной:
f » (g (x)) = (g 2 (x) + 3 g (x) + 1) » = (g 2 (x)) » + (3 g (x)) » + 1 » = = 2 · g 2 — 1 (x) + 3 · g » (x) + 0 = 2 g (x) + 3 · 1 · g 1 — 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g » (x) = (t g x) » = 1 cos 2 x ⇒ y » = (f (g (x))) » = f » (g (x)) · g » (x) = (2 t g x + 3) · 1 cos 2 x = 2 t g x + 3 cos 2 x
Функция вида y = t g x 2 + 3 t g x + 1 не считается сложной, так как имеет сумму t g x 2 , 3 t g x и 1 . Однако, t g x 2 считается сложной функцией, то получаем степенную функцию вида g (x) = x 2 и f , являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что
Однако, t g x 2 считается сложной функцией, то получаем степенную функцию вида g (x) = x 2 и f , являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что
y » = (t g x 2 + 3 t g x + 1) » = (t g x 2) » + (3 t g x) » + 1 » = = (t g x 2) » + 3 · (t g x) » + 0 = (t g x 2) » + 3 cos 2 x
Переходим к нахождению производной сложной функции (t g x 2) » :
f » (g (x)) = (t g (g (x))) » = 1 cos 2 g (x) = 1 cos 2 (x 2) g » (x) = (x 2) » = 2 · x 2 — 1 = 2 x ⇒ (t g x 2) » = f » (g (x)) · g » (x) = 2 x cos 2 (x 2)
Получаем, что y » = (t g x 2 + 3 t g x + 1) » = (t g x 2) » + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x
Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.
Пример 5
Для примера рассмотрим сложную функцию вида y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x · (x 2 + 1)
Данная функция может быть представлена в виде y = f (g (x)) , где значение f является функцией логарифма по основанию 3 , а g (x) считается суммой двух функций вида h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 и k (x) = ln 2 x · (x 2 + 1) . Очевидно, что y = f (h (x) + k (x)) .
Очевидно, что y = f (h (x) + k (x)) .
Рассмотрим функцию h (x) . Это отношение l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 к m (x) = e x 2 + 3 3
Имеем, что l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) является суммой двух функций n (x) = x 2 + 7 и p (x) = 3 cos 3 (2 x + 1) , где p (x) = 3 · p 1 (p 2 (p 3 (x))) является сложной функцией с числовым коэффициентом 3 , а p 1 — функцией возведения в куб, p 2 функцией косинуса, p 3 (x) = 2 x + 1 — линейной функцией.
Получили, что m (x) = e x 2 + 3 3 = q (x) + r (x) является суммой двух функций q (x) = e x 2 и r (x) = 3 3 , где q (x) = q 1 (q 2 (x)) — сложная функция, q 1 — функция с экспонентой, q 2 (x) = x 2 — степенная функция.
Отсюда видно, что h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 · p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) + r (x)
При переходе к выражению вида k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x) видно, что функция представлена в виде сложной s (x) = ln 2 x = s 1 (s 2 (x)) с целой рациональной t (x) = x 2 + 1 , где s 1 является функцией возведения в квадрат, а s 2 (x) = ln x — логарифмической с основанием е.
Отсюда следует, что выражение примет вид k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x) .
Тогда получим, что
y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x · (x 2 + 1) = = f n (x) + 3 · p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) · t (x)
По структурам функции стало явно, как и какие формулы необходимо применять для упрощения выражения при его дифференцировании. Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой.
Пример 2
Найти производную функции
Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильно РАЗОБРАТЬСЯ во вложениях. В тех случаях, когда есть сомнения, напоминаю полезный приём: берем подопытное значение «икс», например, и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
В тех случаях, когда есть сомнения, напоминаю полезный приём: берем подопытное значение «икс», например, и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
1) Сначала нам нужно вычислить выражение , значит, сумма — самое глубокое вложение.
2) Затем необходимо вычислить логарифм:
4) Потом косинус возвести в куб:
5) На пятом шагу разность:
6) И, наконец, самая внешняя функция — это квадратный корень:
Формула дифференцирования сложной функции применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
Вроде без ошибок:
1) Берем производную от квадратного корня.
2) Берем производную от разности, используя правило
3) Производная тройки равна нулю. Во втором слагаемом берем производную от степени (куба).
4) Берем производную от косинуса.
6) И, наконец, берем производную от самого глубокого вложения .
Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Следующий пример для самостоятельного решения.
Пример 3
Найти производную функции
Подсказка: Сначала применяем правила линейности и правило дифференцирования произведения
Полное решение и ответ в конце урока.
Настало время перейти к чему-нибудь более компактному и симпатичному.
Не редка ситуация, когда в примере дано произведение не двух, а трёх функций. Как найти производную от произведения трёх множителей?
Пример 4
Найти производную функции
Сначала смотрим, а нельзя ли произведение трех функций превратить в произведение двух функций? Например, если бы у нас в произведении было два многочлена, то можно было бы раскрыть скобки. Но в рассматриваемом примере все функции разные: степень, экспонента и логарифм.
В таких случаях необходимо последовательно применить правило дифференцирования произведения два раза
Фокус состоит в том, что за «у» мы обозначим произведение двух функций: , а за «вэ» — логарифм: . Почему так можно сделать? А разве — это не произведение двух множителей и правило не работает?! Ничего сложного нет:
Теперь осталось второй раз применить правило к скобке :
Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде — легче будет проверять.
Рассмотренный пример можно решить вторым способом:
Оба способа решения абсолютно равноценны.
Пример 5
Найти производную функции
Это пример для самостоятельного решения, в образце он решен первым способом.
Рассмотрим аналогичные примеры с дробями.
Пример 6
Найти производную функции
Здесь можно пойти несколькими путями:
Или так:
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного , приняв за весь числитель:
В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить?
Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить?
Приведём выражение числителя к общему знаменателю и избавимся от трёхэтажности дроби :
Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных школьных преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
Более простой пример для самостоятельного решения:
Пример 7
Найти производную функции
Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab. | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных. Таблица интегралов. Таблица первообразных. Найти производную. Найти интеграл. Диффуры. / / Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Методический материал для студентов с овз по теме: Производная сложных функций.
План-конспект урока на тему: « Производная сложной функции».
Цели:
1) образовательная – сформировать понятие
сложной функции, изучить алгоритм вычисления производной сложной функции,
показать его применение при вычислении производных.
2) развивающая – продолжить развитие умений логически и аргументировано
рассуждать, используя обобщения, анализ, сравнение при изучении производной
сложной функции.
3) воспитательная – воспитывать наблюдательность в ходе отыскания
математических зависимостей, продолжить формирование самооценки при
осуществлении дифференцированного обучения, повышать интерес к
математике.
Оборудование: таблица производных, презентация к уроку.
Схема урока:
I. Актуализация знаний.
1. Мобилизующее начало (постановка цели работы на уроке).
2. Устная работа с целью актуализации опорных знаний.
3. Проверка домашнего задания с целью мотивации изучения нового
материала.
4. Подведение итогов I этапа и постановка задач следующего.
II. Формирование новых знаний.
1. Эвристическая беседа с целью введения понятия сложной функции.
2. Устная фронтальная работа с целью закрепления определения сложной функции.
3. Сообщение учителем алгоритма вычисления
производной сложной функции.
4. Первичное закрепление алгоритма вычисления производной сложной функции фронтально.
5. Подведение итогов II этапа и постановка задач на следующий.
III. Формирование учебных навыков..
1. Решение задачи с опорой на алгоритм вычисления производной сложной функции
фронтально у доски учеником.
2. Дифференцированная работа по решению задач с последующей проверкой
фронтально у доски.
3. Подведение итогов урока
4. Выдача домашнего задания.
Конспект урока.
На данном уроке мы научимся находить производную сложной функции. Урок является логическим продолжением прошлого занятия, на котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.
На практике с производной сложной функции
приходится сталкиваться очень часто, я бы даже сказала, почти всегда, когда вам
даны задания на нахождение производных.
Смотрим в таблицу на правило дифференцирования сложной функции:
Разбираемся. Прежде всего, обратим внимание на запись . Здесь у нас две функции – и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию я буду называть внешней функцией, а функцию – внутренней (или вложенной) функцией.
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.
Для того, чтобы прояснить ситуацию, рассмотрим:
Пример 1
Найти производную функции
Под синусом у нас находится не просто буква
«икс», а целое выражение , поэтому найти производную сразу по таблице не
получится. Также мы замечаем, что здесь невозможно применить первые четыре
правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус
нельзя:
В данном примере уже из моих объяснений
интуитивно понятно, что функция – это сложная функция, причем
многочлен является
внутренней функцией (вложением), а – внешней функцией.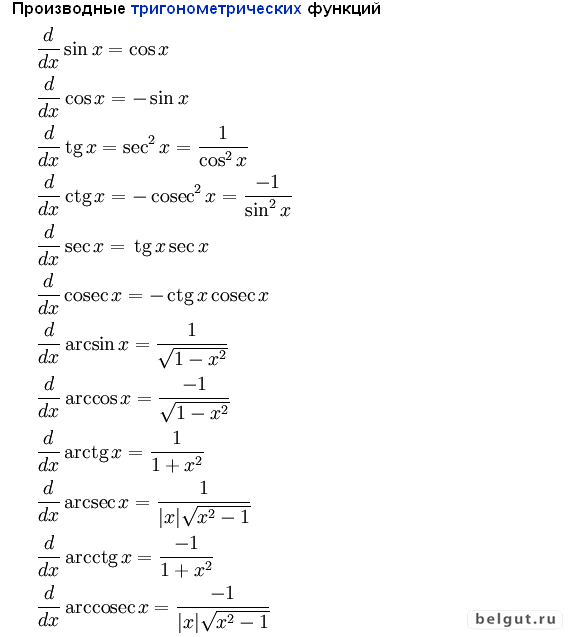
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.
В случае простых примеров вроде понятно, что под синус вложен многочлен . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В
первую очередь нужно будет выполнить следующее действие: , поэтому многочлен и будет внутренней
функцией :
Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями
самое время применить правило дифференцирования сложной функции .
Начинаем решать. Помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:
Сначала находим производную внешней
функции (синуса),
смотрим на таблицу производных элементарных функций и замечаем, что . Все табличные формулы
применимы и в том, случае, если «икс» заменить сложным выражением, в данном
случае:
Все табличные формулы
применимы и в том, случае, если «икс» заменить сложным выражением, в данном
случае:
Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем.
Ну и совершенно очевидно, что
Результат применения формулы в чистовом оформлении выглядит так:
Далее мы берем производную внутренней функции, она очень простая:
Постоянный множитель обычно выносят в начало
выражения:
Готово
Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.
Пример 2
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Пример 3
Найти производную функции
Как всегда записываем:
Разбираемся, где у нас внешняя функция, а где
внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение
выражения при . Что нужно выполнить в первую
очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя
функция:
И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя
функция:
Согласно формуле ,
сначала нужно найти производную от внешней функции, в данном случае, от
степени.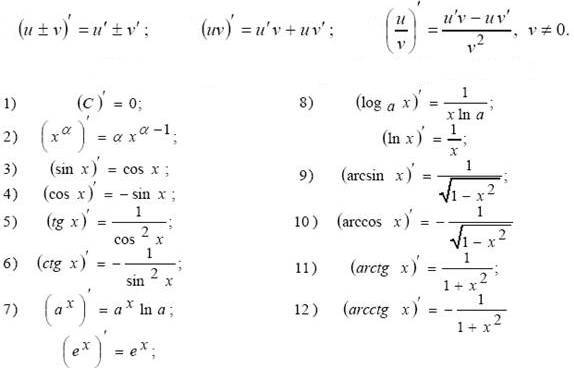 Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула
справедлива не только для «икс», но и для сложного выражения. Таким образом,
результат применения правила дифференцирования сложной функции следующий:
Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула
справедлива не только для «икс», но и для сложного выражения. Таким образом,
результат применения правила дифференцирования сложной функции следующий:
Снова подчеркиваю, что когда мы берем
производную от внешней функции , внутренняя функция у нас не меняется:
Теперь осталось найти совсем простую производную от внутренней функции и
немного «причесать» результат:
Готово.
Пример 4
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?
Пример 5
а) Найти производную функции
б) Найти производную функции
Пример 6
Найти производную функции
Здесь у нас корень, а для того, чтобы продифференцировать
корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в
надлежащий для дифференцирования вид:
Таким образом, сначала приводим функцию в
надлежащий для дифференцирования вид:
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :
Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:
Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Пример 7
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Интересно отметить, что иногда вместо правила
дифференцирования сложной функции можно использовать правило дифференцирования
частного , но такое
решение будет выглядеть как извращение необычно. Вот характерный
пример:
Вот характерный
пример:
Пример 8
Найти производную функции
Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
Косинус – внутренняя функция, возведение в
степень – внешняя функция.
Используем наше правило :
Находим производную внутренней функции, косинус сбрасываем обратно вниз:
Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
Пример 9
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
До сих пор мы рассматривали случаи, когда у
нас в сложной функции было только одно вложение. В практических же заданиях
часто можно встретить производные, где, как матрешки, одна в другую,
вложены сразу 3, а то и 4-5 функций.
Пример 10
Найти производную функции
Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?
Сначала нужно найти , значит, арксинус – самое глубокое вложение:
Затем этот арксинус единицы следует возвести в квадрат :
И, наконец, семерку возводим в степень :
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.
Начинаем решать
Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: Единственное отличие – вместо «икс» у нас сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий:
Под штрихом у нас снова сложная функция! Но
она уже проще. Легко убедиться, что внутренняя функция – арксинус, внешняя
функция – степень. Согласно правилу дифференцирования сложной функции сначала
нужно взять производную от степени:
Легко убедиться, что внутренняя функция – арксинус, внешняя
функция – степень. Согласно правилу дифференцирования сложной функции сначала
нужно взять производную от степени:
Теперь все просто, находим по таблице производную арксинуса и немного «причесываем» выражение:
Готово.
Пример 11
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
На практике правило дифференцирования сложной функции почти всегда применяется в комбинации с остальными правилами дифференцирования.
Пример 12
Найти производную функции
Сначала используем правило дифференцирования суммы , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу :
В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило :
Замечаем, что под некоторыми штрихами у нас
находятся сложные функции , . Каламбур, но это простейшие из сложных функций,
и при определенном опыте решения производных Вы будете легко находить их устно.
А пока запишем подробно, согласно правилу , получаем:
Готово.
! Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь.
Пример 13
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Пожалуй, хватит на сегодня. Хочется еще привести пример с дробью и сложной функцией, но такой пример принципиально ничем не отличается от двух последних заданий, единственное отличие – вместо правила применяем правило .
Ответы:
Пример 2:
Пример 4: Указание: перед дифференцированием необходимо перенести степень наверх, сменив у показателя знак .
Пример 7:
Пример 9:
Пример 11:
Пример 13:
Домашнее задание: В.П. Омельченко. Математика. Стр. 106. №№103-110.
Производная сложной функции — алгебра, уроки
Урок № 19 Дата:
ТЕМА: Производная сложной функции
Цели урока:
образовательная:
формирование понятия сложной функции;
формирование умения находить по правилу производную сложной функции;
отработка алгоритма применения правила нахождения производной сложной функции при решении задач.

развивающая:
развивать умение обобщать, систематизировать на основе сравнения, делать вывод;
развивать наглядно-действенное творческое воображение;
развивать познавательный интерес.
способствовать формированию умения рационально, аккуратно оформить задание на доске и в тетради.
воспитательная:
Обучающийся должен знать:
правила и формулы дифференцирования;
понятие сложной функции;
правило нахождения производной сложной функции.
Обучающийся должен уметь:
Тип урока: урок рефлексия.
Обеспечение урока:
Оборудование:
ХОД УРОКА:
1. Организационный момент (1 мин).
Организационный момент (1 мин).
Вступление
Готовность класса к работе.
Общий настрой.
2. Мотивационный этап (2-3 мин).
(Покажем сами себе, что мы готовы с уверенностью постигать знания, которые нам могут пригодиться!)
— Ответьте мне, какое домашнее задание вы выполнили на этот урок? (на прошлом уроке было задано изучить материал по теме «Производная сложной функции» и как результат составить конспект).
— Какими источниками вы пользовались при изучении данной темы? (видеофильм, учебник, дополнительная литература).
— Какой дополнительной литературой вы воспользовались? (литература из библиотеки).
Таким образом темой урока является …? («Производная сложной функции»)
Открываем тетради и записываем: число, классная работа, и тему урока. (Слайд 1)
Исходя из темы, давайте обозначим цели и задачи урока (формирование понятия сложной функции; формирование умения находить по правилу производную сложной функции; отработать алгоритм применения правила нахождения производной сложной функции при решении задач).
3. Актуализация знаний и осуществление первичного действия (7-8 мин)
Переходим непосредственно к достижению целей урока.
Сформулируем понятие сложной функции (функция вида y = f (g (x)) называется сложной функцией, составленной из функций f и g, где f – внешняя функция и g — внутренняя) (Слайд 2)
Рассмотрим Задание 1: Найти производную функции у = (х2 +sin x)3 (запись на доске)
Данная функция является элементарной или сложной? (сложной)
Почему? (т.к. аргументом служит не независимая переменная х, а функция х2+sinx этой переменной).
Как прочитать эту функцию? (функция суммы тригонометрической и степенной функций в кубе).
Для нахождения производной данной функции необходимо знание основных формул производной элементарных функций и знание правил дифференцирования. Вспомним их, проведя диктант: (Слайд 3)
1) С’=0; 2) (xn)’ = nxn-1; ; 4) ax = ax ln a; 5)
6) 7)
8)
Результат диктанта проверяется (Слайд 4)
Выберем из таблицы производных и правил дифференцирования те, которые нужны для решения данного задания и запишем их в виде схемы на доске.
4. Выявление индивидуальных затруднений в реализации нового знания и умения (4 мин)
Решим пример 1 и найдем производную функции y’ = ((х2 +sin x)3)’
Какие же формулы нужны для решения задания? ((xn)’ = nxn-1;
)
Работа у доски:
(х2 +sin x)3 = U;
y’ = (U3)’ = 3 U2 U`=3(х2 +sin x)2(2х+cos x)
Можно заметить, что без знания формул и правил невозможно взять производную сложной функции, но для правильного расчета нужно видеть в дифференцировании основную функцию.
5. Построение плана по разрешению возникших затруднений и его реализация (8 — 9 мин)
Выявив затруднения, давайте построим алгоритм нахождения производной сложной функции: (Слайд 5)
Алгоритм:
1. Определить внешнюю и внутреннюю функции;
2. Производную находим по ходу чтения функции.
А теперь разберем это на примере
Задание 2: Найти производную функции:
1. Определяем внешнюю и внутреннюю функции:
При упрощении получаем: (5-4х) = U,
т.е. ;
2. Находим производную по ходу чтения функции:
у’ = ’=
Задание 3: Найти производную функции:
1. Определяем внешнюю и внутреннюю функции:
у = 4U – показательная функция
2. Находим производную по ходу чтения функции:
Находим производную по ходу чтения функции:
у’= ’=
6. Обобщение выявленных затруднений (4 мин)
Н.И. Лобачевский “… нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…”
Поэтому обобщая наши знания, решение следующего задания посвятим связи с физическими явлениями (у доски по желанию)
Задание 4:
При электромагнитных колебаниях, возникающих в колебательном контуре, заряд на обкладках конденсатора изменяется по закону q = q0 cos ωt, где q0-амплитуда колебаний заряда на конденсаторе. Найти мгновенное значение силы переменного тока I.
Решение:
‘ = — . Если добавить начальную фазу, то по формулам приведения получим — .
7. Осуществление самостоятельной работы (6 мин)
Ученики выполняют тестирование по индивидуальным карточкам в тетради. Одного ответа не достаточно, должно быть и решение. (Слайд 6)
Одного ответа не достаточно, должно быть и решение. (Слайд 6)
Карточки «Самостоятельная работа к уроку № 19»
Критерии оценки: “3 ответа” — 3 балла; “2 ответа” — 2 балла; “1 ответ” — 1 балл
Ключи ответов (Слайд 7)
№ задания | 1 вариант | 2 вариант | 3 вариант | 4 вариант |
ответ | ответ | ответ | ответ | |
1 | Б | Б | В | А |
2 | Б | В | В | Б |
3 | А | Б | В | В |
После проверки (Слайд 8)
8. Реализация плана по разрешению возникших затруднений (6 — 7 мин)
Реализация плана по разрешению возникших затруднений (6 — 7 мин)
Ответы на вопросы учеников по затруднениям, возникшим в ходе самостоятельной работы, обсуждение типичных ошибок.
Примеры — задания для ответа на возникшие вопросы***:
1) ;
2) ;
3) ;
4) ;
9. Домашнее задание (2 мин) (Слайд 9)
Решить индивидуальное задание по карточкам-заданиям.
Выставление оценок по итогам работы.
10. Рефлексия (2 мин)
«Хочу спросить»
Учащийся задает вопрос, начиная со слов «Хочу спросить…». На полученный ответ сообщает свое эмоциональное отношение: «Я удовлетворен….» или «Я не удовлетворен, потому что …».
По ответам учеников подвести итоги, выяснив при этом, достигнуты ли были цели урока.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Оснащения врачебно-сестринской бригады. Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является. Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒
Таблица производных:
Таблица производных сложных функций
Интегрирование Неопределённый интеграл и непосредственное интегрирование Непосредственное интегрирование – это нахождение неопределенных интегралов с использованием таблицы интегралов и свойств неопределенного интеграла: 1. = 2. =k , где k=const Таблица интегралов
⇐ Предыдущая123Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
2.3: Сложная дифференциация — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 76209
- Хуан Карлос Понсе Кампузано
- Университет Квинсленда
Понятие комплексной производной лежит в основе теории комплексных функций. Определение комплексной производной аналогично определению производной действительной функции. Однако, несмотря на внешнее сходство, комплексная дифференциация представляет собой глубоко иную теорию.
Определение комплексной производной аналогично определению производной действительной функции. Однако, несмотря на внешнее сходство, комплексная дифференциация представляет собой глубоко иную теорию.
Комплексная функция \(f(z)\) является дифференцируемой в точке \(z_{0}\in \mathbb{C}\) тогда и только тогда, когда существует следующее предельное разностное частное
\(\begin{eqnarray}\label{diff01}
f’(z_0) = \lim_{z \rightarrow z_0} \frac{f(z)-f(z_0)}{z-z_0}.
\end{eqnarray}\)
В качестве альтернативы, если \(\Delta z= z-z_{0}\), мы можем записать
\(\begin{eqnarray}\label{diff02}
f'(z_0) = \lim_{\Delta z \rightarrow 0} \frac{f(z_0+\Delta z)-f(z_0)}{\Delta z }.
\end{eqnarray}\)
Мы часто опускаем нижний индекс на \(z_{0}\) и вводим число
.\(\Delta w=f\left ( z+\Delta z \right )-f\left ( z \right )\).
, который обозначает изменение значения \(w=f(z)\), соответствующее изменению \(Δz\) в точке, в которой оценивается \(f\) . Тогда мы можем записать уравнение (2) как
Тогда мы можем записать уравнение (2) как
\(\frac{dw}{dz}=\lim_{Δz\стрелка вправо 0}\frac{\Delta w}{\Delta z}\).
Несмотря на то, что формула (1) для производной по форме идентична формуле производной действительнозначной функции, важно отметить, что \({f}’\left ( z_{0} \ right )\) следует из двумерного предела. Таким образом, для существования \({f}’\left ( z_{0} \right )\) должен существовать соответствующий предел, не зависящий от направления, с которого \(z\) приближается к предельной точке \(z_{0}\ ). Для функции одной действительной переменной у нас есть только два направления, то есть \(x
Рис. 1: Есть бесконечное множество направлений для приближения \(z_{0}\) .
Замечательная особенность комплексного дифференцирования состоит в том, что существование одной комплексной производной автоматически влечет за собой существование бесконечно многих производных! Это отличается от случая функции действительной переменной \(g(x)\), в которой \(g′(x)\) может существовать без существования \(g″(x)\).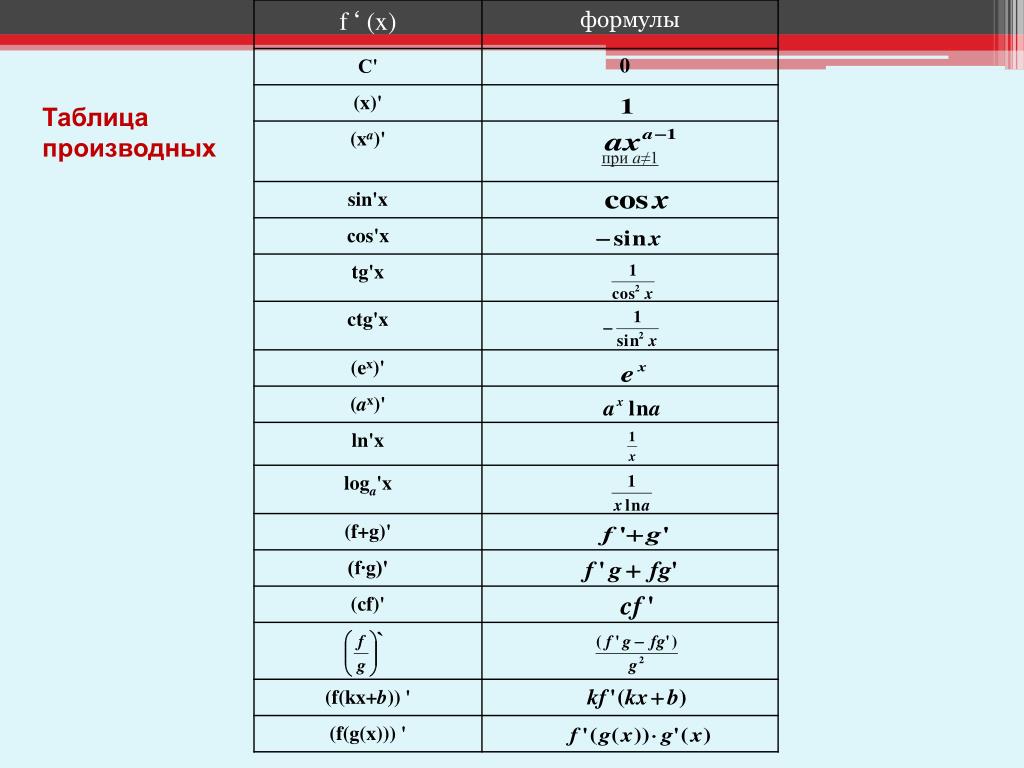
Уравнения Коши-Римана
Теперь давайте посмотрим на замечательное следствие определения (1). Сначала мы посмотрим, что произойдет, если мы приблизимся к \(z_{0}\) в двух простейших направлениях — горизонтальном и вертикальном. Если мы установим
\(z=z_{0}+h=\left ( x_{0} +h\right )+iy_{0}\), \(h\in \mathbb{R}\),
, затем \(z\стрелка вправо z_{0}\) по горизонтальной линии как \(h→0\). Если мы запишем ff через его действительную и мнимую составляющие, то есть
\(f(z)=u(x,y)+iv(x,y)\),
, то
\({f}’\left ( z_{0} \right )=\lim_{h\стрелка вправо 0}\frac{f\left ( z_{0}+h \right )-f\left ( z_{0 } \right )}{h}\)
затем
\({f}’\left ( z_{0} \right )=\lim_{h\rightarrow 0}\frac{f\left ( z_{0 }+h \right )-f\left ( z_{0} \right )}{h}=\lim_{h\стрелка вправо 0}\frac{f\left ( x_{0}+h+iy_{0} \ вправо )-f\влево ( x_{_{0}}+iy_{0} \right )}{h}\\=\lim_{h\стрелка вправо 0}\влево [ \frac{u\left ( x_{0 }+h,y_{0} \right )-u\left ( x_{0},y_{0} \right )}{h} \right ]+i\lim_{h\стрелка вправо 0}\left [ \frac {v\left ( x_{0}+h,y_{0} \right )-v\left ( x_{0},y_{0} \right )}{h}\right ]\\=u_{x} \left (x_{0},y_{0} \right)+iv_{x}\left (x_{0},y_{0} \right)\)
где \(u_{x}\left ( x_{0},y_{0} \right )\) и \(v_{x}\left ( x_{0},y_{0} \right )\) обозначают частные производные первого порядка по \(x\) функции \(u\) и \(v\) соответственно в точках \(\left ( x_{0},y_{0} \right ) \). Если теперь мы установим
Если теперь мы установим
\(z=z_{0}+ik=x_{0}+i\left ( y_{0} +k\right )\), \(k\in \mathbb{R}\) ,
, затем \(z→0\) по вертикальной линии как \(k→0\). Следовательно, мы также имеем
\({f}’\left ( z_{0} \right )=\lim_{k\rightarrow 0}\frac{f\left ( z_{0}+ik \right )-f \left ( z_{0} \right )}{ik}=\lim_{k\стрелка вправо 0}\left [ -i\frac{f\left ( x_{0}+i\left ( y_{0} +k \right )\right )-f\left ( x_{_{0}}+iy_{0} \right )}{k}\right ]\\=\lim_{k\стрелка вправо 0}\left [ \frac{ v\left ( x_{0},y_{0}+k \right )-v\left ( x_{0},y_{0} \right )}{k} -i\frac{u\left ( x_{ 0},y_{0}+k \right )-u\left (x_{0},y_{0} \right )}{k}\right ]\\=v_{y}\left ( x_{0} ,y_{0} \right )-iu_{y}\left ( x_{0},y_{0} \right )\)
, где частные производные от \(u\) и \(v\) на этот раз относятся к \(y\). Приравнивая действительную и мнимую части этих двух формул для комплексной производной \({f}’\left ( z_{0}\), мы замечаем, что действительная и мнимая компоненты \(f(z)\) должны удовлетворять однородная линейная система уравнений в частных производных:
\(u_{x}=v_{y}\), \(u_{y}=-v_{x}\).
Это Коши-Римана уравнения названы в честь известных математиков девятнадцатого века Огюстена-Луи Коши и Бернхарда Римана, двух основоположников современного комплексного анализа.
Теорема \(\PageIndex{1}\)
Комплексная функция \(f(z)=u(x,y)+iv(x,y)\) имеет комплексную производную \(f′(z) \) тогда и только тогда, когда его действительная и мнимая части непрерывно дифференцируемы и удовлетворяют уравнениям Коши-Римана
\(u_{x}=v_{y}\), \(u_{y}=-v_{x}\ )
В этом случае комплексная производная \(f(z)\) равна любому из следующих выражений:
\({f}’\left ( z \right )=u_{x}+iv_ {x}=v_{y}-iu_{y}\).
Пример \(\PageIndex{1}\) 9{n}log\,z\)), а \(c\) – любая комплексная константа. Из экспоненциальных формул для комплексных тригонометрических и гипербоических функций следует, что они также удовлетворяют стандартным правилам
\(\frac{d}{dz}sin\,z=cos\,z\), \(\frac{d {dz}cos\,z=-sin\,z\)
\(\frac{d}{dz}sin\,z=cosh\,z\), \(\frac{d}{dz} ch\,z=sinh\,z\)
Формулы для дифференцирования сумм, произведений, отношений, обратных и композиций комплексных функций идентичны их реальным аналогам с аналогичными доказательствами. Это означает, что вам не нужно изучать какие-либо новые правила для выполнения сложной дифференциации!
Это означает, что вам не нужно изучать какие-либо новые правила для выполнения сложной дифференциации!
Аналитические функции
Пусть \(f:A\стрелка вправо \mathbb{C}\), где \(A\subset \mathbb{C}\) – открытое множество. Функция называется аналитической на \(A\), если \(f\) дифференцируема в каждом \(z_{0}\in A\). Слово «голоморфный», которое иногда используется, является синонимом слова «аналитический». Фраза «аналитическая в \(z_{0}\) » означает \(f\) является аналитической в окрестности \(z_{0}\)
Эта страница под названием 2.3: Комплексная дифференциация распространяется по лицензии CC BY-NC-SA, автором, ремиксом и/или куратором этой страницы является Хуан Карлос Понсе Кампусано.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Хуан Карлос Понсе Кампусано
- Лицензия
- CC BY-NC-SA
- Теги

Список символов исчисления и анализа
В математике исчисление формализует изучение непрерывных изменений, в то время как 9Анализ 0073 дает ему строгую логическую основу. В следующем списке перечислены некоторые из наиболее известных символов и обозначений в исчислении и анализе, а также использование и значение каждого символа.
Для удобства чтения эти символы разбиты на категории по теме и функции в таблицы. Другие полные списки математических символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
Содержание
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в электронной книге формы — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Константы и переменные
В расчетах и анализе константы и переменные часто резервируются для ключевых математических чисел и произвольно малых величин . В следующей таблице приведены некоторые из наиболее заметных символов в этих категориях, а также пример каждого символа и его значение. 92$
В следующей таблице приведены некоторые из наиболее заметных символов в этих категориях, а также пример каждого символа и его значение. 92$
Последовательность, серия и предел
Понятия последовательности , серии и предела составляют основу исчисления (и, соответственно, вещественного и комплексного анализа). В следующей таблице представлены некоторые из наиболее распространенных символов, связанных с этими темами, а также их использование и значение. 9k b_n = \\ b_1 + \cdots + b_k$
$ | е (\ mathrm {х}) — е (\ mathrm {х} _0) | < 2 $

$\displaystyle \lim_{n \to \infty} 0$
$\displaystyle \lim_{n \to \infty} \left( \sup_{m \ge n} b_m \right)$
Производная и интеграл
Часто говорят, что область исчисления (например, многомерное/векторное исчисление, дифференциальные уравнения) вращается вокруг двух противоположных, но дополняющих друг друга понятий: производная и интеграл . В следующих таблицах описаны наиболее известные символы, связанные с ними, а также использование и значение каждого символа.
В следующих таблицах описаны наиболее известные символы, связанные с ними, а также использование и значение каждого символа.
(Обзор функций и связанных с ними операторов см. в разделе , связанные с функциями операторы .)
Одномерные символы, связанные с производными 92(f) = D(D(f))$
Многомерные символы, связанные с производными
| Название символа | Объяснение | Пример |
|---|---|---|
| $f_\mathbf{x}$ | Частная производная от $f$ через $\mathbf{x}$ (обозначения Лагранжа) | $\displaystyle f_x (a, b) = \ lim_{h \to 0}$ $\frac{f(a+h, \, b) \, – \, f(a,\, b)}{h}$ |
| $\dfrac{\ partial}{\partial \mathrm{x}} f, \dfrac{\partial f}{\partial \mathrm{x}}$ | Частная производная от $f$ через $\mathrm{x}$ (стиль Лейбница) | Если $f$ имеет непрерывные вторые частные производные, то $\dfrac{\partial}{\partial y}\dfrac{\partial f}{\partial x} = \dfrac{\partial}{ \partial x}\dfrac{\partial f}{\partial y}$ 92} = \dfrac{\partial}{\partial y}\dfrac{\partial f}{\partial y}$ |
| $\partial_x f$ | Частная производная от $f$ в выражении $ x$ (обозначения Эйлера) | $\partial_{xy} f = \dfrac{\partial}{\partial y} \dfrac{\partial f}{\partial x}$ |
| $\nabla_{\ mathbf{v}} f$ | Производная по направлению от $f$ относительно направления $\mathbf{v}$ | $\nabla _{\mathbb{v}} f(\mathbf{x}) =$ $\displaystyle \lim_{h \to 0} \dfrac{f(\mathbf{x}+h\mathbf{v})-f(\mathrm{x})}{h}$ |
| $\partial \mathrm{x}$ | Частный дифференциал переменной $\mathrm{x}$ | $\dfrac{\partial f}{\partial x} dx \le df$ |
| $df$ | Полный дифференциал функции $f$ | $df = \dfrac{\partial f}{\partial x_1} dx_1 +$ $\displaystyle \cdots + \dfrac{\partial f} {\partial x_n} dx_n$ |
| $\nabla f, \mathrm{grad}\,f$ | Градиент функции $f$ 92}$ | |
| $\nabla \cdot \mathbf{F}, \mathrm{div}\, \mathbf{F}$ | Расходимость векторного поля $\mathbf{F}$ | $\ набла \cdot \mathbf{F} = \dfrac{\partial F_x}{\partial x} +$ $\dfrac{\partial F_y}{\partial y} + \dfrac{\partial F_z}{\partial z} $ |
| $\nabla \times \mathbf{F}, \mathrm{curl} \, \mathbf{F}$ | Curl векторного поля $\mathbf{F}$ | $\nabla \ раз \mathbf{F} =$ $\left( \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right ) \раз$ $\left( F_x, F_y, F_z \right)$ |
| Symbol Name | Explanation | Example |
|---|---|---|
$\displaystyle \left.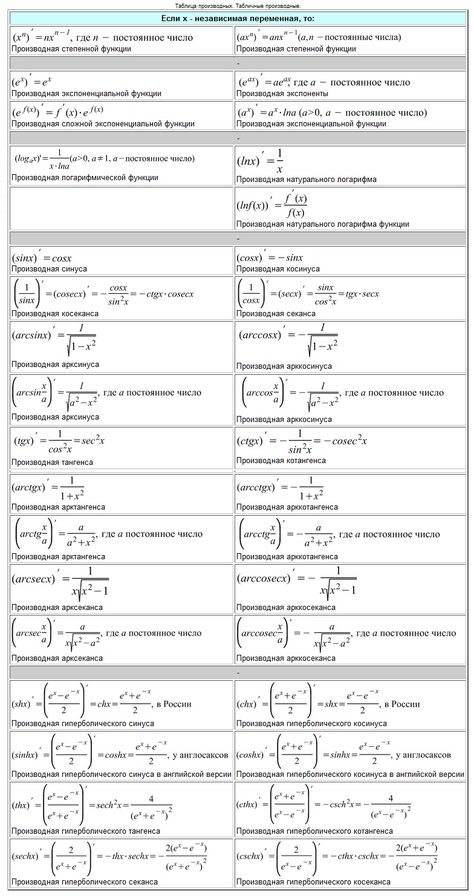 {b}$ 92} \, dx = \dfrac{\pi}{2}$ {b}$ 92} \, dx = \dfrac{\pi}{2}$ | ||
| $\displaystyle \int f(x) \, dx$ | Неопределенный интеграл функции $f$ относительно $x$ | $\displaystyle \int \cos y \, dy = \\ \sin y + C$ |
| $F(x)$ | Первообразная функции $f$ | Для всех констант $c$ , $(F(x) + c)’ = f(x)$. |
| $(Jf)(x)$ | Оператор интегрирования (Интегральная функция от $f$) 93$ |
- Стандартный интеграл
- Линейный интеграл
- Интеграл площадей
- Поверхностный интеграл
(векторного поля)
Асимптотический анализ для анализа различных скоростей роста, сравнения
5 900 функций приводит к изучению асимптотического анализа . В следующей таблице приведены некоторые из наиболее заметных символов, связанных с этой темой, а также их использование и значение.| Symbol Name | Explanation | Example |
|---|---|---|
| $f \equiv g$ | Function $f$ is identically equal to function $g$ | $f \equiv g \iff $ $\mathrm{dom}(f)=\mathrm{dom}(g)$ $\mathrm{and}\, f(x)=g(x) $ $\left( \forall x \in \mathrm{dom}(f) \right)$ |
| $f \sim g$ | Функция $f$ асимптотически равна функции $g$ | $f \sim g \iff $ $\displaystyle \lim_{x \to \infty} \dfrac{f(x)}{g(x)} = 1$ |
| $f \ll g, f \in O(g)$ | $f$ есть , асимптотически ограниченное выше $g$ ($f$ входит в big-O $g$) | $f \ll g \iff \ существует k > 0$ $|f(x)| \le k |g(x)|$ $(\forall x \ge x_0)$ |
| $f \gg g, f \in \Omega(g)$ | $f$ асимптотически ограничено снизу на $g$ ($f$ находится в big-Omega of $g$) | $f \gg g \iff\exists k > 0$ $|f(x)| \ge k |g(x)|$ $(\forall x \ge x_0)$ |
| $f \in \Theta(g)$ | $f$ есть , асимптотически ограниченное выше и ниже $ g$ ($f$ находится в big-Theta $g$) | $f \in \Theta(g) \iff$ $f \ll g \: \mathrm{and} \: f \gg g$ |
| $f \in o(g)$ | $f$ есть асимптотически доминируемое числом $g$ ($f$ находится в small-O of $g$) | $f \in o(g)$ тогда и только тогда, когда для всех $k > 0$ $|f(x)| < k \, |g(x)|$ (для всех $x \ge x_0$).  |
| $f \in \omega(g)$ | $f$ асимптотически доминирует над $g$ ($f$ входит в малую омегу $g$) | $f \in \omega(g)$ тогда и только тогда, когда для всех $k > 0$ $|f(x)| > k \, |g(x)|$ (для всех $x \ge x_0$). |
В следующей таблице представлены некоторые наиболее распространенные функции, расположенные в соответствии с их 9x$
Ключевые функции и преобразования
В расчетах и анализе часто ссылаются на широкий диапазон ключевых функций и преобразований . В следующей таблице описаны наиболее заметные из них, а также использование и значение каждого символа.
(Для обзора элементарных функций см. ключевые функции в алгебре .)
Основные функции
| Название функции | Пояснение | Пример |
|---|---|---|
| $\mathrm{sign}(x)$ | Знаковая функция | $\mathrm{sign}(x) =$ $\begin{case 0 \\ 0 & x=0 \\ 1 & x>0 \end{cases}$ |
| $\mathrm{atan2}(y, x)$ | Функция арктангенса с двумя аргументами | $\ mathrm{atan2}(1, 0) = \pi /2$ |
| $\mathrm{B}(x ,y)$ | Бета-функция | $\mathrm{B}(x, y) =$9{-2\pi i t x} \, dx$ |
Основной список символов см. в разделе Математические символы. Списки символов, классифицированных по типу и предмету , см. на соответствующих страницах ниже.
в разделе Математические символы. Списки символов, классифицированных по типу и предмету , см. на соответствующих страницах ниже.
Вместо этого предпочитаете PDF-версию?
Получите основную сводку математических символов в электронной книге формы — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Дополнительные ресурсы
- Полное руководство по изучению высшей математики : Автономная система из 10 принципов для эффективного изучения высшей математики, мышления и решения задач математика
- Ultimate LaTeX Reference Guide : подробное справочное руководство, которое сделает процесс LaTeX более эффективным и менее болезненным
- Полный глоссарий терминов высшей математики : Основные понятия высшей математики в 106 терминах
Исчисление сложных функций
Базовый код продукта Список ключевых слов: текст; ТЕКСТ; текст/71; ТЕКСТ/71; текст-71; TEXT-71
Распечатать Код продукта: TEXT/71
Онлайн-код продукта:
TEXT/71. E
E
Заголовок (HTML): Исчисление сложных функций
Автор(ы) (Отображение продукта): Уильям Джонстон
Организация(и) (HTML): Университет Батлера, Индианаполис, IN
Рекламный проспект: MAA Press: Выходные данные Американского математического общества
Абстрактный:
Книга знакомит с комплексным анализом как
естественное расширение исчисления вещественнозначных функций.
механизмом для этого является теорема о продолжении, которая утверждает
что любая вещественная аналитическая функция продолжается до аналитической функции
определяется в области комплексной плоскости. Связь с реальным
функции и исчисление тогда естественны. Введение в аналитику
функции кажутся интуитивно понятными, и их основные свойства покрыты
быстро. В результате книга позволяет на удивление широко охватить
темы классического анализа аналитических и мероморфных функций,
гармонические функции, контурные интегралы и представления рядов,
конформные отображения и задача Дирихле. Он также знакомит с несколькими
более сложные понятия, включая гипотезу Римана и оператор
теории в доступной для студентов форме. Последняя глава
описывает ограниченные линейные операторы в гильбертовых и банаховых пространствах,
включая спектральную теорию компактных операторов, таким образом, что также
обеспечивает превосходный обзор важных тем в линейной алгебре и
обеспечивает путь к темам исследований бакалавриата в области анализа.
Он также знакомит с несколькими
более сложные понятия, включая гипотезу Римана и оператор
теории в доступной для студентов форме. Последняя глава
описывает ограниченные линейные операторы в гильбертовых и банаховых пространствах,
включая спектральную теорию компактных операторов, таким образом, что также
обеспечивает превосходный обзор важных тем в линейной алгебре и
обеспечивает путь к темам исследований бакалавриата в области анализа.
Книгу можно гибко использовать в течение одного семестра, всего года или завершающий курс комплексного анализа. Предпосылки могут варьироваться только от многомерного исчисления на переходный курс или на линейную алгебру или реальный анализ. Существует более тысячи упражнений различных виды и уровни. Каждая глава содержит эссе, описывающее часть истории предмета и по крайней мере один связанный сборник упражнения, которые вместе составляют уровень проекта исследование.
Доступны как руководство по решениям, так и руководство для инструктора
в электронном виде для тех инструкторов, которые уже приняли
учебник для занятий в классе. Пожалуйста, отправьте электронное письмо по адресу [email protected] для получения дополнительной информации.
Информация.
Пожалуйста, отправьте электронное письмо по адресу [email protected] для получения дополнительной информации.
Информация.
Название серии книг: Учебники AMS/MAA
Том: 71
Месяц и год публикации: 2022-04-01
Год авторского права: 2022
Количество страниц: 433
Тип крышки: Мягкая обложка
Печать ISBN-13: 978-1-4704-6565-0
Интернет ISBN 13: 978-1-4704-6901-6
Распечатать ISSN: 2577-1205
ISSN в Интернете: 2577-1205
Основной MSC: 30
Вторичный MSC: 47
Учебник?: true
Прикладная математика?: ложь
Книга MAA?: true
Обучение на основе запросов?: false
Домашняя страница?: ложь
Рекомендуемые?: ложь
Образец?: ложь
Ссылка?: false
Электронные носители?: false
Одежда или подарок: false
Уведомления New Pub?: ложь
SXG Тема: AN
Цена онлайн 1 этикетка: Список
Цена онлайн 1: 85.00
Цена печати 1 Этикетка: Список
Цена печати 1:
85. 00
00
Цена онлайн 2 Этикетка: Член АМС
Цена онлайн 2: 63.75
Цена печати 2 Этикетка: Участник AMS
Цена печати 2: 63,75
Цена онлайн 3 Этикетка: Член MAA
Цена онлайн 3: 63.75
Цена печати 3 Этикетка: Член MAA
Цена печати 3: 63.75
Цена комплекта 1 Этикетка: Список
Пакет Цена 1: 127.50
Цена комплекта 2 Этикетка: Участник AMS
Цена комплекта 2: 95,62
Цена комплекта 3: 95.62
Цена комплекта 3 Этикетка: Член МАА
Печать Доступна для заказа: true
Экзамен/настольная копия: https://www.ams.org/exam-desk-review-request?&eisbn=978-1-4704-6901-6&pisbn=978-1-4704-6565-0&epc=TEXT/71.E&ppc=TEXT/71&title= The%20Calculus%20of%20Complex%20Functions&author=William%20Johnston&type=DE
Копия обзора: https://www.ams.org/exam-desk-review-request?&eisbn=978-1-4704-6901-6&pisbn=978-1-4704-6565-0&epc=TEXT/71.E&ppc=TEXT/71&title= The%20Calculus%20of%20Complex%20Functions&author=William%20Johnston&type=R
Читательская аудитория:
Студенты бакалавриата, интересующиеся анализом.
URL изображения обложки: ~~FreeAttachments/text-71-cov.jpg
- Покрытие Обложка11
- Титульная страница iii7
- Авторские права iv8
- Содержание vii11
- Предисловие ix13
- Глава 1. Аналитические функции и производная 119
- 1.1. Комплексная производная 321
- 1.2. Степенные ряды и теорема о продолжении 2038
- 1.3. Многозначные функции и римановы* поверхности. 4462
- 1.4. Уравнения Коши-Римана и* гармонические функции 6785
- 1.5. Аналитическое продолжение 7997
- Примечания к главе 1 86104
- Глава 2. Комплексная интеграция 93111
- 2.1. Сложные линейные интегралы 94112
- 2.2. Теорема Коши-Гурса 112130
- 2.3. Интегральная теорема Коши 121139
- 2.4. Десять главных фактов из теоремы Коши об интеграле* 129147
- Примечания к главе 2 153171
- Глава 3.
 Нецелые функции
155173
Нецелые функции
155173 - 3.1. Особенности 156174
- 3.2. Серия Лоран 168186
- 3.3. Теорема Коши об остатках и* принцип аргумента 186204
- 3.4. Приложения теоремы об остатках 197215
- Примечания к главе 3 213231
- Глава 4. Решение задачи Дирихле. 215233
- 4.1. Конформные карты 217235
- 4.2. Решения с помощью линий тока и* эквипотенциалов 231249
- 4.3. Решения с помощью функций Грина 245263
- 4.4. Решения через интегральное представление 254272
- Примечания к главе 4 265283
- Глава 5. Дальнейшие темы и известные открытия 269287
- 5.1. Интегральные преобразования 269287
- 5.2. Аналитическая теория чисел 284302
- 5.3. Гипотеза Римана 293311
- 5.4. Обобщение основной теоремы алгебры 307325
- Примечания к главе 5 323341
- Глава 6.
 Линейная алгебра и теория операторов
327345
Линейная алгебра и теория операторов
327345 - 6.1. Ограниченные линейные операторы в гильбертовом* пространстве 332350
- 6.2. Изучение операторов конечного ранга: линейная алгебра 350368
- 6.3. Банаховы пространства и компактные операторы 367385
- 6.4. Открытые исследовательские вопросы 384402
- Примечания к главе 6 389407
- Благодарности и кредиты 395413
- Решения странных упражнений 399417
- Библиография 423441
- Индекс 431449
- Задняя обложка Задняя крышка3456
Учебник по исчислению Карла — Вставка 4.4x: Правила для производных
© 1999 Карла ХанаВот он, сваренный и перегнанный. Это основные правила, которые вы должны знать для принятия производных. Нажмите здесь, чтобы увидеть таблицу производных от ряд общих функций.
Правило 1) Производная любой константы всегда равна нулю. Вы можете знать константы, потому что они не изменяются ни с одной переменной . Итак, если С
никогда не меняется независимо от того, что делает x (или любая другая переменная), например, тогда
C является константой и
Вы можете знать константы, потому что они не изменяются ни с одной переменной . Итак, если С
никогда не меняется независимо от того, что делает x (или любая другая переменная), например, тогда
C является константой и
Округ Колумбия
= С'(х) = 0
дх
Примеры: - Число 14 не меняется независимо от других изменений. Значит, производная от 14 равна нулю.
- Значение p не меняется независимо от того, что еще меняется, поэтому производная p всегда равна нулю.
- Если окружность фиксированного размера имеет радиус r, то r постоянна, а производная от r равна нулю.
- Если проблема констатируется что то-то и то-то происходит с постоянной скоростью k, тогда k равно константа, а производная k равна нулю.
Правило 2) Умножение функции на константу умножает
полученную производную на ту же константу. Помните из правила 1, что
константа — это все, что не меняет своего значения независимо от того, что делают переменные. Итак, если f(x) — функция, производная которой равна f'(x), и
g(x) = C f(x), где C — константа, то
Итак, если f(x) — функция, производная которой равна f'(x), и
g(x) = C f(x), где C — константа, то
dg d(Cf) df
= = g'(x) = C = C f'(x)
дх дх дх
Примеры: - Вы знаете, что производная x 2 есть 2x. Тогда производная от 10x 2 равна 20x.
- Производная от sin(x) равна cos(x). Если г постоянной, то производная от r sin(x) равна г cos (х).
- Производная e x также e x . Итак, производная C e x , где C — константа, снова C е х .
Правило 3) Производная суммы есть сумма производные. Это правило суммы. В уравнениях это означает, что если f(x) и g(x) являются функциями от x и h(x) = f(x) + g(x), то
дх дф дг
= h'(x) = + = f'(x) + g'(x)
дх дх дх
Примеры: - Если f(x) = x 2 + 4x, что является
сумма, то чтобы найти f'(x), вы берете производные двух слагаемых,
х 2 и 4х отдельно и взять сумму этих
производные.
 Итак, f'(x) = 2x + 4.
Итак, f'(x) = 2x + 4. - Производная sin(x) + cos(x) равно cos(x) — sin(x).
- Производная e x + ln(x) равна е х + 1/х.
Правило 4) Если поднять х на любой постоянный степени, вы найдете производную, умножив х возведенных в единицу меньше этой мощности самой властью. Это силовое правило. В уравнениях, если у вас есть f(x) = x n , тогда
дф
= f'(x) = n x n-1
дх
Примеры: - Производная от x 3 равна 3x 2 .
- Производная от x 10 равна 10x 9 .
- С
Ох
(то есть sqrt(x))
такой же, как x 1/2 ,
производная от Öx
1 1И да, правило силы применяется, даже если сила не целое число. Мощность может быть любой, лишь бы она была постоянной.
Правило 5) Чтобы найти производную произведения две функции, первую умножить на производную от второй и сложить во второй раз производная от первого. Это правило продукта. В уравнениях если f(x) и g(x) обе являются функциями x и h(x) = f(x)g(x), то
дх дг дф
= h'(x) = f(x) + g(x) = f(x)g'(x) + g(x)f'(x)
дх дх дх
Примеры: Правило 6) Чтобы найти производную от частного или отношения, знаменатель умножить на производную от числителя, вычесть из него числитель умножить на производную от знаменателя, а потом все разделить на квадрат знаменателя. Это частное правило. В уравнениях если f(x) и g(x) являются функциями x и h(x) = f(x)/g(x), тогда
dh g(x)f'(x) - f(x)g'(x)
= h'(x) =
дх г 2 (х)
Примеры: - Производная от
(х + 1) f(x) =Производная как числителя, так и знаменателя равна 1. Так
Так(х - 1) - (х + 1) -2 f'(x) = - Если у вас есть
х 2 + 1 г(х) =тогда(х 3 + 1)(2х) - (х 2 + 1)(3х 2 ) г'(х) =который вы можете упростить, используя алгебру, если хотите. - Поскольку tan(x) = sin(x)/cos(x), можно использовать
Факторное правило для нахождения производной tan(x):
dtan(x) cos 2 (x) + sin 2 (х) 1
Правило 7) Используйте цепное правило найти производную от составных. Если f(x) и g(x) являются функциями от x и h(x) = f(g(x)) (что означает, что вы применяете h к x, сначала применив g к x, а затем применив f к результату), то
дх дф дг
= h'(x) = = f'(g(x)) g'(x)
дх дг дх
Это означает, что нужно применить производную от f к g(x) и умножить
что по производной от g(x).
Примеры:
Правило 8) Если вы умножаете независимую переменную на константа, то вся производная умножается на эту же константу. Это прямое следствие правила цепочки, но оно полезно знать, потому что это дает вам короткий путь. В уравнениях, если f(x) является функция от x и g(x) = f(kx), где k — константа, тогда
g'(x) = k f'(kx)Примеры:
Правило 9) Если добавить константу к независимому переменной, просто относитесь к сумме двух так, как если бы она была независимой. сама переменная. Итак, если g(x) = f(x + a), где а постоянная, то
г'(х) = f'(х + а)Примеры:
- Мы знаем, что e x является собственной производной. Так
согласно этому правилу, если f(x) = e x+3 , то
f'(x) = e x+3
- Вы знаете, как взять производную от x 3 . Так
взять производную от f(x) = (x + n) 3 ,
где n постоянно, у вас есть
f'(x) = 3(x + n) 2
| Производные некоторых элементарных функций: |
|---|
производная функции
|
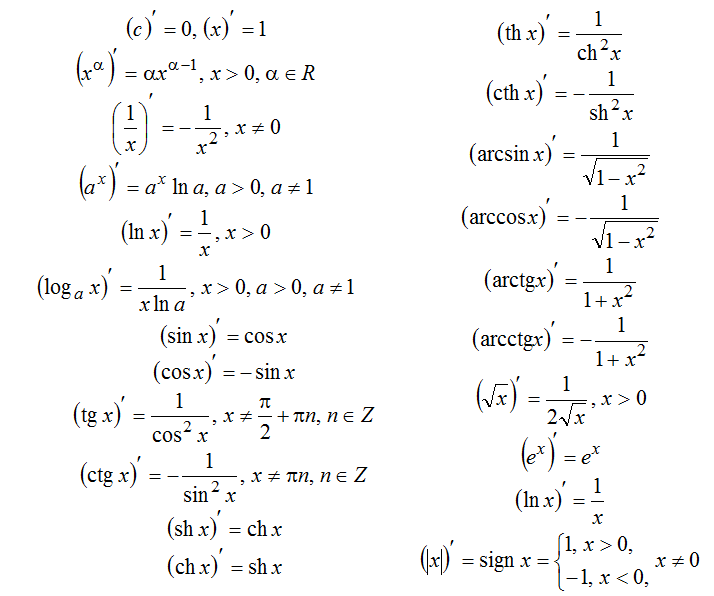 Это означает, что эти функции
содержат элементов для формирования более сложных функций.
Это означает, что эти функции
содержат элементов для формирования более сложных функций.Как и когда делать неявные дифференциация. Цепное правило применяется к композитам, даже если функция внутри состав неизвестен. Так, например, если бы вы только знали, что y(x) является функцией x, и вам нужно было написать выражение для производной от
f(x) = y 2 - 3y + sin(y)затем просто возьмите каждый термин и найдите его производную с помощью относительно y, затем умножьте это на символ, который указывает производную от y. С этой целью символ, у’ делает очень хорошо.
f'(x) = 2y y' - 3y' + cos(y) y'Вы можете вынести y’ и получить (2y — 3 + cos(y)) y’, но вот пример почему лучше начинать с y-простых чисел в каждом термине.
g(x) = xy 2 + y cos(x)Обратите внимание, что для этого вам придется применить правило продукта дважды (один раз для каждого продукта).

g'(x) = [2xyy' + y 2 ] + [-y sin(x) + y' cos(x)]Обратите внимание, что производная каждого из произведений показана на квадратные скобки, чтобы вам было легче увидеть организацию. Но
g'(x) = 2xyy' + y 2 - y sin(x) + y' cos(x)будет так же правильно. Обратите внимание, что когда вы берете производные членов, которые являются чисто функциями независимой переменной, х, вам не нужно умножать на х’, потому что x’ = dx/dx = 1. Вы только умножаете члены которые зависят от y (который является функцией независимого переменная, x) на y’, потому что вообще у’ № 1. Например, в приведенном выше примере у вас есть термин xy 2 , взять производную от. Поскольку это продукт, вам необходимо применить правило продукта. Это означает, что первый фактор, x, раз производная второго множителя, 2yy’, плюс второй фактор, y 2 , умножить на производную первого (и производная от x равна 1). В этом случае, когда вы берете второй множитель, умноженный на производную первого, нет y’, потому что этот первый фактор не содержит у.

Уравнение x и y не обязательно должно иметь f(x) в полном одиночестве на одной стороне равные для того, чтобы вы использовать неявное дифференцирование. У вас могут быть комплексы выражения x и y с обеих сторон. Пример:
_______
Öx 2 + у 2 = ху + у 3 Чтобы применить неявное дифференцирование к этому уравнению, просто приведите
надлежащие правила принятия производных для каждого термина
как вы сталкиваетесь с этим. Не забудьте умножить на y’ везде, где
это уместно. В этом случае вы применяете цепное правило
к sqrt, правило продукта к xy и
правило мощности для y 3 :
1 2x + 2yy'
= у + ху' + 3у 2 у'
2 Ох 2 + у 2 Неявный переход со вторыми производными: Если у вас есть уравнение,
х 3 = гг'и вы хотите применить к нему неявное дифференцирование, вы должны использовать правило питания на x 3 и правило продукта на уу’:
3x 2 = уу" + (у') 2Обратите внимание, что при применении правила произведения к yy’ у вас было взять производную от y’.
 И производная от y’
является его второй производной, y».
И производная от y’
является его второй производной, y».Вернуться к оглавлению
напишите мне по адресу [email protected]
Исчисление — документация по SymPy 1.11
В этом разделе рассказывается, как выполнять основные вычислительные задачи, такие как производные, интегралы, пределы и разложения в ряды в SymPy. Если вы не знакомы с математикой любой части этого раздела вы можете смело пропустить ее.
>>> из импорта sympy *
>>> x, y, z = символы ('x y z')
>>> init_printing(use_unicode=Истина)
Производные
Чтобы взять производные, используйте функцию diff .
>>> diff(cos(x), x)
-грех (х)
>>> разн(ехр(х**2), х)
⎛ 2⎞
⎝х ⎠
2⋅х⋅ℯ
diff может принимать несколько производных одновременно. Чтобы взять несколько производных,
передать переменную столько раз, сколько вы хотите различать, или передать число
после переменной. Например, оба следующих находят третий
производная от \(x^4\). 9{х у г}\).
9{х у г}\).
>>> выражение = выражение (x*y*z) >>> diff(expr, x, y, y, z, z, z, z) 3 2 ⎛ 3 3 3 2 2 2 ⎞ x⋅y⋅z х ⋅y ⋅⎝x ⋅y ⋅z + 14⋅x ⋅y ⋅z + 52⋅x⋅y⋅z + 48⎠⋅ℯ >>> diff(expr, x, y, 2, z, 4) 3 2 ⎛ 3 3 3 2 2 2 ⎞ x⋅y⋅z х ⋅y ⋅⎝x ⋅y ⋅z + 14⋅x ⋅y ⋅z + 52⋅x⋅y⋅z + 48⎠⋅ℯ >>> diff(expr, x, y, y, z, 4) 3 2 ⎛ 3 3 3 2 2 2 ⎞ x⋅y⋅z х ⋅y ⋅⎝x ⋅y ⋅z + 14⋅x ⋅y ⋅z + 52⋅x⋅y⋅z + 48⎠⋅ℯ
diff также можно назвать методом. Два способа вызова diff :
точно такие же, и предоставлены только для удобства.
>>> выр.разн(х, у, у, г, 4) 3 2 ⎛ 3 3 3 2 2 2 ⎞ x⋅y⋅z х ⋅y ⋅⎝x ⋅y ⋅z + 14⋅x ⋅y ⋅z + 52⋅x⋅y⋅z + 48⎠⋅ℯ
Чтобы создать неоцененную производную, используйте класс Derivative . Он имеет
тот же синтаксис, что и diff .
>>> производная = производная (выражение, x, y, y, z, 4)
>>> производное
7
∂ ⎛ х⋅y⋅z⎞
──────────⎝ℯ ⎠
4 2
∂z ∂y ∂x
Чтобы оценить неоцененный производный инструмент, используйте метод doit .
>>> производное.doit() 3 2 ⎛ 3 3 3 2 2 2 ⎞ x⋅y⋅z х ⋅y ⋅⎝x ⋅y ⋅z + 14⋅x ⋅y ⋅z + 52⋅x⋅y⋅z + 48⎠⋅ℯ
Эти необработанные объекты полезны для задержки оценки производное или для целей печати. Они также используются, когда SymPy не уметь вычислять производную выражения (например, если оно содержит неопределенные функции, которые описаны в разделе Решение раздел «Дифференциальные уравнения»).
Производные неуказанного порядка могут быть созданы с использованием кортежа (x, n) , где n — это порядок производной относительно x .
>>> m, n, a, b = символы ('m n a b')
>>> выражение = (a*x + b)**m
>>> выр.разн((х, п))
н
∂ ⎛ м⎞
───⎝(а⋅х + б) ⎠
н
∂х
Интегралы
Чтобы вычислить интеграл, используйте функцию интегрировать . Есть два вида
интегралов, определенных и неопределённых. Чтобы вычислить неопределенный интеграл,
то есть первообразная или примитивная, просто передайте переменную после
выражение.
>>> интегрировать(cos(x),x) грех (х)
Обратите внимание, что SymPy не включает константу интегрирования. Если вы хотите,
вы можете добавить его самостоятельно или перефразировать свою задачу в виде дифференциального уравнения
и используйте dsolve для его решения, что действительно добавляет константу (см. Решение дифференциальных уравнений).
Чтобы вычислить определенный интеграл, передайте аргумент (интеграция_переменная,
нижний_предел, верхний_предел) . Например, чтобы вычислить 9{2}}\, дх\, dy,\]
до
>>> интегрировать(exp(-x**2 - y**2), (x, -oo, oo), (y, -oo, oo)) π
Если интегрировать не удается вычислить интеграл, он возвращает невычисленное Интегральный объект .
>>> выражение = интегрировать (х**х, х) >>> печать (выражение) Интеграл(х**х, х) >>> выражение ⌠ ⎮ х ⎮ х дх ⌡
То же, что и Производная , вы можете создать невычисленный интеграл, используя Интеграл . Чтобы позже оценить этот интеграл, позвоните по номеру
Чтобы позже оценить этот интеграл, позвоните по номеру или .
>>> expr = Integral(log(x)**2, x)
>>> выражение
⌠
⎮ 2
⎮ log (x) dx
⌡
>>> expr.doit()
2
х⋅лог(х) - 2⋅х⋅лог(х) + 2⋅х
интегрировать использует мощные алгоритмы, которые постоянно совершенствуются для вычислений
как определенные, так и неопределенные интегралы, включая эвристическое сопоставление с образцом
алгоритмы типа, частичная реализация алгоритма Риша и алгоритм, использующий
G-функции Мейера, т.е.
полезно для вычисления интегралов с точки зрения специальных функций, особенно
определенные интегралы. Вот выборка некоторой степени интегрировать .
>>> integ = Integral((x**4 + x**2*exp(x) - x**2 - 2*x*exp(x) - 2*x - ... exp(x))*exp(x)/((x - 1)**2*(x + 1)**2*(exp(x) + 1)), x) >>> целое число ⌠ ⎮ ⎛ 4 2 х 2 х х⎞ х ⎮ ⎝x + x ⋅ℯ - x - 2⋅x⋅ℯ - 2⋅x - ℯ ⎠⋅ℯ ⎮ ──────────────────────────────────────── dx ⎮ 2 2 ⎛ х ⎞ ⎮ (х - 1) ⋅(х + 1) ⋅⎝ℯ + 1⎠ ⌡ >>> integ.doit() Икс ⎛ х ⎞ ℯ лог⎝ℯ + 1⎠ + ────── 2 х - 1
>>> целое = Интеграл(sin(x**2),x)
>>> целое число
⌠
⎮ ⎛ 2⎞
⎮ sin⎝x ⎠ dx
⌡
>>> integ.doit()
⎛√2⋅х⎞
3⋅√2⋅√π⋅S⎜────⎟⋅Γ(3/4)
⎝ √π ⎠
──────────────────────
8⋅Г(7/4)
>>> integ = Integral(x**y*exp(-x), (x, 0, oo)) >>> целое число ∞ ⌠ ⎮ у -х ⎮ х ⋅ℯ дх ⌡ 0 >>> integ.doit() ⎧ Γ(y + 1) при re(y) > -1 ⎪ ⎪∞ ⎪⌠ ⎨⎮ у -х ⎪⎮ x ⋅ℯ dx иначе ⎪⌡ ⎪0 ⎩
В этом последнем примере возвращено выражение Кусочная , поскольку интеграл
не сходится, если \(\Re(y) > 1.\)
Ограничения
SymPy может вычислять символьные ограничения с помощью функции limit . Синтаксис для вычисления
\[\lim_{x\to x_0} f(x)\]
— это limit(f(x), x, x0) .
>>> предел(грех(х)/х, х, 0) 1
предел следует использовать вместо подводных лодок всякий раз, когда точка оценки
является особенностью. Несмотря на то, что в SymPy есть объекты для представления \(\infty\), использование
их для оценки не надежен, потому что они не следят за вещами
как скорость роста. Кроме того, такие вещи, как \(\infty — \infty\) и
\(\frac{\infty}{\infty}\) вернуть \(\mathrm{nan}\) (не число). Например
Несмотря на то, что в SymPy есть объекты для представления \(\infty\), использование
их для оценки не надежен, потому что они не следят за вещами
как скорость роста. Кроме того, такие вещи, как \(\infty — \infty\) и
\(\frac{\infty}{\infty}\) вернуть \(\mathrm{nan}\) (не число). Например
>>> выражение = x**2/exp(x) >>> expr.subs(x, oo) нан >>> предел(выражение, х, оо) 0
Подобно Производному и Интегральному , предел имеет неоцененный
аналог, Предел . Чтобы оценить его, используйте doit .
>>> выражение = предел ((cos(x) - 1)/x, x, 0)
>>> выражение
⎛cos(x) - 1⎞
лим ⎜──────────⎟
х─→0⁺⎝ х ⎠
>>> expr.doit()
0
Чтобы оценить предел только с одной стороны, передайте '+' или '-' в качестве четвертого
аргумент до 94\) опущены. Условия заказа
можно создавать и управлять ими за пределами серии . Они автоматически
поглощать члены более высокого порядка.
>>> х + х**3 + х**6 + О(х**4)
3 ⎛ 4⎞
х + х + О⎝х ⎠
>>> х*О(1)
О (х)
Если вам не нужен срок заказа, используйте метод removeO .
>>> выр.серия(х, 0, 4).removeO() 2 Икс ── + х + 1 2
Нотация O поддерживает произвольные предельные точки (кроме 0):
>>> exp(x - 6).series(x, x0=6)
2 3 4 5
(х - 6) (х - 6) (х - 6) (х - 6) ⎛ 6 ⎞
-5 + ──────── + ──────── + ──────── + ──────── + x + O⎝(x - 6) ; х → 6⎠
2 6 24 120
Конечные разности
До сих пор мы рассматривали выражения с аналитическими производными и примитивные функции соответственно. Но что, если мы хотим иметь выражение для оценки производной кривой, для которой нам не хватает представление в закрытой форме, или для которого мы не знаем функционал значения для еще. Одним из подходов было бы использование конечной разности подход.
Самый простой способ дифференцировать с помощью конечных разностей — использовать
функция Different_finite :
>>> f, g = символы ('f g', cls = функция)
>>> Different_finite (f (x) * g (x))
-f(x - 1/2)⋅g(x - 1/2) + f(x + 1/2)⋅g(x + 1/2)
Если у вас уже есть производный экземпляр , вы можете использовать as_finite_difference метод для создания аппроксимаций
производная в произвольном порядке:
>>> f = Функция ('f')
>>> dfdx = f(x). diff(x)
>>> dfdx.as_finite_difference()
-f(x - 1/2) + f(x + 1/2)
diff(x)
>>> dfdx.as_finite_difference()
-f(x - 1/2) + f(x + 1/2)
здесь производная первого порядка была аппроксимирована вокруг x с помощью минимальное количество оцениваемых баллов (2 для производной 1-го порядка) равноудаленно, используя размер шага 1. Мы можем использовать произвольные шаги (возможно, содержащие символические выражения):
>>> f = Функция ('f')
>>> d2fdx2 = f(x).diff(x, 2)
>>> ч = Символ('ч')
>>> d2fdx2.as_finite_difference([-3*h,-h,2*h])
f(-3⋅ч) f(-ч) 2⋅f(2⋅ч)
─────── - ───── + ────────
2 2 2
5⋅ч 3⋅ч 15⋅ч
Если вы просто заинтересованы в оценке веса, вы можете сделать это вручную:
>>> final_diff_weights(2, [-3, -1, 2], 0)[-1][-1] [1/5, -1/3, 2/15]
обратите внимание, что нам нужен только последний элемент в последнем подсписке
возвращено из final_diff_weights . Причина этого в том, что
функция также генерирует веса для младших производных и
с использованием меньшего количества точек (см. документацию
документацию final_diff_weights Больше подробностей).
Если использование final_diff_weights напрямую выглядит сложным, то as_finite_difference метод производных экземпляров
недостаточно гибок, вы можете использовать apply_finite_diff , который
принимает порядок , x_list , y_list и x0 в качестве параметров:
>>> x_list = [-3, 1, 2]
>>> y_list = символы ('a b c')
>>> apply_finite_diff(1, x_list, y_list, 0)
3⋅а б 2⋅с
- ─── - ─ + ───
20 4 5
Введение в комплексный анализ — GeeksforGeeks
Комплексный анализ — это раздел математики, который имеет дело с комплексными числами, их функциями и исчислением. Проще говоря, комплексный анализ — это расширение исчисления действительных чисел на комплексную область. Мы распространим известные из математического анализа понятия непрерывности, производных и интегралов на случай комплексных функций комплексного переменного. При этом мы столкнемся с аналитическими функциями, которые составляют центральную часть этого введения. На самом деле комплексный анализ в значительной степени является изучением аналитических функций.
При этом мы столкнемся с аналитическими функциями, которые составляют центральную часть этого введения. На самом деле комплексный анализ в значительной степени является изучением аналитических функций.
Основным компонентом комплексного анализа является аналитическая функция, или, как мы хорошо знаем в математическом анализе, дифференцируемая функция. Любое комплексное число z можно рассматривать как точку на плоскости ( x,y ), поэтому z = x+iy, , где i=√-1. Аналогичным образом любую комплексную функцию комплексной переменной z можно разделить на две функции, например, f(z)=u(z)+iv(z), или f(x, у)=и(х,у)+iv(х,у). Очевидно, что такие функции зависят от двух независимых переменных и имеют две разделимые функции, поэтому для построения графика функции потребуется четырехмерное пространство, что трудно себе представить.
Конечно, первая отправная точка исчисления комплексных функций состоит в том, чтобы начать с непрерывности функции, а затем постепенно перейти к дифференцируемости в комплексной области.
Непрерывность
Начнем с довольно тривиального случая комплекснозначной функции. Предположим, что f комплекснозначная функция вещественной переменной. Это означает, что если x — действительное число, f(x) — комплексное число, которое можно разложить на действительную и мнимую части: f(x) = u(x)+i v(x) , где u и v — действительные функции действительной переменной; то есть объекты, с которыми вы знакомы из реального исчисления. Мы говорим, что f непрерывна в точке x 0 , если u и v непрерывны в точке x 0 .
Непрерывность комплекснозначной функции комплексной переменной является нетривиальным свойством. Функция называется непрерывной в точке z o , если она приближается к значению f(z o ) , когда z приближается к z или . Поскольку z живет в сложной плоскости (также известной как плоскость Аргана), он может приближаться к точке с разных направлений. Следовательно, нам необходимо уточнить наше определение, чтобы оно соответствовало новым потребностям.
Формально мы говорим, что f(z) непрерывно на z o , если для любого ε>0 существует δ>0 такое, что |f(z)-f(z о )|<ε для всех |z-z о |<δ. Итак, всякий раз, когда z находится внутри диска радиуса δ с центром в z o (называется окрестностью z o ), и функция приближается к значению f(z o ).
Аналитичность
После того, как мы установили понятия непрерывности сложных функций, мы можем погрузиться в дифференциацию сложных функций. Обсуждая дифференцирование сложных функций, мы увидим, что такие функции должны удовлетворять важному критерию, называемому уравнениями Коши-Римана . Если аналогия поможет, мы знаем, что для того, чтобы производная действительной функции существовала конечно в данной точке, функция должна быть непрерывной в этой точке. Аналогичным критерием для комплексных функций являются уравнения Коши-Римана. Вскоре мы увидим доказательство в следующем обсуждении.
Вскоре мы увидим доказательство в следующем обсуждении.
Комплексную функцию действительной переменной можно легко дифференцировать, как f'(x)=u'(x)+iv'(x), , где f(x) — комплексная функция вещественной переменной x. Другими словами, мы расширяем операцию дифференцирования комплексно-линейно. Здесь нет ничего нового.
Однако ситуация меняется, когда f становится функцией комплексной переменной z . Мы знаем, что комплексная переменная z сама по себе является парой двух действительных переменных x 91 666 и 91 665 и 91 666. Мы наносим z как точку на комплексной плоскости с упорядоченной парой ( x,y ) и обозначаем z=x+iy. Таким образом, возникает вопрос, как отличить комплексную функцию от комплексной переменной. Как и следовало ожидать, у нас есть определение производной, похожее на реальное исчисление:
Дифференцирование в комплексной области
Итак, первая проблема состоит в том, как сделать δz исчезающе малым. В комплексной плоскости мы можем делать это с нескольких направлений. Как видно из определения, производная функции не должна меняться при взятии предела. В противном случае мы будем получать новую производную каждый раз, когда будем менять пределы. На самом деле мы занимаемся исследованием того, как функция f(z) меняется, когда мы берем δz⇢0, или, другими словами, δx⇢0 и δy⇢0. По существу, наша производная не должна меняться при изменении порядка взятия пределов. И изменение порядка пределов не всегда гарантирует то же самое значение (каждый математик может придумать функцию, доказывающую это утверждение!). Итак, дифференцируемость — нетривиальное свойство в сложном мире.
В комплексной плоскости мы можем делать это с нескольких направлений. Как видно из определения, производная функции не должна меняться при взятии предела. В противном случае мы будем получать новую производную каждый раз, когда будем менять пределы. На самом деле мы занимаемся исследованием того, как функция f(z) меняется, когда мы берем δz⇢0, или, другими словами, δx⇢0 и δy⇢0. По существу, наша производная не должна меняться при изменении порядка взятия пределов. И изменение порядка пределов не всегда гарантирует то же самое значение (каждый математик может придумать функцию, доказывающую это утверждение!). Итак, дифференцируемость — нетривиальное свойство в сложном мире.
Теперь запишем f(z)=u(z)+iv(z) или, что то же самое, f(x,y)=u(x,y)+iv(x,y) .
Далее возьмем сначала δx⇢0, а затем δy⇢0. Это эквивалентно взятию δz⇢0 вдоль мнимой оси.
Теперь наоборот, возьмем сначала δy⇢0, а затем δx⇢0. Это эквивалентно взятию δz⇢0 вдоль действительной оси.
Два выражения совпадают тогда и только тогда, когда :
Уравнения Коши-Римана
Здесь мы получили уравнений Коши-Римана.
Итак, чтобы проверить, является ли функция f(z) дифференцируемой в точке z o =x o +iy o , нам нужно посмотреть, удовлетворяют ли они уравнениям Коши-Римана. И тогда их производная дается любым выражением, полученным для f'(z o ).
Можно заметить, что дифференцировать в сложном мире действительно непросто, и есть много функций, которые на самом деле не дифференцируемы, даже самые простые (попробуйте дифференцировать z*, комплексно-сопряженную функцию z).
Можно сказать, что функция называется аналитической или голоморфной в окрестности точки z o , если оно дифференцируемо в этой окрестности. Функция, аналитическая во всей комплексной плоскости, называется целой.
Важно понимать, что аналитичность, в отличие от дифференцируемости, является свойством функции не в точке, а на открытом множестве точек.


 ru
ru
 ru:
ru:
 ..
..




 ..
..
 Нецелые функции
155173
Нецелые функции
155173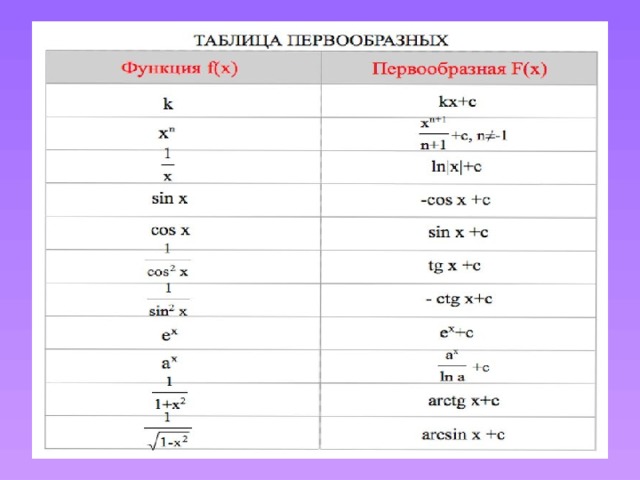 Линейная алгебра и теория операторов
327345
Линейная алгебра и теория операторов
327345 Итак, f'(x) = 2x + 4.
Итак, f'(x) = 2x + 4.
 Так
Так doit()
Икс
⎛ х ⎞ ℯ
лог⎝ℯ + 1⎠ + ──────
2
х - 1
doit()
Икс
⎛ х ⎞ ℯ
лог⎝ℯ + 1⎠ + ──────
2
х - 1
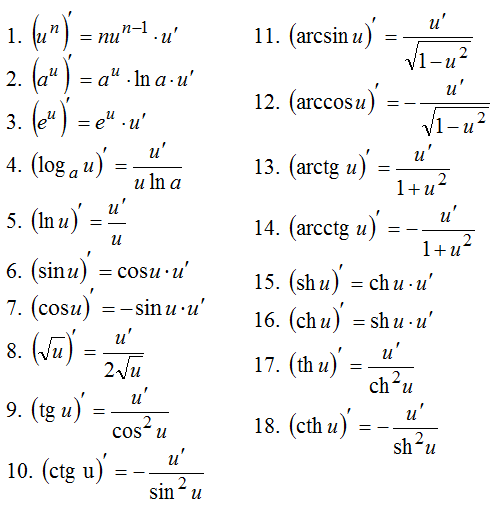 diff(x)
>>> dfdx.as_finite_difference()
-f(x - 1/2) + f(x + 1/2)
diff(x)
>>> dfdx.as_finite_difference()
-f(x - 1/2) + f(x + 1/2)